Introduction

Early investigations on collisions between nuclei with similar masses have indicated that the reaction mechanisms involved are intricate, and the angular distributions of elastic and inelastic scattering exhibit obvious anomalous large-angle scattering (ALAS) [1-6]. The optical model (OM) is an important theoretical model of nuclear reaction analysis. It has been widely used to investigate elastic scattering processes and has achieved significant success in calculations and analyses of experimental data [7-9]. However, the description of elastic scattering between nuclei with similar masses using OM alone is inadequate [10-15]. The experimental data show an obvious enhancement in the elastic scattering angular distributions at intermediate and backward angles. This behavior is typically observed in systems where projectiles and targets share the same core structure [16-20], where the backward angles in the elastic scattering correspond to the forward angles in the transfer process. It is found that the ALAS is a result of specific reaction mechanisms in different reaction systems. For example, the elastic scattering angular distributions of the ⁹Be+¹²C system in the energy range E_lab(⁹Be)= 13.00–21.00 MeV were analyzed using OM and the distorted wave born approximation (DWBA) method [4]. This indicates the significance of the ³He transfer process at intermediate and backward angles. For nα-type systems, where both the projectile and target consist of integer multiples of α particles, such as ¹⁶O+²⁴Mg, ¹⁶O+²⁸Si, and ¹²C+²⁴Mg, the reactions have large α-spectroscopic factors. Therefore, the ALAS behavior is usually attributed to the α transfer process such as in Ref. [3, 21]. However, the spin reorientations of ¹¹B and¹⁴N dominate at intermediate and backward angles in the elastic scattering angular distributions of the ¹¹B+¹⁴N system at E_lab(¹⁴N)= 88 MeV in Ref. [22]. In addition, the spin reorientation of ⁹Be dominates at intermediate and backward angles where the transfer reaction makes only a small contribution to the elastic scattering angular distribution of the ⁹Be+¹⁵N system at E_lab(¹⁵N)= 84 MeV as shown in Ref. [8]. The elastic scattering angular distributions of ¹¹B+¹²C system in a broad energy range E_cm(¹¹B) = 5.00–52.00 MeV were analyzed by the OM and the coupled reaction channels (CRC) method [20], which indicates that the potential scattering dominates at forward angles, the proton transfer process dominates at backward angles, and both these processes and spin reorientation of ¹¹B play important roles at the intermediate angular range. Therefore, various reaction mechanisms may lead to ALAS formation in different reaction systems. Exploring the origin of ALAS allows us to understand nuclear reaction mechanisms more clearly. If the incident projectile and target are both weakly bound light nuclei, another reaction mechanism termed breakup effect, may have a high probability of occurrence, which has been of interest to both experimental and theoretical nuclear physicists [23, 24].

⁶Li+⁷Li system is a good prototype of nuclear reactions between adjacent weakly bound light nuclei, which can be conceptualized as comprising two identical ⁶Li cores accompanied by a neutron bound to one of these cores, i.e. assuming that ⁷Li exhibits a n+⁶Li cluster structure when considering n-transfer processes. The interchange of these identical cores in such a configuration has a considerable probability, which will lead to the notable involvement of neutron transfer in both elastic and inelastic scatterings. Additionally, ⁶Li and ⁷Li are weakly bound nuclei that break easily into +d and +t, respectively. The breakup effect can affect the scattering channels [25-37]. Therefore, the transfer reaction and breakup effect must be considered in the analysis of ⁶Li+⁷Li scattering, and the spin reorientation also be considered according to previous studies [20, 22]. Pottvast et al. presented experimental data [38] on the elastic and inelastic scattering angular distributions of the ⁶Li+⁷Li reaction for the first time to study the reaction mechanism of scattering in asymmetric systems. They employed the OM and DWBA methods to calculate the angular distributions of ⁶Li elastic scattering and inelastic scattering to the first excited state of ⁷Li, taking into account the transfer reaction mechanism. However, their results underestimated the experimental data in the ALAS region. Xu et al. [39] employed the OM and DWBA methods to calculate the ⁶Li elastic scattering angular distributions and the inelastic scattering to the first excited state of 1p-shell nuclei; the calculated results of the elastic scattering angular distributions were in reasonable agreement with the experimental data at forward angles, whereas large discrepancies were observed at backward angles.

The purpose of this study is to investigate the reaction mechanism of ⁶Li+⁷Li scattering and analyze the angular distributions for both elastic and inelastic scatterings at energies $E_{\text{lab}}=10-40\text{ MeV}$. The CRC method is employed in the analysis, and the elastic and inelastic scatterings, ground- and excited-state transfer reaction channels, and their coupling effects are considered. The São Paulo potential obtained using a double-folding model for the ⁶Li+⁷Li system is used as a “bare” potential. Therefore, it is a suitable potential for investigating the coupling effects within the CRC method.

The remainder of this paper is organized as follows. Section 2 outlines the method and theoretical formalism. In Sect. 3, the calculation results and discussion are presented. Finally, a brief summary and conclusions are presented in Sect. 4.

Proposed Method and Theoretical Formalism

To understand the reaction mechanism, ⁶Li+⁷Li scattering is analyzed in the three frameworks. First, routine spherical nucleus OM and DWBA methods are employed to calculate the elastic scattering and inelastic scattering of the first excited state of ⁷Li, respectively. Second, the CRC method is used with consideration of elastic scattering ⁷Li(⁶Li,⁶Li)⁷Li, inelastic scattering ⁷Li(⁶Li,⁶Li)⁷Li_0.48, single neutron ground-state transfer ⁷Li(⁶Li,⁷Li_gs)⁶Li and single neutron excited-state transfer ⁷Li(⁶Li,⁷Li_0.48)⁶Li channels. Third, excluding the four reaction channels, three resonance states of ⁶Li at excited energies of 2.186 MeV (3⁺), 4.312 MeV (2⁺), and 5.65 MeV (1⁺), as well as two resonance states of ⁷Li at excited energies of 4.63 MeV (3.5^-) and 6.68 MeV (2.5^-) are included in the CRC calculation. This is to investigate the approximate influence of the breakup effect, since it is found that the D-wave resonance channels among the ⁶Li breakup channels and the F-wave resonance channels among the ⁷Li breakup channels are significant in couplings to the elastic channel[35, 36]. The calculations are performed using the FRESCO code [40], which considers finite-range transfer and the full complex remnant, and uses the same interaction potential for the initial and final channels.

In the spherical-nucleus OM, the nucleus is assumed to be spherical. Only the shaped elastic scattering channel is highlighted, and the influences of all other channels are expressed as equivalent effects. The spherical-nucleus OM is a typical tool for the analysis of the nucleus-nucleus elastic scattering process. The stationary state Schrödinger equation of the system is defined as follows: $\left(E-T_{\alpha }-U_{\alpha }\left(R\right)\right){\text{Ψ}}_{\alpha }\left(R\right)=0$ (1) where the subscript α denotes the incident channel, E denotes the total energy of the system, $T_{\alpha }$ denotes the relative kinetic energy of the system, $U_{\alpha }\left(R\right)$ denotes the optical model potential between the projectile and the target nucleus, ${\text{Ψ}}_{\alpha }\left(R\right)$ denotes the wave function of the system, and R denotes the distance between the projectile and the target nucleus.

The incident particle moves under the action of the mean field, causing direct reactions owing to residual interactions. When the residual interaction is weak, particularly for spherical nuclei near the full shell, it is appropriate to employ DWBA method for direct reaction calculations. The corresponding equations are defined as follows: $\left(E-E_{\alpha }-T_{\alpha }-U_{\alpha }\left(R\right)\right){\text{Ψ}}_{\alpha }\left(R\right)=V_{\beta }\left(R\mathrm{,}{\xi }_{\alpha }\right){\text{Ψ}}_{\beta }\left(R\right)$ (2) where the subscript β indicates the outgoing channel, $E_{\alpha }$ denotes the excitation energy of the target nucleus, $V_{\beta }\left(R\mathrm{,}{\xi }_{\alpha }\right)$ denotes the residual interaction term between the projectile and target nucleus.

When the residual interaction is strong, the coupling effect cannot be neglected. Therefore, it is appropriate to employ CRC method for direct reaction calculations. The CRC equations are as follows: $\left(E-E_{\alpha }-T_{\alpha }-U_{\alpha }\left(R\right)\right){\text{Ψ}}_{\alpha }\left(R\right)={\displaystyle \sum _{\alpha \ne \beta }}{V}_{\beta }\left(R\right){\text{Ψ}}_{\beta }\left(R\right)$ (3) where $V_{\beta }\left(R\right)={\displaystyle \int {\varphi }^{*}\left({\xi }_{\alpha }\right)\left(V_{\alpha }\left(\overrightarrow{R}\right)-U_{\alpha }\left(R\right)\right)\varphi \left({\xi }_{\beta }\right)\text{d}\text{Ω}\text{d}\xi }$, $V_{\alpha }\left(\overrightarrow{R}\right)$ denotes interaction potential between the projectile and the target nucleus, $\varphi \left({\xi }_{\alpha }\right)$ and $\varphi \left({\xi }_{\beta }\right)$ are the internal wave functions corresponding to the incident channel and outgoing channel, respectively. The channel-channel coupling effects are explicitly included in the CRC method.

The elastic scattering and elastic transfer processes are experimentally indistinguishable, hence both ⁷Li(⁶Li,⁶Li)⁷Li and ⁷Li(⁶Li,⁷Li_gs)⁶Li processes must be considered to obtain the elastic scattering angular distribution, and the same is true for ⁷Li(⁶Li,⁶Li)⁷Li_0.48 and ⁷Li(⁶Li,⁷Li_0.48)⁶Li to obtain the inelastic scattering angular distribution [6, 41]. To consider the interference between elastic scattering and elastic transfer in the theoretical calculation, the elastic transfer amplitude $f_{\text{eltr}}\left(\pi -{\theta }_{\text{c}\text{.m}\text{.}}\right)$ must be added to the elastic scattering amplitude $f_{\text{el}}\left({\theta }_{\text{c}\text{.m}\text{.}}\right)$. The same is true when considering the interference between inelastic scattering amplitude $f_{\text{inel}}\left({\theta }_{\text{c}\text{.m}\text{.}}\right)$ and inelastic transfer amplitude $f_{\text{inltr}}\left(\pi -{\theta }_{\text{c}\text{.m}\text{.}}\right)$ in the theoretical calculation. Subsequently, the elastic scattering angular distribution and the inelastic scattering angular distribution is expressed as follows: $\begin{array}{c}\frac{\text{d}\sigma }{\text{d}\text{Ω}}\left({\theta }_{\text{c}\text{.m}\text{.}}\right)=\frac{1}{\left(2J_{p\mathrm{,}\left(p^{\prime }\right)}+1\right)\left(2J_{t\mathrm{,}\left(t^{\prime }\right)}+1\right)}\cdot {\displaystyle \sum _{m^{\prime }{M}^{\prime }mM}}\\ {\left|f_{\text{el}\left(\text{inl}\right)}\left({\theta }_{\text{c}\text{.m}\text{.}}\right)+f_{\text{eltr}\left(\text{inltr}\right)}\left(\pi -{\theta }_{\text{c}\text{.m}\text{.}}\right)\right|}^2\end{array}$ (4) where Jp, $J_{p^{\prime }}$, Jt and $J_{t^{\prime }}$ are the state spins for the projectile ground, projectile excited, target ground, and the target excited, respectively.

The latest version of the São Paulo potential (SPP2) [42] is used to describe the optical model potential of the ⁶Li+⁷Li system as input to the Fresco code, and is written as follows: $V_{\text{OP}}^{\text{SPP2}}\left(R\right)=\left(N_r+i{N}_i\right)V_{\text{F}}\left(R\right)$ (5) where Nr and Ni are the normalization coefficients, taken as 1 and 0.8, respectively, as suggested in Refs. [43, 44]. The folding potential $V_{\text{F}}\left(\overrightarrow{R}\right)$ depends on the matter density in the following form: $V_{\text{F}}\left(R\right)={\displaystyle \int }{\rho }_{m1}\left({\overrightarrow{r}}_1\right){\rho }_{m2}\left({\overrightarrow{r}}_2\right)v_{mm}\left(\overrightarrow{R}-{\overrightarrow{r}}_1+{\overrightarrow{r}}_2\right)\text{d}{\overrightarrow{r}}_1\text{d}{\overrightarrow{r}}_2$ (6) where ${\rho }_{m1}\left({\overrightarrow{r}}_1\right)$ and ${\rho }_{m2}\left({\overrightarrow{r}}_2\right)$ are the matter densities of the two colliding nuclei, which are the experimental density for ⁶Li and the theoretical Dirac-Hartree-Bogoliubov density for ⁷Li, respectively, obtained from Ref. [42]. vmm is an effective nucleon-nucleon interaction with a Gaussian distribution given by $v_{mm}\left(\overrightarrow{r}\right)=-U_0{e}^{-{\left(r/a\right)}^2}{e}^{-4{\nu }^2/c^2}$ (7) where the values of U₀ and a are 735.813 MeV and 0.5 fm, respectively; c represents the speed of light; and $\nu$ denotes the relative velocity between the interacting nuclei.

The velocity is related to the kinetic energy as follows: ${\text{E}}_K\left(R\mathrm{,}{E}_{\text{c}\text{.m}\text{.}}\right)=E_{\text{c}\text{.m}\text{.}}-V_{\text{C}}\left(R\right)-V_{\text{F}}\left(R\right)$ (8) through the following relativistic expression: ${\nu }^2\left(R\mathrm{,}{E}_{\text{c}\text{.m}\text{.}}/c^2\right)=1-{\left(\frac{\mu c^2}{\mu c^2+E_{\text{K}}}\right)}^2$ (9) V_C denotes the Coulomb potential, and $\mu$ denotes the reduced mass of the system.

To investigate the influence of the coupling effect on the scattering channels, the CRC method is used. The inelastic excitations of ⁶Li and ⁷Li are described by using a rotational model. Such collective motions can be described in terms of permanent deformations of the nuclear shape with deformation lengths δλ. The interaction to which an incident particle is subjected is described by a nonspherical optical-model potential. Because axisymmetric deformation is considered, the deformed nuclear shapes can be expressed as follows: $R({\theta }^{\prime }\mathrm{,}{\phi }^{\prime })=R_0\left[1+{\displaystyle \sum _{\lambda }}{\beta }_{\lambda }{Y}_{\lambda 0}\left({\theta }^{\prime }\mathrm{,}{\phi }^{\prime }\right)\right]$ (10) where $R_0$ denotes the spherical nucleus radius equal to $r_0{A}^{\frac{1}{3}}$<, $Y_{\lambda 0}$ denotes the spherical harmonics, β denotes the multipolarity deformation parameter of the nucleus, $\lambda$ denotes the multipolarity of the transition, ${\theta }^{\prime }$ and ${\phi }^{\prime }$ are angular coordinates in the body-fixed system.

The deformation potential felt by the incident particle can be expressed as follows: $V(\xi \mathrm{,}R)=U(R-\text{Δ}(\widehat{R}\mathrm{,}\xi ))$ (11) where $U(R)$ denotes the OM potential to be deformed using deformation lengths δλ of the multipole and the ’shift function’ has the multipole expansion $\text{Δ}(R^{\prime })={\displaystyle \sum _{\lambda \ne 0}}{\delta }_{\lambda }{Y}_{\lambda }^0\left(R^{\prime }\right)$ (12) where ${\widehat{R}}^{\prime }$ denotes the vector $\widehat{R}$ in the body-centered frame of coordinates defined by $\xi$.

The abovementioned deformation potential $V(\xi \mathrm{,}R)$ can be expanded by the spherical harmonic function in the body-fixed coordinate system. Subsequently, the body-fixed coordinate system is projected to space-fixed coordinate system through the rotational function D. Therefore, the optical model potential of the deformed nucleus in the space-fixed system coordinates can be obtained as follows: $V(\xi \mathrm{,}R)={\displaystyle \sum _{\lambda \mu }}{V}_{\lambda }\left(R\right)D_{\mu 0}^{\lambda }\left(\alpha \mathrm{,}\beta \mathrm{,}\gamma \right)Y_{\lambda \mu }\left(\theta \mathrm{,}\phi \right)$ (13) where α, β, $\gamma$ are the Euler coordinates; θ and $\phi$ are the angular coordinates in the space-fixed system; $V_{\lambda }\left(R\right)$ is unrelated to the angular coordinates and can be expressed as follows: $V_{\lambda }\left(R\right)=\frac{1}{2}{\displaystyle {\int }_{-1}^1}U(r(R\mathrm{,}\cos \theta ))Y_{\lambda }^{\mu }\left(\theta \mathrm{,0}\right)\text{d}(\cos \theta )$ (14) and $r(R\mathrm{,}\cos \theta )=R-\sqrt{\frac{2\lambda +1}{4\pi }}{P}_{\lambda }\left(\theta \right){\delta }_{\lambda }+{\displaystyle \sum _{\lambda }}\frac{{\delta }_{\lambda }^2}{4\pi R_U}$ (15) where RU is the average potential radius.

When the deformation lengths ${\delta }_{\lambda }$ are small, the form factors $V_{\lambda }\left(R\right)$ are simply the first derivatives of the $U(R)$ function as follows [40]. $V_{\lambda }\left(R\right)=-\frac{{\delta }_{\lambda }}{\sqrt{4\pi }}\frac{\text{d}U(R)}{\text{d}R}\mathrm{,}$ (16) with the same shape for all the multipoles $\lambda >0$.

The ground-state reorientation and excited-state reorientation notated by $\langle I_{\text{gs}}^{\pi }{K}_{\text{gs}}|V(\xi \mathrm{,}R)|I_{\text{gs}}^{\pi }{K}_{\text{gs}}\rangle$ and $\langle I_{\text{ex}}^{\pi }{K}_{\text{ex}}|V(\xi \mathrm{,}R)|I_{\text{ex}}^{\pi }{K}_{\text{ex}}\rangle$, as well as the transitions from the ground state to excited state of the ⁶Li and ⁷Li notated by $\langle I_{\text{ex}}^{\pi }{K}_{\text{ex}}|V(\xi \mathrm{,}R)|I_{\text{gs}}^{\pi }{K}_{\text{gs}}\rangle$ is calculated using the CRC method. In the abovementioned transition matrices, $|I_{\text{gs}}^{\pi }{K}_{\text{gs}}\rangle$ and $|I_{\text{ex}}^{\pi }{K}_{\text{ex}}\rangle$ represent the ground- and excited-state wave functions respectively, with spins $I_{\text{gs}}$, $I_{\text{ex}}$ and their projections $K_{\text{gs}}$, $K_{\text{ex}}$ onto the intrinsic symmetry axes. The transitions to these states are calculated using the form factors.

The following reduced deformation length $\begin{array}{ll}{\text{Δ}}_{\lambda }\left(I\to I_{\text{ex}}\right)=\hfill & {\left(-1\right)}^{\left(I-I_{\text{ex}}+|I-I_{\text{ex}}|\right)/2}\hfill \\ \hfill & \cdot \sqrt{2I+1}{\delta }_{\lambda }\langle IK\lambda 0|I_{\text{ex}}K\rangle \hfill \end{array}$ (17) is used in the rotational model for CRC calculations. The quadrupole deformation lengths of ⁶Li, denoted by ${\delta }_2^{ij}$, reflect the transition from the initial state i to the final state j in a rotational nucleus with bandhead K and can be derived from the reduced electric-quadrupole transition probability $B(E2)$: $\begin{array}{ll}\sqrt{B\left(E2;K{J}_i\to K{J}_j\right)}=\hfill & |\langle J_{i}K20|J_{j}K\rangle \hfill \\ \hfill & \cdot \frac{Ze}{A}{\displaystyle {\int }_0^{\infty }}{\rho }_2^{ij}\left(r\right)r^4\text{d}r|\hfill \end{array}$ (18) where ${\rho }_2^{ij}\left(r\right)$ denotes the quadrupole transition density, expressed as ${\rho }_2^{ij}\left(r\right)=-{\delta }_2^{ij}\frac{\text{d}{\rho }_0\left(r\right)}{\text{d}r}$ (19) ${\rho }_0\left(r\right)$ denotes the ground-state charge density of the nucleus, which can be found in Ref. [1].

The ⁶Li+⁷Li elastic and inelastic scattering channels, single neutron transfer reaction channel and breakup effect are included in the coupled reaction channel scheme, as shown in Fig. 1. The spin reorientations of ⁶Li and ⁷Li in the ground and excited states are also included in the CRC calculations. The reorientation quadrupole deformation length, denoted by ${\delta }_2^{ii}$ in (19), for the ground and excited states of ⁶Li and ⁷Li are 1.000 fm and 2.000 fm, respectively.

Fig. 1Full-screen View

(Color online) Coupling schemes for the transitions to the excited states of ⁶Li and ⁷Li, the transitions of the ⁶Li and ⁷Li spin reorientations are marked with arc arrows

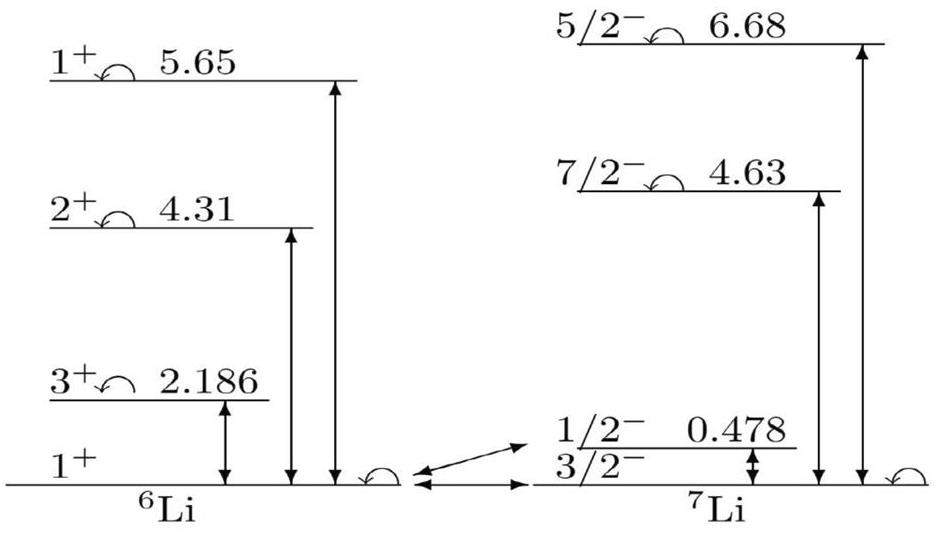
The reduced transition probabilities B(E₂) between the ground state and the 2.186 MeV, 4.312 and 5.650 MeV resonances were obtained from Ref. [45]. The deformation parameters are presented in Table 1.

The neutron transfers to the ⁶Li forming the ground, and the first excited states of ⁷Li are included in the CRC calculations. The bound-state wave functions of $\varphi (n{+}^6\text{Li})$, dependent on the internal coordinates, are obtained by solving the Schrödinger equation using a real Woods-Saxon potential with radius parameters R=3.24 fm and diffuseness $a=0.65\text{ fm}$. The potential depth $V(n{+}^6\text{Li})$ is adjusted to reproduce the binding energies of the ⁷Li ground state E_bind=7.25 MeV and the first excited state E_bind=6.77 MeV. The number of nodes in the bound-state wave function is obtained based on the Wildermuth condition: $2N+L={\displaystyle {\sum }_{i=1}^1\left(2n_i+l_i\right)}$, where N and L represent the number of nodes and the angular momentum of the nucleons respectively, and ni and li are the quantum numbers associated with the Fermi levels (0p_3/2) and (0p_1/2) occupied by nucleons in ⁷Li [3]. It should be noted that the number of nodes defined in the FRESCO code contains the origin; therefore, the number of nodes should be n+1 when calculating using the FRESCO code. The spectroscopic amplitudes $S_{\langle {}^7{\text{Li}}_{\text{g}\text{.s}\text{.}}{|}^6{\text{Li}}_{\text{g}\text{.s}\text{.}}\rangle }^{1/2}$ and $S_{\langle {}^7{\text{Li}}_{\text{0}\text{.48}}{|}^6{\text{Li}}_{\text{g}\text{.s}\text{.}}\rangle }^{1/2}$ are taken from Ref. [38].

Results and Discussion

First, the angular distributions of ⁶Li elastic scattering and inelastic scattering to the first excited state of ⁷Li at incident energies from 10.0 MeV to 40.0 MeV were calculated using the traditional OM and DWBA methods, respectively. The calculated results are shown in Figs. 2(a-g) and Figs. 3(a-g) using the solid curves named OM and DWBA, respectively. In Figs. 2(a-g), the calculated results of the elastic scattering angular distributions are in reasonable agreement with the experimental data at forward angles, whereas large discrepancies were observed at backward angles. A similar situation occurred for the inelastic scattering angular distributions, as shown in Figs. 3(a-g). Therefore, the contributions of other reaction mechanisms to elastic and inelastic scatterings must be considered to describe ALAS, and the CRC method is used for this purpose.

Fig. 2Full-screen View

Comparisons of the calculated elastic scattering angular distributions with the experimental data [38] at energies E_lab(⁶Li)=10–40 MeV. The solid, dashed, short-dashed and dash-dotted curves present the OM, CRC1, CRC2 and CRC3 results, respectively. Details of the calculations are described in the text. (a) E_lab(⁶Li) = 10 MeV, (b) E_lab(⁶Li) = 15 MeV, (c) E_lab(⁶Li) = 20 MeV, (d) E_lab(⁶Li) = 25 MeV, (e) E_lab(⁶Li) = 30 MeV, (f) E_lab(⁶Li) = 35 MeV, (g) E_lab(⁶Li) = 40 MeV

Fig. 3Full-screen View

(Color online) Comparisons of the calculated inelastic scattering angular distributions with the experimental data [38] at energies E_lab(⁶Li)=10–40 MeV. The solid, dashed, short-dashed and dash-dotted curves depict the DWBA, CRC1, CRC2 and CRC3 results, respectively. Details of the calculations are described in the text. (a) E_lab(⁶Li) = 10 MeV, (b) E_lab(⁶Li) = 15 MeV, (c) E_lab(⁶Li) = 20 MeV, (d) E_lab(⁶Li) = 25 MeV, (e) E_lab(⁶Li) = 30 MeV, (f) E_lab(⁶Li) = 35 MeV, (g) E_lab(⁶Li) = 40 MeV

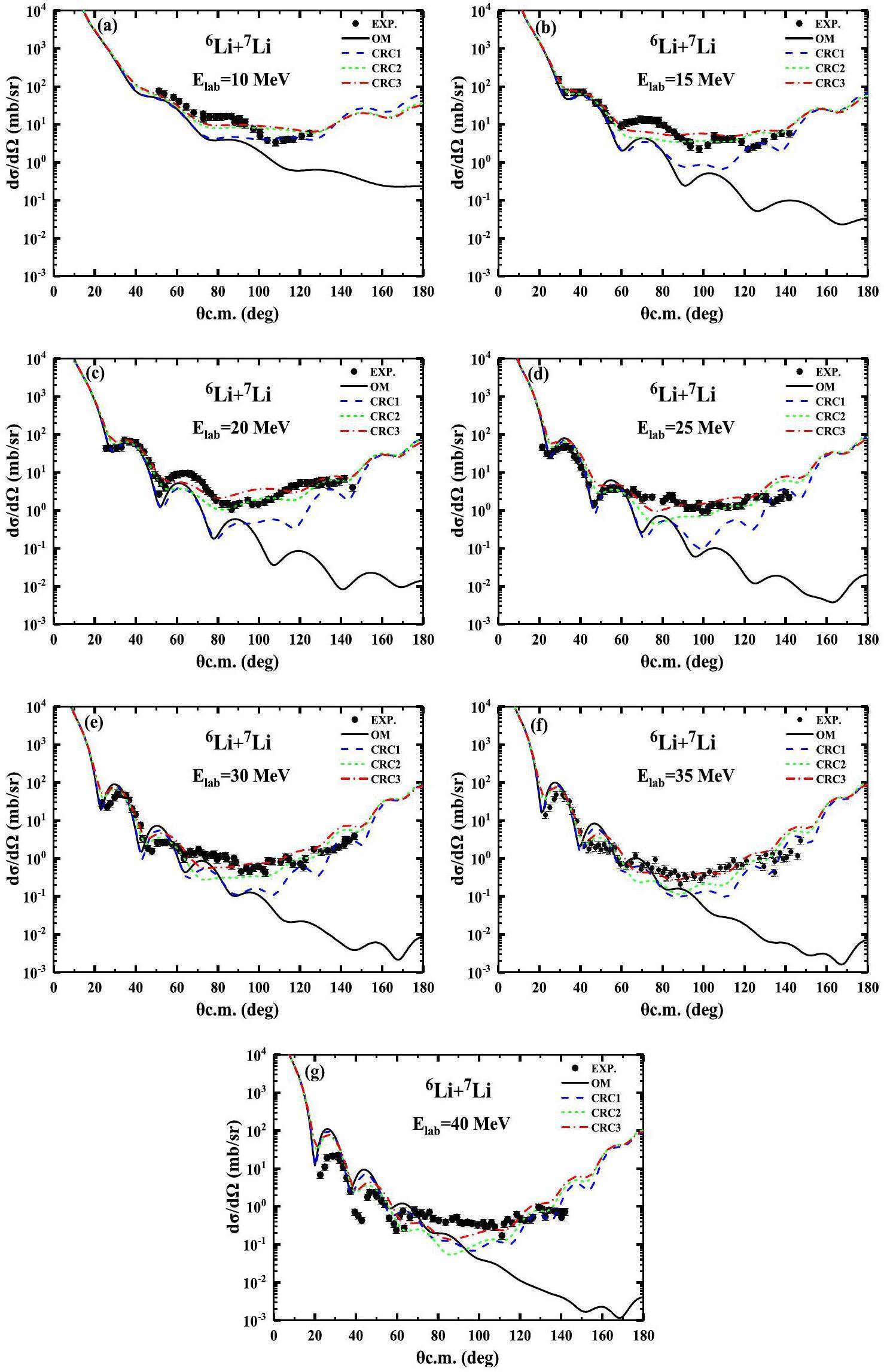
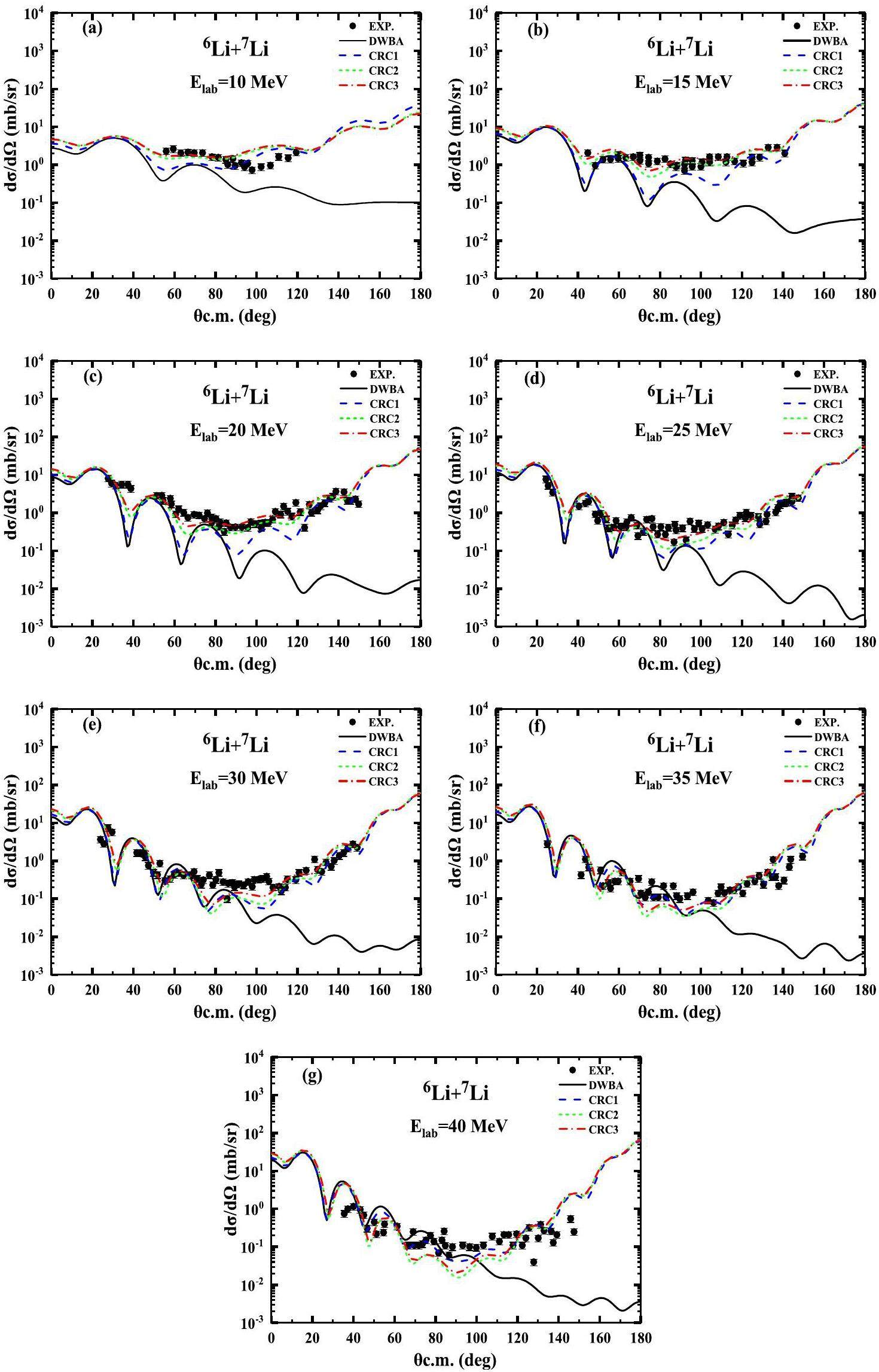
Next, the CRC calculation is performed by coupling the elastic scattering ⁷Li(⁶Li,⁶Li)⁷Li, inelastic scattering ⁷Li(⁶Li,⁶Li)⁷Li_0.48, single neutron ground-state transfer ⁷Li(⁶Li,⁷Li_gs)⁶Li, and single neutron excited-state transfer ⁷Li(⁶Li,⁷Li_0.48)⁶Li channels to explain the ALAS. The calculated results of the elastic scattering and inelastic scattering angular distributions at incident energies from 10.0 MeV to 40.0 MeV are shown by dashed curves named CRC1 in Figs. 2(a-g) and Figs. 3(a-g). Overall, the calculated results were significantly better than the OM and DWBA results. It can be concluded that the transfer reaction mechanism plays a significant role at large angles in elastic and inelastic scattering; however, some of the results are still unsatisfactory. To describe the experimental data better, other reaction mechanisms must be considered.

Finally, the breakup effect was also considered in CRC calculations. Specifically, the coupling reaction framework incorporated contributions from the three resonance states of ⁶Li at excitation energies of 2.186 MeV (3⁺), 4.312 MeV (2⁺), and 5.65 MeV (1⁺), as well as two resonance states of ⁷Li at excited energies of 4.63 MeV (3.5^-) and 6.68 MeV (2.5^-) to investigate the effect of breakup. Based on the four reaction channels of CRC1 scheme, the contributions of the three resonance states of ⁶Li were first added to the coupling channel scheme, and the calculated results are shown by the short-dashed curves named CRC2 in Figs. 2(a-g) and Figs. 3(a-g). The results are better than those of the CRC1 scheme, which highlights the importance of the ⁶Li breakup effect. However, the calculated results underestimate the experimental data over a broad angular range. Then, based on the CRC2 scheme, the contribution of the two resonance states of ⁷Li is added to the coupling channel scheme, and the calculated results are shown by the dashed–dotted curves named CRC3 in Figs. 2(a-g) and Figs. 3(a-g). The results are further improved compared to the CRC2 scheme and provide a reasonable description of the experimental data over the entire angle range. This demonstrates that the breakup effects of ⁶Li and ⁷Li yield non-negligible contributions at intermediate and backward angles.

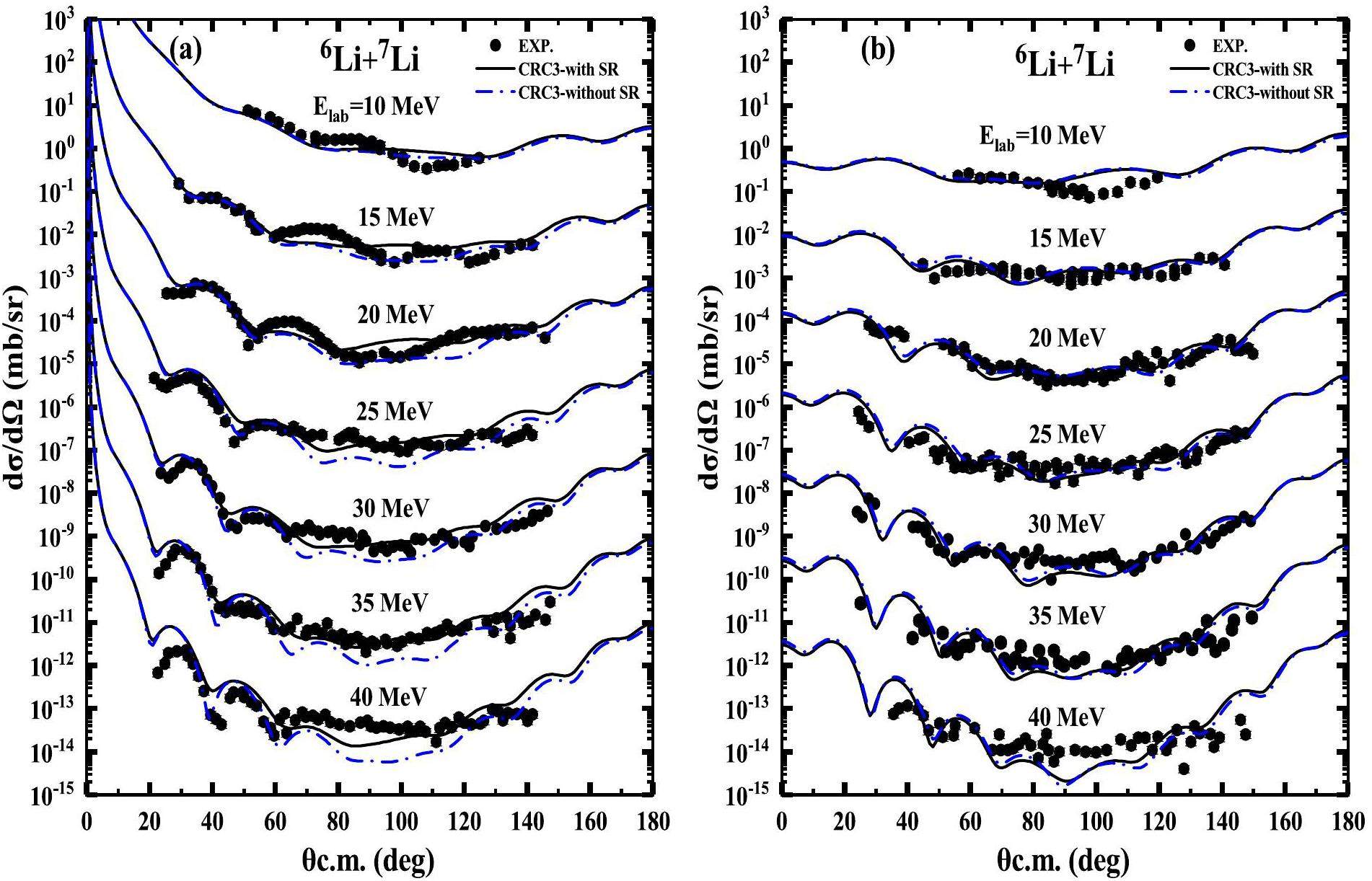
To investigate the influence of spin reorientations of the ⁶Li and ⁷Li, the elastic scattering and inelastic scattering angular distributions are calculated with and without the spin reorientations in the CRC3 scheme, and the results are compared in Fig. 4. The results considering spin reorientation are slightly better, indicating that spin reorientation plays a non-negligible role in the ⁶Li + ⁷Li scattering system.

Fig. 4Full-screen View

(Color online) Comparisons of the calculated results with the experimental data at energies E_lab(⁶Li) = 10–40 MeV. The solid and dash-dotted curves present the results with and without spin reorientations respectively, based on CRC3 scheme. (a) Elastic scattering angular distribution, (b) Inelastic scattering angular distribution

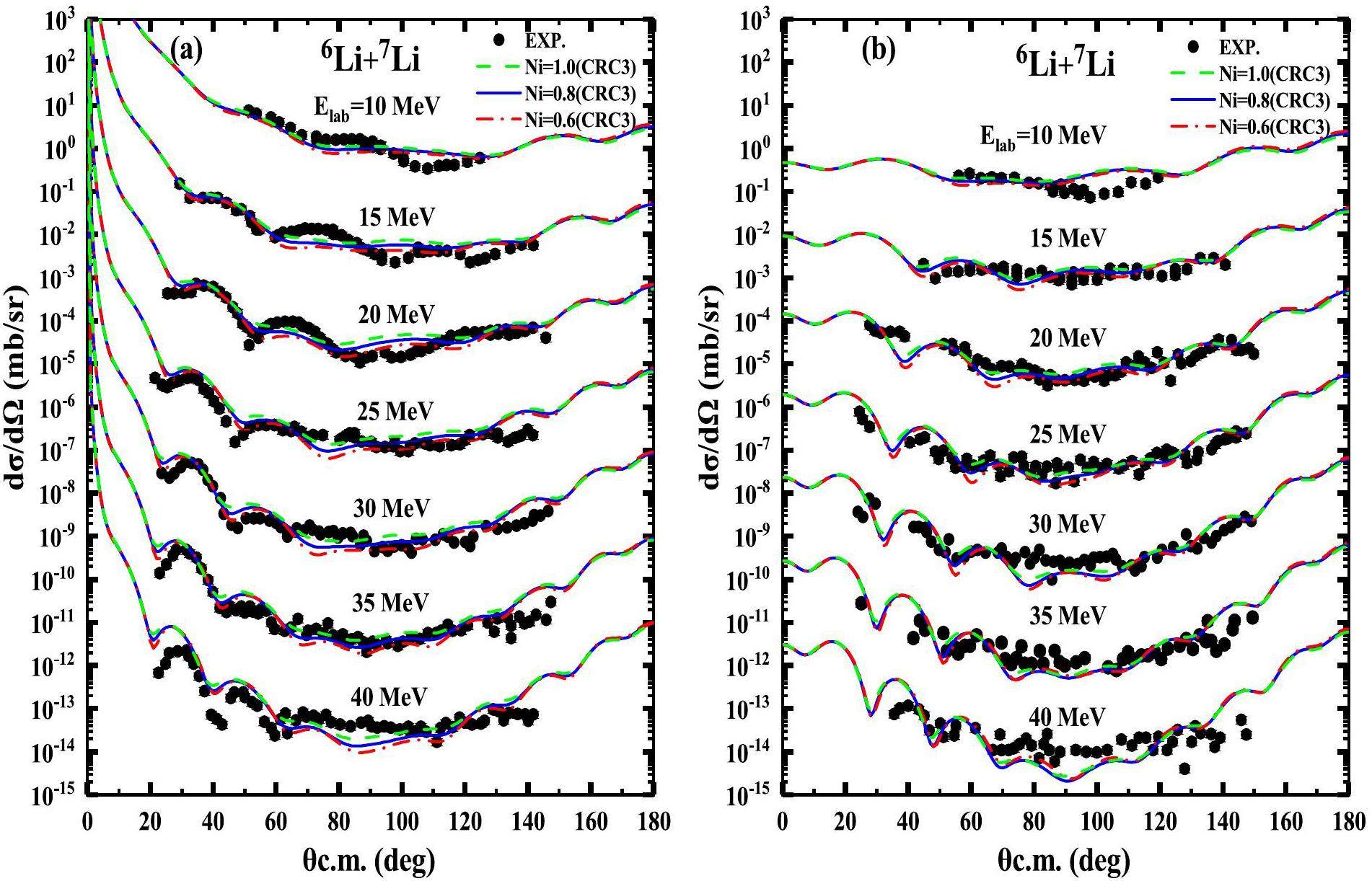
The São Paulo potential is obtained by the double-folding model, which is a bare potential and only gives the real part of the interaction potential; the imaginary part is assumed to be proportional to the real part of the São Paulo potential through the normalization factor Ni. In the calculations above, 0.8 is adopted as the normalization factor, which is the average value for the analyses of different nuclear scattering systems in Refs. [43, 44]. Different normalization factor values are discussed. The calculated results with Ni=0.8, Ni=1.0 and Ni=0.6 are shown by the solid, dashed, and dash-dotted curves, respectively, in Fig. 5. In general, the results calculated with Ni=0.8 are slightly better than the others. Therefore, Ni=0.8 is appropriate for the present analysis.

Fig. 5Full-screen View

(Color online) Comparisons of the calculated results with the experimental data at energies E_lab(⁶Li) = 10–40 MeV.The solid, dashed, and dash-dotted curves present the results with Ni=0.8, Ni=1.0 and Ni=0.6 respectively, based on CRC3 scheme. (a) Elastic scattering angular distribution, (b) Inelastic scattering angular distribution

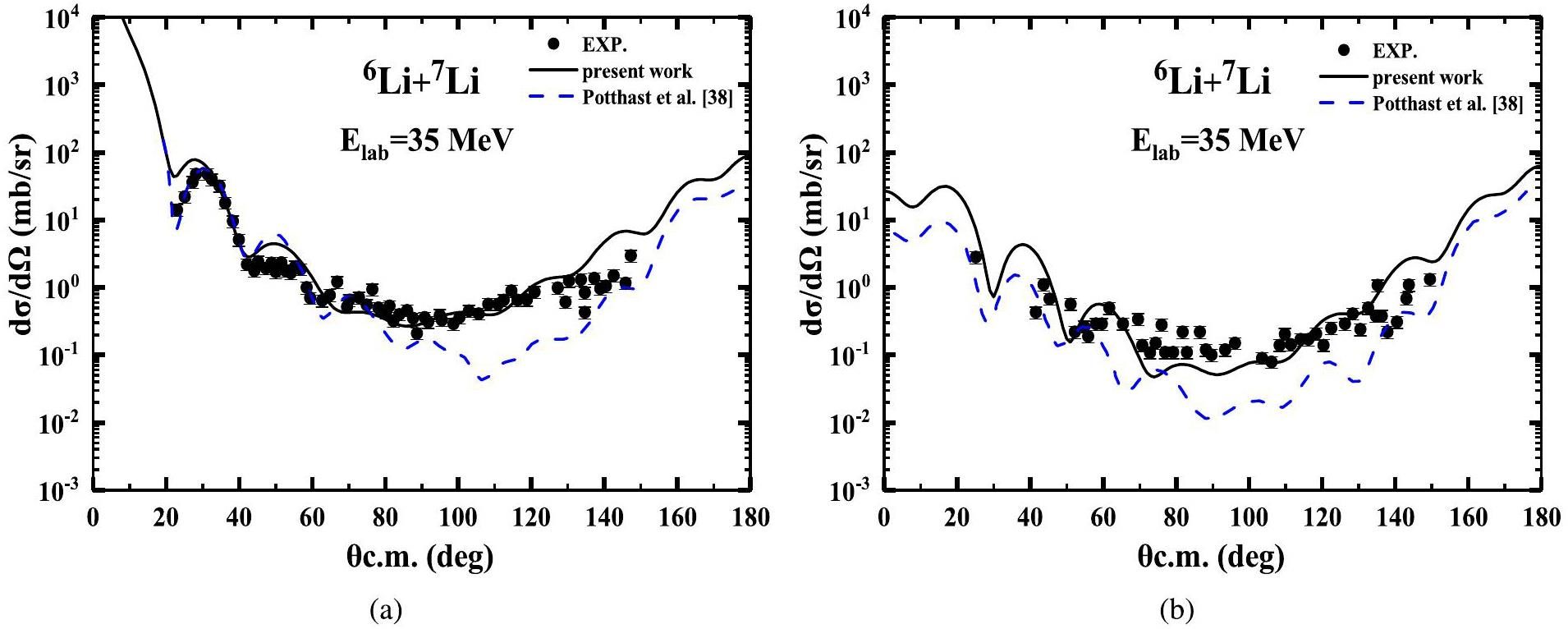
In addition, a comparative analysis of the angular distributions of both elastic and inelastic scatterings at E_lab(⁶Li)=35 MeV is conducted with the previous work [38] which considered only the potential scattering, inelastic scattering and transfer processes using OM and DWBA methods as shown in Fig. 6a and b. The present results can reasonably reproduce the experimental data at large angles θ_c.m.θ_c.m.>60°; however, the previous work could not. This indicates that the breakup and coupling mechanisms are important in the ⁶Li+⁷Li scattering processes.

Fig. 6Full-screen View

(Color online) Comparisons of present calculated results (solid lines) with those given by Ref. [38] (dashed lines) and experimental data at E_lab(⁶Li) = 35 MeV. (a) Elastic scattering angular distribution, (b) Inelastic scattering angular distribution

To further investigate the influence of the breakup effects of ⁶Li and ⁷Li, the elastic scattering and inelastic scattering angular distributions were calculated again in the CRC3 scheme with the ⁶Li–⁷Li optical potential replaced by the phenomenological optical potential V-GL-4 given in Ref. [38]. The calculated results are indicated by dashed curves, named CRC3-POP, in Fig. 7. These results are better than those reported in Ref. [38] denoted by the solid curves, highlighting the importance of the breakup effect. If the spectroscopic amplitude of the (0p_3/2) state of ⁷Li_gs is adjusted from 0.657 to 1.0, the calculated results, denoted by the dash-dotted curves in Fig. 7 better matches the experimental data.

Fig. 7Full-screen View

(Color online) Comparisons of the calculated results with the experimental data at E_lab(⁶Li) = 35 MeV.The solid, dashed, and dash-dotted curves present Potthast et al [38] results, the calculated results in the CRC3 scheme with phenomenological V-GL-4 potential, and with the spectroscopic amplitude of the (0p3/2) state of ⁷Li_gs as 1.0, respectively. (a) Elastic scattering angular distribution, (b) Inelastic scattering angular distribution

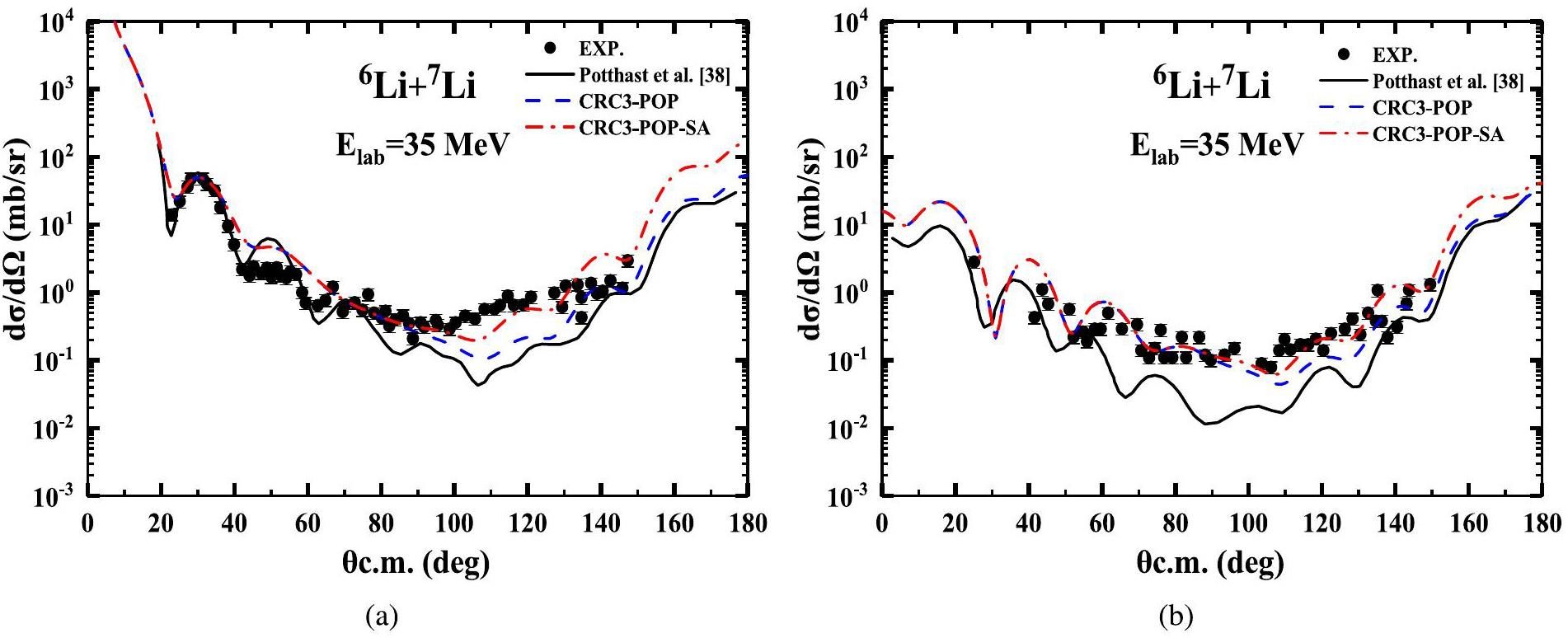
Based on the above analyses, it can be concluded that potential scattering dominates at forward angles where the transfer reaction and breakup effect makes a small contribution, whereas transfer reaction and breakup effects contribute significantly at middle and large angles for both the elastic and inelastic scatterings of the ⁶Li+⁷Li system. The spin reorientations of ⁶Li and ⁷Li provide non-negligible contributions at intermediate and backward angles.

Summary and Conclusion

The angular distributions of a ⁶Li+⁷Li elastic and inelastic scatterings were analyzed in three frameworks. The SPP2 potential provides a reasonable description of ⁶Li+⁷Li elastic scattering angular distributions at forward angles θ_c.m.θ_c.m.>60° in the energy range E_lab=10–40 MeV. ALAS was explained using CRC method that considers the elastic and inelastic scattering reaction channels, spin reorientations of ⁶Li and ⁷Li, ground-state transfer, and excited-state transfer reaction channels. Three resonance states of ⁶Li and two resonance states of ⁷Li were included to approximately consider the breakup effect. The calculated results provide a reasonable description of the experimental data over the entire angle range at incident energies of 10.0 MeV to 40.0 MeV. Moreover, compared with previous works, the present work provides a better description of the experimental data. It was concluded that the transfer and breakup mechanisms are critically important in ⁶Li+⁷Li scattering, and the contributions of the ⁶Li and ⁷Li spin reorientations in the ground and excited states can not be ignored. All of these reaction mechanisms should be considered in the study of nuclear reactions between adjacent weakly bound light nuclei.