Introduction

Carbon fusion is the primary reaction in massive stars [1-4]. It also serves as an ignition reaction for Type Ia supernova explosions [5, 6] and X-ray superbursts [7, 8]. An accurate carbon–carbon fusion-reaction rate can reduce uncertainties in the nucleosynthesis of massive stars and the ignition condition in Type Ia supernova as well as contribute to resolving the ignition problem in superbursts [9, 10].

The carbon–carbon fusion reaction in stars occurs at energies below E_c.m.= 3.0 MeV, which is considerably below the Coulomb barrier at $E_{\text{c}\mathrm{.}m\mathrm{.}}\approx 5.8$ MeV [11, 12], resulting in an extremely low fusion cross section. For example, the fusion cross section at E_c.m.= 2.0 MeV was estimated to be 0.1 pb based on the CF88 recommendation [13]. At $E_{\text{c}\text{.m}\text{.}}<3.0$ MeV, the dominant exit channels are the alpha and proton channels, whereas the neutron channel is closed at its threshold of E_c.m.= 2.597 MeV [14, 15]. Previous measurements relied on detecting light charged particles [16-19] or gamma rays emitted by residual nuclei [20, 21]. Recently, a particle-gamma coincidence method was developed to further suppress background noise and achieve better measurements at stellar energies [22, 23]. LUNA-MV is planned to study the ¹²C+¹²C reaction by detecting the 440 keV and 1634 keV gamma rays emitted by the proton and alpha channels, respectively, in the Gran Sasso underground lab, where natural and cosmic-ray-induced gamma backgrounds are considerably reduced [24]. JUNA, in China, also demonstrates the potential to suppress background noise [25-28].

Although the particle-gamma coincidence method and underground gamma-ray measurements can extend the measurement to even lower energies, the channels of charged particles decaying to the ground states of ²³Na and ²⁰Ne cannot be studied using these methods owing to the absence of gamma rays [18, 29]. We developed a novel technique based on a time-projection chamber (TPC) to measure the nongamma-ray-emitting channels ¹²C(¹²C,α₀)²⁰Ne and ¹²C(¹²C,p₀)²³Na. Our commissioning experiment using the 1024-channel prototype pMATE TPC (multi-purpose time-projection chamber for nuclear astrophysical and exotic-beam experiments) demonstrated that more than 99% of alpha contaminants from the natural environment may be rejected by this technique [30].

An ultrapure carbon target able to withstand beam powers exceeding 400 W is another important factor in carbon-fusion experiments [31, 32]. The background induced by the target impurities, primarily hydrogen and lithium isotopes, may be orders of magnitude higher than the reaction events of interest, limiting the experimental sensitivities. Therefore, obtaining high-purity carbon targets is important to achieve the desired sensitivity. In addition, the small ¹²C+¹²C fusion-reaction cross section at stellar energies requires high beam intensity and a long beam time on the order of weeks. Therefore, target stability is another important feature of carbon targets.

This study reports the first direct measurement of the ¹²C(¹²C,α₀)²⁰Ne reaction at E_c.m.= 2.22 MeV using the highly oriented pyrolytic graphite (HOPG) target and our upgraded TPC-Si detector array. We also investigate the impact of radiation damage on the detected yield of charged particles such as protons and alpha particles. This study consists of four parts. The first part introduces the experimental setup. The second part describes the experimental method. The third part reports the study of the dependence of the detected yield of charged particles on the accumulated dose of the HOPG target. In the fourth part, we present the measurement of the thick target yield of ¹²C(¹²C,α₀)²⁰Ne at E_c.m.= 2.22 MeV using the HOPG target.

Experimental setup

The experimental setup comprises a reaction chamber and detector chamber. A schematic of the setup is shown in Fig. 1. In the reaction chamber, a thick carbon target was mounted on water-cooled stainless-steel backing. The angle between the beam and normal directions of the target surface was set to 135°, allowing the light charged particles from the fusion reaction to be detected by the detectors. A water-cooled collimator with a diameter of 10 mm was installed 40 cm upstream of the target, and the beam spot on the target was limited to ∼10 mm.

Fig. 1Full-screen View

(Color online) Schematic of the experimental setup. In the coordinate system defined in the setup, the target position is deduced to be (10 cm, -21 cm, 10 cm)

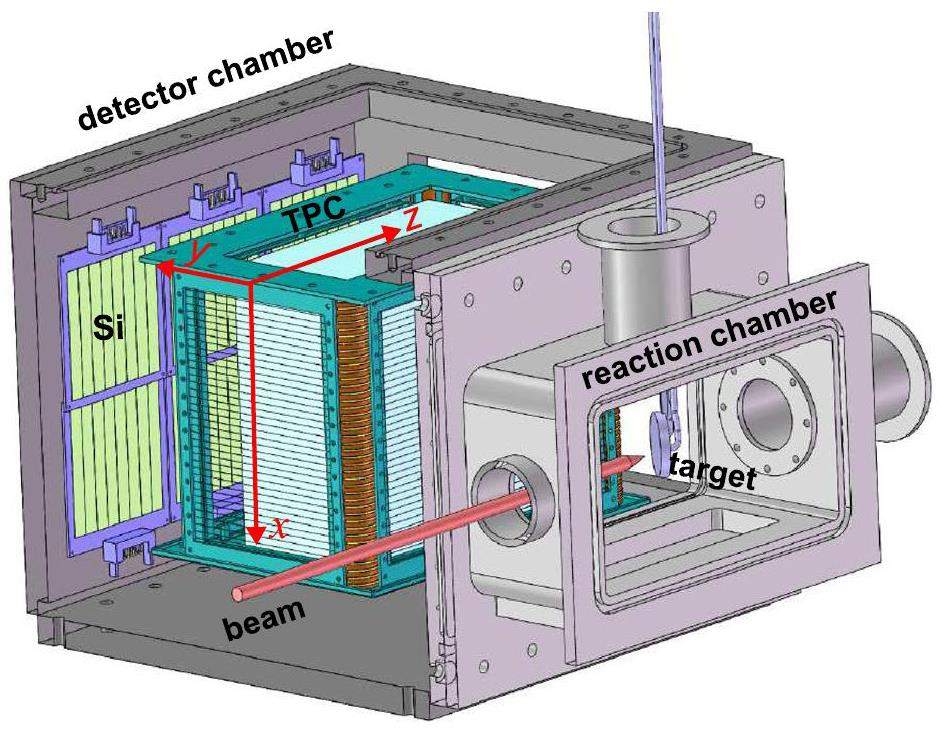
Our detection system comprises a TPC and silicon-detector array. It was installed in the detector chamber filled with counting gas. A large-area Kapton foil with a thickness of 5 μm and an area of 7 cm × 21 cm was used to separate the gas in the detector chamber from the reaction chamber. The Kapton foil was coated with approximately 100-nm-thick aluminum to prevent charge accumulation and shield the silicon detectors from light coming from the beam spot on the carbon target. Two types of stainless-steel hexagonal meshes with transmittances of 77% and 90% were used to support the foil; the typical gas pressure varied from 50 mbar to 300 mbar.

The TPC has an active volume of 100mm(W)×200mm(L)×200mm(H). When the charged particles travel in the TPC gas region, they ionize the gas along their paths. The ionized electrons drift along the electric field towards the anode-readout plate, and an avalanche occurs. The primary and avalanche electrons are collected using an anode plate with rectangular pads.

The three-dimensional position can be determined by measuring the electron drift time. Further details of the TPC detector and its commissioning experiment are provided in Ref. [30, 33].

The silicon array consists of six silicon detectors (Hamamatsu, Japan) with thicknesses of 600 μm [34]. Each silicon detector has eight strips at the junction side in a direction parallel to the electric field of the TPC, dividing the scattering angle into a finer size. The total active area is 90.6 mm × 90.6 mm. The distance between the silicon array and TPC active region can be adjusted from 80 mm to 120 mm. The combination of the silicon detectors and TPC forms a $DE-E$ telescope system. In addition, silicon detectors can provide a starting point for measuring the drift time of electrons in the TPC.

Experiments

A 2-mm thick HOPG target was bombarded by the ¹²C beam delivered by the low-energy high-intensity high-charge-state ion accelerator facility at the Institute of Modern Physics [35]. During the experiments presented in Sections 3 and 5, thick gas electron multipliers [36] were used for gas amplification, and the TPC chamber was placed at a scattering angle of 90. To study the reaction-yield variations using the HOPG target (Sect. 4), the TPC with MicroMegas amplification was used for stable operation at a low gas pressure [37, 38] and was placed at a scattering angle of 120. The gas type and pressure were selected to ensure that the charged particles could penetrate the TPC active volume and stop in the Si detectors while depositing sufficient energy in the gas to generate tracks.

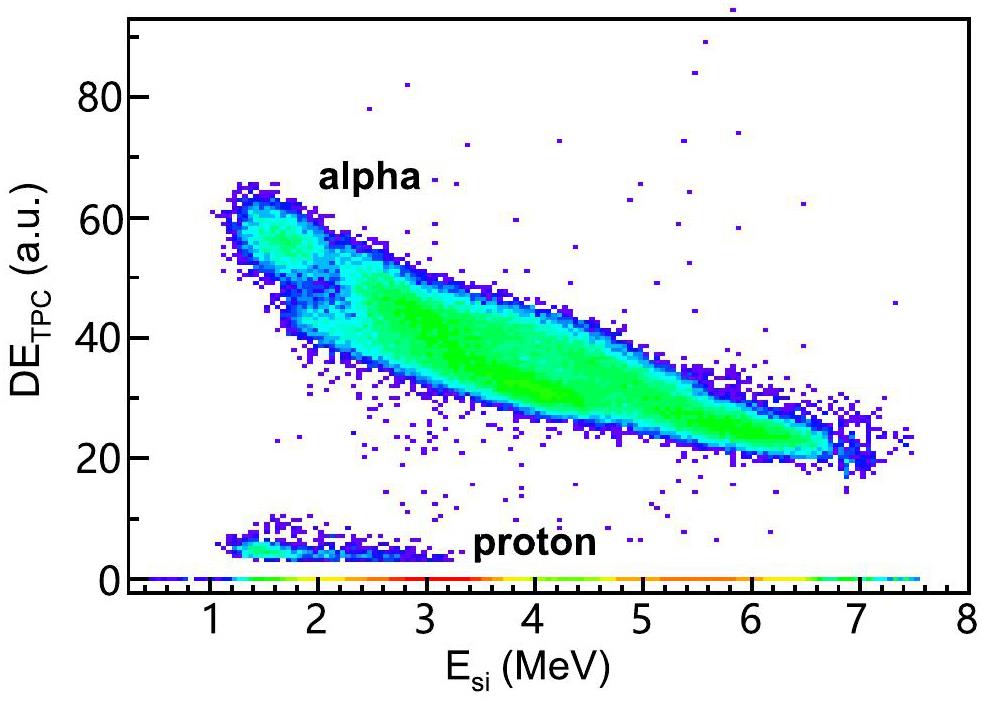
A typical DE_TPC-E_si spectrum measured at E_c.m.= 3.90 MeV is shown in Fig. 2. Here, DE_TPC and $E_{\text{si}}$ are the energy depositions in the TPC and Si detectors, respectively. The TPC chamber was filled with a He+5%CO₂ mixture at 165 mbar. With the energy loss in the TPC and residual energy in the silicon detectors, alpha events were well separated from protons and other events, as shown in Fig. 2. During this measurement, the TPC gain was optimized for the detection of alpha particles, whereas protons with energies above 3 MeV did not generate tracks in the TPC.

Fig. 2Full-screen View

(Color online) Particle identification using the energy loss in TPC versus the energy in silicon detectors for the ¹²C+¹²C fusion reaction at $E_{\text{lab}}\text{=}7.8$ MeV. The detector was placed at 90° with a pressure of 135 mbar. GEM-based readout pads were used. The TPC was optimized for alpha detection, whereas most protons were only recorded by the silicon detectors. The discontinuity in the alpha band around 2 MeV by Si was caused by the energy truncation in the middle silicon detectors, which had a relatively high energy threshold (see Figure 4)

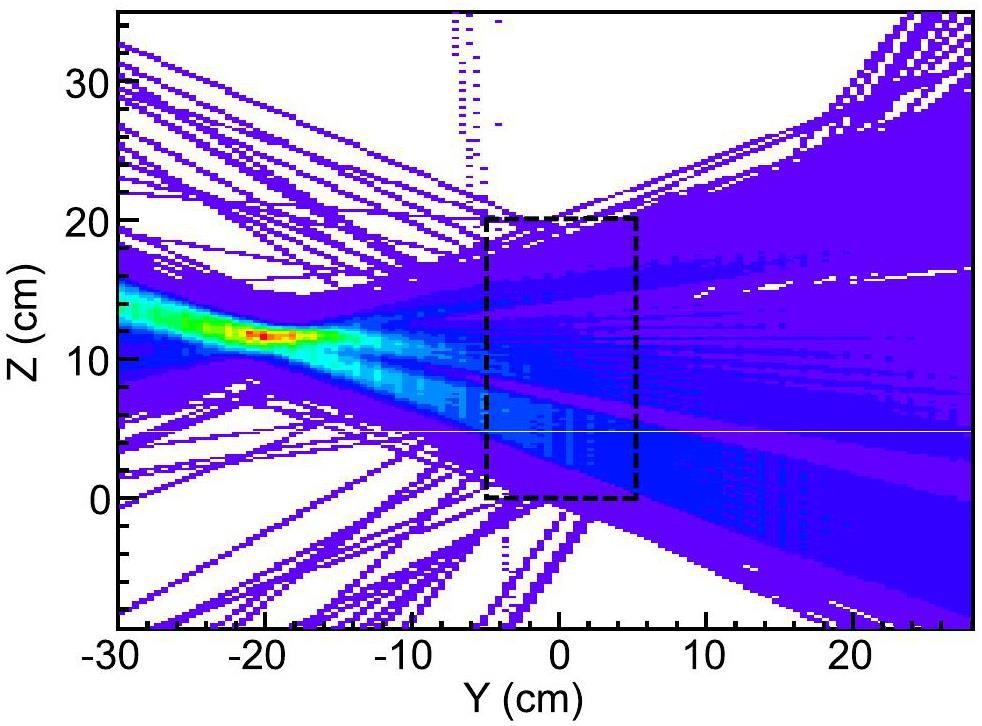
An important advantage of the TPC is its ability to track charged particles [30, 39]. The tracks of the alpha events can be traced back to the beam axis to check whether they originated from the beam spot on the reaction target. An example of track reconstruction in the pad plane (YZ plane) using the selected alpha events is shown in Fig. 3. Most tracks converged around the (-20 cm, 11 cm) point, which clearly defined the beam spot on the reaction target. All other events mostly originated from the natural radioactivity of the surrounding material. The alpha events from the beam spot could be further purified using the TPC drift time [30].

Fig. 3Full-screen View

(Color online) Accumulation of extended alpha tracks in the pad plane for the target reconstruction. TPC active region is indicated by the black dashed line in the plot. Most of the tracks converged to the reaction-target position, which has a diameter of approximately 7 mm. The experimental setup is explained in the caption of Fig. 2

The alpha particles emitted from the target position were selected by gating their $D{E}_{\text{TPC}}$, E_si, and tracks were detected by the TPC. The energy-deposition spectrum in the silicon detectors as a function of strip ID, which corresponds to the polar angle relative to the beam axis, is shown in Fig. 4. The two groups of alpha particles shown in Fig. 4, corresponding to the ground and first excited states of the residual nucleus ²⁰Ne, are identified with their kinematics. The relatively large energy spread of the alpha particles mainly resulted from the combined effects of kinematic broadening, energy loss, and straggling in the thick carbon target, Kapton window, and counting gas.

Fig. 4Full-screen View

(Color online) Energy measured in silicon detectors versus the silicon-strip number, obtained from a graphical representation of alpha events in the $D{E}_{\text{TPC}}-E_{\text{si}}$ matrix in Fig. 1. Silicon IDs from 0 to 23 correspond to the scattering angles of 70° to 110° in the laboratory frame. The ¹³C(¹²C,α)²⁰Ne reaction events are also observed, in which the ¹³C nucleus comes from the natural abundance of 1.1% in the HOPG target. The experimental setup is explained in the caption of Fig. 2

Stability of the HOPG target

The HOPG target was composed of several graphene layers. After beam bombardment, the graphene layers on the surface were damaged and formed a flaky and wrinkled structure as shown in Fig. 5. This radiation damage modified the surface structure and may potentially affect the detection of low-energy charged particles, a phenomenon that has not yet been studied.

Fig. 5Full-screen View

(Color online) Picture of HOPG target before (left) and after 1.34×10⁷ μC beam dose bombardment (right)

We studied the effect of intense beam irradiation on the HOPG target by measuring ¹²C+¹²C reaction yields. In the test, a ¹²C²⁺ beam at a relatively high energy of E_c.m.= 3.55 MeV was chosen to obtain sufficient statistics within a few minutes. The detector was placed at an angle of 120 ° at a gas pressure of 99 mbar. During charge accumulation, the beam was ¹²C²⁺ with a typical current of 40 ∼ 50 pμA. Two types of targets, 4-μm-thick diamond-like carbon (DLC) [40] and 2-mm-thick HOPG targets [41], were used to study the variations in the yields of the carbon–carbon fusion reaction as a function of the beam dose.

An infrared camera was used to monitor the maximum temperature of the target. The observations indicate that the beam spot size on the DLC and HOPG was approximately 1 cm². With water cooling at the back of the target, the maximum temperature of the DLC surface stabilized at approximately 100 ℃. However, the surface temperature of the HOPG target quickly increased to ∼400 ℃ when the beam hit it. This difference might have been caused by the weak interlayer interactions between the individual graphene layers in the HOPG target [42, 41]. Such a structure led to a low through-plane thermal conductivity, which was more than two orders of magnitude lower than that of natural graphite. The formation of flaky and wrinkled structures after irradiation further reduced thermal conduction.

During measurements, the TPC was placed at 120. The detector chamber was filled with a gas mixture of 90% He, 5% CO₂, and 5% Ar at a pressure of 100 mbar. As discussed in the previous section, the alpha yield was determined directly by selecting the alpha band in the $D{E}_{\text{TPC}}-E_{\text{si}}$ condition and the tracking information. Protons can be selected by applying an anti-alpha condition, which excludes alpha events from the $D{E}_{\text{TPC}}-E_{\text{si}}$ spectrum.

4.1

Q-value spectra of the alpha and proton channels

The reaction Q values for the proton (Q_g.s.= 2.24 MeV) and alpha (Q_g.s.= 4.62 MeV) channels were calculated using the following formulas: $Q=\left(\frac{A_a}{A_B}-1\right)E_a+\left(\frac{A_b}{A_B}+1\right)E_b-\frac{2\sqrt{A_a{A}_b{E}_a{E}_b}\cos \theta }{A_b}\mathrm{,}$ (1) where Aa, Ab, and AB are the mass numbers of the projectile, ejected, and residual nuclei, respectively. Ea is the kinetic energy of the projectile during the reaction, Eb is the energy of the ejected light particles, and θ is the scattering angle of particle b. Eb is obtained using the energy detected by the silicon detector and energy losses in the entrance window and gas region [43].

To reduce the systematic error arising from energy-loss correction, only the events measured by the two silicon detectors in the middle were used.

The Q-value spectra of ¹²C(¹²C,α)²⁰Ne and ¹²C(¹²C,p)²³Na at E_c.m.= 3.55 MeV are shown in Fig. 6 and 7, respectively. The green line in Fig. 6 shows the Q-value spectrum for ¹²C(¹²C,α)²⁰Ne using the DLC target at a beam charge of 2.18× 10⁴ μC. This spectrum was measured at the beginning of the beam irradiation. The α₀ and α₁ peaks were located at Q values of 4.62 MeV and 2.99 MeV, respectively. No noticeable change was observed in the Q-value spectrum during the subsequent charge accumulation on the DLC.

Fig. 6Full-screen View

(Color online) Q-value spectrum for ¹²C(¹²C,α)²⁰Ne obtained with different cumulative charge at E_c.m.= 3.55 MeV. The histograms in black and blue represent the Q-value spectra for HOPG with cumulative charges of 4.82×10⁴ μC and 4.94×10⁶ μC, respectively. The Q-value spectrum for DLC at 2.18×10⁴ μC is also plotted for comparison (green line). The vertical solid line indicates the upper limit (5.0 MeV) of integration in calculating the α₀ yield, whereas the three dashed lines correspond to the lower limits (3.1, 3.5, and 4.0 MeV) in different integrations (see Fig. 8 for comparisons of the integrated yields)

Fig. 7Full-screen View

(Color online) Q-value spectrum for ¹²C(¹²C,p)²³Na at E_c.m.= 3.55 MeV. The black and blue histograms represent the Q-value spectra for HOPG at 2.59×10⁵ μC and 4.94×10⁶ μC, respectively. The vertical solid line indicates the upper integral limit (2.4 MeV) when calculating the p₀+p₁ yield, whereas the three dashed lines correspond to the lower limits (0.3, 0.8, and 1.4 MeV) in different integrations (see Fig. 9 for comparisons of the integrated yields)

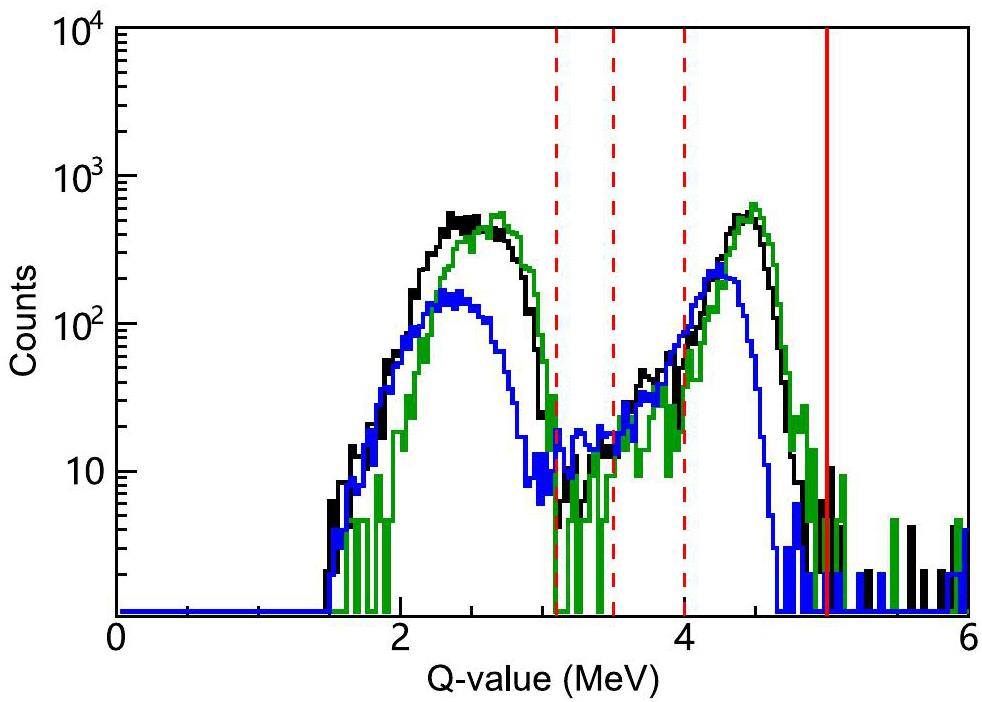
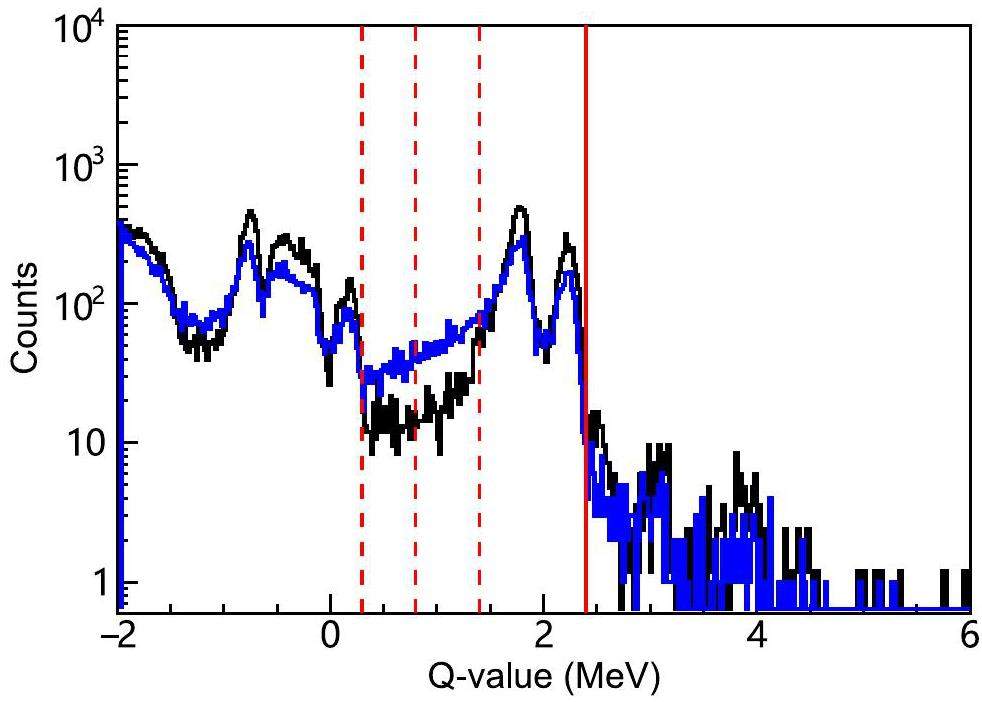
The black and blue lines shown in Fig. 6 represent the HOPG target with the accumulated charges of 4.82×10⁴ μC and 4.94×10⁶ μC, respectively. Comparing the shapes of the Q-value spectra of the HOPG and DLC targets, we can clearly observe a shift and broadening of the α₀ and α₁ peaks for HOPG as the beam dose increases. The black and blue lines shown in Fig. 7 represent the Q-value spectra for protons corresponding to 2.59×10⁵ μC and 4.94×10⁶ μC on the HOPG, respectively. The p₀ and p₁ peaks are located at Q values of 2.24 MeV and 1.80 MeV, respectively. The p₀ and p₁ peaks become broader and develop a longer tail towards the lower Q-value region after approximately 5 C of radiation.

4.2

Dependence of the measured alpha and proton yields on the beam dose

We investigated the dependence of the measured alpha and proton yields on the beam dose. The reaction yields were calculated by integrating the peaks of the protons and alpha particles in the Q-value spectra divided by the incident-beam particles.

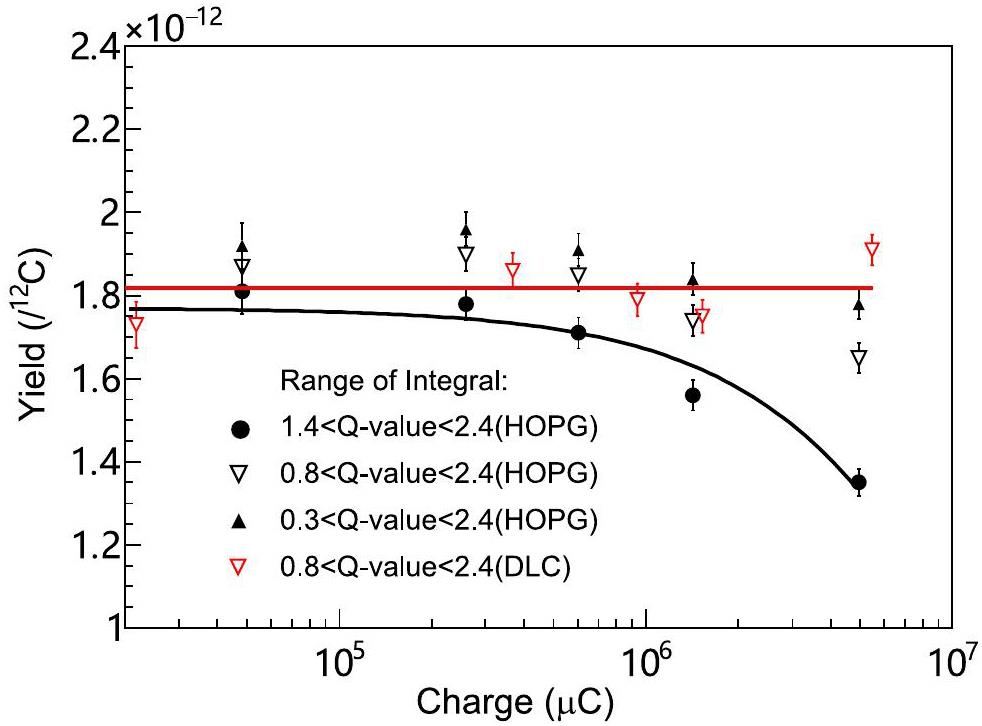
The yield variations in α₀ and p₀ + p₁ are presented in Fig. 8 and 9, respectively, as a function of accumulated charge. For each channel, three different yields corresponding to different integral ranges in the Q-value spectra (indicated by red lines in Fig. 6 and 7) were obtained to account for the change in the Q-value spectra. With an increase in the charge on the HOPG, the yields of both α₀ and p₀ + p₁ exhibited a notable decrease. This scenario worsened for the alpha-emission channels. The decreasing trend in the yield of α₀ (4.0 MeV <Q-value <5.0 MeV)for HOPG can be fitted well by the following exponential function: $\text{Yield}\left({\text{/}}^{\text{12}}\text{C}\right)=\exp \left(-26.68-1.47\times {10}^{-7}\times \text{charge/}\text{μ}\text{C}\right)\mathrm{.}$ (2)

Fig. 8Full-screen View

(Color online) Yield of ¹²C(¹²C,α₀)²⁰Ne versus the accumulated charge at E_c.m.=3.55 MeV. The three sets of labels represent the yields in the HOPG target using different Q-value integral intervals. The black solid curve represents the fitted yield curve for the HOPG within the Q-value-integral interval of [4.0 MeV, 5.0 MeV]. The red triangle represents the yield of the DLC (3 MeV<Q-value<5 MeV), and the red solid line is the fitted yield line (constant) with a mean value of 2.70× 10^-12 /¹²C

Fig. 9Full-screen View

(Color online) Yields of p₀+p₁ for ¹²C(¹²C,p)²³Na versus the accumulated charge at E_c.m.= 3.55 MeV. Three sets of different labels represent the yields of HOPG at different integral intervals. The red triangle represents the yield of DLC within the Q-value integral interval [0.8 MeV, 2.4 MeV] and the red line is the fitted yield line (constant) with a mean value of 1.82× 10^-12 /¹²C. The black solid curve represents the fitted yield curve (1.4 MeV<Q-value<2.4 MeV) by the exponential function: $\text{Yield}\left({\text{/}}^{\text{12}}\text{C}\right)=\exp \left(-27.06-5.76\times {10}^{-8}\times \text{charge/}\text{μ}\text{C}\right)$

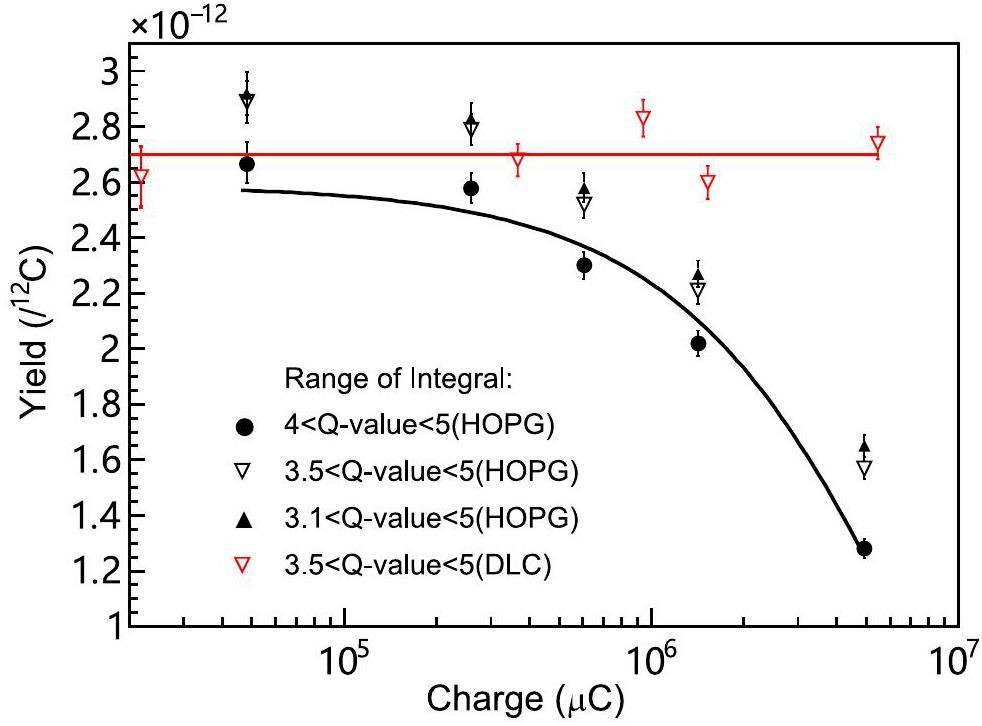
Based on the fitted yield curves shown in Fig. 8, the yield of α₀ decreased by 34.9% when the dose reached 3.0×10⁶ μC and by 51.5% when the dose reached 5.0×10⁶ μC. To mitigate the broadening effect induced by beam irradiation, we employed two extended integral ranges: [3.5 MeV, 5.0 MeV] and [3.1 MeV, 5.0 MeV]. Compared with the integration within [4.0 MeV, 5.0 MeV], the alpha yields increased by 22.0(0.8)% and 28(1)%, respectively, when the dose reached 4.94×10⁶ μC. The α₀ yield obtained from the three integral ranges exhibited a similar trend as the accumulated charge increased from 0 C to ∼5 C.

For comparison, the same test was performed using the DLC target. The maximum beam dose reached 5.5×10⁶ μC. The yield of α₀ was approximately constant at 2.70× 10^-12 /¹²C according to the fitted yield line, as shown in Fig. 8.

The DLC target contained a fraction of hydrogen. The yield difference for the DLC and HOPG targets at a nearly zero dose could be explained by the difference in stopping power.

Regarding the p₀+p₁ yield, the situation differed slightly. When the beam charge accumulated up to 5.0×10⁶ μC, the yield decreased by 25% according to the fitted yield curve shown in Fig. 9. The decrease in the p₀ + p₁ yield could be reduced to 7.0(0.3)% if the integration range is increased to [0.3 MeV, 2.4 MeV].

Measurement of ¹²C(¹²C,α₀)²⁰Ne at E_c.m.= 2.22 MeV

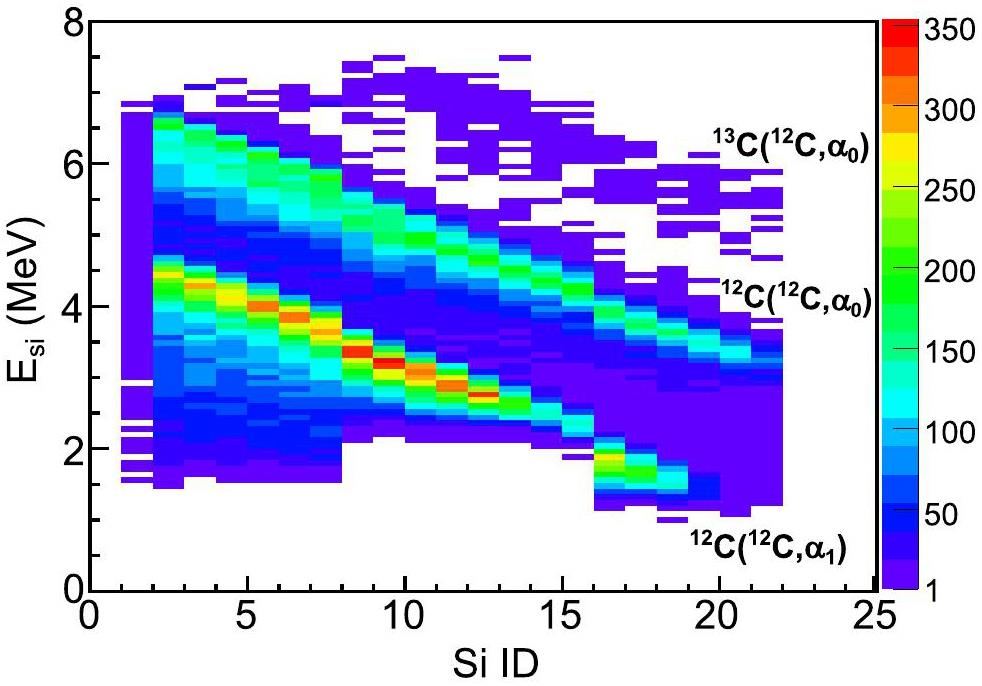
We also measured the ¹²C(¹²C,α)²⁰Ne reaction at E_c.m.= 2.22 MeV using the HOPG target to test the target purity and sensitivity of the TPC-detection technique. The cross section at this energy was estimated to be only a few tens of picobarns, based on the extrapolation of CF88 [11, 13]. The ¹²C⁴⁺ beam intensity was approximately 15 pμA, and the total accumulated charge was 3.26×10⁶ μC. The detector was placed at 90 degrees and filled with 95%He+5%CO₂. Thick GEM-based readout pads were used. For the detection of α particles, the gas pressure in the TPC was optimized to 135 mbar.

Using the same analysis procedure, we obtained the spectrum of the energy deposited in the silicon detectors versus the silicon-strip number for the alpha events. The results are shown in Fig. 10; the top figure is obtained by gating the alpha events in the $D{E}_{\text{TPC}}-E_{\text{si}}$ spectrum through a 15-h run with the beam, and the bottom figure is obtained by gating the alpha events in the $D{E}_{\text{TPC}}-E_{\text{si}}$ spectrum and tracks originating from the beam spot. The difference between the two figures demonstrates the effectiveness of the proposed tracking technique. One α event was identified as originating from the ¹²C(¹²C,α₀)²⁰Ne channel, with the aid of the kinematic curve calculated using the beam energy at the target surface. A total of 570 alpha events from the ¹³C(d,α)¹¹B reaction were also identified, as shown at the bottom of Fig. 10. The high-energy fronts of these events matched well with the expected kinematic curve calculated for the reaction occurring on the surface. A small number of DH⁺ molecular ions could be mixed with the ¹²C⁴⁺ beam and reacted with ¹³C in the HOPG target. This group disappeared in our later measurements when we switched the charge state of the carbon beam from 4⁺ to 2⁺. Although these events contaminated the region of interest for the ¹²C(¹²C,α₁)²⁰Ne channel, they provided valuable information about the beam spot for rejecting natural alpha radioactivity. The natural background of the detector setup was also investigated over a 98-h run without a beam, and the results are shown in Fig. 11. After applying the same cuts to the ¹²C+¹²C measurement, only one α event was observed outside the energy region of interest. As a result, we estimated zero α background counts during the 15-h in-beam measurement. By assuming an isotropic angular distribution in the center-of-mass frame, the thick-target yield for the ¹²C(¹²C,α)²⁰Ne channel was deduced to be ${2.68}_{-1.69}^{+4.69}\times {10}^{-17}{\text{/}}^{12}\text{C}$. Error analysis followed the methodology outlined in Ref. [46]. Considering the effect of the accumulated charge on the HOPG target, the real thick-target yield was ${2.68}_{-1.69}^{+4.69}\times {10}^{-17}{\text{/}}^{12}\text{C}$ after correction, based on the fitted yield curve in Fig. 8. Our result represents the highest sensitivity achieved to date in direct measurements of ¹²C(¹²C,α₀)²⁰Ne.

Fig. 10Full-screen View

(Color online) $E_{\text{si}}$ versus the silicon-ID matrix for alpha particles from the ¹²C+¹²C measurement at E_c.m.=2.22 MeV. Silicon IDs from 0 to 23 correspond to scattering angles of 70–110 degrees in the laboratory frame. The original spectrum (top) and the spectrum obtained after choosing particles coming from the target position (bottom) show one alpha event (marked by the shaded zone), which is assigned to the ¹²C(¹²C,α₀)²⁰Ne reaction based on the kinematic calculation (red solid line). Many alpha particles from the ¹³C(d,α)¹¹B reaction are also observed because a small amount of DH⁺ ions are transported with the ¹²C⁴⁺ beam. This is consistent with the calculated black line

Fig. 11Full-screen View

(Color online) $E_{\text{si}}$ versus the silicon-ID matrix for alpha particles from the natural-background measurement. The original spectrum (top) and the spectrum obtained after choosing particles coming from the target position (bottom) show only one α event outside of the energy region of interest

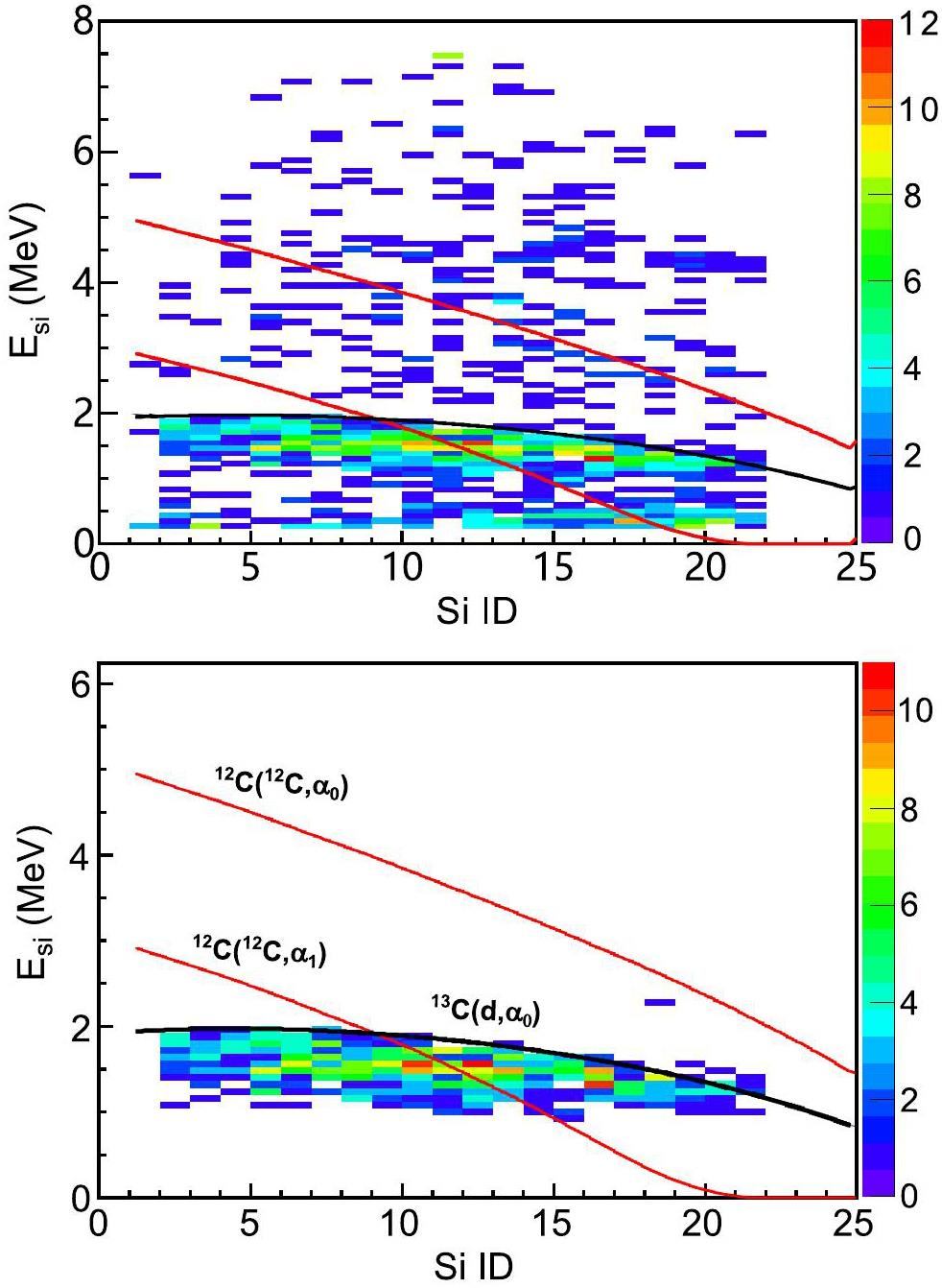
Conclusion

Ultrapure high-power carbon targets are essential for experimental studies of ¹²C+¹²C fusion reactions at stellar energies. HOPG has frequently been adopted as a reaction target in experiments because of its superior purity. In this study, we investigated the reaction-yield dependence on the accumulated beam dose on an HOPG target. Our results showed that the alpha yields were significantly reduced under intense beam bombardment. When the beam dose accumulated to 5 C, the decrease in the alpha yields was 51.5%. Moreover, shifts and broadening of the proton and alpha peaks were clearly observed. To obtain the absolute yield, a correction was required according to the beam dose on the target. Using the TPC-detection technique and HOPG target, we successfully extended the direct measurement of ¹²C(¹²C,α₀)²⁰Ne to E_c.m.= 2.22 MeV, which is within the Gamow window for the carbon burning of massive stars. The thick target yield was determined to be ${2.68}_{-1.69}^{+4.69}\times {10}^{-17}{\text{/}}^{12}\text{C}$, representing the best sensitivity achieved to date for the direct measurement of ¹²C(¹²C,α)²⁰Ne. Further extension to lower energies requires further contaminant reduction in the target and more stable target materials capable of sustaining high beam intensities.