Introduction

Exploring the quantum chromodynamic (QCD) phase structure is one of the most important topics in high-energy nuclear physics. Simulations using lattice QCD revealed that the transition from the quark-gluon plasma (QGP) phase to the hadron phase is a crossover at the vanishing baryon chemical potential (μ∼eq 0) [1-4]. However, effective theories based on QCD predict that this is a first-order phase transition at a finite chemical potential [5-10]. Therefore, it is natural to conjecture the existence of a critical QCD point between the crossover and first-order phase transitions [11, 12].

The characteristic features of the critical point are long-range correlation and large fluctuations. After being created in relativistic heavy-ion collisions, the QGP fireball scans the QCD phase diagram during the evolution process and may reach a critical region. Such fluctuating effects may affect the final observations of heavy-ion experiments. It was conjectured that non-monotonic behavior as a function of the collision energy can be regarded as a signature of the critical point [13-15]. The first-phase Beam Energy Scan (BES-I) program at the RHIC was used to scan the QCD phase diagram by tuning the collision energy [16]. Preliminary measurements of the net proton multiplicity fluctuations showed such non-monotonic behavior with an energy range of 7.7 GeV to 200 GeV [17, 18]. However, the statistics of the BES-I program are insufficient to conclude the observation of non-monotonic behavior, and much higher statistics are required in the second phase of BES and FIX target measurements (see, e.g., Refs. [19, 20] for reviews).

Theoretically, the QGP fireball created in relativistic heavy-ion collisions is a complex system, and several factors may affect the final behavior of net proton multiplicity fluctuations. For instance, owing to the rapidly expanding effect, multiplicity fluctuations may deviate from the equilibrium fluctuations. By considering the dynamic effects induced by an expanding QGP fireball, it was found that the magnitude of the fluctuations could be suppressed [21, 22], the sign could be reversed [23], and the maximum of the fluctuations could be moved from the critical point [24]. Therefore, remarkable progress has been made in the development of dynamic models near the QCD critical point. For example, the dynamics of conserved variables (charge, net-baryon) have been developed [25-29] and the non-monotonic behavior of the fluctuations with respect to the increasing rapidity acceptance window has been observed [25, 28, 29]. Please see e.g., Refs. [30-36] for recent reviews.

In particular, the signs of multiplicity fluctuations are important for exploring the phase structure in heavy ion experiments. A comparison of the magnitudes of the signs can be regarded as a more obvious signature of the phase transition [14, 37]. It predicted the nontrivial behavior of the signs of higher-order cumulants or moments of conserved quantities near the QCD critical point [14, 37]. By developing a dynamic model near the QCD critical point, it was found that critical slowing-down effects may flip the signs of higher-order cumulants [23]. Remarkably, the fourth-order cumulants (or kurtosis) of multiplicity fluctuations in these conserved dynamical models are typically negative [26-29]. This is difficult to achieve using only critical slowing-down effects. This is because the corresponding memory effects preserve the sign of static kurtosis above the phase transition curve, which is not always negative [23]. Thus, the sign of kurtosis is not yet fully understood in a comprehensive and complex simulation of conserved dynamic models. This work focuses on studying the impacts of one of the factors in the conserved dynamic simulation, that is, finite size effects, on the sign of kurtosis. In a realistic detection experiment with a finite acceptance range, only part of the system is collected. This corresponds to the finite size of the system, and the kurtosis is obtained within a finite volume in dynamical models. To understand the typically negative kurtosis near the critical point in dynamically conserved models, this work is dedicated to pointing out that the finite size of the detected system may also modify the sign of the kurtosis by considering the finite volume when calculating the multiplicity fluctuations in a static system.

Multiplicity fluctuations within finite size system

Near the phase transition, the thermal variables (this work focuses on the baryon density n_B) strongly fluctuate, and the corresponding partition function can be written in the Ginzburg-Landau form [26-29]: $\begin{array}{c}Z[\mu ]={\displaystyle \int }D{n}_{\text{B}}\exp \{-\frac{1}{T}{\displaystyle \int }{d}^{3}x[\frac{m^2}{2}{n}_{\text{B}}^2+\frac{K}{2}{\left(\nabla n_{\text{B}}\right)}^2\\ +\frac{{\lambda }_3}{3}{n}_{\text{B}}^3+\frac{{\lambda }_4}{4}{n}_{\text{B}}^4+\mu n_{\text{B}}]\}\mathrm{,}\end{array}$ (1) where T denotes the temperature. The kinetic term with surface tension K is a measure of the interaction range as well as the nonlinear interaction terms. $m=\sqrt{K}/\xi$ is inversely proportional to correlation length ξ. λ₃ and λ₄ are the coupling constants for three- and four-point correlations, respectively. In relativistic heavy-ion experiments, the susceptibility of a conserved quantity is regarded as sensitive to the QCD phase transition [30, 37-39] because it represents the magnitude of the response of the systems against external forces and therefore encodes the correlation between the particles in the system. In particular, people are more interested in the susceptibility of the conserved thermal quantities, such as charge or net-baryon, as they can be obtained unambiguously from the partition function or grand potential by taking the derivatives: ${\chi }_n=\frac{{\partial }^{n}P}{\partial {\mu }^n}\mathrm{,}$ (2) where the pressure has the following form: $P=\frac{T}{V}\ln Z\mathrm{.}$ (3) where V is system volume.

The second-order baryon number susceptibility was proportional to the two-point correlator. ${\chi }_2=\frac{V}{T}\left(\langle n_{\text{B}}^2\rangle -{\langle n_{\text{B}}\rangle }^2\right)\mathrm{,}$ (4) where $\langle \cdots \rangle$ denotes event-by-event averaging. The average correlator over the coordinate space is evaluated using a finite volume $\langle n_{\text{B}}^2\rangle =V^{-2}{\displaystyle {\int }_V}{\text{d}}^3{x}_1{\text{d}}^3{x}_2\langle n_{\text{B}}{\left(x_1)\right)}_{\text{B}}\left(x_2\right)\rangle \mathrm{.}$ (5) That is, spatial integration is performed within a finite volume V. It is noteworthy that $\langle n_{\text{B}}\rangle =0$ can be obtained from Eq. (1). The correlation function $\langle n_{\text{B}}\left(x_1\right)n_{\text{B}}\left(x_2\right)\rangle$ is evaluated as follows: $\langle n_{\text{B}}\left(x_1\right)n_{\text{B}}\left(x_2\right)\rangle =\frac{1}{Z}\frac{{\partial }^{2}Z}{\partial {\mu }^2}=\frac{T}{{\left(2\pi \right)}^3}{\displaystyle \int }{\text{d}}^{3}p\frac{e^{ip\left(x_1-x_2\right)}}{K{p}^2+m^2}\mathrm{,}$ (6) This is the Ornstein-Zernicke form of the correlation function. In the dynamics of conserved baryon density [26-29], the partition function in Eq. (1) is treated as the effective potential in the stochastic diffusion equation. In the linear limit, the dynamic correlation function can be extended to [40] $\begin{array}{l}\langle n_{\text{B}}\left(x_1\right)n_{\text{B}}\left(x_2\right)\rangle \\ =\frac{T}{{\left(2\pi \right)}^3}{\displaystyle \int }{\text{d}}^{3}p\frac{e^{ip\left(x_1-x_2\right)}}{K{p}^2+m^2}\exp \left[-Dt{p}^2\left(K{p}^2+m^2\right)\right]\mathrm{,}\end{array}$ (7) where the factor $\exp \left[-Dt{p}^2\left(K{p}^2+m^2\right)\right]$ is introduced to describe the diffusion of the correlation function as a function of time t and D is the diffusion coefficient. This factor is introduced to consider the dynamic effects in such a static model, and it does not change the following analysis: If the dynamic factor $\exp \left[-Dt{p}^2\left(K{p}^2+m^2\right)\right]$ is neglected, the spatial integration in Eq. (5) is performed in spherical coordinates with radii R, and takes the following form: $\langle n_{\text{B}}^2\rangle =\frac{T}{V}\frac{1}{K}\left[{\xi }^2\left(1-e^{-R/\xi }\right)-R\xi e^{-R/\xi }\right]\mathrm{.}$ (8) At the limit of an infinitely large volume $R\gg \xi$, the second-order baryon number susceptibility approaches the correlation length ${\chi }_2\to {\xi }^2$. This means that the susceptibility of the system is determined only by the correlation length ξ, and not by the size of the system R. This agrees with the results in Ref. [13]. It can be understood that the number of correlated particles is determined by ξ. Particles beyond the correlation length ξ are uncorrelated and do not contribute to the susceptibility value. However, in the limit of small size $R\ll \xi$, the second-order baryon number susceptibility approaches the system size ${\chi }_2\to R^2/\sqrt{K}$. Within this limit, the susceptibility of the system is strongly enhanced by increasing the system size. This is called acceptance dependence, which was proposed [41, 42] and observed experimentally [43]. This can be regarded as another indicator of long-range correlation. When the susceptibility obtained within a scale R is smaller than the correlation length ξ, all detected particles are correlated with each other. An increasing size R indicates that more particles are correlated and contribute to the susceptibility.

Higher-order susceptibilities are important observables for searching the QCD critical point because they are more sensitive to the correlation length, and their signs are more obvious than the magnitudes considering the complex system in relativistic heavy-ion collisions [13, 37]. The fourth-order susceptibility is given by: ${\chi }_4=\frac{{\partial }^{4}P}{\partial {\mu }^4}={\left(\frac{V}{T}\right)}^4\left[\langle n_{\text{B}}^4\rangle -3{\langle n_{\text{B}}^2\rangle }^2\right]\mathrm{,}$ (9) where the four-point correlation function can be calculated using Eq. (1): $\begin{array}{l}\langle n_{\text{B}}\left(x_1\right)n_{\text{B}}\left(x_2\right)n_{\text{B}}\left(x_3\right)n_{\text{B}}\left(x_4\right)\rangle \\ =-6{\lambda }_4{T}^3{\displaystyle \int }{\text{d}}^{3}z{\displaystyle \prod _{i=1}^4}{D}_{zi}+12{\lambda }_3^2{T}^3{\displaystyle \int }{\text{d}}^{3}u{\text{d}}^{3}v{D}_{u1}{D}_{u1}{D}_{v3}{D}_{v4}{D}_{uv}\\ +T^2\left(D_{12}{D}_{34}+D_{13}{D}_{24}+D_{14}{D}_{23}\right),\end{array}$ (10) where the two-point correlator is $\langle n_{\text{B}}\left(x_i\right)n_{\text{B}}\left(x_j\right)\rangle \equiv T{D}_{ij}$. As this work focuses on the susceptibility, the disconnected diagrams $T^2\left(D_{12}{D}_{34}+D_{13}{D}_{24}+D_{14}{D}_{23}\right)$ are canceled because of the subtraction term in Eq. (9): The spatial averages of the four-point correlation function Eq. (10) is evaluated using a finite volume. Appendix 5 provides a more detailed description. Integration could not be performed analytically or evaluated numerically in this study.

Parameterization and discussion

To evaluate the various orders of cumulants (or susceptibilities) near the QCD critical point, the behavior of the correlation length ξ and coupling constants λ₃ and λ₄ is considered. Lattice QCD suffers from sign problems at large chemical potentials [12] and the results of effective theories based on QCD depend on the input parameters. However, a system near the QCD critical point is believed to belong to the same universality class as the three-dimensional (3D) Ising model [44-46]. Therefore, the equations of state and coupling constants near the QCD critical point can be mapped using the 3D Ising model.

Specifically, in the conserved dynamic model [26-29], the coupling constants are related to the net-baryon susceptibility in the zero-mode limit: $\begin{array}{l}{\kappa }_2=\frac{V}{T}\langle n_{\text{B}}^2\rangle =m^{-2}\mathrm{,}{\kappa }_3={\left(\frac{V}{T}\right)}^2\langle n_{\text{B}}^3\rangle =-2{\lambda }_3{m}^{-6}\mathrm{,}\\ {\kappa }_4={\left(\frac{V}{T}\right)}^3\left[\langle n_{\text{B}}^4\rangle -3{\langle n_{\text{B}}^2\rangle }^2\right]=6\left[2{\left({\lambda }_3/m\right)}^2-{\lambda }_4\right]m^{-8}\mathrm{.}\end{array}$ (11) The net-baryon susceptibilities were mapped from the 3D Ising model: ${\kappa }_n=T^{4-n}{\kappa }_n^{\text{Ising}}\mathrm{,}$ (12) where the mapping coefficient is non-universal and $T^{4-n}$ is chosen according to the dimensions of the baryon susceptibility. In the equation of state for the 3D Ising model, the magnetization M of the Ising system is a function of the reduced temperature r and external magnetic field h and can be parameterized as [22]: $\begin{array}{c}M=M_0{\tilde{R}}^{1/3}\theta \mathrm{,}\\ r=h_0\tilde{R}\left(1-{\theta }^2\right)\mathrm{,}\\ h={\tilde{R}}^{5/3}\left(3\theta -2{\theta }^3\right)\mathrm{.}\end{array}$ (13) where the various orders of Ising susceptibility can be obtained by ${{\kappa }_{n+1}^{\text{Ising}}=\frac{{\partial }^{n}M}{\partial h^n}|}_r\mathrm{,}n=\mathrm{1,2,3,}\cdots$ (14) where $\tilde{R}$ is the distance to the critical point in the phase diagram and θ is the corresponding angle with respect to the crossover curve. M₀ and h₀ are normalization constants and $M_0\simeq \mathrm{0.605,}{h}_0\simeq 0.394$. In addition, the reduced temperature r and external magnetic field h are related to the temperature T and baryon chemical potential μ of the QCD system through linear mapping [23, 24, 29]: $\begin{array}{l}\frac{r}{\text{Δ}r}=-\frac{\mu -{\mu }_{\text{c}}}{\text{Δ}\mu }\mathrm{,}\\ \frac{h}{\text{Δ}h}=\frac{T-T_{\text{c}}}{\text{Δ}T}\mathrm{.}\end{array}$ (15) where T_c and μ_c are the critical temperature and the chemical potential of the QCD critical point, respectively. The critical point of the 3D Ising model is located at $r=h=0$. The mapping does not constrain the location of the QCD critical point $\left(T_{\text{c}}\mathrm{,}{\mu }_{\text{c}}\right)$, which is typically treated as a free parameter. The behavior of the critical fluctuations is determined by the position relative to the critical point in the QCD phase diagram, and not by the absolute values of T and μ. Thus, the location of the QCD critical point $\left(T_{\text{c}}\mathrm{,}{\mu }_{\text{c}}\right)$ does not affect the qualitative behavior of $\kappa {\sigma }^2$ and is set as $\left(T_{\text{c}}\mathrm{,}{\mu }_{\text{c}}\right)=(0.145\text{ GeV}\mathrm{,0.16}\text{ GeV})$ in this study. $\text{Δ}T$ and $\text{Δ}\mu$ are the corresponding widths of the critical region and $\text{Δ}h$ and $\text{Δ}r$ are those in the Ising model. These are non-universal parameters and are set as $\text{Δ}T=T_{\text{c}}/\mathrm{8,}\text{Δ}\mu =0.1\text{ GeV}\mathrm{,}\text{Δ}r={\left(5/3\right)}^{3/4}\mathrm{,}\text{Δ}h=1$ in Ref. [29]. By mapping, Eq. (14) and Eq. (15), the net-baryon susceptibilities on the QCD phase diagram ($T\mathrm{,}\mu$) are constructed from those on the $(r\mathrm{,}h)$ plane. Therefore, the coupling constants can be obtained using Eq. (11):

This work is dedicated to understanding the sign of kurtosis in the dynamics of the conserved net-baryon near the QCD critical point. The coupling constants are constructed by mapping from the 3D Ising model, as in Refs. [26-29]. Figure 1 shows the coupling constants with the temperature T=0.138 GeV, below the phase transition curve. The fourth-order net-baryon susceptibility constructed using the Ising model has a small negative value on the crossover side (small μ) and becomes positive on the first-order side (large μ). As expected, the coupling constant $\sqrt{K}/m\equiv \xi$ exhibits a peak close to the critical chemical potential μ_c=0.16 GeV. Because the constants plotted with temperature T<T_c, λ₃ and λ₄ have negative and positive values, respectively.

Fig. 1Full-screen View

(Color online) The coupling constants of the effective potential near the critical point, mapped from the 3D Ising model

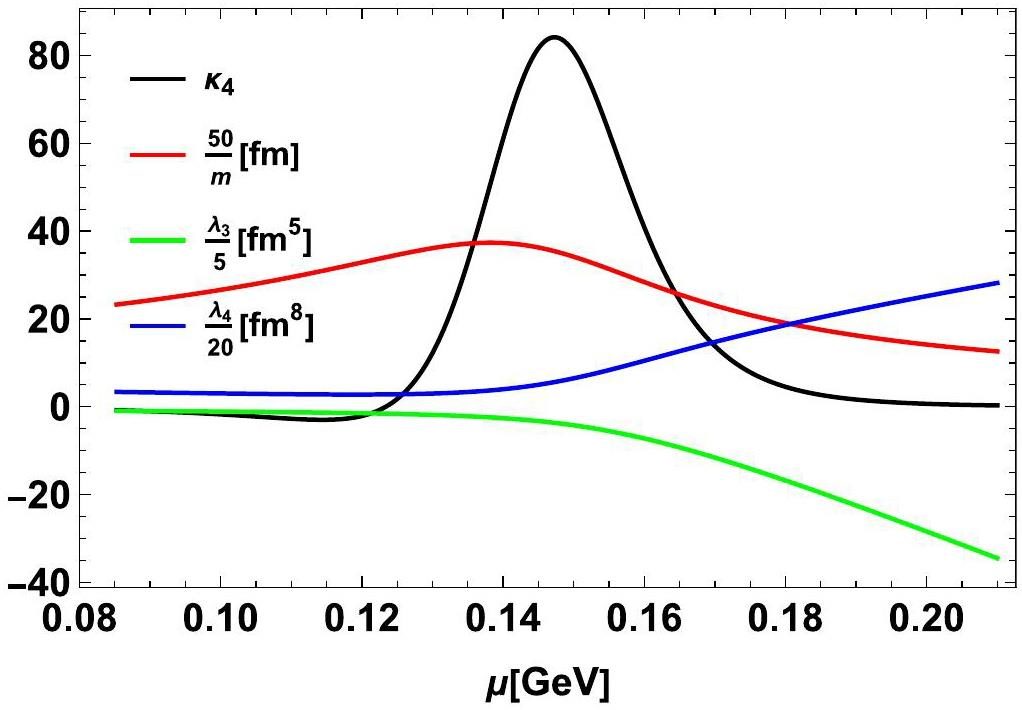
The second-order (4) and fourth-order (9) susceptibilities within the finite system were evaluated using a Monte Carlo integration algorithm. Because the knowledge of the diffusion constant D and surface tension K near the QCD critical point is limited, they are set to D=1 fm^-1 and K=1 fm⁴, respectively, and the evolution time t is chosen as t=10 fm. These were treated as free parameters. As shown in Eq. (7), the dynamical factor $\exp \left[-Dt{p}_i^2\left(K{p}_i^2+m^2\right)\right]$ was introduced to mimic the dynamical effects in the linearized limit [40]. This is far from the realistic dynamic critical fluctuations, which require a full simulation of the dynamic evolution equation [26-29]. In this context, the effect of this dynamic factor is the suppression of the magnitude of the correlation function Dij. As shown below, the sign of $\kappa {\sigma }^2$ is determined by the magnitude of Dij in the model. Different values of D and/or t in this model only affect the critical value of the system size R to obtain the dip behavior of kurtosis. Figure 2 shows the second-order susceptibility within a finite system as a function of the radius of the system, with different correlation lengths ξ. It can be observed that χ₂ increases monotonically with increasing size R. For a large correlation length $\xi =5.0\text{ fm}$, χ₂ strongly depends on the size, particularly $R\ll \xi$, indicating the acceptance dependence of the critical fluctuations in the experiments. However, if the system is significantly larger than the correlation length (e.g., $\xi =2.5\text{ fm}$), χ₂ approaches a constant value when the size is sufficiently large.

Fig. 2Full-screen View

(Color online) Second order baryon susceptibility χ₂ as a function of the radius of the coordinate space R. Different colors represent the input correlation length $\xi =2.5\text{ fm}$ and 5 fm

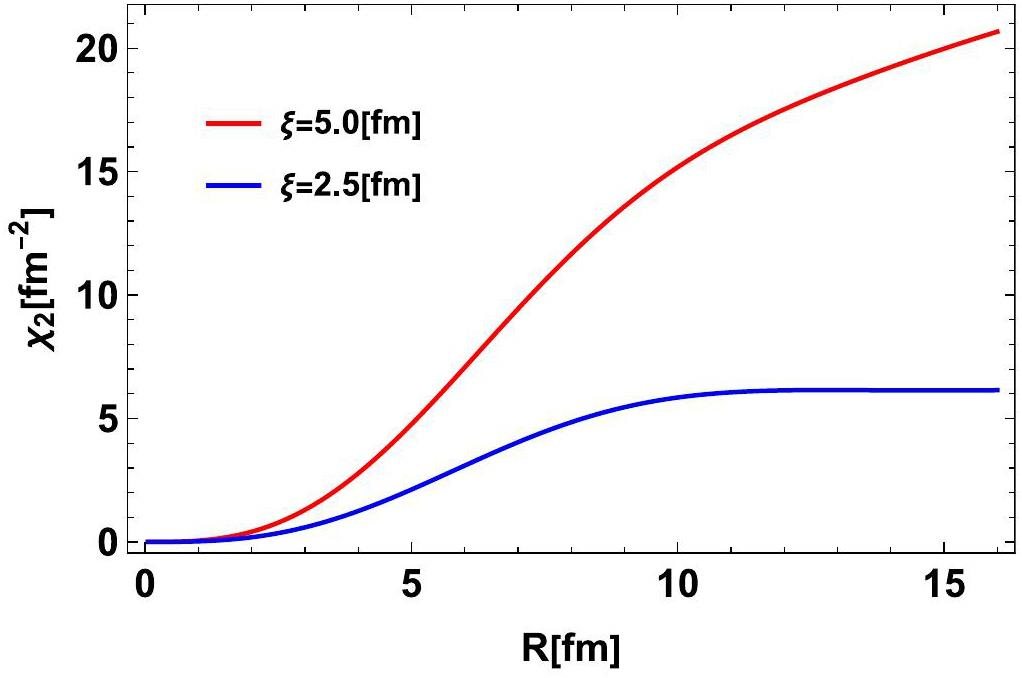
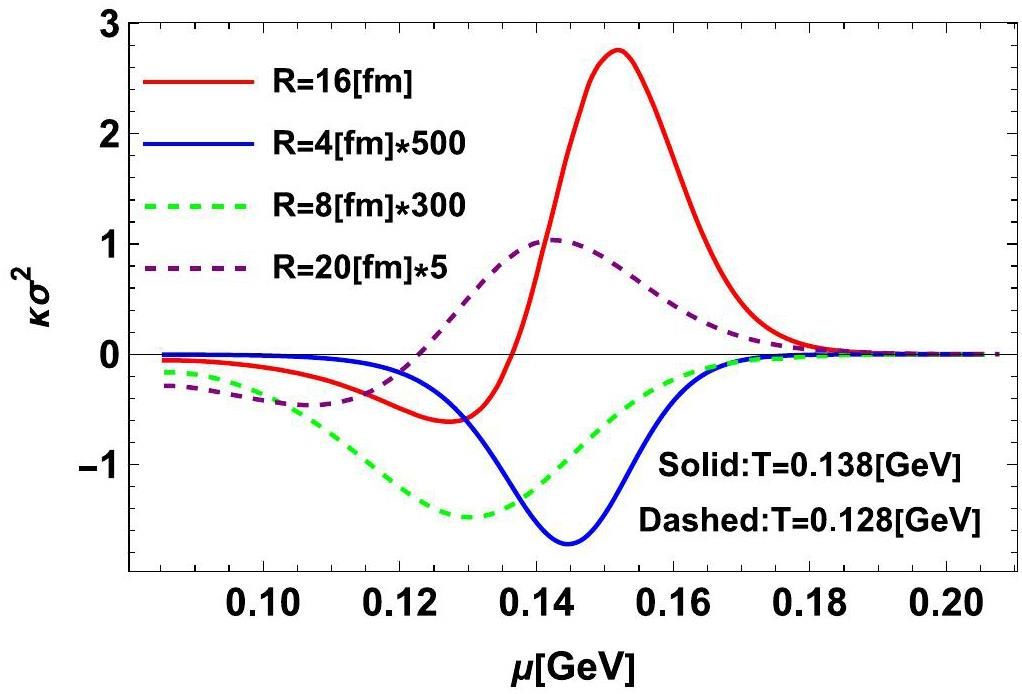
Figure 3 presents the kurtosis $\kappa {\sigma }^2$ of the net-baryon within a finite system near the QCD critical point¹. At the limit of a large system (for example, R=16 fm in Fig.3), $\kappa {\sigma }^2$ behaves non-monotonically as a function of the baryon chemical potential μ and presents a negative value on the crossover side (small μ) and a positive value on the first-order side (large μ). This is consistent with an ideal infinitely large system [14], as shown in Eq. (8) that the second order susceptibility approaches the ideal case ${\chi }_2\to {\xi }^2$. However, $\kappa {\sigma }^2$ within a finite system (for example, R=4 fm in Fig. 3) becomes negative and presents a dip behavior near the critical point. As pointed out in Fig. 2, the correlation Dij or the susceptibility strongly depends on the size of the system and has a small value when the system is small. As shown in Eq. (10), the fourth-order coupling term with λ₄ presents a negative contribution with four terms of correlators Dij, while the third-order coupling term with λ₃ contributes positively with five correlators Dijs. In the case of a small-magnitude correlator Dij, the fourth-order coupling term with λ₄ dominates and the four-point correlation function $\langle n_B^4\rangle$ can be negative, resulting in a negative $\kappa {\sigma }^2$ near the QCD critical point. In addition, Fig.3 also shows that the system is further away from the critical point (T_c=0.145 GeV) with a temperature T=0.128 GeV. Compared with the case of T=0.138 GeV, the critical signal is weaker, and the magnitude of Dij is smaller. The magnitude of $\kappa {\sigma }^2$ is smaller (purple curve), and it is easier to achieve a negative kurtosis (R=8 fm). This means that it is still possible to flip the sign of kurtosis by tuning the system size R, even with different critical signal strengths. Note that $\kappa {\sigma }^2$ with R=4 fm in Fig. 3 was multiplied by a factor of 500 for illustrative purposes, which is a relatively small value compared to the case of R=16 fm. It is notable that the model employed in this work is an ideal system, and the quantitative magnitude of the “dip” in the small system size requires more realistic modeling in heavy-ion collisions. The QGP fireball created in relativistic heavy-ion collisions is a fast-expanding finite-size system, and several factors contribute to the final observables of the QCD critical point. It is typically believed that the dynamical effects ($\sim {\xi }^z$, where the dynamical critical exponent z~3 for the QCD critical point) induced by the expanding effects dominate the finite-size effects (the finite size of the fireball). This motivated the study of dynamic modeling near the QCD critical point in relativistic heavy-ion collisions [30-35]. However, only a part of the system contributes to the final observables, considering the finite acceptance window of the detector in the experiments. The net-proton multiplicity fluctuations in Beam Energy Scan phase I have already shown acceptance dependence, and the fluctuations with a small acceptance window deviate from those with a larger acceptance window [43]. Therefore, comprehensive dynamic modeling of the critical fluctuations with a realistic detector acceptance window as well as the finite size of the QGP fireball is essential for comparison with the experimental measurement in the upcoming Beam Energy Scan phase II.

Fig. 3Full-screen View

(Color online) Kurtosis of the net-baryon $\kappa {\sigma }^2$ within finite system near the QCD critical point. Different colors correspond to the ones with the radius of the coordinate space R=4 fm, 8 fm, 16 fm, 20 fm, respectively. Solid curves are obtained with a temperature (T=0.138 GeV) closer to critical temperature Tc, and the dashed curves are with a temperature (T=0.128 GeV) further away from Tc. The factor after the unit means the kurtosis has been multiplied for illustrative purposes (e.g., blue curve corresponds to $500\kappa {\sigma }^2$)

Conclusion and Outlook

In summary, the signs of higher-order multiplicity fluctuations play an important role in exploring QCD phase transitions. In a simulation of the dynamics of the conserved net-baryon density near the QCD critical point, it was found that the kurtosis of the net-baryon is typically negative [26-29]. To understand negative kurtosis in conserved dynamical models, this study focuses on the sign of the kurtosis obtained within a finite system, which corresponds to only part of the system being detected. It was found that the multiplicity fluctuations (or magnitude of correlation function D_ij) are suppressed with decreasing system size when the scale of the system is small comparing correlation length. This property, called acceptance dependence, results in a negative contribution from the fourth-order coupling term λ₄ (proportional to $\sim D_{ij}^4$), which dominates the fourth-order susceptibility χ₄ when the detected system size is small. However, another term with λ₃ (proportional to $\sim D_{ij}^5$) in χ₄ makes a positive contribution that is much smaller than that with λ₄. In the dynamic models of the conserved net-baryon, the kurtosis is obtained only with part of the system, and this finite number of particles is detected; the corresponding kurtosis can behave with a dip near the critical point instead of a peak.

This work focuses on the finite-size effects on the sign of kurtosis within a static system without considering dynamic modeling in a realistic experimental context. Based on the dynamical model near the QCD critical point (e.g., based on hydrodynamic model [26-29] or transport model [47-52]), the realistic finite size of the QGP fireball, as well as the finite detector acceptance window, requires proper consideration in future studies of higher-order net-proton multiplicity fluctuations. In addition, such an analysis can be performed using other possible observable critical points, such as the light nuclei yield ratio [53-56].