Introduction

The illicit proliferation of special nuclear materials (SNMs) enables terrorists to acquire weapons of mass destruction. The conventional scanning systems deployed at national borders typically use X-rays to obtain the density distribution of the scanned object and cannot differentiate SNMs from other high-density metals, such as lead, tungsten, and bismuth. Therefore, efforts have been made to realize on-site, nondestructive identification of SNMs. SNM detection methods can be categorized as passive and active. Passive interrogation detects naturally emitted γ-rays or neutrons from the radioactive decay of SNMs [1-4]. However, this technique is unsuitable for detecting shielded objects because the intensities and energies of the spontaneous radiation are relatively low. In contrast, active interrogation employs an external radiation source and effectively overcome such limitations. The response was optimized by adjusting the energy and intensity of the interrogation radiation source. The primary radiation sources for interrogation were neutrons, muons, and photons. Neutron fission reactions with fissile materials characterized by both high penetrability and cross sections have been extensively researched [5-8]. However, in the context of radiation safety, neutrons are difficult to handle and the neutron capture reactions induced in nearly all materials generate an additional radiation background, which hinders signal discrimination. Furthermore, neutron-generation devices such as spallation neutron sources or nuclear reactors typically require large areas and are thus unsuitable for widespread applications. Muon scattering tomography technology based on cosmic-ray muons for detecting SNMs has also been extensively investigated [9-11]. However, muon-generation devices are complex, expensive, and unsuitable for broad usage. Photons are often preferred over neutrons and muons because of their lower induction of radioactivity in most materials. To date, photon-induced reactions can be used to detect explosives [12] and identify SNMs based on nuclear resonance fluorescence(NRF) [13-15]. However, owing to the narrow resonance width of NRF reactions (∼meV), γ-ray sources with high spectral and temporal intensities are required to obtain sufficient signals within a reasonable irradiation time. These limitations necessitate the development of photofission-based SNM detection methods.

Photofission is the process in which a fissile nucleus splits into two fragments (light and heavy) after absorbing an incident photon, accompanied by the instantaneous emission of prompt neutrons and prompt γ rays. The radioactive fragments decay into stable nuclides, releasing delayed γ rays. As the thresholds for most photonuclear reactions are typically above 7 MeV, background radiation from photofission is relatively low. Currently, most research on identifying SNMs based on photofission has focused on ^235,238U and ²³⁹Pu. These studies identified and quantitatively analyzed certain nuclides [16-20] and constructed an analysis algorithm for the delayed γ energy spectrum of SNMs in simulations [21, 22]. Additionally, the use of delayed γ-ray ratios for SNM differentiation, which was first proposed by Hollas et al. [23] has received considerable attention. Finch et al. [24] utilized three high-purity germanium (HPGe) detectors to distinguish between ^235,238U and ²³⁹Pu. Nevertheless, the high cost and neutron damage of HPGe detectors make them vulnerable to fission reactions, hindering the repeated implementation and practical applications of this method. Therefore, a detection method that can be widely applied to isotopes is of great significance. Methods for identifying a broader range of SNMs including ^233,235,238U, ^239-242Pu, and ²³²Th, are required. The existence and identification of additional isotopes of U, Pu, and Th must be considered to effectively manage SNMs.

The rapid development of high-intensity γ-ray facilities in China has presented new opportunities for photofission research. Recently, the Shanghai Laser Electron Gamma Source beamline at the Shanghai Synchrotron Radiation Facility was completed and is in operation, providing additional platforms for fields such as photonuclear physics [25, 26]. Moreover, laser-driven γ ray sources can reach extremely high intensities and offer a wide range energies. γ rays with intensities above 10¹⁹/s (10⁸/shot, above 4 MeV) were generated using the 200 TW laser facility at the Compact Laser Plasma Accelerator (CLAPA) Laboratory [27], where significant photonuclear research has been conducted [28-33]. Laser-driven γ-ray sources can be miniaturized and are well-suited for widespread use in customs and railway security. These emerging quasi-monoenergetic γ-source devices [34, 35] and high-intensity γ-ray facilities provide broad application prospects for photofission research and SNM identification.

In this work, we systematically investigated methods to identify the elements and isotopes of SNMs by detecting delayed γ-rays from photofission fragments. Geant4 [36] simulations were performed on the photofission of SNM isotopes, including ^233,235,238U, ^239-242Pu, and ²³²Th. To identify the potential fragment ratios suitable for SNM identification, the mass and charge yield distributions of photofission fragments induced by monochromatic γ sources and their delayed γ spectra recorded by an HPGe detector were obtained. The yields of fission fragments were calculated according to the delayed γ spectrum. The ratios of three high-yield fission fragments, ¹³⁸Cs, ⁹⁴Y, and ⁸⁹Rb, were selected as identification values to differentiate between the SNMs. Additionally, the dependence of the fragment ratios on incident γ-ray energy was investigated. The count rates of delayed γ rays with energies above 3 MeV recorded by a LaBr₃ detector were calculated and used to rapidly detect the presence of nuclear material within the scanned object. This comprehensive approach provides better understanding and control of SNMs.

Method

The fission fragments of different fissile nuclei exhibited variations, and the charge and mass yield distributions shifted towards larger masses as the mass of the fissile nucleus increased. Hence, the yield ratios of the fission fragments may be employed as identification parameters to distinguish between different fission nuclei. In reality, the fragment yields must be calculated from the detected delayed γ-ray spectra according to parameters such as the delayed γ-ray intensity, detection efficiency, and attenuation in the target. Consequently, simulations of delayed γ-ray detection are necessary to obtain insight into the identification of SNMs.

The Geant4 photofission module developed in our laboratory was employed to simulate the detection of delayed γ-rays from photofission fragments [37, 38]. In this module, the mass and charge yield distributions of the fission fragments are based on the Bohr-substitution Gorodisskiy model [38, 39]. The model describes the characteristics of photofission reaction products from actinides, such as prompt neutrons, prompt photons, and fission fragments. The results have been extensively benchmarked against available experimental data and showed good agreement. In addition, the G4RadioactiveDecay physics was implemented in our code to model the delayed γ emissions from fission fragments and simulate the photofission process of SNMs in this study.

An illustration of the simulation setup is shown in Fig. 1. The monoenergetic γ source or the bremsstrahlung γ source was obliquely incident at 45° on eight types of 1-cm-thick SNM targets, resulting in photofission reactions. A LaBr₃ detector with a size of 8 cm × 16 cm was placed perpendicular to the γ beam and parallel to the target to detect γ rays. Owing to the high detection efficiency of LaBr₃ detectors, the count rate of fission γ rays above 3 MeV was obtained, which instantly indicated the presence of SNMs. HPGe detectors, which have high resolution, are suitable for measuring and analyzing the peak structure of complex delayed γ-spectra. Five minutes after the fission reaction, an HPGe detector with a relative efficiency of 80% was used to detect the delayed γ-rays from the fragments. The counts of characteristic γ peak of most high-yield product nuclides was determined using the delayed γ spectrum of photofission products measured by the HPGe detector. The yield of the fission fragments was calculated using γ ray counts, detection efficiency simulations, and self-absorption corrections. The yield ratio, which serves as an identification characteristic for differentiating SNMs, was obtained by screening the most differentiated identification values for each SNM and their uncertainties. Furthermore, the count rates of delayed γ rays with energies above 3 MeV were used to identify nuclear materials.

Fig. 1Full-screen View

(Color online) Schematic diagram for the offline detection of delayed γ rays from the radioactive decay of SNM photofission fragments. Either (1) a monoenergetic γ source or (2) a bremsstrahlung source generated from the interaction between the electron beam and Ta was used for the simulations. The γ-ray source irradiates the target, which induces photofission of the SNMs to be inspected. The resulting radioactive fission fragments emit γ rays during decay. An HPGe or a LaBr₃ detector records the characteristic γ-delayed peaks from fission fragments in a low-background lead chamber

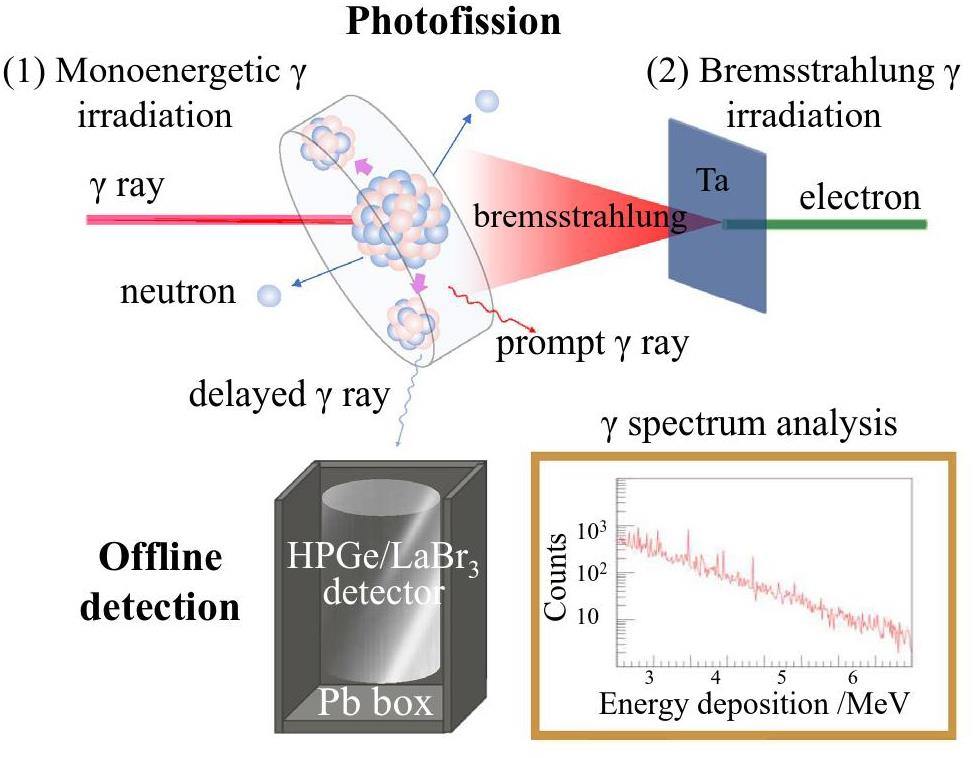
The fragment yields are determined by factors such as the incident photon energy, beam intensity, target nucleus number, and photofission cross section. The fission of a heavy nucleus predominantly produces 600–800 different isotopic fragment species. Therefore, fission fragments with high yields, measurable half-lives, and significant counts of delayed γ rays must be carefully selected. To optimize the yields of the fission products, considering information on the photofission cross section in TENDL-2019 [40], a monoenergetic γ source with energies around 14 MeV was selected because it offered almost the maximum cross sections for uranium, plutonium, and thorium. 10⁹ incident γ-rays were employed for the isotopes of uranium, plutonium, and thorium in Geant4 simulations. Regarding the measurable half-lives, the minute to hour order was suitable for detection. In conclusion, by identifying the characteristic values presented herein, we determined the yield ratios associated with each unique fission nucleus that was significantly different from other fission nuclei.

Results

3.1

Mass and Charge Yield Distribution

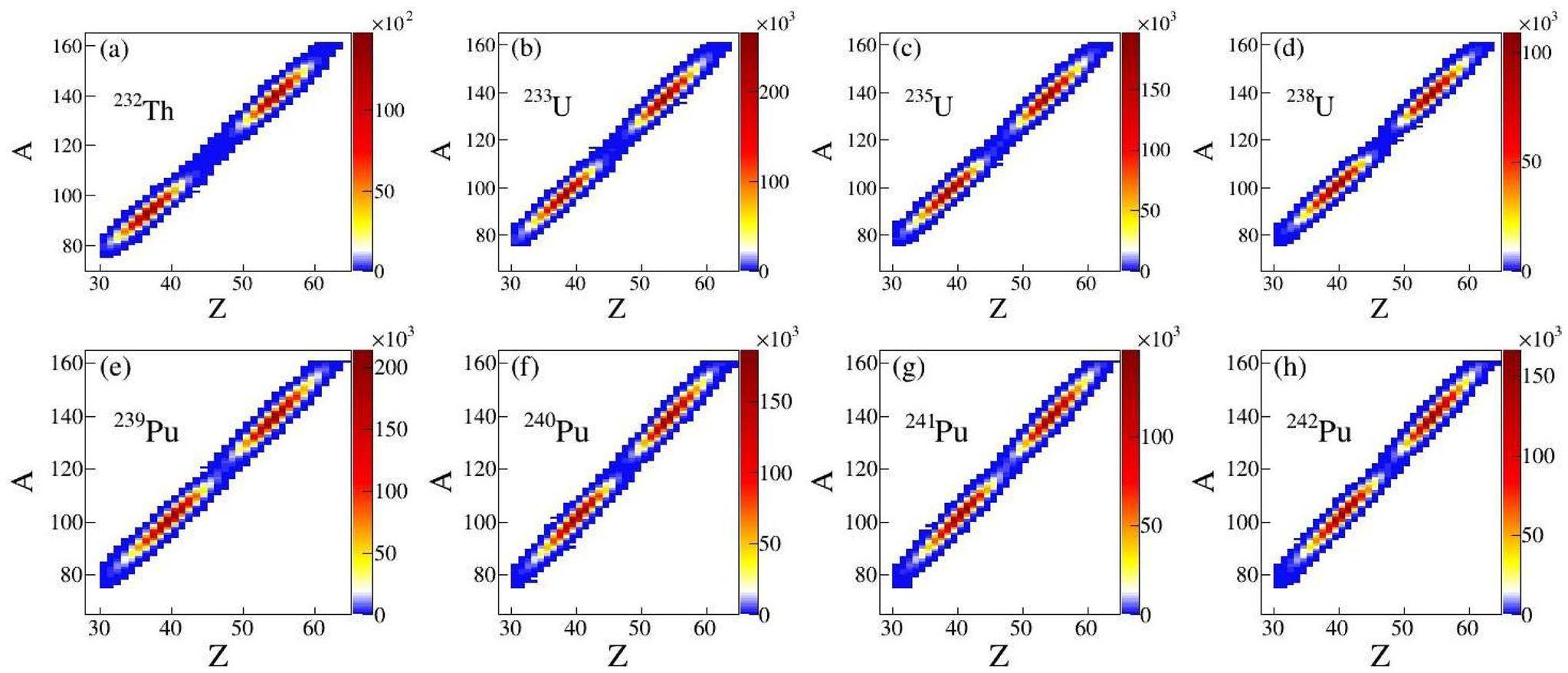
Figure 2 shows the mass and charge yield distributions of the fission fragments from the eight selected SNMs at an incident γ-ray energy of 14 MeV. The number of neutrons and protons in the fission fragments were 40–90 and 25–65, respectively. Typically, the nuclides located in the two peak areas of the figures represent the high-yield fragments; the proton numbers of lighter fragments are primarily concentrated within 36–46, while those of heavier fragments are concentrated within 50-60. Differences in the high-yield fragments among U, Pu, and Th were observed (Fig. 2). Figure 2(b-d) show that the overall fragment yield decreases with increasing target mass numbers for the isotopes of ^233,235,238U. For ^239-242Pu isotopes, the decrease in fragment yields with the target mass number is less linear, as shown in Fig. 2(e-h). Moreover, the mass and charge yield distributions of the eight selected isotopes exhibited discrepancies. These features indicate that fragment yields and ratios can be used to discriminate between SNMs. After a comprehensive analysis of the mass and charge yield distributions, a preliminary candidate list of high-yield fragments that might be suitable for use in further SNM discrimination was identiified: ⁸⁶Se, ⁸⁹Rb, ⁹⁴Y, ⁹⁵Y, ⁹⁸Y, ¹⁰²Nb, ¹²⁹Sb, ¹³²I, ¹³²Cs, ¹³⁸Cs, and ¹³⁸Xe. These high-yield fragments were selected as preliminary screening results to aid the subsequent search for characteristic peaks in the complex delayed γ spectrum and served as a basis for choosing the measurement time of the HPGe detector.

Fig. 2Full-screen View

(Color online) Mass and charge yield distributions of fission fragments of ^233,235,238U, ^239-242Pu, ²³²Th

3.2

Delayed γ-ray Spectrum

The typical delayed γ-ray spectra from the fission fragments of ²³³U, ²³⁹Pu, and ²³²Th recorded by the HPGe detector are shown in Fig. 3. Gamma spectra with energies below 511 keV are complex because of the characteristic peaks from multiple sources and thus, are excluded from the analysis. The data acquisition time was varied from 5 min to 1 h after irradiation. As shown in Fig. 3(a-c), the energies of the delayed γ signals are mostly below 4 MeV. The corresponding characteristic peak counts of the fission fragments range from a few hundred to over a thousand and have good statistical errors within the achievable γ source flux. The detection efficiency of high-energy γ above 4 MeV is low; thus, it is not shown or analyzed in detail.

Fig. 3Full-screen View

(Color online) (a), (b), and (c) are the exemplary full γ ray spectra recorded by the HPGe detector from the fission fragments of the SNM isotopes ²³³U, ²³⁹Pu, and ²³²Th, respectively. The black dashed lines denote the peaks of the characteristic delayed γ signals for the candidate high-yield fission fragments. (d), (e), and (f) are the magnified views of the spectra of the delayed γ signals from the eight SNM isotopes. The incident γ ray energy is 14 MeV

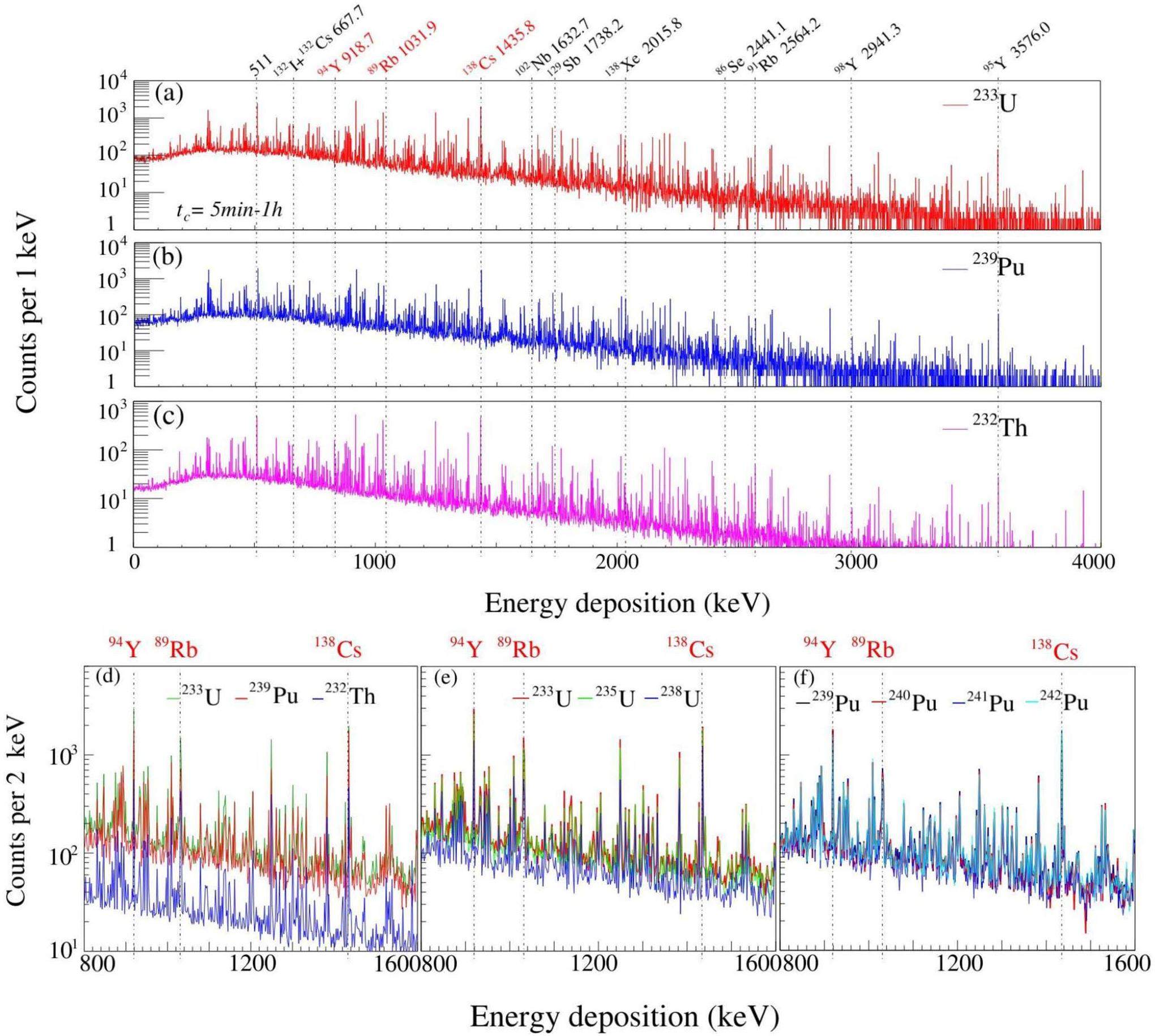
After the initial screening of the candidate fragment nuclides, secondary screening requires a clean source for the characteristic peak (with no other characteristic peaks present within 1 keV) and with significantly different counts for different fission nuclei. For instance, the γ peaks of ¹³²I and ¹³²Cs possess the same energy (667.714 keV) (Fig. 3(d-f)), which is close to the γ peak 668.536 keV of ¹³⁰I. All three fragment nuclides have relatively high yields and non-negligible characteristic peak counts. When the resolution of the detector is insufficient, the overlap of these neighboring peaks affects the fragment yield determination. Furthermore, although the characteristic peaks of the candidate fragments such as ⁹⁵Y and ¹²⁹Sb exhibited relatively large signals, their net counts did not differ significantly among the eight SNMs. Therefore, these characteristic peaks (indicated by black tags at the top of Fig. 3), were not usable as identification fragments. After filtering these unusable candidate signals, three fragments, ⁹⁴Y, ⁸⁹Rb, and ¹³⁸Cs, were identified as usable fragments for SNM discrimination; the corresponding magnified spectra of the signal peaks of the three fragments of the eight SNMs are shown in Fig. 3(d)–(f), respectively. The decay information for the three fragments is presented in Table 1. Furthermore, a detailed analysis of the statistical sources of the characteristic peaks is presented in Table 1 to better reflect the actual detection results. It describes two aspects: the delayed γ peaks of other nuclides with energies close to the characteristic peaks (where the resolution of the detector is insufficient) and some neutron-rich nuclei that undergo β decay to the identified nuclides within the detection time. For example, for the nuclide ⁹⁴Y, which has a half-life of 18.7 minutes, the nuclides ⁹⁴Sr, ⁹⁴Rb, ⁹⁴Kr, and ⁹⁴Br produce ⁹⁴Y through β decay within the detection time. The yield of ⁹⁴Y calculated from the counts of the characteristic peaks is the sum of the yields of these nuclides. The last column of Tab. 1 indicates the productivities of the fragments of interest (the probability of one γ photon generating this nuclide at 14 MeV), which provides a quantitative standard for the high yield of fragments. These nuclides formed three pairs of fragment identification ratios: ⁹⁴Y/⁸⁹Rb, ¹³⁸Cs/⁹⁸Rb, and ¹³⁸Cs/⁹⁴Y, among which the first required the shortest measurement time.

Table 1Full-screen View

Information on the fragment nuclides for identification

Fragments for identification	γ Energy (branch)	Parent nucleus	Half-life	Decay mode(branch)	Productivity (‰)
138Cs	1435.77 keV (76.3%)		32.84 min		0.527812
		138Xe	14.14 min	β-(100%)	0.000222
		138I	6.303 s	β-(100%)	0.000181
		138Te	1.46 s	β-(100%)	0.000018
		138Sb	314 ms	β-(100%)	0.0000002
89Rb	1031.92 keV (63%)		15.39 min		0.451795
		89Br	4.348 s	β-(100%)	0.000067
		89Se	0.41 s	β-(100%)	0.000139
		89Se	1.51 s	β-(100%)	0.000063
		89As	200 ms	β-(100%)	0.000003
94Y	918.74 keV (56%)		18.7 min		0.706307
		94Sr	75.3 s	β-(100%)	0.000120
		94Rb	2.704 s	β-(100%)	0.000241
		94Kr	212.0 ms	β-(100%)	0.000115
		94Br	70.0 ms	β-(100%)	0.000006

Show more

The fragments for identification are the product nuclides finally selected for SNMs identification. The parent nuclei are the fission fragments which decay into the fragments for identification in the detection time. The productivity of fragments for identification is the yield which is obtained by the peak in the γ decay spectrum divided by the total incident γ flux. The productivity of the parent nucleus is the yield obtained from simulation divided by the total incident γ flux. All the productivity values are the data obtained using ²³³U as the reaction target

3.3

Yield Analysis

Considering the differences in the actual detection conditions, such as measurement time variations and interrogation source energy, this study utilized the yield ratio as a convenient and generalized basis for SNM identification. Based on the delayed γ spectra recorded by the HPGe detector, the characteristic γ counts were calculated by subtracting the background±1 keV around the peak from the gross counts. The specific values of the counts and yield ratios are listed in Table 2. The yields were then calculated from the net counts, considering the delayed γ-ray intensity, detection efficiency, and target attenuation. The uncertainties in the yields and their ratios were obtained by performing least-squares fitting of the statistical error of the counts. As shown in Table 2, the net counts of ⁸⁹Rb are lower than those of ⁹⁴Y and ¹³⁸Cs; thus, the relative uncertainty of the yield ratios involving ⁸⁹Rb is higher than that of ¹³⁸Cs/⁹⁴Y.

Table 2Full-screen View

Calculated counts, yield ratios, and associated statistical uncertainty for three pairs of nuclides

Fissile nucleus	Net counts			Yield ratio
	138Cs	89Rb	94Y	138Cs / 89Rb	138Cs / 94Y	94Y / 89Rb
233U	1788	1350	1731	1.168±0.04	0.747±0.03	1.563±0.06
235U	1567	1126	1556	1.324±0.05	0.837±0.03	1.582±0.06
238U	1130	505	776	1.953±0.10	1.207±0.06	1.618±0.09
239Pu	1603	625	1032	2.207±0.10	1.124±0.04	1.963±0.10
240Pu	1506	573	1026	2.416±0.12	1.210±0.05	1.996±0.10
241Pu	1344	487	831	2.509±0.13	1.322±0.06	1.898±0.11
242Pu	1635	500	856	2.906±0.15	1.546±0.07	1.880±0.11
232Th	424	407	325	1.014±0.06	1.067±0.06	0.950±0.06

Show more

The incident γ-ray energy is 14 MeV

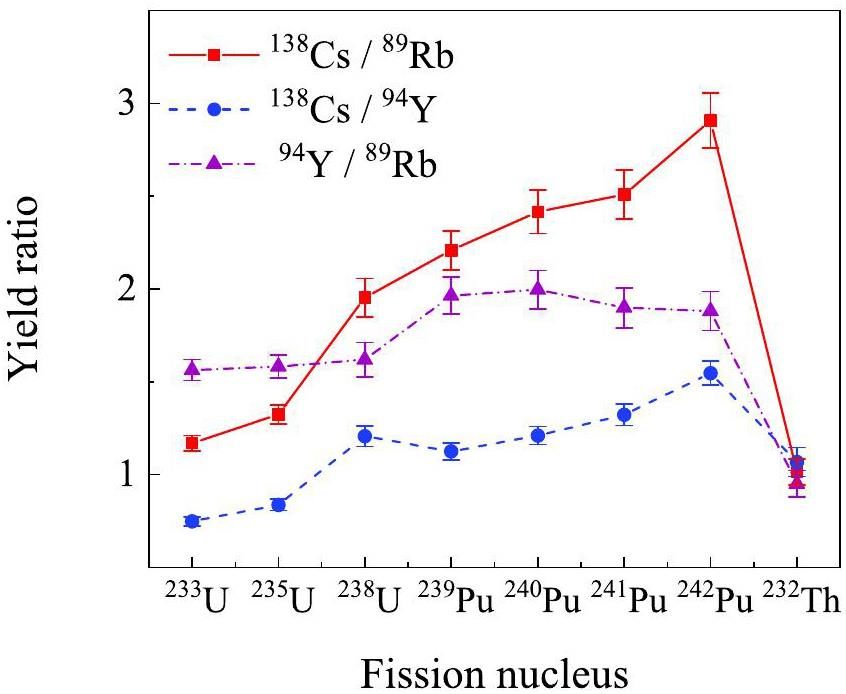
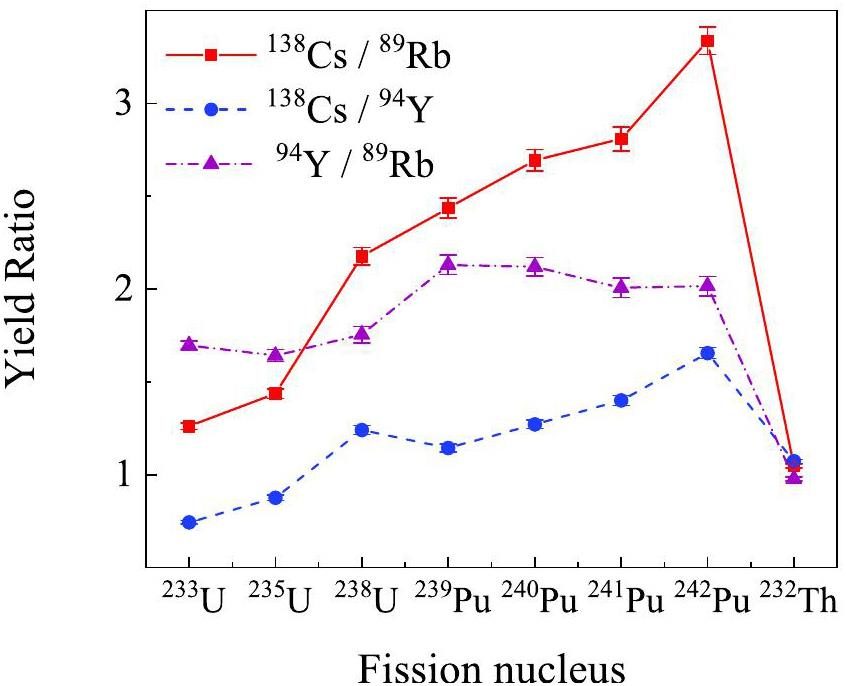
The yield ratios of the three pairs of nuclides comprising the selected fragment nuclides ¹³⁸Cs, ⁹⁴Y, and ⁸⁹Rb were used as indicators to identify the selected SNM isotopes (Fig. 4). The confidence level was calculated to determine whether they could be distinguished from each other within the uncertainty. The yield ratio of ¹³⁸Cs/⁸⁹Rb differs significantly among the SNMs and can be used to distinguish the other seven nuclides except for ^239-241Pu, with a high confidence level above 99.5%. Although the ⁹⁴Y/⁸⁹Rb ratio does not exhibit significance among the isotopes of U, Pu, and Th, it can be used for quick elemental identification. For the isotopes of Pu, the yield ratio of ¹³⁸Cs/⁹⁴Y is the most suitable for isotopic discrimination. This pair of nuclides exhibits the smallest uncertainty in the yield ratio and highlights the most noticeable differences among the fission nuclei, especially for ^239-241Pu. However, the ¹³⁸Cs/⁹⁴Y ratios of ^240,241Pu are similar and cannot be distinguished. When the total number of incident γ-rays increases to 10¹¹, the isotopes of Pu can be distinguished by the yield ratios of ¹³⁸Cs/⁸⁹Rb and ⁹⁴Y/⁸⁹Rb with a high confidence level above 99.5%. Moreover, ¹³⁸Cs has a half-life of 33 min, and thus, requires a longer measurement time.

Fig. 4Full-screen View

(Color online) Fragment ratio yields for the eight SNMs at an incident γ energy of 14 MeV

3.4

High Energy γ Counting Rate

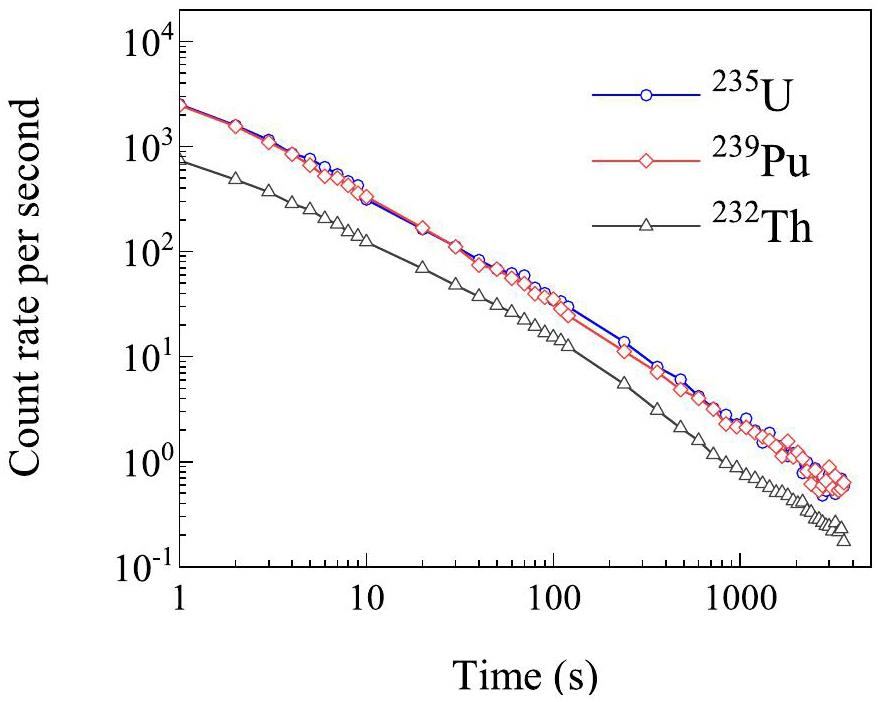
High-energy γ rays above 3 MeV have high penetration capabilities, which have been observed intensively in the aforementioned delayed γ-ray spectra of photofission fragments of SNMs. For common shielding materials such as Pd and Bi, the photofission (or photoinduced spallation) thresholds are typically above 100 MeV, which are much larger than those of SNMs. When irradiated by a γ beam with an energy of approximately 14 MeV, these high-Z benign materials do not undergo photofission, but rather common photonuclear reactions such as (γ, xn). The delayed γ-rays typically released from the reaction residuals are mostly less than 3 MeV. Consequently, delayed γ-rays above 3 MeV from photofission may serve as an effective basis for determining the presence of nuclear materials. The γ counts above 3 MeV resulting from fragment decay were recorded using a LaBr₃ detector. Figure 5 shows the change in the counting rate of the three elements U, Pu, and Th within 1-1000 s of measurement time. As shown in Fig. 5, the count rates of the three SNM elements exhibit differences that are within the error range, which is unsuitable for distinguishing between them. Because nuclear materials primarily generate high-energy γ-rays, these results provide supporting data for identifying whether they are SNMs.

Fig. 5Full-screen View

(Color online) Count rate of delayed γ above 3 MeV recorded by the LaBr₃ detector 1–1000 s after the fission reactions of U, Pu, and Th

Discussion and Summary

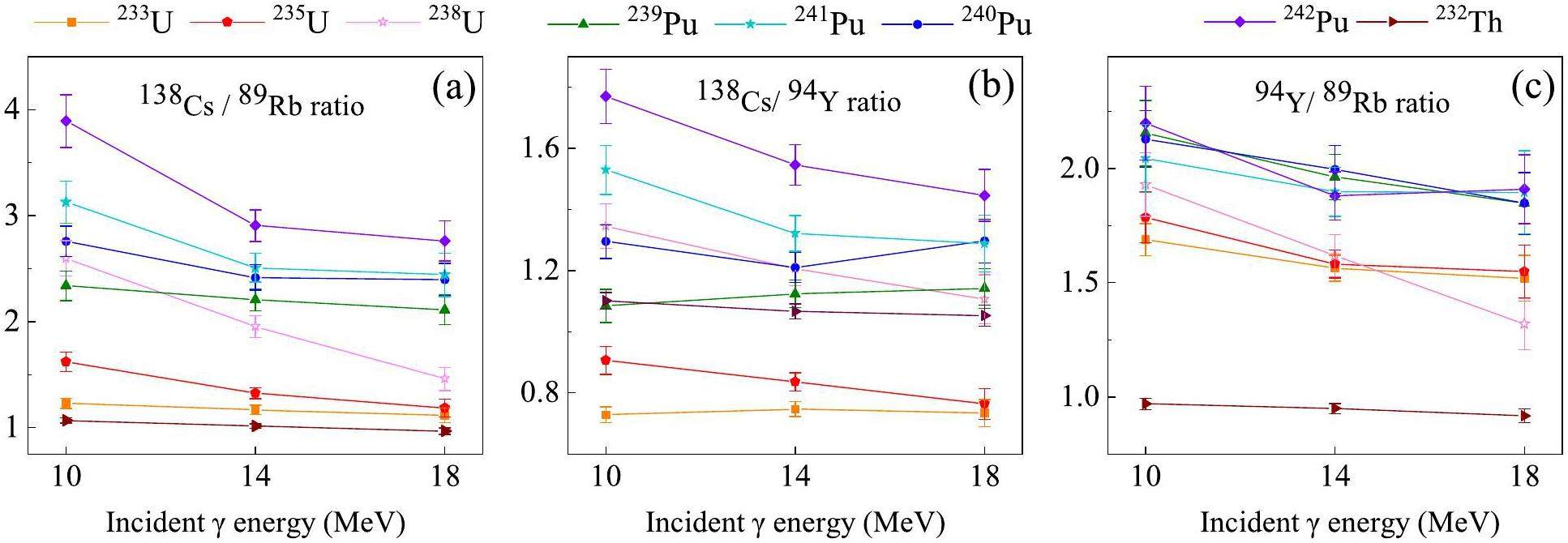
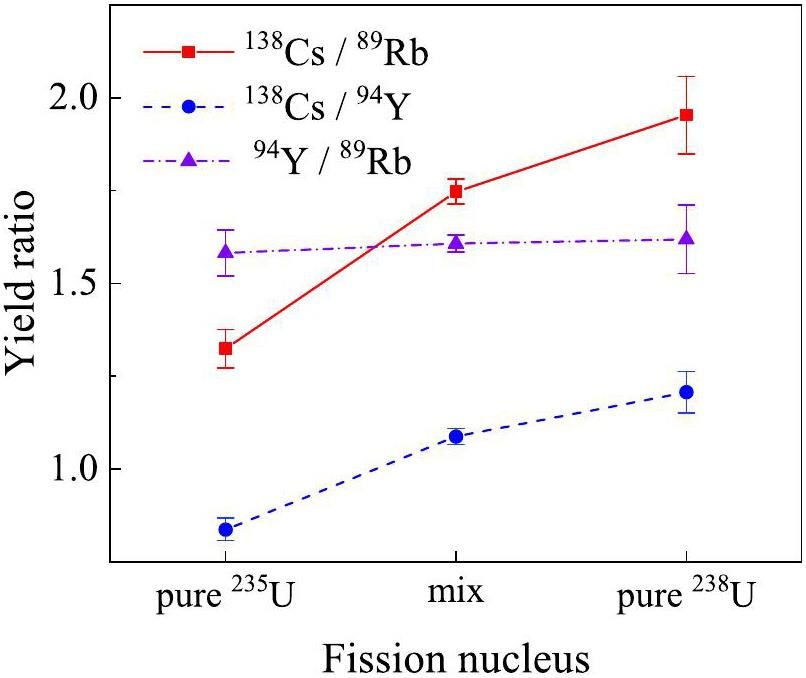
The variation trends of the three pairs of yield ratios at incident photon beam energies of 10 MeV to 18 MeV are illustrated in Fig. 6. The yield ratio is considerably dependent on the fission nucleus. As the energy increases, the yield ratio of ¹³⁸Cs/⁸⁹Rb exhibits diminishing differences across various fission nuclei, while those of ¹³⁸Cs/⁹⁴Y and ⁹⁴Y/⁸⁹Rb demonstrate relatively weak dependence on the incident photon beam energy. Therefore, the method of distinguishing fission nuclei by yield ratio remains effective when γ rays of other energies are incident. When the interrogation source is a bremsstrahlung beam, as illustrated in Fig. 7, the identification method proposed in this paper remains applicable [24]. The yield ratios of the three pairs of nuclides exhibit a good identification effect, and the specific values are consistent with previous results. Because a small proportion of γ rays effectively triggers fission reactions in bremsstrahlung, higher-intensity electrons were used to simulate this process. The yield ratios of the eight nuclides are more distinguishable under beams of higher intensities, leading to improved recognition and higher reliability. Moreover, we discuss the identification under a monoenergetic γ beam of 14 MeV for a mixture of uranium isotopes in nuclear fuel, where ²³⁵U and ²³⁸U accounts for 20% and 80%, respectively. The yield ratios are presented in Fig. 8. Thus, the yield ratios of ¹³⁸Cs/⁸⁹Rb and ¹³⁸Cs/⁹⁴Y can identify the mixture as comprising ²³⁵U and ²³⁸U. Furthermore, the relative abundances of these isotopes depend linearly on the yield ratios. Thus, the detection method remains effective for distinguishing and quantifying isotopes in mixed compositions, thereby extending its applicability to real-world scenarios.

Fig. 6Full-screen View

(Color online) (a), (b), and (c) are the yield ratios corresponding to ¹³⁸Cs/⁸⁹Rb, ¹³⁸Cs/⁹⁴Y, and ⁹⁴Y/⁸⁹Rb, respectively, for the eight SNMs under the incident photon energy of 10-18 MeV

Fig. 7Full-screen View

(Color online) Yield ratios of photofission on SNMs induced by bremsstrahlung from the interaction of 18 MeV electrons with a tantalum target. An electron charge of 10¹³ is used

Fig. 8Full-screen View

(Color online) Yield ratio corresponding to the object to be detected comprising a mixture of ²³⁵U and ²³⁸U

This study provides an identification method for SNM by utilizing the yield ratios of photofission fragments to differentiate among U, Pu, Th, and their isotopes. Photofission was simulated using the self-added photofission module in Geant4, which supplied information on the fission fragments. In the mass and charge yield distribution and decay spectra of fission fragments, the measurable product nuclides with high yields and differences in SNMs were selected. SNMs were identified through the yield ratio of nuclides, in which ^239-241Pu require a higher-intensity γ beam to increase the confidence of the results. The yield ratios of the selected product nuclides at different incident photon beam energies showed good stability and discrimination. The identification method was equally effective in the photofission induced by bremsstrahlung. Hence, the proposed identification method is minimally affected by the light source, providing considerable feasibility and reliability for widespread applications of real SNM detection in the future. In addition, our laboratory successfully detected short-lived isotopes with a half-life of 40 ms, thereby providing an experimental and theoretical foundation for the rapid identification of SNMs in future.