Introduction

L-forbidden M1 transitions have been reported in many odd-mass nuclei, involving pairs of low-lying excited and ground states of single particle nature with the orbital angular momenta differing by two units, such as g_7/2-d_5/2, s_1/2-d_3/2, and p_3/2-f_5/2 [1]. The corresponding orbitals are typically close to each other outside the shell closure. In principle, the M1 transition between them is forbidden. The observation of these non-zero transition strengths indicates the M1 transition of L-forbidden nature beyond a single-particle scheme.

The effective g-factor is necessary to explain the observed magnetic momentum or M1 transition strength. From a physics perspective, such effective operators originate from core polarization and the meson exchange effect [2, 3]. Compared with the spin and orbital terms, the tensor term of the effective M1 operator is almost negligible when a magnetic momentum is produced, as mentioned in Refs. [2-4]. However, in the L-forbidden M1 transition, the tensor term ($[Y_2\mathrm{,}s]$) is essential because it connects the orbitals with Δl = 2.

Meanwhile, the core-excitation, especially when crossing Z = 50 or N = 50 shells [5, 6], increases the number of single-particle orbitals contributing to the M1 transition. However, the quantitative influence of the core polarization effect on the effective g-factor has not yet been elucidated, particularly the tensor term. The L-forbidden M1 transitions in odd-mass isotopes along the N = 82 isotonic chain are potential tools for investigating an effective M1 operator.

The adopted lifetime of the first excited state in ¹³⁹La [7] was determined in previous experiments conducted using the β decay channel from either ¹³⁹La or ¹³⁹Ce. However, because of material limitation, most experiments use two stilbene scintillators to measure the time differences between β-rays and conversion electrons, yielding a half-life of 1.50(10) ns in both cases Refs. [8, 9]. An alternative method is using stilbene and plastic crystals to measure the time difference between conversion electrons and KX-rays, as mentioned in Refs. [10, 11], yielding half-lives of 1.47(6) ns and 1.60(4) ns, respectively. Although the aforementioned experiments employed the best available instruments, the lack (or insufficiency) of energy-resolving power limited the operations of the detectors, accounting for possible uncertainties in the background subtraction. Currently, LaBr₃ detectors are widely used for γ-ray spectroscopy [12-15]. Owing to its excellent time and energy resolution, the LaBr₃ detector together with plastic scintillators is a potential tool for determining the lifetime of the first excited state in ¹³⁹La via β–γ time-difference measurement, an operation that was previously impossible. This novel measurement technique could eliminate the γ-ray background and be applied to investigate complex β-decay channels. Moreover, it could analyze radioactive isotopes such as ¹³³Sn, ¹³⁵Te, and ¹³⁷Xe or determine the lifetime of the first excited states in ¹³³Sb, ¹³⁵I, and ¹³⁷Cs via β–γ time-difference measurement.

This study experimentally performed β–γ measurement to determine the first excited state in ¹³⁹La using LaBr₃ and plastic scintillators. Based on the experimental results, a comprehensive shell-model study on the L-forbidden M1 transition was conducted, focusing on the effect of core-excitation. Experimental details and results are presented in Sect. 2, and the discussion is presented in Sect. 3.

Experimental Setup and Result

The experiment was conducted using the Back-n white neutron beamline [16-21] located at the China Spallation Neutron Source (CSNS) [22]. The Back-n beamline uses backstreaming white neutrons from the spallation target at CSNS, delivering an intense flux of over ~ 10⁷cm^-2s^-1 at the experimental hall, which is 55 m away from the spallation target. With a proton beam power of 100 kW, the Back-n neutron energy ranges from 0.3 eV to several hundreds of megaelectron volts. Three natural Ba targets (71.689% of ¹³⁸Ba) with diameters of 30 mm were placed on the beamline; one target was 3-mm thick, and the others were 5 mm-thick.

During irradiation, ¹³⁹Ba was mainly produced in the ¹³⁸Ba(n,γ) reaction. Given that the β-decay half-life of ¹³⁹Ba is 82.93 ± 0.09 minutes [7], the irradiation time on the beamline was approximately 4 h. After irradiation, the beam was stopped and the targets were displaced to another location for off-beam decay measurement, which lasted 4 h; after which, all the samples were irradiated for 4 h. The procedure was repeated several times. In this experiment, both the irradiation and measurement times were 20 h.

As shown in Fig. 1, for off-line measurement, one plastic scintillator and two LaBr₃ detectors were installed on the samples to detect β and γ rays, respectively. A 2 mm-thick EJ-200 plastic scintillator of size 3 cm×4 cm, coupled with XP2020 photomultiplier tubes (PMTs), was used. The crystal of each LaBr₃ has a diameter of 2 in (50.8 mm) and length of 3 in (76.2 mm). The signal from each LaBr₃ crystal was captured using Hamamatsu PMT R13089, whose anode output has a typical rise time of 2 ns, suitable for fast-timing measurement. The signals from all three detectors were transmitted to a Pixie-16 module from XIA LLC, which is a 14-bit 500 MHz Digital Pulse Processor [23]. To improve the time resolution, a CFD algorithm was applied to detect the zero-crossing of a pulse by subtracting the scaled and delayed copies of the fast-filter pulse in the general-purpose digital data acquisition system (GDDAQ) developed by Peking University. Detailed information on GDDAQ and related CFD logic can be obtained in Ref. [23],

Fig. 1Full-screen View

(Color online) Experimental setup, including two LaBr₃ detectors and one plastic scintillator coupled with a XP2020 photomultiplier tube

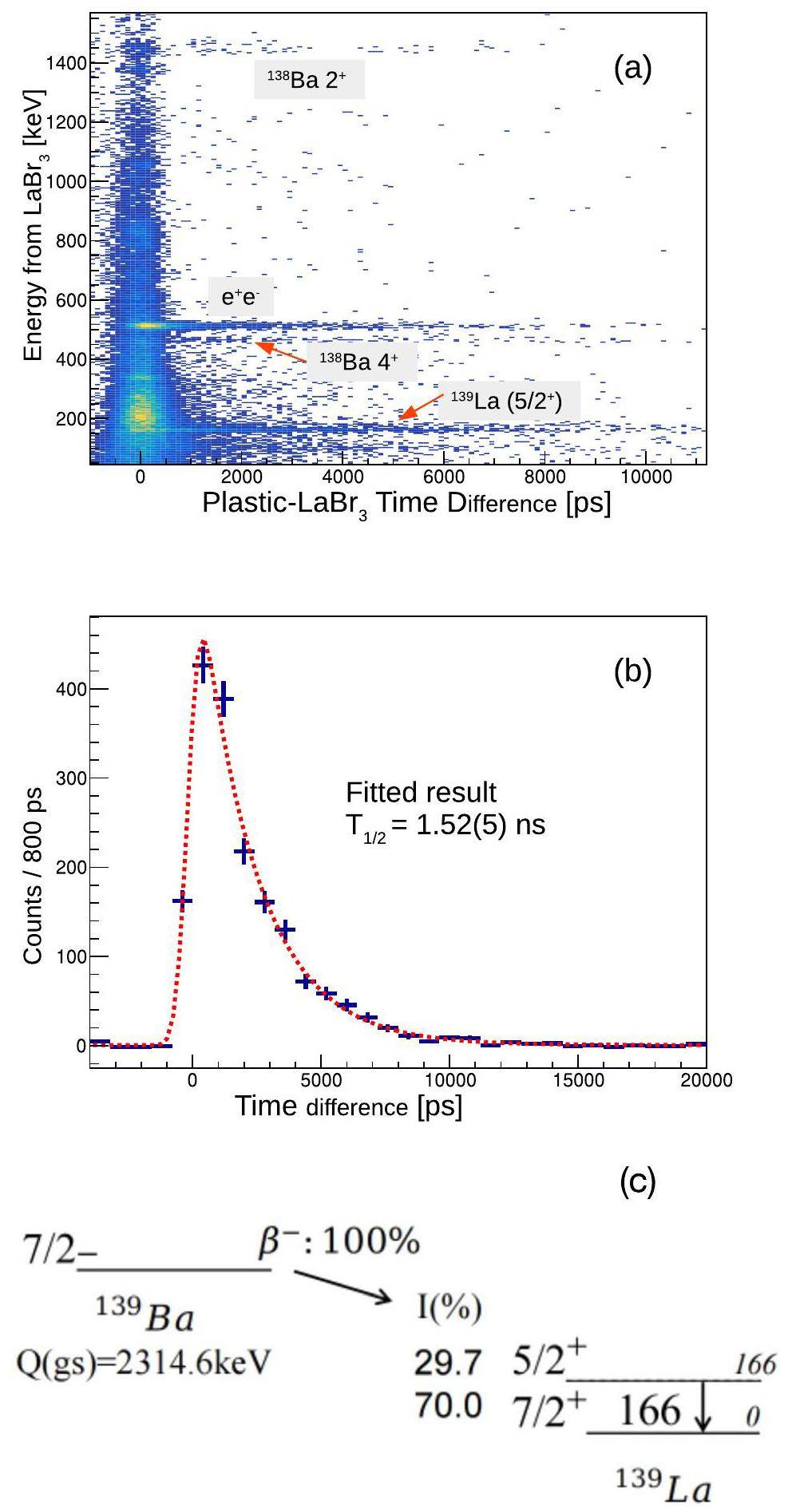
Figure 2(a) shows a two-dimension plot of the β–γ time difference vs γ-ray energy. Following the β decay, three γ lines at 166, 462, and 1436 keV were observed in addition to the 511 keV transition, corresponding to the decay of the first excited state in ¹³⁹La [7] and $2_1^{+}$ and $4_1^{+}$ states in ¹³⁸Ba [24] respectively. These results are consistent with the observation that all the aforementioned transitions attain the highest intensities in their respective β-decay channels [24, 7], whereas the other weak transitions cannot easily be observed, considering the statistics and energy resolution of LaBr₃ detectors.

Fig. 2Full-screen View

(Color online) (a) γ Energy versus β–γ time-difference plot, in which the β decays to excited states in ¹³⁸Ba and ¹³⁹La are separated. (b) β–γ time-difference distribution and fitted result of the half-life of first excited state in ¹³⁹La. (c) Partial β decay scheme illustrating the dominant decay channel from ¹³⁹Ba to the first excited state in ¹³⁹La

When high-energy neutrons impinge on ¹³⁸Ba, ¹³⁹Ba is produced with an excitation energy higher than the proton separation energy (9316(9) keV [7]), producing ¹³⁸Cs using proton evaporation channels. The ground state of ¹³⁸Cs has a β-decay half-life of 32.5(5) min [24] and most of the β-decay branches feed on excited states higher than the $4_1^{+}$ state in ¹³⁸Ba. Considering that the $4_1^{+}$ state is an isomeric state with T_1/2 = 2.160(11) ns, transitions of 462 and 1436 keV may be observed in the β-delayed γ-ray spectrum, as shown in Fig. 2(a).

The following paragraph focuses on the ¹³⁹Ba → ¹³⁹La β-decay channel. The β-decay channel has been extensively investigated [7-11]. The branching ratio information reveals that approximately 70% would directly populate the ground state in ¹³⁹La without emitting γ rays. The strongest among the remaining branches feeds the first excited state in ¹³⁹La with a ratio of 29.7 %, and all the remaining branches only account for 0.3 % of the decay strength. Consequently, most of the measured β–γ coincidence events are related to the ground state of ¹³⁹Ba β decay to the $5/2_1^{+}$ state in ¹³⁹La, followed by the $5/2_1^{+}$ → $7/2_1^{+}$ γ ray at 166 keV. By deconvolution fitting [14, 15] the β–γ time difference with a γ-ray energy of 166 keV, the lifetime of $5/2_1^{+}$ in ¹³⁹La is 1.52(5) ns, as shown in Fig. 2. This value is consistent with that adopted in the NNDC website [7].

The fitting function includes the contributions of both prompt response functions and the exponential decay component. Detailed information about the fitting can be obtained in Ref. [15] and references therein. In the current experiment, owing to the excellent energy resolution of LaBr₃, the 166-keV transition can easily be selected, facilitating background subtraction, as shown in Fig. 2, an operation that was impossible in the 1960s.

Shell-Model Investigation and Discussion

Shell model calculations have been performed to investigate the nature of the L-forbidden M1 transition in ¹³⁹La. To examine the effect of core-excitation, the model space comprises π 0g_9/2, 0g_7/2, 1d_5/2, 1d_3/2, 2s_1/2, 0h_11/2 and ν 0h_11/2, 0h_9/2, 1f_7/2, 1f_5/2, 2p_3/2, 2p_1/2, 0i_13/2 orbitals. The proton (neutron) core-excitation across the Z = 50 (N = 82) shell can be achieved by exciting protons (neutrons) from the π 0g_9/2 (ν 0h_11/2) orbital to higher orbitals.

The effective Hamiltonian is based on the nuclear force V_MU+LS [26], which comprises a Gaussian central force, a π + ρ meson-exchange tensor force, and an M3Y spin-orbit force [27]. The V_MU+LS force has been employed in the psd [28], sdpf [29], pfsdg regions [30], and nearby regions around ¹³²Sn [31, 32] and ²⁰⁸Pb [4, 33-35]. Recently, V_MU+LS had been employed to investigate the level structure of nuclei around ¹³²Sn and ²⁰⁸Pb [36, 37] in a unified manner. Specifically, the separation and excitation energies, as well as the nuclear level densities of $50\le Z\le 56$ and $80\le N\le 84$ nuclei, were reproduced using the interaction proposed in Ref. [38]. All the shell-model calculations were performed using the code KSHELL [39].

1. Influence of effective g-factor on lifetime prediction

In this study, B(M1) calculation employed effective g-factors of $g_{\text{p}}^l=1$, $g_{\text{n}}^l=0$, $g_{\text{p}}^s=5.0274$, and $g_{\text{n}}^s=-3.4424$. The former two are the free-nucleon values, and the latter two are obtained from the free g-factor quenched by 0.9. The proton and neutron effective charges are 1.5e and 0.5e in the B(E2) calculation, respectively.

The theoretical predictions of the $5/2_1^{+}$ → $7/2_1^{+}$ transition strength in ¹³⁹La under different conditions are presented in Table 1. Eliminating core-excitation yields a B(M1) value of 2.2 × 10^-5 [${\mu }_{\text{N}}^2$], increasing the half-life to 97.5 ns, even when the E2 strength is considered. By exciting either one proton or neutron across their respective major shell (noted as “p1” or “n1” in Table 1), the predicted M1 strength becomes one order of magnitude higher. Thus, the predicted half-life is significantly consistent with the experimentally measured half-life, such as 9.5 and 21.5 ns for the proton and neutron cases, respectively. Because of the limitation of computer power, the maximum truncation in the current calculation is that one proton and one neutron can be excited from the ¹³²Sn core, noted as “p1n1” in the last column of Table 1. Here, the maximum B(M1) is 1.3×10^-3 [${\mu }_{\text{N}}^2$], which is approximately two orders of magnitude larger than that in the no core-excitation case. Notably, the influence of the core-excitation on the B(E2) strength is significantly reduced. This study shows that a quenching factor of 0.9 is sufficient considering core-excitation with only a 1p-1h configuration. This value is significantly consistent with the free-nucleon value obtained via the meson exchange calculation (MEC) [40] in the limited model space around the ¹³²Sn region [41, 42].

The calculation in the previous paragraph did not include the tensor term in the effective g-factor [43, 44]. Meanwhile, the tensor part, exhibiting a slight influence on the magnetic moments around the ¹³²Sn region, as reported in Ref. [41, 42], is essential for the L-forbidden M1 transition strength because the $g_{\text{eff}}^t\left[Y_2\mathrm{,}s\right]$ operator can have a non-zero off-diagonal matrix element in the d_5/2 → g_7/2 transition. The last two columns in Table 1 present the shell-model calculation performed by using the effective M1 operator with the tensor part. With a slight correction, $g_{\text{p}}^t=0.15$ (compared with a value greater than 3 obtained via MEC, as shown in Refs. [41, 42]) and $g_{\text{n}}^t=0$, the calculation is consistent with the experimental result in the “p1n1” case, as presented in Table 1.

2. Detailed investigation on M1 matrix element

Furthermore, we analyzed the difference in the M1 matrix element, particularly for the high-J component, between different core-excitation conditions. The decomposition of the M1 matrix element is shown in Fig. 3. First, the inclusion of proton core-excitation significantly enhances the contribution from the π g_7/2 and g_9/2 shells.

Fig. 3Full-screen View

(Color online) Decomposition of the M1 transition matrix elements calculated using the present Hamiltonian. Each matrix element is decomposed of the part involving the π0g_7/2 and π0g_9/2 orbitals (πg), that involving π0h_11/2 (πh), that involving ν0h_9/2 and ν0h_11/2 (νh), and the others

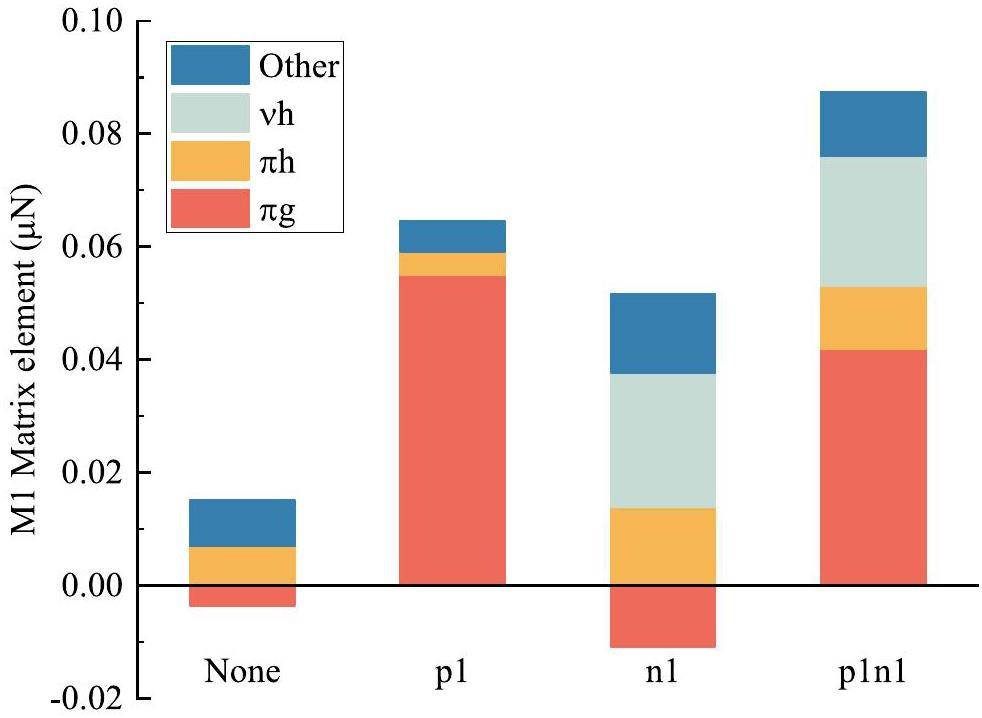
Neutron core-excitation introduces a strong component from νh orbitals similarly. In the one-proton-one-neutron core-excitation condition, all the corresponding components are available, whereas the major components originate from the spin-flip orbitals on both sides of the Z = 50 (g_7/2 and g_9/2) and N = 82 (h_11/2 and h_9/2) shells.

Herein, we aim to investigate the influence of the different components, including central, spin-orbit, and tensor parts, of effective interaction on the M1 transition strength, as shown in Fig. 4. The different nuclear-force components exhibited different behaviors with changes in the core-excitation truncation. In the p1 case, introducing the central force increases the half-life of the $5/2_1^{+}$ state in ¹³⁹La. Involving either tensor or spin-orbit forces significantly reduces the half-life, and an even lower value (as presented in Table 1) can be obtained by considering all forces. This finding is consistent with the experimental results. A different scenario is observed when only neutron core-excitation is involved in the shell model calculation (n1 case). Considering only the central force in the calculation significantly reduces the predicted half-life. Adding the spin-orbit or tensor force does not significantly change the result or even slightly increase the result when the tensor part is considered.

Fig. 4Full-screen View

(Color online) Comparison of half-lives of $5/2_1^{+}$ state in ¹³⁹La, derived with part of or all nuclear force components. "C,""LS," and "T" represent the central, spin-orbit, and tensor forces, respectively. "n1" and "p1" represent the inclusion of at most one neutron or proton core-excitation from theν0h_11/2 and π 0g_9/2 orbitals, respectively. "n1p1(ind.)" is evaluated by considering "n1" and "p1" as independent branches. "n1p1" denotes the condition that both one neutron and proton core-excitations are allowed. For illustration, the experimental values are represented using dashed lines

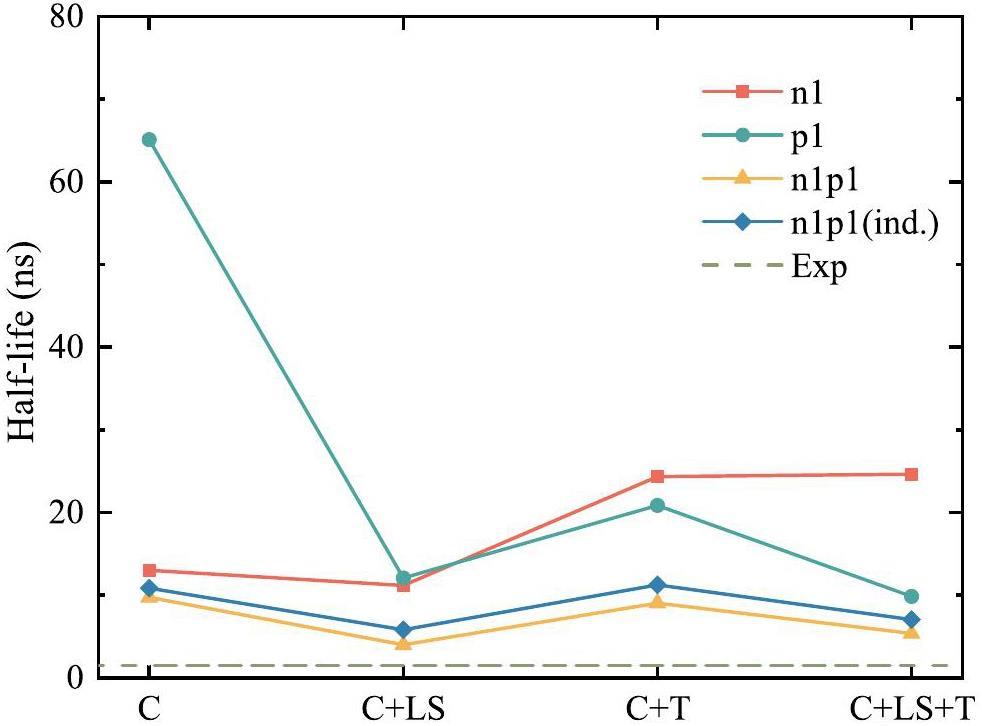
The significant difference between the p1 and n1 cases indicates that the tensor and spin-orbit forces contribute differently in both cases. This was unexpected because, as shown in Fig. 3, within the M1 matrix element, the πg component exhibits constructive and deconstructive interference with the other components in the p1 and n1 cases, respectively. Moreover, the νh component exists in the n1 case but not in the p1 condition, initiating a different situation when spin-orbital or tensor forces are generated. This observation is supported by the n1p1 case, in which the νh component is also a dominant contributor among the matrix elements, and the calculated half-life does not change significantly when spin-orbit and tensor forces are generated; a situation that is similar to the n1 case.

The n1p1(ind.) case, which is evaluated by considering n1 and p1 as independent branches, estimates an overall longer half-life than the "n1p1" condition. However, both cases exhibit similar tendencies. This implies that a consistent interference would be observed between the proton and neutron core-breaking components and that such an interference term between the proton and neutron configurations would not be sensitive to the nuclear force component. Changes in M1 transition strengths with respect to various nuclear forces reflect the modification of effective single-particle energies to adjust the configurations for both $5/2_1^{+}$ and $7/2_1^{+}$ in ¹³⁹ La.

Conclusion

This study measured the lifetime of the first excited state in ¹³⁹La using a state-of-the-art LaBr₃ + plastic scintillator array in a digital data-acquisition system. Compared with previous measurements that used stilbene or plastic scintillators, the proposed measurement effectively separates the background contribution in the gamma line spectrum owing to the high energy resolution of LaBr₃. To measure the lifetime of the ($5/2_1^{+}$) state in ¹³⁹La, a comprehensive shell-model study was conducted in a large model space. Results showed that both proton and neutron core-excitations were necessary to reproduce the measured lifetime of the ($5/2_1^{+}$) state in ¹³⁹ La. To reproduce the measured L-forbidden M1 transition strength, in addition to the core-excitation, a tensor correction was required for the effective M1 operator with a g-factor of 0.15, which is significantly smaller than the previously calculated value in this region or around ²⁰⁸Pb.