Introduction

Relativistic heavy-ion collisions create a unique environment where a quark-gluon plasma with strong collectivity is formed [1-8], accompanied by the strongest known magnetic field generated by spectator protons from the colliding nuclei [9-16]. This environment provides an ideal laboratory for studying the topological properties of the QCD vacuum and anomalous chiral transport phenomena under extreme magnetic field conditions. The chiral magnetic effect (CME), which induces electric charge separation along the magnetic field direction in systems with chiral imbalances, is crucial for detecting these phenomena [17-19].

The charge-dependent azimuthal correlation ${\gamma }_{\alpha \beta }=\langle \cos \left({\varphi }_{\alpha }+{\varphi }_{\beta }-2{\text{Ψ}}_{\text{RP}}\right)\rangle$ was initially proposed as a potential observable for detecting the CME [20]. In this correlator, ${\varphi }_{\alpha \left(\beta \right)}$ denotes the azimuthal angle of a charged particle $\alpha (\beta )$, and Ψ_RP represents the angle of the reaction plane. The difference between opposite-charge and same-charge correlations is represented by Δγ. Early measurements of this correlation by the STAR Collaboration [21-24] at the RHIC and the ALICE Collaboration [25] at the LHC aligned with CME expectations. However, significant background effects, especially those arising from an elliptical flow, influence the measured correlator [26-31]. In recent RHIC–STAR measurements [32], the best measurement was 14.7% in 20–50% centrality for the full-event method, although there could be residual nonflow background as well as discrepancy between a and b. Some measurements incorporating the nonflow effect have limited the CME fraction to approximately 10% [33-37] for Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV. Several methods have been proposed for separating potential CME signals from the dominant background [34, 36, 38-41]. One promising approach involves using isobar collisions, which consist of systems with the same nucleon number but different proton numbers, such as ${}_{44}^{96}\text{Ru}{+}_{44}^{96}\text{Ru}$ and ${}_{40}^{96}\text{Zr}{+}_{40}^{96}\text{Zr}$ collisions [42, 43]. The latest STAR evaluation of the CME signal established an upper limit of approximately 10% for the CME fraction in the Δγ measurement at a 95% confidence level in isobar collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV, after correcting for non-flow contamination [44-46]. However, the nuclear structure effect poses a challenge when searching for the CME in isobar collisions because it introduces differences in the backgrounds of the two isobar systems [47-57]. Based on the AMPT model, the newly developed state-of-the-art Chiral Anomalous Transmission (CAT) module reveals that the upper limit of the CME signal in isobar collisions is 15% [58, 59], which aligns with the STAR data.

Numerous experimental observables have been employed to detect true CME signals while minimizing the background interference in Au+Au and isobar collisions. For this purpose, a two-plane measurement method utilizing charge-dependent azimuthal correlations relative to the spectator plane (SP) and participant plane (PP) was proposed [60, 61]. This method is based on the fact that background and CME signals exhibit different sensitivities or correlations to the two planes [62]. The STAR collaboration applied this method to quantify the fraction of the CME signal within the inclusive Δγ correlation in both Au+Au and isobar collisions. For Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV, the STAR results suggest that the fraction of CME-induced charge separation is consistent with zero in the peripheral centrality bins, whereas finite CME signals may exist in the mid-central centrality bins [32]. This method is believed to eliminate most of the collective flow effect in the background; however, certain nonflow background effects require further investigation [37]. Furthermore, the SP and PP methodology assumes that the ratio a of the elliptical flow relative to different reaction planes is equivalent to the ratio b of the CME signals relative to different reaction planes [32, 37, 63]. However, these two ratios may differ. In our previous study [64], we calculated the CME signal-to-background ratio of b over a (b/a = 0.65 ± 0.18) in isobar collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV using the AMPT model with an initial CME signal, thereby providing theoretical support for the experimental measurement of the CME in isobar collisions. In this study, the experimental search for CME signals in Au+Au collisions and the need to explore the values of b across different collision systems motivated us to extend our calculations to Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV. We aimed to simultaneously fit the experimental observables related to the CME in three different collision systems, Au+Au, Zr+Zr, and Ru+Ru, within the AMPT model framework, thereby achieving a synchronous constraint and extraction of the CME strengths in these three collision systems. We focus on studying how the evolution of different collision systems affects the imported CME signal, which is introduced manually rather than derived from first principles, such as the magnetic field and chirality imbalance.

The remainder of this paper is organized as follows. In Sect. 2, we describe the setup of the AMPT model with an initial CME signal and outline our two-plane method for extracting the fraction of the CME signal from the inclusive Δγ. Our model results are presented and compared with measurements from the STAR experiment in Sect. 3, in which we discuss the implications of our findings for the interpretation of the experimental data and possible physical sources. Finally, Sect. 4 summarizes the main conclusions of the study.

Model and method

2.2

Spectator and participant planes

The two-plane method utilizes distinct plane correlations, that is, the elliptical flow-driven background is predominantly correlated with the PP, whereas the CME signal exhibits a stronger correlation with the SP [60, 61]. The SP and PP can be reconstructed using the following equations: ${\psi }_{\text{S P}}=\frac{\text{atan }2\left(\langle r_{\text{n}}^2\sin \left(2{\varphi }_{\text{n}}\right)\rangle \mathrm{,}\langle r_{\text{n}}^2\cos \left(2{\varphi }_{\text{n}}\right)\rangle \right)}{2}\mathrm{,}$ (2) ${\psi }_{\text{P P}}=\frac{\text{atan }2\left(\langle r_{\text{p}}^2\sin \left(2{\varphi }_{\text{p}}\right)\rangle \mathrm{,}\langle r_{\text{p}}^2\cos \left(2{\varphi }_{\text{p}}\right)\rangle \right)+\pi }{2}\mathrm{,}$ (3) where $r_{\text{n}}$ and ϕ_n represent the displacement and azimuthal angle of the spectator neutrons in the transverse plane, respectively, whereas $r_{\text{p}}$ and ϕ_p represent the displacement and azimuthal angle of the participating partons in the transverse plane, respectively. All spatial information regarding the displacement and azimuthal angle was obtained from the initial state of the AMPT model. $\langle \mathrm{...}\rangle$ means averaged over all partons for each event. The PP can be experimentally determined using the event plane reconstructed from final-state hadrons [76]. In this study, the PP was employed to minimize the non-flow effect [37] in the reconstructed ψ_EP. However, we systematically verified that all conclusions remained quantitatively consistent when the event plane (EP) method was employed. The corresponding elliptic flow coefficients, v₂{SP} and v₂{PP}, using the SP (ψ_SP) and PP (ψ_PP) methods, respectively, are as follows: $v_2\left\{\text{SP}\right\}=\langle \langle \cos 2\left(\varphi -{\psi }_{\text{SP}}\right)\rangle \rangle \mathrm{,}$ (4) $v_2\left\{\text{PP}\right\}=\langle \langle \cos 2\left(\varphi -{\psi }_{\text{PP}}\right)\rangle \rangle \mathrm{.}$ (5) where ϕ represents the azimuthal angle of the final hadrons in the transverse momentum plane, and $\langle \langle \mathrm{...}\rangle \rangle$ means averaged over all charged hadrons for all events. Because the PP in experiments is reconstructed using the momenta of final-state particles, it often introduces non-flow contributions to the experimental measurements of $v_2\left\{\text{PP}\right\}$ [76]. However, our PP is theoretically reconstructed based on the initial parton positions using Eq. (3), which significantly suppresses the non-flow effect [77, 78]. The self-correlation is also significantly reduced because the dynamic evolution of heavy-ion collisions largely breaks the correlation between the final-state hadrons and our initial-state participant parton plane [77, 78].

Figure 1 presents the centrality dependence of v₂{PP} and v₂{SP} for charged hadrons with 0.2<pT<2.0 GeV / c and |η|<1, obtained from the AMPT model with varying CME strengths in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV. As anticipated, v₂{PP} is consistently larger than v₂{SP} in all cases, because the elliptical flow is more strongly correlated with the PP than with the SP. The values of both v₂{PP} and v₂{SP} increase slightly with p for the peripheral collisions. This is because our CME is introduced by reversing the fraction p of the parton momenta, while preserving their spatial positions. This approach intentionally maintains the initial-state geometry but introduces initial-state residual momentum anisotropy. This initial flow likely couples with the final-state interactions, leading to an increase in the elliptical flow v₂ with p for the peripheral collisions [79].

Fig. 1Full-screen View

(Color online) AMPT results on centrality dependence of elliptic flow v₂{PP} (solid symbols) and v₂{SP} (open symbols) in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME. The data points are shifted along the x axis for clarity

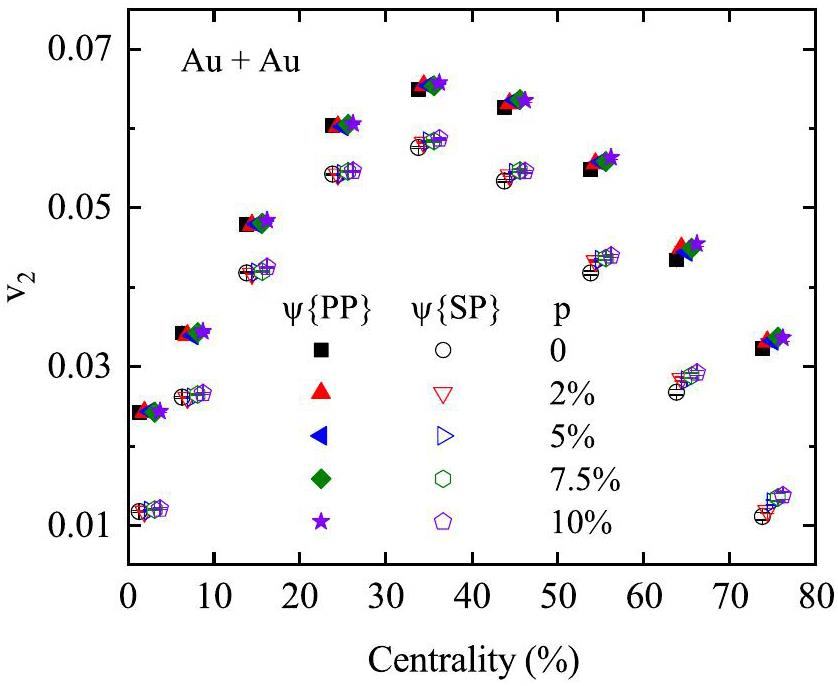
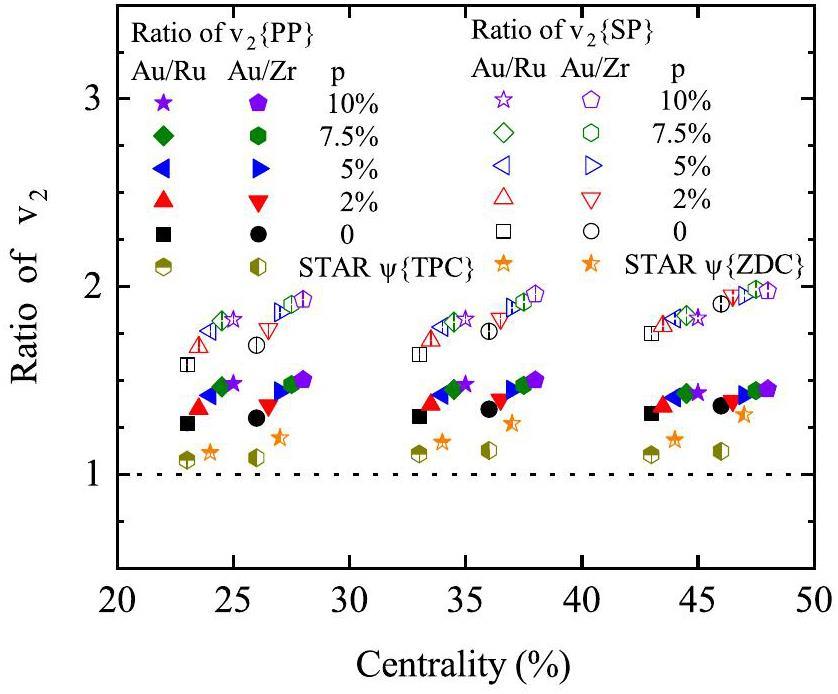
Figure 2 shows the ratios of v₂{PP} and v₂{SP} for Au+Au collisions relative to Ru+Ru and Zr+Zr collisions. Note that all the calculations for the Ru+Ru and Zr+Zr collisions were taken from Ref. [64]. Because the CME is more likely to occur at centrality bins of 20–50%, and to avoid large errors, the comparison is restricted to these centrality bins. The ratio of v₂{PP} is larger than that of v₂{SP}, which is consistent with the experimental trends. Compared with the experimental data, a relatively larger ratio in our results arises because the v₂{PP} and v₂{SP} values calculated from our isobar collision simulations are smaller than the experimental results. Similarly, the v₂{PP} and v₂{SP} ratios of Au+Au to Ru+Ru collisions are smaller than those of Au+Au to Zr+Zr collisions, reflecting the influence of the nuclear structure. This indicates that the v₂{PP} and v₂{SP} values for Ru+Ru collisions are larger than those for Zr+Zr collisions owing to the nuclear structure effect [54, 64]. In the 20–50% centrality bin, the changes in v₂{PP} and v₂{SP} values for Au+Au collisions are mere; however, in isobar collisions, the v₂{PP} and v₂{SP} values decrease with increasing p [64], resulting in an increase in the v₂{PP} and v₂{SP} ratio with the strength of the CME.

Fig. 2Full-screen View

(Color online) Centrality dependence of elliptic flow v₂{PP} (solid symbols) and v₂{SP} (open symbols) ratios of Au+Au collisions to Ru+Ru and Zr+Zr collisions, respectively, at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data [32, 80]. The data points are shifted along the x axis for clarity

Results and Discussions

This section presents the AMPT model results, focusing on the charge-dependent azimuthal correlations for charged particles relative to both the SP and PP. For comparison with the measurements from the STAR experiment, we used kinetic cuts of 0.2<pT<2.0 GeV/c and |η|<1, which are consistent with the STAR experimental setup.

Figure 3 shows the centrality dependence of Δγ{PP} and Δγ{SP} from the AMPT model with varying CME strengths in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV. Compared with the STAR data, the CME signal percentage at p = 5% or 7.5% aligns more closely with the experimental results. Notably, Δγ{SP} exceeds Δγ{PP}, indicating that the SP serves as a more sensitive probe for the CME because of its stronger correlation with the magnetic field direction compared with that of the PP.

Fig. 3Full-screen View

(Color online) Centrality dependence of Δγ{PP} (solid symbols) and Δγ{SP} (open symbols) in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data linked with the dotted line [32]. The data points are shifted along the x axis for clarity

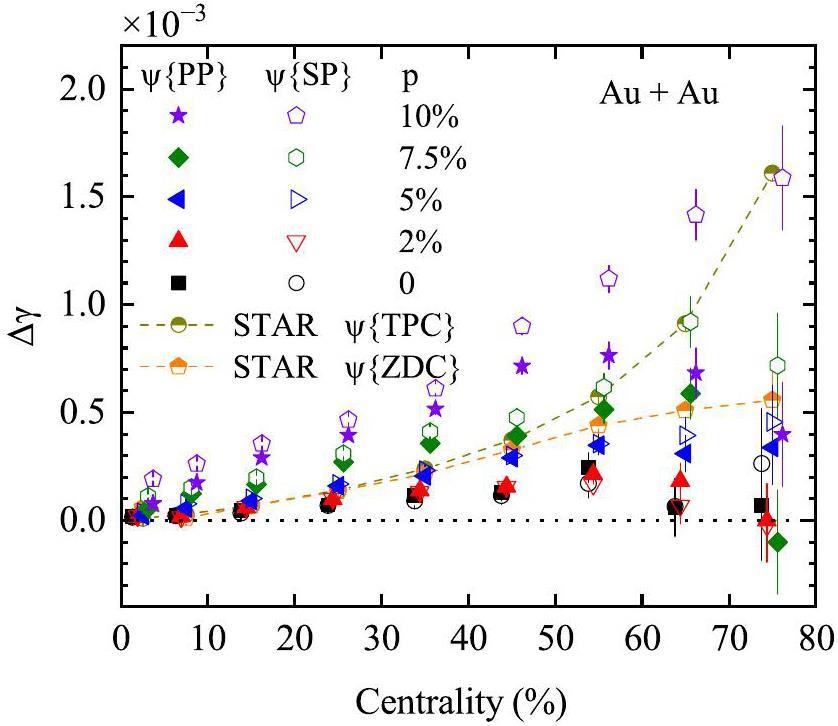
Figure 4(a) and (b) present the centrality dependence of the Δγ{PP} and Δγ{SP} ratios for Au+Au collisions relative to the Ru+Ru and Zr+Zr collisions, respectively. Considering the effect of errors, both the experimental and theoretical results indicate that the Δγ value for Au+Au collisions is smaller than that for isobar collisions, because most of the ratios are less than one. For the ratio of Δγ{PP} in Fig. 4(a), the AMPT results without the CME signal agree closely with the experimental results, whereas for the ratio Δγ{SP} in Fig. 4(b), the AMPT results with the CME signal show better agreement with the experimental results. As the CME signal correlates more strongly with the SP than with the PP, we observe that the ratio of Δγ{SP} in Fig. 4(b) decreases with increasing CME strength. This suggests that Δγ{SP} in isobar collisions increases more rapidly than that in Au+Au collisions as the CME strength increases.

Fig. 4Full-screen View

(Color online) Centrality dependence of Δγ{PP} (a) and Δγ{SP} (b) ratios of Au+Au collisions to Ru+Ru collisions (solid symbols) and Zr+Zr collisions (open symbols), respectively, at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data [32, 80]. The data points are shifted along the x axis for clarity

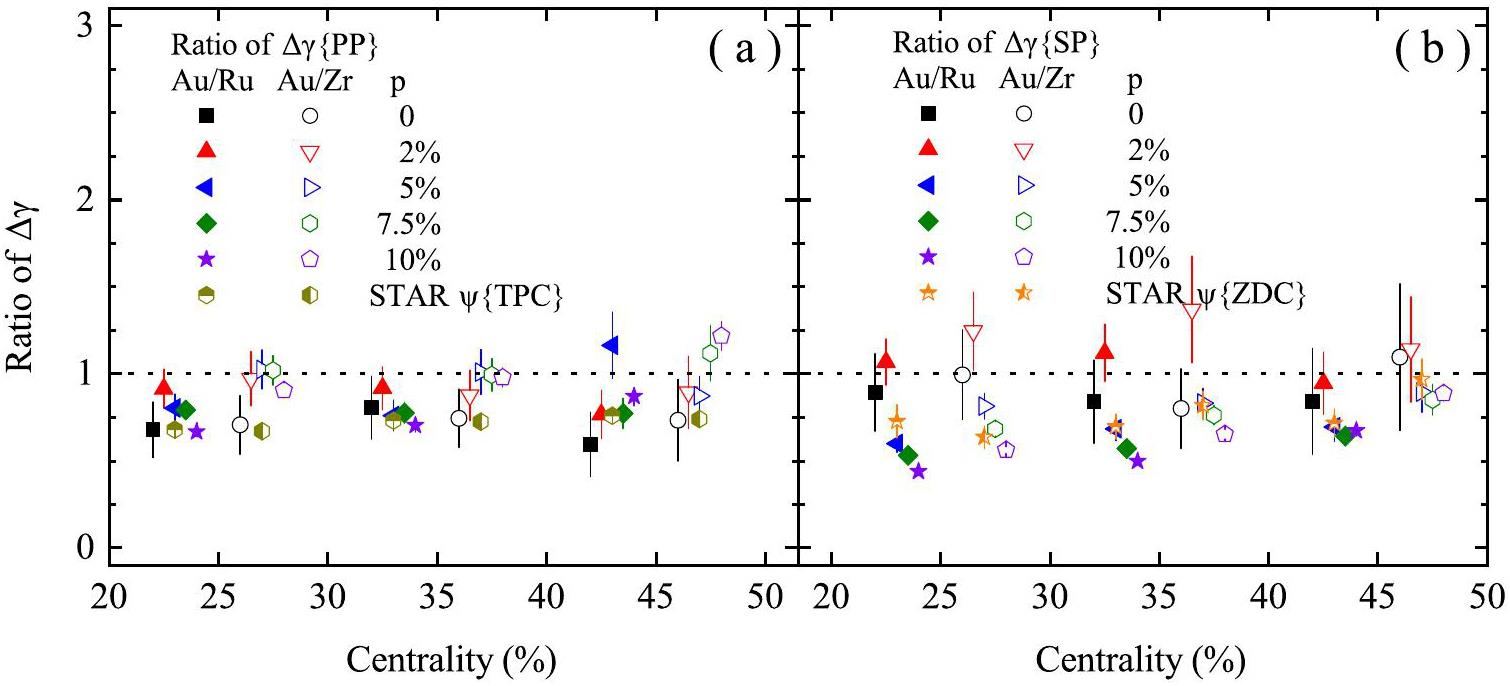
Figure 5 shows the centrality dependence of $A=\text{Δ}\gamma \left\{\text{SP}\right\}/\text{Δ}\gamma \left\{\text{PP}\right\}$ and $a=v_2\left\{\text{SP}\right\}/v_2\left\{\text{PP}\right\}$ from the AMPT model with varying CME strengths, compared with STAR experimental data [32]. As the CME strength in the AMPT model increases, the value of a remains nearly constant and is consistently below unity. It is expected that a follows the expectation $a=\langle \cos 2\left({\psi }_{\text{PP}}-{\psi }_{\text{SP}}\right)\rangle \approx v_2\left\{\text{SP}\right\}/v_2\left\{\text{PP}\right\}$ [60, 81, 82]. In Fig. 6, we utilized the AMPT model to directly calculate the values of $\langle \cos 2\left({\psi }_{\text{PP}}-{\psi }_{\text{SP}}\right)\rangle$ and compared them with the results of $v_2\left\{\text{SP}\right\}/v_2\left\{\text{PP}\right\}$, denoted as a in Fig. 5. We observe that $v_2\left\{\text{SP}\right\}/v_2\left\{\text{PP}\right\}$ closely follows $\langle \cos 2\left({\psi }_{\text{PP}}-{\psi }_{\text{SP}}\right)\rangle$ with small differences that can be attributed to non-flow effects. In contrast, the values of A increase with p, suggesting that the CME affects Δγ differently for the two planes. For small values of p, the model results align more closely with the experimental data.

Fig. 5Full-screen View

(Color online) Centrality dependence of A (solid symbols) and a (open symbols) in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data linked with the dotted line [32]. The data points are shifted along the x axis for clarity

Fig. 6Full-screen View

(Color online) Centrality dependence of $v_2\left\{\text{SP}\right\}/v_2\left\{\text{PP}\right\}$ (solid symbols) and $\langle \cos 2\left({\psi }_{\text{PP}}-{\psi }_{\text{SP}}\right)\rangle$ (open symbols) in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME. The data points are shifted along the x axis for clarity

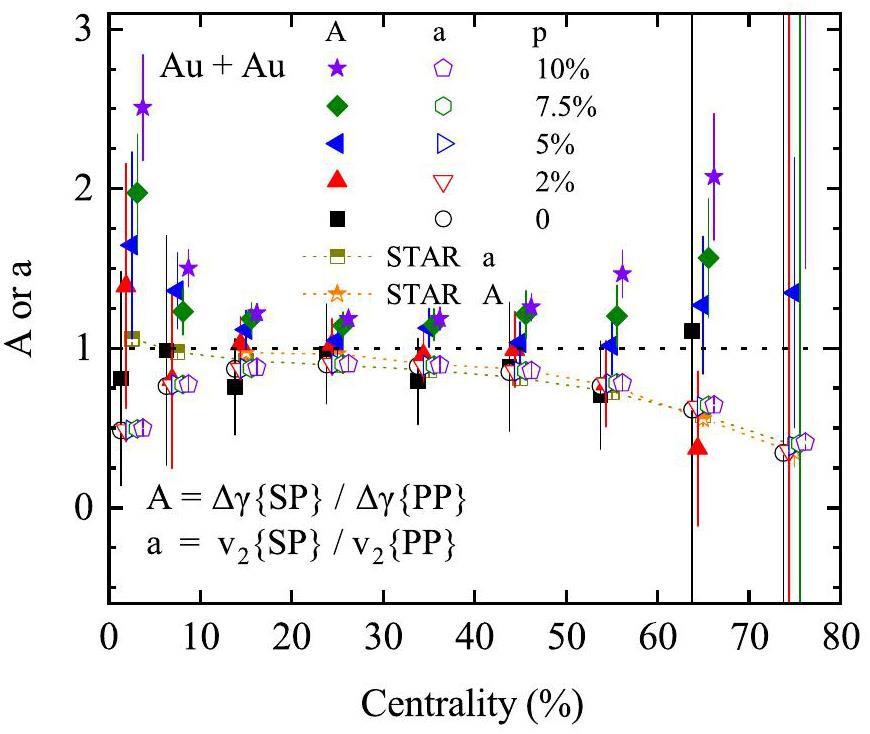
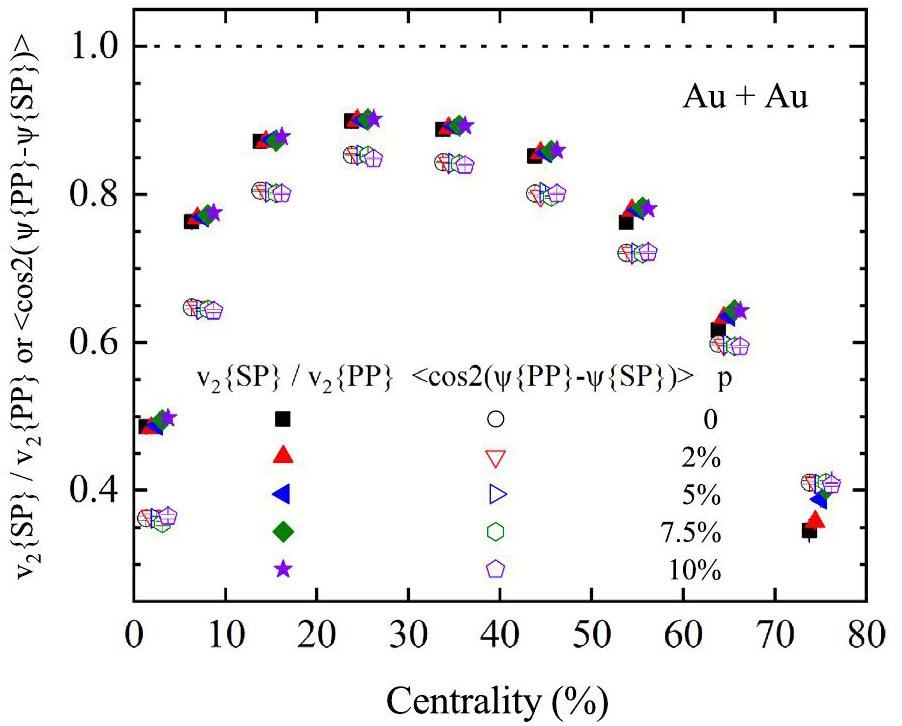
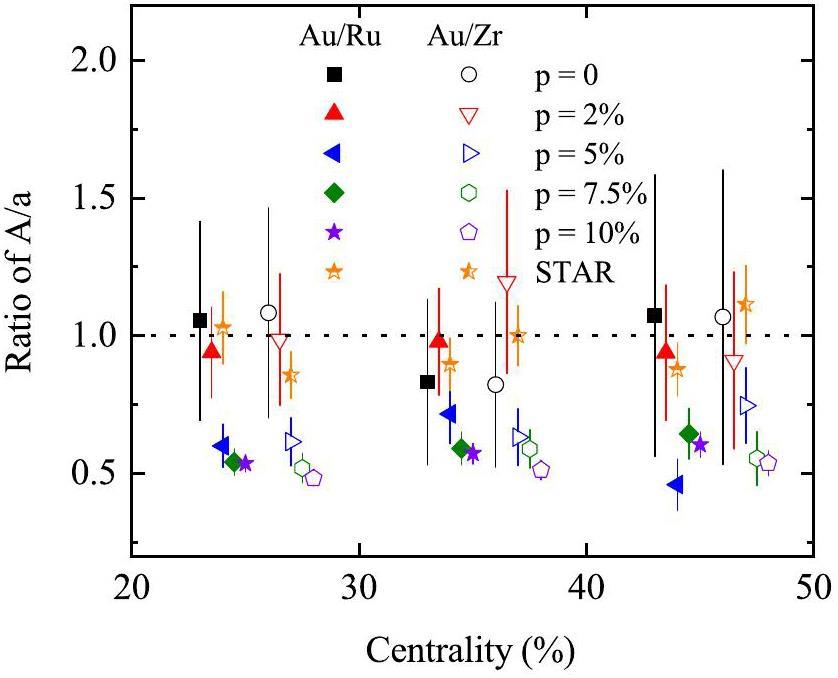
Figure 7 shows the centrality dependence of the A and a ratios for Au+Au collisions relative to Ru+Ru and Zr+Zr collisions, respectively. The ratio of a remains nearly unchanged, which is consistent with the experimental data within error. An a ratio greater than one indicates that the $\langle \cos 2\left({\psi }_{\text{PP}}-{\psi }_{\text{SP}}\right)\rangle$ value is larger, implying a smaller difference angle between ψ_PP and ψ_SP for Au+Au collisions than that for isobar collisions. For larger CME strengths, the ratio of A is less than one, indicating that the ratios of Δγ{SP} and Δγ{PP} are smaller in Au+Au collisions than in isobar collisions, that is, Δγ{SP} and Δγ{PP} are closer in Au+Au collisions than those in isobar collisions.

Fig. 7Full-screen View

(Color online) Centrality dependence of A (solid symbols) and a (open symbols) ratios of Au+Au collisions to Ru+Ru and Zr+Zr collisions, respectively, at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data [32, 80]. The data points are shifted along the x axis for clarity

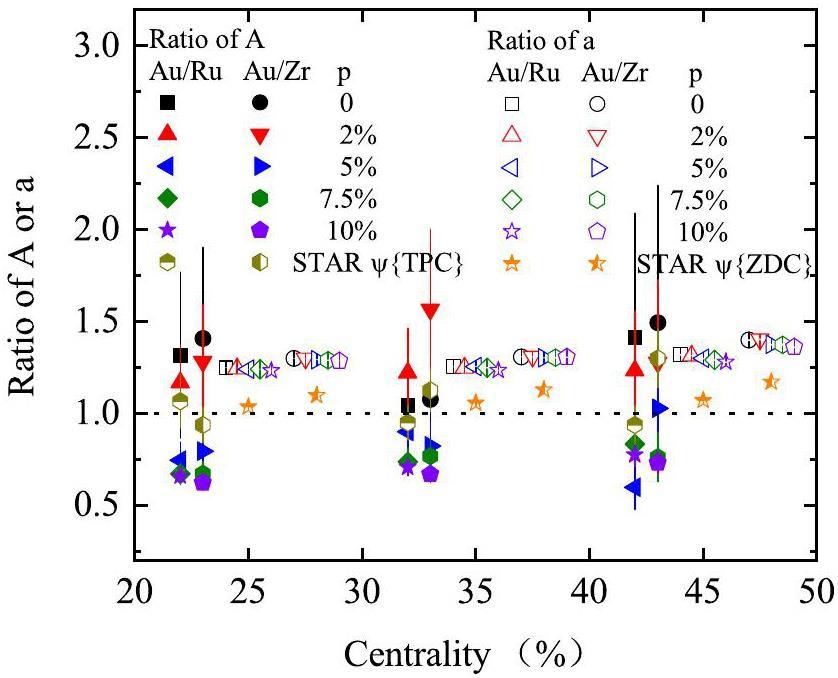
Figure 8 shows A/a as a function of the centrality predicted by the AMPT model with varying CME strengths. According to Eqs. (9) and (12), A/a values greater than unity indicate the presence of a CME signal within the Δγ observable. Focusing on mid-central collisions (20–50% centrality), where the CME effect is more measurable, A/a>1 is observed for all cases except when p=0 and p=2%. Notably, A/a increases with CME strength, suggesting that this ratio reflects the strength of the CME signal. The experimental data are closer to the cases with lower strengths of the CME signal.

Fig. 8Full-screen View

(Color online) Centrality dependence of A/a in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data linked with the dotted line [32]. The data points are shifted along the x axis for clarity

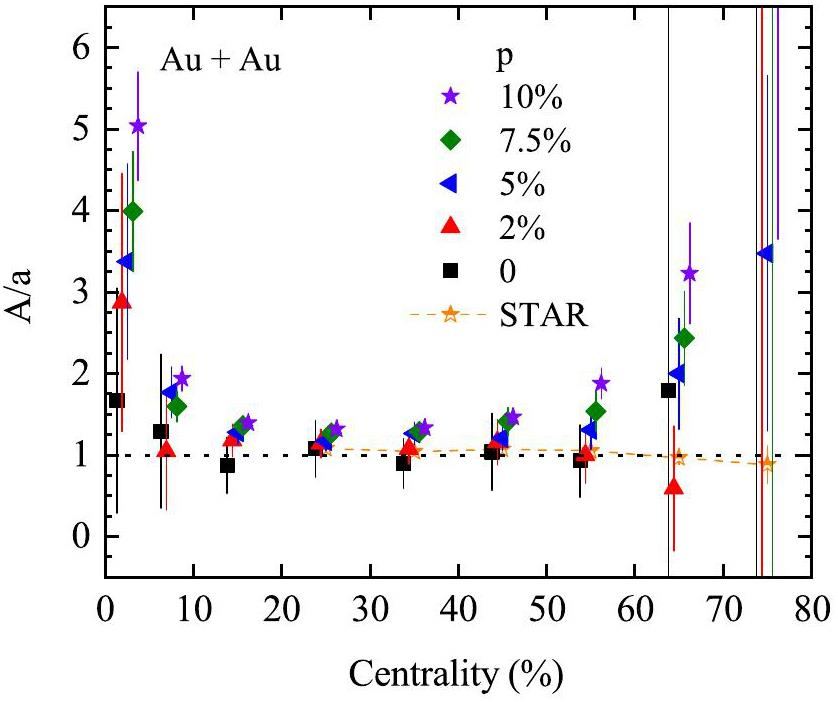
Figure 9 shows the centrality dependence of the A/a ratios for Au+Au collisions relative to Ru+Ru and Zr+Zr collisions. Focusing on mid-central collisions (20–50% centrality), the A/a ratios for the Au+Au and isobar collisions exhibit a trend similar to that of the A ratio shown in Fig. 7, driven by a smaller variation in a and larger variation in A. The experimental data are also closer to the cases with lower strengths of the CME signal.

Fig. 9Full-screen View

(Color online) Centrality dependence of A/a ratios of Au+Au collisions to Ru+Ru and Zr+Zr collisions, respectively, at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data [32, 80]. The data points are shifted along the x axis for clarity

Figure 10 shows the centrality dependence of a and b calculated using Eq. (13), based on the AMPT model with varying CME strengths. Notably, a and b exhibit significant differences. In the 20–50% centrality bins, b remains consistently smaller than a. Moreover, a shows minimal dependence on CME strength, as presented in Fig. 5. By contrast, b reflects the capability of the PP method to capture the CME signal observed in the SP method. Although the statistical errors are substantial, b shows no significant variation with CME strengths, except for the 2% CME strength case, which is excluded because of its large statistical uncertainties.

Fig. 10Full-screen View

(Color online) AMPT results on centrality dependence of a (solid symbols) and b (open symbols) in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME. The data points are shifted along the x axis for clarity

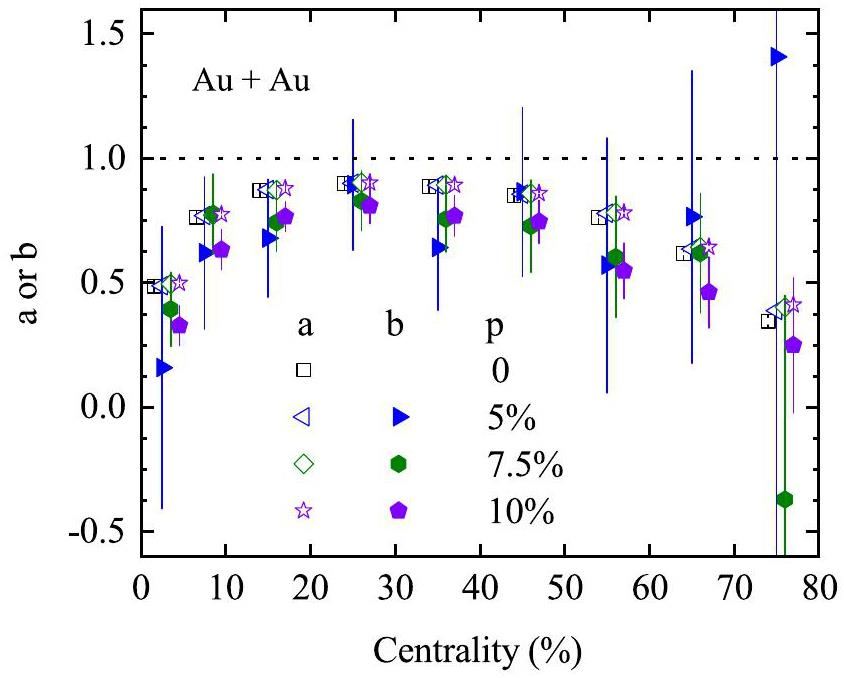
Figure 11 shows the centrality dependence of the a and b ratios for Au+Au collisions relative to Ru+Ru and Zr+Zr collisions, respectively, based on the AMPT model with various CME strengths. Focusing on the 20–50% centrality bins, the a ratio remains nearly unchanged and is smaller than the b ratio. The uncertainties of b ratios are large. According to Eq. (13), a larger b value indicates a smaller difference in the net CME strength between the two planes. Therefore, our results indicate that the difference is smaller in Au+Au collisions than in isobar collisions.

Fig. 11Full-screen View

(Color online) AMPT results on centrality dependence of the a (open symbols) and b (solid symbols) ratios of Au+Au collisions to Ru+Ru and Zr+Zr collisions, respectively, at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME. The data points are shifted along the x axis for clarity

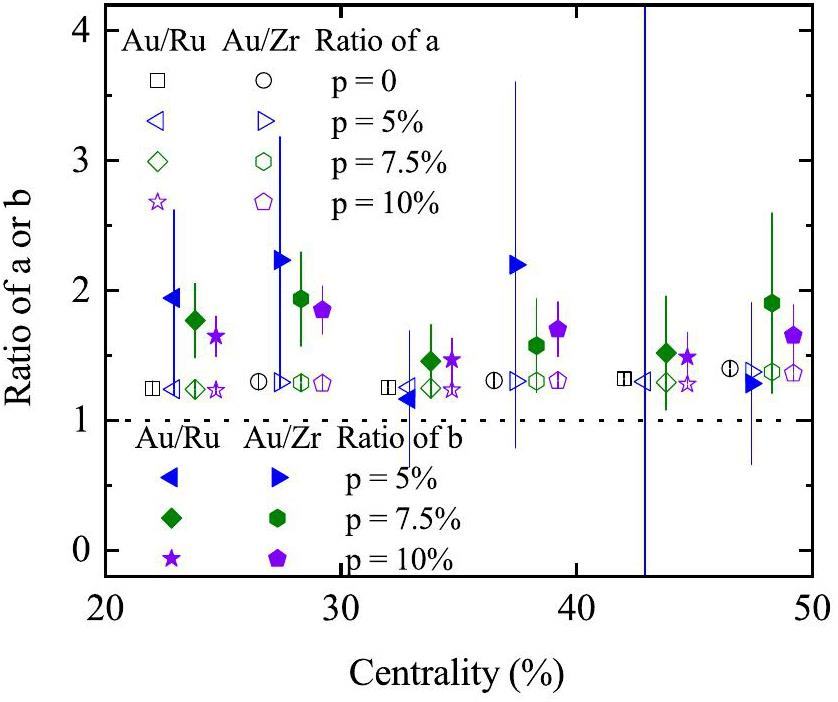
Figure 12 shows the centrality dependence of the b/a ratio as predicted by the AMPT model with varying CME strengths. Focusing on the 20–50% centrality bins in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV, the b/a ratio can be approximated by using a constant function, yielding b/a = 0.88(± 0.08). Our previous study shows that isobar collisions yield b/a = 0.65(± 0.18) [64]. This result implies that the relative ratio of CME signals across different planes does not simply invert the elliptical flow ratio among these planes. This finding has significant implications for extracting the fraction of the CME signal within the Δγ observable, which will be discussed further.

Fig. 12Full-screen View

(Color online) Centrality dependence of b/a in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME. The data points are shifted along the x axis for clarity

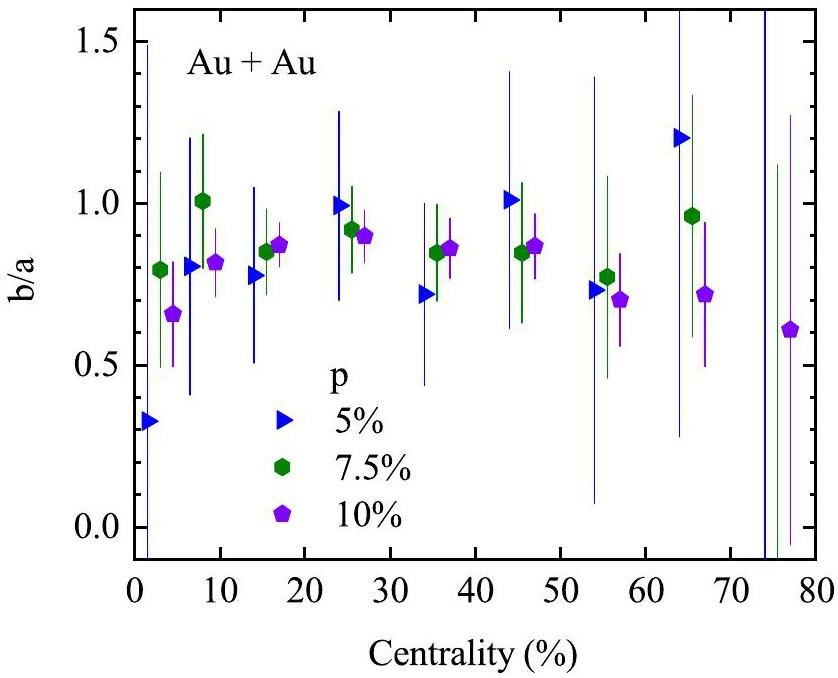
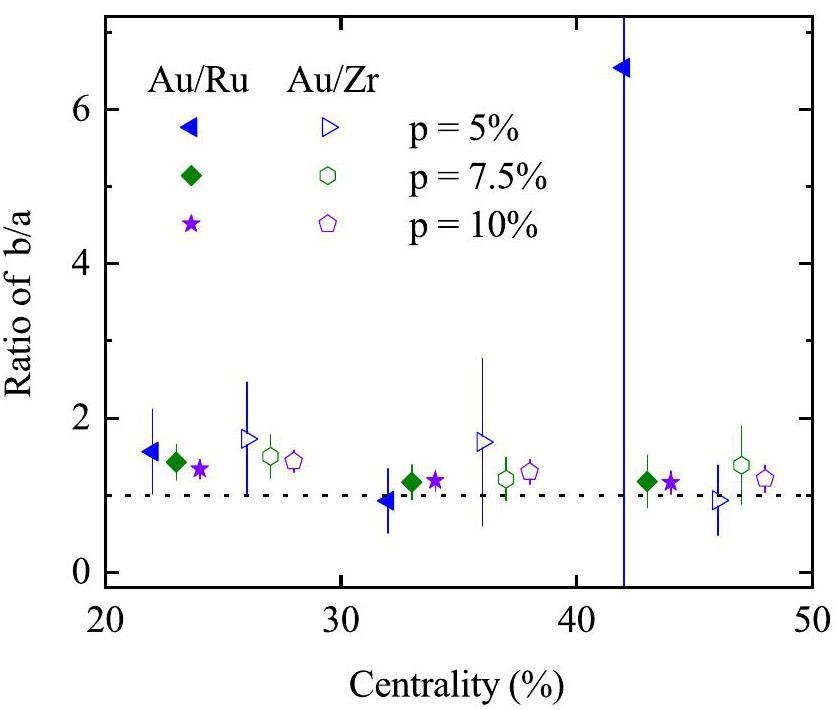
Figure 13 shows the centrality dependence of b/a for Au+Au collisions relative to Ru+Ru and Zr+Zr collisions, respectively, based on the AMPT model with varying CME strengths. Because the value of $a$ remains nearly constant, the ratio $b/a$ follows the trend of the ratio $b$ shown in Fig. 11. The same p input is employed for each centrality in Fig. 11 and Fig. 13. However, it should be pointed out that as the magnetic field is expected to be stronger for Au+Au collisions than for isobaric collisions at the same centrality, the p values should differ for these systems.

Fig. 13Full-screen View

(Color online) Centrality dependence of the b/a ratios of Au+Au collisions to Ru+Ru and Zr+Zr collisions, respectively, at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME. The data points are shifted along the x axis for clarity

The upper panel of Fig. 14 shows the centrality dependence of the two types of f_CME based on the AMPT model with varying CME strengths. The open and solid symbols represent f_CME and f_CME{b} calculated using Eqs. (9) and (12), respectively. Our results are consistent with the STAR experimental data [32], favoring the cases of p=0% and p=2%. Notably, for the 20–50% centrality bins, when $p\ne 0$, f_CME{b} is smaller than f_CME. The negative f_CME values at p=0% arise from statistical fluctuations in the baseline measurement. The lower panel of Fig. 14 shows the centrality dependence of the ratio f_CME{b} to f_CME, which is less than unity for–20–50% centrality bins. This implies that assuming $b=a$ leads to an overestimation of the CME signal fraction within the Δγ observable.

Fig. 14Full-screen View

(Color online) Upper panel: Ccentrality dependence of f_CME{b} and f_CME in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME, in comparison with the STAR data [32]. The solid and open symbols represent the results for f_CME{b} and f_CME, respectively. Lower panel: Centrality dependence of the ratio of f_CME{b} to f_CME. The data points are shifted along the x axis for clarity

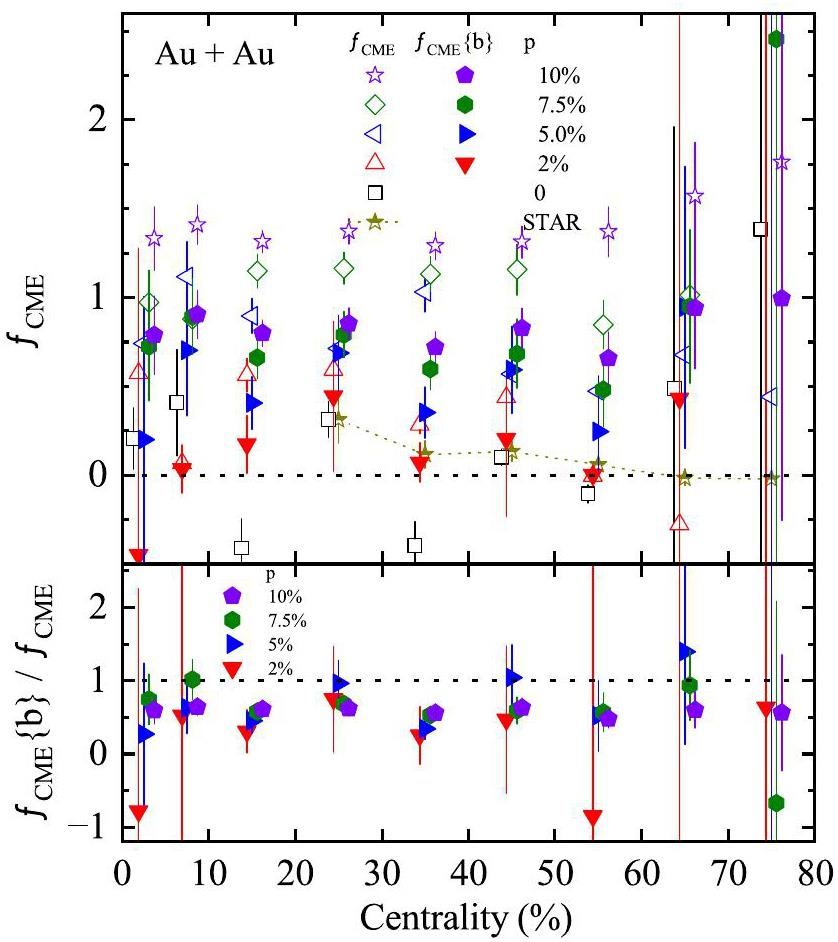
Figure 15 shows the f_CME, f_CME{b}, and f_CME{p} ratios for Au+Au collisions relative to Ru+Ru and Zr+Zr collisions, respectively, in the 20–50% centrality bins at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV. Note that the STAR data for the Ru+Ru and Zr+Zr collisions were obtained by averaging the data reported in Ref [80], which indicates that without accounting for the effect of $b$, the fraction of CME signals in $\text{Δ}\gamma$ is slightly larger in isobar collisions than in Au+Au collisions. The f_CME{p} ratio was calculated using the method described in Ref. [64]. f_CME{p} is defined as follows: $f_{\text{CME}}\left\{p\right\}=\frac{\text{Δ}{\gamma }_{\text{CME}}\left\{\text{PP}\right\}(p\ne 0)}{\text{Δ}\gamma \left\{\text{PP}\right\}(p\ne 0)}\mathrm{,}$ (14) where $\text{Δ}{\gamma }_{\text{CME}}\left\{\text{PP}\right\}(p\ne 0)=\text{Δ}\gamma \left\{\text{PP}\right\}(p\ne 0)-\text{Δ}\gamma \left\{\text{PP}\right\}(p=0)\mathrm{.}$ (15) The observables $\text{Δ}\gamma \left\{\text{PP}\right\}(p=0)$ and $\text{Δ}\gamma \left\{\text{PP}\right\}(\text{p}\ne 0)$ can be obtained from the AMPT model without the CME and with different strengths of the CME, respectively. However, the ratio of Au+Au collisions relative to isobar collisions increases after applying the correction for b, which indicates that, after accounting for b, the fraction of CME signals in $\text{Δ}\gamma$ is greater for Au+Au collisions than for isobar collisions. Therefore, it is important to consider the effect of b to achieve real facts about the CME.

Fig. 15Full-screen View

(Color online) f_CME, f_CME{b}, and f_CME{p} ratios of Au+Au collisions to Ru+Ru and Zr+Zr collisions, respectively, in 20–50% centrality bins at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV from the AMPT model with different strengths of the CME. The solid, open symbols, and open symbols with X represent the results for the AMPT model with different strengths of the CME in comparison with the STAR data [32, 80]. The data points are shifted along the x axis for clarity

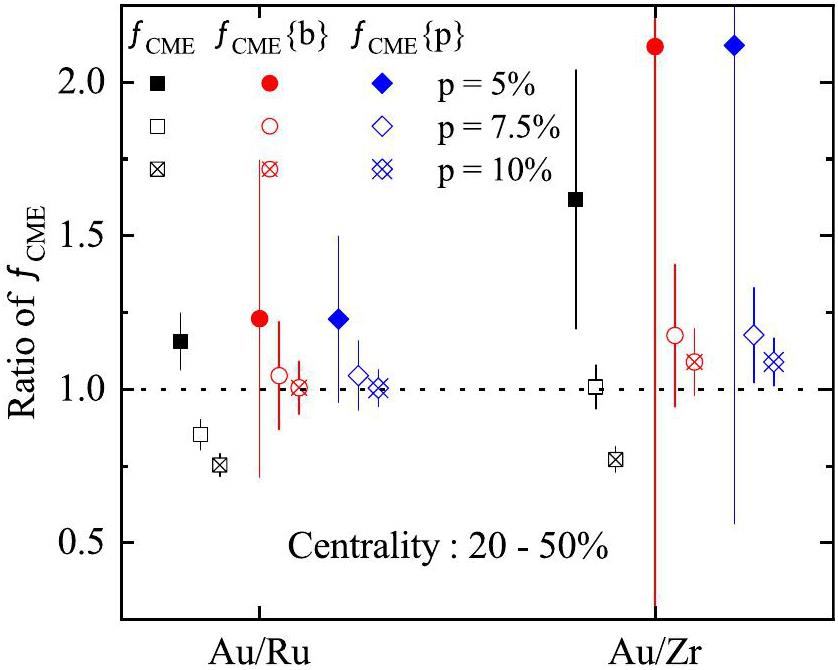
As the introduced CME signal strength increases, the ratios calculated using all the three methods decrease. This is because the A/a value increases more significantly in isobar collisions than in Au+Au collisions, leading to a reduction in the calculated ratios. It is also observed that the Au/Ru ratio is smaller than the Au/Zr ratio in the presence of CME signals, indicating that the fraction of CME signal is higher in Ru+Ru than in Zr+Zr.

The preceding results demonstrate that the ratio b/a = 0.88(± 0.08) significantly influences the final result of f_CME in the 20–50% centrality bins for Au+Au collisions. To elucidate the origin of this relationship, we investigated the evolution of a and b at different stages of the Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV in the AMPT model, assuming a CME strength of p=10%. We focused on four distinct stages: the initial stage, after the parton cascade, after coalescence, and after hadron rescattering. As shown in the upper panel of Fig. 16, the value of a remained constant during the last three stages. The initial stage is excluded from the a calculation because the elliptical flow is initially zero. In contrast, the value of b is consistently smaller than a and decreases with each stage in the 20–50% centrality bins. The lower panel of Fig. 16 illustrates the decreasing trend of the b/a ratio during the evolution stage, which is primarily driven by a decrease in b. This decrease in b suggests weaker correlation between CME signals across different planes, which can be attributed to the effects of final-state interactions during the evolution of heavy-ion collisions [54, 75, 83, 84].

Fig. 16Full-screen View

(Color online) Upper panel: Centrality dependence of $a$ and $b$ in Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV for four different stages of the AMPT model with a CME strength of $p=10\%$. The open and solid symbols represent the results for $a$ and $b$, respectively. Lower panel: centrality dependence of the ratio $b/a$ for the different stages in Au+Au collisions. The same symbols as $b$ in the upper panel are used to indicate different stages. The data points are shifted along the x axis for clarity

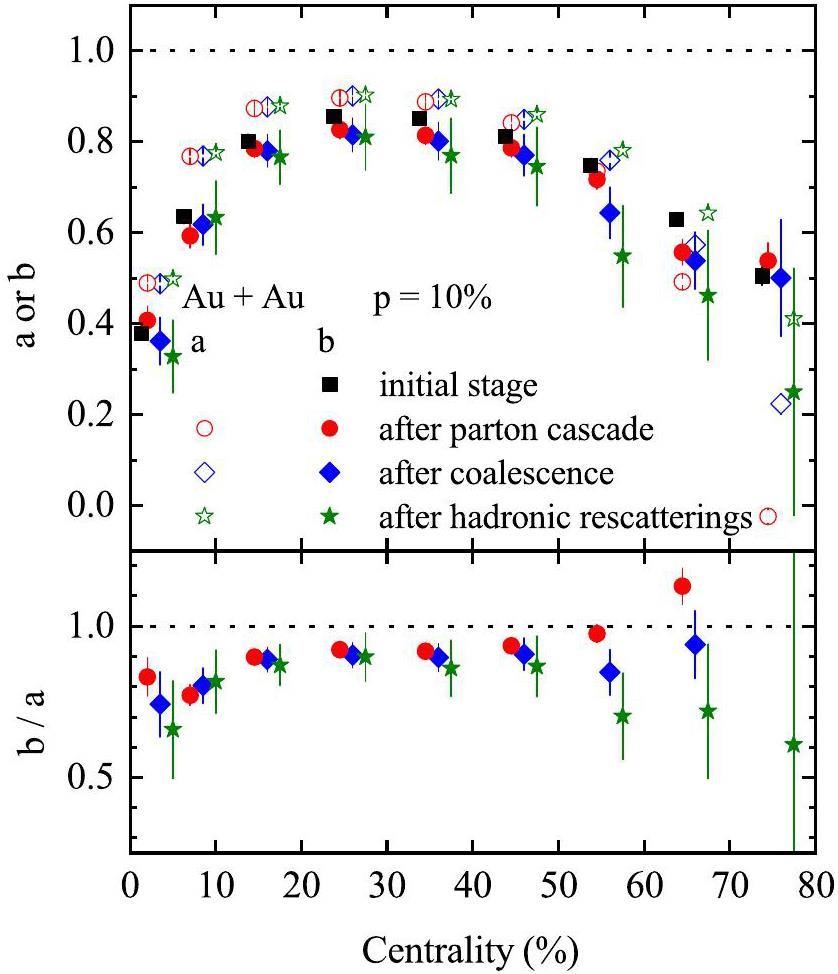
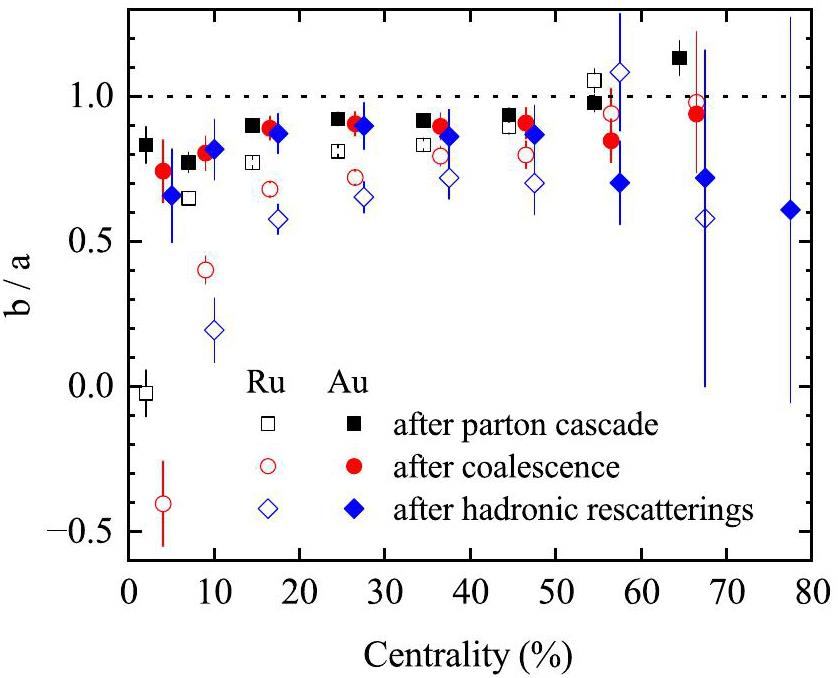
In Ref. [75], the authors demonstrated that the final-state interactions in relativistic heavy-ion collisions significantly suppress the initial charge separation, with a reduction factor reaching up to an order of magnitude. In our previous work [64], we found that, because of the anisotropic overlap zone, these interactions not only reduce the magnitude of the CME current but also alter its direction, resulting in a modified maximum current orientation. Figure 17 shows the centrality dependence of the b/a ratio in the Ru+Ru [64] and Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV for different stages in the AMPT model with a CME strength of p=10%. For the 20–50% centrality bins, the b/a ratios show a decreasing trend with the stage evolution for both Ru+Ru and Au+Au collisions. Furthermore, the b/a values for Ru+Ru collisions are consistently smaller than those for Au+Au collisions across different stages and decrease more rapidly. This observation implies that the effect of the final-state interactions on the decorrelation of CME signals relative to the SP and PP is less pronounced in Au+Au collisions, making it more favorable to detect CME signals using the two-plane method. In our previous AMPT study [64, 75], we showed that assuming $b=a$ in isobar collisions overestimates the final-state CME fraction in the measured $\text{Δ}\gamma$ observable because the signal is subsequently damped and washed out during the final-state evolution of relativistic heavy-ion collisions. We found that $b/a=0.88\pm 0.08$ was larger in Au+Au collisions than in isobar collisions at the same centrality ($b/a=0.65\pm 0.18$), indicating that the signal was damped and washed out to a lesser extent in Au+Au collisions than in isobar collisions.

Fig. 17Full-screen View

(Color online) Centrality dependence of the ratio of b/a in Ru+Ru [64] and Au+Au collisions at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV for different stages from the AMPT model with the CME strength of p=10%. The open and solid symbols represent the results for Ru+Ru and Au+Au, respectively. The data points are shifted along the x axis for clarity

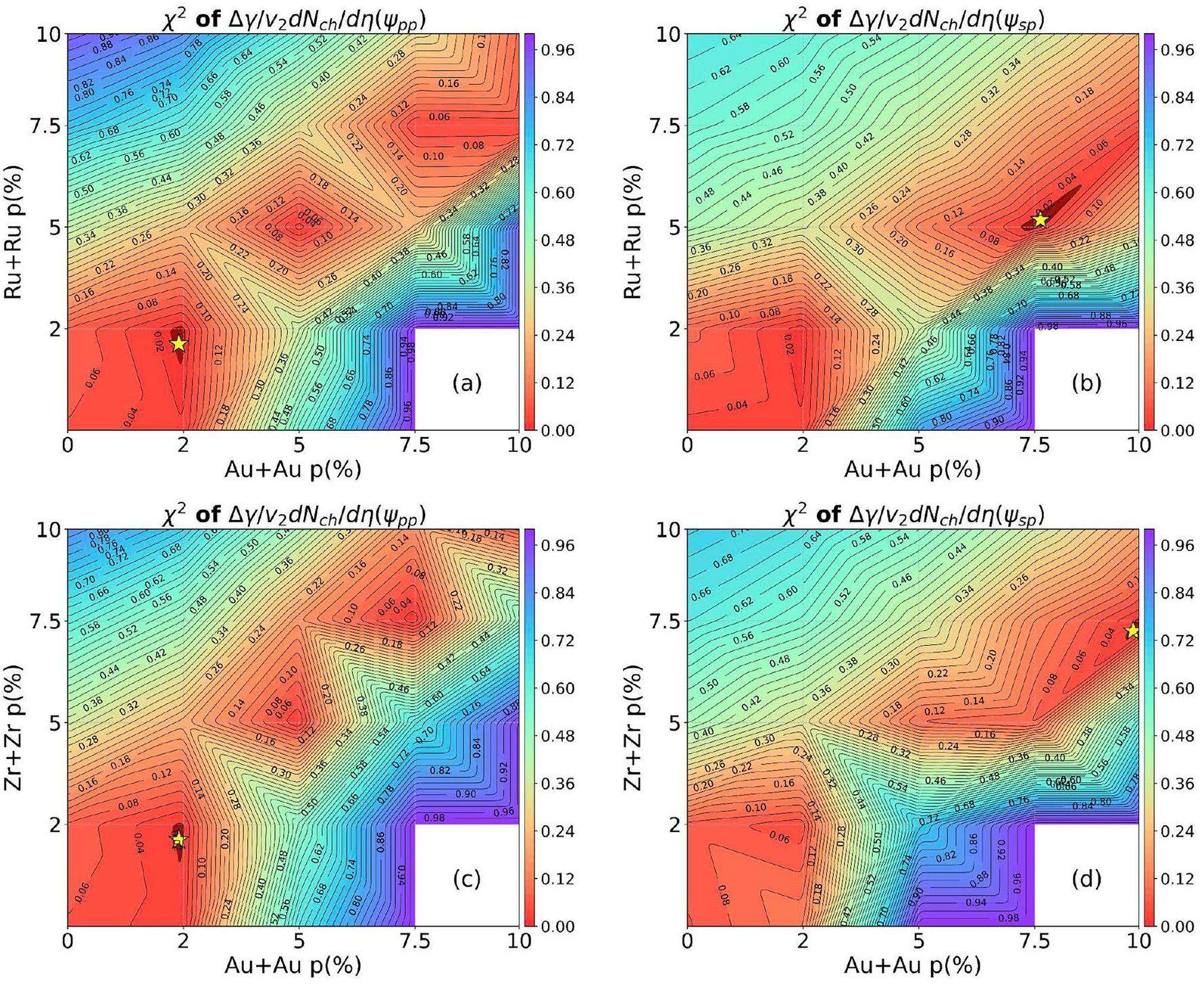
To constrain the CME strengths across Au+Au and isobar collisions simultaneously, we performed a chi-square analysis using the following method. We aimed to compare the CME observable between our results with different CME strengths and the experimental data for those three collision systems simultaneously. The chi-square for a CME observable O in centrality bin i is defined as follows: ${\chi }^2={\displaystyle \sum _{k=0}^n}\frac{{\left(O_i-E_i\right)}^2}{w_o^2}\mathrm{,}$ (16) where we select the CME observable of Oi as the double ratio between Au+Au and isobar collisions to reduce the effect of the background. $O_i=\frac{\frac{{\left\{\text{Δ}\gamma (\psi )\right\}}_{\text{Au}}}{{\left\{v_2\left(\psi \right)\right\}}_{\text{Au}}}\times {\left\{\text{d}{N}_{\text{ch}}/\text{d}\eta \right\}}_{\text{Au}}}{\frac{{\left\{\text{Δ}\gamma (\psi )\right\}}_{\text{Isobar}}}{{\left\{v_2\left(\psi \right)\right\}}_{\text{Isobar}}}\times {\left\{\text{d}{N}_{\text{ch}}/\text{d}\eta \right\}}_{\text{Isobar}}}\mathrm{,}$ (17) where ψ is ψ_PP or ψ_SP, and $\text{d}{N}_{\text{ch}}/\text{d}\eta$ denotes the number of charged particles. Ei represents experimental results. $w_o^2$ represents the error in the calculation results of Oi, and i denotes in the 20–50% centrality bin. Figure 18 shows the results of the two-dimensional normalized chi-square distribution with respect to the different CME signal strengths in Au+Au collisions and the different CME signal strengths in isobar collisions. For the PP plane cases shown in panels (a) and (c), the AMPT simulation results align most closely with the experimental data when the CME strengths for Au+Au, Ru+Ru, and Zr+Zr collisions are all close to 2%. This indicates that, for the PP plane, the experimental results tend to exhibit small CME signals for all three collision systems because the CME signal in the PP plane is relatively insensitive to the SP plane. However, for the SP plane cases shown in panels (b) and (d), the AMPT simulation results align most closely with the experimental data when the CME strength in Au+Au collisions is 7.5% and that in Ru+Ru collisions is 5%, or when the CME strength in Au+Au collisions is 10% and that in Zr+Zr collisions is 7.5%. This indicates that the experimental results for the SP plane tend to exhibit larger CME signals than those for the PP plane for all three collision systems, with stronger signals observed in Au+Au collisions than in isobar collisions because the CME signal exhibits greater sensitivity to the SP plane than to the PP plane.

Fig. 18Full-screen View

(Color online) Two-dimensional normalized chi-square distribution with respect to the different CME signal strengths in Au+Au collisions and the different CME signal strengths in isobar collisions. The chi-square (χ²) value represents the goodness of how well our model describes the experimental data for the CME observable of $\text{Δ}\gamma /v_2\text{d}{N}_{\text{ch}}/\text{d}\eta$. The panels (a) and (b) show the results between Au+Au collisions and Ru+Ru collisions with respect to ψ_PP and ψ_SP, respectively. The panels (c) and (d) show the results between Au+Au collisions and Zr+Zr collisions with respect to ψ_PP and ψ_SP, respectively. Note that the magnitudes of the normalized chi-square value vary with color, where the dark red region, highlighted as a pentagram, indicates the smallest χ² value, which corresponds to the best description

Summary

Using a multiphase transport model with varying CME strengths, we extended our two-plane method analysis from isobar to Au+Au collisions, both at $\sqrt{s_{{}_{\text{NN}}}}=200$ GeV. Our previous isobar collision studies revealed a significant difference (b/a = 0.65 ± 0.18) in the CME signal-to-background ratio between the two planes, complicating CME signal extraction in isobar collisions [64]. However, the current Au+Au analysis demonstrated a reduced difference (b/a = 0.88 ± 0.08) in the CME signal-to-background ratio between the two planes, which enhanced the experimental reliability of the two-plane method for the measurement of Au+Au collisions. Through comprehensive chi-square analysis across the three collision systems, we established that Au+Au collisions exhibit stronger CME signatures compared with isobar systems, which is consistent with a simple picture: Au+Au collisions should have a larger magnetic field because there are more protons [11, 43, 62], particularly when analyzed with respect to the SP. These findings not only validate the improved applicability of the two-plane method in Au+Au collisions but also provide critical insights into the system size dependence of the CME observable, advancing our future experimental measurements of the CME.