Nuclear deformation effects on α-decay half-lives with empirical formula and machine learning

NUCLEAR PHYSICS AND INTERDISCIPLINARY RESEARCH

Nuclear deformation effects on α-decay half-lives with empirical formula and machine learning

Hong-Qiang You，

Xiao-Tao He ，

Ren-Hang Wu，

Shuang-Shuang Zhang，

Jing-Jing Li，

Qing-Hua He，

Hai-Qian Zhang

Nuclear Science and Techniques

Vol.36, No.10

Article number 191

Published in print Oct 2025

Available online 24 Jul 2025

DOI：10.1007/s41365-025-01766-5

CSTR：32136.14.NST.2025.10191

13601

An improved formula considering the deformation effect for the α-decay half-lives is proposed based on WKB barrier penetrability. Using the quadrupole deformation values of the daughter nuclei obtained from the WS4 and FRDM models in the improved formula, the root mean square deviation (RMSD) between the calculated results and experimental data decreased from 0.456 to 0.413 and 0.415, respectively. Although the improved formula did not significantly reduce the overall RMSD, it produced results that better matched the experimental values for nuclei with larger deformations. Additionally, eXtreme Gradient Boosting (XGBoost) models were employed to further reduce the deviations between the calculated α-decay half-lives and experimental data, with the corresponding RMSDs decreasing from 0.413 to 0.295 and from 0.415 to 0.302, respectively. Furthermore, the improved empirical formula and XGBoost models were used to predict the α-decay half-lives of nuclei with Z = 117, 118, 119, and 120. The results suggest that N = 184 is the magic number.

α-decaynuclear deformation effectsmagic numbersSuperheavy nuclei

Introduction

In 1928, α-decay was first described as a quantum mechanical tunneling effect by Gurney and Condon [1] and Gamow [2]. Within Gamow’s picture, the α cluster is preformed in the parent nucleus before it travels through a potential barrier. α-decay has been used as an important tool for understanding nuclear structure. Experimentally, because α-decay is the dominant decay mode of superheavy nuclei, detecting α-decay chains of synthesized superheavy nuclei (SHN) is an important method for identifying them. Consequently, α-decay remains a prominent and active area of study in nuclear physics [3-5].

Many empirical formulas have been proposed to study α-decay half-live. The earliest law for α-decay half-lives was formulated by Geiger and Nutall [6], which states that the logarithm of α-decay half-lives log $\log_{10} T_{1 / 2}$ is linearly correlated with the reciprocal of the square of α-decay energy Qα. Subsequently, many additional empirical formulas have been introduced. Royer developed an analytical formula for α-decay under the framework of the generalized liquid drop model (GLDM) [7, 8]. According to the Viola and Seaborg (VSS) formula, certain parameters are used to describe α-decay half-lives by considering the unpaired nucleon blocking effect [9]. A unified description (UD) formula for the half-life and decay energy of complex cluster radioactivity was presented by Ni et al. [10]. Ren et al. improved the Geiger–Nuttall (G–N) law for α-decay half-lives by incorporating a parameter representing the shell effect in 2012 [11]. Qi proposed a universal decay law (UDL) using the structure of the R-matrix and microscopic mechanism of charged particle emission [12]. Additionally, improved formulas were proposed by adding asymmetry terms or angular momentum effects in Refs. [13, 14, 14-22].

In Refs. [23-30], the authors demonstrated that the deformation of nuclei plays an essential role in α-decay. The total energy, fission barrier, and Coulomb interaction of nuclei have been recalculated by incorporating deformation effects. The penetration probability of α particles is affected by the deformation effects [31]. The deformation and orientation of the daughter nucleus can change the slope and intercept of the linear relationship between $\log_{10} T_{1 / 2}$ and $Q^{- 1 / 2}$ [32]. For SHN, the effects of nuclear deformation on α-decay half-lives were explored [33]. Studies investigating the impact of deformation effects on α-decay half-lives have been conducted based on macro-micro and microscopic models. The results indicate that considering deformation effects in the theoretical model can better describe the experimental values of α-decay half-lives. In this study, the effect of deformation on α-decay half-lives was investigated using an empirical formula. Within the Wentzel-Kramers-Brillouin (WKB) framework, the Coulomb potential containing the quadrupole deformation of daughter nuclei is considered as the total potential energy of the radioactive system. With some approximations and simplifications, the relationship between the deformation term and α-decay half-life is derived. By incorporating the deformation and angular momentum effects [13, 19, 20], an improved empirical formula was used to investigate α-decay half-lives of even Z-even N, even Z-odd N, odd Z-even N, and odd Z-odd N nuclei with $62 ⩽ Z ⩽ 118$ .

Recently, machine learning (ML) algorithms have been used as powerful alternative tools for studying and predicting complex data in nuclear physics [34, 35]. In nuclear structure, ML is used to predict nuclear masses, binding energies, charge radii, etc. [36-49]. ML is a valuable tool for constructing predictive models for nuclear reactions. These models help describe and infer important nuclear reaction data, such as refining the description of reaction data, exploring the initial state of nuclei and reaction geometry, and understanding the reaction mechanism and phase transition [50-53]. Additionally, ML has several advantages in nuclear experiments and the study of dense matter properties [54-59]. Motivated by these advancements, we applied ML to investigate α-decay half-lives of known and unknown nuclei, demonstrating the advantage of this approach in studying α-decay half-lives. In this study, the XGBoost model, which is a powerful and efficient ML algorithm based on gradient boosting decision trees, was employed to further reduce the deviations between experimental and calculated α-decay half-lives of nuclei with $62 ⩽ Z ⩽ 118$ . Additionally, we employed XGBoost models along with an improved formula to predict the behavior of unknown superheavy nuclei.

The remainder of this paper is organized as follows. In Sect. 2, a theoretical method for deducing the improved formula and XGBoost model is presented. The results and discussion are presented in Sect. 3. Finally, a brief summary is presented in the final section.

Theoretical framework

2.1

Improved formula incorporating deformation effect

In 1928, α-decay was described as a quantum tunneling phenomenon through the potential barrier. In the framework of the semiclassical approximation, the α-decay width (or decay constant) is given by $Γ \equiv ℏ ln2 / T_{1 / 2} = P_{0} F P,$ (1) where P₀ is the preformation probability of the α cluster in the parent nucleus. F is the frequency of the α cluster within the barrier, and P is the probability of transmission through the barrier, which is given by the WKB approximation as follows: $P = exp (- \frac{2}{ℏ} \int_{R_{in}}^{R_{out}} \sqrt{2 μ | V (r) - Q |} d r) .$ (2) Here, R_in is the touching radius, given by R_in = Rα + R_d, where Rα and R_d are the hard-sphere radii of the α cluster and daughter nuclei, respectively. R_out is the classical turning point and is given by $R_{out} = Z_{α} Z_{d} e^{2} / Q$ [10]. $μ = A_{α} A_{d} / (A_{α} + A_{d})$ is the reduced mass of the α-core system. $A_{α}$ and $A_{d}$ are the mass numbers of the α cluster and daughter nucleus, respectively.

The deformed Coulomb potential [25, 60] is given by $V (r) = \frac{Z_{α} Z_{d} e^{2}}{r} [1 + \frac{3 R_{0}^{2}}{5 r^{2}} β_{2} Y_{20} (θ)],$ (3) where $R_{0} = 1.15 A_{d}^{1 / 3}$ (fm). $Z_{α}$ and $Z_{d}$ represent the atomic numbers of the α cluster and daughter nucleus, respectively. β₂ is the quadrupole deformation parameter of the daughter nucleus, and $Y_{20} (θ)$ is a harmonic function, where θ is the orientation angle of the emitted alpha particle relative to the symmetric axis of the deformed daughter nucleus. Regarding angle θ, previous studies have shown that the penetration probability $P = \int_{0}^{π} P (θ) \sin (θ) d θ / 2$ is predominantly concentrated around $θ {= 0}^{\circ}$ , which is a pole-to-pole state [61-63]. This alignment minimizes the potential barrier, thereby maximizing penetration probability. Therefore, in this study, adopting $θ {= 0}^{\circ}$ simplifies the model while maintaining its accuracy. Combining the above results, probability P can be expressed as follows: $P = exp (- \frac{2}{ℏ} \int_{R_{in}}^{R_{out}} \sqrt{2 μ} \sqrt{| (\frac{Z_{α} Z_{d} e^{2}}{r} - Q) (1 + 0.162 \frac{Z_{α} Z_{d} e^{2} A_{d}^{2 / 3} β_{2}}{r^{3} (\frac{Z_{α} Z_{d} e^{2}}{r} - Q)}) |} d r),$ (4) By expanding the right-hand term under the square root of Eq. (4) to the first order, we obtain $\begin{array}{l} {log}_{10} P & = - \frac{2}{ℏ ln 10} \sqrt{2 μ} [\int_{R_{in}}^{R_{out}} {(\frac{Z_{α} Z_{d} e^{2}}{r} - Q)}^{1 / 2} d r \\ + 0.081 Z_{α} Z_{d} e^{2} A_{d}^{2 / 3} β_{2} \int_{R_{in}}^{R_{out}} \frac{1}{r^{3} {(\frac{Z_{α} Z_{d} e^{2}}{r} - Q)}^{1 / 2}} d r] \\ = F_{1} + F_{2}, \end{array}$ (5) where F₁ and F₂ are $\begin{array}{l} F_{1} & = - \frac{2}{ℏ ln10} \sqrt{2 μ} \int_{R_{in}}^{R_{out}} {(\frac{Z_{α} Z_{d} e^{2}}{r} - Q)}^{1 / 2} d r, \\ F_{2} & = - \frac{81 \sqrt{2 μ} Z_{α} Z_{d} e^{2} A_{d}^{2 / 3} β_{2}}{500 ℏ ln10} \int_{R_{in}}^{R_{out}} \frac{1}{r^{3} {(\frac{Z_{α} Z_{d} e^{2}}{r} - Q)}^{1 / 2}} d r . \end{array}$ (6) As $R_{out} = Z_{α} Z_{d} e^{2} / Q$ , F₁ can be obtained as follows: $\begin{array}{l} F_{1} & = - \frac{2 \sqrt{2} e^{2}}{ℏ ln10} \sqrt{μ} Z_{α} Z_{d} Q^{- 1 / 2} \\ \times [acrcos (\sqrt{R_{in} / R_{out}}) - (R_{in} / R_{out}) \sqrt{1 - {(R_{in} / R_{out})}^{2}}] . \end{array}$ (7) As the first approximation of the last part of Eq. (7), we obtain $F_{1} = - \frac{\sqrt{2} π e^{2}}{ℏ ln10} \sqrt{μ} Z_{α} Z_{d} Q^{- 1 / 2} + \frac{4 e \sqrt{2 R_{in}}}{ℏ ln10} \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} .$ (8) For α-decay, the variation in R_in is minimal. Therefore, R_in and $\sqrt{R_{in}}$ are treated as constants here. Equation (8) can be simplified to $F_{1} = c_{1} \sqrt{μ} Z_{α} Z_{d} Q^{- 1 / 2} + c_{2} \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2},$ (9) where c₁ and c₂ are constant coefficients.

Similarly, F₂ can be expressed as $\begin{array}{l} F_{2} & = - \frac{81 \sqrt{2 μ} A_{d}^{2 / 3} β_{2}}{1500 ln10 ℏ Z_{α} Z_{d} e^{2}} [- {(\frac{Z_{α} Z_{d} e^{2}}{R_{out}} - Q)}^{3 / 2} + {(\frac{Z_{α} Z_{d} e^{2}}{R_{in}} - Q)}^{3 / 2}] \\ + \frac{81 \sqrt{2 μ} A_{d}^{2 / 3} β_{2} Q}{500 ln10 ℏ Z_{α} Z_{d} e^{2}} (- \sqrt{\frac{Z_{α} Z_{d} e^{2}}{R_{out}} - Q} + \sqrt{\frac{Z_{α} Z_{d} e^{2}}{R_{in}} - Q}) . \end{array}$ (10) As $R_{out} = Z_{α} Z_{d} e^{2} / Q \Rightarrow \frac{Z_{α} Z_{d} e^{2}}{R_{out}} - Q = 0$ , Eq. (10) can be simplified as follows: $\begin{matrix} F_{2} = \frac{81 \sqrt{2 μ} A_{d}^{2 / 3} β_{2}}{1500 ln10 ℏ Z_{α} Z_{d} e^{2}} (\frac{Z_{α} Z_{d} e^{2}}{R_{in}} + 2 Q) \\ \times {(\frac{Z_{α} Z_{d} e^{2}}{R_{in}})}^{1 / 2} {(1 - \frac{Q R_{in}}{Z_{α} Z_{d} e^{2}})}^{1 / 2} . \end{matrix}$ (11) Because $\frac{Q R_{in}}{Z_{α} Z_{d} e^{2}} ≪ 1$ and considering the first approximation of the expression in the last part of Eq. (11), we obtain $\begin{matrix} F_{2} = \frac{81 \sqrt{μ}}{1500 {(R_{in})}^{3 / 2}} A_{d}^{2 / 3} {(Z_{α} Z_{d} e^{2})}^{1 / 2} β_{2} \\ + \frac{81 \sqrt{μ}}{1000 {(R_{in})}^{1 / 2}} A_{d}^{2 / 3} {(Z_{α} Z_{d} e^{2})}^{- 1 / 2} β_{2} Q \\ + \frac{161 \sqrt{μ} {(R_{in})}^{1 / 2}}{1500} A_{d}^{2 / 3} {(Z_{α} Z_{d} e^{2})}^{- 3 / 2} β_{2} Q^{2} \\ = c_{3} \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} A_{d}^{2 / 3} β_{2} + c_{4} \sqrt{μ} {(Z_{α} Z_{d})}^{- 1 / 2} Q A_{d}^{2 / 3} β_{2} \\ + c_{5} \sqrt{μ} {(Z_{α} Z_{d})}^{- 3 / 2} Q^{2} A_{d}^{2 / 3} β_{2}, \end{matrix}$ (12) where c₃, c₄, and c₅ are constants. Similarly, as ${(Z_{α} Z_{d})}^{- 3 / 2} Q^{2} A_{d}^{2 / 3} ≪ {(Z_{α} Z_{d})}^{- 1 / 2} Q A_{d}^{2 / 3}$ , Eq. (12) can be simplified to $F_{2} = c_{3} \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} A_{d}^{2 / 3} β_{2} + c_{4} \sqrt{μ} {(Z_{α} Z_{d})}^{- 1 / 2} Q A_{d}^{2 / 3} β_{2} .$ (13) According to Eq. (1), we have $\begin{array}{l} {log}_{10} T_{1 / 2} & = {log}_{10} (ℏ ln2 / P_{0} F) - {log}_{10} P . \end{array}$ (14) In Ref. [10], $P_{0} {= 10}^{- c_{6} \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} + c_{7}}$ , where c₆ and c₇ are constants based on experimental results. By combining the results of Eqs. (5), (8), and (13), the right-hand side of Eq. (14) can be expressed as the sum of the following terms: $\sqrt{μ} Z_{α} Z_{d} Q^{- 1 / 2}$ , $\sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2}$ , $\sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} A_{d}^{2 / 3} β_{2}$ , $\sqrt{μ} {(Z_{α} Z_{d})}^{- 1 / 2} Q A_{d}^{2 / 3} β_{2}$ , and a constant. The equation for α-decay half-lives can be written as $\begin{array}{l} {log}_{10} T_{1 / 2} & = a \sqrt{μ} Z_{α} Z_{d} Q^{- 1 / 2} + b \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} \\ + c_{1} \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} A_{d}^{2 / 3} β_{2} \\ + c_{2} \sqrt{μ} {(Z_{α} Z_{d})}^{- 1 / 2} Q A_{d}^{2 / 3} β_{2} + h, \end{array}$ (15) where a, b, c₁, c₂, and h are constants to be determined. Additionally, the influence of angular momentum on α-decay half-lives was studied in Refs. [13, 19, 20]. In this paper, we propose an improved empirical formula to investigate the deformation effect on α-decay half-lives, which is given as $\begin{array}{l} \begin{array}{l} {log}_{10} T_{1 / 2} & = a \sqrt{μ} Z_{α} Z_{d} Q^{- 1 / 2} + b \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} \\ + c_{1} \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} A_{d}^{2 / 3} β_{2} \\ + c_{2} \sqrt{μ} {(Z_{α} Z_{d})}^{- 1 / 2} Q A_{d}^{2 / 3} β_{2} \\ + d l (l + 1) + h, \end{array} \end{array}$ (16) where $T_{1 / 2}$ (s) is the half-life of α-decay, and $Q$ (MeV) is the α-decay energy. β₂ denotes quadrupole deformation of the daughter nucleus. $l$ is the minimum angular momentum carried away by an α particle [20]. a, b, c₁, c₂, d, and h are constants to be determined.

To compare the calculated results from Eq. (16) with those obtained when the quadrupole deformation of the daughter nuclei is not taken into account, Eq. (16) becomes $\begin{array}{l} {log}_{10} T_{1 / 2} & = a \sqrt{μ} Z_{α} Z_{d} Q^{- 1 / 2} + b \sqrt{μ} {(Z_{α} Z_{d})}^{1 / 2} \\ + d l (l + 1) + h . \end{array}$ (17)

2.2

Methodology of eXtreme Gradient Boosting (XGBoost) for α-decay half-lives

The XGBoost algorithm is an ensemble ML algorithm that operates within a gradient boosting framework. It utilizes gradient-boosted decision trees, a technique that significantly enhances performance and speed compared with traditional methods. This algorithm efficiently handles classification, regression, and ranked objective functions and offers a more effective solution than its counterparts, such as Decision Trees (DTs) and Random Forests (RFs). In gradient boosting, a series of weak learners or models are combined to create a robust final model, which is derived by considering the weighted sum of all learned models. XGBoost excels in handling small-to-medium-sized, structured, or low-dimensional datasets, making it suitable for various ML problems.

In contrast to the regularized greedy forest model, XGBoost introduces a unique regularized learning objective. This objective is notable for its simplicity, which enhances the efficiency and effectiveness of the model. The predictive function of XGBoost, a key component of this approach, is expressed as follows: ${\hat{y}}_{i} = \sum_{k = 1}^{K} f_{k} (x_{1}), f_{k} \in Γ .$ (18) In this expression, ${\hat{y}}_{i}$ represents the predicted output value for the i-th instance, k denotes the number of regression trees used, and fk represents the structure of each tree. The feature vector for the i-th sample is denoted by xi, and Γ represents the space of all possible regression trees.

To address overfitting, a penalty function is introduced to regularize the learning weights as follows: $O b j^{(t)} = [l (y_{t} - {\hat{y}}_{t}^{(t - 1)}) + g_{t} f_{t} (x_{t}) + \frac{1}{2} h_{t} f_{t}^{2} (x_{t})] + Ω (f_{t}),$ (19) where $g_{i} = \partial_{\hat{y}} (t - 1) l (y_{i}, {\hat{y}}^{(t - 1)})$ and $h_{i} = \partial_{{\hat{y}}^{(t - 1)}}^{2} l (y_{i} - {\hat{y}}^{(k - 1)})$ are the first- and second-order gradient statistics of the loss function, respectively. The constant term is eliminated, yielding the objective function for the i-th step as follows: $O b j^{(t)} = \sum_{t = 1}^{n} [g_{i} f_{t} (x_{l}) + \frac{1}{2} h_{t} f_{t}^{2} (x_{l})] + Ω (f_{t}) .$ (20) The parameters in Eq. (20) can be updated continuously until the stopping criteria are satisfied. Further details on XGBoost can be found in Ref. [64].

In the context of α-decay half-lives, XGBoost considers the experimental α-decay half-lives as the ground truth and learns from the residuals between these data and the predictions made by the empirical formulas in Eqs. (17) and (16). This residual-based learning allows the model to implicitly account for missing physical factors, such as shell effects. The input features include the quadrupole deformation values (β₂) of the daughter nucleus derived from the WS4 and FRDM models, along with the reduced mass (μ) of the α-core system, proton numbers (Zd, Zc) of the daughter nucleus and α cluster, α-decay energy, and other relevant nuclear properties. These features allow the model to identify complex correlations, such as those related to magic and sub-magic numbers, that are not encoded in empirical formulas. Owing to these advantages, XGBoost enhances the ability to capture nonlinear relationships and systematic discrepancies, particularly in regions where empirical formulas typically fail, such as near-shell closures. The XGBoost model is formulated as $R_{n} = T_{1 / 2}^{exp} (x_{n}) - T_{1 / 2}^{cal} (x_{n}) = \sum_{k = 1}^{K} f_{k} (x_{1}), f_{k} \in Γ,$ (21) where Rn represents the residuals for the n-th nucleus, $T_{1 / 2}^{exp} (x_{n})$ is the experimental α-decay half-life, and $T_{1 / 2}^{cal} (x_{n})$ is the calculated α-decay half-life obtained using the empirical formula. The XGBoost model, through its sophisticated learning mechanism, is trained to minimize these residuals, thereby improving the alignment between theoretical predictions and experimental data. The optimization of model parameters, as described in Eq. (20), focuses on minimizing the residuals to achieve the highest possible prediction accuracy.

Results and discussion

3.1

Nuclear deformation effect on α-decay half-lives with improved formula

In this study, the α-decay half-lives of 675 nuclei were extracted, including 183 even-even nuclei, 188 even Z-odd N nuclei, 178 odd Z-even N nuclei, and 126 odd Z-odd N nuclei. The experimental α-decay half-lives, spins, and parities were obtained from the evaluated properties table NUBASE2020 [65], and the α-decay energy was obtained from the evaluated atomic mass table AME2020 [66]. The quadrupole deformation values of the daughter nuclei in Eq. (16) were obtained from the WS4 [67] and FRDM [68] mass models. For different nuclei types, the parameters in Eqs. (17) and (16) were obtained by fitting the experimental α-decay half-lives. The fitting coefficients are listed in Tables 1, 2, and 3. Note that the parameters in Table 1 are fitted by the experimental α-decay half-lives of the nuclei with an absolute quadrupole deformation of less than 0.1. The parameters in Tables 2 and 3 were fitted using the experimental α-decay half-lives of all nuclei.

Parameter values of Eq. (17)

Nuclei	a	b	d	h
Even Z-even N	0.4052	-1.5073	0	-12.1265
Even Z-odd N	0.4101	-1.5008	0.04556	-12.6194
Odd Z-even N	0.4181	-1.4863	0.05270	-14.0310
Odd Z-odd N	0.4163	-1.4782	0.04998	-13.6438

Parameter values of Eq. (16) obtained by fitting the experimental α-decay half-lives, where the values of the quadrupole deformation of the daughter nuclei were taken from the WS4 model [67]

Nuclei	a	b	c₁	c₂	d	h
Even Z-even N	0.4124	-1.5354	-0.0072	0.1536	0	-12.2610
Even Z-odd N	0.4138	-1.4461	-0.0032	0.0693	0.0453	-14.4611
Odd Z-even N	0.4148	-1.4657	-0.0059	0.1316	0.0507	-14.1217
Odd Z-odd N	0.4145	-1.4866	0.0074	-0.0178	0.0511	-13.2610

Same as Table 2, but the values of the quadrupole deformation of the daughter nuclei were taken from the FRDM model [68]

Nuclei	a	b	c₁	c₂	d	h
Even Z-even N	0.4117	-1.5500	-0.0067	0.1527	0	-11.8213
Even Z-odd N	0.4140	-1.4474	-0.0031	0.0647	0.0453	-14.4561
Odd Z-even N	0.4146	-1.4723	-0.0061	0.1420	0.0511	-13.9411
Odd Z-odd N	0.4176	-1.4695	-0.0020	0.0946	0.0516	-14.0118

To precisely compare the different formulas, the root mean square deviation (RMSD) of the nuclei can be calculated as follows: $σ = \sqrt{\sum_{i = 1}^{n} {(\log_{10} T_{1 / 2}^{cal} - \log_{10} T_{1 / 2}^{exp})}_{i}^{2} / n},$ (22) where $T_{1 / 2}^{cal}$ is the calculated α-decay half-life and $T_{1 / 2}^{exp}$ is the experimental α-decay half-life. The RMSDs for the different formulas are listed in Table 4. Using the quadrupole deformation values of the daughter nuclei in Eq. (16), taken from the WS4 and FRDM models, the corresponding σ values are denoted as σ₂ and σ₃, respectively. Additionally, σ₁, σ₄, and σ₅ represent the σ values between the experimental data and calculated results obtained from Eq. (17) and other formulas [8, 13], respectively.

Root mean square deviations between experimental α-decay half-lives and the calculated results obtained by Eq. (17), Eq. (16), and other formulas [8, 13]. σ₁, σ₄, and σ₅ represent the σ deviations between the experimental data and calculated results from Eq. (17) and other formulas [8, 13], respectively. With the quadrupole deformation values of the daughter nuclei in Eq. (16) taken from the WS4 and FRDM models, the corresponding σ deviations are denoted as σ₂ and σ₃, respectively

	Eq. (17)	Eq. (16)		Ref. [8]	Ref. [13]
Nuclei	σ₁	σ₂	σ₃	σ₄	σ₅	No. of nuclei
Even Z-even N	0.406	0.363	0.368	0.376	0.375	183
Even Z-odd N	0.475	0.445	0.445	0.668	0.457	188
Odd Z-even N	0.469	0.412	0.409	0.653	0.425	178
Odd Z-odd N	0.472	0.432	0.439	0.634	0.475	126
Total	0.456	0.413	0.415	0.589	0.428	675

When the quadrupole deformation of the daughter nuclei in Eq. (16) is taken from the WS4 mass model, the σ values decrease from 0.406 to 0.363 for even Z-even N nuclei, from 0.475 to 0.445 for even Z-odd N nuclei, from 0.469 to 0.412 for odd Z-even N nuclei, and from 0.472 to 0.432 for odd Z-odd N nuclei. A similar trend was observed when the quadrupole deformation values were taken from the FRDM model. Among all subsets, the σ values for even Z-even N nuclei were the lowest, with σ₁, σ₂, and σ₃ values of 0.406, 0.363, and 0.368, respectively. This can be attributed to the fact that in the α-decay of even Z-even N nuclei, the angular momentum l carried away by the α particle is always zero, eliminating the ambiguity in determining l, which is not true for other subsets. For the total dataset, the σ₂ and σ₃ values, when compared with the σ₁ value from Eq. (17), decrease from 0.456 to 0.413 and 0.415, respectively. From the σ values, including deformation effects in the empirical formula does not significantly improve describing experimental α-decay half-lives.

Additionally, by fixing the parameters a, b, d, and h in Eq. (17), the deformation-related parameters c₁ and c₂ are independently fitted by the experimental α-decay half-lives. Using this approach, Eq. (16) produces σ= 0.419 and 0.421 with the quadrupole deformation values obtained from WS4 and FRDM, respectively. Compared with the values of σ₂ and σ₃ shown in Table 4, their σ values are higher. Hence, the results calculated from Eq. (16), where the parameters of Eq. (16) are fitted using the experimental α-decay half-lives of all nuclei, will be used in the subsequent discussions on XGBoost optimization and the prediction of α-decay half-lives for superheavy nuclei.

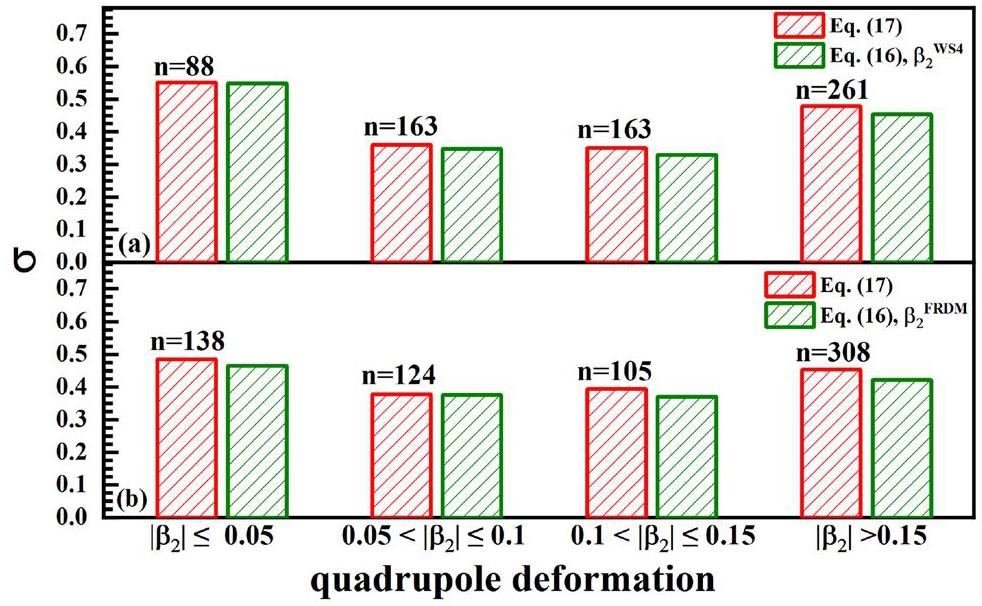
In Fig. 1, the σ deviations of Eqs. (17) and (16) across different quadrupole deformation regions are presented, with the deformation values derived from the WS4 and FRDM models, respectively. For nuclei with small deformations ( $| β_{2} | \leq 0.05$ ), the difference between the two formulas (Eqs. (17) and (16)) is negligible. This suggests that the deformation effect is minimal in this range. In the intermediate deformation range ( $0.05 < | β_{2} | \leq 0.15$ ), the σ values in Eq. (16) are slightly lower than those in Eq. (17), indicating a better consistency with the experimental data in this range. For nuclei with large deformation (|β₂| > 0.15), the deformation-inclusive equation (Eq. (16)) shows a further reduction in the σ values, indicating that considering deformation improves the agreement with experimental data for highly deformed nuclei. Overall, the σ deviations in Eq. (16) are consistently smaller than those in Eq. (17) across all deformation ranges, as shown in Figs. 1(a) and 1(b). Although deformation has little impact on near-spherical nuclei, it becomes increasingly relevant as deformation increases. Although the improved formula does not significantly reduce the overall σ value, it achieves better consistency with experimental data for highly deformed nuclei, with minimal effect on less deformed nuclei.

Fig. 1

(Color online) Root mean square deviations of Eqs. (17) and (16) for nuclei across different deformation regions of the daughter nuclei, with the quadrupole deformation values of daughter nuclei taken from WS4 (a) and FRDM (b) models. The horizontal axis represents the range of deformation values for the daughter nuclei, whereas the vertical axis indicates the root mean square values for nuclei within each deformation range. n represents the number of nuclei present in each deformation interval

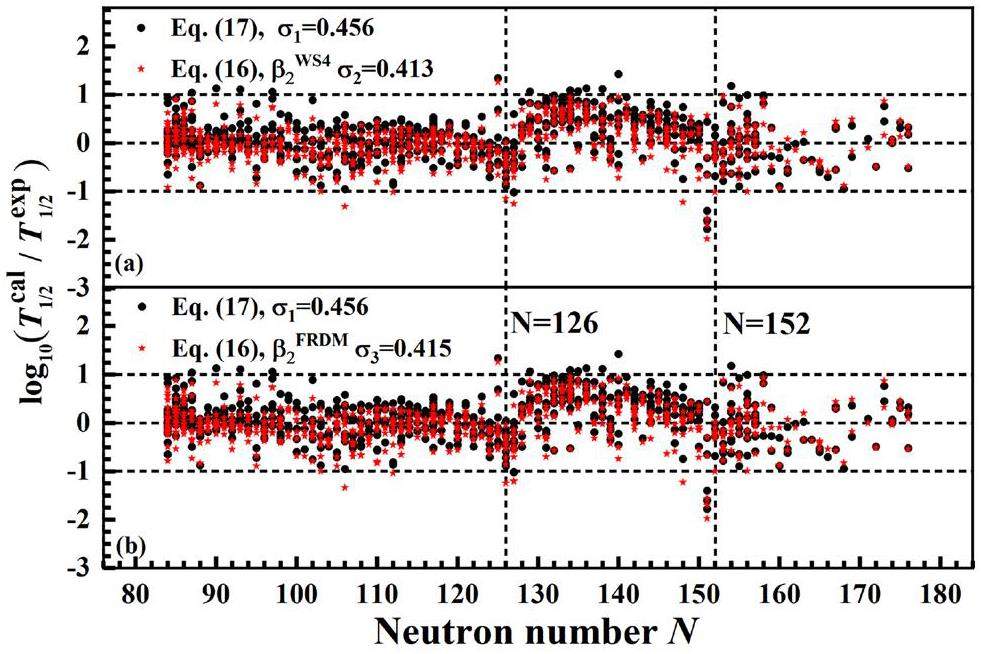
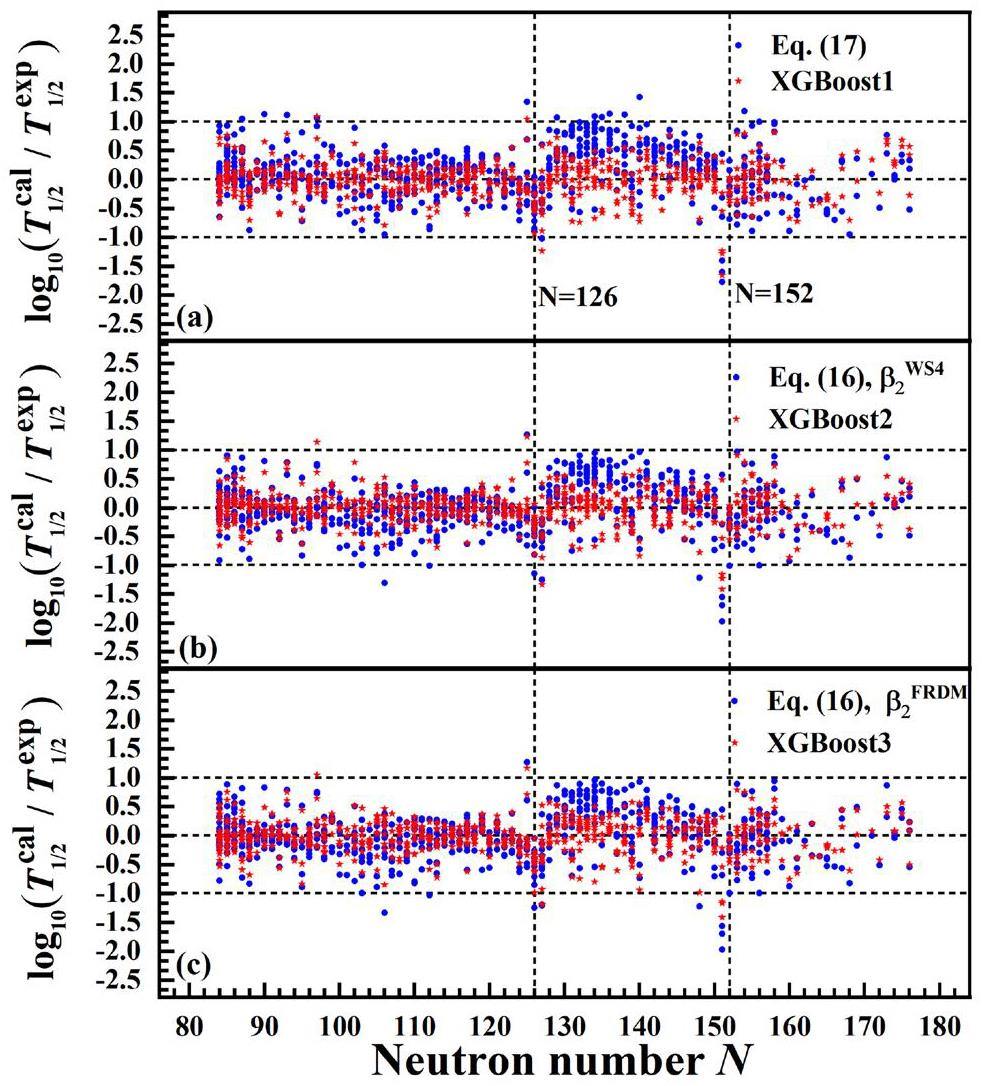
Using the RMSD as an indicator of the accuracy of the formula provides only a rough estimate of its performance. For a more detailed insight, Fig. 2 presents the logarithmic deviations between the experimental data and the results calculated using Eqs. (17) and (16). In Fig. 2(a), the black circles and red stars represent the deviations for Eqs. (17) and (16), respectively, using the deformation values from the WS4 model [67]. Similarly, Fig. 2(b) presents the same analysis using the deformation values from the FRDM model [68]. Points closer to zero indicate better agreement with experimental data, and evidently, the deviations of Eq. (16) (red stars) are more concentrated near zero than those of Eq. (17) (black circles) for both models. A notable feature in Fig. 2 is the large deviations observed near neutron numbers N = 126 and N = 152, where both formulas exhibit significant discrepancies from the experimental data. Previous studies identified N = 126 and N = 152 as magic and sub-magic numbers, respectively [69-71]. These deviations can be attributed to shell effects associated with these neutron numbers, which are not explicitly accounted for in either Eq. (17) or (16). To address this issue, in the following sections, we explore using the XGBoost algorithm to further reduce the σ values of empirical formulas, including nuclei near the magic and sub-magic numbers.

Fig. 2

(Color online) Logarithmic differences between the experimental α-decay half-lives and calculated results obtained by Eqs. (17) and (16), with values of the quadrupole deformation of the daughter nuclei taken from the WS4 (a) and FRDM (b) models, respectively. The dashed lines represent the neutron numbers N = 126, 152, and the deviations of the decimal logarithms of

T_{1 / 2}^{cal} / T_{1 / 2}^{exp}

are 0, -1, and 1, respectively

To gain further insight into the deformation effect on α-decay half-lives, we compared the improved formula of Eq. (16) with other formulas [8, 13]. The experimental data used in this study differ from those in Refs. [8] and [13]. The parameters of the empirical formulas in Refs. [8, 13] were recalibrated using the experimental data obtained in this study. This recalibration resulted in σ values of 0.589 and 0.428, respectively, which were lower than the original σ values of 0.779 and 0.429 with the parameters obtained from Refs. [8] and Ref. [13], respectively. The recalibrated σ values for the four subsets and total dataset are displayed in the fifth and sixth columns of Table 4, respectively. As indicated in the table, the improved formula of Eq. (16) exhibits smaller σ values for the entire set of data than those of the other formulas [8, 13]. This indicates that the improved formula, which incorporates the deformation effect, can be used to study α-decay half-lives.

3.2

Study on α-decay half-lives with eXtreme Gradient Boosting

In this study, we built three XGBoost models to further improve the prediction accuracy of α-decay half-lives, denoted as XGBoost1, XGBoost2, and XGBoost3. For the XGBoost2 and XGBoost3 models, the quadrupole deformation values of the daughter nuclei were obtained from the WS4 and FRDM models, respectively. Additionally, in the XGBoost models, the physical terms of Eqs. (17) and (16) were used as inputs, and the residuals between the calculated and experimental α-decay half-lives served as the output.

The experimental data for 675 nuclei were extracted and divided into two sets: the training set (540 nuclei) and testing set (135 nuclei). The corresponding σ values calculated using the formulas and XGBoost1, XGBoost2, and XGBoost3 models are presented in Table 5. The σ values of the XGBoost1, XGBoost2, and XGBoost3 models show an obvious decrease compared with those of Eqs. (17) and (16) for the training and testing sets. For the entire set, the σ values of XGBoost1, XGBoost2, and XGBoost3 models reduced from 0.456 to 0.316, from 0.413 to 0.295, and from 0.415 to 0.302, respectively. This indicates that XGBoost models can further reduce the deviation between the calculated and experimental α-decay half-lives.

Root mean square deviations between experimental α-decay half-lives and calculated results using Eq. (17), Eq. (16), XGBoost1, XGBoost2, and XGBoost3 for training, testing, and entire sets

	inputs	σ (training set)	σ (testing set)	σ (entire set)
Eq. (17)	-	0.462	0.418	0.456
XGBoost1	(Qα, μ, Zc, Zd, l)	0.310	0.346	0.316
(Eq. (16), $β_{2}^{W S 4}$ )	-	0.427	0.345	0.413
XGBoost2	(Qα, μ, Zc, Zd, l, $β_{2}^{W S 4}$ )	0.288	0.318	0.295
(Eq. (16), $β_{2}^{FRDM}$ )	-	0.430	0.345	0.415
XGBoost3	(Qα, μ, Zc, Zd, l, $β_{2}^{FRDM}$ )	0.301	0.308	0.302

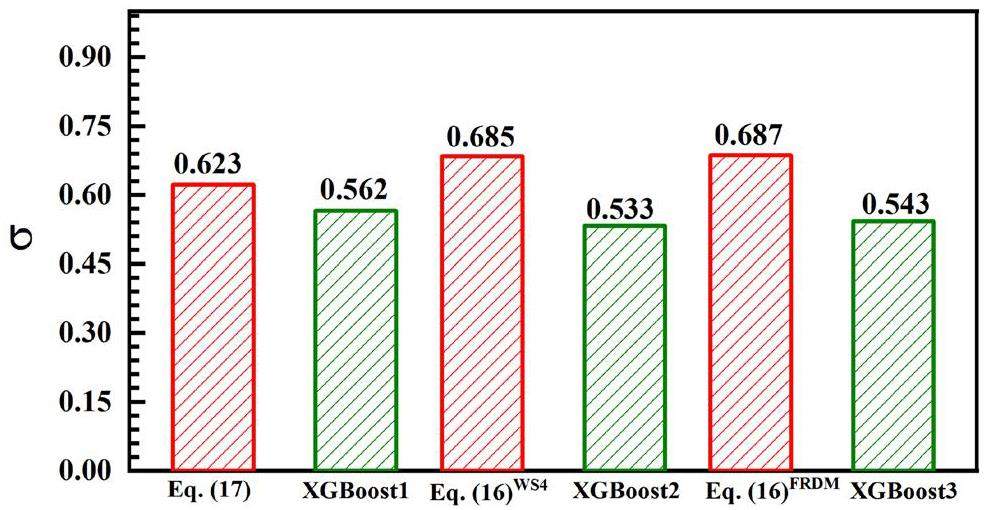
The deviations between the experimental data and results calculated using the empirical formula (blue circles) and XGBoost models (red stars) are illustrated in Fig. 3. As shown in Fig. 3, the majority of blue circles are scattered in the range of ± 1, suggesting larger deviations. By contrast, most red stars fall within the range of ± 0.5, indicating a closer alignment to the zero line. For nuclei near the neutron magic number N = 126 and sub-magic number N = 152, the deviations obtained by XGBoost models are smaller than those from the empirical formulas in Eqs. (17) and (16). To further quantify these differences, Fig. 4 shows the σ values in Eq. (17), Eq. (16), and the XGBoost models (XGBoost1, XGBoost2, and XGBoost3) for nuclei with N=125, 126, 127, 151, 152, and 153. The comparison shows that the σ values for the XGBoost models were reduced from 0.623 to 0.562, from 0.685 to 0.533, and from 0.687 to 0.543, respectively, indicating better consistency with the experimental data than with the empirical formulas. For these nuclei, the larger deviations of the empirical formulas can be attributed to their lack of consideration of shell effects. By contrast, the XGBoost models effectively capture missing physical effects, such as shell effects, by learning from the residuals between the empirical formulas and experimental data. Consequently, the XGBoost models further reduced the deviations for nuclei near the neutron magic number N = 126 and sub-magic number N = 152, providing more accurate predictions.

Fig. 3

(Color online) Logarithmic differences between the experimental data and calculated α-decay half-lives using (a) Eq. (17) and XGBoost1, (b) Eq. (16) and XGBoost2, and (c) Eq. (16) and XGBoost3. The values of quadrupole deformation of the daughter nuclei in Eq. (16) are taken from the WS4 and FRDM models, respectively. The dashed lines represent the deviation of the decimal logarithms of

T_{1 / 2}^{cal} / T_{1 / 2}^{exp}

of 0, -1, and 1, respectively

Fig. 4

(Color online) Root mean square deviations between the experimental data and calculated α-decay half-lives using Eq. (17), Eq. (16), XGBoost1, XGBoost2, and XGBoost3 models for the 53 nuclei at N= 125, 126, 127, 151, 152, and 153

3.3

Predictions of α-decay half-lives of nuclei with Z = 117, 118, 119, and 120

Using the improved formula of Eq. (16), along with the XGBoost2 and XGBoost3 models, we predict the α-decay half-lives of SHN with Z = 117, 118, 119, and 120. In Table 6, the first column lists the α-decay, followed by the α-decay energy and quadrupole deformation of the daughter nuclei (columns 2-5), obtained from WS4 [67] and FRDM [68] mass models, respectively. The spin and parity values of the parent and daughter nuclei in the nuclear ground state were taken from Ref. [72]. Because of challenges in determining the spin and parity of doubly odd SHN, we assume that the minimum angular momentum l carried away by the α particle is zero. As shown in the eighth to last columns, the decimal logarithms of α-decay half-lives, calculated using the improved formula Eq. (16), are shown as $\log_{10} T_{1 / 2}^{Cal 1}$ and $\log_{10} T_{1 / 2}^{Cal 2}$ , with the values of the quadrupole deformation taken from WS4 and FRDM models, respectively. Additionally, $\log_{10} T_{1 / 2}^{XGBoost 1}$ and $\log_{10} T_{1 / 2}^{XGBoost 2}$ were calculated using the XGBoost2 and XGBoost3 models, respectively.

α-decay half-lives of nuclei with Z = 117, 118, 119, and 120, with the α-decay energy and quadrupole deformation obtained by the WS4 [67] and FRDM [68] mass models, respectively. The logarithms of α-decay half-lives were calculated using Eq. (16), denoted by

\log_{10} T_{1 / 2}^{Cal 1}

and

\log_{10} T_{1 / 2}^{Cal 2}

, with the values of the quadrupole deformation obtained from the WS4 and FRDM models, respectively. Additionally,

\log_{10} T_{1 / 2}^{XGBoost 1}

and

\log_{10} T_{1 / 2}^{XGBoost 2}

were calculated using the XGBoost2 and XGBoost3 models, respectively

α transition	$Q_{α}^{WS 4}$ (MeV)	$Q_{α}^{FRDM}$ (MeV)	$β_{2}^{WS 4}$	$β_{2}^{FRDM}$	l	$\log_{10} T_{1 / 2}^{Cal 1}$	$\log_{10} T_{1 / 2}^{XGBoost 1}$	$\log_{10} T_{1 / 2}^{Cal 2}$	$\log_{10} T_{1 / 2}^{XGBoost 2}$
²⁷⁹Ts→²⁷⁵Mc	13.36	12.97	0.1792	0.198	2	-5.734	-5.391	-4.904	-4.306
²⁸⁰Ts→²⁷⁶Mc	13.42	12.79	0.1825	0.198	0	-4.876	-5.454	-4.097	-4.388
²⁸¹Ts→²⁷⁷Mc	13.21	12.32	0.1822	0.198	2	-5.440	-5.619	-3.633	-3.525
²⁸²Ts→²⁷⁸Mc	13.00	12.59	0.1803	0.032	0	-4.039	-4.495	-4.376	-4.512
²⁸³Ts→²⁷⁹Mc	12.86	12.96	-0.0141	-0.011	2	-5.150	-4.800	-5.402	-4.909
²⁸⁴Ts→²⁸⁰Mc	12.66	12.65	-0.0239	0.021	0	-5.023	-5.008	-4.548	-4.447
²⁸⁵Ts→²⁸¹Mc	12.42	12.45	0.0404	0.032	2	-4.123	-4.319	-4.240	-4.287
²⁸⁶Ts→²⁸²Mc	12.24	12.18	-0.0573	0.064	0	-4.385	-4.455	-3.357	-3.201
²⁸⁷Ts→²⁸³Mc	12.02	12.11	-0.0719	0.064	2	-3.403	-3.743	-3.441	-3.446
²⁸⁸Ts→²⁸⁴Mc	11.95	12.01	0.0618	0.064	0	-2.743	-3.121	-2.976	-3.170
²⁸⁹Ts→²⁸⁵Mc	11.96	11.98	0.0707	0.064	2	-3.076	-2.888	-3.152	-2.743
²⁹⁰Ts→²⁸⁶Mc	11.81	11.85	0.0676	0.075	0	-2.364	-2.774	-2.567	-2.752
²⁹¹Ts→²⁸⁷Mc	11.69	11.75	-0.1016	0.064	2	-2.647	-2.806	-2.630	-2.549
²⁹²Ts→²⁸⁸Mc	11.72	11.71	0.0654	0.064	0	-2.178	-2.141	-2.282	-2.021
²⁹³Ts→²⁸⁹Mc	11.60	11.40	0.062	0.064	2	-2.255	-2.294	-1.805	-1.565
²⁹⁴Ts→²⁹⁰Mc	11.35	11.29	0.0544	0.053	0	-1.363	-1.204	-1.306	-0.965
²⁹⁵Ts→²⁹¹Mc	11.27	11.55	-0.0729	-0.042	2	-1.570	-1.741	-2.312	-2.218
²⁹⁶Ts→²⁹²Mc	11.48	11.64	-0.062	-0.042	0	-2.678	-2.359	-2.511	-2.007
²⁹⁷Ts→²⁹³Mc	11.59	11.76	-0.0555	-0.021	2	-2.363	-2.621	-2.786	-2.712
²⁹⁸Ts→²⁹⁴Mc	11.49	11.86	-0.0392	-0.021	0	-2.523	-2.811	-2.956	-3.001
²⁹⁹Ts→²⁹⁵Mc	11.43	11.86	-0.0334	-0.021	2	-1.951	-1.686	-3.021	-2.512
³⁰⁰Ts→²⁹⁶Mc	11.53	11.88	-0.0319	-0.011	0	-2.536	-2.401	-2.964	-2.679
³⁰¹Ts→²⁹⁷Mc	11.59	11.93	-0.0276	-0.011	2	-2.323	-1.957	-3.166	-2.612
³⁰²Ts→²⁹⁸Mc	12.20	12.75	-0.0154	-0.011	0	-3.959	-4.070	-4.891	-4.898
³⁰³Ts→²⁹⁹Mc	12.75	12.74	-0.0087	0	2	-4.918	-4.509	-4.918	-4.417
³⁰⁴Ts→³⁰⁰Mc	12.52	12.82	-0.0145	0	0	-4.642	-5.088	-4.988	-5.366
³⁰⁵Ts→³⁰¹Mc	12.06	12.69	-0.0214	0	2	-3.413	-3.229	-4.813	-4.475
³⁰⁶Ts→³⁰²Mc	11.58	12.40	-0.0277	0.011	0	-2.629	-2.864	-4.046	-4.195
³⁰⁷Ts→³⁰³Mc	10.90	12.24	-0.0466	0.011	1	-0.785	-0.473	-4.026	-3.480
³⁰⁸Ts→³⁰⁴Mc	10.33	11.49	-0.0575	0.021	0	0.375	0.186	-1.908	-1.883
³⁰⁹Ts→³⁰⁵Mc	9.99	10.80	-0.1822	-0.011	3	2.346	2.788	-0.048	0.579
³¹⁰Ts→³⁰⁶Mc	9.73	10.37	-0.1855	0.044	0	0.974	1.273	1.115	1.415
³¹¹Ts→³⁰⁷Mc	9.42	10.15	-0.2	0.054	2	3.924	3.842	1.488	1.311
³¹²Ts→³⁰⁸Mc	9.05	9.78	-0.2111	0.065	0	2.968	2.905	2.923	2.805
²⁸¹Og→²⁷⁷Lv	13.77	13.15	0.1787	0.186	5	-5.274	-5.254	-4.129	-3.825
²⁸²Og→²⁷⁸Lv	13.49	13.12	0.1799	0	0	-6.582	-6.431	-6.335	-5.864
²⁸³Og→²⁷⁹Lv	13.32	13.20	0.1792	0.032	7	-3.262	-3.395	-3.171	-3.062
²⁸⁴Og→²⁸⁰Lv	13.21	13.56	-0.0262	0	0	-6.475	-6.502	-7.191	-7.133
²⁸⁵Og→²⁸¹Lv	13.05	13.24	0.0363	0.032	0	-5.399	-5.362	-5.788	-5.692
²⁸⁶Og→²⁸²Lv	12.89	13.05	0.0479	0.053	0	-5.698	-5.463	-6.066	-5.741
²⁸⁷Og→²⁸³Lv	12.77	12.96	0.056	0.064	0	-4.820	-4.884	-5.204	-5.084
²⁸⁸Og→²⁸⁴Lv	12.59	12.86	-0.0765	0.064	0	-5.257	-5.026	-5.662	-5.215
²⁸⁹Og→²⁸⁵Lv	12.56	12.76	0.0711	0.075	0	-4.370	-4.664	-4.787	-4.914
²⁹⁰Og→²⁸⁶Lv	12.57	12.68	0.075	0.075	0	-5.008	-4.771	-5.273	-4.896
²⁹¹Og→²⁸⁷Lv	12.39	12.55	0.075	0.075	2	-3.728	-3.781	-4.075	-3.934
²⁹²Og→²⁸⁸Lv	12.21	12.39	0.0735	0.075	0	-4.248	-4.392	-4.671	-4.676
²⁹³Og→²⁸⁹Lv	12.21	12.34	0.0711	0.075	2	-3.344	-3.807	-3.624	-3.867
²⁹⁴Og→²⁹⁰Lv	12.17	12.37	0.0687	0.064	0	-4.163	-3.963	-4.649	-4.223
²⁹⁵Og→²⁹¹Lv	11.88	11.92	0.0617	0.064	0	-2.857	-3.270	-2.962	-3.192
²⁹⁶Og→²⁹²Lv	11.73	12.28	0.0532	-0.073	0	-3.176	-3.102	-4.703	-4.420
²⁹⁷Og→²⁹³Lv	12.08	12.38	-0.0789	-0.063	0	-3.385	-3.801	-4.055	-4.241
²⁹⁸Og→²⁹⁴Lv	12.16	12.49	-0.0651	-0.042	0	-4.279	-3.902	-5.112	-4.549
²⁹⁹Og→²⁹⁵Lv	12.02	12.51	-0.0507	-0.021	2	-2.968	-2.939	-4.044	-3.709
³⁰⁰Og→²⁹⁶Lv	11.93	12.51	-0.0441	-0.011	0	-3.733	-3.926	-5.093	-5.066
³⁰¹Og→²⁹⁷Lv	12.00	12.56	-0.0396	0	2	-2.903	-3.012	-4.138	-4.000
³⁰²Og→²⁹⁸Lv	12.02	12.62	-0.0336	0	0	-3.923	-3.913	-5.305	-5.175
³⁰³Og→²⁹⁹Lv	12.58	13.38	-0.0197	0	4	-3.566	-3.666	-5.179	-5.227
³⁰⁴Og→³⁰⁰Lv	13.10	13.39	-0.0136	0	0	-6.232	-5.888	-6.863	-6.450
³⁰⁵Og→³⁰¹Lv	12.89	13.45	-0.0188	0	2	-4.837	-4.617	-5.950	-5.621
³⁰⁶Og→³⁰²Lv	12.46	13.35	-0.0264	0	0	-4.906	-5.248	-6.785	-7.042
³⁰⁷Og→³⁰³Lv	11.90	12.57	-0.0397	0.011	2	-2.690	-2.802	-4.152	-4.016
³⁰⁸Og→³⁰⁴Lv	11.18	12.10	-0.0484	0	0	-1.893	-1.810	-4.168	-3.900
³⁰⁹Og→³⁰⁵Lv	10.70	11.07	-0.0584	0.022	2	0.359	0.422	-0.626	-0.288
³¹⁰Og→³⁰⁶Lv	10.41	10.74	-0.1812	0.044	0	0.268	0.534	-0.795	-0.415
³¹¹Og→³⁰⁷Lv	10.08	9.98	-0.2049	-0.042	2	2.177	2.561	2.441	2.917
³¹²Og→³⁰⁸Lv	9.74	10.05	-0.207	0.055	0	2.406	1.999	1.131	0.706
³¹³Og→³⁰⁹Lv	8.63	9.72	-0.2135	0.066	0	6.890	7.432	2.925	3.570
²⁸⁵119→²⁸¹Ts	13.60	14.06	0.0304	0	2	-5.998	-5.813	-6.979	-6.712
²⁸⁶119→²⁸²Ts	13.42	13.75	0.0401	0.043	0	-5.494	-5.914	-6.112	-6.442
²⁸⁷119→²⁸³Ts	13.26	13.37	0.0524	0.064	2	-5.288	-5.535	-5.497	-5.466
²⁸⁸119→²⁸⁴Ts	13.20	13.57	-0.0751	0.075	0	-6.040	-5.900	-5.620	-5.264
²⁸⁹119→²⁸⁵Ts	13.13	13.47	-0.0845	0.075	2	-5.310	-5.027	-5.656	-5.025
²⁹⁰119→²⁸⁶Ts	13.04	13.31	0.0721	0.075	0	-4.465	-4.804	-5.117	-5.316
²⁹¹119→²⁸⁷Ts	13.02	13.24	0.0773	0.075	2	-4.773	-4.409	-5.215	-4.657
²⁹²119→²⁸⁸Ts	12.87	13.08	0.0776	0.086	0	-4.073	-3.611	-4.610	-4.013
²⁹³119→²⁸⁹Ts	12.69	12.92	0.0746	0.075	2	-4.099	-3.580	-4.581	-3.869
²⁹⁴119→²⁹⁰Ts	12.70	12.85	0.0739	0.075	0	-3.731	-3.474	-4.187	-3.790
²⁹⁵119→²⁹¹Ts	12.73	12.94	0.0732	0.075	2	-4.191	-4.541	-4.620	-4.776
²⁹⁶119→²⁹²Ts	12.45	12.98	0.0733	0.075	0	-3.191	-3.550	-4.452	-4.671
²⁹⁷119→²⁹³Ts	12.40	12.90	-0.0856	-0.073	2	-3.716	-3.561	-4.890	-4.418
²⁹⁸119→²⁹⁴Ts	12.69	13.09	-0.0806	-0.073	0	-5.037	-5.387	-5.335	-5.430
²⁹⁹119→²⁹⁵Ts	12.74	13.08	-0.0721	-0.052	2	-4.453	-4.813	-5.218	-5.312
³⁰⁰119→²⁹⁶Ts	12.55	13.04	-0.0601	-0.032	0	-4.559	-4.939	-5.048	-5.185
³⁰¹119→²⁹⁷Ts	12.40	13.08	-0.0494	-0.032	0	-3.977	-4.229	-5.474	-5.483
³⁰²119→²⁹⁸Ts	12.40	13.05	-0.0431	0	0	-4.096	-4.639	-4.925	-5.282
³⁰³119→²⁹⁹Ts	12.39	13.11	-0.0355	0	2	-3.632	-3.256	-5.147	-4.523
³⁰⁴119→³⁰⁰Ts	12.91	13.86	-0.02	0	0	-4.972	-4.737	-6.519	-6.215
³⁰⁵119→³⁰¹Ts	13.40	13.86	0.0147	0	2	-5.650	-5.384	-6.607	-6.250
³⁰⁶119→³⁰²Ts	13.18	13.92	-0.0198	0	0	-5.525	-5.464	-6.631	-6.501
³⁰⁷119→³⁰³Ts	12.76	13.39	-0.0287	0	0	-4.721	-5.152	-6.012	-6.358
³⁰⁸119→³⁰⁴Ts	12.04	12.17	-0.0396	0.011	0	-3.247	-2.919	-2.970	-2.456
³⁰⁹119→³⁰⁵Ts	11.35	11.70	-0.0508	0	3	-0.836	-1.338	-1.722	-2.005
³¹⁰119→³⁰⁶Ts	10.86	10.67	-0.0616	-0.032	0	-0.517	-0.651	0.666	0.752
³¹¹119→³⁰⁷Ts	10.76	10.32	-0.1895	0	0	0.098	0.171	1.315	1.434
³¹²119→³⁰⁸Ts	10.56	9.90	-0.1936	-0.397	0	-0.908	-0.512	1.916	2.463
³¹³119→³⁰⁹Ts	9.37	10.06	-0.2055	0.066	2	4.825	5.333	2.398	2.812
³¹⁴119→³¹⁰Ts	8.97	9.55	-0.2136	-0.407	0	3.896	4.091	3.085	3.233
³¹⁵119→³¹¹Ts	8.65	9.36	-0.2137	-0.406	1	7.318	7.005	4.635	4.535
³¹⁶119→³¹²Ts	8.67	9.20	-0.2369	-0.406	0	7.050	6.877	5.404	5.308
³¹⁷119→³¹³Ts	9.20	9.06	-0.4273	-0.416	3	5.859	5.518	6.462	6.180
²⁸⁷120→²⁸³Og	13.84	13.96	-0.0531	0.043	4	-5.595	-5.706	-5.729	-5.590
²⁸⁸120→²⁸⁴Og	13.71	13.85	-0.0663	0.064	0	-7.039	-7.317	-7.068	-7.147
²⁸⁹120→²⁸⁵Og	13.69	13.75	-0.0797	0.075	0	-6.253	-6.497	-6.213	-6.227
²⁹⁰120→²⁸⁶Og	13.68	13.75	-0.0872	0.075	0	-7.028	-6.996	-6.852	-6.641
²⁹¹120→²⁸⁷Og	13.48	13.87	-0.096	0.075	2	-5.586	-6.056	-6.164	-6.394
²⁹²120→²⁸⁸Og	13.44	13.78	0.0788	0.086	0	-6.222	-6.226	-6.874	-6.743
²⁹³120→²⁸⁹Og	13.37	13.65	0.0786	0.086	2	-5.206	-4.958	-5.741	-5.304
²⁹⁴120→²⁹⁰Og	13.22	13.49	-0.1098	0.086	0	-6.132	-5.759	-6.338	-5.857
²⁹⁵120→²⁹¹Og	13.25	13.46	0.0762	0.075	2	-4.954	-4.862	-5.386	-5.101
²⁹⁶120→²⁹²Og	13.32	13.59	0.0752	0.075	0	-5.989	-6.199	-6.554	-6.624
²⁹⁷120→²⁹³Og	13.12	13.65	0.0751	0.075	0	-4.970	-5.153	-6.021	-6.065
²⁹⁸120→²⁹⁴Og	12.98	13.24	-0.0863	0.064	0	-5.595	-5.896	-5.915	-6.019
²⁹⁹120→²⁹⁵Og	13.23	13.73	-0.0849	-0.084	0	-5.343	-5.652	-6.325	-6.379
³⁰⁰120→²⁹⁶Og	13.29	13.70	-0.075	-0.063	0	-6.233	-6.400	-7.155	-7.105
³⁰¹120→²⁹⁷Og	13.04	13.62	-0.065	-0.042	2	-4.654	-4.944	-5.800	-5.842
³⁰²120→²⁹⁸Og	12.87	13.55	0.0382	-0.032	0	-5.155	-5.582	-6.773	-7.067
³⁰³120→²⁹⁹Og	12.79	13.51	-0.0448	-0.011	2	-4.104	-3.690	-5.556	-4.860
³⁰⁴120→³⁰⁰Og	12.74	13.55	-0.0355	0	0	-4.999	-5.520	-6.684	-7.019
³⁰⁵120→³⁰¹Og	13.26	14.26	-0.0214	0	2	-5.060	-4.988	-6.954	-6.729
³⁰⁶120→³⁰²Og	13.77	14.28	0.0139	0	0	-6.971	-6.621	-8.042	-7.641
³⁰⁷120→³⁰³Og	13.50	13.62	0.0191	0	4	-4.873	-4.879	-5.125	-5.078
³⁰⁸120→³⁰⁴Og	12.95	12.96	-0.0297	0	0	-5.426	-5.655	-5.503	-5.616
³⁰⁹120→³⁰⁵Og	12.14	11.77	-0.0416	-0.021	0	-2.932	-3.279	-2.053	-2.157
³¹⁰120→³⁰⁶Og	11.48	11.29	-0.0527	0	0	-2.063	-1.779	-1.673	-1.204
³¹¹120→³⁰⁷Og	11.18	10.76	-0.1882	-0.397	2	-0.300	-0.385	0.877	1.003
³¹²120→³⁰⁸Og	11.20	10.71	-0.1933	-0.397	0	-1.344	-1.316	-0.251	-0.074
³¹³120→³⁰⁹Og	11.01	10.50	-0.194	-0.407	2	0.160	0.431	1.648	2.098
³¹⁴120→³¹⁰Og	10.74	10.33	-0.2019	-0.407	0	-0.043	0.109	0.961	1.208
³¹⁵120→³¹¹Og	9.41	10.16	-0.2323	-0.407	0	4.792	5.516	2.425	2.993
³¹⁶120→³¹²Og	9.17	9.94	0.3893	-0.416	0	4.035	3.735	2.277	2.114
³¹⁷120→³¹³Og	9.91	9.83	-0.4157	-0.416	3	3.757	4.187	4.041	4.669
³¹⁸120→³¹⁴Og	9.91	9.66	-0.425	-0.416	0	2.772	2.722	3.266	3.408

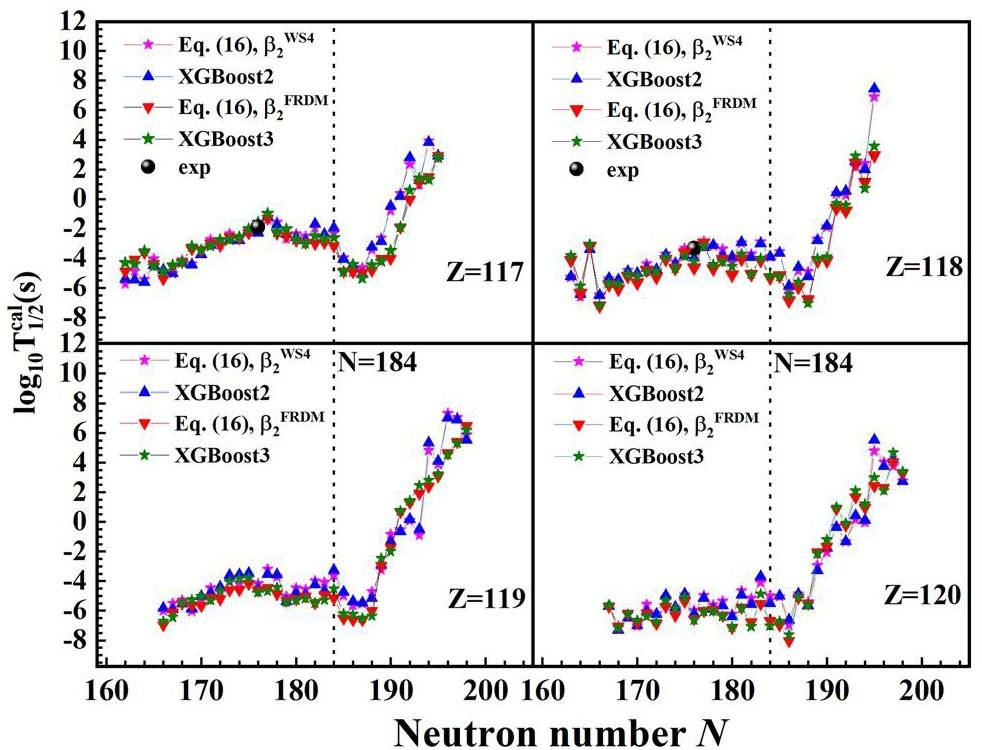
The calculated α-decay half-lives of the nuclei with Z = 117, 118, 119, and 120 are plotted in Fig. 5, respectively. As shown in Fig. 5, the calculated α-decay half-lives for ²⁹³Ts, obtained using the improved formula ( $\log_{10} T_{1 / 2}^{Cal 1}$ and $\log_{10} T_{1 / 2}^{Cal 2}$ ) and the XGBoost models( $\log_{10} T_{1 / 2}^{XGBoost 1}$ and $\log_{10} T_{1 / 2}^{XGBoost 2}$ ), are in good agreement with the experimental α-decay half-lives. For ²⁹⁴Og, the calculated α-decay half-life obtained by the XGBoost2 model was much closer to the experimental α-decay half-lives than those obtained by other models. Fig. 5 reveals that when neutron numbers surpass N = 184, the α-decay half-lives of nuclei Z = 117, 118, 119, and 120 exhibit a rapid decrease of more than 1.8 orders of magnitude. This phenomenon reflects strong shell effects, suggesting that N = 184 is a neutron magic number. Additionally, the decimal logarithms of α-decay half-life values for nuclei with Z = 117, 118, 119, and 120 ranged from -8 to 10. If these nuclei could be synthesized in a laboratory, the majority could be detected experimentally.

Fig. 5

(Color online) Logarithms of α-decay half-lives of nuclei with Z = 117, 118, 119, and 120 using Eq. (16), XGBoost2, and XGBoost3 with Qα obtained by the WS4 [67] and FRDM [68] nuclear mass table. The black dashed lines denote the neutron number N = 184

Summary

In summary, this study investigated the impact of deformation effects on α-decay half-lives using an improved formula within the WKB framework. By incorporating the quadrupole deformation of the daughter nucleus into the Coulomb potential, the improved formula provides a refined description of the α-decay half-lives of nuclei with $62 ⩽ Z ⩽ 118$ . Although the improved formula does not significantly reduce the overall σ value, it provides calculations that align more closely with the experimental values for nuclei with larger deformations. Furthermore, XGBoost models have been employed to further reduce the deviations between experimental and calculated α-decay half-lives using the improved formula. The results suggest that the XGBoost model can effectively reduce the RMSDs between the calculated and experimental values across all nuclei, including those near magic and sub-magic numbers. Additionally, the improved formula and XGBoost models that yield low σ values were extended to predict α-decay half-lives for nuclei with Z = 117, 118, 119, and 120. When neutron numbers surpass N = 184, the α-decay half-lives of nuclei Z = 117, 118, 119, and 120 exhibit a rapid decrease of more than 1.8 orders of magnitude. These results indicate that N = 184 is a magic number.

References

R.W. Gurney, E.U. Condon,

Wave mechanics and radioactive disintegration

. Nature 122, 1476-4687 (1928). https://doi.org/10.1038/122439a0