Irradiation terminal and beam line control system of accelerator

Figure 1a shows the passive beam delivery system installed on the shallow-seated (80.55 MeV/n carbon ions) FLASH irradiation terminal of the HIRFL. Because the accelerator can provide a constant beam current, the scanning magnet deflects the pencil beam quickly and continuously in a zigzag scanning manner to achieve transverse beam diffusion and generate a larger radiation field [31]. The X and Y directions are high- and low-frequency zigzag periodic current-driven magnets that control the target volume of irradiation by adjusting different frequencies in the X and Y directions. Thus, the magnetic scanning system guides the focused beam to draw the target volume at the center of the treatment terminal in a Lissajous or raster-like pattern depending on the difference between the fast and slow frequencies. The terminal monitoring system consisted of three large-area penetrating ICs (Fig. 1a): a dose IC, an integrated dose-position monitoring FLASH IC, and a position monitoring IC. The output signal of the FLASH IC was directly connected to the FEMTO variable-gain low-noise amplifier for I/V conversion, and a small current was directly converted into the available voltage. The data acquisition system was based on a National Instruments (NI) cRIO 9063 with a real-time operating system and an NI 9215 analog input card to achieve rapid acquisition. During the irradiation process, when the dose measured by the dose IC reached a set value, the automatic sample-change system changed to the next sample. If the position IC monitors that the beam profile uniformity does not meet the experimental requirements, the irradiation of the interlocking system is stopped [32, 33].

Fig. 1Full-screen View

(Color online) FLASH shallow-seated irradiation terminal beam monitoring and dose measurement schematic at HIRFL (a). Schematic of the generation of a pulse beam (b)

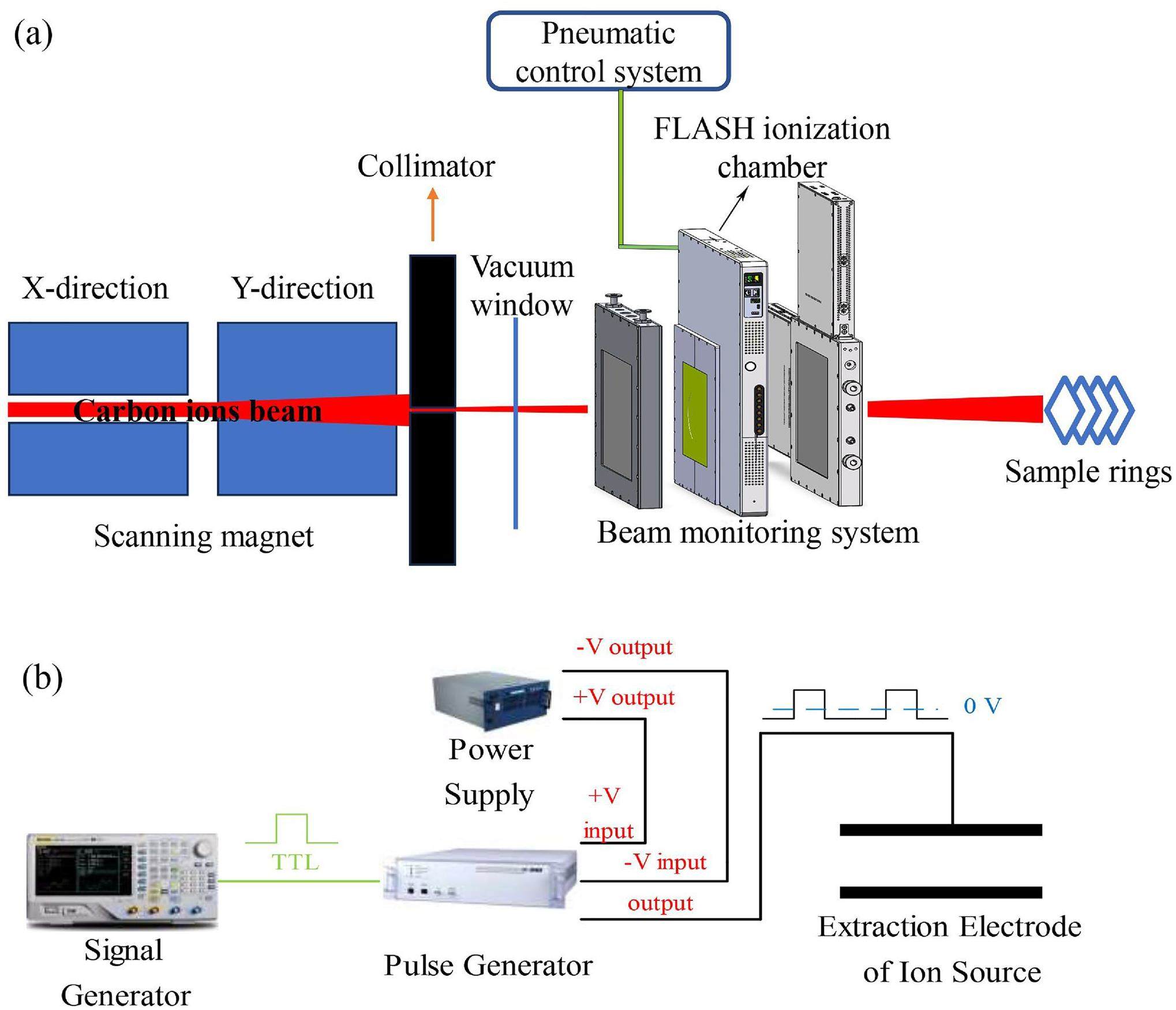
Through the chopper system, a pulse beam was generated and cut off, and the response accuracy reached the nanosecond level to satisfy the FLASH irradiation requirements. The beam-time structure adjusts the signal characteristics to excite the pulse generator by setting parameters such as the frequency, amplitude, and duty cycle of the pulse through the signal generator. The direct-current (DC) voltage generated by the high-voltage DC power supply enters the pulse generator and is modulated by the transistor-–transistor logic gate signal generated by the signal generator. The output voltage of the high-voltage power supply was compared with the set reference voltage. When the difference between the two reaches a specified threshold, the counter triggers the output pulse signal, and its output is loaded onto the ion source extraction electrode. When the carbon-ion beam is extracted, pulse modulation of the carbon-ion beam current is achieved. A schematic of this process is shown in Fig. 1b.

Physical process analysis

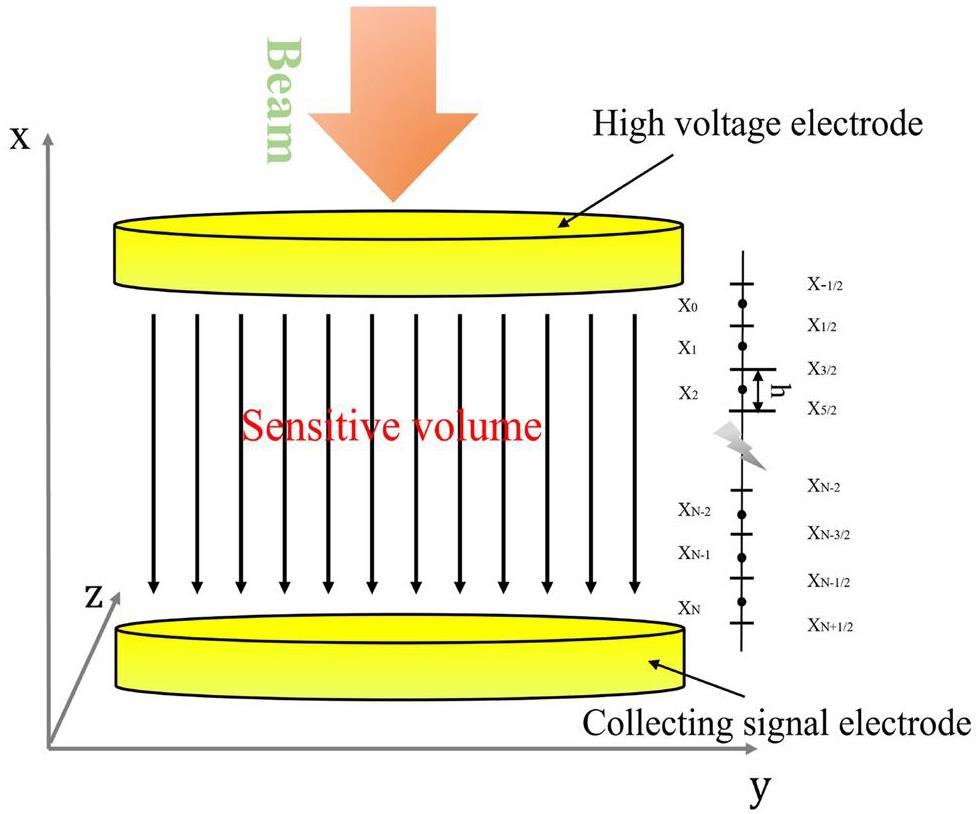
The FLASH IC is based on a parallel-plate IC. The chamber can be simplified as a high-voltage electrode, gas gap, and collection-signal electrode. The air gap thickness was 4 mm. Air was used as the working gas in the experiments. During the experiment, the entire sensitive volume was ensured to have a uniform electric field in the FLASH IC. Simultaneously, there is a high line-energy transfer of the radiation mass, such as carbon ions. We should consider not only volume recombination but also initial recombination based on the amorphous track structure theory [34, 35].

To this end, the following four-step procedure was implemented: (1) Electrons and cations are generated according to the intensity distribution of the ion beam and the resulting ionization density between the two electrodes with a gap size of d. (2) The corresponding charge is recombined according to the coefficients (recombination, attachment, and diffusion coefficients). (3) The electric field in the sensitive volume of the FLASH IC was calculated, and the superposition of the external electric field caused by the applied voltage and the internal electric field generated by the charge carrier was calculated. (4) The electron-ion pair drifts with the calculated electric field.

In the experiment, the particle current density ${\overrightarrow{J}}_{\pm }$ of the positive and negative ions is in units of charge carriers per unit area per unit time, which consists of the contribution of drift caused by the electric field $\overrightarrow{E}$ and diffusion D_± caused by the concentration gradient, and is given as ${\overrightarrow{J}}_{\pm }\left(\overrightarrow{r}\mathrm{,}t\right)=-D_{\pm }\nabla {\rho }_{\pm }\left(\overrightarrow{r}\mathrm{,}t\right)\pm \frac{p_0}{p}\overrightarrow{E}{\mu }_{\pm }{\rho }_{\pm }\left(\overrightarrow{r}\mathrm{,}t\right),$ (7) where n_± is the charge carrier density and μ_± is the mobility of the positive and negative ions. We introduced ion recombination and attachment coefficients into the continuous equation as follows: $\frac{\partial {\rho }_{\pm }\left(\overrightarrow{r}\mathrm{,}t\right)}{\partial t}+\overrightarrow{\nabla }\cdot {\overrightarrow{J}}_{\pm }=-\alpha {\rho }_{+}\left(\overrightarrow{r}\mathrm{,}t\right)\rho \left(\overrightarrow{r}\mathrm{,}t\right)\pm \gamma {\rho }_{\text{e}}.$ (8) Equation (8) can be written as $\frac{\partial {\rho }_{\pm }}{\partial t}=D_{\pm }{\nabla }^2\rho \mp {\mu }_{\pm }\frac{p_0}{p}\left(\overrightarrow{E}\cdot \overrightarrow{\nabla }{\rho }_{\pm }+\rho \overrightarrow{\nabla }\cdot \overrightarrow{E}\right)-\alpha {\rho }_{+}{\rho }_{-}\pm \gamma {\rho }_{\text{e}}.$ (9) ${\mu }_{\pm }\frac{p_0}{p}\overleftarrow{E}\cdot \overleftarrow{\nabla }{\rho }_{\pm }$ is expressed in units of charge carriers per unit sensitive volume per unit time, and ${\mu }_{\pm }\frac{p_0}{p}\rho \overleftarrow{\nabla }\cdot \overleftarrow{E}$ represents the change in ion drift velocity caused by the space-charge effect in the sensitive volume. The space-charge effect shields the charge carriers released from the external electric field and causes the observed charge carriers (electron-ion pairs) to change the drift velocity to the opposite polarity electrode. This effect is very obvious at ultra-high dose rates. To simulate the ion transport process of the sensitive volume in the FLASH IC at an ultra-high dose rate, Equations (10)—(12) are used to describe the physical process of charge carriers. In our model, we considered three types of carriers (positive ions, negative ions, and electrons) for formation, interaction, and motion in the FLASH IC. The evolution equations describing the time-dependent processes of various carriers can be obtained as follows: $\begin{array}{c}\frac{\partial {\rho }_{+}}{{\partial }_t}=+R\left(t\right)-\frac{\alpha }{e}{\rho }_{+}{\rho }_{-}-\frac{\beta }{e}{\rho }_{+}{\rho }_{\text{e}}-D_{+}{\nabla }^2{\rho }_{+}\\ -{\mu }_{+}\frac{p_0}{p}\overrightarrow{E}\cdot \overrightarrow{\nabla }{\rho }_{+}+{\mu }_{+}\frac{p_0}{p}{\rho }_{+}\overrightarrow{\nabla }\cdot \overrightarrow{E}\end{array}$ (10) $\begin{array}{l}\frac{\partial {\rho }_{-}}{{\partial }_t}=+\gamma {\rho }_{\text{e}}-\frac{\alpha }{e}{\rho }_{+}{\rho }_{–}{D}_{-}{\nabla }^2{\rho }_{-}\hfill \\ +{\mu }_{-}\frac{p_0}{p}\overrightarrow{E}\cdot \overrightarrow{\nabla }{\rho }_{-}-{\mu }_{-}\frac{p_0}{p}{\rho }_{-}\overrightarrow{\nabla }\cdot \overrightarrow{E}\hfill \end{array}$ (11) $\begin{array}{c}\frac{\partial {\rho }_{\text{e}}}{{\partial }_t}=+R\left(t\right)-\gamma {\rho }_{\text{e}}-\frac{\beta }{e}{\rho }_{+}{\rho }_{\text{e}}-D_{\text{e}}{\nabla }^2{\rho }_{\text{e}}\\ +{\mu }_{\text{e}}\frac{p_0}{p}\overrightarrow{E}\cdot \overrightarrow{\nabla }{\rho }_{\text{e}}-{\mu }_{\text{e}}\frac{p_0}{p}{\rho }_{\text{e}}\overrightarrow{\nabla }\cdot \overrightarrow{E}\end{array}$ (12) R(t) is the charge production rate due to irradiation, and ${\rho }_i\left(i=+,-,e\right)$ are the positive, negative, and electron densities, respectively. $\gamma {\rho }_{\text{e}}$ is the contribution rate of the electron attachment. α is the positive and negative ion recombination coefficient, and β is the positive ion and electron recombination coefficient. ${\mu }_i$ denotes the mobility of species i, $\overrightarrow{E}$ denotes the electric field strength, and $P/P_0$ is the standard air pressure in units of air pressure. The electric field dependence of the chamber due to the space-charge effect can be calculated by solving the following one-dimensional Poisson equation: $\begin{array}{l}\frac{\partial E(x\mathrm{,}t)}{\partial x}=\frac{e}{ϵ}\left[{\rho }_{+}\left(x\mathrm{,}t\right)-{\rho }_{-}\left(x\mathrm{,}t\right)-{\rho }_{\text{e}}\left(x\mathrm{,}t\right)\right]\hfill \end{array}$ (13) where ϵ is the medium’s dielectric constant.

The finite-element method

The above equations (10–12) are coupled with the partial differential equations without analytical solutions. Therefore, we can obtain the numerical solutions by converting them into ordinary differential equations using a first-order upwind technique, as shown in Equation 15. To this end, the spatial derivative is first used to discretize the term, which produces an ordinary differential equation set (only the time derivative remains). The obtained system can then be integrated numerically [36]. The specific finite-element analysis method is introduced as follows:

The k_s values for the ion recombination and space-charge shielding effects were calculated. Equations (10)—(12) were solved using the finite-element method. The spatial first-order upwind technique was used to implement discretization in Equation (15), and the forward Euler method was used for time integration in Equations (20)–(21). For the numerical solution, the sensitive volume perpendicular to the electrode direction was divided into N bins of size h and two bins outside the sensitive volume (Fig. 2). The standard advection–diffusion reaction model deals with the time evolution of species in a flowing medium such as water or air. The mathematical equations describing this evolution are partial differential equations derived from mass balances. If $\overline{\rho }\left(x\mathrm{,}t\right)$ is uniform, then t≥0 and 0<h<D_p, and in $\left[x-\frac{1}{2}h,x+\frac{1}{2}h\right]$ $\begin{array}{ll}\overline{\rho }\left(x\mathrm{,}t\right)\hfill & =\frac{1}{h}{\displaystyle {\int }_{x-\frac{1}{2}h}^{x+\frac{1}{2}h}}\rho \left(s\mathrm{,}t\right)\text{d}s\hfill \\ \hfill & =\rho \left(x\mathrm{,}t\right)+\frac{1}{24}{h}^2\frac{{\partial }^2}{\partial x^2}\rho \left(x\mathrm{,}t\right)+\cdots \hfill \end{array}$ (14) The model conditions satisfy the law of conservation of mass; therefore, the change in $\overline{u}\left(x,t\right)$ per unit time is the net balance of the inflow and outflow over the bin boundaries. $\begin{array}{ll}\frac{\partial }{\partial t}\rho (x\mathrm{,}t)\hfill & =\frac{1}{h}[v\left(x-\frac{1}{2}h\mathrm{,}t\right)\rho \left(x-\frac{1}{2}h\mathrm{,}t\right)\hfill \\ \hfill & -v\left(x+\frac{1}{2}h\mathrm{,}t\right)\rho \left(x+\frac{1}{2}h\mathrm{,}t\right)]\hfill \end{array}$ (15) where $v\left(x\mp \frac{1}{2}h,t\right)\rho \left(x\mp \frac{1}{2}h,t\right)$ denotes the mass flux over the left and right bin boundaries. Therefore, the advection equation can be written as follows: $\begin{array}{l}\frac{\partial }{\partial t}\rho \left(x\mathrm{,}t\right)+\frac{\partial }{\partial x}\left(v\left(x\mathrm{,}t\right)\rho \left(x\mathrm{,}t\right)\right)=0\hfill \end{array}$ (16) We considered the effects of diffusion in the same manner. $\begin{array}{l}\frac{\partial }{\partial t}\rho (x\mathrm{,}t)=\frac{\partial }{\partial x}\left(D(x\mathrm{,}t)\frac{\partial }{\partial x}\rho (x\mathrm{,}t)\right)\hfill \end{array}$ (17) There may also be a local change in $\rho \left(x,t\right)$ that is described by $\begin{array}{l}\frac{\partial }{\partial t}\rho \left(x\mathrm{,}t\right)=f(t\mathrm{,}\rho (x\mathrm{,}t))\hfill \end{array}$ (18) In summary, the advection–diffusion reaction equation is $\begin{array}{ll}\frac{\partial }{\partial t}\rho (x\mathrm{,}t)\hfill & +\frac{\partial }{\partial x}(v(x\mathrm{,}t)\rho (x\mathrm{,}t))\hfill \\ \hfill & =\frac{\partial }{\partial x}\left(D\left(x\mathrm{,}t\right)\frac{\partial }{\partial x}\rho \left(x\mathrm{,}t\right)\right)+f(t\mathrm{,}\rho (x\mathrm{,}t))\hfill \end{array}$ (19) Therefore, the integral of each step is obtained as $\rho \left(t_i+\text{Δ}t\right)-\rho \left(t_i\right)={\displaystyle {\int }_{t_i}^{t_i+\text{Δ}t}}f(t\mathrm{,}\rho (t)\text{d}t\approx \text{Δ}tf(t_i\mathrm{,}\rho \left(t_i\right)$ (20) where $\text{Δ}t\le \frac{h}{\left|v\right|}$, and the forward Euler method is used for the iterative calculation $\begin{array}{l}\rho \left(t_{i+1}\right)=\rho \left(t_i\right)+\text{Δ}tf(t_i\mathrm{,}\rho \left(t_i\right)\hfill \end{array}$ (21) The first-order upwind technique was used for discretization, and the forward Euler method was used for step iteration. We attempt to require $h\to 0$ and $\text{Δ}t\to 0$ to ensure that the calculation results converge more strictly to a real physical understanding. Therefore, the first-order upwind technique first takes the value of the upstream node directly on the boundary surface. Although the definition of upstream depends on the flow direction, the calculated flux is consistent. Therefore, the upwind scheme is conservative. The second condition is the boundary condition. The upwind scheme satisfies the Scarborough boundedness criterion. The coefficient matrix obtained after discretization is diagonally dominant; therefore, the numerical results do not exhibit an “oscillation” phenomenon, similar to the central difference scheme. However, false diffusion occurs when the number of grids is large. Grid encryption is often required to avoid this problem. The maximum upper limit of the bin size (h) was determined using the Einstein–Smoluchowski relation [37-39] $\begin{array}{l}{D}_{\text{p}}=\frac{{\mu }_{\text{e}}{k}_{\text{B}}T}{q}\hfill \end{array}$ (22) where q is the particle charge, k_b is the Boltzmann constant, and T is the temperature. In addition, the physical diffusion must be greater than the numerical diffusion $\left(D_{\text{p}}>D_{\text{n}}=\frac{1}{2}hv\right)$. Considering that $v=P_0/P{\mu }_{\text{e}}E$ and that the electron has a charge q=e, the equation can be transformed into $h=2k_{\text{B}}T/(Ee)$, where T = 300 K and the pressure is the standard atmospheric pressure, that is, $P_0/P=1$. It is evident that the first-order upwind scheme considers the directionality of the flow; thus, it has good transportability.

Fig. 2Full-screen View

(Color online) Discrete internal schematic of the sensitive volume of the flat IC, where X₀,..., XN are the main grid points, and $X_{{-}_2^1}$, ..., $X_{N+\frac{1}{2}}$ are auxiliary grid points. Concentration is defined at the main grid points and can be regarded as the average value of the entire unit, while electric field intensity and related input parameters are calculated at the unit boundary

Parameters of the numerical solution

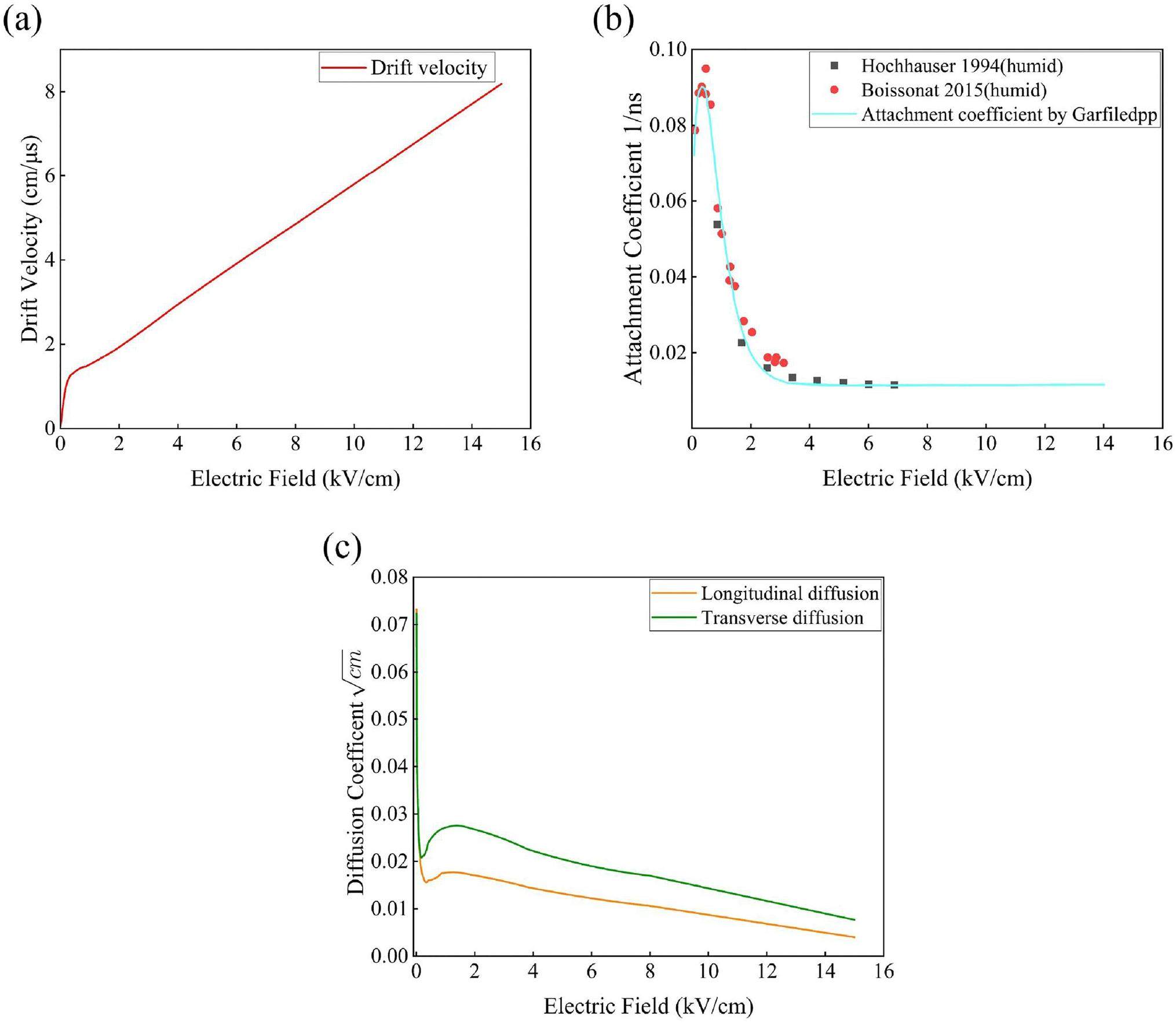
Air was used as the working gas in the experiment. The equation contains several physical parameters: recombination coefficient (α), electron attachment coefficient (γ), diffusion coefficient (D), and ion mobility (μi) (including positive ions, negative ions, and electrons). The electron drift velocity (Fig. 3a) and diffusion coefficient (Fig. 3c) under different electric field strengths were determined using the Garfield++ simulation. We used test data from Hochhäuser et al.[40] and Boissonnat et al. [41] for the spline interpolation to determine the electron attachment coefficient (Fig. 3b). Simultaneously, the positive and negative ion mobilities and diffusion coefficients were good approximation constants for the variation range of the electric field strength of the IC during the experiment. The specific parameters are listed in Table 1.

Fig. 3Full-screen View

Figure shows the electric field-dependent parameters used in the calculation. Figure (a) shows the electron drift velocity ($v=P_0/P{\mu }_{\text{e}}E$) by the Garfield++ simulation for humid air. Figure (b) shows the attachment coefficient (γ) of the electrons. The regression spline used in the numerical calculation is shown together with experimental data from Hochhäuser et al. [40] and Boissonnat [41] for humid air. Figure (c) shows the transverse and longitudinal diffusion coefficients (D_e) in different field strengths of electrons simulated by Garfield++ for humid air

Experimental correction factor $k_{\text{s}}{}_{-\exp }$ determination

A Faraday cup was used to calibrate the reference dose of the FLASH IC. A relevant description is provided in Ref. [33]. The liberated charges $Q_0=c\times \left(FC-F{C}_0\right)$, FC and FC₀ are the signal and background of the Faraday cup, and c is the conversion factor. The measured charge of the IC is given by $Q_{\text{c}}=IC-I{C}_0$, where IC and IC₀ are the signal and background of the FLASH IC, respectively. Therefore, the correction factor k_s is expressed as follows: $\begin{array}{l}{k}_{\text{s}}{}_{-\exp }=\frac{Q_0}{Q_{\text{c}}}=\frac{c\times \left(FC-F{C}_0\right)}{IC-I{C}_0}\hfill \end{array}$ (23) The background of the FLASH IC and Faraday cup must be deducted before each measurement. According to physical theory, when Q₀ = 0, there must be Q_c = 0, which means that there is no recombination in the FLASH IC; therefore, $k_{\text{s}}{}_{-\exp }=1$, which is of significant importance for dose measurement.

Dose measurement and profile monitoring of ionization chamber under low pressure

The beam current of the terminal was tested using a Faraday cup to ensure that the PTW Roos-34001 IC was within the normal working range. The extrapolation of the Faraday cup measurements at an ultra-high dose rate (approximately 50 Gy/s) demonstrates that the beam current can fulfill the requirements of FLASH irradiation. Considering the experimental field environment, the carbon-ion beam current at an ultra-high dose rate was measured by reducing the air pressure of the chamber. The replacement of the working gas (such as helium) can alleviate ion recombination but cannot obtain completely satisfactory results at ultra-high dose rates. Considering the experimental environment within the field, the beam current at an ultra-high dose rate was measured by reducing the air pressure within the chamber. The replacement of the working gas (for example, helium) can mitigate ion recombination; however, the results obtained at an ultra-high dose rate are not entirely satisfactory. The large-area real-time beam-monitoring system for carbon-ion FLASH irradiation is susceptible to the effects of reduced electrode plate spacing, owing to the limitations of processing technology and the accuracy of the electrode plate. Additionally, this reduction is prone to a “light” phenomenon, which results in irreversible damage to the detector.

Figure 4(a) shows the dose measurement results of the FLASH IC at a dose rate of approximately 0.2 Gy/s under standard atmospheric pressure. The output of the PTW Roos-34001 IC was used as the reference dose. Fig. 4(b) shows the dose residuals of the FLASH IC. Under the condition of IC pressure of 10 mbar and a dose rate of approximately 50 Gy/s, the dose linear curve (Fig. 4c) and residual diagram (Fig. 4d) of the FLASH IC were obtained. A Faraday cup was used to verify the reference dose of the FLASH IC. The results in Fig. 4 show that the IC can simultaneously meet the beam monitoring and dose measurement requirements of carbon-ion irradiation under conventional clinical and FLASH RT. The residuals were less than 2%, and as the dose increased, the deviation gradually decreased and approached 0%, which meets the requirements for preclinical dose monitoring.

Fig. 4Full-screen View

Dose linear curve and residual diagram of FLASH IC at different pressures and dose rates

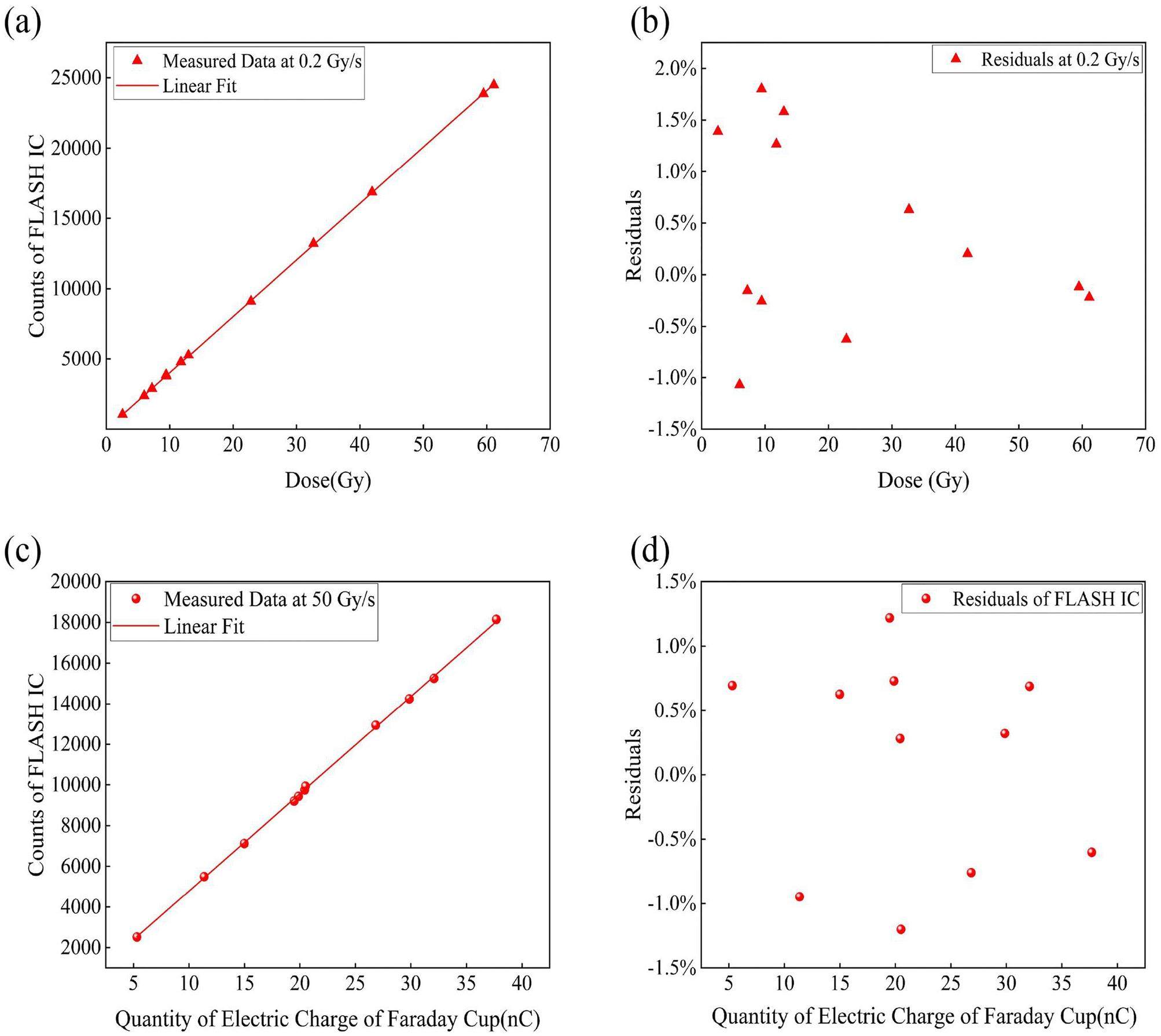
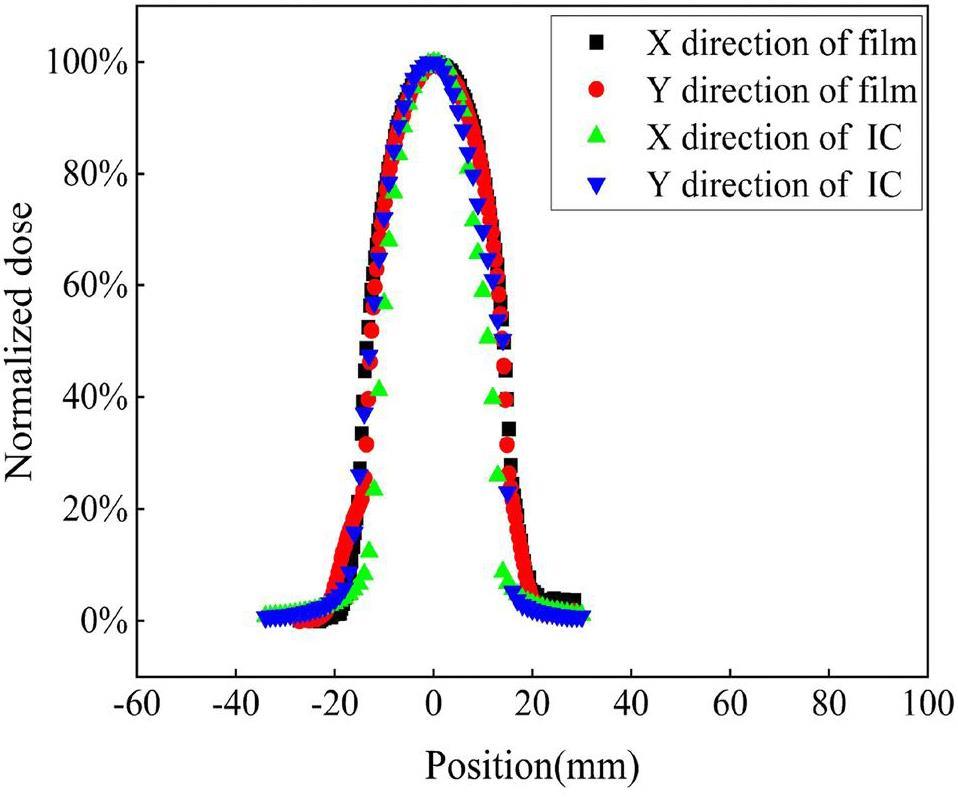
Figure 5 shows that the beam spot was adjusted to approximately 40 mm in diameter, and the beam profile was measured using the FLASH IC and EBT3 films. Because the beam was defocused at the measurement position and the film was placed on the lower surface of the FLASH IC, the results for the film were slightly larger. The FLASH IC can measure the position profile of carbon-ion beams at ultra-high dose rates. During the experiment, the beam-scanning system was adjusted so that different volume targets at the isocenter could be irradiated.

Fig. 5Full-screen View

(Color online) Beam profile position measurement of FLASH IC and EBT3 film at a dose rate of 50 Gy/s

Measuring saturation curve and calculating correction factor

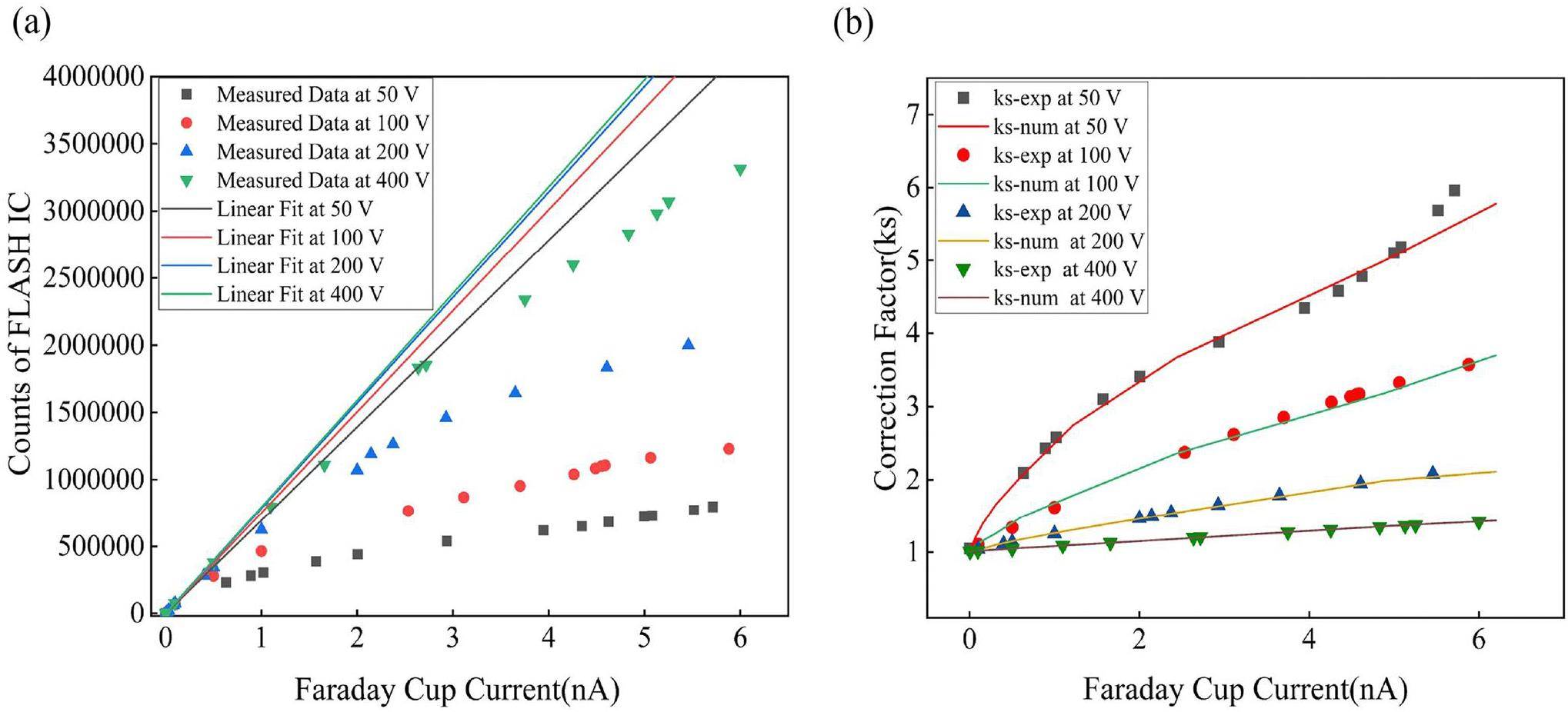
Figure 6a shows that the ion recombination effect at different dose rates was tested by increasing the polarization voltage of the IC. The response of FLASH IC was characterized by a Faraday cup monitoring the beam current to obtain the saturation curve using Eq. (23). The results showed that the recombination effect of ions decreased with increasing polarization voltage. Theoretically, the voltage can be increased in the ionization region to obtain a linear dose curve. However, owing to the high polarization voltage applied at the ultra-high dose rate, the IC will be “light”; thus, the maximum polarization voltage is set to 400 V. Figure 6b shows the correction factor obtained by experimental calculation and model calculation. The results indicate that the correction factor calculated using the model is in good agreement with the experimental results. During the experiment, when a higher polarization voltage was applied, such as 200 or 400 V, the maximum deviation in the results was less than 5%. However, when the polarization voltages were 100 V and 50 V, the maximum deviation was less than 10%.

Fig. 6Full-screen View

Figure (a) shows the scatter plot of the saturation curve and corrected linear fitting under different applied voltages of IC to change beam current (dose rate). The scatter plot in (b) represents the experimental correction factor calculated by Equation (23), and the curve represents the correction factor calculated by the finite-element model