Introduction

The number of naturally occurring nuclides on Earth is 339, including 256 stable nuclides and 83 radioactive nuclides. The possible number of bound nuclides has been predicted by nuclear models to be approximately 6000∼9000 [1-3], for which only 3340 nuclides have been experimentally observed [4]. The nuclear drip line is the boundary beyond which the atomic nuclei are unbound with respect to the emission of one or more proton(s) or neutron(s). Although the proton drip line has been extensively explored experimentally over the past decades, the neutron drip line has only been confirmed for light elements up to Ne [5].

The limit of nuclear existence is at fundamental subject in nuclear physics. Nuclei at or near drip lines can exhibit extreme structures [6], offering unique opportunities to study exotic open quantum behaviors and asymmetric nuclear matter. In addition to the naturally occurring radioactive nuclei, the most unstable nuclei are artificially produced in accelerator facilities. Production methods are predominantly divided into two categories [7]: Isotope Separation On-Line (ISOL) and In-Flight fragment separation (IF). ISOL facilities are renowned for generating high-purity isotopes with precise energies and low emittance but suffer from poor extraction efficiencies for refractory materials and long extraction times for certain chemical elements. The In-Flight method effectively delivers all reaction products with lifetimes longer than several hundred ns, making it the most productive route for isotope discovery in recent years [8, 9]. Fission during flight, primarily involving actinide elements, is highly competitive for generating medium-mass neutron-rich nuclei (see Ref. [10]). Hybrid methods that integrate the strengths of ISOL and In-Flight techniques have attracted considerable interest because they offer promising opportunities to enhance the production yield of the most neutron-rich isotopes [11-13].

Despite significant progress in studying neutron-rich nuclei worldwide, exploring “terra incognita” near the neutron drip line remains challenging, where no data are available, primarily because of their small yield. In fragmentation reactions, the evaporation of neutrons from excited pre-fragments reduces the production cross sections of more neutron-rich nuclei [14, 15]. To address these challenges, numerous experimental strategies have been proposed to enhance beam intensity, spectrometer acceptance, and particle identification resolution at existing facility [16, 17]. However, they cannot fully compensate for the decreased production cross sections toward the neutron drip line.

There are various theoretical models from the empirical formula [18-20] to the hybrid method using Bayesian neural networks (BNNs) as well as Qg systematics [21-23]. However, their extrapolations to systems with significant $n/p$ asymmetry often exhibit large deviations. Transport models such as isospin-dependent quantum molecular dynamics [24] offer a microscopic description of the reaction mechanism and can reproduce experimental elemental fragmentation data fairly well [14, 25]. However, QMD calculations are generally time-consuming and unsuitable for the comprehensive calculation of multi-step fragmentation.

In this work, we investigate multi-step fragmentation reactions at relativistic energies of ~GeV/nucleon on a thick target to increase the yield of neutron-rich nuclei far from the stability line. In multi-step fragmentation, neutron-rich fragments can undergo further fragmentation processes, producing even more neutron-rich nuclei. This is due to the inherent “memory effect” in fragmentation reactions, which works efficiently to produce fragments with mass-to-charge ratios similar to those of neutron-rich projectile nuclei. Additionally, the diversity of intermediate nuclei increases the ejection probability of neutron-rich fragments to a certain extent [26-28].

In the present study, the effect of multi-step processes was illustrated using the drip line nucleus ³⁴Ne as an example. We simulated its production and transmission processes to evaluate the effectiveness and advantages of multi-step reactions. After optimizing the yields of neutron-rich nuclei, we estimated the production rates of the neutron drip line nuclei above oxygen.

Production in the multi-step fragmentation

For a specific isotope of interest, the yield Y can be expressed as the product of three independent factors: $\begin{array}{l}Y=\varphi PS\hfill \end{array}$ (1) where ϕ is the incident beam flux. P represents the probability of producing the nucleus of interest in the target, which depends on multiple factors such as nuclear interaction, beam energy, and target thickness. The third parameter S is the total transmission efficiency, which is determined by the momentum distribution of the fragments and acceptance of the detection system. Estimations of P and S for drip line nuclei were the main focus of the present study. To evaluate the factor P, one must consider not only the reactions of the projectile but also those of all the nuclei produced in the intermediate steps. In addition, the angular and energy spreads of these product nuclei should be evaluated for the transmission factor S.

The production probability of the desired nuclide in a target, along with its angular and energy distribution, was calculated using the computer code LISE++ (version 16.18.20) [28, 29]. The fragment cross sections were calculated using the semi-empirical formula EPAX 2.15 [18], which has good precision in predicting the existing data near the neutron drip line in this mass region [30]. The slowing down processes, including energy loss, energy-loss straggling, and angular straggling, were evaluated using the ATIMA 1.2 code [31, 32], with the results serving as input for subsequent calculations. The momentum distribution of the fragments was assessed based on Goldhaber theory [33]. A higher energy projectile is preferable to optimize the contribution of multi-step reactions; however, the accelerator facility imposes constraints on the energy choice. This study focuses on producing drip line nuclei near ³⁴Ne at the High-Intensity heavy-ion Accelerator Facility (HIAF) [17] under construction. Therefore, the projectile energy was set to 1500 MeV/nucleon.

The calculated production probability (P) of ³⁴Ne is shown in Fig. 1(a) as a function of target thickness for a ⁴⁸Ca beam incident on a Be target. The target thickness is expressed in units of the mean free path (λ), calculated using the reaction cross section of 1547 mb for ⁴⁸Ca on Be. In this case, the thickness λ corresponds to 9.68 g/cm² or 5.2 cm. As indicated in Fig. 1(a), the single-step production probability saturates at a thickness of approximately 1.03λ, which is significantly smaller than the thickness required for multi-step yields to plateau. Multi-step fragmentation dominates the production of thick targets, accounting for more than 95% of the total yield when the thickness exceeds λ. The corresponding peak value, observed at 3.33λ, was nearly 50 times higher than that obtained under the assumption of a single-step process alone. We also note that this optimized thickness holds true for beam energies above 0.8 GeV/nucleon. However, as the target thickness increases, the effects of the incident particle attenuation and fragmentation of the objective nuclei become more pronounced, reducing the final production probability. Consequently, optimizing the target thickness is crucial to achieve a high yield of neutron-rich nuclei.

Fig. 1Full-screen View

(Color online) (a) Production probability of ³⁴Ne as a function of target thickness for the reaction of 1500 MeV/nucleon ⁴⁸Ca on Be. The single-step and multi-step processes are represented by black and colored lines, respectively. Solid and dashed lines distinguish the results from LISE++ and our code, respectively. (b) Same as Panel (a) but for the relative yields of Ne isotopes calculated using LISE++. The yields have been normalized to that at the 0.2λ thickness. The hollow pentagons indicate the peak positions

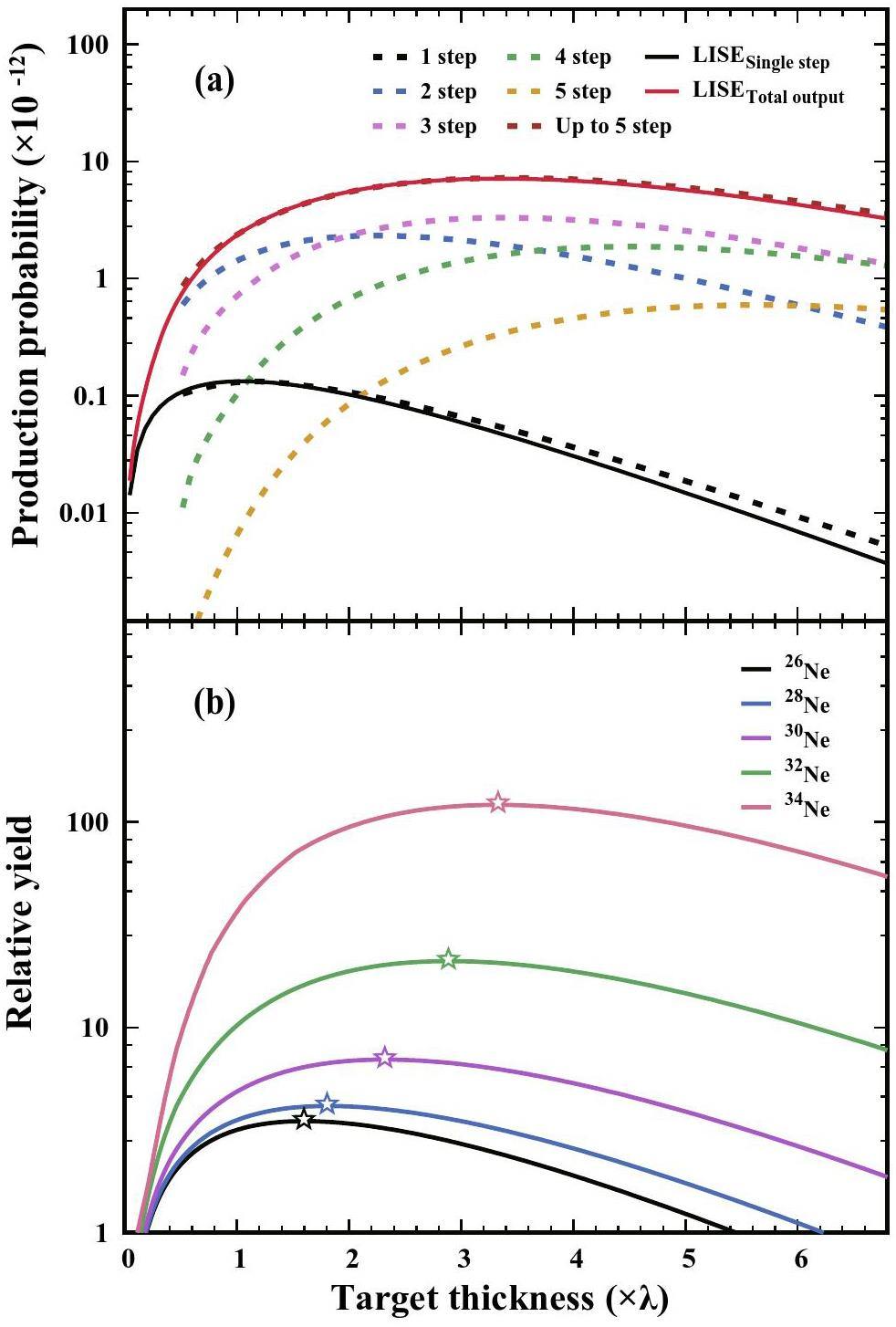
To determine which component plays a key role in multi-step fragmentation, we developed a dedicated code to compute the fragmentation yield similar to Ref. [27]. In this calculation, the reaction target was uniformly segmented along the beam direction. Each segment thickness is much smaller than the mean free path of projectile-like ions, so at most one reaction occurs per segment. The probability of fragment generation at each reaction point was calculated individually. The total probability was determined by evaluating all possible combinations of reaction positions and multi-step pathways. Figure 1(a) presents the calculated production probabilities from the single step to the fifth step. For target thicknesses of up to 2λ, the second-step reaction is the most crucial process. Above this thickness, the third-step process became predominant, steadily increasing its contribution. Contributions of the fifth step account for less than 4% of the total yield, while that beyond the fifth step is negligible. Inclusion of up to 5 steps in our simulation is sufficient for the absolute yield estimates, and is well consistent with the LISE++ results.

We computed the yields using other reaction models. Despite discrepancies in absolute values across models, the overall trends in the production probability of drip line fragments as a function of target thickness remained consistent, indicating that the enhancement via a multi-step mechanism in thick targets is a robust and model-independent feature.

To assess the yield of isotopes with varying neutron excesses, we present the relative yields of ^{26,28,30,32,34}Ne isotopes from the multi-step fragmentation in Fig. 1(b). A small scaling factor was introduced for the production probabilities to match the corresponding results at 0.6 GeV/nucleon. The yield curve for each isotope was normalized to the corresponding value at a thickness of 0.2λ. Although the curves exhibit a similar pattern across isotopes, the peak positions shift to a thicker thickness with increasing neutron excess. Two important tendencies were observed: First, the yield enhancement at a larger λ is more pronounced for neutron-rich nuclei, indicating that multi-step fragmentation contributes more efficiently to their production. Second, the yield peaks at greater target thicknesses for more neutron-rich nuclei, highlighting the advantage of multi-step reactions in producing extremely neutron-rich nuclides. This pattern also holds for all neutron-rich isotopes. In contrast, increasing the target thickness to more than 1λ has little effect on the production of nuclei near the stability line. This pronounced disparity in yields implies that employing a thick target for a relativistic projectile, where the multi-step fragmentation process gradually plays a leading role, can compensate for the limitations associated with the smaller production cross-sections of the most exotic nuclei. This approach has a clear advantage in pushing the limits of new isotope discoveries.

Transmission of Multi-step fragments

Reactions and penetration in a thick target inevitably lead to a notable increase in the beam transverse emittance and momentum spread, owing to the cumulative effects of fragmentation reactions and multiple scattering. Therefore, the fragments are eventually characterized by a high production rate but a broad momentum distribution. For experimental purposes, the separation, purification, and delivery of cocktail fragments to the terminal using a spectrometer or separator are often essential. The final yield at the experimental terminal is determined by the momentum distribution and transmission efficiency of the spectrometer.

In the following, we take the HIgh-rigidity Radioactive Ion Beam Line (HIRIBL) of the HIAF facility (in construction) as a realistic case to illustrate the transmission of ejective fragments from a thick target. The HIRIBL, formerly known as the High-energy FRagment Separator (HFRS), was designed to produce, separate, and purify rare isotopes with a maximum magnetic rigidity of 25 Tm. It is characterized by an angular acceptance of ±30 mrad (x) and ±15 mrad (y), and a momentum acceptance of ±2.0%. Details of the HIRIBL can be found in Refs. [34, 35]. The arrangement of the HIRIBL is shown in Fig. 2(a), with a Be production target at PF0. The reaction products were simulated for different focal planes. A clear particle identification is expected in the desired mass range.

Fig. 2Full-screen View

(Color online) (a) Schematic layout of the HIRIBL. PF0-PF4 are the focal planes of the pre-separator, while MF0-MF6 correspond to the focal planes of the main separator. Dipole magnets are shown in blue, and multipole magnets in red. (b) Momentum distributions of ³⁴Ne expected after the reaction target at PF0 (solid lines), PF4 (dashed lines), and MF6 (dotted lines) for the target thicknesses of 0.5λ, 1.5λ, and 3.0λ. The projectile beam energy is fixed at 1500 MeV/nucleon with a beam intensity of 3×10¹¹ ppp. (c) Production rate of ³⁴Ne (in particles per pluse) transmitted through HIRIBL as a function of target thickness. Solid and dashed lines represent results immediately after the target and at MF6 of HIRIBL, respectively, considering the multi-step fragmentation process. The black dots indicate the transmission efficiency at different target thicknesses

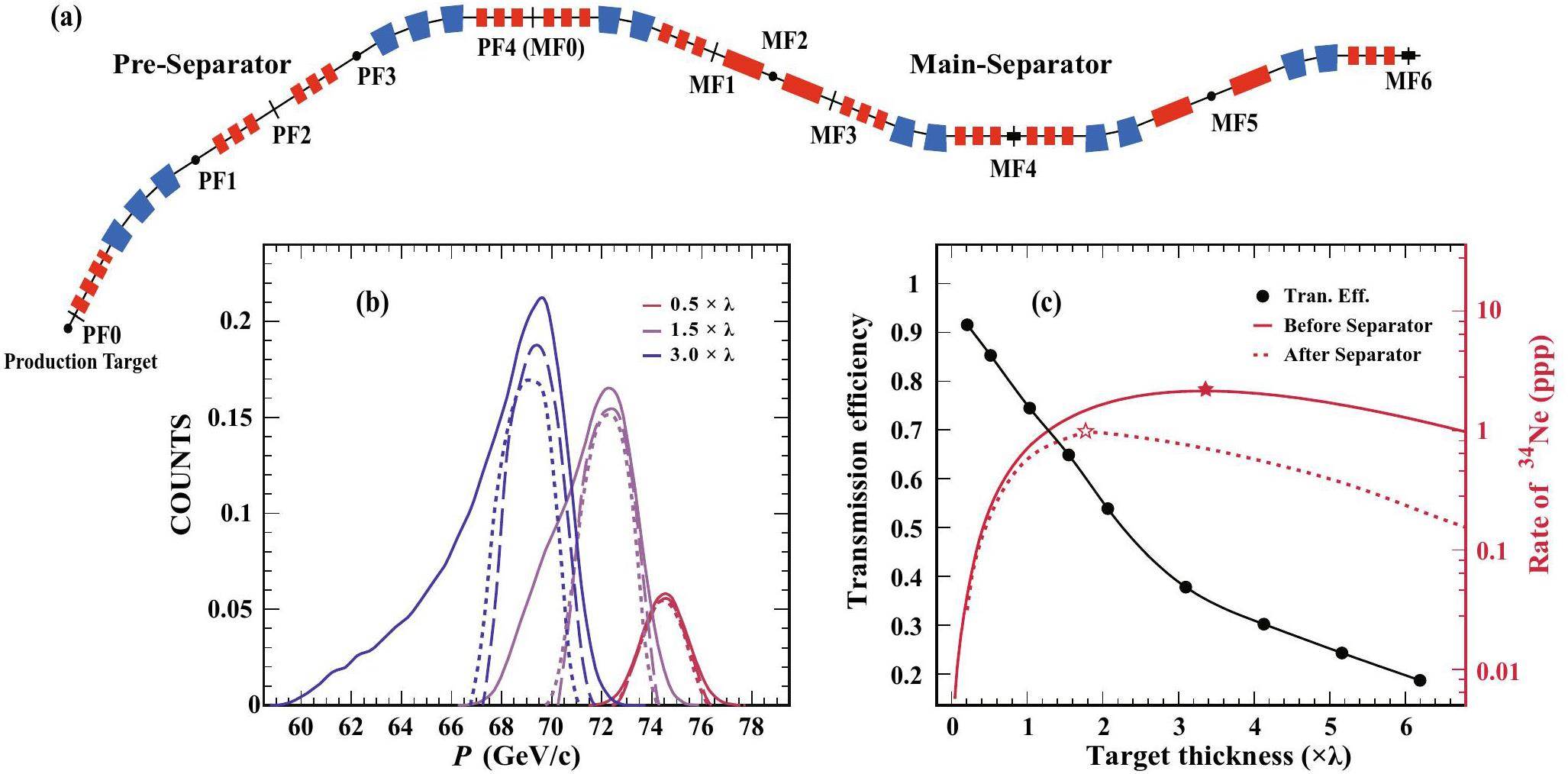
The fragments are produced by bombarding a 1500 MeV/nucleon ⁴⁸Ca beam on Be, then transmitted and separated by HIRIBL. The beam intensity was 3×10¹¹ particles per pulse (ppp). Each pulse lasted for 13 s. Acceptance calculations were performed using the Monte Carlo method implemented in LISE++. A high incident energy was beneficial for reducing the influence of the momentum distribution of the final product. Figure 2(b) illustrates the momentum distribution of ³⁴Ne fragments produced for various target thicknesses. A distinct asymmetric distribution is observed with a broad shoulder on the low momentum side as the target thickness increases from 0.5λ to 3.0λ. The broadening is due to the energy loss difference between the projectile beam and the fragment. The distributions become symmetric after considering the momentum acceptance of the spectrometer for the optimized yield of ³⁴Ne.

Under identical target thicknesses, the momentum distributions at PF4 and MF6 exhibit similarity, reducing the yields from PF4 to MF4 by only 2.6% and 4.5% to MF6. In subsequent analyses, MF6 was used as the experimental terminal. Utilizing a thick target significantly reduces the transmission efficiency, as shown by the transmission efficiency curve in Fig. 2 (c). The transmission efficiency decreased from 92% at 0.21λ to 38% at 3.10λ. The impact of spectrometer acceptance on the final yield is illustrated in Fig. 2 (c). The optimized target thickness with the HIRIBL transmission is slightly reduced from 3.33λ to 1.76λ, and the maximum yield decreases to 45% of the peak value obtained after the reaction target. However, using a thick target enhances the daily yield of ³⁴Ne by more than a factor of 30 compared with the case involving only single-step reactions. Moreover, utilizing a Ni projectile beam at the same beam intensity can enhance the ³⁴Ne yield rate by more than a factor of 130, as indicated in Fig. 3.

Fig. 3Full-screen View

(Color online) Estimated daily event rate of the most neutron-rich nuclei at HIRIBL, using the 1500 MeV/nucleon ⁶⁴Ni beam with an intensity of 3×10¹¹ ppp on Be. The values in the square indicate the corresponding daily event rates. Color code represents the enhancement factors of the production rates for the multi-step fragmentation relative to those for the single-step process. The black line denotes the boundary of the observed nuclei experimentally. Nuclei to the right of the black line remain to be discovered. The neutron drip lines predicted by the WS4 [1] and UNEDF1 [36] mass models are shown by the blue dotted and red dashed lines, respectively

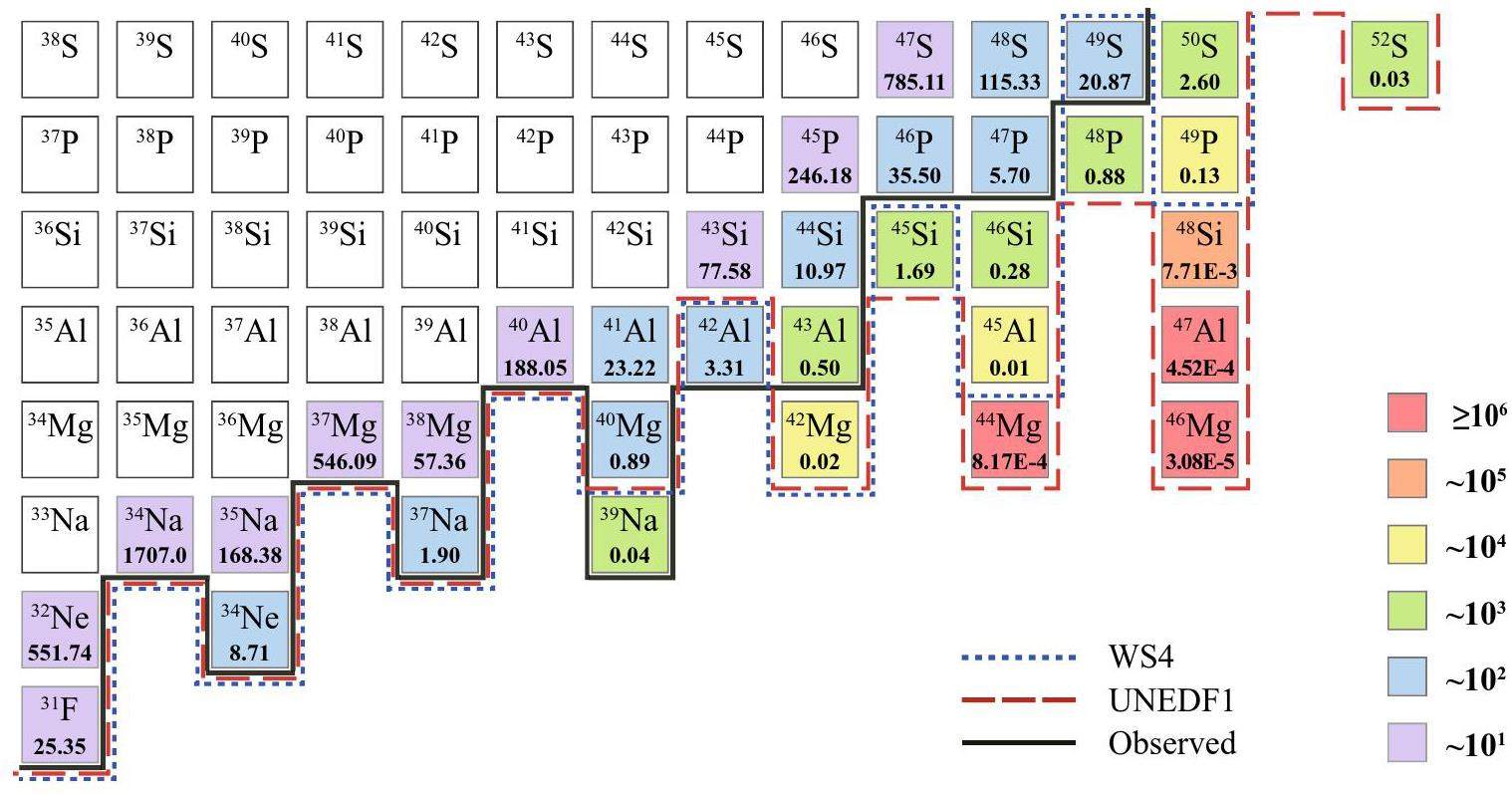
Finally, Fig. 3 summarizes the optimized production rates and the enhancement factor in producing the most neutron-rich isotopes between oxygen and chlorine using HIRIBL. The neutron drip lines predicted by the WS4 [1] and UNEDF1 [36] mass models are shown for comparison. The enhancement factor is the ratio between the production rates calculated with multi-step fragmentation and those calculated with only the single-step process. The projectile beam of ⁶⁴Ni is assumed to be at 1500 MeV/nucleon and has an intensity of 3×10¹¹ ppp. Each isotope was calculated to achieve the best production rate by optimizing the target thickness and transmission in the HIRIBL. Compared to single-step reactions alone, an increase of more than two orders of magnitude in the yields of the most exotic nuclei can typically be achieved. For example, the expected daily event rate of ⁴⁵Si increases from 1.28×10^-3 to approximately 1.69. Other projectile nuclei such as ⁸²Se may help achieve even higher yields [37]. These enhancements provide new possibilities for locating the drip line above sodium, and thus significantly expanding the research horizon.

Conclusion

In summary, the multi-step fragmentation of relativistic ions occurring in a thick target can significantly enhance the yields of neutron drip line nuclei, effectively compensating for their low production cross section. This enhancement is a robust feature that is independent of the reaction model. The fragment separator HIRIBL is expected to be commissioned this year, and a proof-of-principle run will be planned during the first experimental run, which can be coupled naturally with charge-changing reaction studies [38-40]. When coupled with the fragment separator HIRIBL, the production rates can be boosted by several orders of magnitude. Employing a higher-acceptance separator will further highlight such improvements. Thus, the multi-step fragmentation processes open new avenues for searching for new isotopes at the edge of nuclear stability and exploring novel structures and phenomena in extremely neutron-rich nuclei.

Enhancing production rates is expected to be more effective at higher projectile energies, which will be available at HIAF and FAIR facilities. Although we have restricted the discussion to multi-step fragmentation, one can naturally extend the study to other combinations of reactions, such as, projectile fission followed by multi-step fragmentation. Different combinations of multi-step processes can help increase specific isotope rates. We would also like to note that the effect of multi-step fragmentation is present at energies below GeV/nucleon, albeit with reduced efficacy.