Searching for specific distributions leading to effective basis wave functions

In the GCM, the mesh points for the generator coordinates were not predetermined. Although it is theoretically feasible to obtain exact solutions by enumerating a large number of wave functions with different configurations, this approach is computationally impractical. Instead, we hypothesize that the effective basis wave functions may follow specific distributions. To test this hypothesis, we generated coordinate sets {R} using various random distributions and applied them to calculate the ground state energy of the di-neutron halo nucleus ⁶He. By analyzing the relationship between the number of superimposed basis wave functions and the resulting ground state energies, we aim to derive global empirical rules that can enhance the efficiency of the GCM.

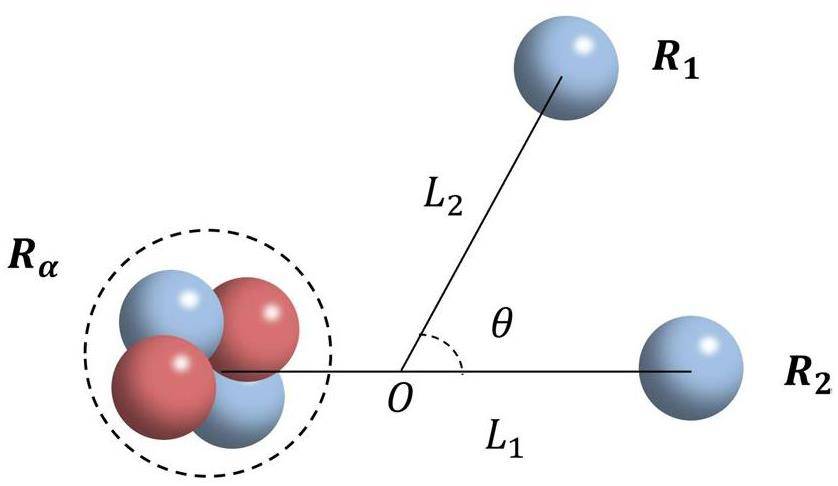
As a benchmark test, we first calculated the ground state of the di-neutron halo ⁶He nucleus using traditional mesh points for the Brink wave functions. As shown in Fig. 1, different sets of coordinates can be generated by adjusting the relative distances L₁, L₂, and angle θ relative to the x-axis. Where L₁ is the distance between the α particle and neutron, and L₂ is the distance between the other neutron and the center-of-mass of the α particle and neutron. Subsequently, various configurations with different sets (L₁, L₂, θ) were superposed. The mesh points for L₁ were established at intervals of 0.35 fm, resulting in 14 points, whereas for L₂, the intervals were set at 0.5 fm, accumulating 18 points. The values for angle $\theta$ were sequentially determined to be 0°, 30°, 60°, and 90°. By employing this traditional method, 1008 basis wave functions were generated. Subsequently, the ground state energy was computed after diagonalization. Due to large overlap between some wave functions or their lack of physical significance, 539 out of the initial 1008 basis wave functions were removed during the calculations. This outcome is shown in the last column of Table 1, along with other results recorded in the same table. Furthermore, Fig. 2 displays how the energy varies with the superposition of wave functions.

Fig. 1Full-screen View

(Color online) This schematic figure illustrates the Brink wave function of ⁶He (α + n + n). Blue spheres represent neutrons, while red spheres denote protons. The α cluster and the two neutrons are aligned in the same plane

Fig. 2Full-screen View

(Color online) Energy convergence of the ground state (0⁺) of ⁶He using various methods to generate basis wave functions. The brown and gray lines represent the results from the spherical shell and traditional methods, respectively. The curves in other colors represent the calculation result of the generated coordinates generated by the random distribution

Another common method for selecting mesh points is to distribute them within a spherical shell structure. The spherical structure of the latter is depicted as a three-dimensional, multi-layered spherical shell. The initial radius of the spherical shell was set at 1 fm, with spacing between adjacent layers at 1 fm, producing a total of five layers from the inside out. The Marsaglia algorithm [66] was employed to ensure a uniform distribution of points on each spherical shell. For each layer, 200 random three-dimensional coordinate values were generated. Following a procedure similar to the earlier one, the coordinates of the 1000 points generated are designated as ${\text{R}}_1{}_i\left(x_{1i}\mathrm{,}{y}_{1i}\mathrm{,}{z}_{1i}\right)$. This randomization process was repeated three times to obtain the generation coordinates for the α particles and two neutrons. By superposing these 1000 basis wave functions, the ground state of ⁶He was calculated. Detailed information regarding the results is presented in Fig. 2 and Table 1.

In addition to the above common methods, we also introduce other random distribution functions for generating mesh points, such as Gamma distribution, Uniform distribution, Chi-square distribution, Logistic distribution, and Normal distribution. Considering the halo feature of ⁶He, which is characterized by a diffuse density distribution around the nucleus, specific parameters for various random distribution functions have been selectively determined to assess their impact on the tail region. Although no quantitative relationships for parameter values under different distributions have been specified, we fortuitously discovered that the results remained relatively stable within a reasonable range of parameter values after experimenting with various settings. The probability density functions and specific parameter values for random distributions are listed in Table 1. Furthermore, GCM calculations are performed within the center-of-mass coordinate system; consequently, the results depend solely on the relative distances between the clusters. Thus, in the Normal and Logistic distributions, the results are influenced only by the standard deviation σ, independent of the mean μ. For computational convenience, μ is set to zero in these cases. Each random distribution is utilized to generate 1000 basis wave functions for the GCM calculations.

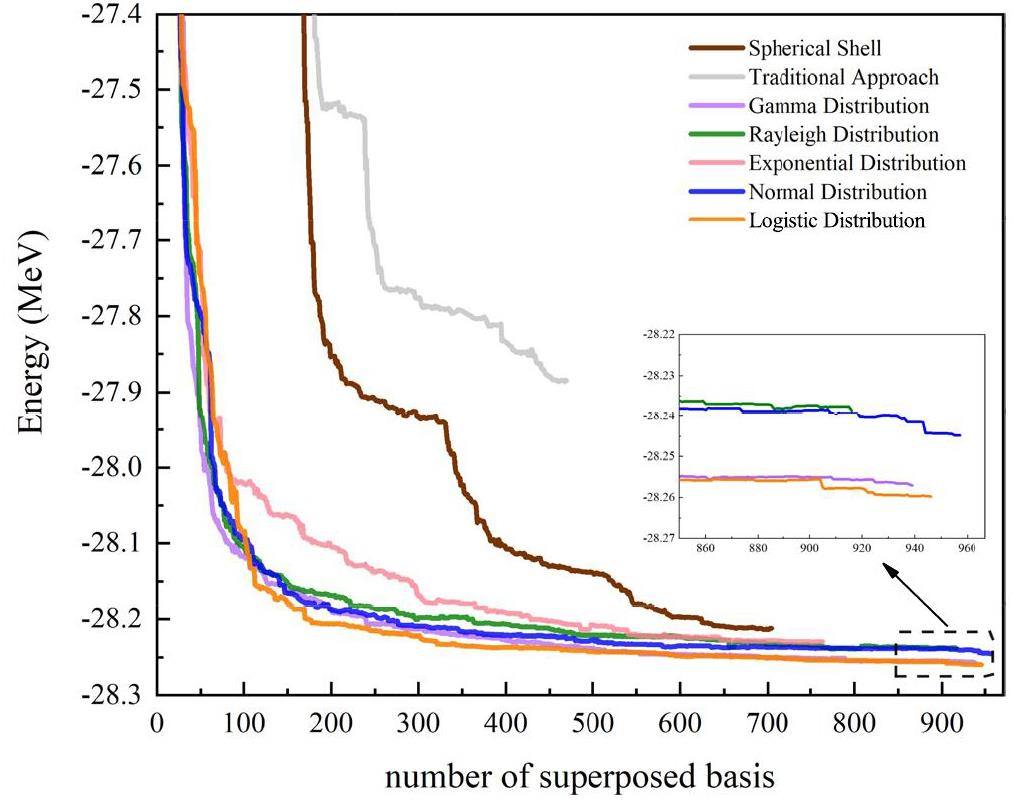
Figure 2 shows the energy convergence of the ground state using the various methods presented here to generate the basis wave functions. As one can see, the convergence rate of the energy variation curves corresponding to random distributions is significantly faster than that derived from manually configured structures. Table 1 provided qualitative insights. The ground state energies obtained using the traditional and spherical shell methods are -27.884 MeV and -28.212 MeV, respectively, both of which are obviously higher than those from all random distributions.

From Fig. 2 and Table 1, it is interesting to see that the Logistic distributions outperform other random distributions, with the 0⁺ state energies calculated at -28.260 MeV. Note that the Gamma distribution is also effective, although it is determined by two parameters (α,β), which provide a wider range of adjustments. Single-parameter Normal and Logistic distributions offer significant advantages for practical calculations. This superiority is attributed to the assumption of independence in the Normal distribution, which mirrors the relative spatial near independence of the clusters in the nuclei. Furthermore, the thicker asymptotic tails of the probability density function in the Normal distribution closely corresponded to the halo characteristics of ⁶He. Similarly, although the Logistic distribution resembles the Normal distribution, it features notably heavier tails. This characteristic better captures the extended features of the ⁶He halo nucleus structure, thereby encompassing a broader distribution of the effective basis states.

To substantiate this conclusion further, we compared the ground state energy by maintaining approximate equality between the standard deviations of the Logistic and Normal distributions according to the theoretical formula $\gamma =\left(\sqrt{3}\sigma \right)/\pi$. In this case, the two distributions have similar shapes but slightly different tail thicknesses. We selected four sets of generation coordinates with varying parameters for comparison, where each set generates 1000 basic wave functions. Specifically, the parameters for the Logistic distribution were set at γ = 1.2, 1.3, 1.4, 1.5 and for the Normal distribution at σ= 1.8, 2.0, 2.3, 2.5. The calculated ground state (0⁺) energies of ⁶He are presented in Table 2, and Fig. 3 illustrates the energy convergences with an increasing number of basis. From Table 2, it can be seen that among the computations employing Normal distributions, the best performance is achieved with a standard deviation σ of 2.3, where the ground state energy converges to -28.245 MeV. Conversely, for σ values of 1.8, 2.0, and 2.5, the energies converge to -28.224 MeV, -28.222 MeV, and -28.231 MeV, respectively. On the other hand, the Logistic distribution clearly outperforms the Normal distribution, with ground state energies uniformly converging around -28.26 MeV. Notably, even at its poorest performance with parameter γ = 1.2, the energy convergence reaches -28.260 MeV, surpassing the mean performance of the Normal distribution groups. Additionally, Fig. 3 illustrates that the rate of energy convergence for the Logistic distribution group is substantially faster than that for the Normal distribution group, thereby exhibiting greater robustness. This indicates that the Logistic distribution includes a more effective basis, which could be because of its heavy tail part.

Fig. 3Full-screen View

(Color online) Energy convergence of the ground state (0⁺) of ⁶He. To compare the results of Normal distribution and Logistic distribution, 1000 ground state wave functions are generated using four sets of different parameters. In addition, the red line denotes the results of Adam optimization

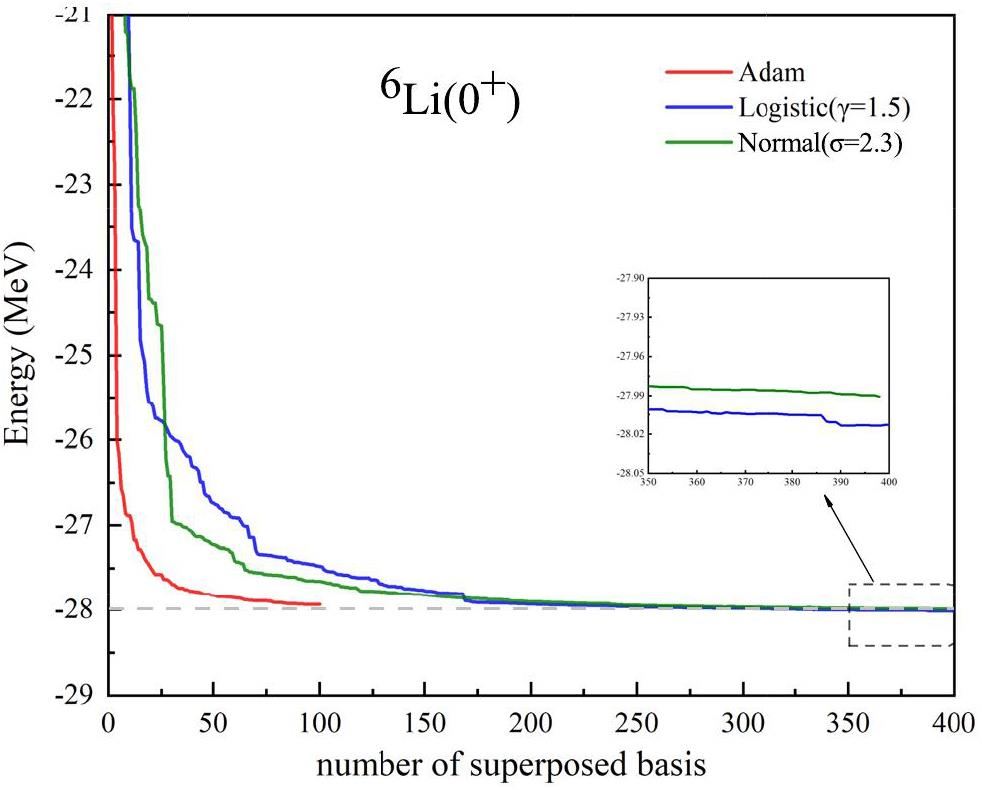
It is worth mentioning that the ground state (1⁺) of ⁶Li converges rapidly, requiring only a minimal number of basis wave functions. Calculations using various parameters for the Logistic and Normal distributions also quickly converged to approximately -30.02 MeV, indicating that there is no need for further optimization of the basis wave functions. Therefore, further discussion of the ⁶Li ground state is omitted in this work.

To confirm the aforementioned conclusions and ascertain the universality of the Logistic distribution in halo nuclear structures, we studied the excited states (0⁺) of ⁶Li and generated three sets of Logistic and Normal distributions under conditions of similar standard deviations for comparative analysis. Parameters for the Logistic distribution were set at γ = 1.0, 1.3, and 1.5, whereas those for the Normal distribution were set at σ = 1.8, 2.0, and 2.3. Considering the proton-neutron halo structure of ⁶Li, whose excited state energy converges more readily than the ground state energy of ⁶He, we generated 400 basis wave functions for each parameter set to perform the GCM calculations. The results are shown in Fig. 4 and Table 3. It is gratifying to observe that compared with the Normal distribution, the Logistic distribution still performs well in each group. According to the excitation energy of the 0⁺ state in Table 3, it can be observed that the Logistic distribution parameters γ are set at 1.0, 1.3, and 1.5, yielding convergence values of energy at -27.945 MeV, -27.999 MeV, and -28.013 MeV, respectively. These values slightly surpass those derived from the Normal distribution parameter σ set at 1.8, 2.0, and 2.3, which resulted in energy convergences of -27.933 MeV, -27.969 MeV, and -27.991 MeV. As shown in Fig. 4, the energy gradually converges as the number of basis wave functions increases, with the Logistic distribution exhibiting a slightly faster rate of convergence than the Normal distribution. These results indicate that the thick-tail characteristic of the Logistic distribution is not only suitable for calculating the ground state (0⁺) energy of ⁶He with a di-neutron halo, but also applicable to the excited state (0⁺) of ⁶Li with a proton-neutron halo. Furthermore, the Logistic distribution encompasses a broader range of effective basis wave functions, thereby providing crucial empirical insights for the subsequent selection of effective basis wave functions. It is important to analyze the underlying mechanisms behind this distribution.

Fig. 4Full-screen View

(Color online) Energy convergence of the excited state (0⁺) of ⁶Li. To compare the results of Normal distribution and Logistic distribution, 400 wave functions are generated using three sets of different parameters. The red line represents the results of Adam optimization

Adam optimization based on gradient descent principle

In GCM calculations, determining an appropriate distribution of optimized basis wave functions is of paramount importance for practical computations. However, studying the optimal basis wave functions mathematically at a local level is indispensable.

As shown in Eq. (3), the eigen energy E can be considered as a multivariable function with a set of {R} as its independent variables. Thus, solving for the energy using the variational principle is analogous to finding the minimum of a multivariable function $f\left({\left\{R\right\}}_1\mathrm{,}\{R{\}}_2\mathrm{,}\dots \mathrm{,}\{R{\}}_i\right)$. The computational procedure for optimizing the superposition of 100 basis wave functions is as follows: To begin this process, a random set of generated coordinates $\left\{\right\{R{\}}_1\mathrm{,}\{R{\}}_2\mathrm{,}\dots \mathrm{,}\{R{\}}_i\}$ is created as the starting position. For the first basis wave function $\text{Φ}\left({\left\{R\right\}}_1\right)$, the energy gradient must be calculated to adjust the coordinates ${\left\{R\right\}}_1$ in the gradient direction. When a local minimum was reached, this position was recorded as the effective basis wave function location ${\left\{R\right\}}_1^{\text{opt}}$. Next, for the second basis wave function $\text{Φ}\left({\left\{R\right\}}_2\right)$, we superimpose it onto the previously optimized ${\left\{R\right\}}_1^{\text{opt}}$. This results in a simplified expression for the wave function as $\text{Φ}\left({\left\{R\right\}}_1^{\text{opt}}\right)$ + $\text{Φ}\left({\left\{R\right\}}_2\right)$. Then, only coordinates ${\left\{R\right\}}_2$ are adjusted in the direction of the gradient, while coordinates $\text{Φ}\left({\left\{R\right\}}_1^{\text{opt}}\right)$ are held constant. Once the local minimum is achieved, the current position is designated as the effective basis wave function position, $\text{Φ}\left({\left\{R\right\}}_2^{\text{opt}}\right)$. For the third basis wave function $\text{Φ}\left({\left\{R\right\}}_3\right)$, the same procedure was followed. The adjustment process focuses solely on coordinates ${\left\{R\right\}}_3$ in the direction of the gradient, keeping ${\left\{R\right\}}_1^{\text{opt}}$ and ${\left\{R\right\}}_2^{\text{opt}}$ constant.This method was repeated for each subsequent wave function, ensuring that the optimized coordinates remained fixed, while the new coordinates underwent gradient descent. This iterative approach continues until all basis wave functions are optimized. In principle, a set of optimal generating coordinates for the basis wave functions can be obtained with sufficient computational precision.

We used the Adam algorithm for gradient descent [58]. The Adam algorithm was chosen for its efficiency in optimizing the basis wave functions, particularly for handling complex and flat energy surfaces. By adapting learning rates and leveraging historical gradients, Adam outperformed traditional methods, reducing computational costs and improving the convergence speed. This makes it well-suited for challenging calculations, such as those involving halo nuclei.

Given the gradual slowing of energy convergence with increasing number of basis wave functions, distinct treatments were applied to the initial and terminal functions. In the early superposition phase, owing to the rapid decrease in energy, the Adam algorithm’s learning rate α was set at 0.3 with a maximum iteration count of 12 and an allowance for four oscillations to prevent missing minimal value points. When the fifth wave function was reached, as the rate of energy decline slowed, the learning rate was adjusted to 0.7 with the maximum iterations increasing to 40, and oscillations allowed up to eight to minimize time consumption.

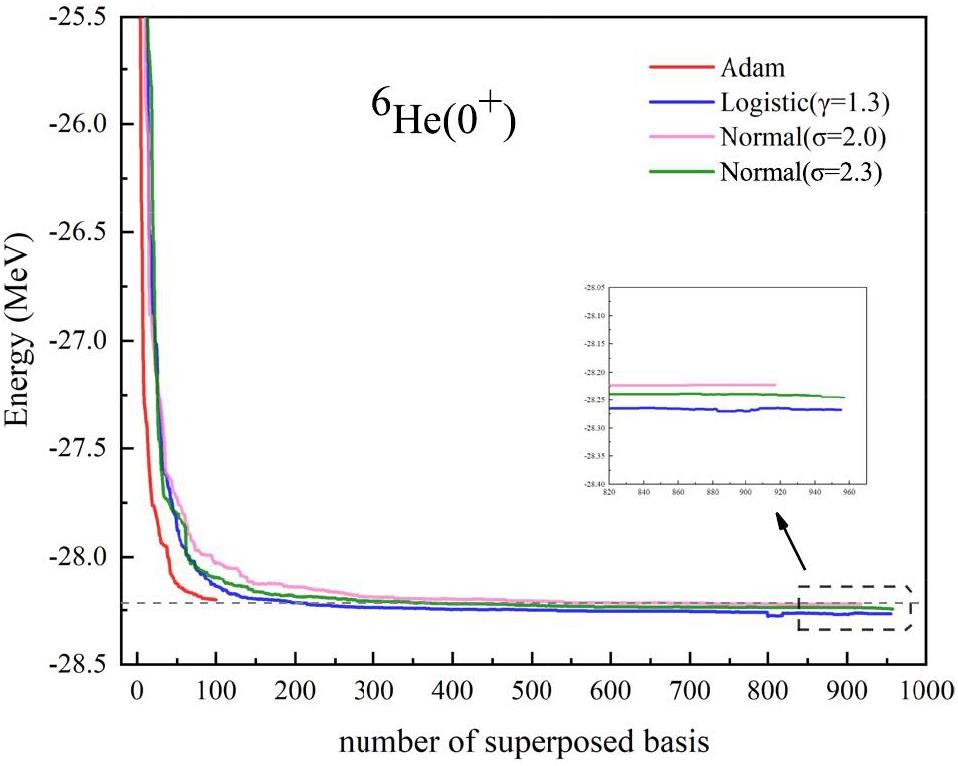
Although Sect. 3.1 shows the Logistic distribution outperforming Normal distributions and other models, we used the Normal distribution with σ = 2.3 to generate 100 initial coordinates {R} for a clearer comparative analysis. The optimization results for the ground state (0⁺) of ⁶He, as shown in Fig. 3. Compared to -28.064 MeV with unoptimized basis wave functions, the energy significantly decreases to -28.203 MeV after Adam optimization. Even compared to the well-performing Normal distribution, the superposition of 100 optimized basis wave functions through the Adam method equates to the effects of adding 200 or even 500 basis wave functions in the Normal distribution. This outcome not only confirms the feasibility and effectiveness of gradient descent optimization using the Adam method but also demonstrates that a small number of basis wave functions can achieve the effects of superposing multiple wave functions, and that Adam optimization includes a large number of effective basis wave functions.

To further validate this conclusion, the Adam algorithm was applied to the calculation of the excited state (0⁺) energy of ⁶Li, and the results are depicted in Fig. 4. Compared to -27.656 MeV with non-optimized basis wave functions, the energy decreased significantly to -27.937 MeV after Adam optimization. Compared with other parameter settings in the Normal distribution, the superposition effect of 100 optimized basis wave functions is equivalent to adding 200-300 ones in the Normal distribution. This suggests that there is still room for improvement in determining better distributions for the mesh points in the GCM. It is worth noting that owing to the differing nuclear structures of various nuclei, the optimized basis functions derived by the Adam algorithm for one nucleus in principle cannot be directly applied to another.