I. INTRODUCTION
The Monte Carlo method is a type of stochastic simulation method that approximates solutions to quantitative problems with the help of different statistical sampling techniques. It is also considered as a random sampling technique or a statistical test method. The Monte Carlo method is widely used in atomic energy research, radiation protection, dosimetry and radiation biophysics, and other fields of nuclear science to address neutron and photon transport in nuclear reactor design, physics experiments, and radiation shielding [1]. Several simulation programs are based on the Monte Carlo method, including electron gamma shower, Monte Carlo N-Particle, and Geant4 procedures [2]. Nonetheless, the Monte Carlo method must be developed based on numerous simulations to obtain reasonable and accurate results given that it is a method based on probability and statistics theories. Errors in the Monte Carlo method can be described by
The Monte Carlo program can be accelerated in two ways: hardware and software acceleration [4, 5]. With respect to hardware acceleration, the University of Toronto in Canada investigated the parallel computing of Monte Carlo based on a field programmable gate array (FPGA) in addition to improving computer performance [6]. The software acceleration method for the Monte Carlo program is divided into two parts. One part aims to improve the algorithm by enhancing the structure of the program and to reduce the number of simulation processes using programming techniques or algorithms, thereby limiting simulation time. Another software acceleration method is parallel computing, which facilitates multi-threaded simulation in the program by enhancing the implementation of the Monte Carlo program structure.
Graphics processing units (GPUs) are significantly advantageous over central processing units (CPUs) in terms of high-speed float point arithmetic performance. The current study attempts to apply the parallel computing capabilities of GPU, to re-write the photon and electron simulation processes of the Geant4 simulation program with an open programming language, to write the Geant4 simulation program into a GPU kernel executable program using an open programming language, and to generate a new Geant4 simulation program based on GPU. In the process of developing this new Geant4 simulation program, the main calculation component of the simulation is implemented in GPUs while the overall process is coordinated by the CPU. Simulation models are also established to verify the feasibility of the new Geant4 simulation program based on GPU.
II. MATERIALS AND METHODS
The parallel computing capability of GPU has been improved significantly in recent years [7]. Given its powerful parallel computing capability and sophisticated programmable performance, increasing numbers of researchers focuses on the application of GPU to the field of non-graphics processing. Thus, a new field of study is developed, namely, the general-purpose computation of GPUs (GPGPU). This study field emphasizes the expansion of the range of scientific computing on GPU to beyond conventional graphics processing. To date, GPGPU has been applied successfully in algebraic computations, database applications, fluid simulation, spectrum analyses, and in the commercial implementation of data mining tools and intelligent information processing systems [8, 9]. The rapid development of GPGPU generates a novel research direction for the acceleration of the Monte Carlo program and of GPU-based parallel computing [10, 11]. The target can be reached using GPU programming languages such as OpenCL and CUDA. The present study establishes two models: One model verifies and compares the feasibilities of OpenCL and CUDA, whereas the other determines the accelerating effects of this method.
A. Simplified model of photon transport
This study utilizes a simplified model of photon transport. This model adopts an energy-tunable, monoenergetic photon source and an iron target of infinite incident cross-sectional areas and variable thickness. In this simplified model, only the Compton scattering is taken into account and the program gives the energy spectrum of the photon and normalizes the output. Various programming languages can be used to calculate this model. Therefore, this study programs miniMC, miniMC_O, and miniMC_C using Geant4, OpenCL, and CUDA, respectively. The differences among these three programs are presented in the succeeding sections of this paper. Fig. 1 shows the process of the parallel computing program that describes photon transport based on GPU using the OpenCL programming language. The algorithm process of CUDA is similar to the aforementioned one.
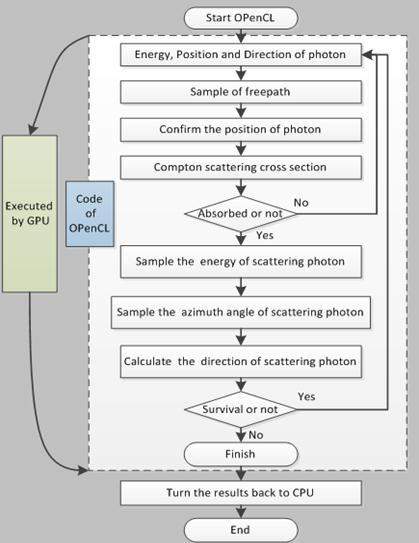
First, the miniMC_O program must establish the kernel program using the OpenCL programming language. This program is divided into two sections, namely, the OpenCL starting section and the kernel code section. OpenCL mainly establishes a link between CPU and GPU and can check whether the hardware of the current system meets the requirements for parallel computing. It can also manage the parallel computing program, such as how the kernel can be sent to the GPU and how the number of threads can be controlled. The process initiated in the kernel code section is similar to that of the miniMC program in Geant4, with the exception of some differences in syntax. With the completion of the kernel program, the results are tentatively saved to the GPU chip memory. The program must therefore return the calculated results to the CPU through the storage mechanism established in the start section of the OpenCL to collect and subsequently analyze the results.
B. Simple coupling model of photon and electron transport
This model aims to determine the acceleration effect achieved with the GPU-based parallel computing method for the Monte Carlo program. The Geant4 program (version 4.8.2) is chosen as the standard computing program. Base on GPU, parallel computing tools (BOGPT) are developed to solve the simulation model for electronic energy deposition in the material. This model involves an energy-tunable monoenergetic electron source whose energy ranges from 0.1 MeV to 10 MeV. This source is positioned in the Z-axis direction. The target geometry is defined as an infinite rectangular with a thickness of the incident electron range, which is divided into 100 layers. The material of the target consists of a single element, such as Cu, Al, or C. BOGPT is then used to conduct a statistical analysis of the energy deposition of particles in each layer. Figure 2 depicts the algorithm process of this program.
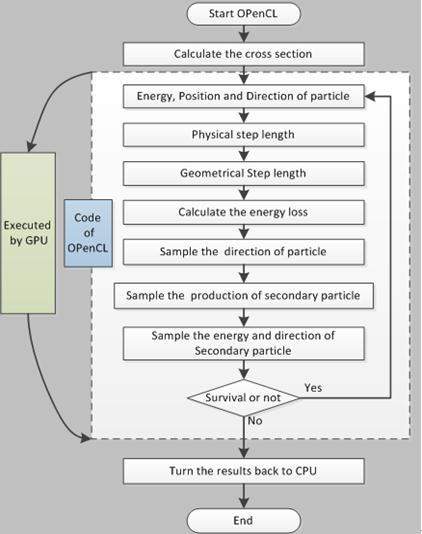
In the parallel computing of Geant4 photon electron transport based on GPU, the steps executed within GPU must be identified to shorten the execution time and to enhance program effectiveness. Given that data transfer between the GPU and CPU may delay the transmission of large data significantly in relation to BOGPT procedures, parallel calculation procedures should ensure that data communication between GPU and CPU is as limited as possible. BOGPT calculates the cross-section in the CPU and conveys the results to GPU for follow-up calculations. The simulation process of the photon electronic simulation program in Geant4 is written into the kernel program using OpenCL. The program is then transmitted to GPU for execution.
III. RESULTS AND DISCUSSIONS
A. Simulation results of the simplified photon transport model
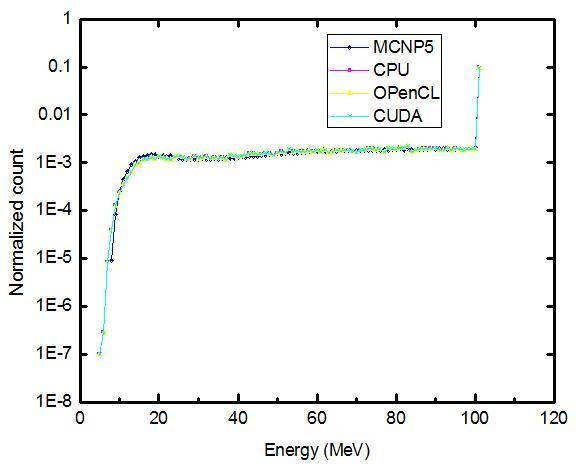
Figure 3 presents the simulation of the simplified photon transport model when photon energy is 1 MeV and the thickness of the iron target is 10 cm. Four curves in the figure represent the simulation results of the MCNP5, miniMC, miniMC_C, and miniMC_O programs. The reasonable conclusion is that the simulation results of parallel computing based on GPU are similar to those of the original program under the same conditions. Moreover, all findings are consistent with the simulation results of the MCNP5 program, thus confirming that the parallel computing results of the GPU-based Monte Carlo program are reliable.
This section discusses the acceleration effect of the program. Table 1 lists the simulation times of the different programs and the variable thicknesses of the target given 107 incident photons at 1 MeV. The GPU-based parallel computing process for the Monte Carlo program, which utilizes OpenCL (miniMC_O), is approximately 88 times shorter than that of the original program (miniMC). Furthermore, the process of the miniMC_C is approximately 94 times shorter. These results indicate that GPU can induce the acceleration effect by efficient parallel computing, thus confirming that the computational efficiency of the Monte Carlo program can be improved with the help of parallel computing based on GPU. In addition, OpenCL may have relatively more technical support and broader development prospects than CUDA. Thus, OpenCL is used as the programming language in this study.
| Target thickness (cm) | miniMC (s) | MiniMC_O (s) | MiniMC_C (s) |
|---|---|---|---|
| 5 | 32.04 | 0.37 | 0.34 |
| 10 | 31.87 | 0.36 | 0.33 |
| 15 | 31.99 | 0.36 | 0.33 |
| 30 | 32.26 | 0.38 | 0.35 |
B. Simulation results of the simple coupling model of photon and electron transport
The simple coupling model of photon and electron transport is simulated using three programs after electron energy and target materials are selected. These three programs are Geant4, BOGPT, and the non-parallel computing simulation for the BOGPT program (CPU). The simulation results are then compared with one another. Figs. 4 and 5 display the simulation results of these three programs under the same condition (where De is the energy deposition; E0 is the incident electron energy; r0 is the range of the electron; and z is the particle penetration depth). The X-axis represents the penetration depth in normalized values and the Y-axis is the energy deposition value of each layer. Fig. 4 suggests that the incident electron is 1.0 MeV and that the target is Cu, whereas Fig. 5 shows that the incident electron is 1.0 MeV and the target is Al. These results indicate that the BOGPT program simulation results are roughly similar to those of the original Geant4 program, thereby indicating that the simulation results are credible.
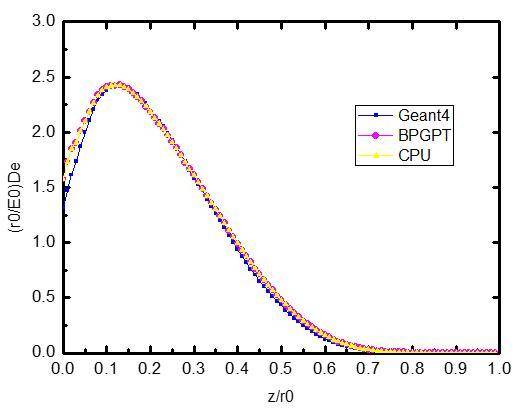
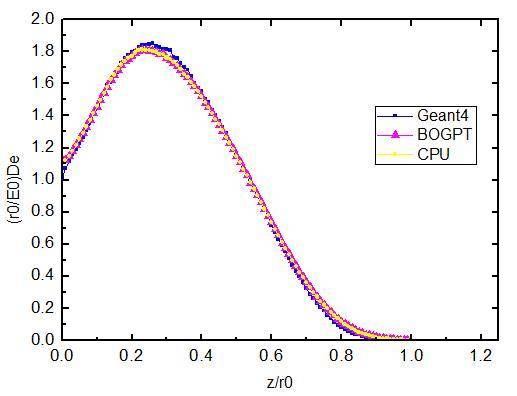
Table 2 lists the simulation times of the BOGPT, CPU, and Geant4 programs given different target materials under the condition that electron energy is 1 MeV and the number of incident particle is 106. The costs of the BOGPT program are approximately two times less than those of the CPU and Geant4 programs. Therefore, the parallel efficiency of the BOGPT program is roughly three times better than those of the other two programs.
| Material | CPU (s) | BOGPT (s) | Geant4 (s) |
|---|---|---|---|
| C | 329.3 | 105.8 | 305 |
| Al | 327.5 | 103.5 | 301 |
| Cu | 330.2 | 109.33 | 308 |
However, the acceleration effect of the BOGPT program is inferior to those of the miniMC_O and miniMC_C programs, which are nearly 100 times better than the effects obtained with parallel computing. This finding is attributed to the fact that the simulation of the BOGPT program is much more complex than those of the simplified models. MiniMC_O and miniMC_C are simple and consider only the Compton scattering effect. By contrast, the BOGPT program involves the coupling model of photon and electron transport, the simulation process of which is substantially similar to that of Geant4. It involves numerous judgment and branch operations in which GPU is ineffective. BOGPT is the initial completion of the reproduction of the simulation processes of Geant4, which optimizes programs by parallel computing based on GPU without effective program optimization. This process limits the effect of parallel computing to some extent.
The simulation of CPU program time is slightly longer than that of Geant4, as shown in the Table. This result is primarily ascribed to the fact that the optimization processes of calling cross-section in the original Geant4 have been deleted to enhance the execution of the BOGPT program. Thus, the BOGPT program considers cross-sections directly and not through judgments and branches, which take certain time cost and lengthen the simulation time of the CPU program in comparison with that of Geant4.
IV. CONCLUSION
This research is a preliminary study on a GPU-based parallel computing method for the Monte Carlo program. The Geant4 procedures and the BOGPT program are simulated and compared, and the results indicate that the use of GPU programming can facilitate the parallel computing of the Monte Carlo program. Furthermore, the increase in speed by a maximum of 100 times is ideal for simple procedures. It is also effective in complex Monte Carlo procedures, such as Geant4. However, this method remains limited in terms of hardware and software. Therefore, it must be further optimized to expand the prospects of GPU programming application in the parallel computation of the Monte Carlo program.

