Introduction
The T1/2=2.54-min Jπ=19/2- isomer at 3.0 MeV in 53Fe is unique in atomic nuclei in that it has a direct decay branch to the Jπ=7/2- ground state, requiring a hexacontatetrapole electric transition E6 [1-3]. This was recently experimentally confirmed with improved precision [4], providing a sensitive probe for nuclear structures [5, 6]. More generally, this scenario provides unique insights into the highest-order shapes and correlations in nuclei, and tests the applicability of nuclear models under extreme conditions. In the present work, we focus on ab initio calculations with bare nucleon charges, which can explain both 53Fe excited-state energies and electromagnetic decay transition rates.
In nature, a free photon has an angular momentum of 1 ħ, whereas in a high multipole transition, a single photon carries away a large angular momentum. Naively, the probability of emitting a high-spin photon should be very small. In 53Fe, a single E6 photon brings a spin change as large as 6ħ. No other isolated physical system is known to exhibit high multipole or single-photon emission. By comparison, infrared spectra have revealed 6ħ absorption in solid hydrogen [7], and magneto-optical studies of atomic 85Rb have reported 6ħ spontaneous emissions [8]. Thus, there is a small group of physical environments where high multipole radiation provides access to novel and exceptional physics.
In a recent experimental study by Palazzo et al. [4], the existence of E6 decay in 53Fe was firmly established using empirical shell model calculations. However, Ref. [4] does not provide calculations of high multipole electromagnetic transition probabilities. This is because that the empirical calculations require both proton and neutron effective charges that cannot be determined at present by only one available set of experimental E6 transition rate data. In empirical models, different effective charges are used for different multipolarities of the transitions. To improve such ad hoc features, ab initio calculations that use realistic interactions and bare nucleon charges are required. This provides the prospect of gaining insight into rare high-multipole transitions and testing the ab initio method itself. The ab initio nuclear theory is at the forefront of the current nuclear structure studies. Over the past two decades, significant progress has been made in ab initio many-body methods [9-13] using nuclear forces based on chiral effective field theory [14].
In this study, we employed the ab initio valence-space in-medium similarity renormalization group (VS-IMSRG) [15-18] to derive the valence-space effective Hamiltonian and effective multipole transition operators for further shell model calculations of the observed excited states and their electromagnetic transitions in 53Fe. Unique bare nucleon charges were used in the calculation of all the multipolar transitions. We aim to provide solid calculations to explain the experimental observations and provide deep insight into the structure of the Jπ=19/2- isomer.
Theoretical framework
Our calculations start from the intrinsic Hamiltonian of the A-nucleon system [19, 20]
The IMSRG evolves the normal-ordered Hamiltonian to a block diagonal, which gives the valence-space effective Hamiltonian. Using this technique, we can also derive valence-space effective operators for other observables, including multipolar transitions. The Magnus expansion [25] was used in the IMSRG evolution. Operators appearing in the IMSRG equations are truncated at the two-body level, which is referred to as IMSRG(2) [21]. The technique of using IMSRG to obtain a valence-space Hamiltonian for shell model calculations is called VS-IMSRG [21].
The normal-ordering approximation of the Hamiltonian and the evolution of the VS-IMSRG were implemented with a closed-shell reference state in the Hartree-Fock basis. However, to reduce the effect of the residual 3NF, which is neglected, the fractional filling of open-shell orbitals in an open-shell nucleus has been suggested, called ensemble normal ordering (ENO) [17]. Using the ENO approximation of the VS-IMSRG, we can obtain the nucleus-dependent valence-space effective Hamiltonian and the effective operators of the other observables. The effective Hamiltonian obtained is diagonalized using the large-scale shell model code KSHELL [26], giving eigenenergies and one- and two-body transition densities (OBTD and TBTD, respectively) for further calculations of states.
The reduced transition probability is calculated by
Calculations and discussions
The 53Fe Jπ=19/2- isomer is the only case in which the highest multipole E6 transition is observed [1-4]. In a recent experimental study [4], shell model calculations using two empirical interactions, GFPX1A and KB3G, were performed with a model space of only the 0f7/2 or the full fp shell. In empirical calculations of electromagnetic transitions, effective nucleon charges are used with different effective charges for different multipolarities of transitions, determined by fitting the data. The problem is that only one E6 transition has been observed to date, that is, from the 19/2- isomer to the 7/2- ground state in 53Fe. One E6 transition data cannot simultaneously determine both the proton and neutron effective charges. In the present work, we performed ab initio calculations using the shell model with a full fp model space above the 40Ca core. The valence-space shell model effective Hamiltonian, including the one-body single-particle energies of the valence particles, is obtained using the IMSRG evolution with the ENO approximation [17, 21]. In ab initio calculations of multipole transitions, unique bare nucleon charges are used, meaning that the same bare charges are used for different multipolarities of the transitions.
In our calculations, two different versions of the chiral NN plus 3N interaction were used to test its dependence on the interaction used. The potential labeled 1.8/2.0(EM) [29-31] takes the NN force (2NF) at N3LO [32] and 3NF at N2LO. This potential can globally reproduce the ground-state properties of nuclei, from light-to heavy-mass regions, with the harmonic-oscillator (HO) basis frequency optimized at
The basis space is another important issue that must be addressed. The present calculation starts by using a spherical HO basis with
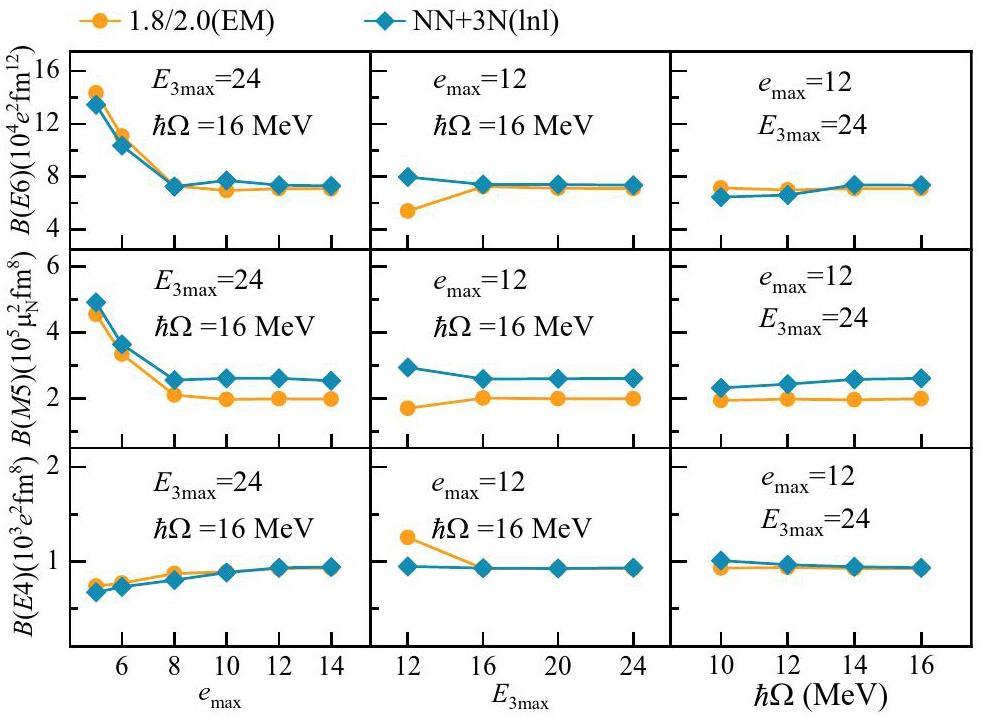
The present calculations reproduce the excitation spectrum of 53Fe. However, for the sake of simplicity, as shown in Fig. 2 we show only a limited set of levels associated with the 19/2- isomer. The calculations reproduced experimental data [38]. In particular, the calculation using the NN+3N(lnl) interaction was in better agreement with the data. Both calculations yield the correct energy ordering of the 19/2- level, which is lower than the 13/2- level. The lower energy of the 19/2- level compared to that of the 17/2- and 15/2- levels makes it natural that the M1 and E2 transitions cannot occur from the 19/2- state, which leads to the formation of the 19/2- metastable isomeric state.
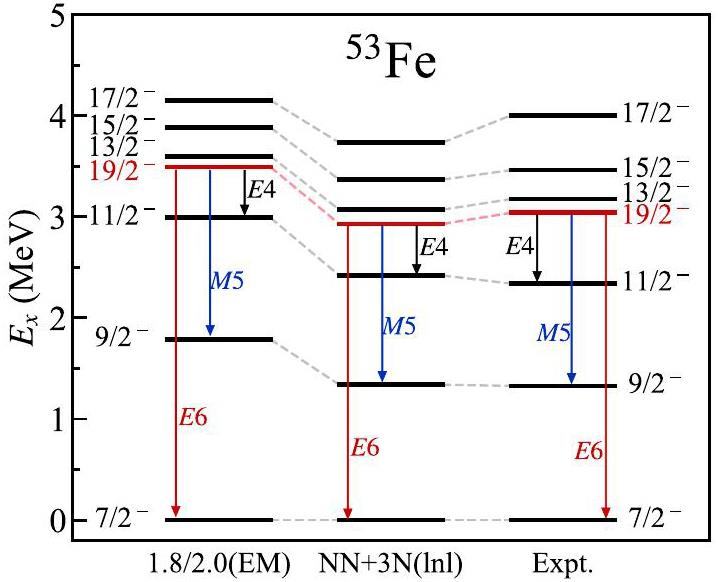
Experiments [1=4] observed that the 19/2- states decayed to lower 11/2-, 9/2- and 7/2- states by high-multipole E4, M5 and E6 transitions, respectively. Higher multipole γ decays have lower transition probabilities, which can lead to long-lived isomers. Experimental observations [1-4] of the rare high multipole γ decay in 53Fe provide a unique laboratory for the study of electromagnetic transitions with high multipolarity. Table 1 shows the calculated reduced probabilities of the observed highest-multipole transitions E6, M5 and E4 compared with the experimental data [4]. The NN+3N(lnl) potential provides an improved result for the M5 transition probability that is closer to the data. However, the calculated E6 transition probability differed from the experimental data by a factor of approximately three, although the experimental error was large for this transition. The present VS-IMSRG calculation is approximated with operators truncated at a two-body level by IMSRG(2) [21], whereas a recent study has developed the IMSRG with operators truncated at the three-body level labeled by IMSRG(3) [39, 40]. Another study indicated that the IMSRG combined with the generator coordinate method can capture more collective correlations in deformed nuclei [41]. In Refs. [42, 43], it was found that the inclusion of two-body currents can improve the calculation of magnetic dipole moments (transitions). It is clear that the consideration of these factors can improve calculations, but such an investigation goes beyond the scope of the present work and will be addressed separately. In empirical shell model calculations, effective nucleon charges are used to compensate for missing correlations. The values of the proton and neutron effective charges were determined by fitting the corresponding experimental data to the electromagnetic transitions. Different effective charges of protons and neutrons are used for different multipolarities of the transitions. Unfortunately, only one E6 experimental data point is available at present, which is not sufficient to determine both the proton and neutron effective charges of the E6 transition.
| Transitions | ||||
|---|---|---|---|---|
| 1.8/2.0(EM) | NN+3N(lnl) | Expt. | ||
| E6 | 0.706×105 | 0.725×105 | 2.61(81)×105 | |
| M5 | 1.98×105 | 2.53×105 | 3.31(16)×105 | |
| E4 | 9.28×102 | 9.58×102 | 6.46(5)×102 | |
Using bare nucleon charges, we also calculated the 53Fe E2 and M1 reduced transition probabilities that were available experimentally, as shown in Table 2. We observe that the observed E2 and M1 transition probabilities can be reproduced reasonably well (all are well within
| σλ | Transitions | |||
|---|---|---|---|---|
| 1.8/2.0(EM) | NN+3N(lnl) | Expt. | ||
| E2 | 108 | 104 | 106(47) | |
| 139 | 127 | 94(59) | ||
| M1 | 0.81 | 0.79 | 0.63(14) | |
| 0.51 | 0.51 | 0.98(41) | ||
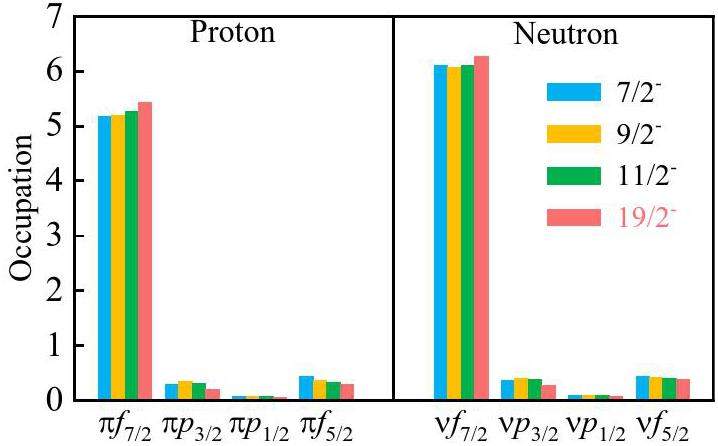
To better understand the long-lived 19/2- isomer of 53Fe, we discuss the state configurations. Figure 3 shows the configurations of the 7/2-, 9/2-, 11/2- and 19/2- states obtained from the calculation. We see that the 0f7/2 component dominates the states, which can be understood by the simple three-hole (3h) coupling
Summary
High-multipole electromagnetic transitions are of particular interest in the study of nuclear structures, providing a sensitive test of the theories used. To date, the highest multipole transition is the electric hexacontatetrapole E6 transition from the Jπ=19/2- isomer to the 7/2- ground state in 53Fe, accompanied by M5 and E4 transitions to the first 9/2- and 11/2- excited states, respectively. A recent experiment [4] provided clear detection of the highest-multipole transitions with greater precision for the transition rates. Shell-model calculations with empirical interactions were performed in an experimental study [4]. However, empirical calculations cannot definitively determine the E6 transition probability. The empirical shell model uses the effective charges determined by fitting the experimental data. To date, only one E6 transition was observed, i.e., that from the Jπ=19/2- isomer to the Jπ=7/2- ground state in 53Fe. An experimental E6 transition rate cannot simultaneously determine both the proton and neutron effective charges.
In this study, we performed ab initio calculations of the highest multipole electromagnetic transitions observed from the 19/2- isomer of 53Fe. Two different versions of the chiral two- plus three-nucleon interactions were used in the calculations. Using the valence-space in-medium similarity renormalization group, the free-space interaction matrix was decoupled to form a low-momentum valence space, obtaining the valence-space effective interaction for the shell-model calculation. The calculation convergence of the excitation spectrum and the electromagnetic transitions of 53Fe has been well tested. The present ab initio calculations reproduce the experimental spectrum well. The 19/2-isomerism is due to its lower energy compared to those of the 17/2- and 15/2- levels, which leads to the absence of natural E2 and M1 transitions from the 19/2- state. Using the same decoupling method, free-space bare operators of electromagnetic transitions evolve into the valence space. With the unique bare nucleon charges, we can reproduce the measured highest multipole E6, M5 and E4 transition strengths. The low multipole E2 and M1 transitions observed in this nucleus can also be reproduced using bare nucleon charges. Moreover, we provide the configurations of the 7/2-, 9/2-, 11/2- and 19/2- states, and reveal the structure of the Jπ=19/2- isomer.
E6 and M5 transitions observed in Fe53m decay
. Phys. Rev. Lett. 26, 451-454 (1971). https://doi.org/10.1103/PhysRevLett.26.451Decays of the f72 isomers 53Feg and 53Fem
. Phys. Rev. C 11, 939-951 (1975). https://doi.org/10.1103/PhysRevC.11.939Yrast states in 52Fe, 52Mn and the decay of 52Fem
. Phys. Rev. C 19, 1938-1947 (1979). https://doi.org/10.1103/PhysRevC.19.1938Direct measurement of hexacontatetrapole, E6γ decay from 53mFe
. Phys. Rev. Lett. 130,E6 gamma decay
. AIP Conference Proceedings 1355, 145-152 (2011). https://doi.org/10.1063/1.3584058Shell-model description of nuclear isomers
. Eur. Phys. J. Special Topics 233, 893-902 (2024). https://doi.org/10.1140/epjs/s11734-024-01137-yHigh-resolution infrared spectroscopy of solid hydrogen: The tetrahexacontapole-induced Δj=6 transitions
. Phys. Rev. Lett. 62, 32-35 (1989). https://doi.org/10.1103/PhysRevLett.62.32Pump-probe nonlinear magneto-optical rotation with frequency-modulated light
. Phys. Rev. A 73,A guided tour of ab initio nuclear many-body theory
. Front. Phys. 8, 379 (2020). https://doi.org/10.3389/fphy.2020.00379Ab initio predictions link the neutron skin of 208Pb to nuclear forces
. Nat. Phys. 18, 1196-1200 (2022). https://doi.org/10.1038/s41567-022-01715-8Progress in ab initio in-medium similarity renormalization group and coupled-channel method with coupling to the continuum
. Nucl. Sci. Tech. 35, 215 (2024). https://doi.org/10.1007/s41365-024-01585-0Physics of exotic nuclei
. Nat. Rev. Phys.. https://doi.org/10.1038/s42254-024-00782-5Unbound 28O, the heaviest oxygen isotope observed: a cutting-edge probe for testing nuclear models
. Nucl. Sci. Tech. 35, 21 (2024). https://doi.org/10.1007/s41365-024-01373-wChiral effective field theory and nuclear forces
. Phys. Rep. 503, 1-75 (2011). https://doi.org/10.1016/j.physrep.2011.02.001In-medium similarity renormalization group for open-shell nuclei
. Phys. Rev. C 85,The in-medium similarity renormalization group: A novel ab initio method for nuclei
. Phys. Rep. 621, 165 (2016). https://doi.org/10.1016/j.physrep.2015.12.007Nucleus-dependent valence-space approach to nuclear structure
. Phys. Rev. Lett. 118,Ab initio multishell valence-space hamiltonians and the island of inversion
. Phys. Rev. C 102,The roles of three-nucleon force and continuum coupling in mirror symmetry breaking of oxygen mass region
. Phys. Lett. B 827,Ab initio descriptions of A=16 mirror nuclei with resonance and continuum coupling
. Phys. Rev. C 108,In-medium similarity renormalization group for nuclei
. Phys. Rev. Lett. 106,Contribution of chiral three-body forces to the monopole component of the effective shell-model hamiltonian
. Phys. Rev. C 100,Coupled-cluster theory for three-body hamiltonians
. Phys. Rev. C 76,Medium-mass nuclei with normal-ordered chiral NN+3N interactions
. Phys. Rev. Lett. 109,Magnus expansion and in-medium similarity renormalization group
. Phys. Rev. C 92,Thick-restart block lanczos method for large-scale shell-model calculations
. Computer Physics Communications 244, 372-384 (2019). https://doi.org/10.1016/j.cpc.2019.06.011Ab initio electromagnetic observables with the in-medium similarity renormalization group
. Phys. Rev. C 96,Improved nuclear matter calculations from chiral low-momentum interactions
. Phys. Rev. C 83,Exploring sd-shell nuclei from two- and three-nucleon interactions with realistic saturation properties
. Phys. Rev. C 93,Saturation with chiral interactions and consequences for finite nuclei
. Phys. Rev. C 96,Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory
. Phys. Rev. C 68,Ab initio limits of atomic nuclei
. Phys. Rev. Lett. 126,Converged ab initio calculations of heavy nuclei
. Phys. Rev. C 105,Novel chiral hamiltonian and observables in light and medium-mass nuclei
. Phys. Rev. C 101,Discrepancy between experimental and theoretical β-decay rates resolved from first principles
. Nat. Phys. 15, 428 (2019). https://doi.org/10.1038/s41567-019-0450-7In-medium similarity renormalization group with three-body operators
. Phys. Rev. C 103,In-medium similarity renormalization group with flowing 3-body operators, and approximations thereof
. Phys. Rev. C 110,Ab initio treatment of collective correlations and the neutrinoless double beta decay of 48Ca
. Phys. Rev. Lett. 124,Impact of two-body currents on magnetic dipole moments of nuclei
. Phys. Rev. Lett. 132,Magnetic dipole transition in 48Ca
. Phys. Rev. Lett. 132,Nuhamil: A numerical code to generate nuclear two- and three-body matrix elements from chiral effective field theory
. Eur. Phys. J. A 59, 150 (2023). https://doi.org/10.1140/epja/s10050-023-01039-yFu-Rong Xu is an editorial board member for Nuclear Science and Techniques and was not involved in the editorial review, or the decision to publish this article. All authors declare that there are no competing interests.

