First-principles study on the diffusion behavior of Cs and I in Cr coating

NUCLEAR ENERGY SCIENCE AND ENGINEERING

First-principles study on the diffusion behavior of Cs and I in Cr coating

Shu-Ying Lin，

Xiao-Jing Li，

Lin-Bing Jiang，

Xi-Jun Wu，

Hui-Qin Yin，

Yu Ma，

Wen-Guan Liu

Nuclear Science and Techniques

Vol.35, No.6

Article number 100

Published in print Jun 2024

Available online 18 Jun 2024

DOI：10.1007/s41365-024-01460-y

78002

Cs and I can migrate through fuel-cladding interfaces and accelerate the cladding corrosion process induced by the fuel-cladding chemical interaction. Cr coating has emerged as an important candidate for mitigating this chemical interaction. In this study, first-principles calculations were employed to investigate the diffusion behavior of Cs and I in the Cr bulk and grain boundaries to reveal the microscopic interaction mitigation mechanisms at the fuel-cladding interface. The interaction between these two fission products and the Cr coating were studied systematically, and the Cs and I temperature-dependent diffusion coefficients in Cr were obtained using Bocquet’s oversized solute-atom model and Le Claire’s nine-frequency model, respectively. The results showed that the Cs and I migration barriers were significantly lower than that of Cr, and the Cs and I diffusion coefficients were more than three orders of magnitude larger than the Cr self-diffusion coefficient within the temperature range of Generation-IV fast reactors (below 1000 K), demonstrating the strong penetration ability of Cs and I. Furthermore, Cs and I are more likely to diffuse along the grain boundary because of the generally low migration barriers, indicating that the grain boundary serves as a fast diffusion channel for Cs and I.

First-principles calculationFuel cladding chemical interactionCr coatingFission productDiffusionGrain boundary

Introduction

Fuel cladding chemical interaction (FCCI) is considered one of the major factors limiting the lifetime of fuel pins in fast reactors, especially for oxide fuel pins with stainless-steel cladding [1], as severe oxidative corrosion can occur at the interface of the fuel and the cladding inner wall. Some fission products that migrate through the fuel-cladding interface can accelerate the FCCI-induced cladding corrosion process. The main fission products involved in this process are volatile Cs and I [1, 2] considering their production yield and penetration depth. Because the cladding attack rate depends on reactant diffusion at the cladding surface, Cs and I diffusion in the fuel pins is a key factor in the FCCI-induced corrosion problem.

Because of the complex and multi-scale coupled physical and chemical FCCI mechanisms, previous studies have mainly focused on experimentally exploring materials that can mitigate FCCI, and a buffer-getter material coating on the cladding inner surface is considered an effective method [1]. Buffer-getter materials, including V, Nb, Cr, Zr, U, Ti, and certain rare-earth metals, can reduce oxidation of the cladding owing to their high affinity for oxygen [1]. Specifically, Cr coatings have a high melting point, superior oxidative corrosion resistance [3, 4], good crack resistance [5-7], and mature preparation processes [8-10], making them important candidates for FCCI mitigation. However, the underlying micromechanisms remain unknown. First-principles density functional theory (DFT) is recognized as a powerful tool for revealing micro-mechanisms, especially in terms of elemental diffusion behavior when coupled with harmonic transition state theory [11], as demonstrated by numerous previous studies for impurity diffusion, including its consequent effects in Ni [11-16], Fe [17-24], Al [25-27], SiC [28], among others. Recently, Yang et al. [22] performed first-principles calculations of lanthanide diffusion in Cr and α-Fe to identify FCCI-mitigating mechanisms for metallic fuel and ferritic/martensitic steel cladding systems. To the best of our knowledge, there are few reported studies on FCCI-involved elements in oxide fuels, in which Cs and I dominate. Further research is warranted to comprehensively understand the effects of Cr coating on cladding inner surface functions for FCCI mitigation in oxide fuel pin systems.

In this study, first-principles was employed to investigate the diffusion behavior of important fission products (e.g., Cs and I) in body-centered cubic (BCC) Cr coating. Cs and I are very large in the Cr matrix, and the interstitial atom diffusion mechanism [29-33] is deemed unrealistic. Instead, the vacancy-mediated mechanism is the main diffusion mode for large-atomic-size impurity atoms [34], such as Cs and I. The remainder of this paper is organized as follows. Section 2 describes the vacancy-mediated diffusion models and the first-principles calculations. The methodology used to determine the inputs for the diffusion models is also described. Section 3 discusses the interactions between the impurity atoms and the surrounding Cr atoms or vacancies. The Cs and I diffusion coefficients in BCC Cr were obtained by applying the diffusion model, and the possible diffusion paths of Cs and I at the grain boundary (GB) were predicted based on the migration barriers between different sites. Finally, Section 4 summarizes the study and its findings.

Computational methods

2.1

Diffusion models for vacancy-mediated solutes

In this section, two diffusion models for impurity diffusion coefficient determination are introduced: Le Claire’s nine-frequency model [35-37] (hereon referred to as Le Claire’s model) and the oversized solute-atom (OSA) model [21]. As shown in Fig. 1, the impurity and matrix atoms are represented by orange and blue spheres, respectively, and the vacancies are represented by gray squares. The numbers on the atoms and vacancies indicate their positions as nearest neighbors (nn) to the impurity atom. The corresponding jump frequencies for different atom-vacancy exchange processes are shown in Fig. 1. The main difference between the two diffusion models lies in the configuration formed by the impurity atom and its 1nn vacancy, as described in detail next.

Fig. 1

(Color online) Diffusion model schematics: (a) Le Claire’s model [35-37]; (b) OSA model [21]

According to Le Claire’s model [35-37], the self-diffusion coefficient ( $D_{self - diff}$ ) and solute diffusion coefficient (D_solute) in a BCC lattice can be obtained as follows: $D_{self - diff} = a^{2} ω_{0} f_{0} C_{V},$ (1) $D_{solute} = a^{2} ω_{2} f_{x} C_{V} \exp (\frac{E_{1}^{b}}{k_{B} T}),$ (2) where a is the lattice parameter, $E_{1}^{b}$ is the vacancy-solute binding energy when the vacancy is located at the 1nn solute site, k_B is the Boltzmann constant, T is the temperature in K, f₀ is the correlation factor for self-diffusion, which is a constant equal to 0.727 for diffusion in BCC crystals. The correlation factor for solute diffusion fx is expressed as follows [35-37]: $f_{x} = \frac{3 ω_{3} + 3 ω_{3^{'}} + ω_{3^{″}} - \frac{ω_{3} ω_{4}}{ω_{4} + F ω_{5}} - \frac{2 ω_{3^{'}} ω_{4^{'}}}{ω_{4^{'}} + 3 F ω_{0}} - \frac{ω_{3^{″}} ω_{4^{″}}}{ω_{4^{″}} + 7 F ω_{0}}}{2 ω_{2} + 3 ω_{3} + 3 + ω_{3^{″}} - \frac{ω_{3} ω_{4}}{ω_{4} + F ω_{5}} - \frac{2 ω_{3^{'}} ω_{4^{'}}}{ω_{4^{'}} + 3 F ω_{0}} - \frac{ω_{3^{″}} ω_{4^{″}}}{ω_{4^{″}} + 7 F ω_{0}}},$ (3) where F=0.512. This expression applies to cases in which the impurity atom is close in size to the matrix atom, with $ω_{6} \approx ω_{0}$ . Based on transition-state theory [38], the average atomic jump frequency ωi with respect to the migration energy ( $E_{i}^{m}$ ) can be written as $ω_{i} = ν_{i} \exp (- \frac{E_{i}^{m}}{k_{B} T}),$ (4) where νi and $E_{i}^{m}$ are the attempt frequency and corresponding migration barrier for jump i, respectively. νi is defined as $ν_{i} = \prod_{j = 1}^{3 N - 3} / ν_{j}^{I} / \prod_{j = 1}^{3 N - 4} ν_{j}^{T}$ , where $ν_{j}^{I}$ is the normal vibration frequency of the initial migration state (I), and $ν_{j}^{T}$ is the nonimaginary normal frequency of the transition state (T). The vacancy concentration at equilibrium at temperature T is given by $C_{V} = \exp (- \frac{E_{v}^{f}}{k_{B} T}) \exp (\frac{S_{v}^{f}}{k_{B}})$ , with vacancy formation energy $E_{v}^{f} = E^{I} - (N - 1) E^{B} / N$ and vacancy formation entropy $S_{v}^{f} = k_{B} [\sum_{j = 1}^{3 N - 3} \ln (\frac{k_{B} T}{h ν_{j}^{I}}) - \frac{N - 1}{N} \sum_{j = 1}^{3 N} \ln (\frac{k_{B} T}{h ν_{j}^{B}})]$ , where E^I and E^B are the corresponding energy of the initial state structure and the bulk structure containing $N - 1$ and N atoms, respectively, and $ν_{j}^{B}$ is the normal vibration frequency of the bulk structure (B).

Le Claire’s model is a widely used diffusion model that describes the diffusion of substitutional solutes. Nevertheless, owing to the strong attraction of the OSA to the vacancies (as illustrated in Fig. 1 (b)), the OSA diffusion cannot be described using Le Claire’s model. Bocquet et al. [21] proposed a diffusion model applicable to OSA, namely, the OSA model, where the OSA diffusion coefficient is given by [21] $D_{OSA} = \frac{λ^{2}}{12} Γ_{MJ} f,$ (5) where λ is the distance between the vacancy and its nearest atom, i.e., $λ = \sqrt{3} a$ /2 in BCC crystals, $Γ_{MJ}$ is the frequency attached to a macrojump (MJ), and f is the correlation factor. An MJ is formed by two elementary displacements: the OSA located on a substitutional site (S) is pushed onto a transitional site (T), i.e., S → T, and then moved onto an S (T→S). Accordingly, the frequency attached to an MJ is defined as: $Γ_{MJ} = Γ_{ST} Γ_{TS} / (Γ_{ST} + Γ_{TS})$ , with $Γ_{ST} = 8 C_{V} [3 ω_{4} \exp (\frac{E_{2}^{b}}{k_{B} T}) + 3 ω_{4^{'}} \exp (\frac{E_{3}^{b}}{k_{B} T}) + ω_{{4^{'}}^{'}} \exp (\frac{E_{5}^{b}}{k_{B} T})]$ and $Γ_{TS} = 2 \times (3 ω_{3} + 3 ω_{3^{'}} + ω_{{3^{'}}^{'}})$ . $E_{i}^{b}$ is the binding energy between the solute and its i^th nn vacancy (a positive value for attraction and vice versa) and can be calculated as $E_{i}^{b} = E^{V} + E^{S} - E^{I} - E^{B} .$ (6) where the right-hand-side terms represent the energies of the different configurations. The number of Cr atoms, vacancies, and impurity atoms in each configuration are (127, 1, 0), (127, 0, 1), (126, 1, 1), and (128, 0, 0), respectively. The correlation factor f for OSA diffusion in BCC crystals is $1 + Q^{BCC}$ , where Q^BCC is the average cosine between a T→S jump vector and the next S→T jump in the BCC lattice. Bocquet et al. [21] obtained the exact formula for Q^BCC using double Laplace and Fourier transforms of the transport equation for vacancies. For simplicity, in this study, we applied the formula with “one-shot” approximation as follows: $\begin{matrix} Q_{1shot}^{BCC} = - \frac{1}{3 ω_{3} + 3 ω_{3^{'}} + ω_{3^{″}}} \\ \times (\frac{4 ω_{3} ω_{4}}{4 ω_{4} + 4 ω_{5}} + \frac{4 ω_{3^{'}} ω_{4^{'}}}{2 ω_{4^{'}} + 6 ω_{0}} + \frac{ω_{3^{″}} ω_{4^{″}}}{ω_{4^{″}} + 7 F ω_{0}}) . \end{matrix}$ (7) The “one-shot” approximation hypothesis is that, after the OSA dissociation with its nearby vacancy, only one jump is needed for the vacancy to return close to the OSA. It has been proven that the vacancy-solute interaction is very strong at 1nn, which is exactly the case for OSA diffusion.

Our preliminary calculation shows that Cs combines with its 1nn vacancy and forms a “V/2 + Cs + V/2” (V denotes vacancy) configuration, as shown in Fig. 1(b)). In contrast, I does not exhibit a strong attraction to 1nn V, as shown in Fig. 1(a). According to the application conditions for different diffusion models, in this study, the OSA model was used for the Cs diffusion coefficient calculation and Le Claire’s model was used for I.

2.2

First-principles calculation

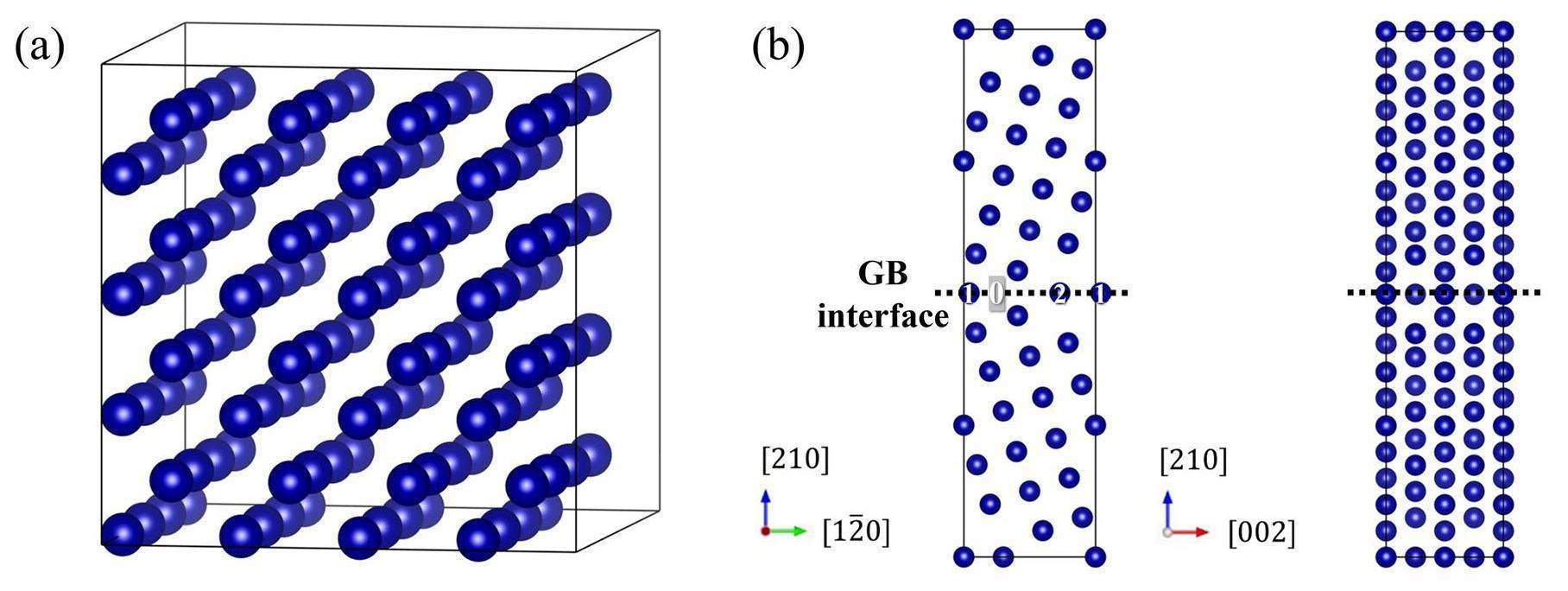
To investigate the diffusion behavior of Cs and I in the BCC Cr coating, density functional theory (DFT) calculations were performed with the Vienna ab initio simulation package (VASP) [39-41] using projector augmented wave (PAW) [42] pseudopotentials and the Perdew-Burke-Ernzerhof (PBE) [43] parameterization. Razumovskiy et al. [44] found that disordered local moment calculations for pure Cr in the paramagnetic state can be reduced to a nonmagnetic solution. A 4 × 4 × 4 supercell containing 128 atoms was adopted for the Cr matrix simulation, and a ∑5(210) GB supercell consisting of 76 sites was used for the simulation at the Cr GB, as shown in Fig. 2. The Brillouin area was sampled with 4 × 4 × 4 and 5 × 5 × 1 k-point meshes for the Cr matrix and GB, respectively. The total energy and force convergence criteria were set as 1.0×10^-5 eV and 0.01 eV/Å, respectively, with a cutoff energy of 400 eV. All transition states and migration barriers were obtained by applying the climbing image nudged elastic band (cNEB) method using three intermediate images. To determine the diffusion coefficients in the Cr matrix, phonon calculations were performed by considering only the vibrational modes of the migrating atoms [22, 45-48]. For both the transition state search and phonon calculations, the force convergence criterion was reset to 0.001 eV/Å because the results were highly sensitive to this parameter.

Fig. 2

(Color online) Simulation models for the Cr matrix and GB. (a) 4 × 4 × 4 supercell containing 128 atoms representing the Cr matrix; (b) Cr ∑5(210) GB with 76 atoms, where the atomic sites at the GB interface are labeled with numbers (0 for the interstitial site, 1 & 2 for substitutional sites)

Results and discussion

3.1

Impurity diffusion in the Cr matrix

3.1.1

Atomic structure and electron distribution in the matrix

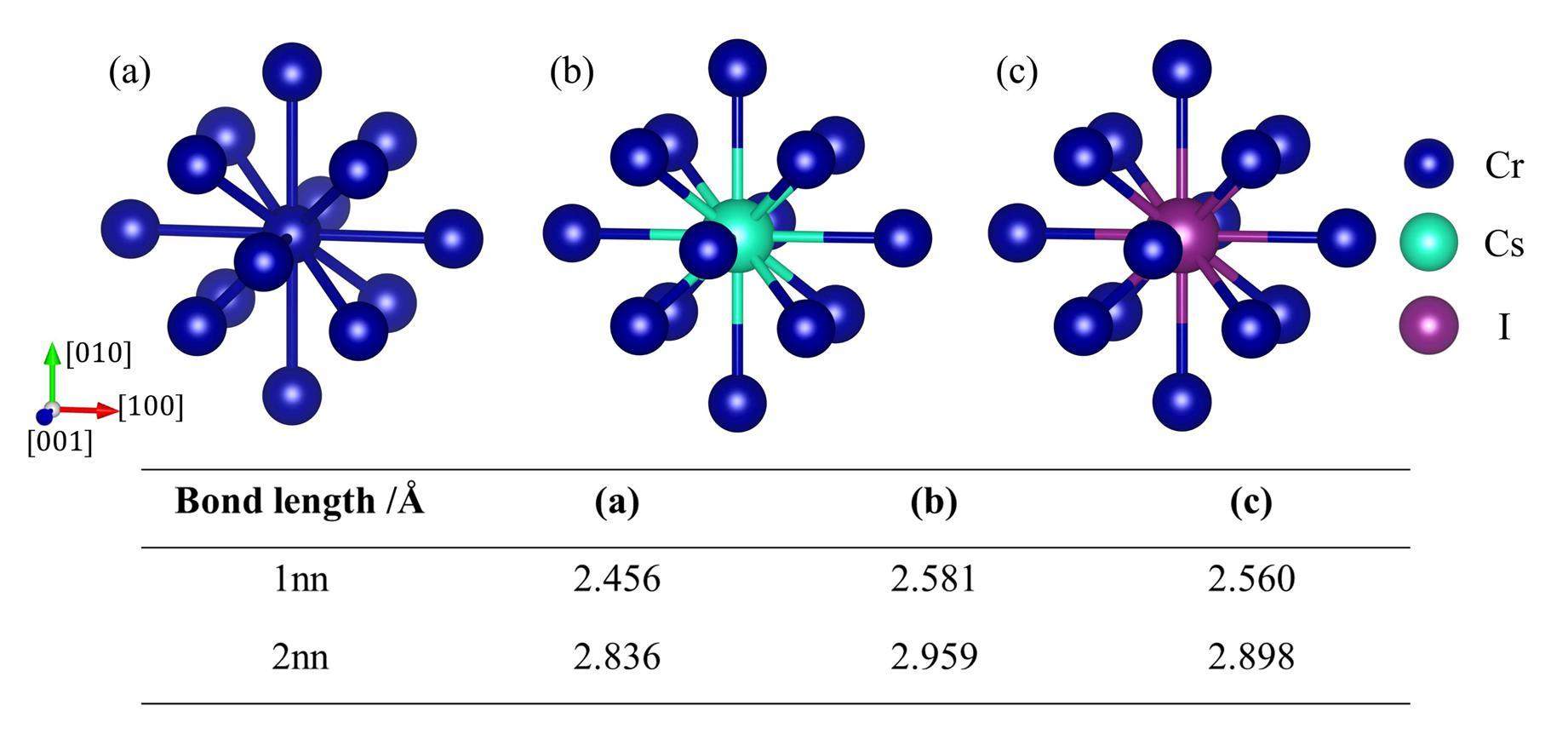
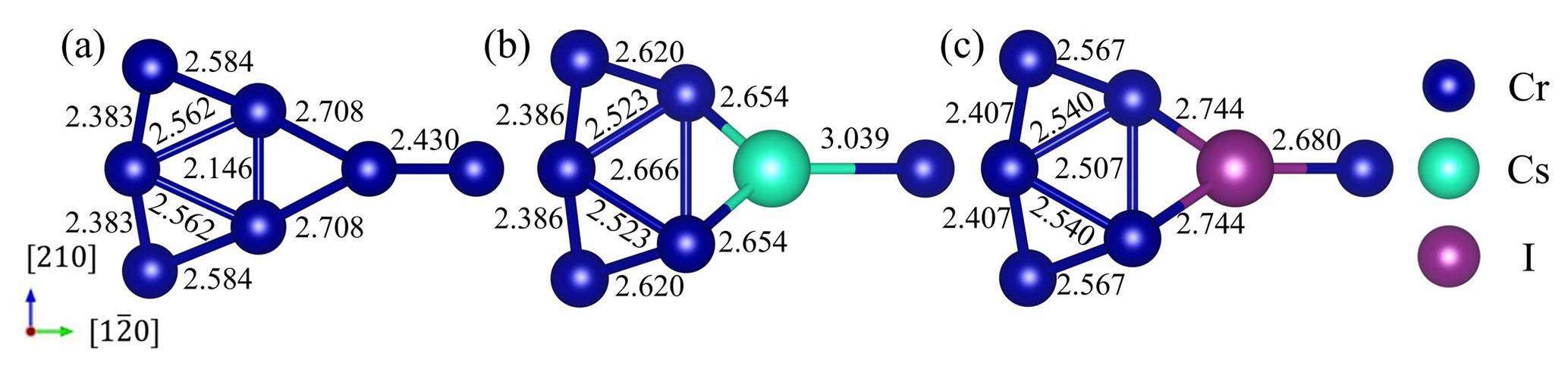
The interaction between atoms can change the forces applied to the impurity; therefore, it is an important factor affecting the migration behavior. Figure 3 illustrates the changes in bond lengths caused by substitutional impurities. It can be seen that both Cs and I exert a repulsive effect on the surrounding Cr atoms, as the Cs and I Bader radii listed in Table 1 are both larger than that of Cr. The effect of Cs is more significant, with the 1nn and 2nn bond lengths increasing by more than 0.1 Å.

Fig. 3

(Color online) Calculated bond lengths (Å) in the Cr matrix for the (a) pure matrix, (b) matrix with a substitutional Cs atom, and (c) matrix with a substitutional I atom

Calculated Bader charge, volume, and radius for atoms in the Cr matrix with Cs or I substitution

	Cs	Cr(Cs)	I	Cr(I)
Bader charge, e^-	9.369	5.997	7.784	5.994
Atomic volume (Å³)	18.778	11.346	19.056	11.344
Atomic radius (Å)	1.649	1.394	1.657	1.394

Cr(Cs) and Cr(I) denote the Cr atoms in the Cs-doped and I-doped Cr matrix, respectively

To better understand the effect of impurities, the electronic structure with impurities was further analyzed. The Bader charges, volumes, and radii [49], determined using the Bader decomposition method [50], are listed in Table 1. For the Cr atoms, it is found that the Bader charge and atomic volume of the 127 Cr atoms are almost the same; therefore, their average values are given directly in the table. As can be seen, both Cs and I gain electrons from the matrix. In addition, the non-metallic I atom gained more electrons than the metallic Cs atom. The Cs and I atomic volumes are almost the same when they occupy a substitutional site in the Cr matrix; therefore, their migration behavior is expected to be similar.

The binding effect between impurity atoms and their surrounding Cr atoms was weaker than that between Cr atoms, which can be observed from the charge densities between the impurity atoms and their 1nn Cr atoms, as shown in Fig. 4. The charge density around the impurity atoms decreased significantly compared with the corresponding profile for the pure Cr system (Fig. 4(a)), which is in agreement with the effect of increasing the bond length shown in Fig. 3. In addition, the presence of impurity atoms increases the charge density between the Cr atoms in the diagonal direction, indicating an enhanced interaction between them. Taken together, the Cr atoms near the impurity atoms tend to move away from the impurity atoms and have weak binding interactions with the impurity atoms, favoring the impurity atom diffusion in the matrix.

Fig. 4

(Color online) Calculated charge density distribution (electron/Bohr³) in the (101) plane for the (a) pure Cr matrix, (b) Cr matrix with a substitutional Cs atom, and (c) Cr matrix with a substitutional I atom

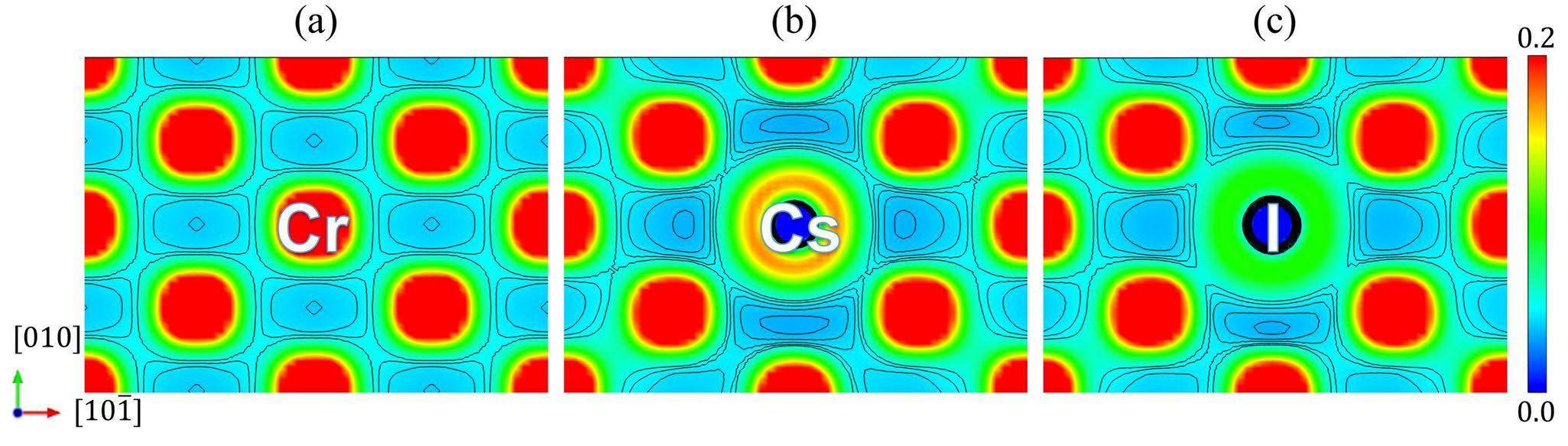
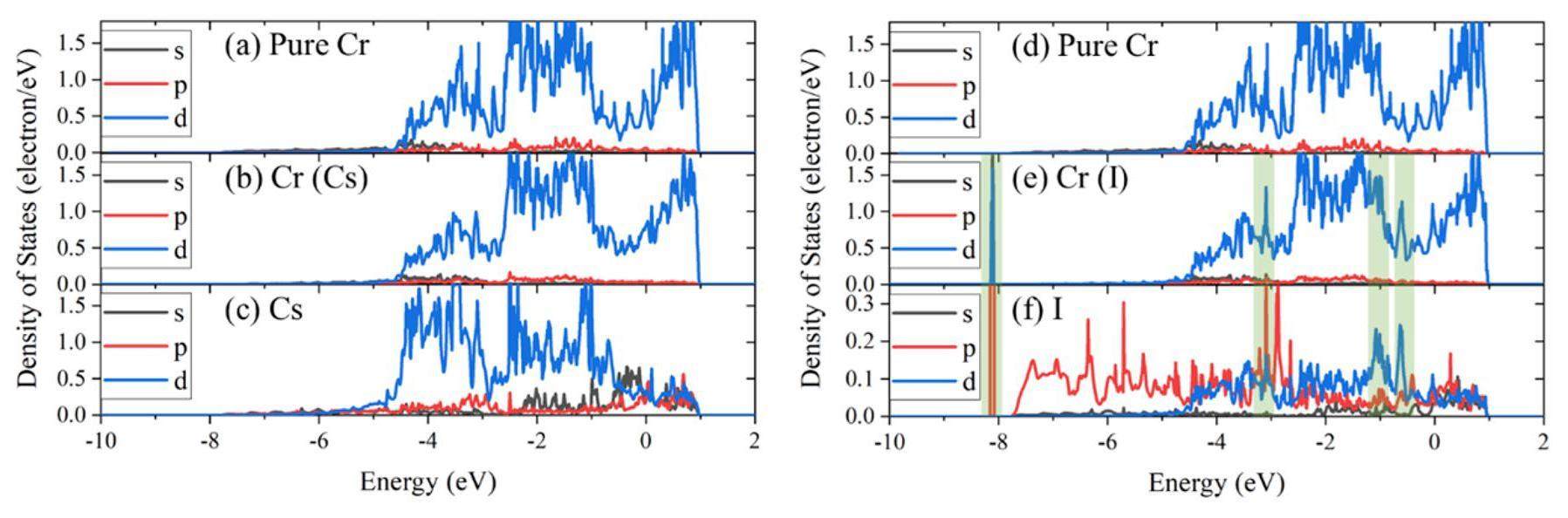
In addition, the binding effect of Cr atoms to Cs was slightly weaker than that of I. A comparison of the results for Cs and I (Fig. 4(b) & (c)) reveals that their charge density distributions are similar. However, in terms of equipotential lines, the charge density around Cs is more dilute, and the interaction with Cr atoms is weaker than that of I. This is consistent with the fact that the Cs-Cr bonds are longer than the I-Cr bonds, as shown in Fig. 3, which can also be observed in Fig. 5. There was no hybridization peak between the Cs and Cr atoms, indicating metallic bonds. Several hybridization peaks appeared between the I and Cr atoms, indicating covalent-like bonds. Specifically, the Cr d electrons and the I p electrons are mainly involved in hybridization between -9 and -3 eV, while the I and Cr d electrons are mainly involved in hybridization between -2 and 0 eV. Overall, Cs and I had a similar effect on the Cr matrix, with slightly weaker interactions around Cs than I.

Fig. 5

(Color online) Density of states (DOS) with respect to energy: (a) & (d) Cr in the pure Cr matrix; (b) & (e) 1nn-Cr of a substitutional Cs or I atom; (c) & (f) substitutional Cs and I atoms, respectively. Main hybridization peaks are marked with light green bars

3.1.2

Diffusion process and diffusion coefficient in the matrix

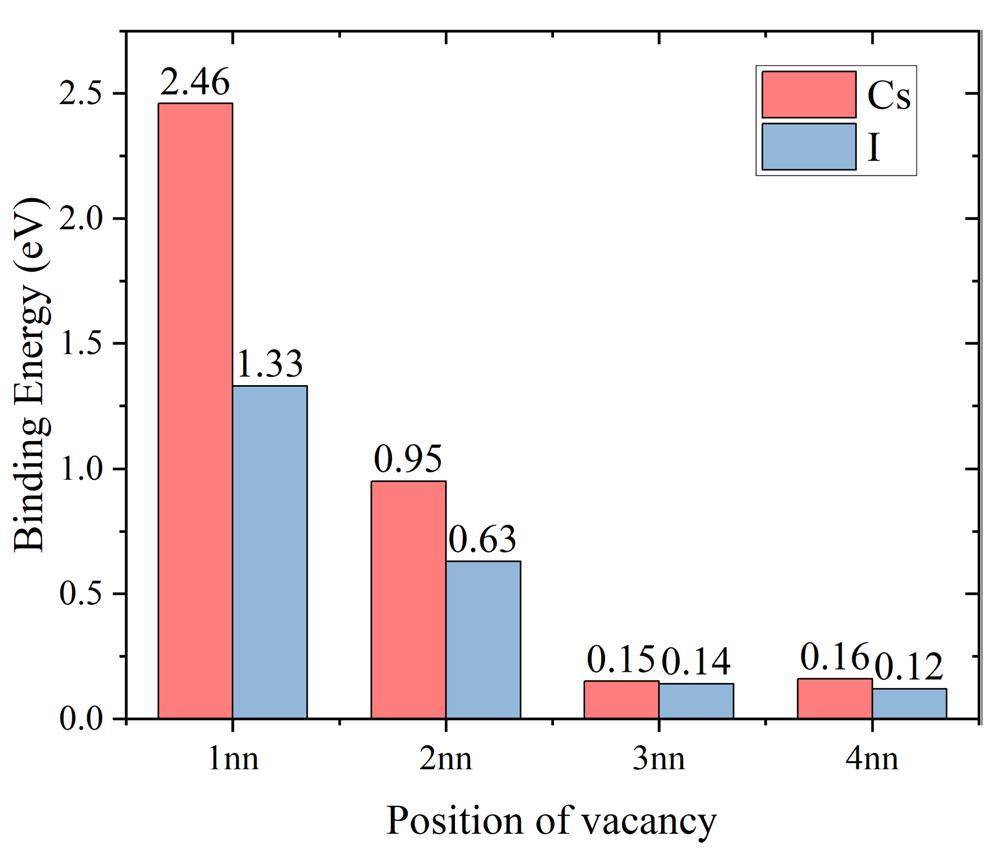
To investigate the effect of impurity atoms on neighboring vacancies, the binding energies of the impurity atoms to neighboring vacancies were calculated using Eq. (6), the results from 1nn to 4nn are shown in Fig. 6. The binding energy involving the 5nn vacancy is not presented because the 5nn vacancy slides spontaneously into the 1nn position, that is, the Cr atom at the 1nn position of the impurity slides spontaneously into the 5nn position. Both impurity atoms have an attractive effect on the vacancies from 1nn to 4nn. The binding energy of Cs to the 1nn vacancy is up to 2.46 eV, which is a possible reason for the formation of the “V/2 + Cs + V/2" configuration. The relatively low binding energy between I and its 1nn vacancy may explain why I remained stable at the substitution site. The binding energies of Cs atoms to vacancies are generally higher than those of I atoms, especially for 1nn and 2nn vacancies. However, for the 3nn and 4nn vacancies, the binding energies are almost identical, indicating that the impurity atoms mainly affect the 1nn and 2nn vacancies.

Fig. 6

(Color online) Calculated impurity-vacancy binding energies

The migration energy and attempt frequency required for the vacancies near the impurity to move to different sites are also important factors affecting the migration processes. The results in Table 2 indicate that impurity atoms compete with the surrounding matrix atoms for vacancies. The migration barriers of vacancies moving away from the impurity atoms ( $E_{3}^{m}$ , $E_{3^{'}}^{m}$ , $E_{5}^{m}$ ) are generally higher than those in the direction close to the impurity atoms ( $E_{4}^{m}$ , $E_{4^{'}}^{m}$ , $E_{6}^{m}$ ), and the energy required for the vacancies located in 3nn of the impurity atoms to migrate to 1nn is lower than that required for self-diffusion in the pure Cr system (0.92 eV, as shown in Fig. 7). In terms of the attempt frequency, the attempt frequencies of vacancies moving away from the impurity atoms (ν₃, $ν_{3^{'}}$ , ν₅) are also generally lower than those near the impurity atoms (ν₄, $ν_{4^{'}}$ , ν₆). This indicates that vacancies are more likely to be attracted to stay near impurity atoms, which is consistent with the results shown in Fig. 6, and this attractive effect to vacancies facilitates the diffusion of impurity atoms.

Vacancy migration energies and attempt frequencies for vacancies near Cs or I atoms

	Cs	I
$E_{2}^{m}$	-	0.36
$E_{3}^{m}$	2.70	1.66
$E_{4}^{m}$	1.19	0.96
$E_{3^{'}}^{m}$	2.66	1.77
$E_{4^{'}}^{m}$	0.35	0.59
$E_{5}^{m}$	-	1.09
$E_{6}^{m}$	-	0.59
ν₂	-	2.85
ν₃	5.56	7.22
ν₄	12.80	10.12
$ν_{3^{'}}$	9.79	10.04
$ν_{4^{'}}$	12.95	15.12
ν₅	-	8.74
ν₆	-	12.63

Fig. 7

(Color online) Schematics of the Cs and I diffusion characteristics. (a) Spontaneous Cs diffusion; (b) Non-spontaneous I diffusion; (c) I and Cr migration barriers. The energies are relative to the corresponding initial states

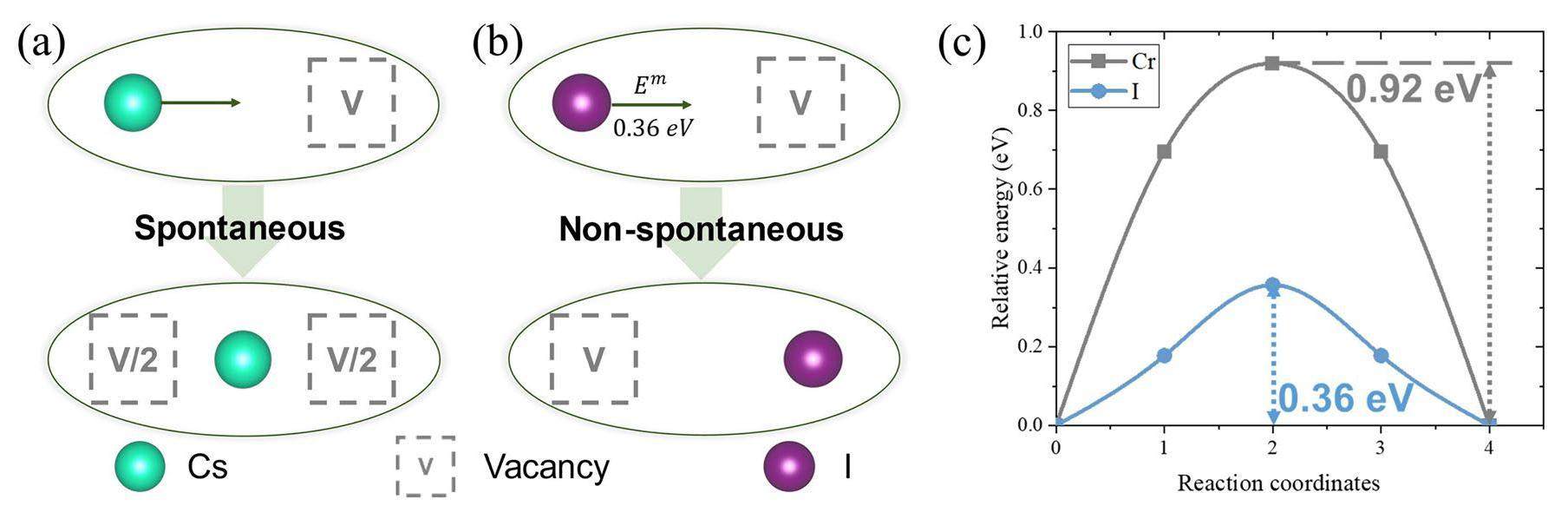
Both Cs and I can easily diffuse into the Cr matrix because of their low migration barriers. As illustrated in Fig. 7(a) & (b), Cs will spontaneously move from the substitutional site to the middle point of the two lattice sites, while I should overcome a migration barrier of 0.36 eV to move to another substitutional site. Although I migration is not spontaneous, the migration barrier is lower than that for Cr atoms (0.92 eV according to our calculations). As a result, the Cs and I diffusion was easier than that of Cr. Nevertheless, the migration barrier results do not necessarily imply that Cs diffusion is faster than I diffusion because the displacement of I that occurs by diffusion is $\sqrt{3} a$ /2, which is twice the displacement of Cs.

Before determining the Cs and I diffusion coefficients in Cr, approximations are required for the spontaneous sliding of the 5nn vacancy of the impurity to the 1nn position. Because this process proceeds spontaneously, it is impossible to determine the corresponding vacancy jump frequency using Eq. (4). According to the assumptions of the Le Claire and OSA models, the exchange frequency of the 5nn vacancy with the atom further away from the impurity is considered to be the jump frequency of the Cr atom self-diffusion. In our DFT simulations, the 5nn vacancy will only slide into the 1nn position; therefore, we can define $ω_{4^{″}} = ω_{0}, ω_{3^{″}} = 0.$ (8)

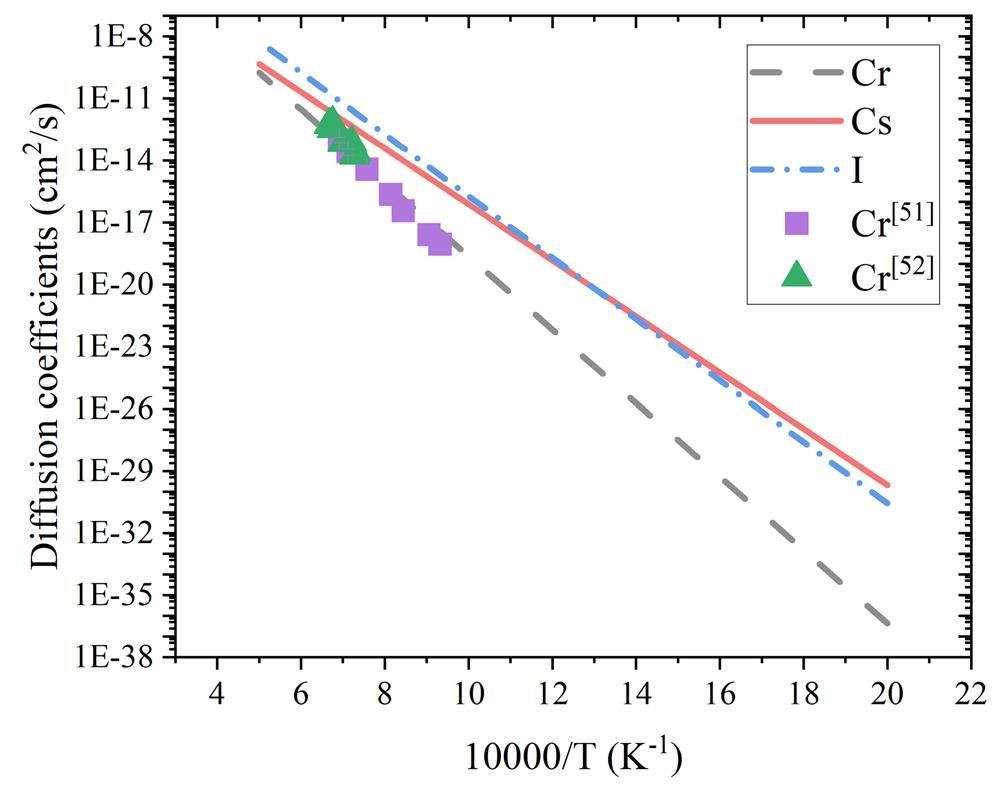
Based on the aforementioned assumptions, the Cs and I diffusion coefficients in the Cr matrix at 500–2000 K were calculated according to the OSA and Le Claire models, respectively, as shown in Fig. 8. The Cr self-diffusion coefficient results are shown for comparison, which are in good agreement with the experimental results [51, 52]. It can be seen that the diffusion coefficients of the impurity atoms are larger than the Cr self-diffusion coefficients in the considered temperature interval. This can be attributed to the combined effect of the three factors analyzed in the preceding discussion: a weaker bonding effect by the surrounding Cr atoms, a stronger attraction effect for nearby vacancies, and lower migration barriers compared to the Cr self-diffusion process. In the temperature range of Generation-IV fast reactors (approximately 500–1000 K), the Cs and I diffusion coefficients are three to seven orders of magnitude larger than the Cr self-diffusion coefficients, which also indicates the strong penetration ability of Cs and I. The diffusion coefficients of all three elements increase exponentially with increasing temperature. Despite the different Cs and I diffusion characteristics shown in Fig. 7, the Cs and I diffusion coefficients are very similar in the considered temperature range. Because our Cr self-diffusion coefficient calculations agree well with the experimental results, it can be concluded that the Cs and I diffusion coefficients in BCC Cr obtained from the DFT calculations are reliable.

Fig. 8

(Color online) Temperature dependence of the impurity diffusion coefficient in the Cr matrix. Self-diffusion coefficients are given for comparison. Our results are denoted by lines and the experimental results are denoted by dots

Based on the parameters obtained in this study, the BCC Cr self-diffusion coefficient, D_Cr (cm²/s), can be recalculated as follows: $D_{Cr} = 0.1323 \times \exp (- \frac{4.0861 \times 10^{4}}{T}),$ (9) and the Cs and I diffusion coefficients in BCC Cr, D_Cs and D_I (cm²/s), respectively, can be fitted from Fig. 8 as follows: $D_{Cs} = \exp [(- 5.8676 \pm 0.0051) - \frac{(2.6915 \pm 0.0004) \times 10^{4}}{T}],$ (10) $D_{I} = \exp [(- 1.8582 \pm 0.0158) - \frac{(3.4297 \pm 0.0016) \times 10^{4}}{T}] .$ (11)

3.2

Impurity diffusion at the Cr GB

3.2.1

Atomic structure and electron distribution at the GB

The GB serves as a fast diffusion channel for impurity atoms, and the existence of Cs and I atoms on the GB plane changes the GB structures, including the bond lengths and charge distributions. To analyze the changes and differences between the matrix and the GB, impurity atoms were placed at site 1 on the GB plane. As shown in Fig. 9, the presence of impurity atoms at the GB does not lead to an increase in any of the bond lengths, which is different from that in the matrix. Nevertheless, the impurity atoms located at this substitution site significantly increase the bond length in the [210] direction by distancing the atoms on both sides of the GB plane. This facilitates the diffusion of impurity atoms along the interface. In addition, Cs had a more pronounced effect on increasing the bond length than I, which is in accordance with the results shown in Fig. 3.

Fig. 9

(Color online) Calculated bond lengths (Å) at the Cr GB for (a) pure GB, (b) GB with a substitutional Cs atom, and (c) GB with a substitutional I atom

As in the matrix, the Bader charges, volumes, and radii [50] of the atoms at the GB were obtained using the Bader decomposition method [49], and the results are presented in Table 3. Similarly, the Bader results of the 75 Cr atoms at the GB were close; therefore, their average values were used for analysis. By comparing the results in Table 1 with those in Table 3, it was found that the I atom gains electrons both in the matrix and at the GB, whereas the Cs atom loses electrons at the GB, which is different from the case of the matrix. For the I substitution, the number of electrons gained at the GB is slightly less than that in the matrix, probably because the atomic structure at the GB is not as compact as that in the matrix, and fewer electrons are transferred between the different nuclei. The Cs and I atomic volumes at the Cr GB are essentially the same as those in the Cr matrix. However, the Bader volume of all atoms at the GB is slightly larger than that in the matrix, which is reasonable because the atomic arrangement at the GB is sparser. This is also favorable for Cs and I atom migration, and it is expected that the impurity atoms on the GB plane will migrate more easily than those in the matrix.

Calculated Bader charge, volume, and radius of atoms at the Cr GB. The Cr values are averaged values

	Cs	Cr(Cs)	I	Cr(I)
Bader charge, e^-	8.962	6.001	7.600	5.992
Atomic volume (Å³)	21.286	11.881	21.968	11.872
Atomic radius (Å)	1.719	1.416	1.737	1.415

Cr(Cs) and Cr(I) denote the Cr atoms in Cs-doped and I-doped Cr GB, respectively

Both Cs and I have similar effects at the Cr GB as in the matrix, with slightly lower interactions around Cs than around I, as shown by the charge density distribution in Fig. 10. It can be seen that the charge density around the impurity atoms is significantly lower compared to that at the pure Cr GB, which is similar to the Cr matrix (Fig. 4). The dilute charge density indicates a weak interaction between the impurity atoms and their surrounding Cr atoms, which favors impurity atom migration along the GB plane. By comparing the charge distributions shown in Fig. 10(b) and (c), it can be seen that the charge density around Cs is smaller than that around I, that is, the Cs-Cr binding is weaker than the I-Cr binding, which also agrees with the change in the bond length in the [210] direction shown in Fig. 9. Compared to the charge density distribution in the matrix (Fig. 4), the charge density distribution at the GB is more dilute. As a result, it can be predicted that the Cs and I diffusion rates at the GB should be comparable, and the diffusion should be much easier than in the matrix.

Fig. 10

(Color online) Calculated charge density distribution (electron/Bohr³) in the (001) plane for (a) pure GB and GB with a substitutional (b) Cs or (c) I atom at site 1

3.2.2

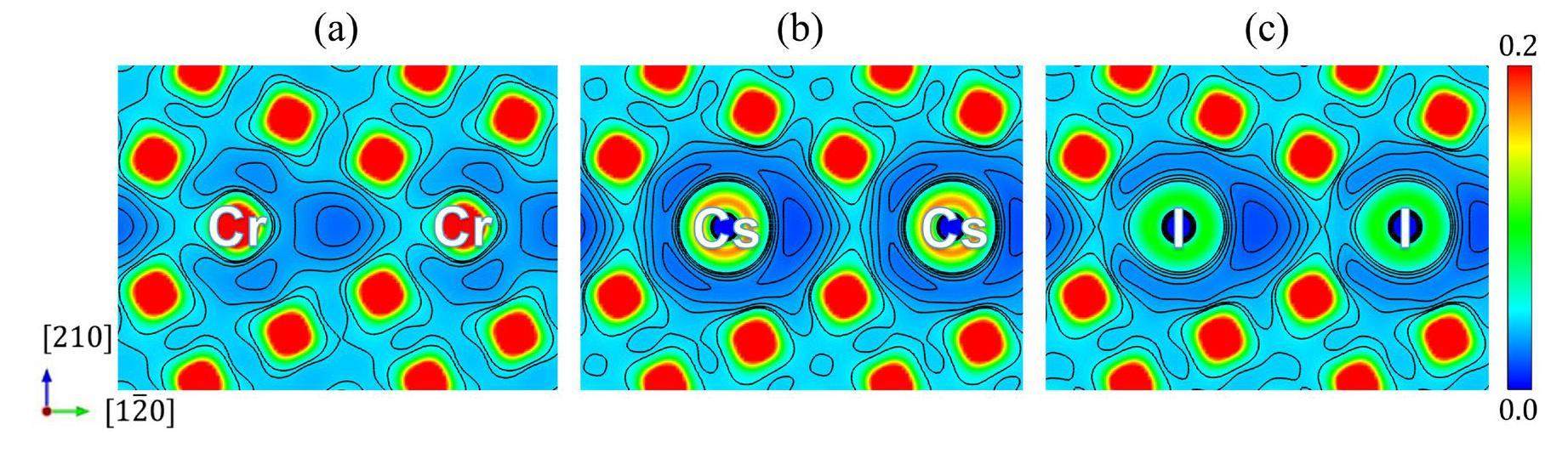
Diffusion barrier and diffusion path along the GB

To investigate the impurity diffusion behavior along the GB, impurity atoms were placed at the interstitial site 0 and substitutional sites 1 and 2 on the GB plane (as shown in Fig. 2(b)) as the initial structures of the different migration processes; the optimization results for these initial structures are presented in Table 4. It can be seen that the impurity atoms located in site 0 will spontaneously migrate to the non-occupied site 2, which is more stable than site 0. If a vacancy is introduced at site 1, the impurity atoms located at site 2 spontaneously migrate to site 1, which is more stable than site 2. Both migration processes occur spontaneously such that the impurity atoms can readily diffuse along the GB direction.

Atomic structures after ionic optimization by first-principles calculation

Migration process	Initial structure (vacancy site, impurity site)	Final Cs position after optimization	Final I position after optimization
site 2 → site 0	(site 0, site 2)	site 2	site 2
site 0 → site 2	(site 2, site 0)	Between site 0 and site 2	site 2
site 1 → site 2	(site 2, site 1)	Between site 1 and site 2, closer to site 1	site 1
site 2→ site 1	(site 1, site 2)	Between site 1 and site 2, closer to site 1	site 1
site 1 → site 0	(site 0, site 1)	site 1	site 1
site 0 → site 1	(site 1, site 0)	site 0	site 0

The calculated migration barriers between sites 0 and 1 are shown in Fig. 11. The migration barriers from site 0 to site 1 for Cs and I are smaller than those in the matrix (Table 2), indicating that GBs are fast channels for impurity diffusion in Cr. Nevertheless, it can be seen that Cs or I needs to overcome a high energy barrier (up to 4.90 or 3.53 eV) to migrate from site 1 to site 0, indicating that impurity diffusion is directional in some GB regions.

Fig. 11

(Color online) Energy evaluation during the Cs or I migration process between sites 0 and 1 at the GB. The energies are with respect to the initial structure with impurity atoms at site 1

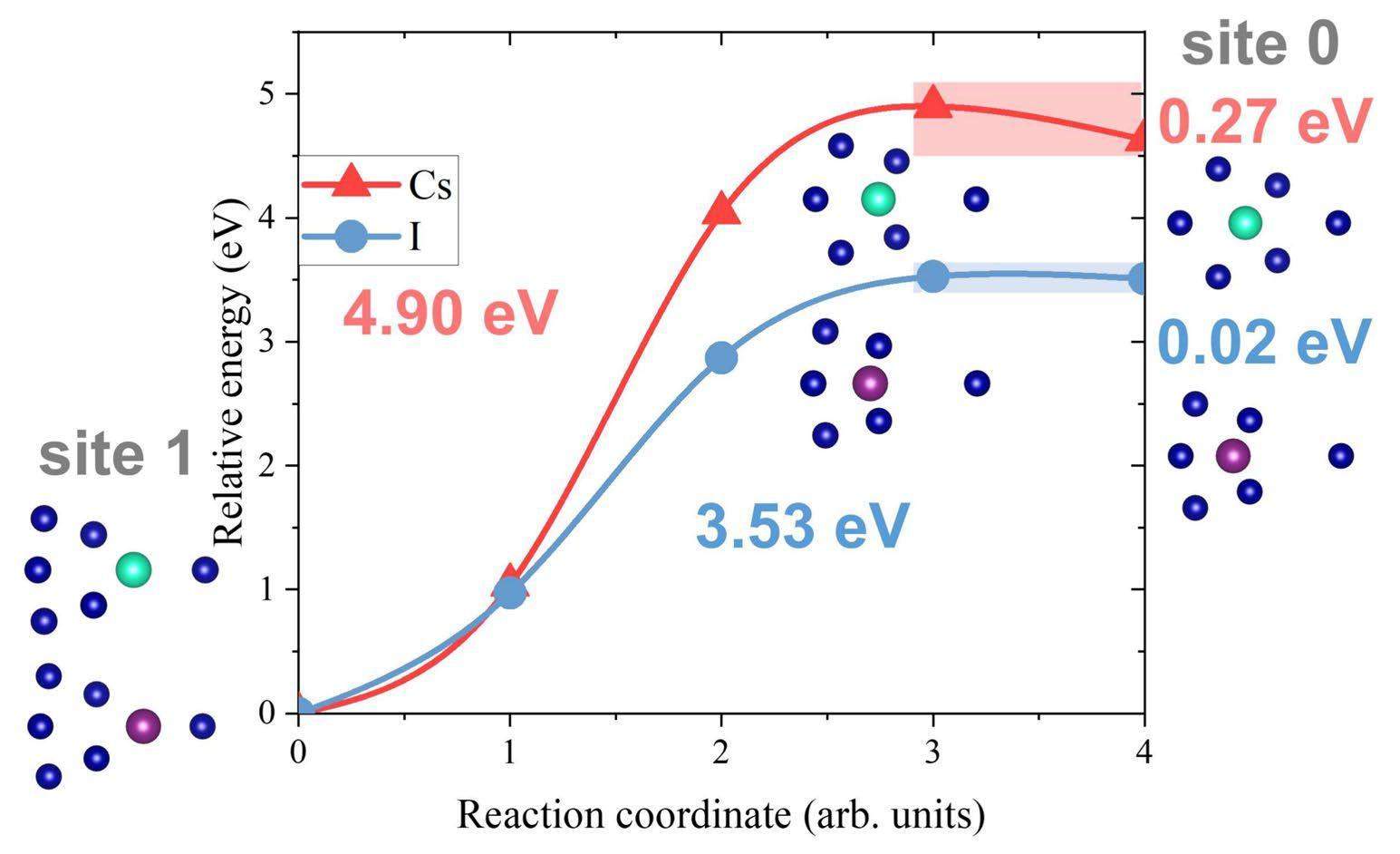
In summary, two additional possible paths were predicted for impurity atom diffusion along the GB plane, as shown in Figs. 12 & 13. Both migration paths require the introduction of vacancies at the GB plane, and many vacancies exist in the GB region of real materials. Furthermore, the vacancy concentration can be significantly increased by the combined effects of high temperature and irradiation under the service conditions on the cladding inner surface in a nuclear reactor. In Fig. 12, vacancies at sites 2 and 1 were introduced in succession, and the impurity atoms at site 0 moved spontaneously, sliding sequentially to sites 2 and 1. In Fig. 13, one vacancy was introduced at site 1, and because of the low migration barrier from sites 0 to 1, the impurity atoms could easily move to site 1.

Fig. 12

(Color online) First-principles-predicted spontaneous impurity diffusion paths along the GB plane: (a) impurity atoms initially located at site 0; (b) introduction of a vacancy at site 2; (c) spontaneous movement of impurity atoms to site 2; (d) introduction of a vacancy at site 1; (e) spontaneous movement of impurity atoms to site 1

Fig. 13

(Color online) First-principles-predicted impurity atom diffusion paths along the GB plane by overcoming a low migration barrier: (a) impurity atoms initially located at site 0; (b) introduction of a vacancy at site 1; (c) impurity atom diffusion to site 1 with a low energy barrier

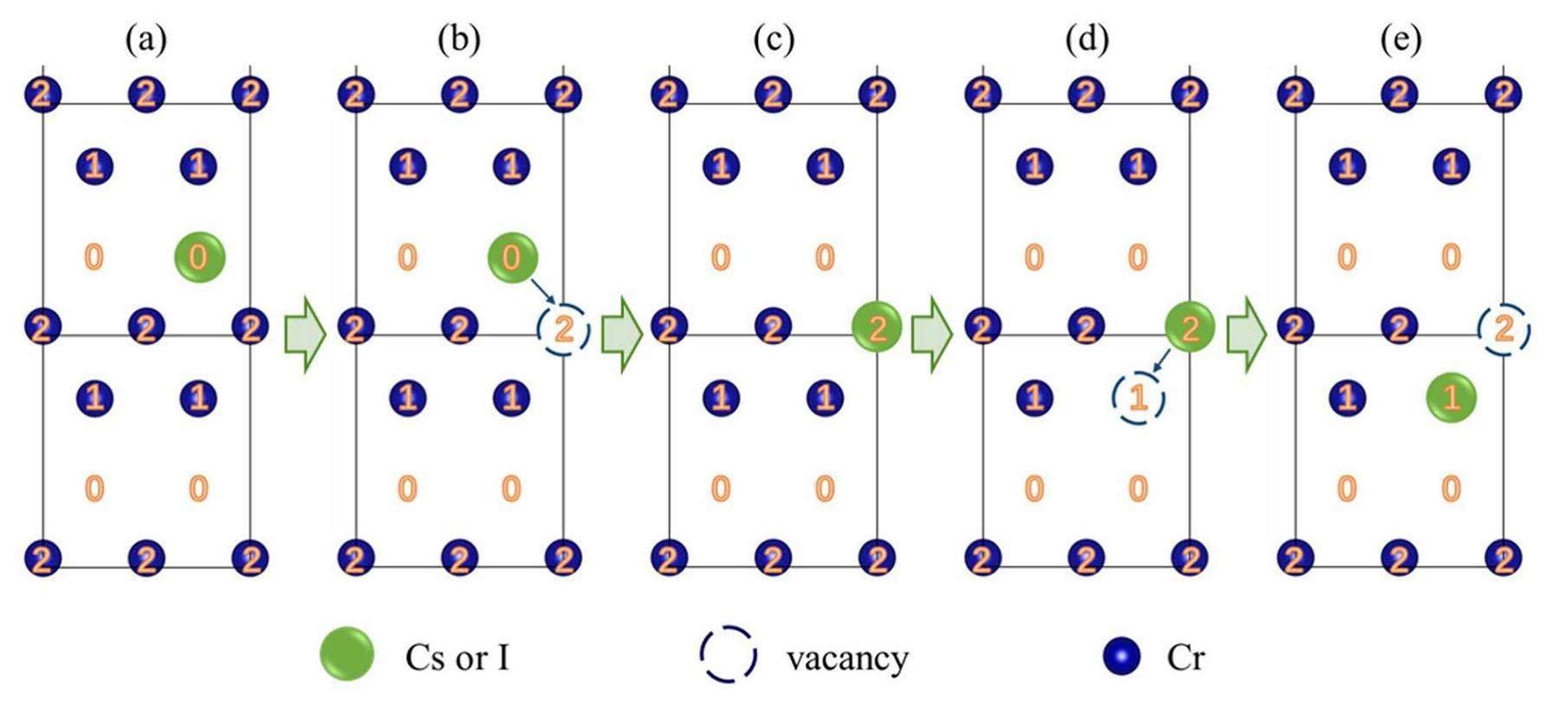
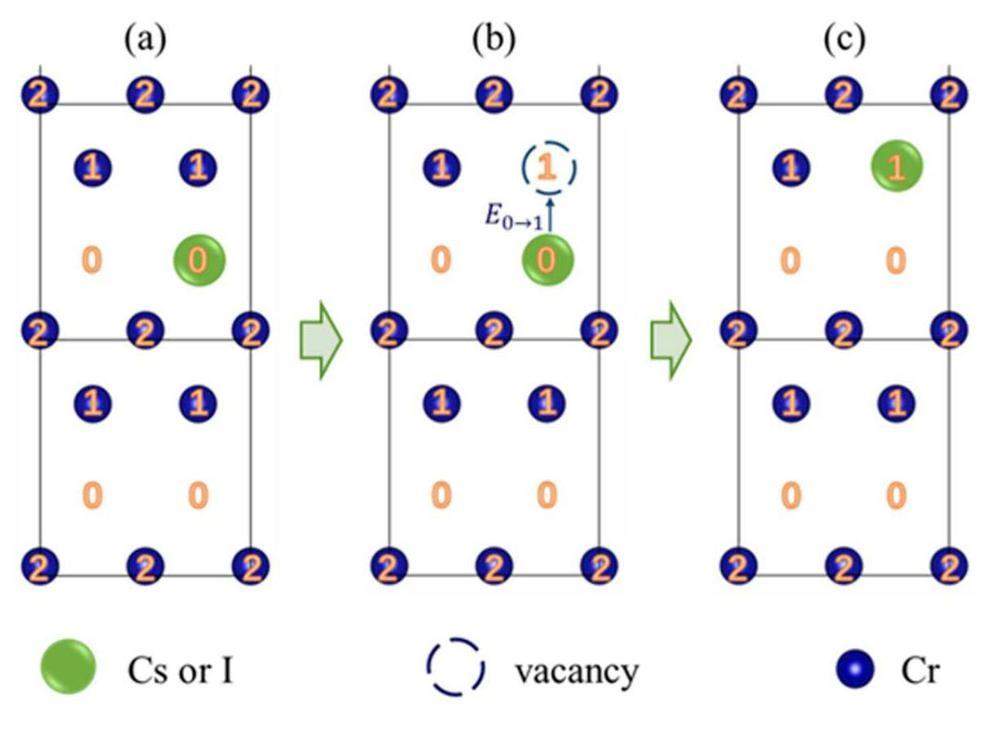
Summary

The diffusion behavior of Cs and I, which are key FCCI elements, in Cr coating were investigated using DFT calculations combined with the Le Claire and OSA diffusion models. Under the combined effect of low binding with matrix atoms and strong binding with nearby vacancies, the migration barriers of Cs and I were both lower than that of Cr. As a result, the Cs and I diffusion coefficients are both 3–7 orders of magnitude larger than the Cr self-diffusion coefficient below 1000 K, which corresponds to the temperature range of Generation-IV fast reactors. Despite the differences in the migration barriers and displacements of the elemental diffusion process of Cs and I, as well as the different models used, the diffusion coefficients obtained for I and Cs were of the same order of magnitude at the considered temperature. The Cr self-diffusion results agreed well with the experimental results, demonstrating the accuracy of our results. Based on the results, the Cs and I diffusion paths in the inner-surface Cr coating of the cladding were predicted. Cs and I are more likely to diffuse along the GB, and intergranular corrosion still requires further research.

References

K. Maeda, 3.16 - Ceramic Fuel–Cladding Interaction, in: R.J.M. Konings (Ed.) Comprehensive Nuclear Materials, Elsevier, Oxford, 2012, pp. 443-483.

R. Parrish, A. Aitkaliyeva,

A review of microstructural features in fast reactor mixed oxide fuels

. J. Nucl. Mater. 510, 644-660 (2018). https://doi.org/10.1016/j.jnucmat.2018.05.076