INTRODUCTION

The neutron skin thickness, defined as the difference between the root mean square of the neutron and proton density distributions of a nucleus ${\delta }_{\text{np}}\equiv {\langle r_{\text{n}}^2\rangle }^{1/2}-{\langle r_{\text{p}}^2\rangle }^{1/2}$, is an important parameter for neutron-rich nuclei. With the advanced ability of new rare isotope facilities to produce nuclei near proton and neutron drip lines, a new era has commenced for nuclei with exotic structures, particularly for neutron-rich isotopes at extremes [1, 2]. The exact value of δ_np is important in research on symmetry energy [3] and neutron stars [4]. It is more important to study δ_np of extreme nuclei because they may have a much lower density distribution in the surface region than stable nuclei. Along the history of studying δ_np of neutron-rich nuclei, many probes have been proposed based on different theoretical frameworks and via different types of experiments. Projectile fragmentation reactions induced by neutron-proton asymmetric nuclei, as one type of heavy-ion reactions, are typical experimental tools to investigate properties of neutron-rich nuclei, in which the light particle emissions [5, 6], fragment production ratios [7, 8], fragment mass or charge distributions through information entropy analysis [9, 10], etc, are proposed as probes to study the neutron-skin of projectile nuclei to varying degrees of accuracy. Due to the difficulties in measuring neutron density distributions, the neutron-skin thickness of asymmetric nuclei are usually determined in experiments through indirect probes, for example, the giant dipole resonance [11, 12], spin dipole resonance [13], neutron-removal cross section [14], and parity violating electron scattering (for ²⁰⁸Pb [15, 16] and for ⁴⁸Ca [17]), etc. The momentum distribution of nucleons is widely used to study the structure and properties of atomic nuclei [18-21]. The short-range correlation between nucleons can be experimentally studied by detecting the high-momentum tail of the nucleon momentum distribution using bremsstrahlung γ rays in heavy-ion nuclear reactions [22-24]. The parallel momentum distribution ($p_{\parallel }$) of fragments in breakup or few-body reactions is usually the first evidence of halo or skin nuclei, as in ¹¹Li [18], ²⁹P [25], ²³Al [26], ³¹Ne [27]. Thus, $r_{\text{p}}^2$ of the residual fragments can also be employed to determine δ_np within the framework of optical models [28-30]. Experimentally, the $p_{\parallel }$ of fragments is usually used to determine their yields or cross-sections after integration [31], which directly connects the yields of fragments and the nuclear density (and neutron skin thickness) of the projectile nucleus. This makes the $p_{\parallel }$ of fragment in potential be a probe for δ_np of projectile nucleus. In this study, $p_{\parallel }$ of the residual fragments in projectile fragmentation reactions was investigated using the Lanzhou quantum molecular dynamics (LQMD) model [32, 33]. It is suggested that the width of $p_{\parallel }$ of the fragment produced in the peripheral collisions is sensitive and could serve as a probe for δ_np of the projectile nucleus.

Model Description

2.1

The LQMD model

The LQMD model is an isospin- and momentum-dependent transport model that includes all possible elastic and inelastic collision reaction channels during charge exchange. The temporal evolution of nucleons, hyperons, and mesons in a reaction system under a self-consistently generated mean field is governed by Hamilton’s equations of motion [32-35]. Based on the Skyrme interactions, isospin-, density-, and momentum-dependent Hamiltonians were constructed [34]. The Hamiltonian of baryons consists of the relativistic energy, effective interaction potential, and momentum-related components. $H_{\text{B}}={\displaystyle \sum _i\sqrt{{\text{p}}_i^2+m_i^2}}+U_{\text{int}}+U_{\text{mom}}\mathrm{,}$ (1) where p_i and mi denote the momentum and mass of the baryons, respectively. U_int comprises the Coulomb interaction and the local interaction potential. The local interaction potential is expressed as follows: $U_{\text{loc}}={\displaystyle \int }{V}_{\text{loc}}\left[\rho \left(\text{r}\right)\right]d\text{r}\mathrm{,}$ (2) derived from the Skyrme energy density functional. $V_{\text{loc}}\left(\rho \right)$ can be written as: $\begin{array}{l}{V}_{\text{loc}}\left(\rho \right)=\frac{\alpha }{2}\frac{{\rho }^2}{{\rho }_0}+\frac{\beta }{1+\gamma }\frac{{\rho }^{1+\gamma }}{{\rho }_0^{\gamma }}+E_{\text{sym}}^{\text{loc}}\left(\rho \right)\rho {\delta }^2\hfill \\ +\frac{g_{\text{sur}}}{2{\rho }_0}{\left(\nabla \rho \right)}^2+\frac{g_{\text{sur}}^{\text{iso}}}{2{\rho }_0}{\left[\nabla \left({\rho }_{\text{n}}-{\rho }_{\text{p}}\right)\right]}^2\mathrm{,}\hfill \end{array}$ (3) where ρ_n, ρ_p and $\rho ={\rho }_{\text{n}}+{\rho }_{\text{p}}$ are the neutron, proton, and total densities, respectively, and $\delta =\left({\rho }_{\text{n}}-{\rho }_{\text{p}}\right)/\left({\rho }_{\text{n}}+{\rho }_{\text{p}}\right)$ is isospin asymmetry. The coefficients $\alpha \mathrm{,}\beta \mathrm{,}\gamma \mathrm{,}{g}_{\text{sur}}\mathrm{,}{g}_{\text{sur}}^{\text{iso}}$, and ρ₀ were set to -215.7 MeV, 142.4 MeV, 1.322 23 MeV fm², -2.7 MeV fm², and 0.16 fm^-3, respectively. $E_{\text{sym}}^{\text{loc}}\left(\rho \right)$ is the local part of the symmetry energy, which can be adjusted to mimic the predictions of the symmetry energy calculated using microscopic or phenomenological many-body theories. $\begin{array}{l}{E}_{\text{sym}}^{\text{loc}}\left(\rho \right)=\frac{1}{2}{C}_{\text{sym}}{\left(\rho /{\rho }_0\right)}^{{\gamma }_{\text{s}}}\mathrm{.}\hfill \end{array}$ (4) The values of C_sym and γ_s are 52.5 MeV and 2.0, respectively, which correspond to hard-symmetry energy with a baryon density [34].

U_mom takes the form $\begin{array}{c}{U}_{\text{mom}}=\frac{1}{2{\rho }_0}{\displaystyle \sum _{i\mathrm{,}j\mathrm{,}j\ne i}{\displaystyle \sum _{\tau \mathrm{,}{\tau }^{\prime }}{C}_{\tau \mathrm{,}{\tau }^{\prime }}}}{\delta }_{\tau \mathrm{,}{\tau }_i}{\delta }_{{\tau }^{\prime }\mathrm{,}{\tau }_j}{\displaystyle \int }{\displaystyle \int }{\displaystyle \int }\text{d}\text{p}\text{d}\text{p}\text{'}\text{d}\text{r}\\ \times f_i\left(\text{r}\mathrm{,}\text{p}\mathrm{,}t\right)\ln {\left[ϵ{\left(\text{p}-\text{p}\text{'}\right)}^2+1\right]}^2{f}_i\left(\text{r}\mathrm{,}\text{p}\text{'}\mathrm{,}t\right)\mathrm{,}\end{array}$ (5) where $C_{\tau \mathrm{,}\tau }=C_{\text{mom}}\left(1+x\right)$, $C_{\tau \mathrm{,}{\tau }^{\prime }}=C_{\text{mom}}\left(1-x\right)\left(\tau \ne {\tau }^{\prime }\right)$ and the isospin symbols $\tau ({\tau }^{\prime })$ represent protons and neutrons, respectively. The parameters C_mom and ϵ were determined by fitting the real part of the optical potential as a function of the incident energy from the proton-nucleus elastic scattering data, and the obtained values of C_mom and ϵ were 1.76 MeV and 500c²/GeV², respectively. Thus, the effective mass of the nuclear medium at saturation density is $m^{*}/m$=0.75. The parameter x is the strength of the isospin splitting, for which a value of -0.65 is adopted in this study, and the mass splitting is $m_{\text{n}}^{*}>m_{\text{p}}^{*}$ in the nuclear medium [36].

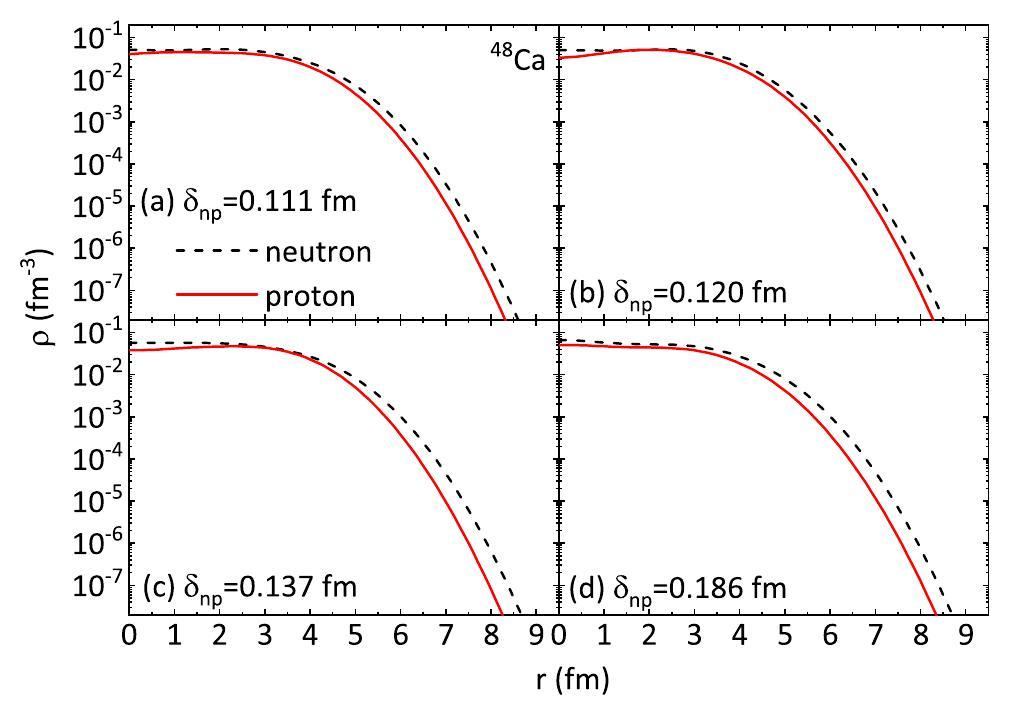
During the initialization of the projectile nucleus in LQMD, the initial coordinates of the nucleons are obtained by random sampling according to the two-parameter Fermi-type density distribution [38]: ${\rho }_i\left(r\right)=\frac{{\rho }_i^0}{1+\exp \left(\frac{r-C_i}{f_i{t}_i/4.4}\right)}\mathrm{,}i=\text{n}\mathrm{,}\text{p}\mathrm{,}$ (6) where ${\rho }_i^0$ is a normalization constant that ensures that the integrated density distribution is equal to the number of protons or neutrons, fi is a parameter for adjusting the diffuseness parameter [39, 7], ti is the diffuseness parameter, Ci is the half-density radius. Nuclei with reliable stability and an expected neutron skin thickness were selected as candidates for collisions, and the values of δ_np were 0.111, 0.120, 0.136, 0.168, and 0.186 fm for the corresponding initial ⁴⁸Ca nuclei after LQMD initialization (see Fig. 1). The fragments were analyzed in phase space at t= 300 fm/c in the LQMD simulation, and nucleons with a relative distance smaller than 3.0 fm and a relative momentum smaller than 200 MeV/c were considered in the coalescence model [33].

Fig. 1Full-screen View

(Color online) The proton and neutron physical density distributions in the initialization of ⁴⁸Ca in the LQMD simulation with different δ_np. In panels (a), (b), (c), and (d), δ_np are 0.111, 0.120, 0.137, and 0.186 fm, respectively

Results and discussion

$p_{\parallel }$ of a fragment is generally influenced by the incident energy of the reaction, nuclear density of the reaction system, impact parameter, and the fragment itself (such as isospin). The experimental δ_np determined from the proton elastic scattering for ⁴⁰Ca was $-{0.010}_{-0.024}^{+0.022}$ fm [37], and for ⁴⁸Ca, it was $0.121\pm 0.026\left(\text{exp}\right)\pm 0.024\left(\text{model}\right)$ fm from the parity-violating method [17]. To compare the sensitivity of $p_{\parallel }$ to the projectile nuclear density distribution, the ³³P produced in the 140A MeV ⁴⁰Ca + ⁹Be (δ_np=- 0.030 fm of ⁴⁰Ca) and ⁴⁸Ca + ⁹Be (δ_np= 0.168 fm of ⁴⁸Ca) reactions are simulated and fitted by Eq. (7), as shown in Fig. 2. $p_{\parallel }$ for ³³P in the symmetric ⁴⁰ Ca-induced reaction is also symmetric in Γ_L and Γ_R, whereas Γ_L is larger than Γ_R for ³³P in the asymmetric ⁴⁸ Ca-induced reaction, indicating a neutron-skin effect for the neutron-rich projectile.

Fig. 2Full-screen View

(Color online) The $p_{\parallel }$ of ³³P fragments produced in the LQMD model simulated 140A MeV ^40,48Ca + ⁹Be reactions within b= [1–8] fm. The circles and triangles denote results for the ³³P fragments in the ⁴⁸Ca (δ_np= 0.168 fm) and ⁴⁰Ca (δ_np=- 0.030 fm) induced reactions, respectively. The lines with different types denote the fitting results by a function according to Eq. (7)

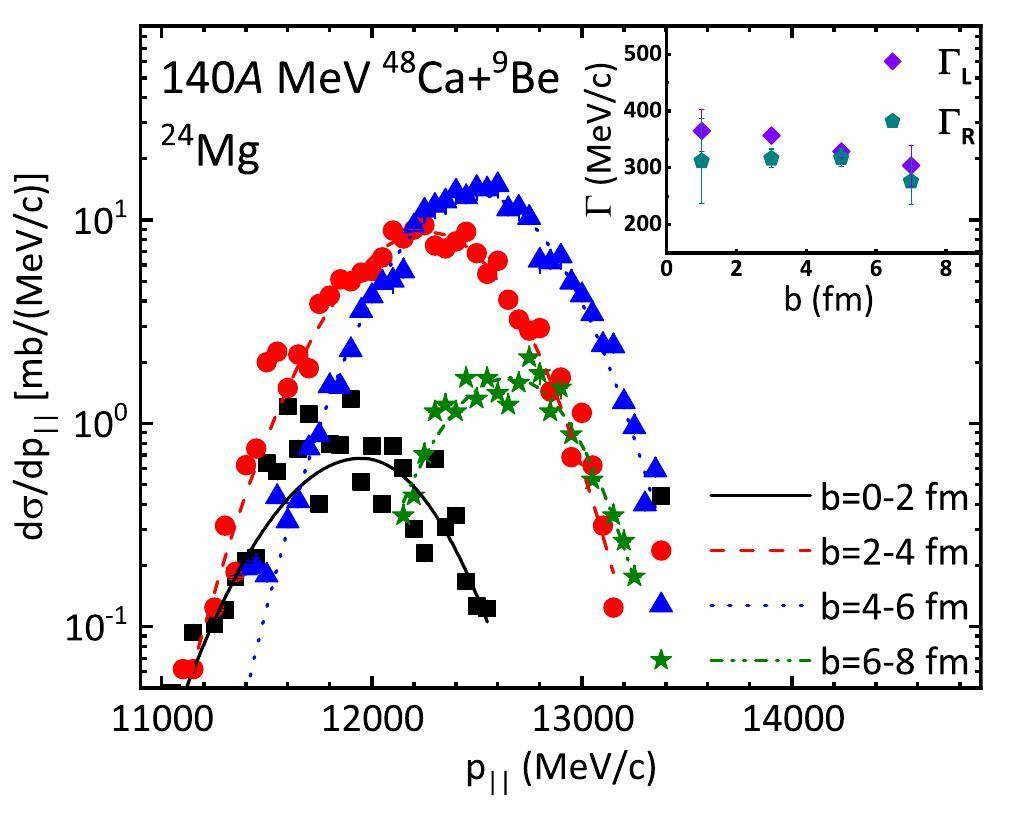
With the varying impact parameters in projectile fragmentation reactions, the $p_{\parallel }$ of a specific fragment is also influenced by the significant change in nuclear density from central to peripheral collisions [23], and the $p_{\parallel }$ of a fragment thus carries significant information on reactions, such as nuclear density distribution and nucleon-nucleon cross section [1]. The $p_{\parallel }$ values of the neutron-proton symmetric fragment ²⁴Mg produced in the 140A MeV ⁴⁸Ca + ⁹Be reaction within b= [0-2], [2-4], [4-6], and [6-8] fm are plotted in Fig. 3. From the central to the peripheral collisions, $p_{\parallel }$ for ²⁴Mg shifts from the low-momentum side to the high-momentum side as b increases. Both Γ_L and Γ_R depend on impact parameters. For different $p_{\parallel }$, the value of Γ_L tends to decrease with an increase in b. Γ_L > Γ_R (Fig. 3), with the uncertainty of the Γ_R larger than that of Γ_L, (particularly for the central collisions). Γ_R remains constant when b<6 fm whereas Γ_L decreases with increasing b. The reason for Γ_L > Γ_R may be the difference in the centrality in the reaction; that is, the larger the centrality, the deeper the collision with the target, and the significant $p_{\parallel }$ lost, as well as the wider width of Γ_L.

Fig. 3Full-screen View

(Color online) The $p_{\parallel }$ for ²⁴Mg produced in the 140A MeV ⁴⁸Ca + ⁹Be (δ_np= 0.111 fm of ⁴⁸Ca) projectile fragmentation reactions at different ranges of impact parameter from central collisions to peripheral collisions. The ranges of b are within [0-2], [2-4], [4-6], and [6-8] fm, respectively. The lines of different types denote the fitting results by a function according to Eq. (7). The inserted figure are for Γ_L and Γ_R for the $p_{\parallel }$

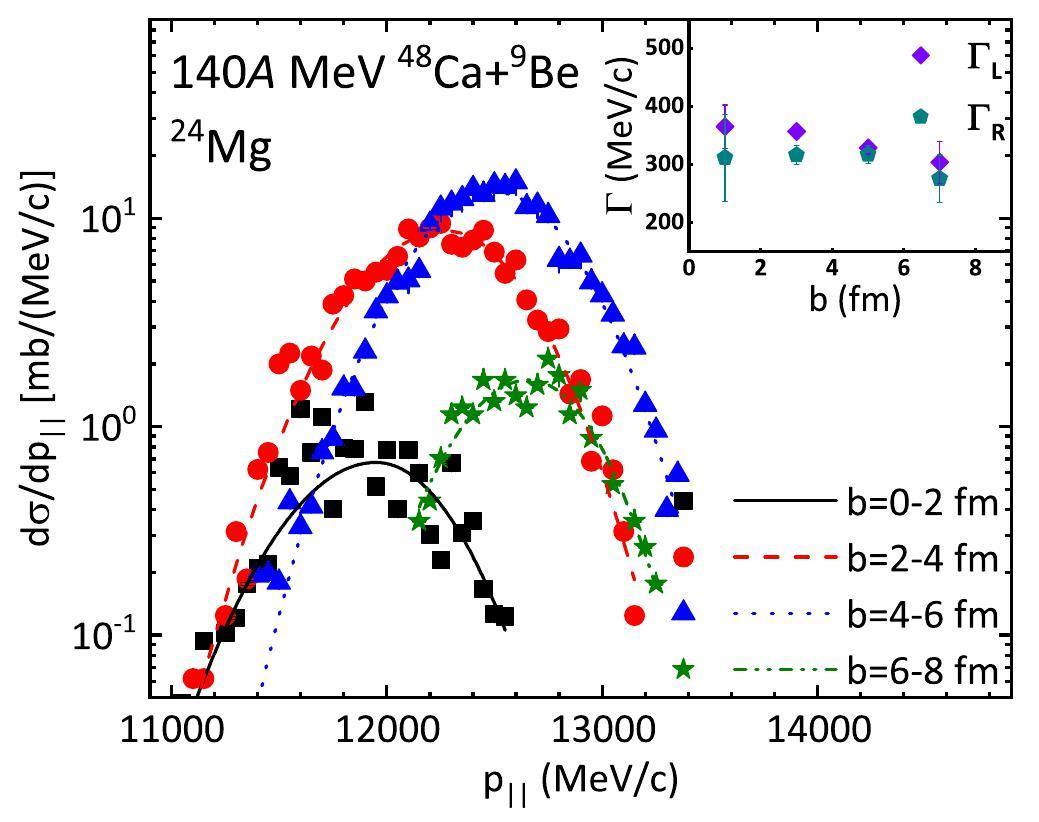
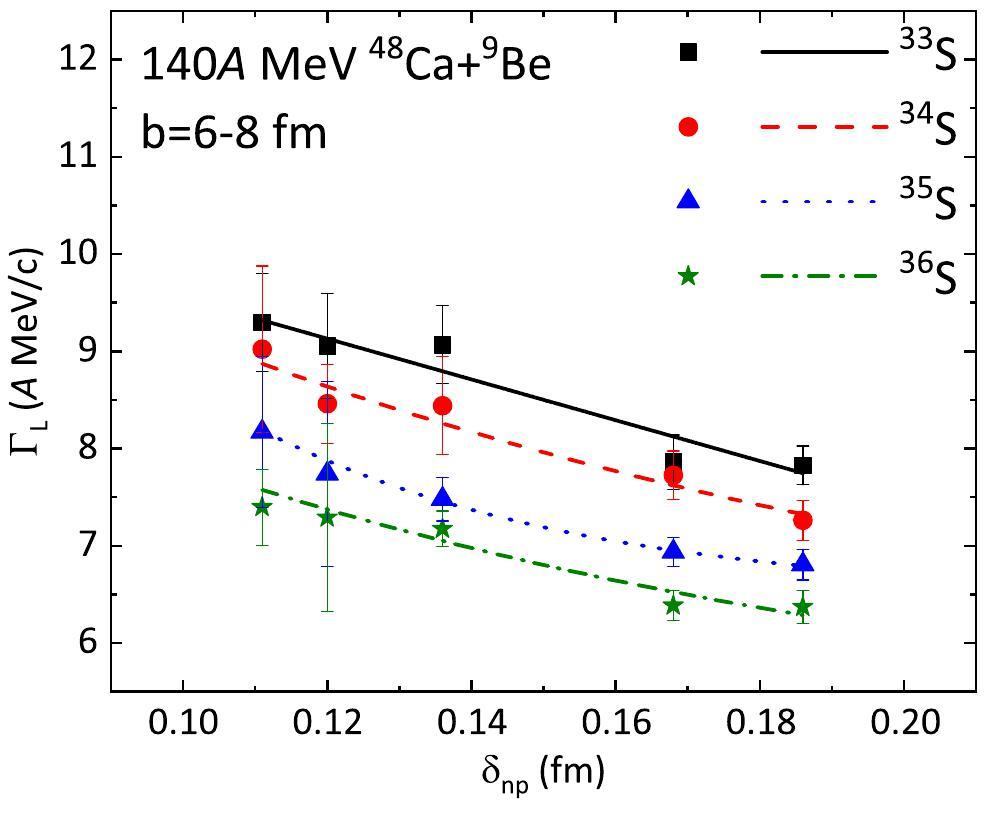
Finally, the $p_{\parallel }$ values for the isotopic fragments with different isospins were studied to determine whether they are sensitive to the neutron skin thickness of the projectile. The neutron skin of the asymmetric nucleus mainly influences the products of peripheral collisions. The $p_{\parallel }$ of the fragments was simulated for peripheral collisions of 140A MeV ⁴⁸Ca + ⁹Be within b= [6–8] fm. To compare $p_{\parallel }$ values for isotopic fragments with different mass numbers, $p_{\parallel }$ per nucleon ($p_{\parallel }$/A) was chosen. Based on the different values of δ_np for ⁴⁸Ca, as shown in Fig. 1, the $p_{\parallel }$/A distributions for neutron-rich sulfur isotopes (from ³³S to ³⁶S) are plotted in Fig. 3 together with the fitting results by Eq. (7). The values of Γ_L for $p_{\parallel }$ were obtained and the Γ_L correlations for the sulfur isotopes with δ_np of ⁴⁸Ca are plotted in Fig. 4, in which the correlations are fitted using the decaying exponential function. A strong exponential dependence of Γ_L for neutron-rich sulfur isotopes on δ_np of the projectile nucleus ⁴⁸Ca is shown, which indicates that Γ_L can be an effective probe for the neutron skin thickness of the projectile nucleus in the projectile fragmentation reaction. Further simulations of the fragment de-excitation were performed using the GEMINI code [40]. Compared with the obvious correlation between Γ_L and δ_np in the LQMD simulations, Γ_L becomes constant as δ_np varies in the LQMD + GEMINI simulations, indicating that the GEMINI de-excitation erases the correlation between Γ_L and δ_np. It is also noted that the correlation between Γ_L and δ_np is an indirect probe for the neutron-skin thickness of the projectile nucleus because fragments are obtained after the compression-expansion process of the colliding system. Further investigations are also needed to study the ${\text{Γ}}_{\text{L}}\sim {\delta }_{\text{np}}$ correlation, including the de-excitation effects, since they may modify the intermediate mass fragments in projectile fragmentation reactions, as has been found in Refs. [7, 8].

Fig. 4Full-screen View

(Color online) The LQMD simulated $p_{\parallel }$/A in peripheral collisions (within b= [6–8] fm) for the 140A MeV ⁴⁸Ca + ⁹Be reaction. The values of δ_np for ⁴⁸Ca are 0.111, 0.120, 0.136, 0.168, and 0.186 fm, respectively. Panel (a) is for ³³S, (b) for ³⁴S, (c) for ³⁵S, and (d) for ³⁶S. The lines denote the fitting results by Eq. (7)

Based on the eikonal distorted-wave impulse approximation (DWIA) explanation by Ogata et al. [30], the high-momentum side reflects the phase-volume effect owing to energy and momentum conservation, whereas the low-momentum side reflects the momentum shift caused by the attractive potential of the residual nucleus when the incident energy is not very high (below 200A MeV). Because the impact parameters are restricted to b= [6–8] fm, the width of Γ_L reflects the Heisenberg uncertainty principle in quantum mechanism; that is, from $\text{Δ}x\cdot \text{Δ}p\ge \frac{h}{4\pi }$, $\text{Δ}x$ is inversely correlated to Δ p [21]. Thus, it can be considered that the larger the Γ_L, the closer the nucleons contained in the fragment are to the center of the nucleus. In contrast, the smaller the Γ_L, the closer the nucleons in the fragment to the edge of the nucleus. With an increased neutron-skin thickness, the valence neutrons are further pushed away from the center of the nucleus, resulting in a narrower Γ_L as observed in Fig. 5 for the neutron-rich sulfur fragments.

Fig. 5Full-screen View

(Color online) The correlation between Γ_L of $p_{\parallel }$ for neutron-rich sulfur fragments in Fig. 4 and δ_np of ⁴⁸Ca in the LQMD simulated peripheral collisions for 140A MeV ⁴⁸Ca + ⁹Be reactions within b= [6–8] fm. The lines of different types denote the exponential fits to the correlations for ^33-36S

Summary

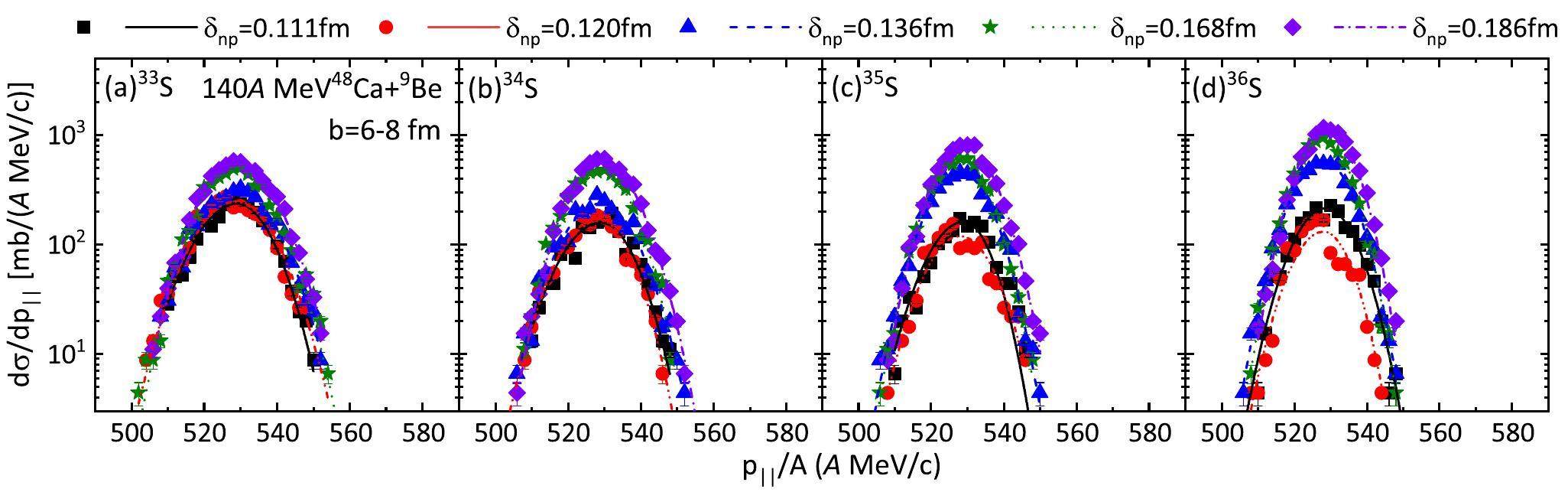
In summary, a possible probe for the neutron skin thickness of a neutron-rich projectile nucleus was studied by simulating the 140A MeV ⁴⁸Ca + ⁹Be reaction in the framework of the LQMD model. The neutron skin thickness of ⁴⁸Ca was adjusted by varying the diffuseness of the neutron density distributions. A combined Gaussian function with different widths of the left (Γ_L) and right (Γ_R) halves was employed to fit $p_{\parallel }$ of the fragments. The $p_{\parallel }$ values of the fragments are influenced by the projectile nucleus, impact parameters, and the isospin of isotope. It was found that Γ_L of the $p_{\parallel }$ of the projectile-like fragments produced in peripheral collisions was sensitive to δ_np of the projectile nucleus. Considering that $p_{\parallel }$ of fragments is easy to measure in experiments, the correlation between Γ_L of the projectile-like fragments and δ_np of the projectile nucleus potentially provides a new probe for the neutron skin thickness of neutron-rich projectile nuclei.