A new observable in heavy ion collision experiments was identified to be sensitive to the hexadecapole deformation of the colliding nuclei. Such deformation is difficult to measure in traditional nuclear electric transition measurements, as it is often overwhelmed by the nuclear quadrupole deformation. This opens the door to gain new insight into nuclear structure with experiments that were designed to study hot and dense nuclear matter.

Atomic nuclei are extended objects whose detailed structures are determined by the nuclear force, providing fundamental insight into the laws of nature. Deformations, quantified by deviations from a spherical shape, are a consequence of the interaction between the nuclear shell structure and the residual valence nucleons, whose detailed knowledge is crucial for understanding for example nucleo-synthesis, nuclear fission, and neutrinoless double-beta decay.

Characterizing the deformations with spherical harmonics allows a systematic expansion of the nuclear shape, going from larger scale deformations to finer structures. A leading large scale deformation, present in the ground states of many nuclei, is the quadrupole moment, with uranium-238 having one of the largest. It can be accessed in nuclear electric transition measurements [1], where nuclei are excited and the transition probabilities determined from the emitted gamma radiation. The electric quadrupole transition is related to the corresponding ground state deformation. Higher order moments, for example the hexadecapole moment is not precisely known for the majority of nuclei [2]. In particular for uranium-238, it is challenging to measure with the conventional methods, as it is overwhelmed by the effects of the large quadrupole deformation.

This is where rather different experiments, namely high energy heavy-ion collisions, can provide an alternative venue. It has been well established that the many particles produced in every individual heavy in collisions, performed for example at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory, or the Large Hadron Collider (LHC) at CERN, carry information about the initial spatial structure of the overlap region between the colliding nuclei. This is possible because the strong interactions between the produced particles convert the spatial information into momentum distributions of the final particles that reach the detectors. One can picture this in a hydrodynamic framework, where the initial pressure gradients drive the expansion of the hot and dense system, generating an anisotropic flow of the produced matter [3]. When the system expands and becomes more dilute, eventually interactions will cease and the system ‘freeze out’ into particles, whose momentum distributions are strongly affected the flow of the medium they emerge from.

The analysis of transverse momentum distributions thus provides deep insights into the properties of the created fluid, such as its equation of state and viscosities, and also the detailed structure of the initial geometry of the collisions. The latter is naturally affected by how much the nuclei overlapped in the direction transverse to the beam. Less overlap leads to less produced particles and a more elliptical interaction region, while for larger overlap one becomes more and more sensitive to the detailed shape of the incoming nuclei.

Measurements of elliptic flow, a typically very large component of the harmonic expansion of the azimuthal angle distribution of the transverse momentum spectrum have been performed in many collision systems and were a crucial ingredient in establishing our understanding of the produced nuclear matter as a nearly perfect fluid of deconfined quarks and gluons – the quark gluon plasma [4]. It is also well known that for very central collisions (those with the most overlap), the quadrupole deformation of colliding nuclei can have a large effect on the elliptic flow coefficient [5]. In more peripheral collisions, its effect is easily overwhelmed by the intrinsically elliptic shape of the overlap region. At RHIC, the effects of the large quadrupole deformation of uranium-238 have clear signatures in the elliptic flow in very central collisions.

Besides elliptic flow, higher flow harmonics exist and have been measured. To first approximation, elliptic flow is the response to the initial ellipticity of the interaction region, triangular flow the response to initial triangularity, quadrangular flow the response to the fourth order harmonic in an expansion of the initial transverse geometry, and so on. Such initial geometry is fluctuating event by event because of fluctuations in the nucleon positions, leading to fluctuations of observed flow harmonics. One can then study moments of the event-by-event flow distributions that carry a lot of information.

Effects of an hexadecapole deformation of uranium are hard to measure as they are typically overwhelmed by those from the large quadrupole deformation. There have been indications of a significant hexadecapole deformation from the comparison of elliptic flow in U+U and Au+Au collisions at RHIC. Those results seem inconsistent when using the measured quadrupole deformation of uranium in model calculations. However, including a large hexadecapole deformation and carefully distinguishing between the nature of the measured deformation and the model deformation parameters, would reduce the model parameter for quadrupole deformation and restore consistency between the measurements in U+U and Au+Au [6].

Nevertheless, this consistency could also be established by changing the used quadrupole deformation in Au, which is not very well known. A more direct measurement of the hexadecapole deformation of uranium is thus desired. Enter the work by the team from Huzhou University, NSFC, Fudan University, and Purdue University [7]. Here, an observable was identified that uses data from both Au+Au and U+U collisions and is insensitive to the quadrupole deformation of the uranium or gold nuclei, but shows a strong sensitivity to the hexadecapole deformation of uranium alone. To understand this observable, let us return to the discussion on how the initial geometry drives the final flow of the system. We have discussed that an initial elliptic shape leads to an elliptic flow component in momentum space, a triangular shape to triangular flow and so on. In fact, to first approximation, there is a linear relation between the n-th order eccentricity (the n-th harmonic of an expansion of the initial shape of the interaction region) and the n-th order flow harmonic, which we call vn. The proportionality constant is a response coefficient that depends on the properties of the fluid.

However, hydrodynamics, which describes the evolution of the system and the conversion of initial shape to final flow via pressure gradients, is a non-linear theory. That means one can have coupling between different modes [8]. For example, the fourth order harmonic has a linear component, proportional to the 4-th order initial eccentricity, but also a non-linear component that is proportional to the square of the 2-nd order initial eccentricity. As the 2nd order flow harmonic v₂ does not have a large non-linear component, one can write v₄ as a combination of a linear part and a part proportional to $v_2^2$. The proportionality coefficient for the non-linear part is called the non-linear response coefficient, written as χ_4,22. The relative difference of this quantity between U+U and Au+Au systems $R\left({\chi }_{\mathrm{4,22}}\right)=2\frac{\left({\chi }_{\mathrm{4,22}}^{\text{UU}}-{\chi }_{\mathrm{4,22}}^{\text{AuAu}}\right)}{\left({\chi }_{\mathrm{4,22}}^{\text{UU}}+{\chi }_{\mathrm{4,22}}^{\text{AuAu}}\right)}\mathrm{,}$ is the observable that turns out to be uniquely sensitive to the hexadecapole deformation of uranium.

To show this, the authors of [7] have performed simulations of 1 million events using 2+1 dimensional hydrodynamics with a fluctuating initial state that allows the variation of the deformation properties of the incoming nuclei. They have varied the quadrupole deformations of uranium-238 and gold-197 as well as the hexadecapole deformation of uranium-238, demonstrating that the observable R(χ_4,22) is only sensitive to variations in the hexadecapole moment.

The result is illustrated in Fig. 1, where one can see that the observable, plotted as a function of collision centrality (the smaller the centrality, the more overlap between the colliding nuclei), is insensitive to varying ${\beta }_2^{\text{U}}$, the quadrupole deformation of uranium, but strongly sensitive to variation of ${\beta }_4^{\text{U}}$, the hexadecapole deformation of uranium. The parameters for gold are kept the same, except for the solid line, for which a different ${\beta }_2^{\text{Au}}$ was used. Comparing this result with the blue band, for which only ${\beta }_2^{\text{Au}}$ is different, one can also see the insensitivity to the quadrupole deformation of the gold nucleus.

Fig. 1Full-screen View

(Color online) Model results for the observable R(χ_4,22) as a function of collision centrality for different choices of quadrupole deformation of the uranium and gold nuclei, and different hexadecapole deformations of the uranium nucleus. Comparing the results clearly demonstrates the insensitivity to either quadrupole deformation, and sensitivity to the hexadecapole deformation of uranium. Figure adapted from [7]

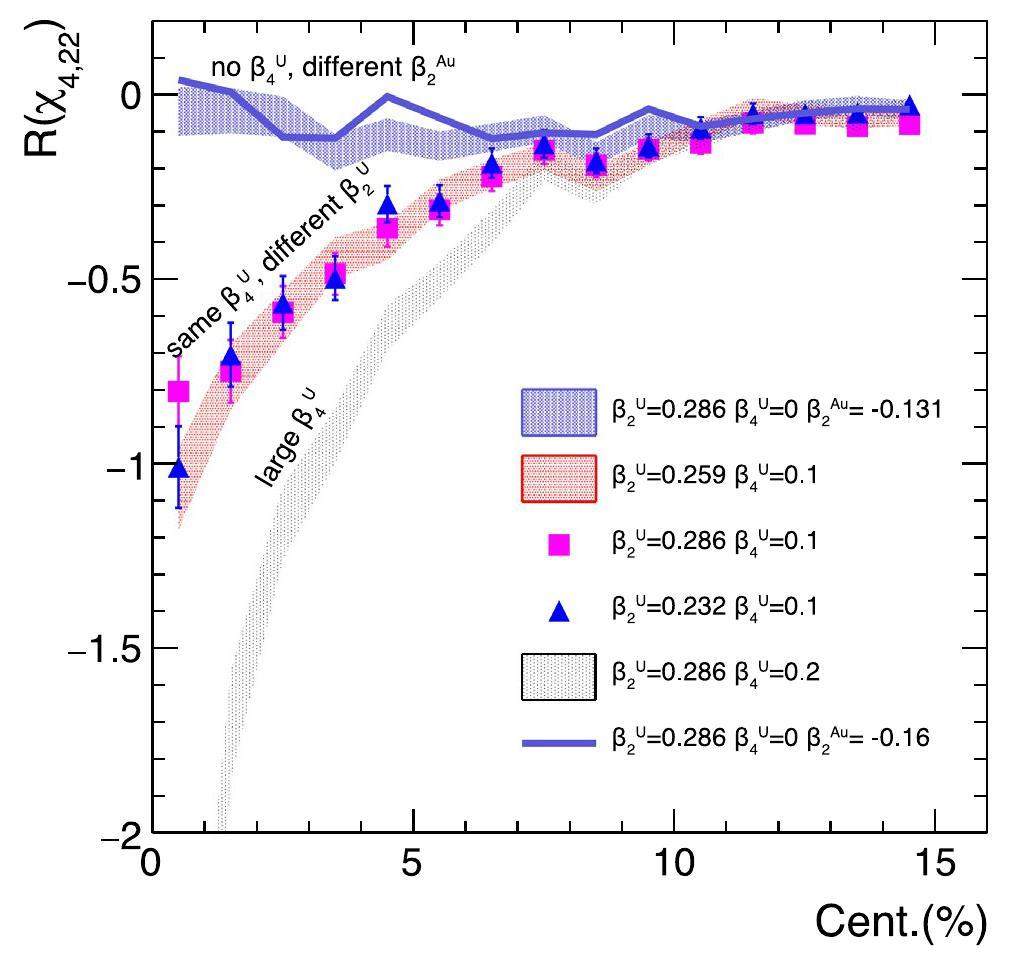
In practice, the measurement of χ_4,22 requires the measurement of v₄ with respect to the second order event plane, which is the symmetry axis defined by the elliptic flow distribution, as well as the second order four-particle cumulant used mainly for normalization. The authors further demonstrated that other potentially sensitive observables, like the R(v₄), which should naively be sensitive to the hexadecapole deformation in central events, cannot distinguish between different hexadecapole moments in uranium because they are too sensitive to the quadrupole moments of uranium or gold or are simply not sensitive enough to the hexadecapole deformation.

Consequently, a measurement using data from the STAR Collaboration at RHIC, which has already been taken, could provide a clean determination of the hexadecapole deformation of uranium-238, without any ambiguity caused by our lack of precise knowledge of the quadrupole deformation of the gold nucleus. This would uniquely resolve the otherwise puzzling inconsistency between elliptic flow measurements in central Au+Au and U+U collisions. The same method can further be applied to relativistic isobar collisions to extract the hexadecapole deformation of isobar nuclei. The work [7] stresses further the versatility and extraordinary potential of heavy ion collisions in studying a great variety of nuclear physics questions.