Introduction
In fusion reactors, excellent thermal transport properties are crucial for the regular service of plasma-facing materials (PFMs), which suffer from steady and transient heat loads. As a primary PFM candidate, tungsten (W) crystals have good thermal conductivity (κ), but significant degradation of κ is inevitable owing to the drastic increase in defect density under high-dose irradiation from the plasma [1-4]. Specifically, during high-energy neutron irradiation, collisions between neutrons and lattice atoms trigger cascade processes, leading to the production of numerous point defects in the PFM on femtosecond timescales [5]. These point defects then recombine or evolve into extended defects, resulting in severe material damage such as swelling and hardening [6]. Throughout the irradiation process, the κ value changes with the drastic structural alteration. Experiments measuring κ after irradiation have demonstrated that the κ of W samples decreases with increasing irradiation dosage, whereas high temperatures capable of inducing significant dynamic annealing in W can partially restore κ [7-10]. However, real-time experimental measurement of κ during irradiation remains challenging, despite the ability to directly observe the evolution of defects in situ [11-13]. Therefore, computer simulations are necessary to study the behavior of κ during irradiation under various conditions.
To date, most theoretical studies have used classical molecular dynamics (MD) methods employing a primary knock-on atom (PKA) to investigate complex structures under different cascade conditions. These studies explored the effects of the kinetic energy of the PKA, temperature [14], and the presence of helium atoms [15] on the surviving defects in tungsten systems. As the PKA energy increases or interstitial helium atoms are introduced, the number of surviving defects increases, whereas the temperature has little effect on the defects. Additionally, there has been significant interest in understanding the influence of grain boundaries (GBs) during cascades, as GBs can act as effective sinks for point defects and exhibit a bias-absorption effect on interstitials [16-22]. These studies have succeeded in obtaining complex structures during cascade processes, whereas few models can predict the thermal conductivities of such intricate atomistic configurations [18], particularly for structures arising during cascade processes in which drastic structural changes occur in an extremely short period. Consequently, most thermal conductivity calculations rely on structures that have reached steady states, allowing researchers to explore only the effects of various types of irradiation-induced defects on thermal conductivities or post-cascade changes in the thermal conductivities [23-29]. In tungsten systems, the lattice thermal conductivity decreases in the presence of voids or GBs, with a further reduction when these defects trap significant amounts of helium or hydrogen atoms. The overall thermal conductivity κ decreases in the presence of GBs and further decreases when the GBs are covered by voids. Additionally, the introduction of the impurity rhenium also reduces κ. Furthermore, it is worth noting that the majority of research on metal W has focused on lattice thermal conductivity using non-equilibrium molecular dynamics simulations [25-27] and the overall thermal conductivity based on the phase-field model [23, 24], whereas research on the electronic thermal conductivity (κe) that dominates metal thermal transport is relatively limited.
In this study, we employed a tight-binding (TB) potential model developed for W-based systems [30] to simulate cascade processes and calculate the corresponding κe at the quantum theory level. We accounted for the effects of PKA energy, temperature, the presence of hydrogen (H) atoms, and the presence of a GB on the κe of W systems during cascades.
Methods
In this study, cascade simulations and calculations of κe were performed based on the developed WHTB model [30], where the Hamiltonian matrix of each system is parameterized to handle large-scale systems within the framework of quantum mechanics. For our investigations into the effects of low-energy PKA, H atoms, and temperature on κe, we applied a 9×9×14 supercell consisting of 2268 W atoms (Fig. 1(a)). To study the effect of the GB, we constructed a common symmetric tilt GB structure,
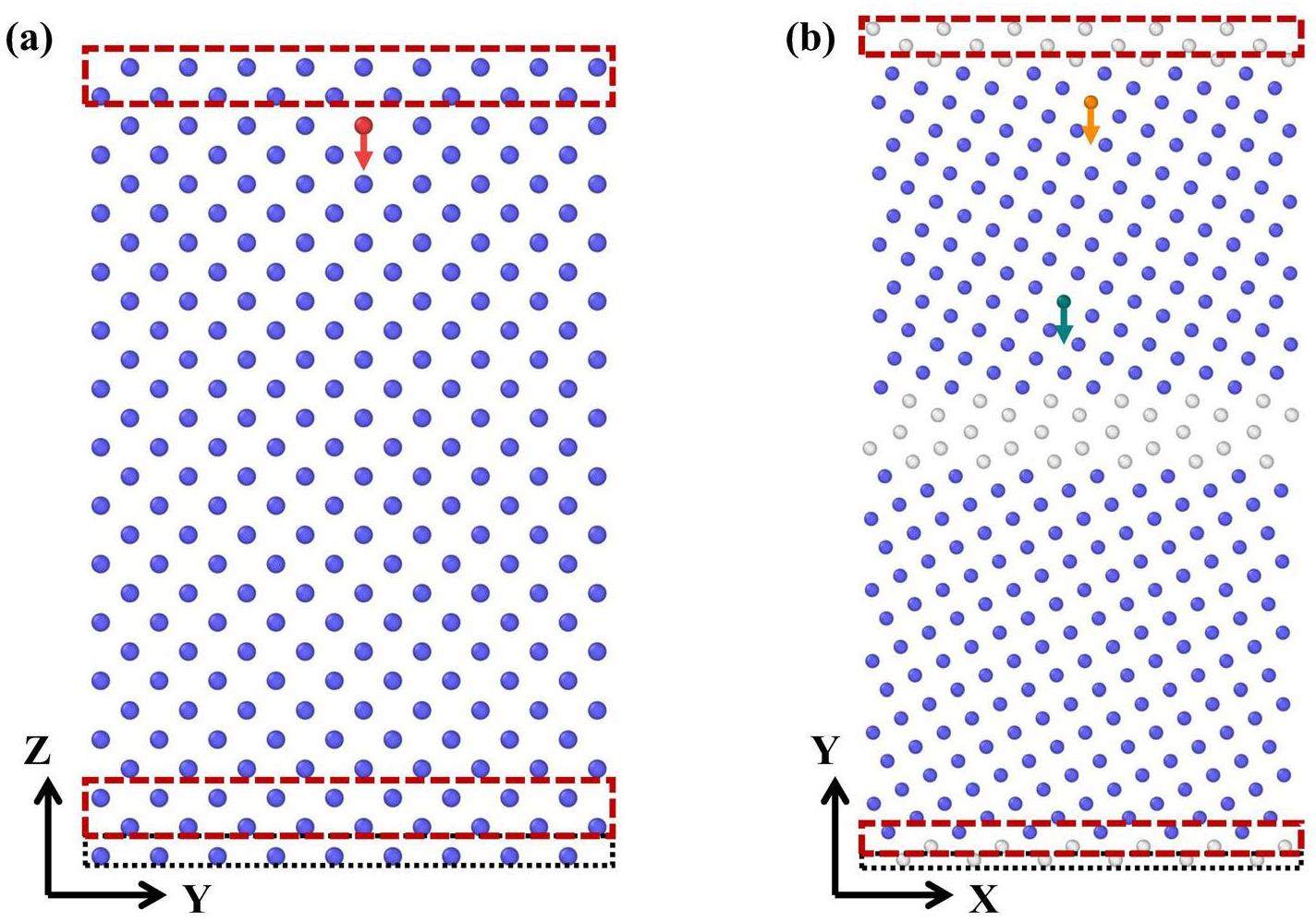
To achieve thermodynamic equilibrium states, we conducted tight-binding molecular dynamics (TBMD) simulations of up to 5-8 picoseconds (ps) at the NPT ensemble (N represents the number of particles, P represents pressure, and T represents temperature) for the considered systems. Then, to simulate the cascade processes, the atomic layer at the bottom of the supercell was fixed to prevent system translation, and four atomic layers (two at the bottom and two at the top) were used as thermostat regions to control the temperature of the simulation system using the Berendsen temperature control technique [31]. For general systems (Fig. 1(a)), the PKA was chosen beneath the top thermostat region, and the incident direction was in the negative Z direction. Regarding the GB systems, two PKAs at different distances from the GB were selected, with the incident direction perpendicular to the GB along the negative Y direction (Fig. 1(b)). Additionally, we adopted an adaptive time-stepping scheme based on the method proposed by Nordlund [32] and set a maximum step time of 1 fs. To obtain the statistical average results, we performed three sets of cascade simulations under different conditions.
Furthermore, we extracted the structures at different times during the cascades and calculated their κe values. The Kubo-Greenwood method was used to obtain κe values, and the average electron mean free path (MFP) was calculated to evaluate the strength of electron scattering. In our theoretical approach, based on the Kubo formula [33-35] and the Chester-Tellung version of the Kubo-Greenwood formula [36, 37], κe can be obtained as follows:
In addition, we counted the defects in the systems, including displaced atoms (with a displacement exceeding half the nearest-neighbor distance) and Frenkel pairs (identified using the Wigner-Seitz cell method [41]), and evaluated the centrosymmetry parameters (CSPs) of the atoms to understand the change in κe from the perspective of the structure. The CSP is defined as
Results and discussion
Effects of PKA energies and H atoms on electronic thermal conductivity
The calculations in this section were performed at 800 K, which is the operating temperature for W-PFM. Fig. 2a illustrates the variation in κe values for pure tungsten systems during cascades, where the initial kinetic energy of PKA (represented as EPKA) is 300 eV and 500 eV, respectively. It is evident that κe undergoes a significant decrease during the initial stage (approximately 0.3 ps), followed by a partial recovery at a slow pace. As EPKA increases, κe further decreases during the initial stage, whereas the recovery rate remains almost unchanged during the recovery period. In addition, it should be noted that even after approximately 4 ps, κe values for cases with EPKA values of 300 eV and 500 eV recover to only approximately 64% and 55% of the pristine crystal's value, respectively. We will provide a discussion of this phenomenon later.
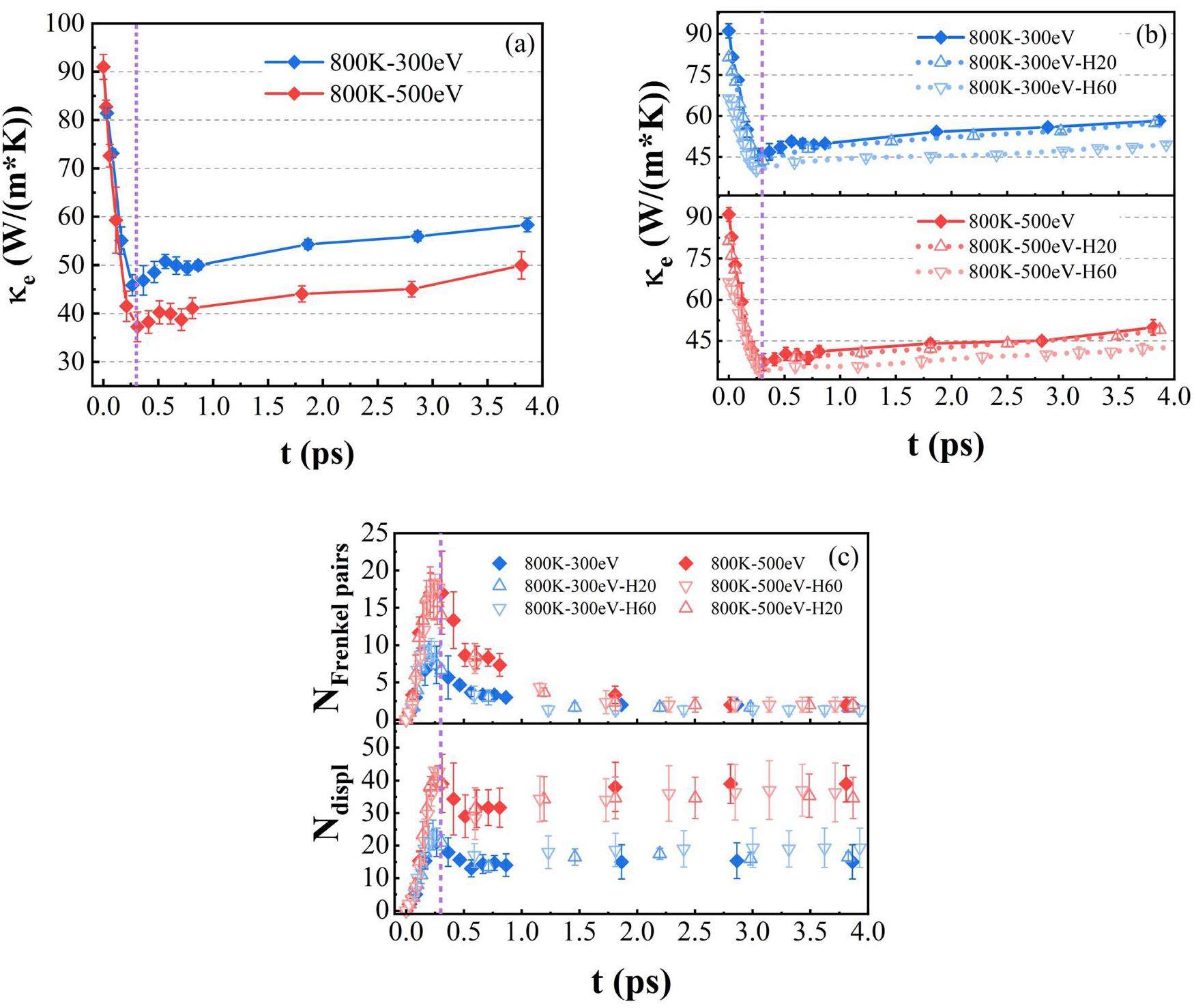
Similar trends in κe variation were observed for systems containing H atoms, as shown in Fig. 2b. In the case of the system with 20 H atoms (H concentration: 0.88%), κe closely resembled that of pure tungsten systems, except for a reduction of approximately 10 W m-1K-1 at 0 ps. For systems with 60 H atoms (H concentration: 2.65%), κe in EPKA=300 eV cascade exhibited a clear reduction compared to that of pure tungsten systems. In contrast, the reduction in κe in the EPKA=500 eV cascade appeared to be less significant. This suggests that a high concentration of H atoms in tungsten can further reduce κe, particularly in low-energy cascades. Additionally, the rates of reduction and recovery in κe for H-containing systems are lower than those for pure tungsten systems, as reflected by the slopes of the curves in Fig. 2b.
To gain a deeper understanding of the variations in κe, we examined the numbers of displaced atoms and Frenkel pairs. We focused on the defects associated with W atoms for a clear comparison between systems with and without H atoms. As shown in Fig. 2c, the numbers of both defects first sharply increase and then reach local maxima at 0.3 ps. Subsequently, the number of Frenkel pairs gradually decreases and approaches zero, after which the number of displaced atoms gradually stabilizes. Furthermore, both defect numbers noticeably increase as EPKA increases, whereas the introduction of H atoms has little effect on these quantities, indicating that the reduction in κe may be attributed to the H atom itself. The behavior of these defect variations roughly matches the κe behavior because an increase in the defect numbers enhances electron scattering and ultimately degrades the electronic transport performance. However, it is worth noting that although the number of Frenkel pairs approaches zero after 2 ps, the corresponding κe value remains close to its minimum and is significantly lower than the value at 0 ps. This suggests that despite the decrease in the number of vacancies and interstitials, the electrons in the system continue to experience severe scattering. In this scenario, we speculate that the severe electron scattering is due to the accumulation of slight structural distortions. These distortions likely arise from the incomplete restoration of displaced atoms to their initial thermal equilibrium state within a few picoseconds during the recombination of the point defects.
To validate this hypothesis, we extracted the centrosymmetry parameter (P) for each W atom in the systems. This parameter qualifies the deviation from centrosymmetry in the immediate vicinity of an atom. Table 1 presents representative data for both pure tungsten systems and systems containing 60 H atoms, where EPKA is 500 eV. Initially (at 0 ps), approximately 2.12% of the W atoms in pure tungsten exhibit P values greater than 1, indicating significant deviations from centrosymmetry in the immediate vicinity of only a few atoms due to atomic thermal motion. As the cascade event progresses, the structural evolution leads to changes in the number of W atoms, with P values greater than 1. At approximately 4 ps, the number of W atoms with P values above 1 is slightly lower than that at approximately 0.3 ps but remains significantly higher than that at the initial thermal equilibrium state (0 ps). This indicates that a few picoseconds after the PKA incidents, the local environment of some W atoms still substantially deviates from the thermal equilibrium state. The accumulation of these deviations can result in strong electron scattering, as evidenced by a 1.66 nm decrease in MFP around 4 ps compared to the initial state (0 ps). When 60 H atoms are present in the system, two notable differences emerge in the analysis of centrosymmetry parameters. First, the presence of H atoms exacerbates the deviation from centrosymmetry near the W atoms. Second, the rate of change of Psum decreases when H atoms are present. These differences are consistent with the observed alterations in κe.
| Time | 0 ps | 0.15 ps | 0.3 ps | 4 ps | |
|---|---|---|---|---|---|
| Pure | Number of W atoms with P>1 | 48 | 283 | 502 | 384 |
| Summation of P > 1(Psum) | 268.30 | 1846.24 | 3571.75 | 2096.01 | |
| Change rate of Psum | - | 5.88 | 12.31 | 6.81 | |
| Average electron MFP | 3.77 | 2.03 | 1.50 | 2.11 | |
| 60 H atoms | Number of W atoms with P>1 | 129 | 350 | 533 | 516 |
| Summation of P > 1 (Psum) | 789.78 | 2337.96 | 3722.90 | 2809.53 | |
| Change rate of Psum | - | 1.96 | 3.71 | 2.56 | |
| Average electron MFP | 2.76 | 1.66 | 1.32 | 1.52 | |
Effect of temperature on electronic thermal conductivity
It is widely acknowledged that the influence of temperature on defect generation during a cascade is relatively minor [43]. However, the effect of temperature on κe values of defective systems is complex [44]. To further investigate the impact of temperature on κe during cascades, we studied the κe values of tungsten systems with varying EPKA and different numbers of H atoms under a high temperature of 1300 K.
As shown in Fig. 3a, an increase in temperature leads to a noticeable improvement in κe values throughout the considered cascades. Specifically, at 0.3 ps, the corresponding minimum κe values for all examined systems exhibit a relatively high value of approximately 50 W m-1 K-1. Subsequently, κe values are consistently significantly higher than those observed at 800 K. In addition, the disparity in κe between the pure tungsten system and the tungsten system containing H atoms remains nearly unchanged with increasing temperature, except at 0 ps. At 0 ps, κe of the pure tungsten system remains almost constant, whereas that of the system with H atoms shows a significant improvement.
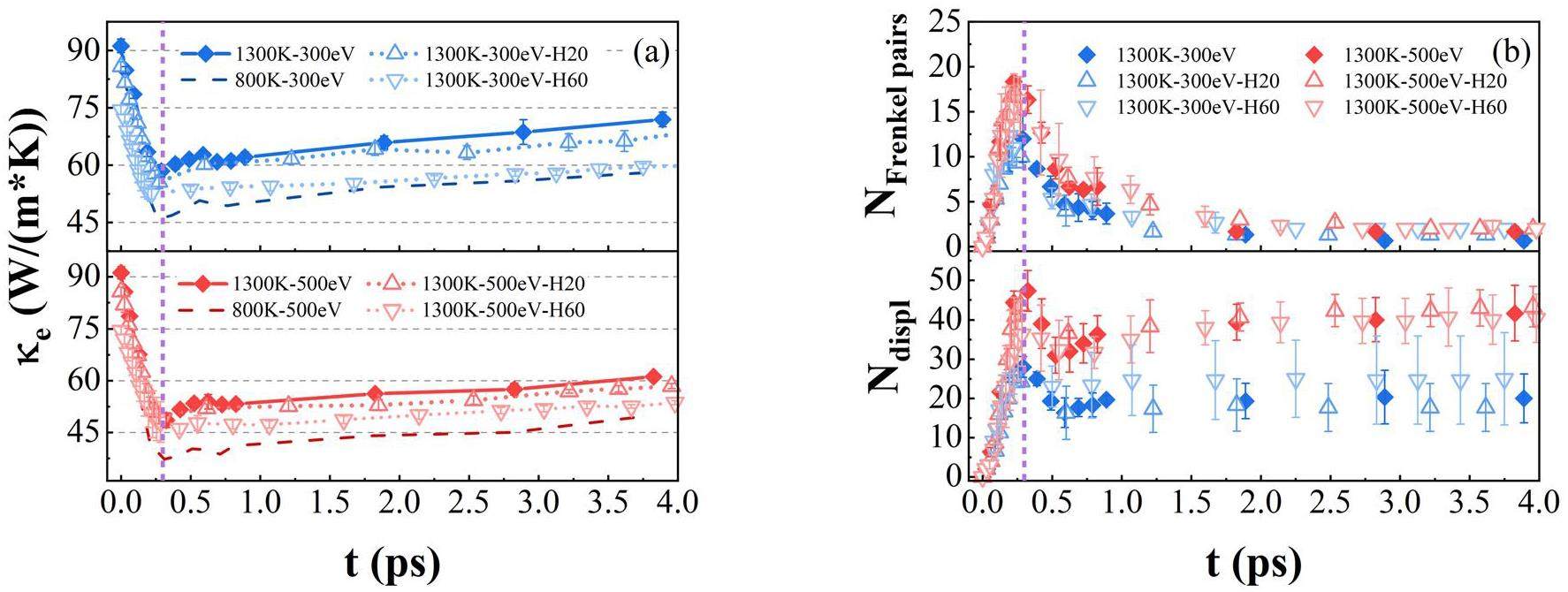
A count of typical defects in the cascades at 1300 K was performed, as illustrated in Fig. 3b. It was observed that the local maxima for both types of defects slightly increase compared to those at 800 K (Fig. 2c. After approximately 2 ps, the defect counts at both temperatures become similar. Moreover, Table 2 provides representative data on the CSP and MFP for the pure tungsten system and the system containing 60 H atoms at 1300 K with an EPKA value of 500 eV. The major distinction between the two temperature cases lies in the significant increase in the number of W atoms with P values greater than 1 and the corresponding Psum throughout the entire process with increasing temperature. This indicates that an elevated temperature causes a greater deviation from centrosymmetry in the immediate vicinity of the W atoms, leading to enhanced electron scattering. However, the thermal transport properties of the electrons are enhanced at 1300 K compared to those at 800 K. This phenomenon arises from the complex effect of temperature on κe. On the one hand, a temperature rise strengthens the thermal motion of atoms, thereby augmenting the electron scattering, as supported by the CSP and MFP analyses; on the other hand, the energy carried by electrons also increases with a higher temperature, directly facilitating heat transport. The complex effect of temperature is also reflected in the Wiedemann-Franz law [45], as discussed in our previous work [44].
| Time | 0 ps | 0.23 ps | 0.3 ps | 4 ps | |
|---|---|---|---|---|---|
| Pure | Number of W atoms with P>1 | 414 | 888 | 1015 | 955 |
| Summation of P > 1 (Psum) | 2290.73 | 5555.25 | 6630.40 | 5319.31 | |
| Change rate of Psum | - | 1.43 | 1.89 | 1.32 | |
| Average electron MFP | 2.18 | 1.10 | 0.99 | 1.32 | |
| 60 H atoms | Number of W atoms with P>1 | 504 | 928 | 1054 | 991 |
| Summation of P > 1 (Psum) | 2676.19 | 5918.74 | 6910.15 | 5562.22 | |
| Change rate of Psum | - | 1.21 | 1.58 | 1.08 | |
| Average electron MFP | 1.69 | 0.96 | 0.91 | 1.11 | |
In summary, although an increase in temperature has a slight effect on defect production and even enhances electron scattering, the accompanying increase in the energy carried by electrons significantly improves electronic thermal transport.
Effect of grain boundary on electronic thermal conductivity
Previous studies [16, 20] have demonstrated that GBs can serve as effective sinks for point defects, particularly interstitials, leading to self-healing of irradiation damage. Additionally, the extent of overlap between the cascade center and the GB is known to influence the absorption effect of the GB for point defects [17, 19, 22], which may affect the electron transport properties. Hence, we examined the influence of different levels of overlap between the cascade center and the GB on κe during cascades. We employed a common symmetric tilt GB in W,
Then, we calculated the κe values for systems with a specific GB during the cascades. Because the GB exhibited anisotropy, we extracted κe values separately along the X, Y, and Z directions. Figure 4a shows a substantial reduction in κe values in all three directions compared to the cases of the pure tungsten systems throughout the cascades. In particular, κe in the Y direction experienced the most pronounced decrease, primarily due to the strong electron scattering at the GB interface. Throughout the cascades, the presence of the GB itself reduced the electronic transport properties (0 ps), and the reduction (0 ps–0.3 ps) and subsequent recovery (0 ps-4 ps) of κe were relatively slow compared to those in the pure tungsten systems. Notably, the degree of overlap between the cascade center and GB does not significantly affect κe for the considered systems.
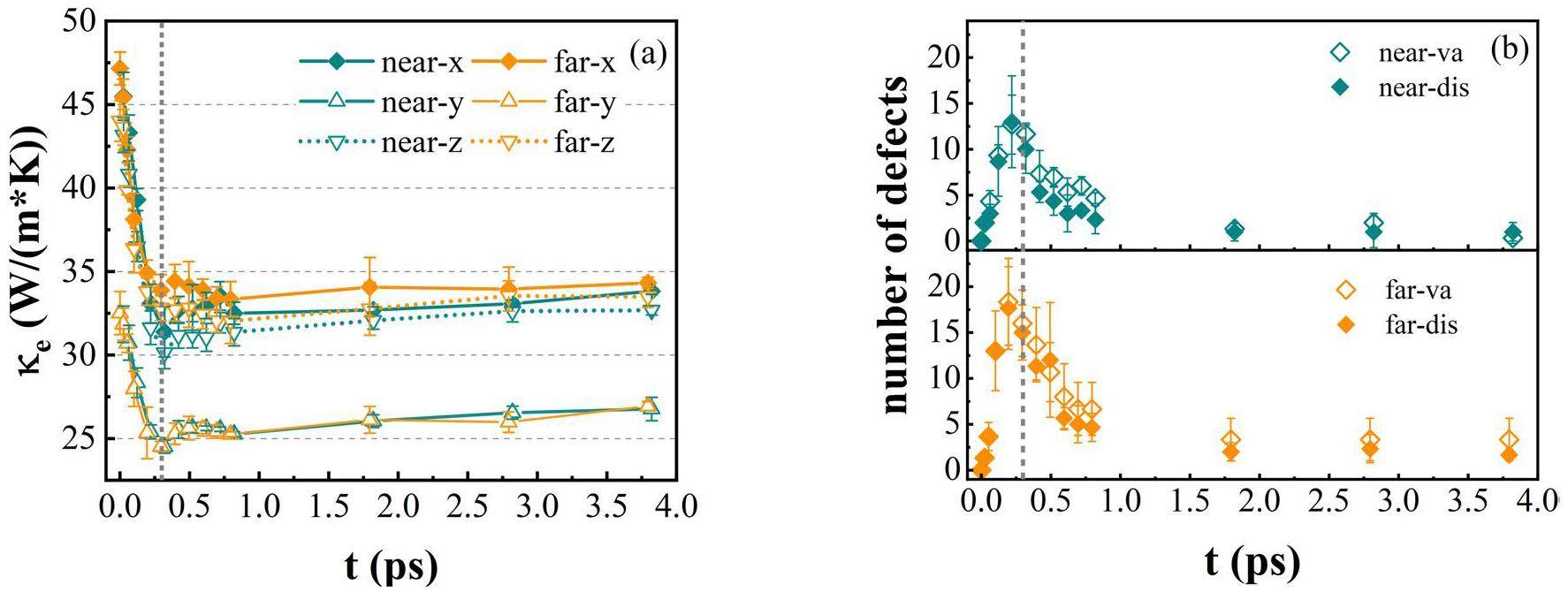
To better understand the variation of κe, we counted the numbers of vacancies and interstitials outside the GB. Throughout the cascades, the vacancies outnumbered the interstitials for both degrees of overlap between the cascade center and GB. Moreover, increasing the degree of overlap decreased the number of vacancies and interstitials outside the GB. These results were consistent with those of previous studies [17, 19, 22]. However, the enhancement in the absorption effect of the GB does not improve κe but rather slightly weakens it at approximately 0.3 ps in the X and Z directions. This indicates that point defects absorbed by the GB continue to negatively impact electronic transport in the short term, despite reducing the defects within the grain interior. The corresponding data in Table 3 for both cases support this observation. Specifically, similar CSP data and comparable MFP for the two cases indicate similar deviations from centrosymmetry in the immediate vicinity of the atoms and comparable electron scattering intensities.
| Time | 0 ps | 0.2 ps | 0.3 ps | 4 ps | ||
|---|---|---|---|---|---|---|
| Cascade center overlaps with GB | Number of W atoms with P>1 | 404 | 827 | 894 | 921 | |
| Summation of P > 1 (Psum) | 3431.19 | 6286.75 | 6764.72 | 6221.36 | ||
| Change rate of Psum | - | 0.83 | 0.97 | 0.81 | ||
| Average | X | 1.94 | 1.23 | 1.18 | 1.26 | |
| electron | Y | 1.27 | 0.91 | 0.87 | 0.96 | |
| MFP | Z | 1.73 | 1.13 | 1.08 | 1.18 | |
| Cascade edge overlaps with GB | Number of W atoms with P>1 | 404 | 871 | 933 | 899 | |
| Summation of P > 1 (Psum) | 3431.19 | 6586.79 | 6858.80 | 6133.09 | ||
| Change rate of Psum | - | 0.92 | 1.00 | 0.79 | ||
| Average | X | 1.94 | 1.31 | 1.26 | 1.29 | |
| electron | Y | 1.27 | 0.90 | 0.89 | 1.01 | |
| MFP | Z | 1.73 | 1.22 | 1.19 | 1.23 | |
Discussion on using TB model for calculation
First, we highlight the reliability of the WHTB potential model for calculating the electronic thermal conductivities of tungsten-based systems. In this work, electronic thermal conductivity was obtained based on electrical conductivity through the Kubo-Greenwood method; therefore, an accurate calculation of electrical conductivity is crucial. Reference [46] compared the electrical conductivities of pristine tungsten calculated using the WTB potential model (on which the WHTB potential is based) and measured experimentally at different temperatures. Notably, a favorable alignment between the theoretical and experimental values at high temperatures (
A similar underestimation is evident in the calculations of the electronic thermal conductivity of pristine tungsten systems, and this underestimation also intensifies with decreasing temperature. However, it is noted that the referenced work compared the electronic thermal conductivity calculated by the Kubo-Greenwood method and the total thermal conductivity measured directly in experiments, with the latter including not only the electronic thermal conductivity but also the lattice thermal conductivity. Hence, some of the underestimation stems from the absence of the lattice thermal conductivity. In experiments, electronic thermal conductivity can be indirectly determined by measuring the electrical conductivity and applying the Wiedemann-Franz law [47]. In our previous work [44], we conducted a comparative analysis of the electronic thermal conductivity of pristine tungsten at 800 K obtained by TB calculations and experiments. The respective values were 95.92 W m-1 K-1 and 102.36 W m-1 K-1, which are close to each other. Therefore, the electronic thermal conductivity data for tungsten-based systems at high temperatures (
Next, we discuss the significance of our investigation using the TB model. In this study, we focused on the dynamic evolution of the electronic thermal conductivity of tungsten during the displacement cascade process under diverse conditions, which is difficult to directly measure experimentally. This process corresponds to the early stage of neutron irradiation, leading to the generation of a significant number of vacancies and interstitials in the materials within a brief timeframe at the picosecond level. The resulting alterations in the thermal transport properties are substantial, potentially affecting the normal service of PFM. Hence, the electronic thermal conductivity variation in tungsten during the cascade process must be investigated. Currently, research on the electronic thermal conductivity of tungsten during cascade processes is limited because of the difficulty of handling electronic structures in large and complex systems. Although the WHTB model can be used to determine the electronic thermal conductivity of tungsten under low-energy cascades, it is difficult to directly compare the results with the conductivities of materials experiencing high-energy and sustained neutron irradiation at the macroscopic level. Nevertheless, our research contributes to this field in two ways. First, the results reveal the influence of diverse cascade conditions on the electronic thermal conductivity of tungsten; second, our study can provide foundational data for simulations using the phase-field model, facilitating simulations that more accurately reflect the actual evolution of thermal transport properties of tungsten under neutron irradiation.
Conclusion
In conclusion, we employed the WHTB model and the Kubo-Greenwood method to investigate how PKA energy, H atoms, temperature, and GB affect κe of tungsten systems during collision cascades. Our findings revealed a rapid reduction in κe within the initial 0.3 ps, followed by a gradual recovery. A higher PKA energy and high concentration of H atoms worsen the reduction in κe during the cascades. With increasing temperature, κe shows a significant improvement during cascades due to the increased energy carried by electrons, despite exhibiting fewer changes in defect production and an apparent enhancement in electron scattering. The presence of the considered GB has a notable negative impact on κe, and the absorption of point defects by GB does not improve the κe performance. In addition, the evolution of the defect count approximately matched the changes in κe, whereas the accumulation of microstructural distortion keeps κe relatively low when the number of point defects approaches zero.
The interactions between rhenium and interstitial-type defects in bulk tungsten: a combined study by molecular dynamics and molecular statics simulations
. J. Nucl. Mater. 522, 200-211 (2019). https://doi.org/10.1016/j.jnucmat.2019.05.003Defect characterization, mechanical and thermal property evaluation in CVD-W after low-dose neutron irradiation
. Int. J Refract. Hard. Met. 85,The heat flux and temperature distribution of W fuzz layers under fusion-relevant He/D ion irradiations
. J. Nucl. Mater. 557,Degradation of thermal conductivity of the damaged layer of tungsten irradiated by helium-plasma
. Fusion Eng. Des. 137, 97-103 (2018). https://doi.org/10.1016/j.fusengdes.2018.08.014Multiscale modelling of plasma-wall interactions in fusion reactor conditions
. J. Phys. D 47(22),Multiscale modelling of plastic flow localization in irradiated materials
. Nature 406, 871-874 (2000). https://doi.org/10.1016/S0168-583X(01)00392-5Thermal conductivity degradation and recovery in ion beam damaged tungsten at different temperature
. J. Nucl. Mater. 511, 141-147 (2018). https://doi.org/10.1016/j.jnucmat.2018.09.002Thermal diffusivity of tungsten irradiated with protons up to 5.8 dpa
. J. Nucl. Mater. 509, 152-157 (2018). https://doi.org/10.1016/j.jnucmat.2018.06.041Response of unalloyed tungsten to mixed spectrum neutrons
. J. Nucl. Mater. 520, 193-207 (2019). https://doi.org/10.1016/j.jnucmat.2019.03.045Deuterium retention and thermal conductivity in ion-beam displacement-damaged tungsten
. Nucl. Mater. Energy 12, 164-168 (2017). https://doi.org/10.1016/j.nme.2017.03.024Damage-tolerant nanotwinned metals with nanovoids under radiation environments
. Nat. Commun. 6, 7036 (2015). https://doi.org/10.1038/ncomms8036Direct observation of the spatial distribution of primary cascade damage in tungsten
. Acta. Mater. 144, 905-917 (2018). https://doi.org/10.1016/j.actamat.2017.10.031Direct observation of size scaling and elastic interaction between nano-scale defects in collision cascades
. Epl 110(3), 36001 (2015). https://doi.org/10.1209/0295-5075/110/36001Displacement cascades and defects annealing in tungsten, part I: defect database from molecular dynamics simulations
. J. Nucl. Mater. 462, 329-337 (2015). https://doi.org/10.1016/j.jnucmat.2014.12.056Molecular dynamics simulation of the displacement cascades in tungsten with interstitial helium atoms
. Fusion Sci. Technol. 66(1), 112-117 (2014). https://doi.org/10.13182/fst13-742An energetic and kinetic perspective of the grain-boundary role in healing radiation damage in tungsten
. Nucl. Fusion 53(12),The evolution of interaction between grain boundary and irradiation-induced point defects: symmetric tilt GB in tungsten
. J. Nucl. Mater. 500, 42-49 (2018). https://doi.org/10.1016/j.jnucmat.2017.12.013Effect of irradiation on mechanical properties of symmetrical grain boundaries investigated by atomic simulations
. J. Nucl. Mater. 491, 154-161 (2017). https://doi.org/10.1016/j.jnucmat.2017.04.051Primary radiation damage near grain boundary in bcc tungsten by molecular dynamics simulations
. J. Nucl. Mater. 458, 138-145 (2015). https://doi.org/10.1016/j.jnucmat.2014.11.135Efficient annealing of radiation damage near grain boundaries via interstitial Emission
. Science 327(5973), 1631-1634 (2010). https://doi.org/10.1126/science.1183723Effects of grain boundaries on the radiation-induced defects evolution in BCC Fe-Cr alloy: a molecular dynamics study
. Nucl. Mater. Energy 22,Effects of atomic grain boundary structures on primary radiation damage in alpha-Fe
. Nucl. Instrum. Methods Phys. Res. B 362, 1-8 (2015). https://doi.org/10.1016/j.nimb.2015.08.074Numerical simulations of thermal conductivity in void-containing tungsten: Topological feature of voids
. J. Nucl. Mater. 543,Understanding the thermal conductivity of pristine W and W-Re alloys from a physics-based model
. J. Nucl. Mater. 529,Thermal conductivity of tungsten: effects of plasma-related structural defects from molecular-dynamics simulations
. Appl. Phys. Lett. 111(8),Study of lattice thermal conductivity of tungsten containing bubbles by molecular dynamics simulation
. Fusion Eng. Des. 161,Simulation study of effects of grain boundary and helium bubble on lattice thermal resistance of tungsten
. Fusion Eng. Des. 168,The effect of temperature and cascade collision on thermal conductivity of 3C-SiC: a molecular dynamics study
. Int. J. Heat Mass Transf. 180,Graphene coated 3C-SiC with improved irradiation resistance and enhanced heat conduction property after collision cascade
. Int. J. Heat Mass Transf. 194,Interplay between the edge dislocation and hydrogen in tungsten at electronically excited states
. Adv. Phys. Res. 2(8),Molecular-dynamics with coupling to an external bath
. J. Chem. Phys. 81(8), 3684-3690 (1984). https://doi.org/10.1063/1.448118Molecular dynamics simulation of ion ranges in the 1-100 keV energy range
. Comput. Mater. Sci. 3(4), 448-56 (1995). https://doi.org/10.1016/0927-0256(94)00085-qStatistical-mechanical theory of irreversible processes. I. general theory and simple applications to magnetic and conduction problems
. J. Phys. Soc. Japan 12(6), 570-586 (1957). https://doi.org/10.1143/JPSJ.12.570Topological nature of anomalous hall effect in ferromagnets
. J. Phys. Soc. Japan 71(1), 19-22 (2002). https://doi.org/10.1143/JPSJ.71.19Quantum transport of massless dirac fermions
. Phys. Rev. Lett. 98(7),Ab initio determination of electrical and thermal conductivity of liquid aluminum
. Phys. Rev. B 72(10),The law of wiedemann and franz
. Proc. Phys. Soc. 77(5), 1005 (1961). https://doi.org/10.1088/0370-1328/77/5/309Electrical transport in carbon nanotubes: Role of disorder and helical symmetries
. Phys. Rev. B 69(12),Electronic transport through Si nanowires: Role of bulk and surface disorder
. Phys. Rev. B 74(24),Effect of charged line defects on conductivity in graphene: Numerical Kubo and analytical Boltzmann approaches
. Phys. Rev. B 87(19),Defect production in collision cascades in elemental semiconductors and fcc metals
. Phys. Rev. B 57(13), 7556-7570 (1998). https://doi.org/10.1103/PhysRevB.57.7556Dislocation nucleation and defect structure during surface indentation
. Phys. Rev. B 58(17), 11085-11088 (1998). https://doi.org/10.1103/physrevb.58.11085The primary damage state in fcc, bcc and hcp metals as seen in molecular dynamics simulations
. J. Nucl. Mater. 276, 1-12 (2000). https://doi.org/10.1016/s0022-3115(99)00165-8Effect of lattice defects, hydrogen impurity and temperature on electronic thermal conductivity in first wall tungsten materials
. J. Nucl. Mater. 581,Thermal conductivity in metallic nanostructures at high temperature: Electrons, phonons, and the Wiedemann-Franz law
. Phys. Rev. B 82(7),An empirical law on the finite-size effects in electronic transport calculations of tungsten
. AIP Adv. 9(9),Temperature dependence of thermal conductivity in W and W-Re alloys from 300 to 1000 K
. Mater. Lett. 57(19), 2950-2953 (2003). https://doi.org/10.1016/s0167-577x(02)01403-9The authors declare that they have no competing interests.


