Introduction
The Shanghai Laser Electron Gamma Source (SLEGS) is a beamline station constructed in the Shanghai Synchrotron Radiation Facility (SSRF) project II. The SLEGS is the first pioneering Laser Compton Slanting Scattering (LCSS) gamma source, and it is characterized by its innovative approach of employing a continuously changing collision angle of 20 degrees to 160 degrees, which can produce an adjustable γ-ray energy within the range of 660 keV to 21.7 MeV [1-3]. The SLEGS is an important platform for basic and applied scientific research in photonuclear physics [4-8]. The γ-ray beam flux is a crucial parameter for the SLEGS, and its measurement can be accomplished through direct or indirect measurements via a photonuclear reaction. Large-volume scintillator detectors such as LaBr3(Ce), BGO, and NaI(Tl) detector offer direct measurements by attenuating the γ-ray beam intensity. However, limitations arise at high count rates (less than 106 cps) because of the long decay time of scintillators and limited readout rate of PMTs. The plastic scintillator paddle detectors employed at the High Intensity Gamma-ray Source (HIγS) allow beam flux measurements of up to 3×107 photons/s, with an accuracy of at least 2% [9].
At the SLEGS, a large-volume Φ 76.2 mm × 101.6 mm LaBr3(Ce) detector, manufactured by Saint-Gobain [10], and a Φ 76.2 mm × 200 mm BGO detector were employed to directly monitor the attenuated beam. Indirect methods rely on nuclear reactions induced by γ-rays, such as d(γ,n)p in D2O and deuterated benzene cell (C6D6) targets, to monitor the beam flux by counting the neutrons at HIγS. The γ-ray flux calculated at 3 MeV was 1.2×107 photons/s with the simulation detector efficiency, and the overall systematic uncertainty could be limited to below 5% [11, 12]. Another indirect method involves Compton scattering by a copper target employed at the ELI-NP to measure the relative beam flux [13]. Additionally, the photon activation method, which involves photon-nuclear reactions such as 197Au(γ, n)196Au, 27Al(γ, x;x=2pn,pd3 [14-16], 93Nb(γ, n)92m,gNb, and others, provides another means for determining the beam flux. Specifically, for the LCSS γ-ray beams at the SLEGS, 197Au(γ, n)196Au and 64Zn(γ, n)63Zn were selected to measure the γ-ray beam flux. This article is organized as follows. Section 2 introduces the basic principles and methods for Photon Activation Analyses (PAA) [17-19], including the γ-ray beam source and detection system. Section 3 outlines our data analysis procedure. Section 4 discusses the prospects of the PAA, such as the improvement of nuclear reaction data, development of new γ-ray sources, and integration of PAA with other techniques.
SLEGS beamline and PAA setup
γ-ray beam characterization
A laser Compton scatter γ-ray beam was generated in a interaction chamber by employing a CO2 laser (wavelength: 10.64 μm) operating at a low frequency of 1 kHz, with a pulse width of 50 μm (equivalent to 5 W laser power). This laser beam was collided with a 3.5 GeV electron in the SSRF storage ring, resulting in the production of quasi-monochromatic γ-rays beam with energies varying from 0.66 MeV to 21.7 MeV. The γ-ray beam flux ranged from 4.8×105 ph/s to 1.5×107 ph/s [1]. The main parameters of the SLEGS are listed in Table 1. The LCSS γ-ray beam was then directed through a vacuum pipeline, passing sequentially through a coarse collimator, fine collimator, and attenuator [20-23] before ultimately reaching the experimental hall. This well-controlled transport setup ensured precise delivery of the γ-ray beam to the experimental hall.
| parameter | Value | Comments |
|---|---|---|
| E-beam bunch interval (ns) | 2 | |
| E-beam energy (GeV) | 3.5 | |
| E-beam current (mA) | 180–210 | Topup mode |
| γ-ray energy (MeV) | 0.66–21.7 | CO2 Laser |
| Total flux (γ /s) | 4.8×105-1.5×107 | 20°-180° |
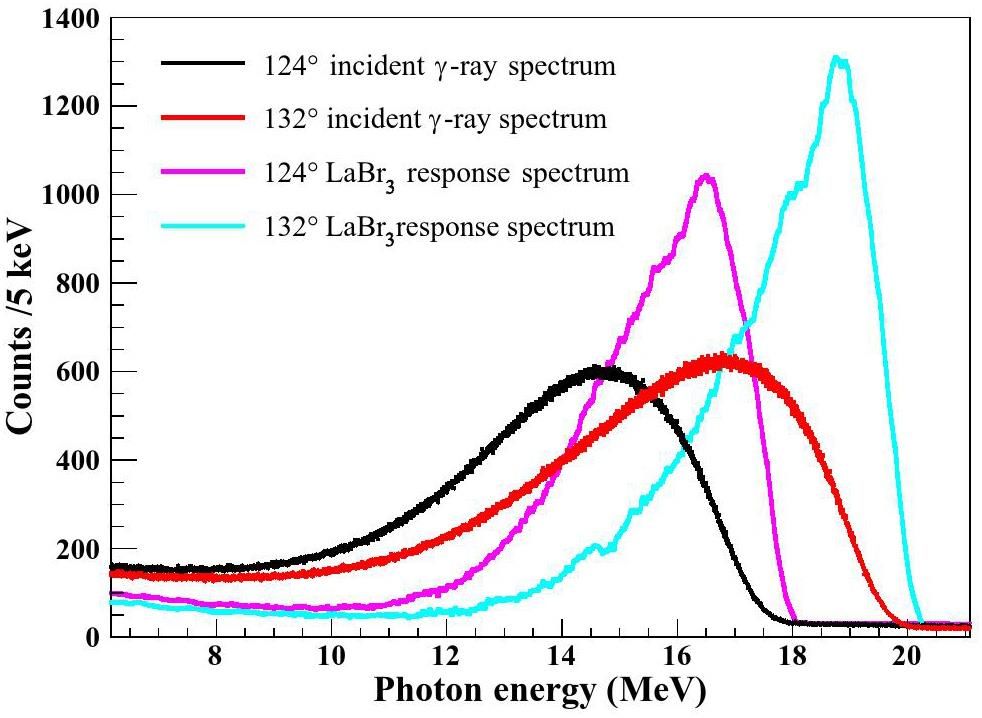
Figure 1 shows a diagram illustrating the online activation and offline measurements. The activation platform, featuring a multi-slot target holder, was strategically positioned behind the beam pipe exit. A silicon pixel imaging detector (MiniPIX) was used to facilitate beam spot imaging and reaction target localization. Additionally, a Φ 76.2 mm × 101.6 mm LaBr3(Ce) detector was placed at the termination point of a LCS γ-ray beamline to measure both the γ-ray beam flux and energy. Figure 2 shows the detector response to γ-ray beam at collision angles of 124° and 132° using a 3 mm coarse collimator under 200 mm copper attenuation. The energy and efficiency calibrations of the LaBr3(Ce) detector were performed using monoenergetic gamma rays from nuclear reactions (6.13 MeV, 9.17 MeV, 10.76 MeV, 17.6 MeV) and the radioactive source 60Co [24-27]. The profile of a quasi-monoenergetic γ-ray beam overlaid on a continuous bremsstrahlung background was clearly visible. Using the unfolding method, the corresponding γ-ray energy spectrum without detector response was successfully solved, as shown in Fig. 2 (pink and blue). The details of the unfolding method for the γ-ray beam are presented in [28].

Low background HPGe detector systems
The characteristic γ-rays emitted from a nuclide sample were measured using a HPGe detector (ORTEC GEM70200-p). This detector showed a relative efficiency of 55.2% at 1333 keV and an impressive energy resolution of 5.99 keV at 1333 keV (0.45%). To minimize background interference, 10 cm thick lead shields were employed to ensure low background counts (less than 5 cps) within a range of 60 keV to 3000 keV.
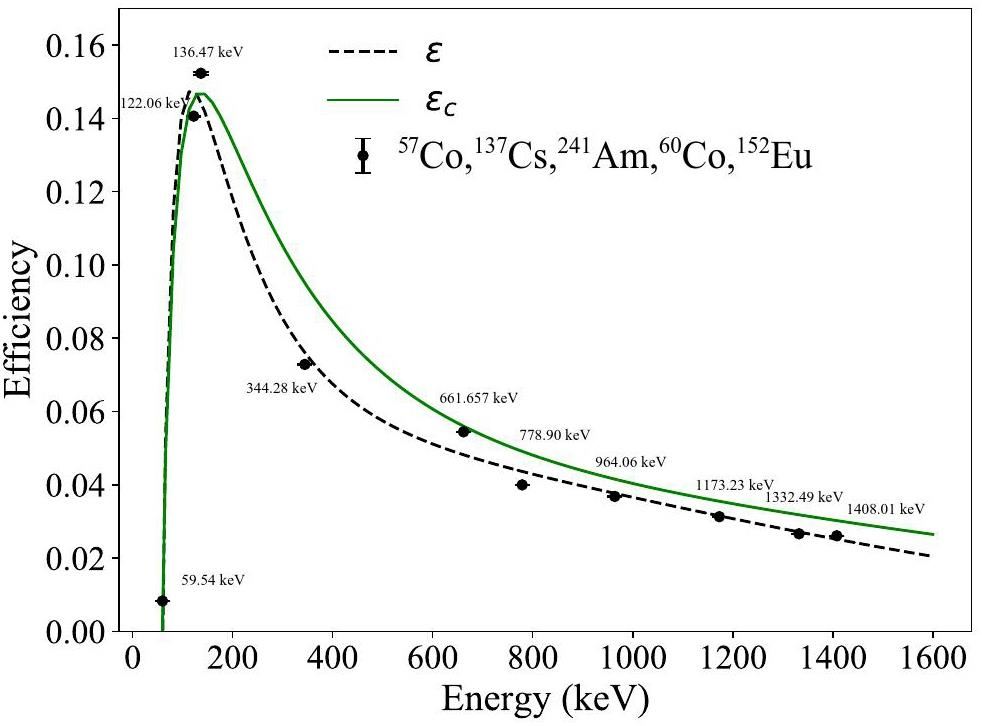
Calibration of the HPGe detector efficiency was meticulously carried out using standard gamma sources, including 152Eu (24.5 kBq), 137Cs (8.177 kBq), 57Co (80.73 kBq), and 241Am (6.516 kBq). The absolute efficiency (η) of the gamma source positioned at an identical distance from the HPGe detector was determined using Eq. (1). This rigorous calibration ensured the accurate and reliable measurement of the activity of the irradiated target.
The fitted curves of the interpolated and measured detector efficiencies are shown in Fig. 3. ϵ is the efficiency curve obtained from the experimental data, and ϵc is the correction efficiency for summing the coincidence effects. Furthermore, the correction for the summing coincidence effects was accomplished through a Geant4 simulation [29], to ensure accurate corrections and enhance the reliability of the calibration process.
Activation Data Analysis
Gold, a commonly utilized activated material, was selected for comparison with zinc, a short-lived activated material. In this study, the γ-ray beam flux extracted from the 197Au(γ, n)196Au and 64Zn(γ, n)63Zn reactions was meticulously measured. The measurements spanned from 102° (13.16 MeV) to 139° (19.08 MeV), providing valuable insights into the beam flux characteristics.
Calculation of the γ-ray beam flux
The γ-ray beam flux ϕ(t) was determined using Eq. (3).
The self-attenuation coefficients (fs) owing to the interactions of the γ-rays within the sample thickness are given by Eq. 8. μ is the attenuation coefficient obtained from NIST [30], and t is the mass thickness.
Target material for activation
The 197Au(γ, n)196Au and 64Zn(γ, n)63Zu reactions were specifically chosen to monitor the γ-ray beam flux at the SLEGS. The single-neutron separation energies for 197Au and 64Zn are 8.073 MeV and 11.86 MeV, respectively. Consequently, for these reactions, the γ-ray beam flux can be effectively monitored within the energy ranges of 8.07-21.00 MeV and 11.96-25.00 MeV, respectively, ensuring comprehensive coverage across the desired γ-ray beam energies. They exhibited a broader monitoring energy range, and the giant resonance excitation functions for these reactions are shown in Figs. 4(a) and (b). This presentation encompasses previously reported experimental data from the EXFOR experimental database and evaluated cross-sectional data from the ENDF/B-VIII.0 and IAEA/PD-2019 libraries. Owing to their substantial cross sections, these reactions facilitated short activation times, making them versatile for a variety of experiments. The half-lives of 196gAu and 63Zn were 6.1669 days and 38.47 minutes, respectively.
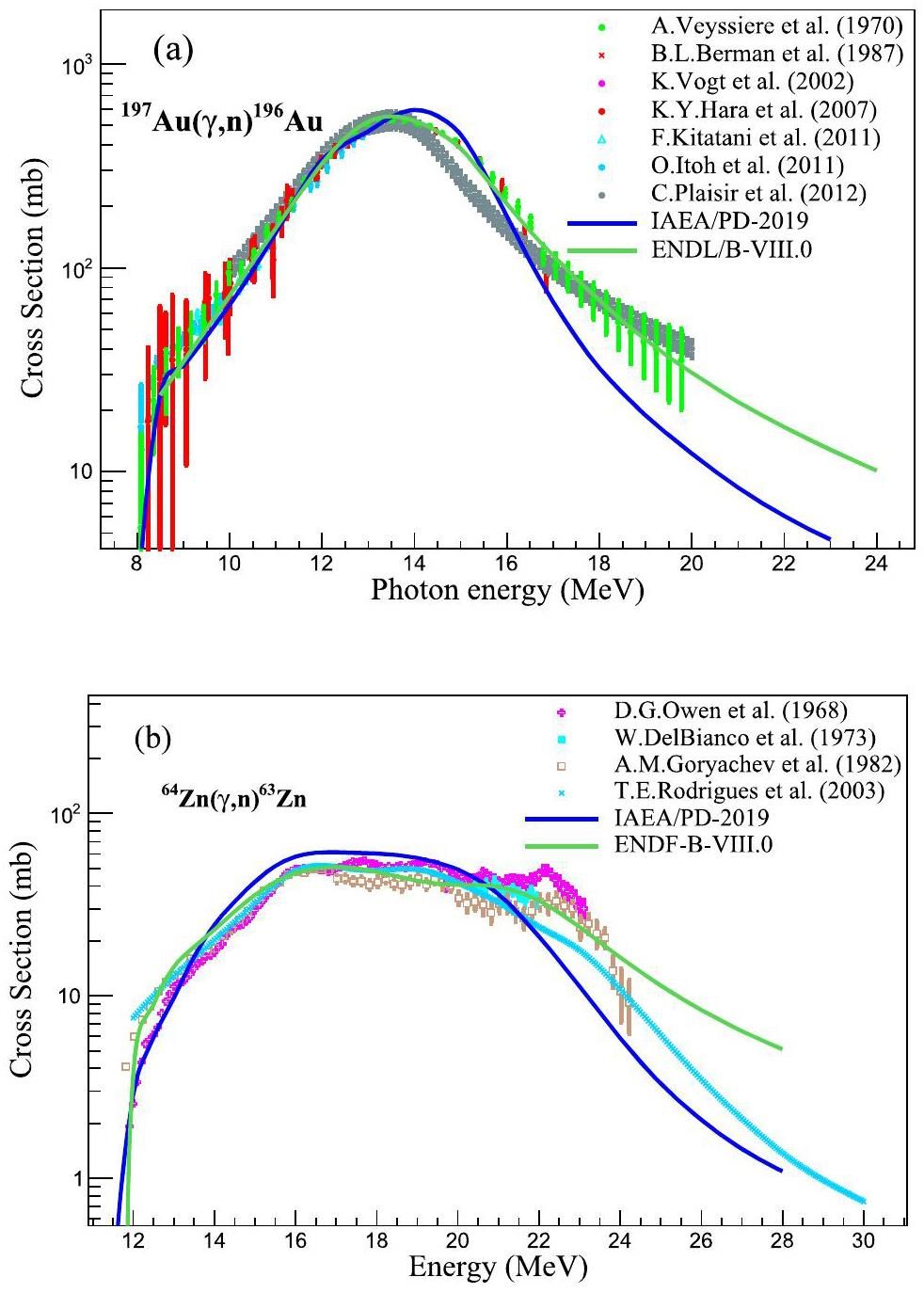
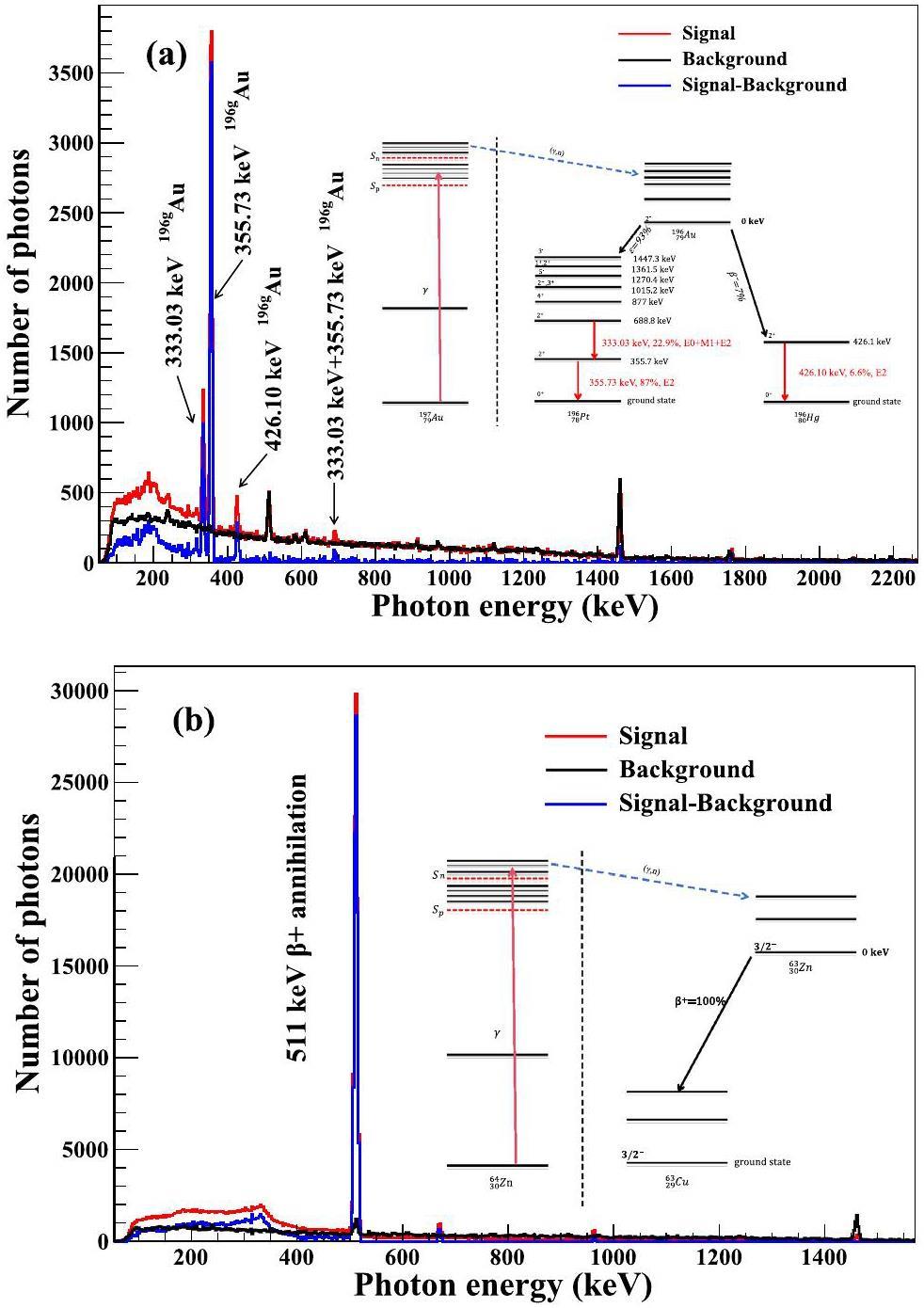
Fig. 5 shows the level scheme of 196gAu and 63Zn decays, along with the characteristic γ-ray energies and intensities associated with each. The relative nuclear spectroscopic data were sourced from the NuDat 3.0 database [31]. In addition to their utility in experimental settings, both reactions were well suited for offline measurements.
The beam-flux activation monitor utilized a natural gold target (197Au 100%) with a purity of 99.99% and thickness of 0.5 mm. In addition, natural Zn targets (64Zn 49.2%, 66Zn 27.7%, 67Zn 4.0%, 68Zn 18.5%, and 70Zn 0.6%) with a purity of 99.99% and thickness of 2 mm were employed. The target had a diameter of 10 mm, which exceeded the diameter of the γ-ray beam restricted by a 3 mm coarse collimator. The target was strategically positioned on a multi-slot target holder along the beam axis and precisely placed in front of the experimental hall. The target underwent meticulous irradiation using a focused γ-ray beam. This deliberate irradiation resulted in well-controlled 197Au(γ, n)196Au and 64Zn(γ, n)63Zn reactions, which played a crucial role in the experimental procedure. The accuracy of cross-section data for nuclear reactions is crucial in beam monitoring. Experimental measurements of cross sections for the 197Au(γ, n)196gAu reaction [32–40] were conducted using γ-rays produced by several sources, including bremsstrahlung γ-rays [32, 40], positron annihilation in flight-generated quasi-monochromatic γ-rays [33, 34, 39], and LCS-generated quasi-monochromatic γ-rays [35–38]. The experimental cross-section data for the 64Zn(γ,n)63Zn reaction [41–47] were measured using monoenergetic γ-rays produced by nuclear reactions, including the 3H(p,γ)4He reaction [41, 47], the 7Li(p,γ)8Be reaction [45], and bremsstrahlung γ-rays [42–44, 46]. The IAEA provides the evaluated data for photonuclear reactions [48].
The 197Au(γ, n)196Au reaction produces unstable nuclei, such as 196mAu and 196gAu. Subsequently, 196mAu is de-excited by emitting γ-rays, leading to the formation of 196gAu. The decay of 196gAu proceeds through either electron capture (93%), yielding 196Pt, or through β- decay (7%), resulting in 196Hg. The decay profiles are shown in Fig. 5(a). Additional reaction details are summarized in Table 2.
| product nuclide | Reaction | Sn (MeV) | T1/2 | Eγ(keV) | Iγ |
|---|---|---|---|---|---|
| 196gAu | 197Au(γ, n)196Au | 8.073 | 6.1669 day | 355.73 | 0.87 |
| 63Zn | 64Zn(γ, n)63Zn | 11.86 | 38.47 min | 511.00 | 1.855 |
Characteristic γ-ray de-excitation spectrum
The γ-ray beam flux was quantified by identifying the characteristic transition peaks associated with the ground state of 196gAu, following the photon-neutron reaction with 197Au. This ground state of 196gAu has a half-life of 6.1669 days, making it a reliable marker for assessing the strength of the γ-ray beams. The irradiation, cooling, and counting times were carefully selected as ti = 0.5637 days, Tw = 2.24, and Tc=224, 309 s, respectively. Notably, the cooling time exceeded two days, ensuring 99% decay of the excited state of 196mAu (Elevel=0.5957 MeV, T1/2=9.6 hours) to reach the ground state. This meticulous time allocation enhanced the reliability and precision of the experimental measurements. Figure 5(a) shows the distinct characteristic the γ-ray transitions resulting from the irradiation of the 197Au target using a 19.08 MeV γ-ray beam. Notably, the characteristic γ-rays of 196gAu include peaks at 355.73 keV and 333.03 keV, originating from the β- decay of 196gAu, along with the peak at 426.10 keV, corresponding to the inner transition (IT) decay of 196gAu. These features contribute to a comprehensive understanding of the experimental spectra.
63Zn undergoes β+ decay, resulting in the emission of a characteristic peak at 511 keV because of the annihilation of positrons with electrons. The gamma-ray energy spectra recorded for zinc samples irradiated with 19.08 MeV photons are illustrated in Fig. 5(b). The experimental conditions included an irradiation time of ti = 2 h, cooling period of Tw = 3.1 min, and counting time of Tc = 2 h. Notably, the statistical errors associated with these measurements were all below 1%, highlighting the precision of the experimental data.
Results and discussion
The γ-ray beam flux was determined through the activation reactions 197Au(γ, n)196g+mAu and 64Zn(γ, n)63Zu, as well as by direct measurements using a LaBr3(Ce) detector. The results presented in Fig. 6, obtained from the activation reactions, exhibit excellent agreement with the LaBr3(Ce) detector and Geant4 simulation outcomes.
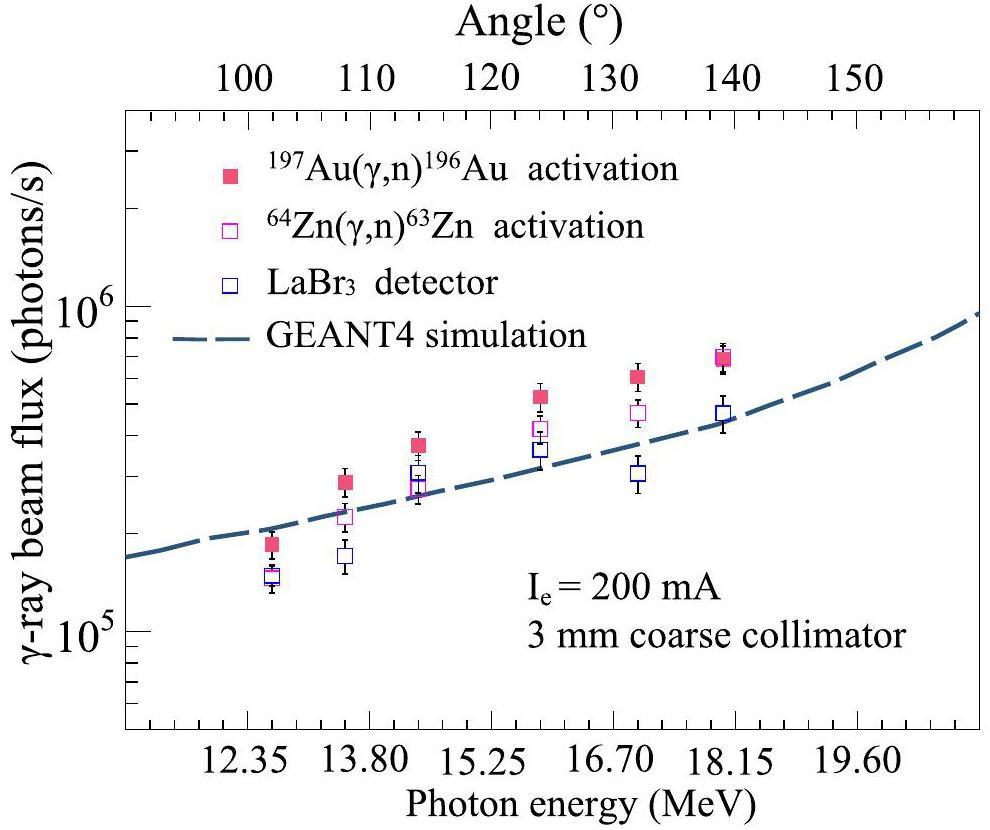
Under the conditions of a 3 mm coarse collimator aperture, the γ-ray beam flux ranged from 1.8×105 photons/s to 7×105 photons/s, depending on the collision angle between the laser and electron beam (ranging from 102° to 139°, corresponding to the γ-ray beam energies of 13.16-19.08 MeV). This substantiates the reliability and convenience of the PAA method, proving that it is as effective as classical beam-monitoring methods. When suitable short-lived target materials are utilized, this approach allows for sensitive and rapid online monitoring across different energy regions.
Direct monitoring is challenging at high γ-ray beam flux levels. In such cases, photon activation monitoring is an excellent method for flux indexing. Our group also developed a rapid monitoring method for short-lived target materials, as detailed in subsequent studies. The total uncertainties in the measured γ-ray beam flux for the 197Au(γ, n)196g+mAu and 64Zn(γ, n)63Zu reactions and LaBr3(Ce) detectors are listed in Table 3.
| Reaction | ϵλ (%) | ϵη (%) | |||
|---|---|---|---|---|---|
| 197Au(γ, n)196g+mAu | 0.69 | 0.01 | 0.71 | 0.028 | 3.71 |
| 64Zn(γ, n)63Zn | 0.72 | 0.13 | 0.05 | 0.09 | 3.71 |
The error analysis of the γ-ray beam flux measurements included several factors, including the statistical error of the characteristic γ-ray counts (
The efficiency calibration relative errors of the HPGe detector are denoted by ϵη, and the relative errors of the number of targets per unit area (
Conclusion
A flux monitoring system utilizing PAA was developed for the SLEGS. This system served as a supplementary crosschecking tool for direct measurements. The monitoring system comprised both online activation and offline low-background HPGe detector components. In this setup, natural materials such as gold and zinc were selected as the preferred target materials. This choice was based on the relatively short half-lives of 196gAu and 63Zn, which rendered them stable for use at γ-ray flux levels exceeding 105 photons/s. The chosen materials were effective within the energy range of 13.16-19.08 MeV. This system is particularly beneficial for high-flux γ-ray beam experiments.
Through this newly established flux-monitoring system, the SLEGS activity platform enhances its experimental capabilities. This enhancement makes it well-suited for conducting photoneutron cross-sectional measurements using quasi-monochromatic energy γ-ray beams.
Commissioning of laser electron gamma beamline SLEGS at SSRF
. Nucl. Sci. Tech. 33, 87 (2022). https://doi.org/10.1007/s41365-022-01076-0Simulation and test of the SLEGS TOF spectrometer at SSRF
. Nucl. Sci. Tech. 34, 47 (2023). https://doi.org/10.1007/s41365-023-01194-3An X-ray source based on Compton backscattering of laser and 100 MeV electrons
. Nucl. Instrum. Methods A 580, 1184-1190 (2007). https://doi.org/10.1016/j.nima.2007.07.007A potential photo-transmutation of fission products triggered by Compton backscattering photons
. Nucl. Instrum. Methods A 599, 118-123 (2009). https://doi.org/10.1016/j.nima.2008.10.031A high intensity beam line of gamma-rays up to 22 MeV energy based on Compton backscattering
. Nucl. Instrum. Methods A 578, 457-462 (2007). https://doi.org/10.1016/j.nima.2007.05.322Simulation study on the production of medical radioisotopes 186gRe by photonuclear reaction
. Radiat. Phys. Chem. 218,233Pa(n, γ) cross section extraction using the surrogate reaction 232Th(3He, p) 234Pa involving spin-parity distribution
. Phys. Rev. C 109,Photo-transmutation of long-lived nuclear waste 135Cs by intense Compton γ-ray source
. Ann. Nucl. Energy 89, 109-114 (2016). https://doi.org/10.1016/j.anucene.2015.11.017Photon flux monitor for a mono-energetic gamma ray source
. Nucl. Instrum. Methods A 606, 517-522 (2009). https://doi.org/10.1016/j.nima.2009.04.014Luxium solutions, formerly Saint-Gobain crystal.
, https://www.luxiumsolutions.com/news/saint-gobain-crystals-now-luxium-solutionsInvestigation of the d(γ,n)p reaction for gamma beam monitoring at ELI-NP
. J. Instrum. 11, P05025-P05025 (2016). https://doi.org/10.1088/1748-0221/11/05/P05025Photoneutron reaction cross section measurements on 94Mo and 90Zr relevant to the p-Process nucleosynthesis
. Phys. Rev. C 99,Investigation of compton scattering for gamma beam intensity measurements and perspectives at ELI-NP
. Nucl. Instrum. Methods A 921, 27-32 (2019).Monitor reactions for high energy bremsstrahlung beams
. Nucl. Instrum. Methods 93, 77-81 (1971). https://doi.org/10.1016/0029-554X(71)90140-6Cross-sections for the 27Al(γ,x)24Na multiparticle reaction at eγmax= 35-95 MeV
. Eur. Phys. J. A 57, 207 (2021). https://doi.org/10.1140/epja/s10050-021-00483-yCross section measurements of 27Al(γ, x)24Na reactions as monitors for laser-driven bremsstrahlung γ-ray
. Nucl. Phys. A 1043,Photon activation analysis
. Encyclopedia of Analytical Chemistry. https://doi.org/10.1002/9780470027318.a6211.pub2Principles, methodologies, and applications of photon activation analysis: a review
. J. Radioanal. Nucl. Ch. 312, 443-459 (2017). https://doi.org/10.1007/s10967-017-5238-6Effective extraction of photoneutron cross-section distribution using gamma activation and reaction yield ratio method
. Nucl. Sci. Tech. 34, 170 (2023). https://doi.org/10.1007/s41365-023-01330-zCollimator system of SLEGS beamline at Shanghai Light Source
. Nucl. Instrum. Methods A 1013,A new annular collimator system of SLEGS beamline at Shanghai Light Source
. Nucl. Instrum. Methods B 519, 9-14 (2022). https://doi.org/10.1016/j.nimb.2022.02.010Interaction chamber for laser compton slant-scattering in SLEGS beamline at Shanghai Light Source
. Nucl. Instrum. Methods A 1033,Interaction chamber design for an energy continuously tunable sub-MeV laser-Compton gamma-ray source
. IEEE Trans. Nucl. Sci. 63, 906-912 (2016). https://doi.org/10.1109/TNS.2015.2496256A Ge(Li) counter investigation of the γ-ray decay of 29Si produced in the reaction 27Al(p,γ)28Si
. Can. J. Phys. 44, 3075-3081 (1966). https://doi.org/10.1139/p66-253Thick-target yield of 17.6 MeV γ-ray from the resonant reaction 7Li(p,γ)8Be at Ep = 441 keV
. Nucl. Instrum. Methods B 529, 56-60 (2022). https://doi.org/10.1016/j.nimb.2022.08.005Study on γ-ray source from the resonant reaction 19F(p, αγ)16O at Ep = 340 keV
. Chinese Phys. B 29,New measurement of thick target yield for narrow resonance at Ex = 9.17 MeV in the 13C(p,γ)14N reaction*
. Chinese Phys. B 28,Energy profile of laser Compton slant-scattering gamma-ray beams determined by direct unfolding of total-energy responses of a BGO detector
. Nucl. Instrum. Methods A 1063,Summing coincidence correction for γ-ray measurements using the hpge detector with a low background shielding system
. Nucl. Instrum. Methods A 880, 22-27 (2018). https://doi.org/10.1016/j.nima.2017.09.043X-ray mass attenuation coefficients: Tables of X-ray mass attenuation coefficients and mass energy-absorption coefficients from 1 keV to 20 MeV for elements Z = 1 to 92 and 48 additional substances of dosimetric interest
. NIST Standard Reference Database 126. https://doi.org/10.18434/T4D01FNational nuclear data center NuDat 3.0.
, https://www.nndc.bnl.gov/nudat3/Measurement of the 85Rb(γ, n)84mRb cross-section in the energy range 10-19 MeV with bremsstrahlung photons
. Eur. Phys. J. A 48, 68 (2012). https://doi.org/10.1140/epja/i2012-12068-7Absolute photoneutron cross sections for Zr, I, Pr, Au, and Pb
. Phys. Rev. C 36, 1286-1292 (1987). https://doi.org/10.1103/PhysRevC.36.1286Photoneutron cross-section measurements on gold using nearly monochromatic photons
. Phys. Rev. 127, 1273-1279 (1962). https://doi.org/10.1103/PhysRev.127.1273Measurements of the 152Sm(γ,n) cross section with laser-compton scattering γ rays and the photon difference method
. J. Nucl. Sci. Technol. 44, 938-945 (2007). https://doi.org/10.1080/18811248.2007.9711333Photoneutron cross sections for au revisited: Measurements with laser compton scattering γ-rays and data reduction by a least-squares method
. J. Nucl. Sci. Technol. 48, 834-840 (2011). https://doi.org/10.1080/18811248.2011.9711766Measurement of 76Se and 78Se (γ, n) cross sections
. J. Nucl. Sci. Technol. 48, 1017-1024 (2011). https://doi.org/10.1080/18811248.2011.9711787Measurement of the 80Se(γ, n) cross section using laser-compton scattering γ-rays
. J. Nucl. Sci. Technol. 47, 367-375 (2010). https://doi.org/10.1080/18811248.2010.9711967Photoneutron cross sections of 208 Pb and 197 Au
. Nucl. Phys. A 159, 561-576 (1970). https://doi.org/10.1016/0375-9474(70)90727-XMeasurement of the (γ, n) cross section of the nucleus 197Au close above the reaction threshold
. Nucl. Phys. A 707, 241-252 (2002). https://doi.org/10.1016/S0375-9474(02)00922-364Zn(γ,n)63Zn cross section from 20.4 to 21.9 MeV
. Can. J. Phys. 51, 1302-1303 (1973). https://doi.org/10.1139/p73-173Statistical and direct aspects of decay channels in the giant dipole resonance and quasideuteron energy regions
. Phys. Rev. C 68,Photonuclear production of the medical isotope 67Cu
. Nucl. Instrum. Methods B 498, 48-51 (2021). https://doi.org/10.1016/j.nimb.2021.04.016The studying of the photoneutron reactions cross sections in the region of the giant dipole resonance in zinc, germanium, selenium, and strontium isotopes
. Voprosy Teoreticheskoy i Yadernoy Fiziki 8, (1982).Absolute Cross Sections of the (γ, n) Reaction for 63Cu, 64Zn and 109Ag
. J. Phys. Soc. Jpn. 14, 693-698 (1959). https://doi.org/10.1143/JPSJ.14.693Structure in the giant resonance of 64Zn and 63Cu
. Nucl. Phys. A 122, 177-183 (1968). https://doi.org/10.1016/0375-9474(68)90711-2Photonuclear activation by 20.5-MeV gamma rays
. Phys. Rev. 126, 709-717 (1962). https://doi.org/10.1103/PhysRev.126.709IAEA Photonuclear Data Library 2019
. Nucl. Data Sheets 163, 109-162 (2020). https://doi.org/10.1016/j.nds.2019.12.002Nuclear Data Sheets for A = 196
. Nucl. Data Sheets 108, 1093-1286 (2007). https://doi.org/10.1016/j.nds.2007.05.001Hong-Wei Wang is an editorial board member for Nuclear Science and Techniques and was not involved in the editorial review, or the decision to publish this article. All authors declare that there are no competing interests.


