Study of the momentum correlation of nucleons in 4496Ru + 4496Ru and 4096Zr + 4096Zr collisions at sNN=7.7 and 200 GeV from a multiphase transport model

NUCLEAR PHYSICS AND INTERDISCIPLINARY RESEARCH

Study of the momentum correlation of nucleons in $_{44}^{96} Ru$ + $_{44}^{96} Ru$ and $_{40}^{96} Zr$ + $_{40}^{96} Zr$ collisions at $\sqrt{s_{NN}} = 7.7$ and 200 GeV from a multiphase transport model

Bao-Shan Xi，

Jin-Hui Chen，

Long Ma ，

Yu-Gang Ma ，

Ting-Ting Wang

Nuclear Science and Techniques

Vol.36, No.12

Article number 228

Published in print Dec 2025

Available online 29 Sep 2025

DOI：10.1007/s41365-025-01826-w

CSTR：32136.14.NST.2025.12228

29208

By using A MultiPhase Transport (AMPT) model in the string melting scenario, the influences of nuclear structure on the momentum correlation functions between nucleons in the isobaric collisions of $_{44}^{96} Ru$ + $_{44}^{96} Ru$ and $_{40}^{96} Zr$ + $_{40}^{96} Zr$ at $\sqrt{s_{NN}} = 7.7$ and 200 GeV were investigated. The results, including the centrality dependence of the correlation functions, were compared across different parameterizations of the Woods-Saxon distribution corresponding to varying deformation configurations in the simulation. A maximum difference of 4% was observed between the isobaric systems for the proton-proton correlation functions when including quadrupole (β₂) and octupole (β₃) deformation. In peripheral collisions, the Ru + Ru and Zr + Zr systems exhibited maximum differences of 4% and 5%, respectively, when comparing different parametrization cases. Furthermore, neutron-proton correlation has been studied, showing a sensitivity to nuclear structure comparable to proton-proton correlations. Our results indicate that in peripheral collisions, there may be measurable effects of momentum correlation functions from nuclear deformation and neutron skin in high-precision experimental data, whereas in central collisions, both effects may show negligible influence on momentum correlation functions.

Momentum correlationNuclear deformationHeavy-ion collision

Introduction

Relativistic heavy-ion collisions provide a unique laboratory for studying quantum chromodynamics (QCD) under extreme conditions, including the formation of quark-gluon plasma (QGP) [1]. Extensive studies have been conducted at both RHIC and LHC energies across various collision systems to investigate the properties of the QGP matter [2-7]. Among various collision systems, isobaric collisions, such as $_{44}^{96} Ru$ + $_{44}^{96} Ru$ and $_{40}^{96} Zr$ + $_{40}^{96} Zr$ , proposed experimentally for the search of the anomalous phenomenon of the chiral magnetic effect (CME), also offer an effective tool for investigating the influence of the initial nuclear structure on final-state observables, such as anisotropic flow [8-10]. The upgrade of detectors also provides new avenues for exploring the CME [11-13]. These collision systems have identical mass numbers, but differ in nuclear deformation and density distributions, making them ideal for isolating deformation effects from other variables [14-19]. Notably, Ru nuclei exhibit quadrupole deformation, whereas Zr nuclei display octupole deformation. By comparing these systems, researchers can disentangle the initial-state geometry from medium-induced effects, offering deeper insights into the QGP properties as well as the nuclear structure [20, 21]. As recently reported in the results of the STAR experiment, differences were observed in the elliptic flow coefficient (v₂) and triangular flow coefficient (v₃) ratios between the two isobaric collision systems at $\sqrt{s_{NN}} = 200$ GeV, revealing the nuclear structure effects on source collectivity [8].

The two-particle momentum correlation function, known as femtoscopy, originating from Hanbury-Brown Twiss (HBT) interferometry [22], is a powerful tool for accessing the expanding source dynamics of heavy-ion physics [23-27]. Femtoscopy in relativistic heavy-ion collisions extracts space-time information about particle emission sources and probes collision dynamics. Studies have been performed on the momentum correlation of various particle species, including mesons, nucleons, light charged particles, and even antiprotons, revealing details about source size and interaction mechanisms [28]. At LHC energies, the ALICE Collaboration precisely measured the initial energy density, effective temperature, system size, lifetime, and interactions between various hadron pairs via femtoscopy, extracted the scattering parameters, and demonstrated the feasibility of detecting three-body correlations [5, 29, 30]. Notably, momentum correlations have confirmed charge-parity-time (CPT) symmetry in proton-proton and antiproton-antiproton interactions [31]. Recent advances have extended the femtoscopy studies to exotic systems, including strange hadrons (e.g., Ω and ∑ hyperons), charm hadrons (e.g. D mesons), light nuclei (e.g., deuterons, tritons), and test predictions from lattice QCD and chiral effective field theory [32-34]. Measurements have been performed for the correlations between Λ-Λ, p-Λ and p-Ω, particularly for the study of hyperon-hyperon and hyperon-nucleon interaction in dense matter [35-41]. Momentum correlation studies have also been conducted for proton-deuteron and deuteron-deuteron systems, with the scattering parameters measured, offering valuable insights into strong interactions in exotic nuclear systems [42, 43]. In addition to heavy-ion collisions, analyses have been extended to smaller collision systems with further constraints on the dynamics of particle production during high-energy collisions [44-46].

In this study, we explore the effects of nuclear structure on the momentum correlation of nucleons in isobar collisions by considering the different deformation configurations of Ru and Zr nuclei. In contrast to femtoscopy studies in non-deformed nuclear systems (e.g. Au+Au and Pb+Pb), the distinct deformation profiles of Ru (quadrupole) and Zr (octupole) nuclei in isobaric collisions introduce differences in the initial-state geometry. In addition, different nuclear deformation parameters correspond to different neutron skin thicknesses. Because two-particle correlations are sensitive to source size, comparing Ru + Ru and Zr + Zr systems can reveal how nuclear deformation affects particle emission dynamics and final-state momentum correlation, which may offer an appropriate way to explore the interplay between nuclear deformation and collective dynamics inside the QGP.

This paper is organized as follows: In Sect. 2, a multiphase transport model is described, and different cases of the Woods-Saxon parameters for Ru and Zr are introduced. In Sect. 3, the results of the momentum correlation functions of nucleon pairs for different isobaric deformation configurations are discussed. In Sect. 4, a brief summary will be given.

Model and Methodology

2.1

The AMPT model

A multiphase transport model [47, 48] has been applied extensively and successfully to study heavy-ion collisions at relativistic energies [49-54]. In the string melting version of the model, the initial state phase space information of partons considering fluctuating initial conditions is generated by the heavy ion jet interaction generator (HIJING) model, where minijet partons and excited strings are produced by hard and soft processes, respectively [55]. To study the collisions of deformed nuclei, we altered the nucleon distribution, which is discussed in more detail in Sect. 2.2. The interaction between partons is then simulated by Zhang’s parton cascade (ZPC) model which includes only two-body parton elastic scatterings [56]. During the hadronization process, a quark coalescence model was used to combine partons into hadrons. Then, the final-state hadronic evolution is described by a relativistic transport (ART) model that considers baryon-baryon, baryon-meson, and meson-meson elastic and inelastic scatterings, as well as resonance decay processes [57].

2.2

The nuclear deformation configuration

In AMPT, the default spatial distribution of nucleons in the nucleus rest frame is given by Woods-Saxon (WS) distribution, defined as follows [15, 58-60]: $ρ (r, θ) = \frac{ρ_{0}}{1 + \exp [\frac{r - R_{0} [1 + β_{2} Y_{2}^{0} (θ) + β_{3} Y_{3}^{0} (θ)]}{a}]},$ (1) where r and θ denote radial position and polar angles of nucleons, respectively. The parameters R₀ and "a" denote "radius" and the surface diffuseness parameter of the nucleus, respectively, both of which influence the initial overlap area of the collision [14, 61]. ρ₀ is the nuclear density normalization factor, determined by nucleon number A.

The quadrupole deformation parameter β₂ and the octupole deformation parameter β₃ describe the deformation of the nucleus from a spherical shape. These parameters have been widely used in recent studies [15, 58, 62-65].

In this study, we investigated the influence of the nuclear structure on the nucleon momentum correlations in relativistic isobar collisions (Ru + Ru and Zr + Zr). Because the Woods-Saxon parameters for these two isobaric systems have not been determined, we explored four cases of parameter sets in our study, as shown in Table 1 [15, 62, 64, 66-68]. Case 1 is without deformation, and values of R₀ and "a" for Ru and Zr are set to be the same, while in case 2, Ru (β₂ = 0.13) has a bigger quadrupole deformation than Zr (β₂ = 0.06). Case 3 is based on calculations using the energy density functional theory (DFT), which also assumes that the nuclei are spherical. The differences in R₀ and "a" between Zr and Ru result in a thicker neutron skin for Zr. Case 4 also includes the deformation effect and neutron skin effect. In this study, the distribution of nucleons (protons and neutrons) inside the nuclei was initialized according to Eq. (1) based on the nuclear matter density configuration.

The Woods-Saxon parameters used for the Ru and Zr nuclei in the AMPT model

Nucleus	Ru				Zr
Para.	R₀ (fm)	a (fm)	β₂	β₃	R₀ (fm)	a (fm)	β₂	β₃
Case 1	5.096	0.540	0	0	5.096	0.540	0	0
Case 2	5.13	0.46	0.13	0	5.06	0.46	0.06	0
Case 3	5.067	0.5	0	0	4.965	0.556	0	0
Case 4	5.09	0.46	0.162	0	5.02	0.52	0.06	0.20

In the AMPT model, the shape of the initial geometry produced by collisions is primarily determined by the collision event impact parameter "b" and nuclear structure parameters. To facilitate an experimental comparison, we divided the centrality classes based on the number of final-state charged particles with pseudorapidity |η| < 0.5, instead of directly using the impact parameter. The charged-particle multiplicity distributions of the four cases of the Woods-Saxon parameterization for Ru + Ru and Zr + Zr collisions at $\sqrt{s_{NN}} = 200$ GeV are shown in Fig. 1. Similar distributions with tiny differences across all four cases were also observed for isobaric collisions at $\sqrt{s_{NN}} = 7.7$ GeV. The multiplicity intervals corresponding to different centrality classes in Ru + Ru and Zr + Zr collisions at $\sqrt{s_{NN}} = 7.7$ GeV and 200 GeV are presented in Table 2. By comparing the multiplicity distribution of various collision systems with different Woods-Saxon configurations, we note that the effect of the nuclear deformation parameters on the multiplicity distribution is small.

Fig. 1

(Color online) Charged-particle multiplicity distribution in mid-rapidity for Ru + Ru and Zr + Zr collisions at

\sqrt{s_{NN}} = 200

GeV. Results are compared for four different parameterization cases, shown in distinct colors

Centrality defintion based on charged-particle multiplicity

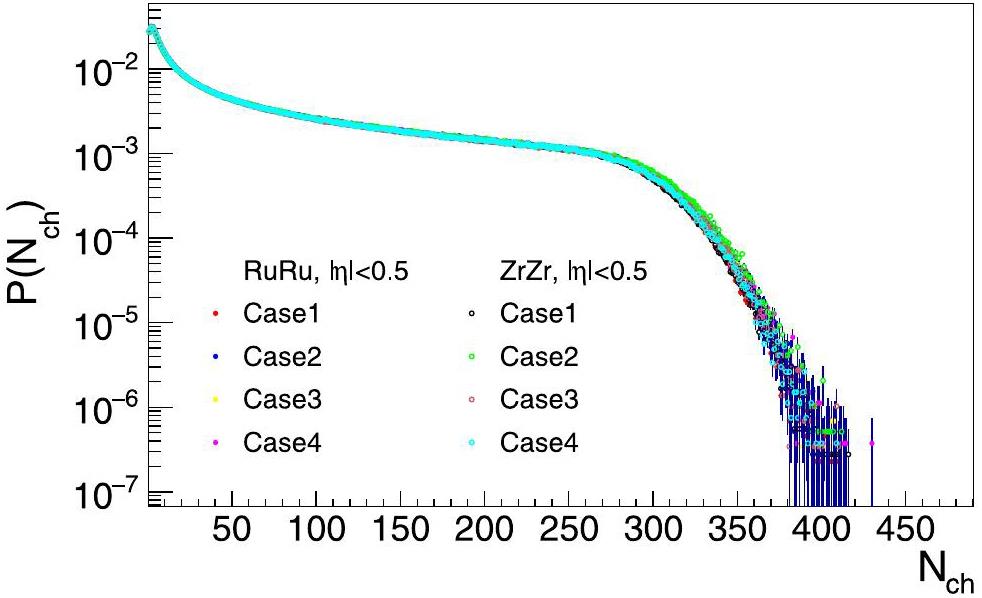
	Multiplicity cut (>)
	Ru + Ru				Zr + Zr
7.7 GeV	Case 1	Case 2	Case 3	Case 4	Case 1	Case 2	Case 3	Case 4
0% – 20%	61	62	62	62	61	62	61	61
20% – 40%	31	33	32	33	31	33	32	32
40% – 60%	14	15	15	15	14	15	14	15
60% – 80%	6	6	6	6	6	6	6	6
200 GeV	Case 1	Case 2	Case 3	Case 4	Case 1	Case 2	Case 3	Case 4
0% – 20%	150	154	153	154	150	155	151	151
20% – 40%	69	73	71	73	69	73	69	70
40% – 60%	28	29	29	29	28	29	27	28
60% – 80%	10	10	10	10	10	10	9	10

2.3

Correlation function

The Lednický-Lyuboshitz method [69-72] was used to calculate the momentum correlation function. Firstly, the s-wave scattering amplitude for proton-proton (p-p) pair is obtained by $f_{p - p}^{S} (k^{*}) = {[\frac{1}{f_{0}^{S}} + \frac{1}{2} d_{0}^{S} k^{* 2} - \frac{2}{a_{c}} h (k^{*} a_{c}) - i k^{*} A_{c} (η)]}^{- 1},$ (2) where $k^{*} = | k^{*} |$ and $r^{*} = | r^{*} |$ represent magnitude of half of the relative momentum difference and relative position vector between the two particles in their pair rest frames, respectively. $f_{0}^{S}$ denotes the scattering length and $d_{0}^{S}$ is the effective range. These two parameters characterize strong interactions and further determine the interactions between particles [73]. The superscript S denotes the total spin, where S=0 corresponds to the singlet state, and S=1 corresponds to the triplet state. $A_{c} (η) = 2 π η {[\exp (2 π η) - 1]}^{- 1}$ denotes the Coulomb penetration factor. For the p-p pair, $η = {(k^{*} a_{c})}^{- 1}$ , where a_c=292.1 fm is the Bohr radius. $h (x) = \frac{1}{x^{2}} \sum_{n = 1}^{\infty} \frac{1}{n (n^{2} + x^{- 2})} - C + \ln | x |,$ (3) where C = 0.5772 denotes the Euler constant. Because neutrons are uncharged, there is no Coulomb interaction between the neutron and proton (n-p) pairs: $f_{n - p}^{S} (k^{*}) = {[\frac{1}{f_{0}^{S}} + \frac{1}{2} d_{0}^{S} k^{* 2} - i k^{*}]}^{- 1} .$ (4) In the following discussion, we denote $f_{p - p}^{S} (k^{*})$ and $f_{n - p}^{S} (k^{*})$ as $f^{S} (k^{*})$ . For p-p pair, the scattering length $f_{0}^{S}$ is 7.8 fm for singlet state and -5.4 fm for triplet state. Effective range parameter d₀ is 2.77 fm for singlet state and 1.7 fm for triplet state, while for n-p pair, the scattering length parameter f₀ is 23.7 fm and -5.4 fm, d₀ is 2.7 fm and 1.7 fm, for singlet and triplet state, respectively. The values of f₀ and d₀ in this study were obtained using the Lednický-Lyuboshitz method [69-72].

The equal-time reduced Bethe-Salpeter amplitude for p-p pair is calculated approximately as $\begin{matrix} ψ_{- k^{*}; p - p}^{S (+)} (r^{*}) = e^{i δ_{c}} \sqrt{A_{c} (η)} [e^{- i k^{*} \cdot r^{*}} F (- i η,1, i ξ) \\ + f^{S} (k^{*}) \frac{\tilde{G} (ρ, η)}{r^{*}}]; \end{matrix}$ (5) $\begin{matrix} ψ_{k^{*}; p - p}^{S} (r^{*}) = e^{i δ_{c}} \sqrt{A_{c} (η)} \\ \times [e^{i k^{*} \cdot r^{*}} F (- i η,1, i (ρ - k^{*} \cdot r^{*})) \\ + f^{S} (k^{*}) \frac{\tilde{G} (ρ, η)}{r^{*}}] . \end{matrix}$ (6) Here F denotes the confluent hypergeometric function, $ρ = k^{*} r^{*}$ is used to describe the phase factor of plane waves and scattered spherical waves, $ξ = k^{*} \cdot r^{*} + ρ$ and $\tilde{G} (ρ, η) = \sqrt{A_{c} (η)} (G_{0} (ρ, η) + i F_{0} (ρ, η)),$ (7) where F₀ denotes the regular s-wave Coulomb function and G₀ denotes the singlet s-wave Coulomb function [69, 74, 75].

For the n-p pair, η is set to 0, and the Coulomb wave function $\tilde{G} (ρ,0)$ degenerates into a free spherical wave eiρ. Coulomb phase shift: $e^{i δ_{c}} = e^{0} = 1$ . The forms are as follows: $ψ_{- k^{*}; n - p}^{S (+)} (r^{*}) = e^{- i k^{*} \cdot r^{*}} + f^{S} (k^{*}) \frac{e^{i ρ}}{r^{*}};$ (8) $ψ_{k^{*}; n - p}^{S} (r^{*}) = e^{i k^{*} \cdot r^{*}} + f^{S} (k^{*}) \frac{e^{i ρ}}{r^{*}} .$ (9) The forms are denoted as $ψ_{- k^{*}}^{S (+)}$ and $ψ_{k^{*}}^{S}$ . Incorporating these terms, the weight of the particle pair can be obtained as $w (k^{*}, r^{*}) = \sum_{S} R_{S} {〈 {| ψ_{- k^{*}}^{S (+)} (r^{*}) |}^{2} 〉}_{S},$ (10) assuming that particles were unpolarized. We set R₀ = 1/4 and R₁ = 3/4 for the pairs in the singlet and triplet states, respectively. Finally, for both p-p and n-p pairs, the theoretical correlation function can be written as: $C_{NN} (k^{*}) = \frac{\sum_{pairs} δ (k_{pair}^{*} - k^{*}) w (k^{*}, r^{*})}{\sum_{pairs} δ (k_{pair}^{*} - k^{*})} .$ (11) where $k_{pair}^{*}$ denotes the actual relative momentum of a real pair in its resting frame.

Results and Discussion

Based on the centrality definition and initial nuclear configuration described above, we studied the nucleon momentum correlation in the Ru and Zr collision systems.

The final-state phase space information can be obtained from the AMPT model for collisions with different deformed nuclei. We derived the correlation functions of p-p and n-p for four cases of nuclear deformation in different centrality classes in isobaric collisions at $\sqrt{s_{NN}} = 7.7$ and 200 GeV. For the protons and neutrons selected for pair correlation, a fundamental particle cut criterion (|p_T| > 0.2 GeV/c, |η| < 1.0 and p < 10 GeV/c) was applied.

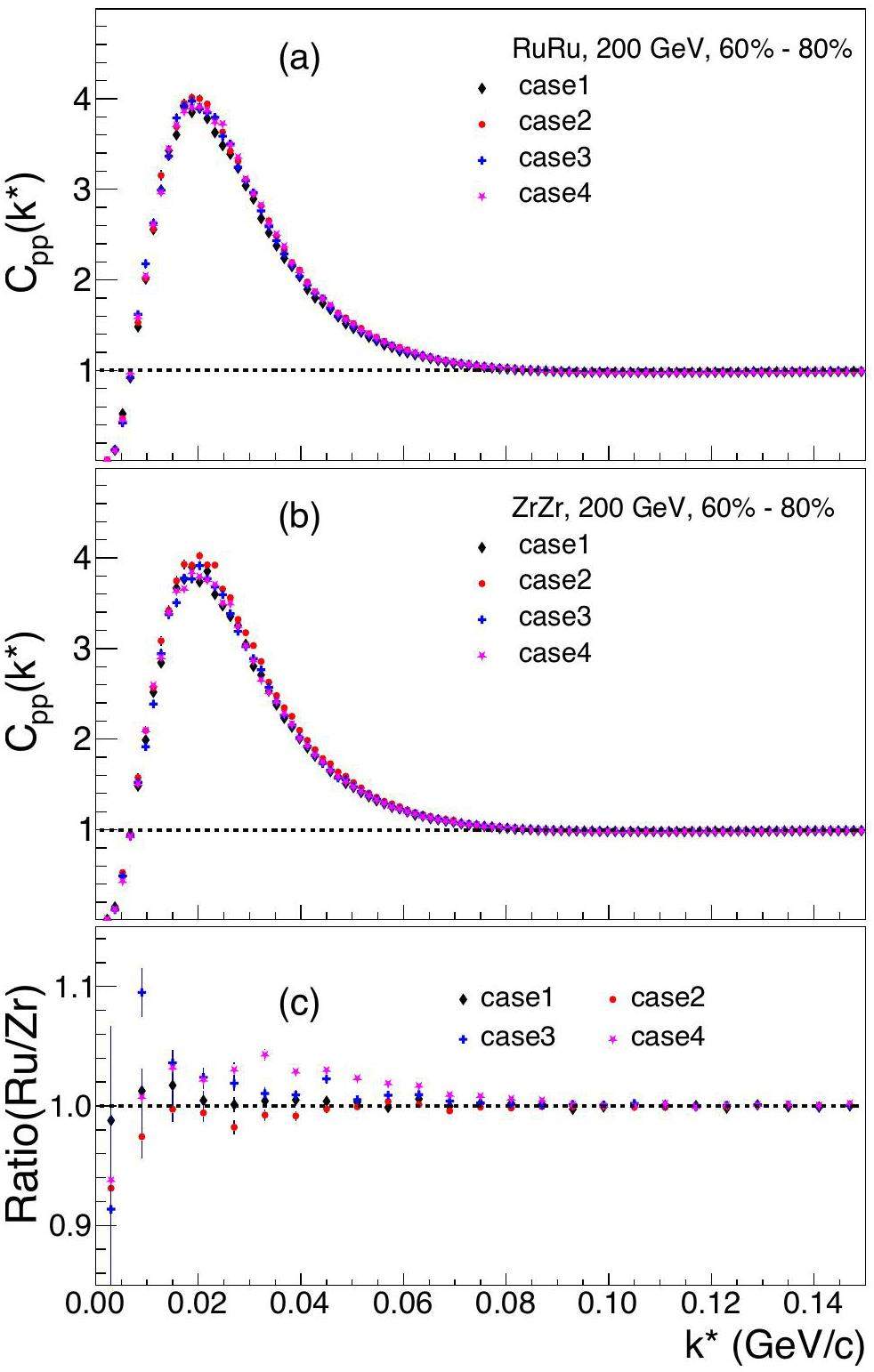
Figure 2 shows the AMPT results of the p-p correlation functions for Ru + Ru and Zr + Zr collisions at $\sqrt{s_{NN}} = 7.7$ GeV. The data points in different colors represent the results of the isobaric system with different deformation cases at a centrality of 0–20%. It can be seen that the differences between the correlation functions across collision systems and deformation parameters are very small. As the correlation function is highly sensitive to the fireball radius, the observed small differences in the correlation functions could be attributed to the relatively small deformation coefficients and neutron skin differences between the isobaric systems, which induce tiny variations in the initial-state geometry, and consequently, the fireball size. It is also possible that the correlation function itself is insensitive to nuclear deformation.

Fig. 2

Proton-proton correlation function for 0–20% central Ru + Ru (Panel a) and Zr + Zr (Panel b) collisions. Panel (c) shows the ratio between the two systems (Ru/Zr) for four different cases of Woods-Saxon parametrization as shown in Table 1

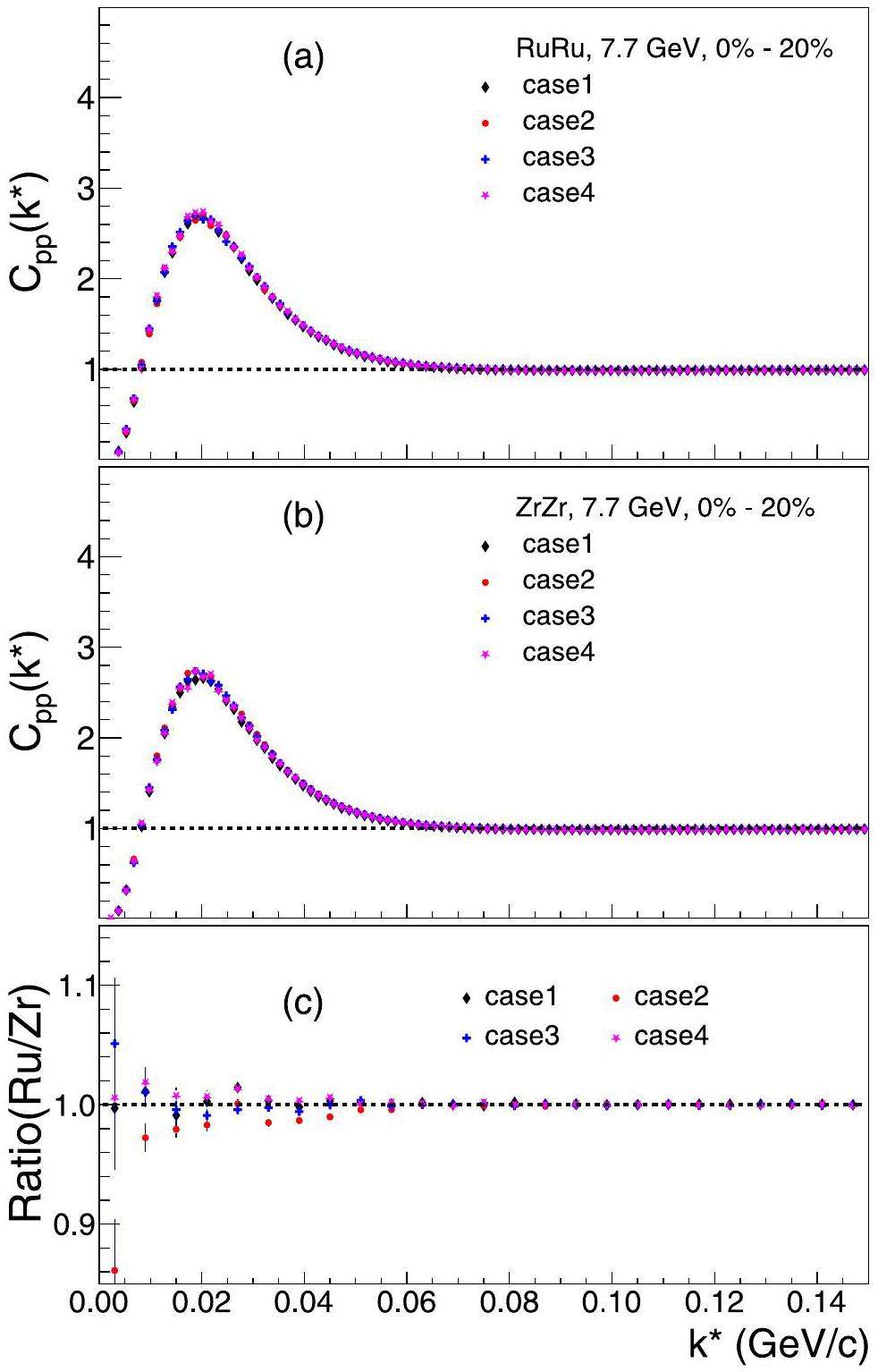
In panel (c) of Fig. 2, the ratios of the correlation functions are calculated for each deformation parameterization case, allowing for a quantitative study of the initial-state effects on the two collision systems. It can be seen that in Case 1, the parameters of both systems are identical. Despite the difference in the number of nuclear charges between the two systems, little difference is observed between the correlation functions. Case 3 does not involve a nuclear shape change but incorporates the neutron skin effect. Our results demonstrate that the neutron skin effect caused by different density distributions of protons and neutrons might have a negligible influence on the correlation function in central collisions, consistent with the understanding that neutron skin effects are largely suppressed in central collisions, as they predominantly manifest in peripheral collisions [76].

In Case 2, the ratio of the correlation functions between the two systems for 0–20% centrality is less than 1 with a 1–2% offset in the low k^* region. As β₃ is 0 for both Ru and Zr, the relative magnitude of the correlation function is determined by the radius parameter R₀ and quadrupole deformation parameter β₂. In contrast, the ratio results of Case 4 are slightly larger than 1, with a relative difference of ∼ 1%, indicating that β₃ may have a potential influence on the correlation results. The ratios of these four cases are generally consistent with 1 at large k^* (>0.05 GeV/c), indicating that the effects of nuclear deformation are negligible in this region.

Figure 3 shows the results of the correlation functions for four different cases of deformation configuration in Ru + Ru (Panel a) and Zr + Zr (Panel b) collisions at $\sqrt{s_{NN}} = 7.7$ GeV in centrality class 60–80%. Since the fireball size in peripheral collisions is smaller than central collisions, their correlation signal intensities are generally stronger than those in central collisions. For the ratios of the two systems presented in Panel (c), it is evident that within the k^* interval of 0.01–0.08 GeV/c, the ratio is less than 1 for Case 2, whereas it exceeds 1 for the other three cases. The results of Case 1 show little deviation from unity within statistical uncertainties. Case 2 has a maximum deviation of 2% suggesting that a smaller deformation induces a stronger correlation, while Case 3, which includes differences in the nuclear skin and size between the isobar nuclei, also shows a maximum deviation of 2%, indicating that a thinner neutron skin induces a stronger correlation. A larger deviation from unity, reaching up to 4%, was observed in Case 4, suggesting that the deformation parameter β₃ may have sizable effects on the correlation functions in peripheral collisions. By comparing the results with those of the 0–20% central collisions, a centrality dependence was revealed, with the deviation value increasing from central to peripheral collisions.

Fig. 3

Proton-proton correlation function for 60–80% central Ru + Ru (Panel a) and Zr + Zr (Panel b) collisions at center-of-mass energy

\sqrt{s_{NN}} = 7.7

GeV. Panel (c) shows the results of the ratio (Ru/Zr) for different nuclear deformation configurations

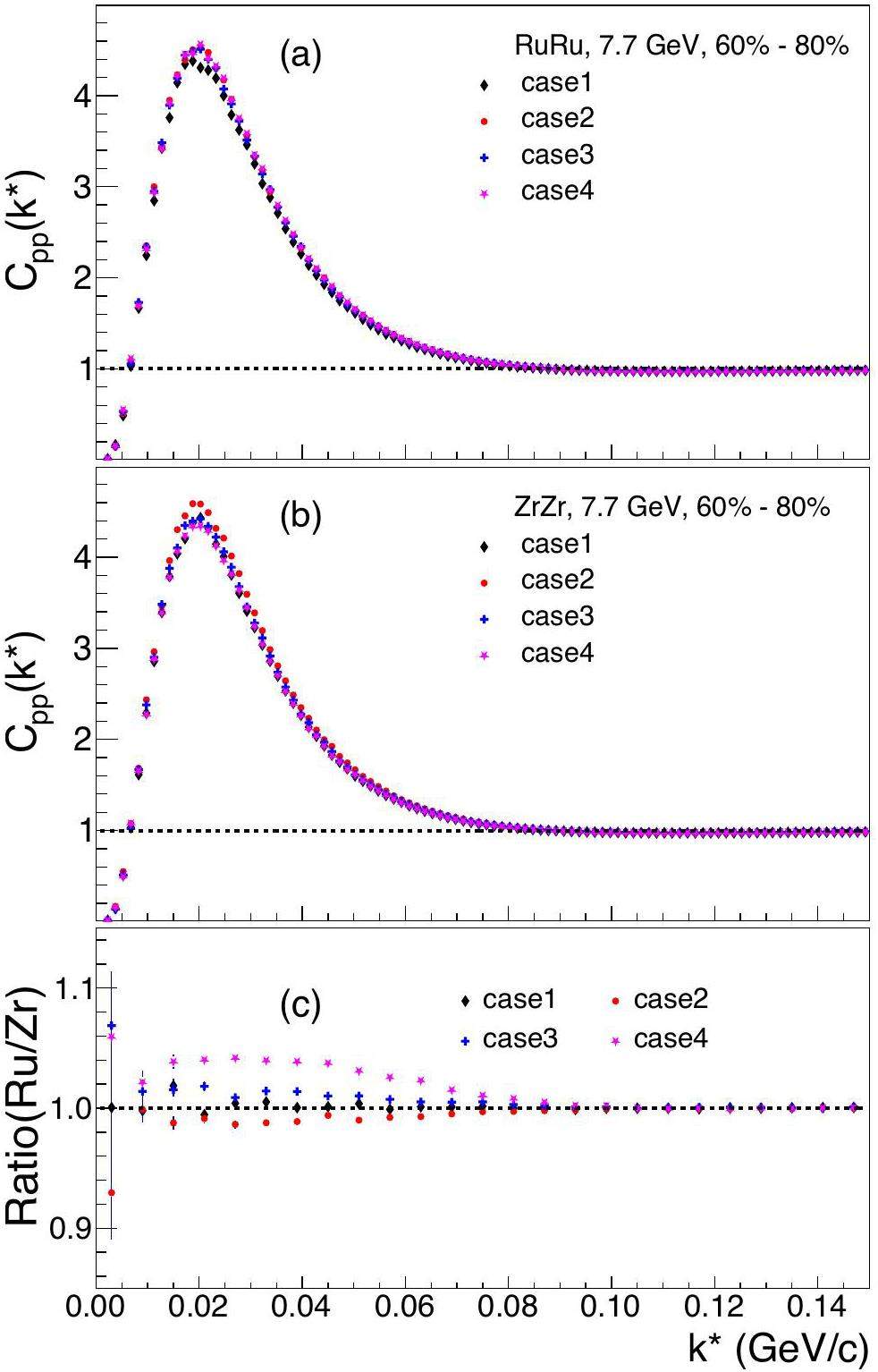
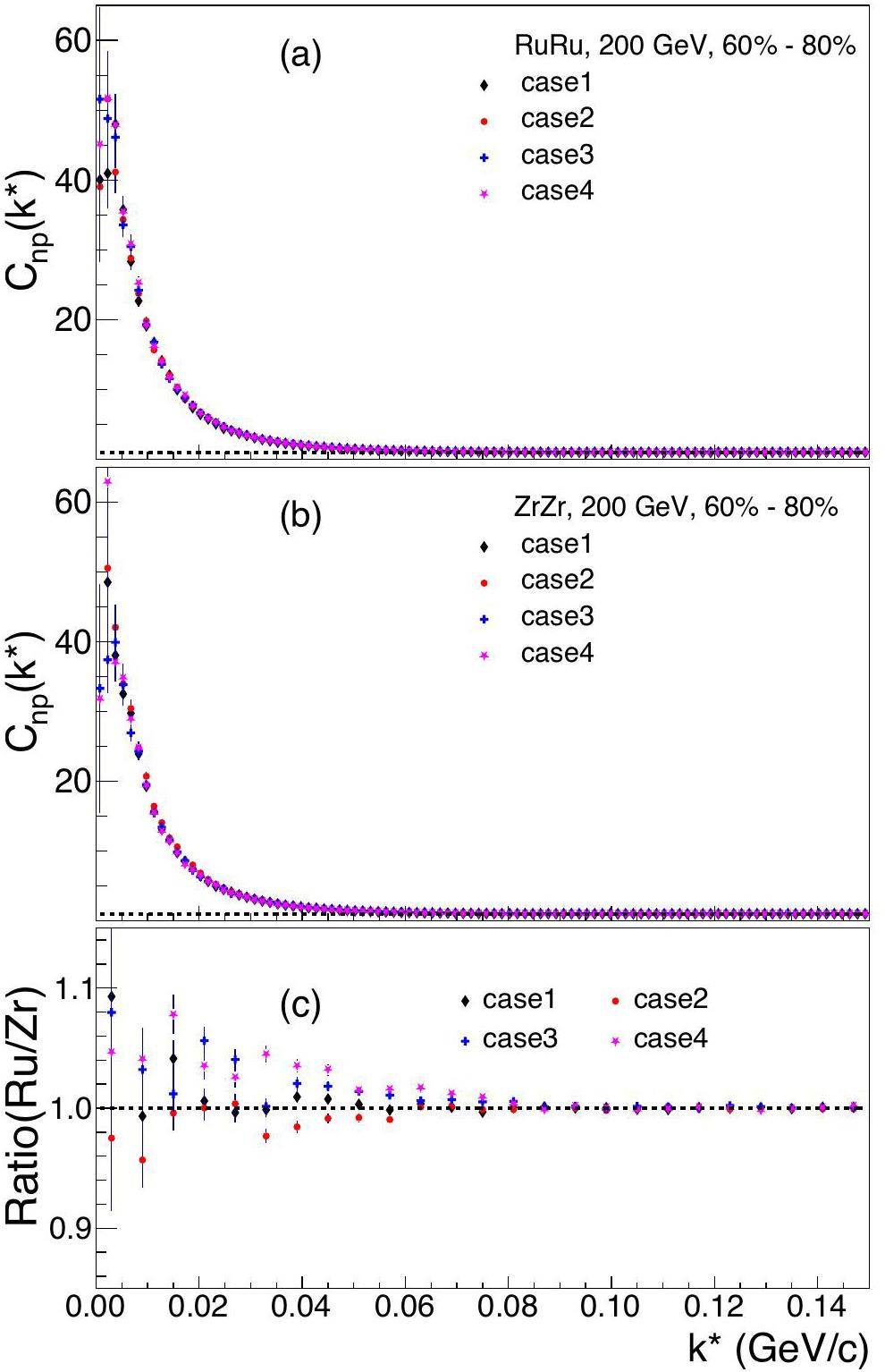
Figures 4 and 5 show the results of central and peripheral collisions at $\sqrt{s_{NN}} = 200$ GeV for four cases of Woods-Saxon parametrization of Ru + Ru and Zr + Zr collisions. Because the source size at $\sqrt{s_{NN}} = 200$ GeV collisions is expected to be larger than that at $\sqrt{s_{NN}} = 7.7$ GeV collisions, the correlation functions in both central and peripheral collisions are supposed to be smaller in magnitude than those at $\sqrt{s_{NN}} = 7.7$ GeV. In 0–20% central collisions, the ratios of the four cases are consistent with unity within statistical uncertainties at large k^* and show only tiny differences (<2%) at small k^*, indicating a negligible effect of the neutron skin and nuclear deformation on the correlation functions in central collisions at higher energies.

Fig. 4

Proton-proton correlation function in 0–20% central Ru + Ru (Panel a) and Zr + Zr (Panel b) collisions at

\sqrt{s_{NN}} = 200

GeV. Panel (c) shows the ratios (Ru/Zr) for various Woods-Saxon parameterization cases as shown in Table 1

Fig. 5

Proton-proton correlation function for 60–80% central Ru + Ru (Panel a) and Zr + Zr (Panel b) collisions at

\sqrt{s_{NN}} = 200

GeV. The ratios (Ru/Zr) of the correlation functions between the two systems are shown in Panel (c) for different cases

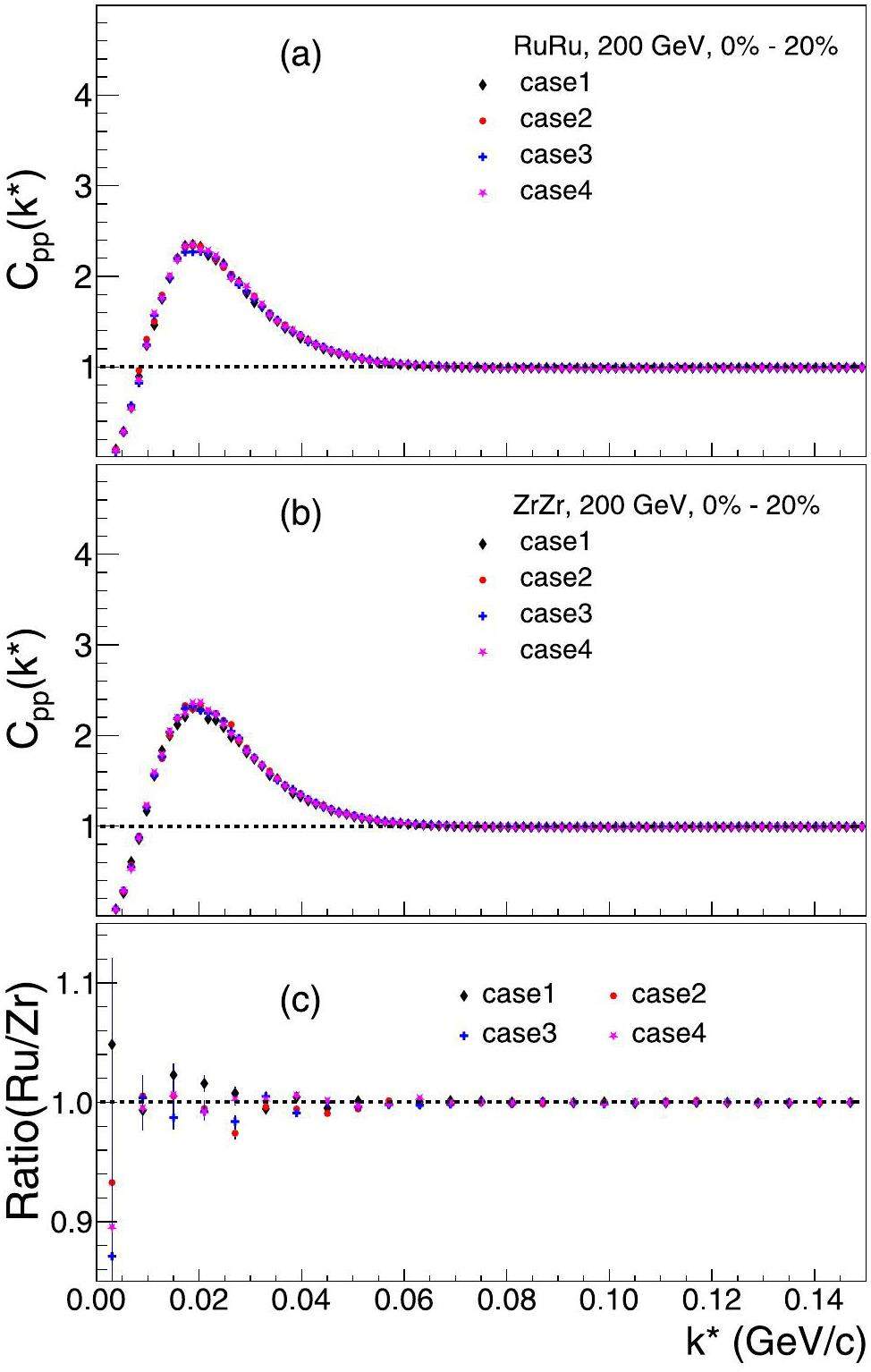
In peripheral collisions, the ratio (Ru/Zr) in Case 1 is consistent with unity. The ratios for Case 2 show deviations from unity with magnitudes similar to those at $\sqrt{s_{NN}} = 7.7$ GeV, suggesting that the energy dependence of the ratio is relatively weak. It can be seen that the differences between the two isobaric systems caused by β₂ deformation are negligible in peripheral collisions at $\sqrt{s_{NN}} = 200$ GeV.

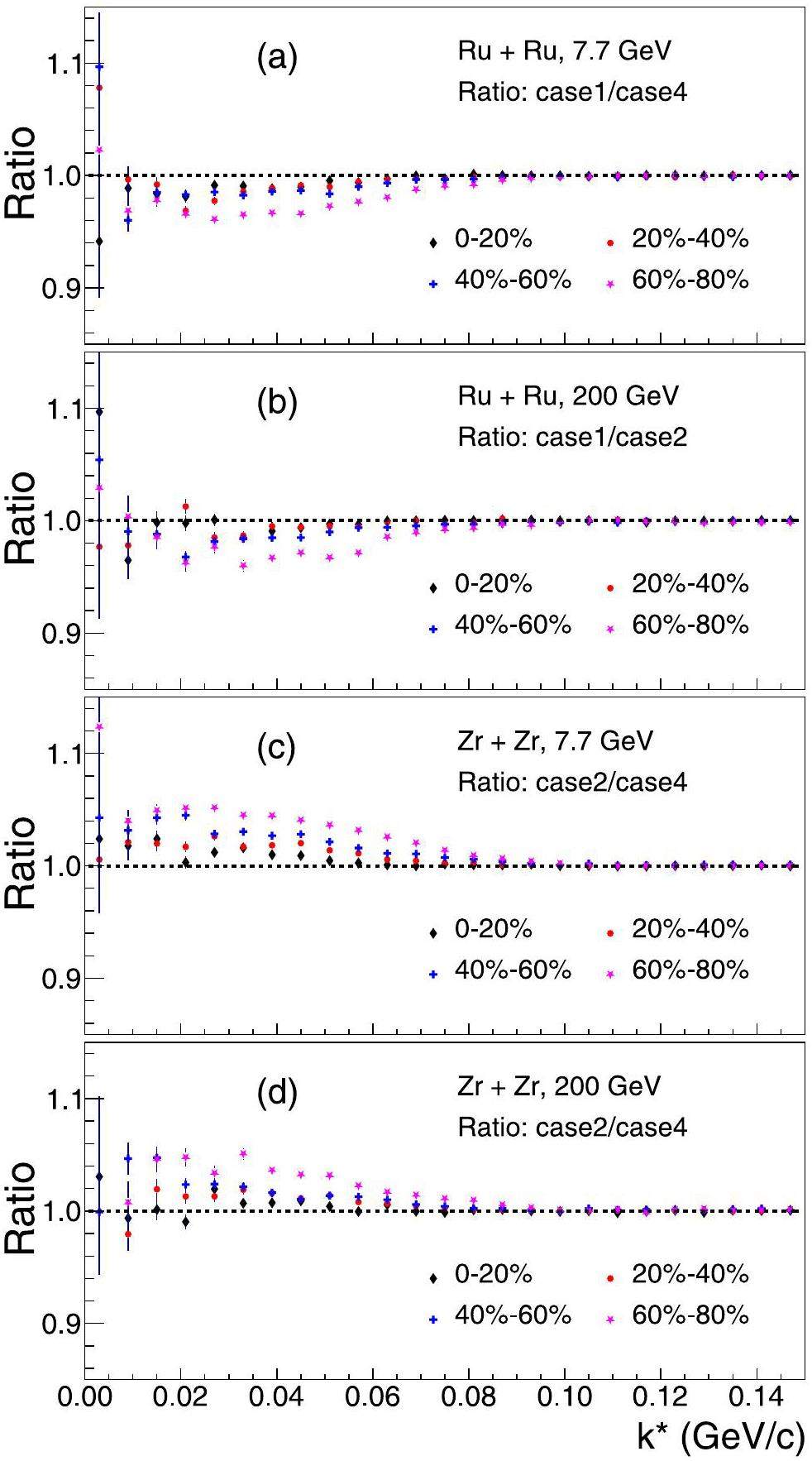
We calculated the ratios of the correlation functions between different parameterization cases across the centrality classes from 0–20% to 60–80%. Figure 6 shows the results for Zr + Zr and Ru + Ru collisions at $\sqrt{s_{NN}}$ of both 7.7 and 200 GeV. We find that the results show a relatively small dependence on collision energy, but exhibit significant centrality dependence. We systematically compared case1 with case2, case1 with case4, and case2 with case4. Through these comparisons, we quantitatively evaluated the influence of the nuclear deformation effects in the two collision systems. A maximum deviation of 4% and 5% was observed at small k^* (0.02–0.04 GeV/c) for Ru + Ru and Zr + Zr, respectively. According to the Woods-Saxon configurations in our model simulation, the deformation and neutron skin effects were found to be more pronounced in peripheral collisions, consistent with our expectations based on studies of observables such as particle yield in isobaric collision systems [64, 68].

Fig. 6

Ratio of proton-proton correlation function for case1/case4 in Ru + Ru at

\sqrt{s_{NN}} = 7.7

GeV (Panel a), case1/case2 in Ru + Ru at

\sqrt{s_{NN}} = 200

GeV (Panel b), case2/case4 in Zr + Zr at

\sqrt{s_{NN}} = 7.7

GeV (Panel c) and case2/case4 in Zr + Zr at

\sqrt{s_{NN}} = 200

GeV (Panel d) in different centrality classes

Studies have also been performed for n-p correlation. Figures 7 and 8 show the results of central and peripheral Ru + Ru and Zr + Zr collisions at $\sqrt{s_{NN}} = 200$ GeV. Owing to the absence of charge interactions, all the data points of the correlation function were all greater than 1. For central collisions, the correlation functions for all four cases are consistent within the statistical uncertainties, with only a tiny difference observed at small k^*. For the peripheral collisions, the differences between the n-p correlations are similar to that of p-p, indicating that the n-p pair is sensitive to the nuclear structure similar to that of the p-p pair.

Fig. 7

Neutron-proton correlation function of 0–20% central Ru + Ru (Panel a) and Zr + Zr (Panel b) collisions at

\sqrt{s_{NN}} = 200

GeV. The ratios (Ru/Zr) are shown in Panel (c)

Fig. 8

Neutron-proton correlation function of 60–80% central Ru + Ru (Panel a) and Zr + Zr (Panel b) collisions at

\sqrt{s_{NN}} = 200

GeV. The ratios (Ru/Zr) are shown in Panel (c)

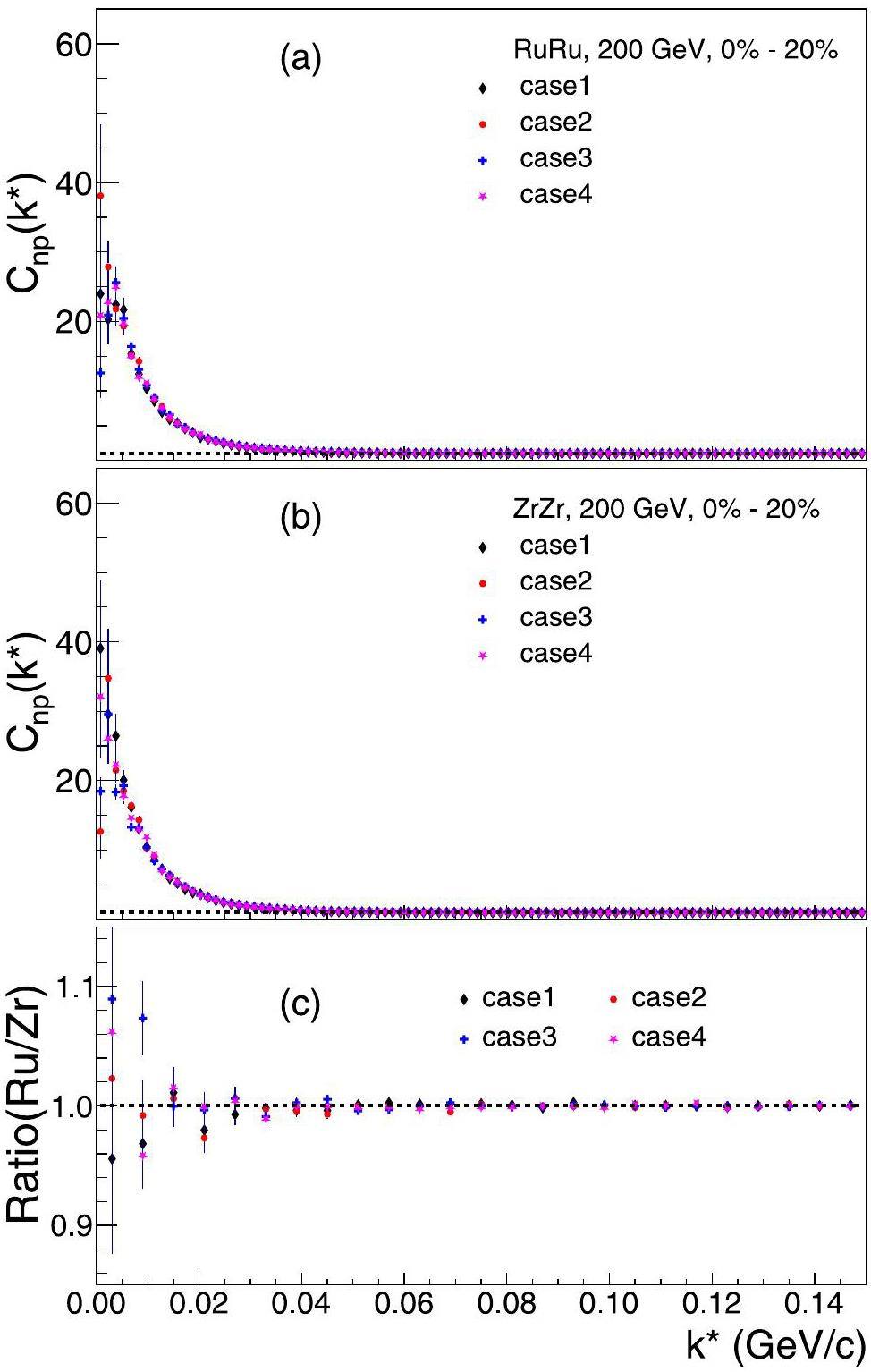
The ratios of the correlation functions between the two systems (Ru/Zr) for the different cases are shown in the bottom panels of Figs. 7 and 8. It was found that the ratio results at $\sqrt{s_{NN}} = 200$ GeV were similar to the p-p correlation. No significant deviations are observed in the central collisions, indicating minimal differences between the two systems. Neither the neutron skin nor the nuclear deformation effects manifest in the correlation functions in central collisions. For peripheral collisions, similar differences to p-p correlations were observed between the four deformation cases with a maximum deviation of 4% from the unity observed, taking into consideration the statistical uncertainties. The results suggest that in n-p correlations, both the neutron skin effect and the deformation effect make non-negligible contributions. In addition, the correlation functions of both n-p and p-p show a clear centrality dependence.

Summary

Using the AMPT model, we investigated the nucleon momentum correlation in the relativistic collisions of Ru + Ru and Zr + Zr at $\sqrt{s_{NN}} = 7.7$ and 200 GeV. The correlation functions of p-p and n-p for different cases with various deformation parameters were calculated to quantitatively study the effects of nuclear structure and system size.

The ratios of the correlation functions between the two isobaric systems (Ru/Zr) for four different cases of Woods-Saxon parametrization were evaluated based on the simulation data with a clear centrality dependence. The ratio shows no deviation from unity in case 1 for nuclei with the same nuclear size and without deformation. We observed a deviation from unity in the ratios for cases 2-4 in both central and peripheral collisions, which could be attributed to the deformation effect. We found that the influence of the nuclear structure becomes more significant in peripheral collisions. A maximum deviation of 5% from unity was observed between all the Woods-Saxon parameterization cases and 4% between collision systems in 60–80% peripheral collisions, incorporating nuclear size and the neutron skin effect. Meanwhile, it was found that the energy dependence of both the neutron skin effect and deformation effect in the p-p correlation is shallow. In addition, we found that in both p-p and n-p, the intensity of the correlation function in central collisions is greater than that in peripheral collisions. The results of the p-p correlation at $\sqrt{s_{NN}} = 7.7$ GeV are greater than those at 200 GeV, which reflects the fireball size produced in the corresponding collision scenarios.

Notably, our simulation study did not consider the evolution and interactions of magnetic fields related to the charge number of the colliding nuclei. Further theoretical studies incorporating magnetic field effects in nucleon momentum correlation, along with experimental measurements at RHIC energies, would enable more precise examinations of nuclear structure and size, providing stronger constraints on the nuclear structure parameters of the isobar systems [77].

References

E. Shuryak,

Strongly coupled quark-gluon plasma in heavy ion collisions

. Rev. Mod. Phys. 89, 035001 (2017). https://doi.org/10.1103/RevModPhys.89.035001