Introduction
Clustering is a fundamental phenomenon in the nucleus [1-8]. Cluster models are widely used and have been shown to be effective in describing the characteristics of light nuclei [9, 10]. With the cluster model, the study of diproton and dineutron correlations is crucial for understanding nucleon-nucleon interactions and the underlying nuclear structure, providing information on pairing mechanisms and the behavior of nucleons in short-range interactions, which are essential for understanding phenomena such as nuclear stability and reaction dynamics [11-14].
6He, the lightest Borromean halo nucleus, together with its mirror nucleus 6Be, the lightest two-proton emitter, has attracted extensive studies on the dinucleon correlations in their decaying modes and structures [15-21]. Previous studies have described the structure of 6He [22-24], a more precise description can be found in [25], which addresses both six-body correlations and clustering in the 6He ground state using the no-core shell model with continuum (NCSMC), where the “dineutron” configuration is shown to prevail over the “cigar” structure. Recently, the
Dineutron and diproton correlations have been intensively discussed through 2n and 2p emissions from unbound nuclei in connection with recent experiments [30-33]. In the case of 6He, experiments have investigated the decay mode of its
The main objective of this study was to investigate the correlations between diprotons and dineutrons in 6He and 6Be in several low-lying states of 6He and 6Be at the structural level using a microscopic nuclear model. We employed the Generator Coordinate Method (GCM) with Brink wave functions [39, 40] as a robust framework to model and analyze these correlations.
By calculating the Two-Cluster Overlap Amplitude (TCOA), we aim to quantify the spatial distribution and correlation strength of nucleon pairs, providing insights into the nucleon-nucleon interactions within these nuclei [41, 42]. This approach enables detailed examination of the structural and correlation properties of 6He and 6Be, contributing to a deeper understanding of nucleon correlations in light nuclear systems [43, 44].
Theoretical framework
In the present GCM calculations, the total wave function of 6He (6Be) can be written as the superposition of angular-momentum-projected and parity-projected Brink wave functions
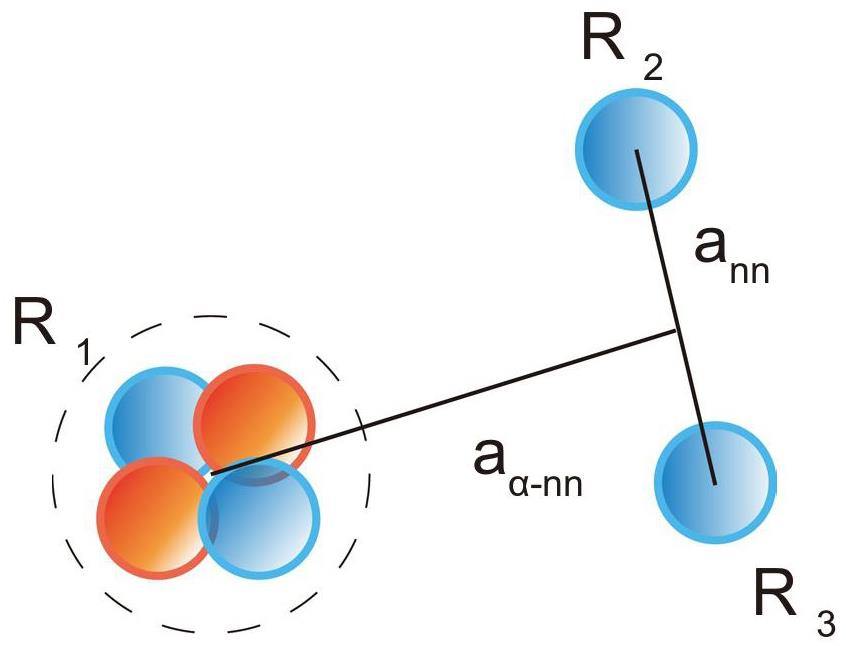
TCOA was introduced as an extension of the RWA method to quantitatively analyze the spatial distribution and correlation strength of nucleon pairs [50]. This approach has been successfully applied to study core + N + N + N structures [51], providing a detailed description of clustering dynamics.
To illustrate the three-cluster structure, the TCOA [52] of 6He is defined as:
To characterize the relative motion between the α cluster and the two neutrons, we introduce the relative-motion coordinates r1 and r23, which are defined as
The TCOA provides the spatial distribution of valence nucleons in terms of the distance between the two valence nucleons,
Results and discussion
By superposing 600 distinct three-body spatial configurations,
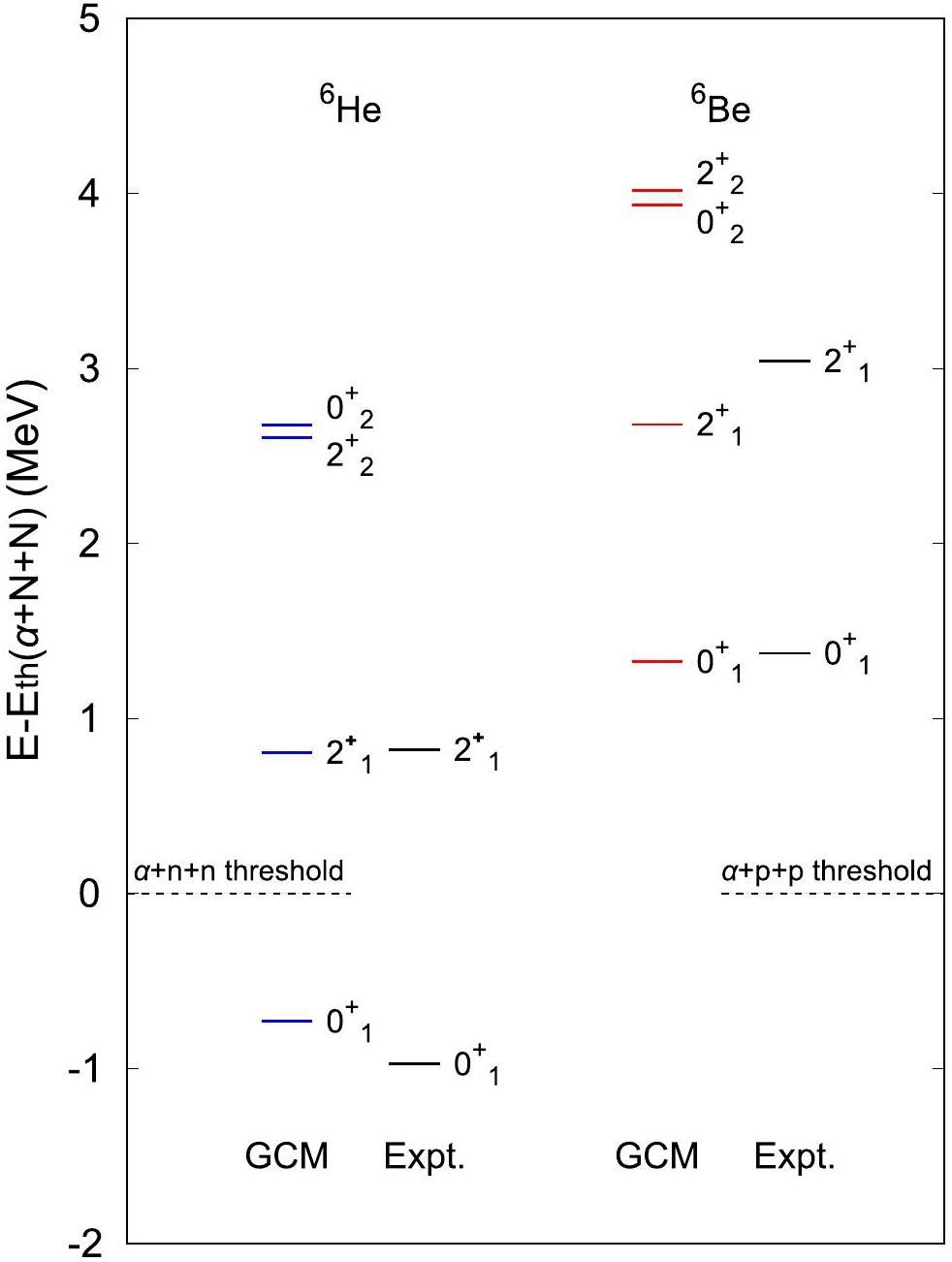
Based on the definition of the TCOA discussed above, this framework effectively characterizes critical three-body cluster correlations, with specific emphasis on the dineutron correlation in 6He and the diproton correlation in 6Be. Figures 3 and 4 present the TCOA distributions for three-cluster systems in 6He and 6Be, where the orbital angular momenta quantum numbers l1 = l23 = 0 and l1 = l23 = 1 were chosen because these specific combinations exhibited the most pronounced TCOA distribution amplitudes. In a purely non-correlated scenario, the distributions would exhibit equal weights on both sides of the dashed lines in the figure, which divide two distinct regions in the hyperspherical description of three-body nuclei [53]. For the ground states of 6He and 6Be, two distinct peaks were observed: a dinucleon-like peak in the region
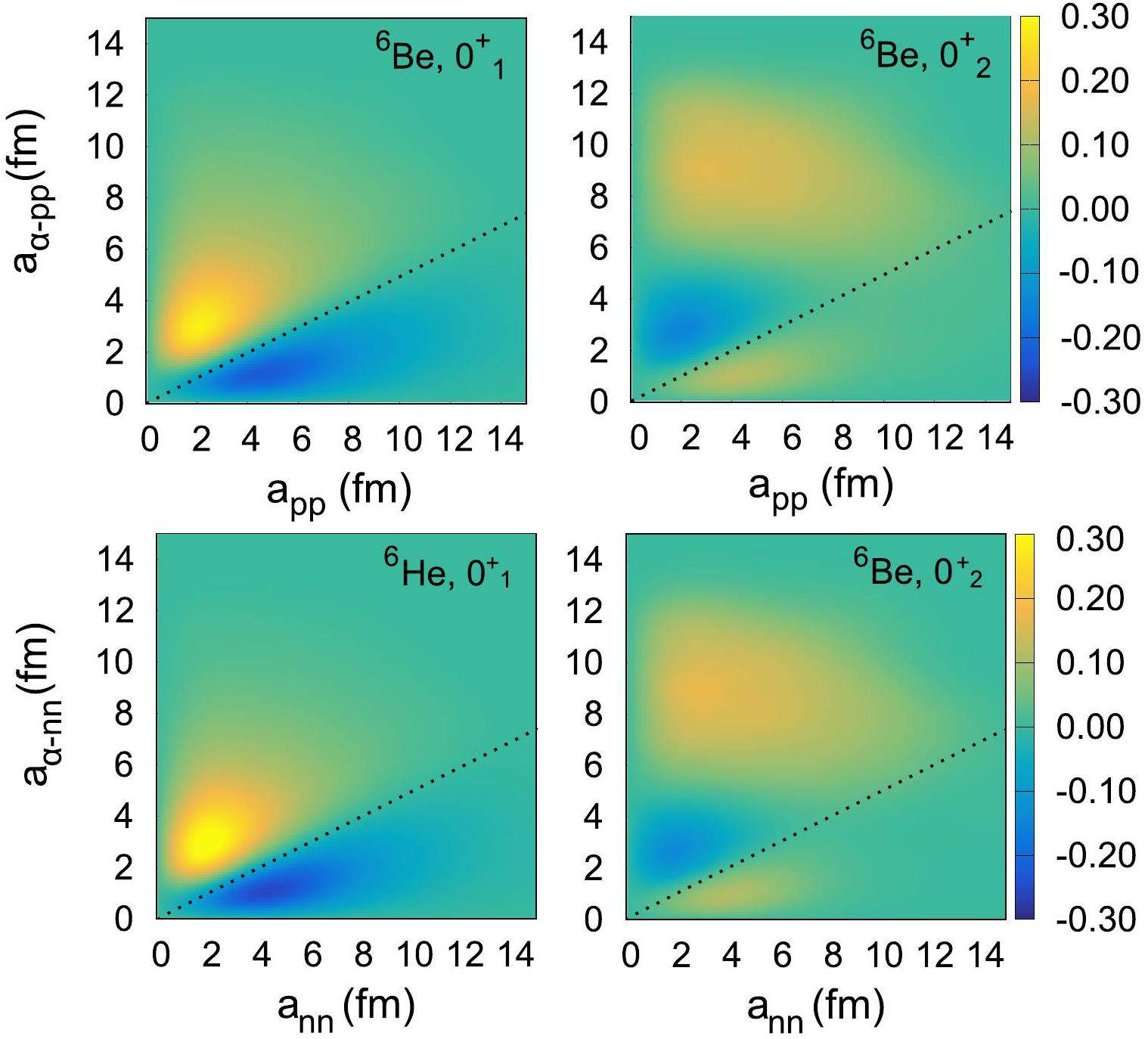

The conclusion of the favored dineutron correlation in the ground state of 6He is consistent with a recent experimental work [15], which extracted
Compared to the ground states, the
For the first excited state
The TCOA distributions of the
Summary
In this study, we investigated the diproton and dineutron correlations in the ground and low-lying 2+ states of 6Be and 6He using the TCOA method within the GCM framework. Our calculations reveal that both 6Be and 6He exhibit pronounced diproton and dineutron correlations in their ground states, characterized by a cigar-like spatial configuration with a localized nucleon pair. The TCOA distributions for the
The present theoretical framework, combining the GCM with TCOA analysis, has proven effective in providing a detailed description of nucleon-nucleon correlations and clustering behavior in light nuclear systems, offering insights into the structural evolution of mirror nuclei across different excitation energies.
Microscopic clustering in light nuclei
. Rev. Mod. Phys. 90,Nonlocalized clustering: A new concept in nuclear cluster structure physics
. Phys. Rev. Lett. 110,Physics of exotic nuclei
. Nat. Rev. Phys. 7, 21-37 (2025). https://doi.org/10.1038/s42254-024-00782-5Giant dipole resonance as a fingerprint of αclustering configurations in 12C and 16O
. Phys. Rev. Lett. 113,Effects of neutron-skin thickness on direct hard photon emission from reactions induced by the neutron-rich projectile 50Ca
. Phys. Rev. C 105,Bubble 36Ar and its new breathing modes
. Phys. Lett. B 857,Effects of α-clustering structure on nuclear reaction and relativistic heavy-ion collisions
. Nucl. Tech. 46,α-clustering effects in relativistic heavy-ion collisions (in chinese)
. Sci Sin-Phys Mech Astron 54,A unified theory of the nucleus
. Physics Today 30,. https://doi.org/10.1063/1.3037638Nuclear clusters and nuclear molecules
. Phys. Rep. 432, 43-113 (2006). https://doi.org/10.1016/j.physrep.2006.07.001Pair correlations near the neutron drip line
. Ann. Phys. 209, 327-363 (1991). https://doi.org/10.1016/0003-4916(91)90033-5Pairing correlations in nuclei on the neutron-drip line
. Phys. Rev. C 72,Two-proton radioactivity and three-body decay: General problems and theoretical approach
. Phys. Rev. C 64,The 5αcondensate state in 20Ne
. Nat. Commun. 14, 8206 (2023). https://doi.org/10.1038/s41467-023-43816-9Three-body breakup of 6He and its halo structure
. Phys. Lett. B 814,Dineutron in the 21+ state of 6He
. Phys. Rev. C 105,Two-neutron correlations in microscopic wave functions of 6He, 8He, and 12C
. Phys. Rev. C 84,Ground state properties of beryllium isotopes studied by amd+gcm method
. Phys. Scr. 71, 349 (2005). https://doi.org/10.1238/Physica.Regular.071a00349Bound state properties of borromean halo nuclei: 6He and 11Li
. Phys. Rep. 231, 151-199 (1993). https://doi.org/10.1016/0370-1573(93)90141-YRecent progress in two-proton radioactivity
. Nucl. Sci. Tech. 33, 105 (2022). https://doi.org/10.1007/s41365-022-01091-1Fermion pair dynamics in open quantum systems
. Phys. Rev. Lett. 126,Microscopic description of translationally invariant core+ n+ n overlap functions
. Phys. Rev. C 89,Three-body systems with lagrange-mesh techniques in hyperspherical coordinates
. Phys. Rev. C 67,Two-neutron overlap functions for 6he from a microscopic structure model
. Nucl. Phys. A 847, 1-23 (2010). https://doi.org/10.1016/j.nuclphysa.2010.06.012How many-body correlations andαclustering shape 6He
. Phys. Rev. L 117,Cluster structure in Be isotopes within point-coupling covariant density functional
. Chin. Phys. Lett. 30,Two-proton emission and related phenomena
. Prog. Part. Nucl. Phys. 132,Role of diproton correlation in two-proton-emission decay of the 6Be nucleus
. Phys. Rev. C 90,Dependence of two-proton radioactivity on nuclear pairing models
. Phys. Rev. C 96,Different mechanism of two-proton emission from proton-rich nuclei 23Al and 22Mg
. Phys. Lett. B 743, 306-309 (2015).Two-proton emission and related phenomena
. Prog. Part. Nucl. Phys. 132,Ab initio Gamow shell-model calculations for dripline nuclei
. Nucl. Tech. 46,Exploring the edge of nuclear stability on the proton-rich side
. Nucl. Phys. News 33, 11-16 (2024). https://doi.org/10.1080/10619127.2023.2168911Two neutron decay from the 21+ state of 6He
. Phys. Rev. C 88,Complete correlation studies of two-proton decays: 6Be and 45Fe
. Phys. Lett. B 677, 30-35 (2009). https://doi.org/10.1016/j.physletb.2009.04.085Democratic decay of 6Be exposed by correlations
. Phys. Rev. Lett. 109,Sensitivity of three-body decays to the reactions mechanism and the initial structure by example of 6Be
. Phys. Rev. C 86,Three-body decay of 6Be
. Phys. Rev. C 80,The cluster model in nuclear physics
. Nucl. Phys. 109, 1-30 (1966). https://doi.org/10.1016/0375-9474(66)90685-5Alpha cluster condensation in 12C
. Phys. Rev. Lett. 87,Cluster structures in light nuclei
. Prog. Theor. Phys. Suppl. 123, 773-801 (2010). https://doi.org/10.1143/PTP.123.773Microscopic theory of nuclear structure
. Prog. Part. Nucl. Phys. 50, 106-142 (2003). https://doi.org/10.1016/S0146-6410(03)90039-5Nuclear clustering in light nuclei
. Rev. Mod. Phys. 81, 1359-1410 (2009). https://doi.org/10.1103/RevModPhys.81.1359New description of light nuclei by extending the amd approach
. Phys. Rev. C 68,Microscopic calculations of 6He and 6Li with real-time evolution method
. Eur. Phys. J. A 58, 25 (2022). https://doi.org/10.1140/epja/s10050-021-00648-9Equilibrium deformation calculations of the ground state energies of 1p shell nuclei
. Nucl. Phys. 74, 33-58 (1965). https://doi.org/10.1016/0029-5582(65)90244-0Potential models of nuclear forces at small distances
. Prog. Theor. Phys. 39, 91-107 (1968). https://doi.org/10.1143/PTP.39.91Effective interaction with three-body effects
. Prog. Theor. Phys. 62, 1018-1034 (1979). https://doi.org/10.1143/PTP.62.1018The reduced-width amplitude in nuclear cluster physics
. (2024). arXiv:2412.20928 https://arxiv.org/abs/2412.20928Spectroscopic amplitudes in microscopic three-cluster systems
. Phys. Rev. C 107,The 3αcorrelations of ground and excited 0+ states of 12C within the microscopic cluster model
. (2025). arXiv:2501.10664 https://arxiv.org/abs/2501.10664Bound state properties of borromean halo nuclei: 6he and 11li
. Phys. Rep. 231, 151-199 (1993).Analysis of the effect of core structure upon dineutron correlation using antisymmetrized molecular dynamics
. Phys. Rev. C 93,Nonlocalized clustering in 18O
. Eur. Phys. J. A 59, 49 (2023). https://doi.org/10.1140/epja/s10050-023-00961-5Yu-Gang Ma is the editor-in-chief for Nuclear Science and Techniques and was not involved in the editorial review, or the decision to publish this article. All authors declare that there are no competing interests.

