Introduction

The production of new superheavy nuclei (SHN) is a challenging frontier in low-energy nuclear reactions. Over the years, experimental and theoretical nuclear physicists have explored SHN synthesis since the prediction of the “island of stability” around Z = 114, N = 184 [1, 2]. The Skyrme–Hartree–Fock method considers Z = 120, 124, or 126 and N = 172 or 184 as magic numbers [3]. The synthesis of superheavy elements (SHEs) Z = 107–112 was accomplished in GSI using cold fusion reactions with Pb and Bi targets [4]. However, despite the successful synthesis of SHE Z = 113 via the cold fusion reaction ⁷⁰Zn + ²⁰⁹Bi at RIKEN [5], the evaporation residue cross section (ERCS) ${\sigma }_{\text{ER}}$ was only 0.03 pb, reaching the limit of experimental detection at that time [6]. To overcome this challenge, researchers in Dubna focused on hot-fusion reactions with ⁴⁸Ca beams and actinide targets. This method produces SHEs with Z = 114–118 [7-12], which complete the seventh period of the periodic table.

In recent years, several new isotopes with Z≤118 have been synthesized using modern accelerators, such as the DC-280 and U-400 of the Dubna SHE factory, RILAC of RIKEN, SFC of HIRFL, and UNILAC of GSI [7, 12-16]; however, the production of SHEs with Z>118 remains a challenge. Previous attempts to produce SHEs with Z=120 using ⁵⁸Fe+²⁴⁴Pu [6] and ⁵⁴Cr + ²⁴⁸Cm [17] reactions at Dubna and GSI, respectively, did not observe any α decay chains associated with this element. The three events reported by the GSI in Ref. [17] were later determined to be random events [18]. In 2020, with the gas-filled recoil separator TASCA at GSI, the search for synthesizing SHEs with Z=119 and Z=120 was conducted via the reactions ⁵⁰Ti + ²⁴⁹Bk and ⁵⁰Ti + ²⁴⁹Cf, yet neither was detected [19]. In 2022, RIKEN estimated the optimal incident energy for synthesizing SHE Z=119 through the reaction ⁵¹V+²⁴⁸Cm [20]. Therefore, the synthesis of SHEs Z>118 requires not only more advanced detection and identification techniques but also an appropriate reaction system.

Several models and different fusion mechanisms have been proposed to accurately describe the process of fusion-evaporation reactions. The improved quantum molecular dynamics (ImQMD) model [21], time-dependent Hartree-Fock theory [22-25], fusion-by-diffusion model [26], cluster dynamical decay model [27], two-step model [28, 29], dinuclear system (DNS) model [30-44], and other methods [45-48] have proved to be reliable in reproducing experimental data and have provided predictions about the synthesis of unknown nuclei [22, 45, 49-56].

The synthesis and decay of elements Z = 119 and Z = 120 have been extensively studied [22, 33, 35, 45, 52, 57-59], whereas only a limited number of calculations have been conducted for the synthesis of SHE Z = 121. To address this research gap, this study aims to investigate the optimal projectile-target combinations for synthesizing SHE Z = 121 and provide a reference for future experimental attempts.

The remainder of this paper is organized as follows: In Sect. 2, the DNS model is described, and its reliability is examined. The ERCSs of Z = 121 isotopes in different reaction channels are discussed in Sect. 3. Finally, the conclusions are provided in Sect. 4.

Theoretical descriptions

In the DNS model, the ERCS for synthesizing SHN in the center-of-mass frame can be obtained using the following expression: $\begin{array}{c}{\sigma }_{\text{ER}}\left(E_{\text{c}\text{.m}\text{.}}\right)=\frac{\pi {\hslash }^2}{2\mu E_{\text{c}\text{.m}\text{.}}}{\displaystyle \sum _J\left(2J+1\right)}T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)\\ \times P_{\text{CN}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)W_{\text{sur}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right).\end{array}$ (1) Here, $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ represents the transmission probability of the colliding system overcoming the Coulomb barrier V_b. $P_{\text{CN}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ is the fusion probability for the formation of a compound nucleus [60]. $W_{\text{sur}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ denotes the probability that the excited compound nucleus emits neutrons instead of undergoing fission to reach the ground state [61]. The nucleus–nucleus interaction potential considering quadrupole deformation is expressed as follows [62]: $\begin{array}{c}V\left(R\mathrm{,}{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}{\theta }_1\mathrm{,}{\theta }_2\right)=\frac{1}{2}{C}_1{\left({\beta }_1-{\beta }_1^0\right)}^2+\frac{1}{2}{C}_2{\left({\beta }_2-{\beta }_2^0\right)}^2\\ +V_{\text{C}}\left(R\mathrm{,}{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}{\theta }_1\mathrm{,}{\theta }_2\right)\\ +V_{\text{N}}\left(R\mathrm{,}{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}{\theta }_1\mathrm{,}{\theta }_2\right)\mathrm{,}\end{array}$ (2) where ${\beta }_{\mathrm{1,2}}$ and ${\beta }_{\mathrm{1,2}}^0$ denote the dynamic quadrupole and static deformation parameters of the projectile and target nucleus, respectively. θ_1,2 are the collision angles of the deformed projectile and target nucleus, respectively. The stiffness parameters $C_{\mathrm{1,2}}$ are expressed as follows [63]: $C_i=\left(\lambda -1\right)\left[\left(\lambda +2\right)R_{\mathrm{0,}i}^2\sigma -\frac{3}{2\pi }\frac{Z_i^2{e}^2}{R_{\mathrm{0,}i}\left(2\lambda +1\right)}\right]\mathrm{.}$ (3) λ = 2 represents the quadrupole deformation. The Coulomb potential V_C is determined using Wang’s formula [64]: $\begin{array}{c}{V}_{\text{C}}\left(R\mathrm{,}{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}{\theta }_1\mathrm{,}{\theta }_2\right)=\frac{Z_1{Z}_2{e}^2}{R}+\sqrt{\frac{9}{20\pi }}\frac{Z_1{Z}_2{e}^2}{R^3}\\ \times {\displaystyle \sum _{i=\mathrm{1,2}}{R}_i^2}{\beta }_2^{\left(i\right)}{P}_2\left(\cos {\theta }_i\right)+\frac{3}{7\pi }\\ \times \frac{Z_1{Z}_2{e}^2}{R^3}{\displaystyle \sum _{i=\mathrm{1,2}}{R}_i^2}{\left[{\beta }_2^{\left(i\right)}{P}_2\left(\cos {\theta }_i\right)\right]}^2.\end{array}$ (4) The nuclear potential V_N is given by the Woods–Saxon potential [64]: $\begin{array}{l}{V}_{\text{N}}\left(R\mathrm{,}{\beta }_1\mathrm{,}{\beta }_2\mathrm{,}{\theta }_1\mathrm{,}{\theta }_2\right)=-V_0\times \\ {\left\{1+\text{exp}\left[\frac{r-{\displaystyle {\sum }_{i=\mathrm{1,2}}{R}_i}\left(1+\sqrt{5/4\pi }{\beta }_2^{\left(i\right)}{P}_2\left(\cos {\theta }_i\right)\right)}{a}\right]\right\}}^{-1}\mathrm{.}\end{array}$ (5) During the capture process, the transmission probability $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}B\mathrm{,}J\right)$ is described using Ahmed’s formula [65, 66]: $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}B\mathrm{,}J\right)=\frac{1-\exp \left(-4\pi \alpha \right)}{1+\exp \left(2\pi \left({\beta }_J-\alpha \right)\right)}\mathrm{.}$ (6) Here $\alpha =\frac{\sqrt{2\mu E_{\text{c}\text{.m}\text{.}}}}{\hslash }{\alpha }_{\text{M}}$ and ${\beta }_J=\frac{\sqrt{2\mu \left(B+\frac{{\hslash }^2}{2\mu R_{\text{B}}^2\left(J\right)}J\left(J+1\right)\right)}}{\hslash }{\alpha }_{\text{M}}$. μ represents the reduced mass, and ${\alpha }_{\text{M}}$ denotes the Morse parameter [67].

Considering the barrier distribution function $f\left(B\right)$, $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ can be written as: $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)={\displaystyle \int }f\left(B\right)T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}B\mathrm{,}J\right)\text{d}B\mathrm{.}$ (7) The asymmetric barrier distribution parameters are presented in Refs. [68]. The capture cross-section ${\sigma }_{\text{cap}}$ is calculated as follows [62]: ${\sigma }_{\text{cap}}\left(E_{\text{c}\text{.m}\text{.}}\right)=\frac{\pi {\hslash }^2}{2\mu E_{\text{c}\text{.m}\text{.}}}{\displaystyle \sum _J\left(2J+1\right)}T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)\mathrm{.}$ (8) The fusion of the colliding nuclei is determined by the potential energy surface, expressed as [62] $\begin{array}{c}U\left(N_1\mathrm{,}{Z}_1\mathrm{,}{N}_2\mathrm{,}{Z}_2\mathrm{,}R\mathrm{,}{\beta }_1\mathrm{,}{\beta }_2\right)\\ =E_{\text{B}}\left(N_1\mathrm{,}{Z}_1\right)+E_{\text{B}}\left(N_2\mathrm{,}{Z}_2\right)-E_{\text{B}}\left(N_3\mathrm{,}{Z}_3\right)\\ +V_{\text{CN}}\left(N_1\mathrm{,}{Z}_1\mathrm{,}{N}_2\mathrm{,}{Z}_2\mathrm{,}R\mathrm{,}{\beta }_1\mathrm{,}{\beta }_2\right).\end{array}$ (9) The data of the binding energies of the colliding nucleus $E_{\text{B}}\left(N_{\text{1,2}}\mathrm{,}{Z}_{\text{1,2}}\right)$ and the formed compound nucleus $E_{\text{B}}\left(N_{\text{3}}\mathrm{,}{Z}_{\text{3}}\right)$ is taken from Ref. [69]. V_CN denotes the nucleus–nucleus interaction potential.

Nucleon transfer is treated as a diffusion process at the lowest point on the potential energy surface, known as the driving potential [62]. To form a compound nucleus, the dinuclear system must surpass the inner fusion barrier B_fus along the mass asymmetry degree $\eta =\left(A_{\text{P}}-A_{\text{T}}\right)/\left(A_{\text{P}}+A_{\text{T}}\right)$, which denotes the potential energy disparity between the incident point and the Businaro–Gallone (B.G.) point (the peak of the driving potential) [70], defined as $B_{\text{fus}}=U\left({\eta }_{\text{B}\text{.G}\text{.}}\right)-U\left({\eta }_{\text{i}}\right)$. The fusion probability $P_{\text{CN}}(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J)$ is determined through the summation of the distribution probabilities of crossing the B.G. point $P\left(N_{\text{1}}\mathrm{,}{Z}_{\text{1}}\mathrm{,}{E}_{\text{1}}\mathrm{,}t\right)$ as follows: $P_{\text{CN}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)={\displaystyle \sum _{N_1=1}^{N_{\text{B}\text{.G}\text{.}}}{\displaystyle \sum _{Z_1=1}^{Z_{\text{B}\text{.G}\text{.}}}P}}\left(N_1\mathrm{,}{Z}_1\mathrm{,}{E}_1\mathrm{,}t={\tau }_{\text{int}}\left(J\right)\right).$ (10) Here, the interaction time ${\tau }_{\text{int}}\left(J\right)$ is calculated using the deflection function method [71]. $P\left(N_{\text{1}}\mathrm{,}{Z}_{\text{1}}\mathrm{,}{E}_{\text{1}}\mathrm{,}t\right)$ is calculated by solving the two-dimensional master equation. $\begin{array}{c}\frac{\text{d}P\left(N_1\mathrm{,}{Z}_1\mathrm{,}{E}_1\mathrm{,}t\right)}{\text{d}t}\\ ={\displaystyle \sum _{N_1^{\text{'}}}{W}_{N_1\mathrm{,}{Z}_1;N_1^{\text{'}}\mathrm{,}{Z}_1}}\left(t\right)\\ \times \left[d_{N_1\mathrm{,}{Z}_1}P\left(N_1^{\text{'}}\mathrm{,}{Z}_1\mathrm{,}{E}_1\mathrm{,}t\right)-d_{N_1^{\text{'}}\mathrm{,}{Z}_1}P\left(N_1\mathrm{,}{Z}_1\mathrm{,}{E}_1\mathrm{,}t\right)\right]\\ +{\displaystyle \sum _{Z_1^{\text{'}}}{W}_{N_1\mathrm{,}{Z}_1;N_1\mathrm{,}{Z}_1^{\text{'}}}}\left(t\right)\\ \times \left[d_{N_1\mathrm{,}{Z}_1}P\left(N_1\mathrm{,}{Z}_1^{\text{'}}\mathrm{,}{E}_1\mathrm{,}t\right)-d_{N_1\mathrm{,}{Z}_1^{\text{'}}}P\left(N_1\mathrm{,}{Z}_1\mathrm{,}{E}_1\mathrm{,}t\right)\right]\\ -\left[{\Lambda }_{\text{qf}}\left(\Theta \left(t\right)\right)+{\Lambda }_{\text{fis}}\left(\Theta \left(t\right)\right)\right]P\left(N_1\mathrm{,}{Z}_1\mathrm{,}{E}_1\mathrm{,}t\right)\mathrm{.}\end{array}$ (11) Here $W_{N_1\mathrm{,}{Z}_1;N_1^{\text{'}}\mathrm{,}{Z}_1}$ denotes the mean transition probability from state $\left(N_1\mathrm{,}{Z}_1\right)$ to state $\left(N_1^{\text{'}}\mathrm{,}{Z}_1\right)$ [72], and $d_{N_1\mathrm{,}{Z}_1}$ is the microscopic dimension of state $\left(N_1\mathrm{,}{Z}_1\right)$. The quasi-fission rate ${\Lambda }_{\text{qf}}$ and fission rate ${\Lambda }_{\text{fis}}$ are given by the one-dimensional Kramers formula [73].

The survival process is determined primarily by the rivalry between fission and neutron emissions [74]. The survival probability at excitation energy $E_{\text{CN}}^{*}$ can be expressed as $\begin{array}{l}{W}_{\text{sur}}\left(E_{\text{CN}}^{*}\mathrm{,}x\mathrm{,}J\right)\\ =P\left(E_{\text{CN}}^{*}\mathrm{,}x\mathrm{,}J\right){\displaystyle \prod _{i=1}^x}\left[\frac{{\text{Γ}}_{\text{n}}\left(E_i^{*}\mathrm{,}J\right)}{{\text{Γ}}_{\text{n}}\left(E_i^{*}\mathrm{,}J\right)+{\text{Γ}}_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)}\right].\end{array}$ (12) $P\left(E_{\text{CN}}^{*}\mathrm{,}x\mathrm{,}J\right)$ denotes the realization probability of emitting x neutrons [75]. $E_i^{*}$ represents the excitation energy of a compound nucleus that emits i-1 neutrons [57].

The neutron decay width ${\text{Γ}}_{\text{n}}\left(E_i^{*}\mathrm{,}J\right)$ was calculated using the Weisskopf–Ewing theory [76]: $\begin{array}{c}{\text{Γ}}_{\text{n}}\left(E_i^{*}\mathrm{,}J\right)=\frac{\left(2s_{\text{n}}+1\right)m_{\text{n}}}{{\pi }^2{\hslash }^2\rho \left(E_i^{*}\mathrm{,}J\right)}\\ \times {\displaystyle {\int }_{I_{\text{n}}}}\epsilon \rho \left(E_i^{*}-B_{\text{n}}-\epsilon \mathrm{,}J\right){\sigma }_{\text{inv}}\left(\epsilon \right)\text{d}\epsilon .\end{array}$ (13) Here, $I_{\text{n}}=\left[\mathrm{0,}{E}_i^{*}-B_{\text{n}}-\delta -\frac{1}{a}\right]$. δ and $B_{\text{n}}$ represent the pairing correction and the neutron separation energies [33], respectively. The level density ρ is expressed as in Refs. [77], and ${\sigma }_{\text{inv}}$ denotes the inverse reaction cross section [78].

${\text{Γ}}_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)$ is the fission decay width given by the Bohr–Wheeler transition-state method [79]: $\begin{array}{c}{\text{Γ}}_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)=\frac{1}{2\pi {\rho }_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)}\\ \times {\displaystyle {\int }_{I_{\text{f}}}}\frac{{\rho }_{\text{f}}\left(E_i^{*}-B_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)-\epsilon \mathrm{,}J\right)\text{d}\epsilon }{1+\exp \left[-2\pi \left(E_i^{*}-B_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)-\epsilon \right)/\hslash \omega \right]},\end{array}$ (14) with $I_{\text{f}}=\left[\mathrm{0,}{E}_i^{*}-B_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)-\delta -\frac{1}{a_{\text{f}}}\right]$, $a_{\text{f}}=1.1A/12$ [80, 81]. The temperature-dependent fission barrier $B_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)$ was calculated using the following expression [82, 83]: $\begin{array}{c}{B}_{\text{f}}\left(E_i^{*}\mathrm{,}J\right)=B_{\text{f}}^{\text{LD}}\left(1-x_{\text{LD}}{T}_i^2\right)\\ +B_{\text{f}}^{\text{M}}\left(E_i^{*}=\mathrm{0,}J\right)\exp \left(-\frac{E_i^{*}}{E_{\text{D}}}\right)\\ -\left(\frac{{\hslash }^2}{2J_{\text{g}\text{.s}\text{.}}}-\frac{{\hslash }^2}{2J_{\text{s}\text{.d}\text{.}}}\right)J\left(J+1\right)\mathrm{,}\end{array}$ (15) where $B_{\text{f}}{}^{\text{LD}}$ denotes the macroscopic portion of the fission barrier. Ti and $x_{\text{LD}}$ represent the nuclear temperature and temperature-dependent parameters, respectively, [82]. $B_{\text{f}}{}^{\text{M}}$ is the microscopic shell correction energy in the ground state [69] and $E_{\text{D}}=25$ MeV [50]. $J_{\text{g}\text{.s}\text{.}}$ and $J_{\text{s}\text{.d}\text{.}}$ are as expressed in Refs. [84, 85].

To evaluate the accuracy of our model in predicting the ERCSs of SHN, Fig. 1 presents the comparisons between the calculated ERCSs and the experimental data in the reactions ⁴⁸Ca + ²⁴⁵Cm [12, 86], ⁴⁸Ca + ²⁴⁸Cm [87], ⁴⁸Ca + ²⁴⁹Bk [88] and ⁴⁸Ca + ²⁴⁹Cf [12, 89, 90]. Calculation uncertainties arise from the relatively subjective choice of the $E_{\text{D}}$ range [91]. The fission barrier relies heavily on the contribution of the shell correction energy, and the reduction in the shell correction energy with increasing excitation energy is described by $E_{\text{D}}$ values, which lie in the range of $\text{10}\text{MeV}\le E_{\text{D}}\le \text{30}\text{MeV}$ [92].

Fig. 1Full-screen View

(Color online) Comparison of the predicted ERCSs with the experimental results [12, 86-90] for the synthesis of Lv (a, b), Ts (c), and Og (d). The calculated ERCSs in the 2n-, 3n-, 4n-, and 5n-emission channels are denoted by the dashed, solid, dash-dot, and dotted lines, respectively. The shades indicate the uncertainties of the calculated ERCSs. The experimental results for the 2n-, 3n-, 4n-, and 5n-emission channels are denoted by inverted triangles, circles, squares and triangles, respectively

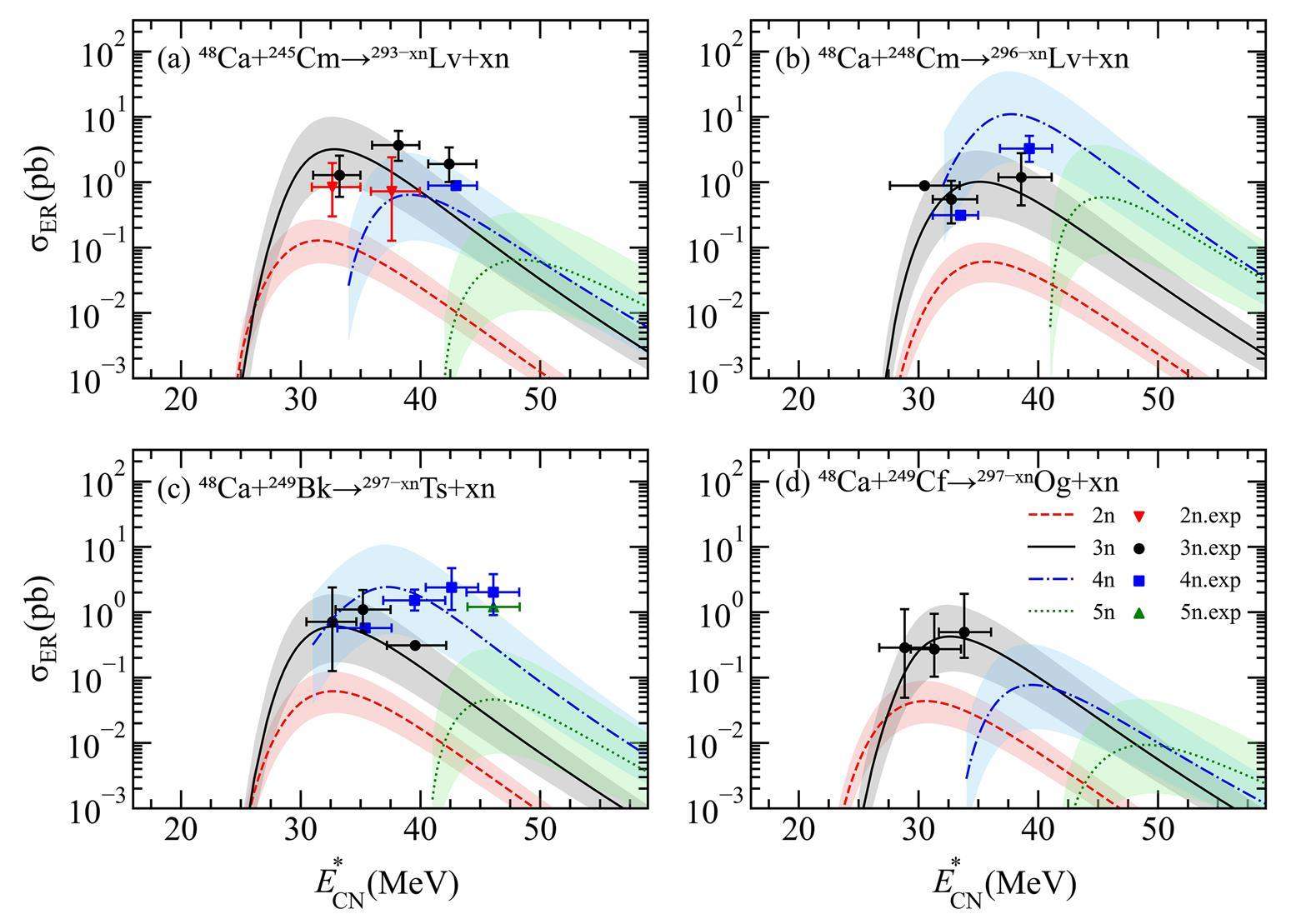
As shown in Figs. 1(a)-(d), the ERCSs show a decreasing trend with increasing proton number of compound nucleus. For the reactions ⁴⁸Ca + ²⁴⁵Cm and ⁴⁸Ca + ²⁴⁹Cf, the maximal ERCSs of both the calculation and experiment appeared in the 3n-emission channels. The 4n-emission channels are more favorable for the synthesis of SHN with the reactions ⁴⁸Ca + ²⁴⁸Cm and ⁴⁸Ca + ²⁴⁹Bk. The predicted ERCSs aligned well with the experimental results, particularly for the reaction ⁴⁸Ca + ²⁴⁹Cf. A maximal ERCS of ${0.42}_{-0.30}^{+0.87}$ pb for the reaction ⁴⁸Ca + ²⁴⁹Cf was predicted at the 3n-emission channel at $E_{\text{CN}}^{*}$ = 32.0 MeV, This is consistent with the experimental value of ${0.5}_{-0.3}^{+1.6}$ pb with $E_{\text{CN}}^{*}$ = 32.1-36.6 MeV in the same channel. This validates the applicability of the DNS model for predicting the synthesis of new elements via fusion–evaporation reactions.

Results and discussion

To prevent facility contamination by unstable beams, we chose stable projectiles with Z=21–30 and actinide targets with half-lives exceeding 50 d for the experimental duration; the optimal reaction systems are summarized in Table 1. The most favorable reactions and ERCSs (optimal E_c.m.) for producing isotopes ^295-302121 are ²⁵²Es (⁴⁶Ti, 3n) ²⁹⁵121, 4.123 fb (223.9 MeV), ²⁴⁸Cf (⁵⁰V, 3n) ²⁹⁶121, 0.566 fb (239.1 MeV), ²⁵⁴Es (⁴⁶Ti, 3n) ²⁹⁷121, 6.619 fb (219.9 MeV), ²⁵⁴Es (⁴⁷Ti, 3n) ²⁹⁸121, 1.331 fb (222.3 MeV), ²⁵⁷Fm (⁴⁵Sc, 3n) ²⁹⁹121, 8.778 fb (213.6 MeV), ²⁵⁴Es (⁴⁹Ti, 3n) ³⁰⁰121, 0.453 fb (228.5 MeV), ²⁵⁴Cf (⁵⁰V, 3n) ³⁰¹121, 3.705 fb (229.0 MeV), and ²⁵⁴Cf (⁵¹V, 3n) ³⁰²121, 0.524 fb (234.1 MeV).

As mentioned in the previous paragraph, the largest maximal ERCS corresponding to the synthesis of the SHE with Z = 121 is 8.778 fb in the reaction ⁴⁵Sc+²⁵⁷Fm. In addition, the reactions ⁴⁶Ti+²⁵²Es and ⁴⁶Ti+²⁵⁴Es offer large maximal ERCSs of 4.123 and 6.619 fb, respectively. Considering its experimental feasibility, the ²⁵⁴Es target is currently available among several Es targets in the laboratory [94], with a half-life of 275.70 d. The ²⁵²Es target has a comparatively long half-life (1.29 y), making it a potential target for experimental purposes. Therefore, despite the slightly higher ERCS of the reaction ⁴⁵Sc+²⁵⁷Fm, the reactions ⁴⁶Ti+^252,254Es are more feasible for experimental purposes.

In Figs. 2a-c, we present the calculated ERCSs of the reactions ⁴⁵Sc+²⁵⁷Fm, ⁴⁸Ti+²⁵⁴Es, and ⁵¹V+²⁵¹Cf. These reactions yield the same compound nuclei of ³⁰²121. Notably, our analysis revealed a consistently decreasing trend in the maximal ERCSs for synthesizing the same isotopes, ²⁹⁹121 via the 3n-emission channel and ²⁹⁸121 via the 4n-emission channel, as the charge number of the projectiles increased. This trend can be attributed to the reduced fusion probability resulting from the increased mass asymmetry. To further investigate the influence of mass asymmetry on the fusion-evaporation reaction, the fusion probabilities and driving potentials for the reactions ⁴⁵Sc+²⁵⁷Fm, ⁴⁸Ti+²⁵⁴Es, and ⁵¹V+²⁵¹Cf are presented in Figs. 3 and 4.

Fig. 2Full-screen View

(Color online) Predicted ERCSs of the reactions ${}^{45}\text{Sc}{+}^{257}\text{Fm}$, ⁴⁸Ti+²⁵⁴Es, and ⁵¹V+²⁵¹Cf. The 3n- and 4n-emission channels are indicated by the blue solid and red dotted lines, respectively. The shades indicate the uncertainties of the calculated ERCSs

Fig. 3Full-screen View

(Color online) Calculated fusion probabilities of the reactions ⁴⁵Sc+²⁵⁷Fm (black solid line), ⁴⁸Ti+²⁵⁴Es (red dashed line), and ⁵¹V+²⁵¹Cf (blue dash-dot line)

Fig. 4Full-screen View

(Color online) Driving potential for the reaction ⁴⁵Sc+²⁵⁷Fm, ⁴⁸Ti+²⁵⁴Es, and ⁵¹V+²⁵¹Cf as a function of mass asymmetry. The arrows indicate the entrance channel

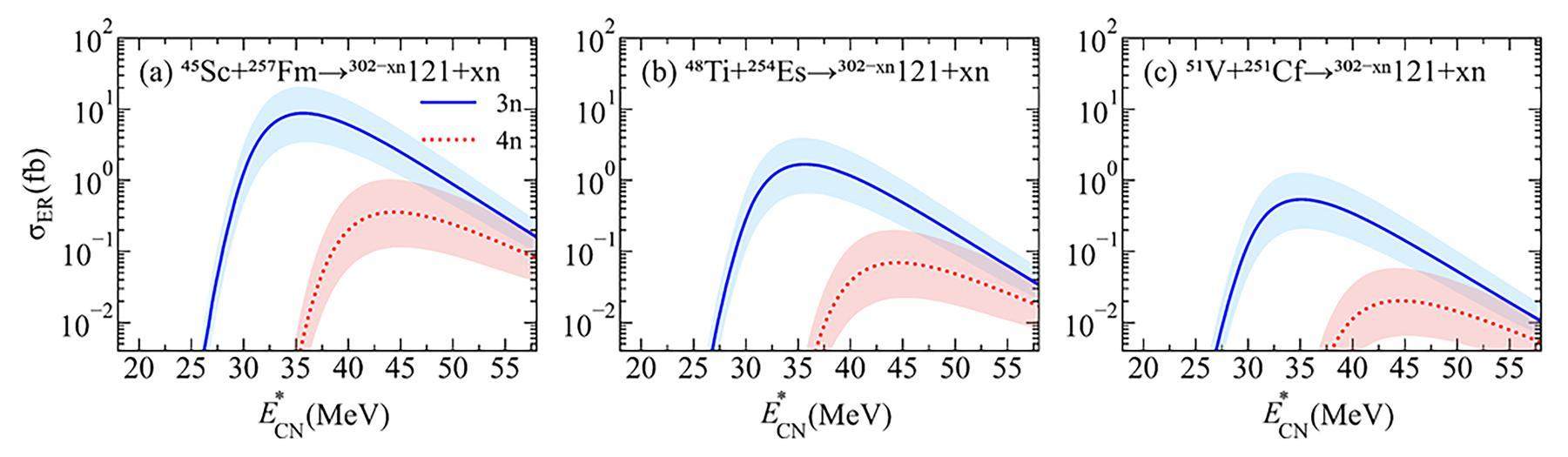
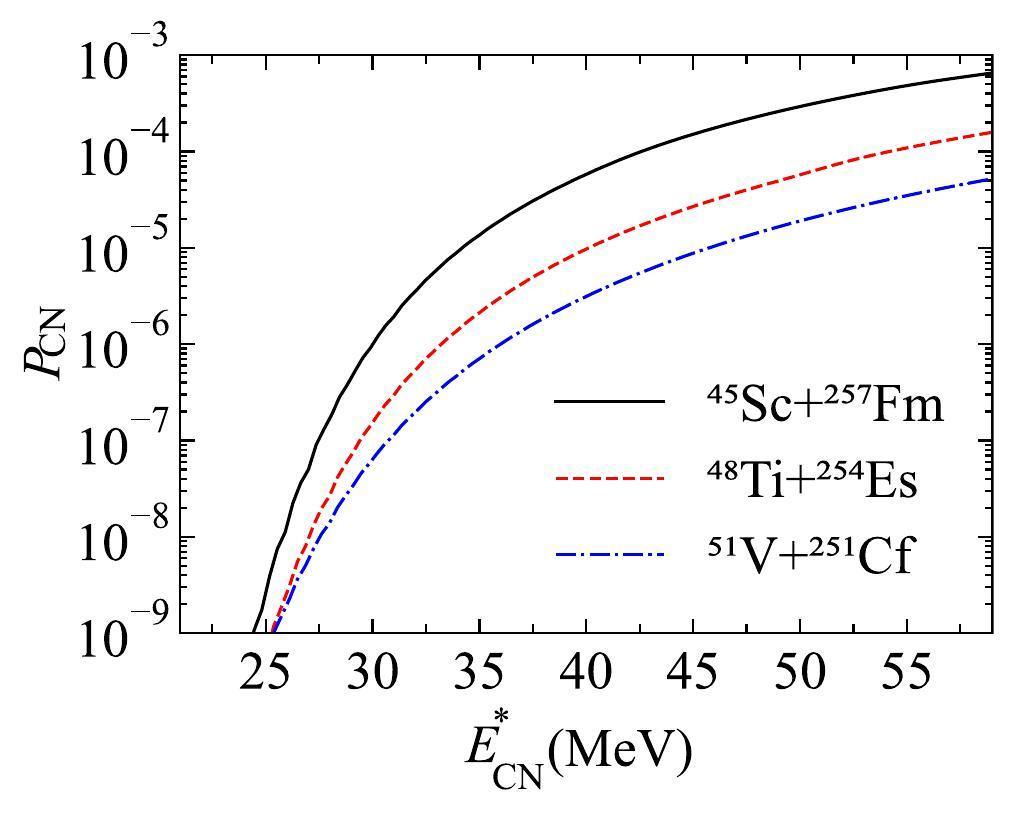
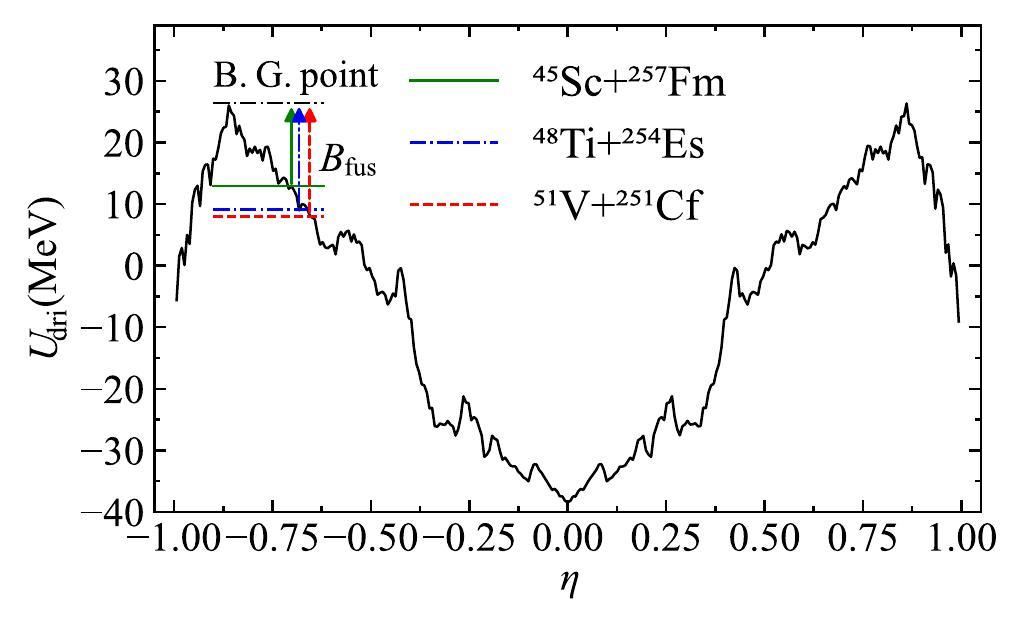
Figure 3 reveals that the fusion probabilities exhibit an increasing trend with increasing $E_{\text{CN}}^{*}$. This occurred because of the heightened dissipated energy within the dinuclear system at higher $E_{\text{CN}}^{*}$, thus rendering the reaction system more likely to overcome the inner fusion barrier. Additionally, Fig. 3 shows that the reaction ⁴⁵Sc+²⁵⁷Fm exhibits a much larger fusion probability than the other two reactions. Conversely, the reaction ⁵¹V+²⁵¹Cf exhibits the lowest fusion probability. This significant difference can be attributed to the different B_fus values influenced by the change in mass asymmetry.

Figure 4 shows that as the mass asymmetry of the reaction system decreases, the entrance channel approaches the B.G. point, resulting in a corresponding decrease in B_fus. For the reaction ⁴⁵Sc+²⁵⁷Fm, the B_fus is 13.1 MeV, which is lower than the reactions ⁴⁸Ti+²⁵⁴Es (B_fus=17.1 MeV) and ⁵¹V+²⁵¹Cf (B_fus=17.8 MeV). Consequently, the reaction ⁴⁵Sc+²⁵⁷Fm is more likely to overcome the inner fusion barrier, resulting in an enhanced fusion probability, as shown in Fig. 3. Evidently, the heightened fusion probabilities, stemming from the reduced mass asymmetry, establish the superiority of Sc- and Ti-induced reactions for producing the SHE with Z = 121.

In Fig. 5, we present an analysis of the calculated maximal ERCSs, corresponding incident energies, and Q values for reactions involving ^46-50Ti projectiles and ^252,254Es targets. Figure 5(a) reveals that the reactions employing the neutron-rich ²⁵⁴Es target consistently yielded larger maximal ERCSs than those employing the ²⁵²Es target. Moreover, the maximum ERCSs decreased as the neutron number of the projectile increased. Notably, odd–even effects also impact the maximal ERCSs, with even-A Ti projectiles resulting in relatively enhanced ERCSs. Figure 5(b) illustrates that the optimal incident energies for reactions with the ²⁵²Es target are approximately 3–4 MeV higher than those with the ²⁵⁴Es target. Additionally, the optimal incident energies exhibited a discernible increase, with evident odd–even effects as the neutron number of the projectiles increased.

Fig. 5Full-screen View

(Color online) (a) Calculated maximal ERCSs, (b) corresponding optimal incident energies, and (c) the Q values of the reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es

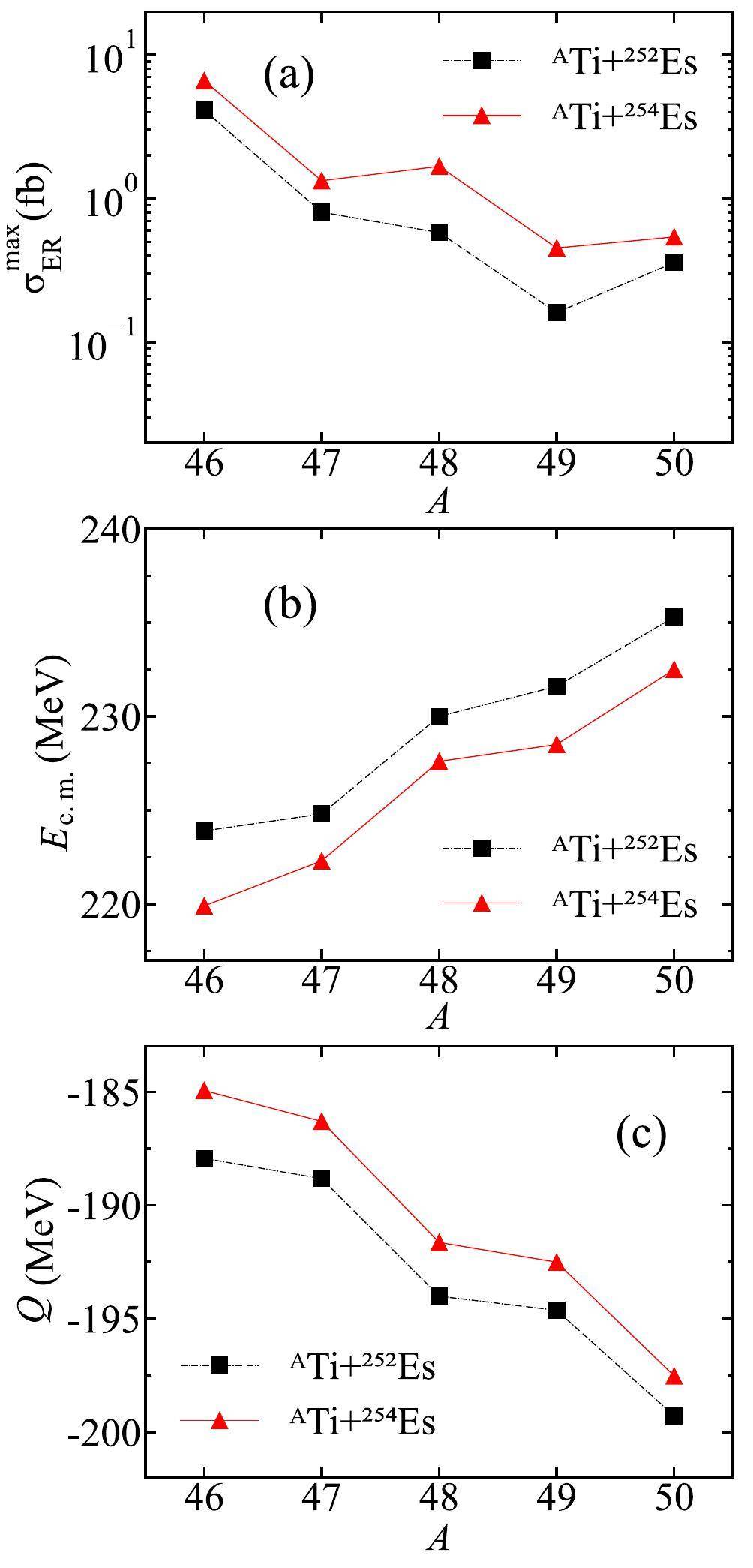
For all reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es, the corresponding $E_{\text{CN}}^{*}$ falls within the range of 35–37 MeV. This range has a limited effect on the optimal incident energy. The increasing trend in the optimal incident energy can be attributed to the differences in the Q values. Figure 5(c) reveals that a high neutron excess of the target nuclei enhances the Q values of the reaction system, whereas a high neutron excess of the projectile nuclei exerts the opposite effect. The odd–even effects of the projectiles also have a significant influence on the Q values, with reactions utilizing even-A Ti projectiles displaying relatively suppressed Q values compared to those employing odd-A Ti projectiles.

A comprehensive investigation of the capture, fusion, and survival stages is essential for determining the isotopic dependence of the maximal ERCSs and the corresponding optimal incident energies. In Fig. 6(a), we present the capture cross sections for the combinations involving ^46-50Ti projectiles colliding with ²⁵²Es and ²⁵⁴Es targets at excitation energies of $E_{\text{CN}}^{*}$ = 35 MeV and 50 MeV. Notably, the capture cross sections exhibit an increasing trend with increasing $E_{\text{CN}}^{*}$, as the ability to surpass the Coulomb barrier increases with higher $E_{\text{CN}}^{*}$. Furthermore, the capture cross-sections of the reactions involving ²⁵²Es targets are notably enhanced compared to those with ²⁵⁴Es targets. Additionally, there is an upward trend in the capture cross sections with a higher neutron excess in the projectiles. These trends can be attributed to a decrease in the Coulomb barrier.

Fig. 6Full-screen View

(Color online) (a) Calculated capture cross sections of the reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es with $E_{\text{CN}}^{*}$ = 35 MeV and $E_{\text{CN}}^{*}$ = 50 MeV. (b) Excitation energies of the corresponding Coulomb barriers V_b+Q of the reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es

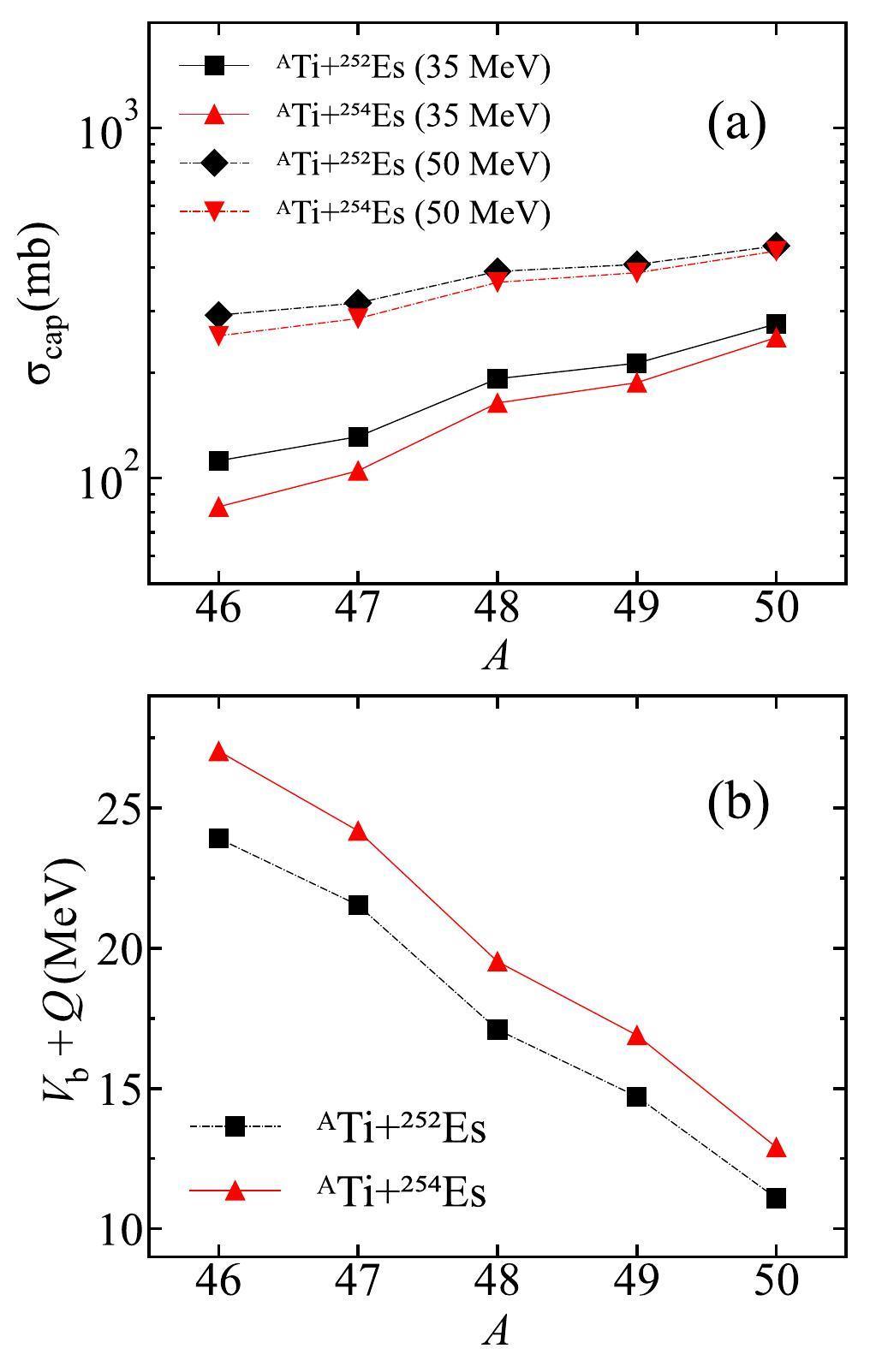
In Fig. 6(b), the excitation energies associated with the Coulomb barriers V_b+Q of the corresponding reactions are plotted. The V_b+Q values decreased with increasing neutron excess in the projectiles. Moreover, the reaction systems with the ²⁵²Es target exhibited lower V_b+Q values than those with ²⁵⁴Es targets. Consequently, reactions involving ²⁵²Es as target nuclei coupled with neutron-rich Ti projectiles have an increased likelihood of overcoming the Coulomb barrier, thereby enhancing the corresponding capture cross sections.

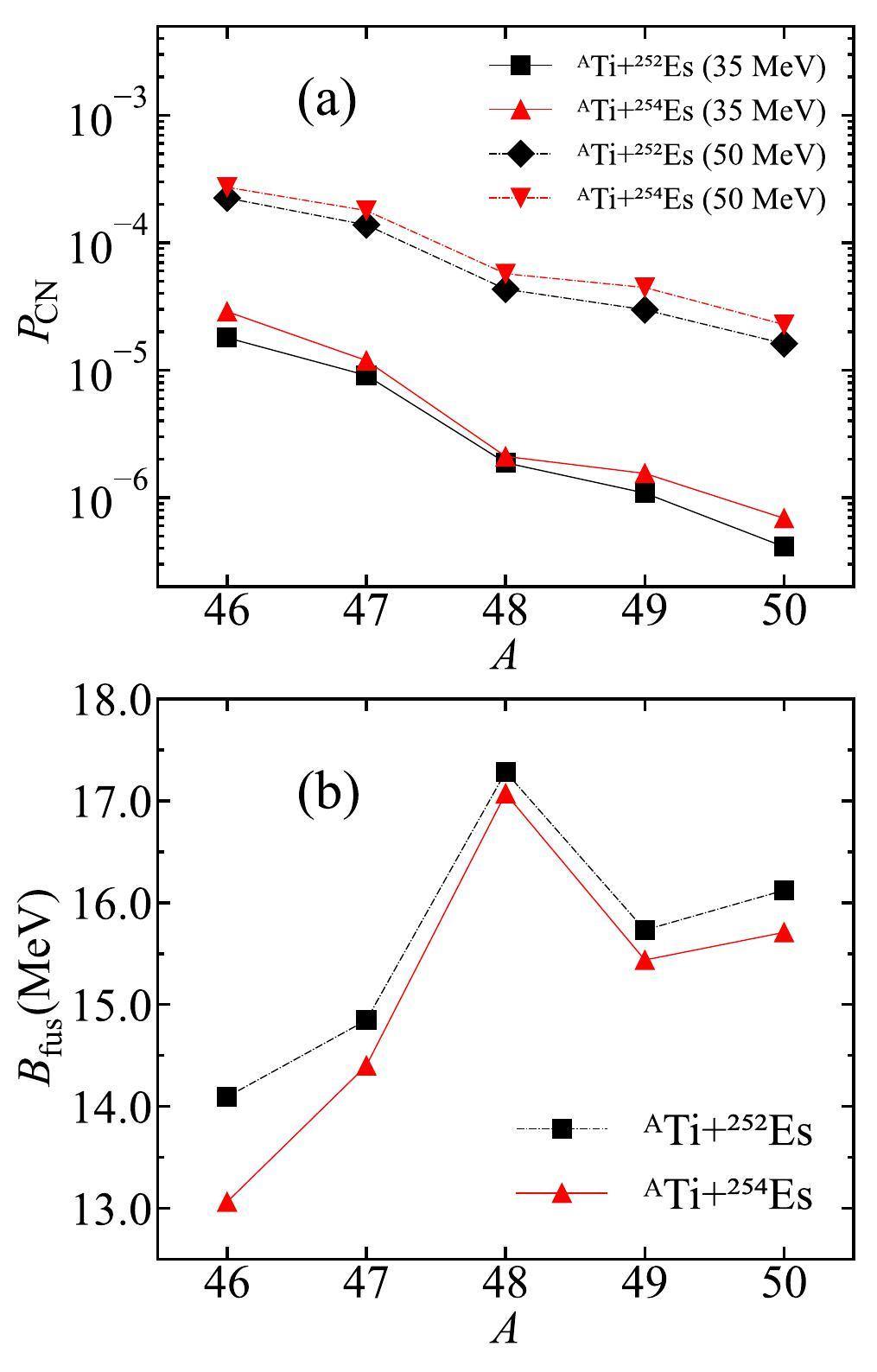
The fusion process in Fig. 7(a) shows the fusion probabilities of reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es at $E_{\text{CN}}^{*}$ = 35 MeV and 50 MeV. As the probability of overcoming the inner fusion barrier increased, the fusion probabilities were amplified with a higher $E_{\text{CN}}^{*}$. These fusion probabilities exhibit a decreasing trend with increasing neutron excess in the projectile. Notably, the employment of the neutron-rich ²⁵⁴Es target leads to a relative enhancement in the fusion probability, which can be attributed to the reduced inner fusion barrier. Fig. 7(b) shows the inner fusion barriers for the corresponding reactions. Notably, the B_fus values increase with increasing neutron excess in the projectiles and are higher in reaction systems with lighter ²⁵²Es targets. This can be attributed to the increased mass asymmetry of projectiles with a higher neutron excess and targets with a lower neutron excess, which subsequently enhances the B_fus values and hinders the fusion process.

Fig. 7Full-screen View

(Color online) (a) Calculated fusion probabilities of the reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es with $E_{\text{CN}}^{*}$ = 35 MeV and $E_{\text{CN}}^{*}$ = 50 MeV. (b) $B_{\text{fus}}$ values of the reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es

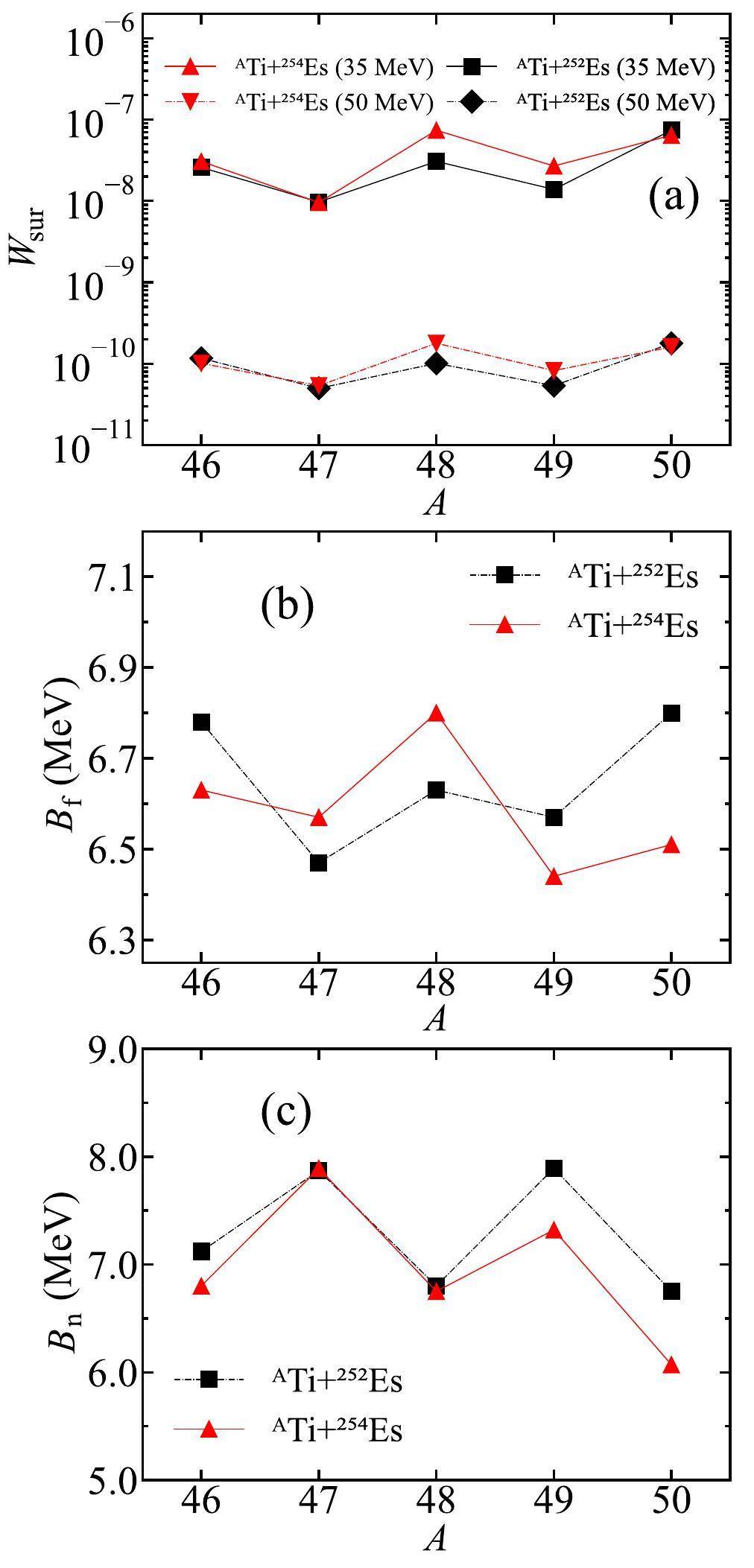
In Fig. 8(a), the survival probabilities of the compound nuclei in the 3n-emission channel for reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es at $E_{\text{CN}}^{*}$ = 35 MeV and 50 MeV are plotted. Notably, the survival probabilities exhibited a decreasing trend as $E_{\text{CN}}^{*}$ increased. This is due to the damped shell effect at increased $E_{\text{CN}}^{*}$, which results in diminished compound nucleus stability. Additionally, the ²⁵⁴Es based reactions exhibited relatively high fusion probabilities with an evident odd–even staggering pattern. This can be ascribed to the influences of the B_n and B_f values of the corresponding compound nuclei, as shown in Figs. 8(b) and Fig. 8(c)). The compound nuclei formed via the even-A projectiles are more likely to de-excite through neutron emission because of their relatively higher B_f values and lower B_n values. This behavior results in odd–even staggering in both the survival probabilities and maximal ERCSs of the Ti-induced reactions. Furthermore, the combined effect of the B_n and B_f values contributes to the generally higher survival probabilities in reactions with the ²⁵⁴Es target compared with those with ²⁵²Es targets. This dual enhancement in the fusion and survival stages highlights the advantage of employing a ²⁵⁴Es target for the synthesis of isotopes with Z = 121.

Fig. 8Full-screen View

(Color online) (a) Calculated survival probabilities of the compound nuclei in the 3n-emission channel for the reactions ^46-50Ti+²⁵²Es and ^46-50Ti+²⁵⁴Es with $E_{\text{CN}}^{*}$ = 35 MeV and $E_{\text{CN}}^{*}$ = 50 MeV. (b) $B_{\text{f}}$ values and (c) $B_{\text{n}}$ values of the corresponding compound nuclei

Summary

The calculated ERCSs using the DNS model were assessed using the experimental results of the reactions ⁴⁸Ca + ²⁴⁵Cm, ⁴⁸Ca + ²⁴⁸Cm, ⁴⁸Ca + ²⁴⁹Bk, and ⁴⁸Ca + ²⁴⁹Cf. Our analysis indicates consistency between the theoretical predictions and the experimental results. Based on the DNS model, we investigated the synthesis of the SHE Z = 121 using stable projectiles with Z=21-30 and actinide targets with half-lives longer than 50 d, revealing that this element is expected to be produced via reactions ⁴⁵Sc+²⁵⁷Fm, ⁴⁶Ti + ²⁵⁴Es, and ⁴⁶Ti + ²⁵²Es. Considering the experimental feasibility, the reactions ⁴⁶Ti + ²⁵⁴Es and ⁴⁶Ti + ²⁵²Es are more favorable with maximal ERCSs and optimal incident energies of 6.619 fb at 219.9 MeV and 4.123 fb at 223.9 MeV.

We investigated the mass asymmetry effect, revealing enhanced fusion probabilities for Sc- and Ti-induced reactions. Additionally, the influences of the Q values, Coulomb barriers, inner fusion barriers, fission barriers, and neutron separation energies on the isotopic dependence of the reactions with Ti projectiles and Es targets were analyzed in detail. Our results indicate that employing a ²⁵⁴Es target and even-A Ti projectiles with a smaller neutron excess is favorable for synthesizing the element Z = 121.