Introduction

The study of nuclide production and its properties in the N=126 neutron-rich region is of great significance for expanding the nuclear landscape, revealing the evolution of the shell structure, and understanding astrophysical nucleosynthesis. According to the theory of nuclear astrophysics, approximately half of the nuclei in nature heavier than iron are considered to be produced by a rapid neutron capture process, also known as the r-process [1-3]. The properties of N=126 neutron-rich nuclei, such as mass and lifetime, play a crucial role in understanding the r-process abundance peak around A=195 [4-6]. However, reaching this region experimentally is difficult because of the low production cross sections and the great challenge of separation and identification. The lack of experimental data leads to significant uncertainty in predicted abundance patterns [7-10]. Therefore, research on the production and properties of neutron-rich nuclei around $N=126$ is extremely important.

In recent decades, producing N=126 neutron-rich nuclei in the laboratory has become a challenging problem. Multi-nucleon transfer (MNT) reactions at near-barrier energies are expected to be powerful techniques for synthesizing and studying nuclides in the neutron-rich N=126 region [11-14]. Several facilities based on MNT reactions have been constructed or are in planning or under construction around the world, such as KISS at RIKEN [15], IGISOL at JYFL [16], the N=126 factory at ANL [17], and INCREASE at GSI [18]. Some neutron-rich isotopes of Pt, Ir, and Os, produced as target-like fragments using the ¹³⁶Xe+¹⁹⁸Pt reaction system, were successfully extracted using the KISS facility [19, 20]. However, to reduce the plasma density in a gas cell induced by the primary beam and elastic products [15, 21, 22], experiments using these facilities are typically performed at low primary beam intensities. Moreover, thin reaction targets must be used because of the low beam energies used in experiments. Low beam intensity and thin reaction targets are not beneficial for obtaining high fragment yields. To increase the available primary beam intensity, a new design using a gas-filled solenoid to suppress unwanted elastic particles has been proposed for future facilities such as NEXT at Groningen [23] and KISS-II at RIKEN [24].

Except for MNT reactions at near-barrier energies, the experimental results indicate that the projectile fragmentation reaction of ²⁰⁸Pb or ²³⁸U at relativistic energies may be an effective method for producing heavy neutron-rich nuclei in this region [25, 26]. However, this method requires a high beam intensity, relativistic beam energy, and high performance of the in-flight separator to be met simultaneously. A high beam intensity is necessary to produce products with low cross sections. Relativistic energy is required to reduce the number of populated ionic charge states, thereby increasing collection efficiency. High-performance separators are crucial for separating and identifying heavy neutron-rich fragments [27]. The future Super-FRS in-flight facility at FAIR [28] satisfies these conditions. Searching for new isotopes and studying their properties in the region along the N=126 line below ²⁰⁸Pb has been proposed as one of the main physical objectives of FAIR Phase-0 experiments [29].

High-energy FRagment Separator (HFRS) [30, 31], an in-flight separator at relativistic energies, is now under construction at the High-Intensity heavy-ion Accelerator Facility (HIAF) [32, 33] and will start operation a few years later. It is also characterized by high ion-optical acceptance, high-resolution power, high magnetic rigidity, and excellent particle identification, similar to the Super-FRS separator. In combination with the HIAF accelerator facility, which will provide beams up to 34 Tm corresponding to ²³⁸U³⁵⁺ ions of 833 MeV/nucleon and with intensity as high as 1e11 ions per pulse, the neutron-rich nuclei around N=126 from projectile fragmentation at relativistic energies can be produced and purified by using the HFRS separator. This provides a new opportunity to study the properties of N=126 neutron-rich nuclei and understand the third abundance peak in the r-process.

In this study, we primarily focused on the production of N=126 neutron-rich nuclei and the feasibility of studying their properties using the HIAF-HFRS facility. Measurement methods for nuclear properties, such as mass and lifetime, as well as the layout of related experimental setups, are introduced first. Subsequently, simulation results are presented to verify its feasibility.

Experimental setups and methods

Nuclear masses and lifetimes are of fundamental importance in r-process simulations. Using the HFRS separator at the HIAF facility, some neutron-rich nuclei in the region along the N=126 line below ²⁰⁸Pb could be produced, and the properties of these nuclei, such as their mass and lifetime, can be experimentally measured.

The experimental setup for the HFRS separator is illustrated in Fig. 1. A relativistic ²⁰⁸Pb or ²³⁸U primary beam will be extracted from the HIAF accelerator facility in the slow extraction mode and implanted into the carbon production target at the entrance of the HFRS separator. The fragments of interest produced via the fragmentation reaction will be collected and separated using the Bρ-Δ E-Bρ method [34, 35], in which the analysis of magnetic rigidity (Bρ) is combined with the energy loss in an achromatic degrader (Δ E) at the pre-separator stage. An achromatic degrader will be placed on the PF2 dispersion plane. The unreacted primary beam will be intercepted in the beam dump systems installed after each dipole magnet in the pre-separator, according to Bρ deviation between the primary beam and the desired isotope.

Fig. 1Full-screen View

(Color online) Schematic layout of experimental setups of the HFRS separator

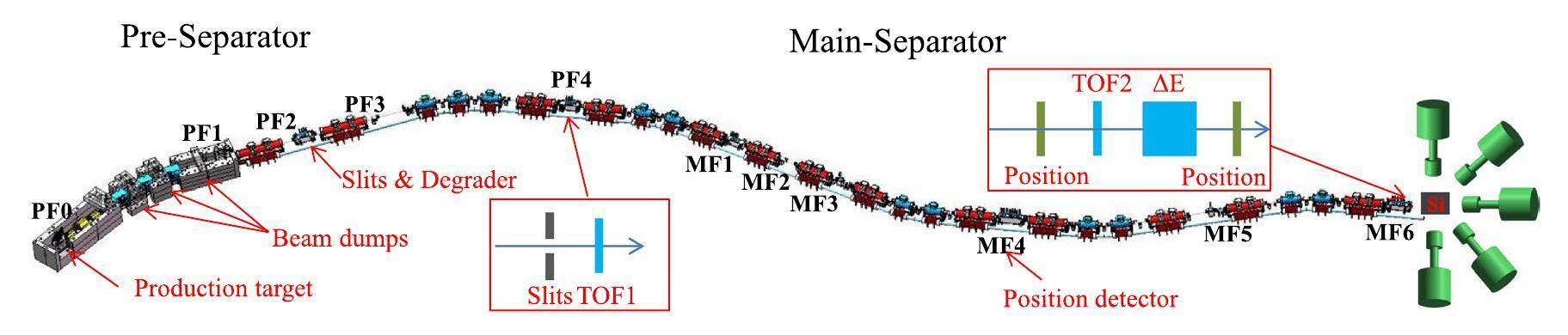
The main separator will be used as a spectrometer. Cocktail products are identified at this stage by combining the Δ E-TOF-Bρ method and isomer-tagging technique [36-38]. The energy loss (Δ E), time of flight (TOF), and Bρ are measured and used to determine the atomic number Z and mass-to-charge ratio A/Q of each fragment. Cocktails can be unambiguously identified by detecting delayed γrays emitted from the short-lived isomeric states of certain fragments. A schematic diagram of the particle identification setup is shown in Fig. 1. Multiple sampling ionization chambers (MUSIC) placed at MF6 will be used for the Δ E measurements [39, 40]. The TOF information will be obtained using TOF detectors installed at the PF4 and MF6 foci with a flight path of 118.03 m [31, 41]. The Bρ value will be determined from position measurements at the MF4 dispersive plane. At the final focal plane of the HFRS, a decay detector array consisting of a silicon array stopper surrounded by an array of high-purity germanium detectors will be used for isomer tagging of the selected fragments.

In the Δ E-TOF-Bρ method, the mass-to-charge ratio A/Q of a fragment is determined using the following equation: $\text{TOF}=\frac{L}{v}\mathrm{,}$ (1) $\frac{A}{Q}=\frac{B\rho }{\gamma v}\mathrm{,}$ (2) where L is the length of the flight path, v is the velocity of the fragment, and γ is the relativistic Lorentz factor. The fragment mass m can then be expressed as $m=Q\frac{B\rho }{c}\sqrt{{\left(\frac{c\text{TOF}}{L}\right)}^2-1}\mathrm{,}$ (3) where c represents the velocity of light. From this equation, the nuclear mass can be determined from the measured TOF and Bρ values while performing particle identification. This nuclear mass measurement method is known as the Bρ–TOF method [42, 43]. Usually, precise Bρ determination is achieved using the trajectory reconstruction method [44]. Assuming a negligible object spot size, the Bρ values can be calculated using the following formula: $B\rho =B{\rho }_0\left[1+\frac{x_{\text{D}}}{\left(x|\delta \right)}\right]\mathrm{,}$ (4) where $B{\rho }_0$ represents the central magnetic rigidity. Here, x_D and $(x|\delta )$ denote the horizontal position and momentum dispersion in the dispersive plane, respectively. The Bρ-TOF method has the characteristics of simple equipment, high measurement accuracy, low fragment yield requirements, and short measurement time, making it particularly suitable for measuring the mass of short-lived nuclei with very low yield far from the stability line. Using this method, the masses of some neutron-rich nuclei have been accurately measured for the first time, such as the masses of ^{48, 49}Ar and ^{56, 57}Sc measured with the combination of the A1900 separator and S800 spectrometer at NSCL [45, 46], the masses of ^55-57Ca, ^58-60Sc, ^60-62Ti, and ^62-64V measured with the combination of the BigRIPS separator and the SHARAQ spectrometer at RIKEN [47, 48].

From Eqs. (3) and (4), the mass resolution σ_m/m of the Bρ–TOF method can be expressed as $\begin{array}{l}{\left(\frac{{\sigma }_{\text{m}}}{m}\right)}^2={\left(\frac{{\sigma }_{B\rho }}{B\rho }\right)}^2+{\left(\frac{{\gamma }^2{\sigma }_{\text{TOF}}}{\text{TOF}}\right)}^2\\ ={\left(\frac{{\sigma }_{x_{\text{D}}}}{\left(x|\delta \right)+x_{\text{D}}}\right)}^2+{\left(\frac{{\gamma }^2{\sigma }_{\text{TOF}}}{\text{TOF}}\right)}^2\mathrm{,}\end{array}$ (5) where ${\sigma }_i$ is the standard deviation of measured values of "i". To improve the mass measurement accuracy, a common method is to simultaneously improve the position resolution of the position detector placed at the dispersive plane, the time resolution of the TOF system, and the momentum dispersion. For position measurements at the dispersion focal plane, detectors with a thin material thickness should be used to reduce the impact of beam energy loss and multiple scattering on the beam trajectory. A position-sensitive micro-channel-plate (MCP) tracking detector with a resolution of ~0.5 mm (σ) [49] and a low-pressure delay-line parallel-plate avalanche counter (DL-PPAC) with a resolution of ~0.43 mm (σ) [50] were used for the Bρ-TOF mass measurement experiments at NSCL and RIKEN, respectively. Using a typical resolution of ~0.5 mm (σ) of the position detector at the dispersive plane, combined with a high-resolution optical mode with a momentum dispersion of ~10 cm/% specially designed for the HFRS main separator, the uncertainty ${\sigma }_{B\rho }/B\rho$ can be estimated to be about 5×10^-5.

For the TOF measurement, the lower the ion energy, the longer the flight time, which is more conducive to improving TOF measurement accuracy. However, for N=126 neutron-rich heavy nuclei, low ion energy can cause changes in the charge-state population passing through the materials placed at the foci, thereby affecting the collection efficiency. Figure 2 (a) shows the fractions of fully stripped ions in the equilibrium charge state after passing through an Al degrader for elements in the N=126 region as a function of the kinetic energy behind the degrader. This was calculated using the Global code [51]. One can observe that the fraction of fully stripped ions decreased with increasing charge number and decreasing kinetic energy. When the ion energy behind the Al degrader is greater than 350 MeV/nucleon, even for the heaviest Hg element, the proportion of fully stripped ions is greater than 50 %. This proportion is acceptable for the mass measurement experiments. The flight path length of the HFRS is 118.03 m. Figure 2 (b) shows the effect of the time resolution of the TOF system on mass measurement accuracy under different ion energies. For an ion with a kinetic energy of 350 MeV/nucleon, the contribution of TOF resolution to the final mass resolution is ~9.9×10^-5 at a system resolution of ~30 ps (σ). This TOF resolution requirement is achieved experimentally. For example, at NSCL, two plastic scintillator detectors read out by photomultiplier tubes were used for the TOF measurement, and the resolution was measured to be ~30 ps (σ) with primary beam tests [52]. An upgraded TOF system for Bρ–TOF mass measurement experiments was developed at the NSCL and achieved a better time resolution (σ) of 7.5 ps [53]. In addition, two CVD diamond detectors formed the TOF system used in RIKEN mass-measurement experiments, with a system resolution of 27 ps (σ) [54].

Fig. 2Full-screen View

(Color online) (a) Fractions of fully stripped ions in the equilibrium charge state after passing through an Al degrader for the elements in the N=126 region calculated with the Global code. (b) The effect of the time resolution of the TOF system on mass measurement accuracy under different ion energies

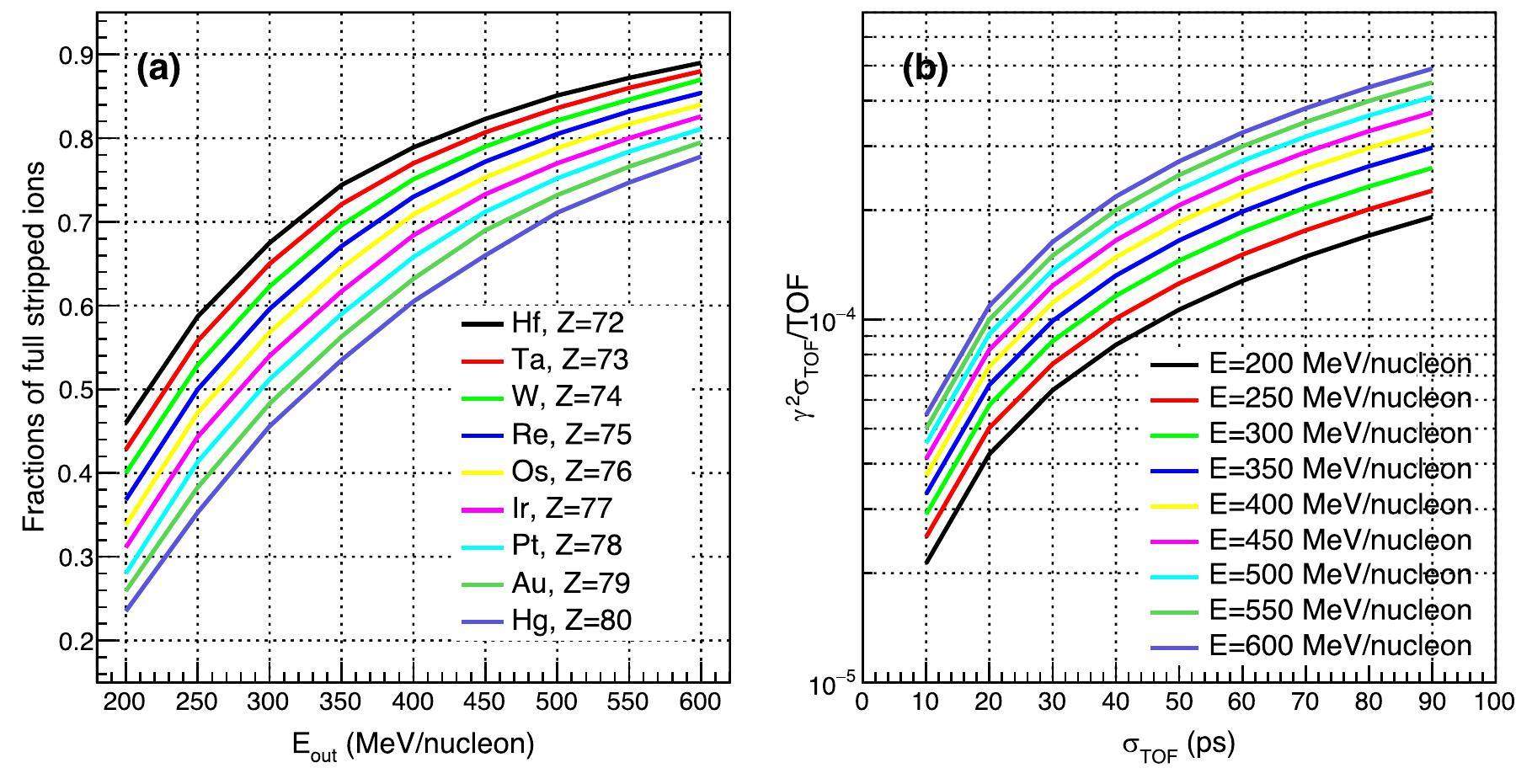
Based on the contributions of the position measurement accuracy (~9.9×10^-5) and TOF measurement accuracy (~5×10^-5) obtained above, the mass resolution of ~1.1×10-4 can be obtained from Eq. (5), which corresponds to ${\sigma }_{\text{m}}$ 460 keV for ~ 2000 statistical events and neutron-rich nuclei with mass numbers ~200 near N=126. The accuracy of the mass excess is generally sufficient to reveal the evolution of the shell structure and to constrain mass models far from the stability [55].

In addition, the mass shifts contributed by the isomers will be estimated from isomer measurements using the decay detector array at the final focal plane of the HFRS. The fragments will be stopped in the silicon array stopper after the mass measurement, and the germanium detectors installed close to the stopper will be used to detect isomeric $\gamma$-rays. From the measurement of the time elapsed between implantation and the subsequent decay, the isomeric lifetime of the implanted ion can be obtained by correlating the particle identification of the HFRS. Simultaneously, using a stopper composed of multiple highly pixelated Double-Sided Silicon Strip Detectors (DSSDs) such as AIDA [56] or WAS3ABi [57], the implanted nuclei and decay-emitting β -rays can be directly correlated within each pixel of the detector, providing a direct measurement of the β -decay lifetimes. This is critical for understanding the third abundance peak in the r-process.

Simulation and analysis

With the HFRS separator at the HIAF facility, many neutron-rich nuclei around N=126 can be produced, and their properties, such as mass and lifetime, can be experimentally measured. This is of great significance for expanding nuclide maps, developing nuclear theories, and understanding the origins of heavy elements in the universe. In this section, we first introduce the high-resolution optical mode of the HFRS specifically developed for Bρ–TOF mass measurement experiments. The production, separation, identification, and nuclear mass measurement accuracy are then studied with the Monte Carlo simulation program MOCADI [58] using high-resolution ion optics for neutron-rich nuclei around N=126.

3.1

High resolution ion-optics

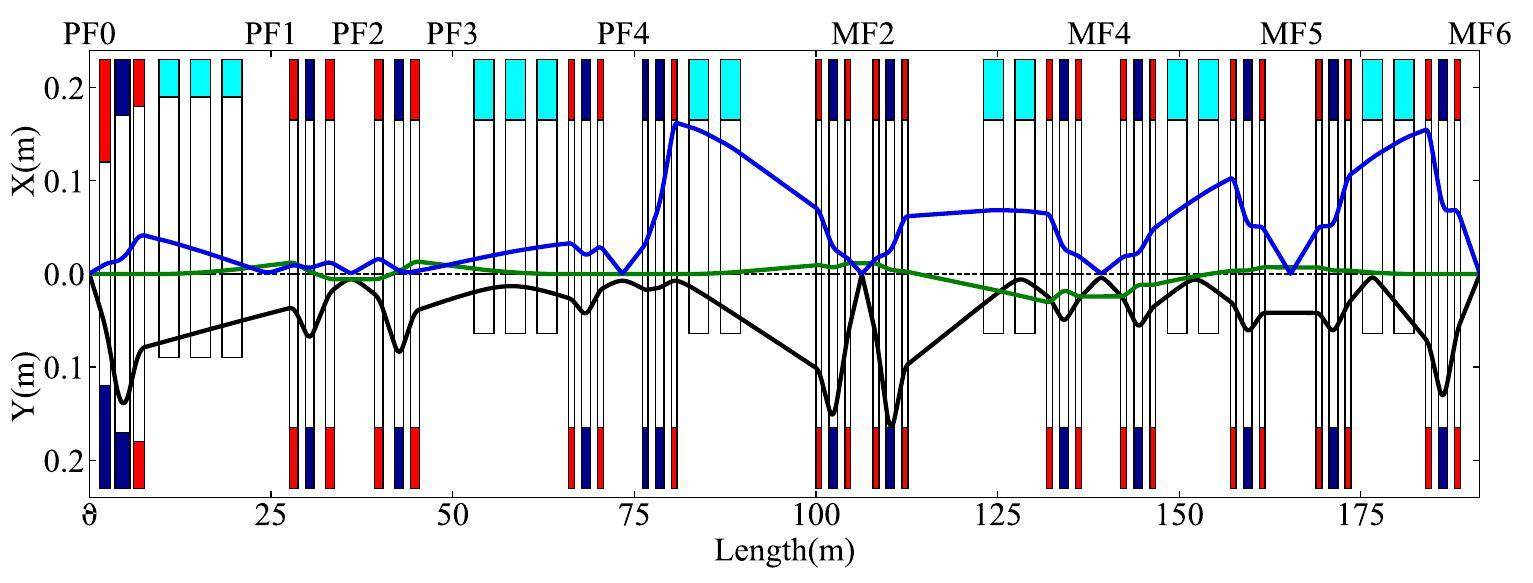
For Bρ –TOF mass measurement experiments, the pre-separator of the HFRS will be used as a separator, and the main separator will be used as a spectrometer. A high-resolution ion optics of the spectrometer is necessary to accurately measure the ion magnetic rigidities. Using parameterized magnetic field distributions [31], the high-resolution ion optics were designed using the codes of Winagile [59] and GICOSY [60]. Figure 3 shows the beam envelopes with initial beam spot sizes X=± 1 mm and Y=± 1.5 mm. To improve the momentum resolution compared with the normal mode [31], the horizontal angular acceptance is decreased to ± 5 mrad, and the momentum acceptance is reduced to ± 0.2 %. The maximum magnetic rigidity also decreases from 25 Tm to 15 Tm. The vertical angular acceptance remains unchanged at 25 mrad. The momentum-resolving powers at PF2 and MF4 are 1270 and 7440, respectively, for an emittance of 5  mm mrad and a horizontal beam spot size of ± 1 mm. The momentum dispersion at MF4 is 12 cm/%. With this dispersion, the uncertainty of ${\sigma }_{B\rho }/B\rho$ can be estimated to be approximately ~4.17×10^-5 using a typical resolution of ~0.5 mm (σ) for the position detector in the dispersive plane.

Fig. 3Full-screen View

(Color online) Beam envelopes for high-resolution ion-optics. The blue line and the black line correspond to an emittance in the X-direction and Y-direction of 5 πi and 37.5  mm mrad, with an object size of ± 1 mm and ± 1.5 mm at the PF0, respectively, while the dispersion line (green) represents a momentum deviation of +0.2 %

3.2

Production and separation

To produce neutron-rich nuclei around N=126 via a fragmentation reaction, the available projectiles primarily include ²⁰⁸Pb and ²³⁸U. Both types of projectiles were used in the simulations. For a specific nucleus of interest, the use of Pb or U fragmentation is determined based on the calculated yields. The Booster Ring (BRing) synchrotron of the HIAF facility has a maximum magnetic rigidity of 34 Tm, and can accelerate ²⁰⁸Pb³¹⁺ and ²³⁸U³⁵⁺ ions to 850.74 and 833.15 MeV/nucleon, respectively. The beam intensities of Pb and uranium were as high as those of 1.1×10¹¹ and 1.0×10¹¹ ions per pulse, respectively. The typical beam extraction time in slow extraction mode was 3 s with a repetition period of 13 s. The corresponding beam spots in the X and Y directions on the production target were assumed to be Gaussian distributions with standard deviations of 0.4 mm and 0.6 mm, respectively.

Taking the production of ²⁰⁴Au ions as an example, the production and separation ability of neutron-rich nuclei around N=126 is simulated and studied using the high-resolution ion optics of the HFRS. In the simulation, a graphite target installed on the PF0 focal plane was used as the production target. The thickness of the graphite target was set to 4.4 g/cm² for both Pb and U fragmentation reactions, which corresponded to 50.1 % of the Pb range and 56.5 % of the U range, respectively. In addition, 75 mg/cm² niobium foil was placed behind the production target to achieve efficient electron stripping in both reactions. More than 75 % of the ²⁰⁴Au ions are fully stripped, which is important for high transmission.

To purify the fragments of interest, an achromatic Al degrader placed on the PF2 dispersive plane was used. As mentioned above, when the ion energy behind the Al degrader is greater than 350 MeV/nucleon, the fraction of fully stripped ions is higher than 50 % for neutron-rich nuclei around N=126. Therefore, the thickness of the degrader was optimized such that the energy of the fragments of interest was greater than 350 MeV/nucleon. The center thickness of the Al degrader was set to 44 % and 36.8 % of the ²⁰⁴Au range for the Pb and U fragmentation reactions, respectively. This thickness combination of the production target and degrader ensures that the ²⁰⁴Au ion has approximately 356 MeV/nucleon of kinetic energy after passing through the degrader. The Global calculations show that the proportion of fully stripped ²⁰⁴Au ions at this energy is as high as 57 %. Considering the proportion of fully stripped ions, the HFRS magnetic rigidity was set according to the fully stripped ions in both reactions.

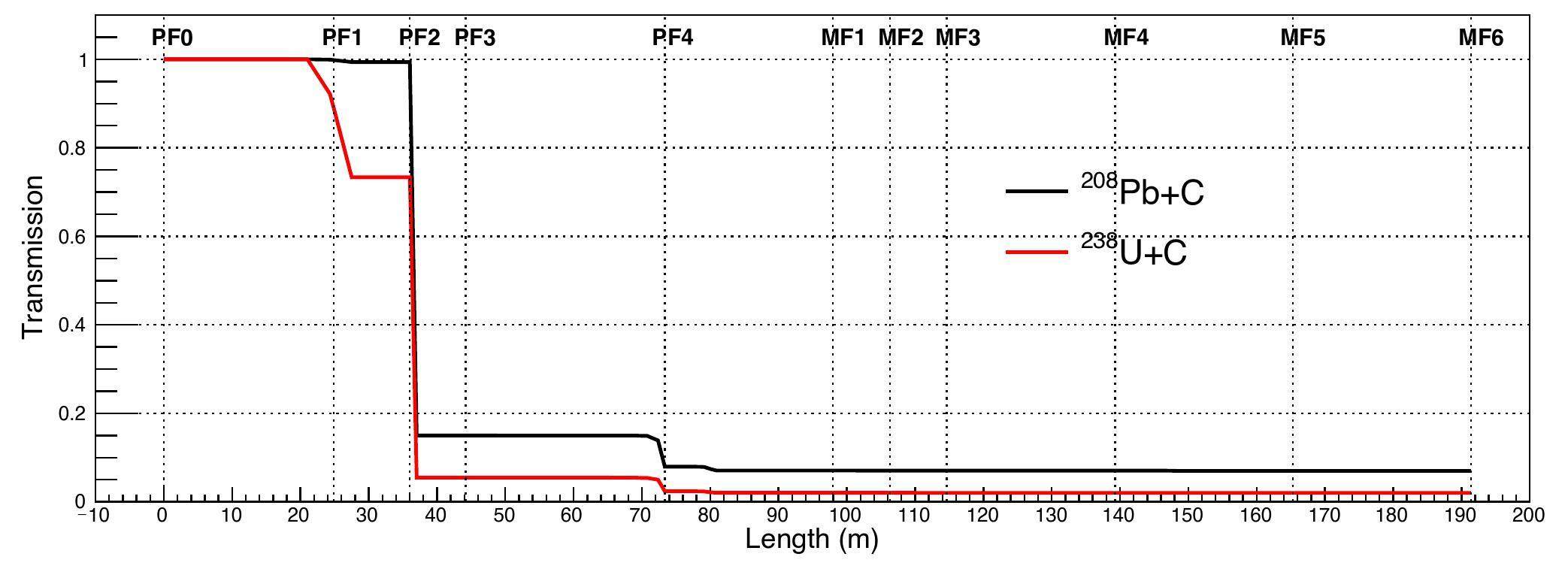
Figure 4 shows the simulated transmissions of the ²⁰⁴Au fragment from the Pb and U fragmentation reactions as functions of the separator length. A significant decrease is observed near PF1 and PF2. This is primarily caused by momentum deviation. At the PF2 focal plane, the momentum slits were set to allow fragments with ± 0.2 % momentum deviation to pass through. In addition, the transmission of the ²⁰⁴Au fragments produced by U fragmentation exhibits a greater reduction than that of Pb fragmentation owing to the larger momentum deviation. This is because in the U fragmentation reaction, more nucleons need to be eliminated to produce ²⁰⁴Au, which results in a greater momentum deviation of ²⁰⁴Au fragments according to the Goldhaber model [61]. The opening of the mass slits placed at the PF4 focal plane can be adjusted based on the desired transmission and the number of nuclei required for mass measurements. In the simulations, the mass slits were set to ± 5 mm. They also cause a decrease in the transmission owing to the charge-state population of the fragments. In the final focal plane, the transmission of ²⁰⁴Au ions is 7 % and 2 % for Pb and U fragmentation, respectively. These transmissions are significantly lower than those under the normal optical modes described in Ref. [31] primarily because of the lower momentum and horizontal angular acceptances of the high-resolution optical mode.

Fig. 4Full-screen View

(Color online) Simulated transmissions of the fragmentation product ²⁰⁴Au as a function of the length of the HFRS separator under the high-resolution mode

The yields and purities of the ²⁰⁴Au ions produced from the Pb and U fragmentation reactions were estimated and are shown in Fig. 5 (a) and (b). The area of the isotopes in the $N-Z$-plane represents the corresponding yields in the MF6 focal plane. The yields were obtained from the product of the production cross-section, number of target nucleons per unit area, and transmission. The parameterized FRACS formula can provide a good description of the production cross-section estimations [62]. The number of target nucleons per unit area was calculated based on target thickness. The transmission was obtained from the MOCADI simulations. In addition, to assess the purity, nuclei located in the region of $Z\pm 10$ and $N\pm 10$ around the ²⁰⁴Au nucleus were selected for the simulation. Purity is defined as the ratio of the yield of the fragment of interest to the total. From Fig. 5, one can observe that for ²⁰⁴Au ions, the Pb fragmentation reaction has a yield of up to 9.09×10⁴ ppp and a purity of approximately 3.69 %. The yield and purity of the ²⁰⁴Au ions from the Pb fragmentation are higher than those from the U fragmentation reaction. Therefore, Pbfragmentation will be used to produce ²⁰⁴Auions in future experiments.

Fig. 5Full-screen View

(Color online) Purification quality of the HFRS for the ²⁰⁴Au ions produced by (a) ²⁰⁸Pb fragmentation and (b) ²³⁸U fragmentation under high resolution optical mode

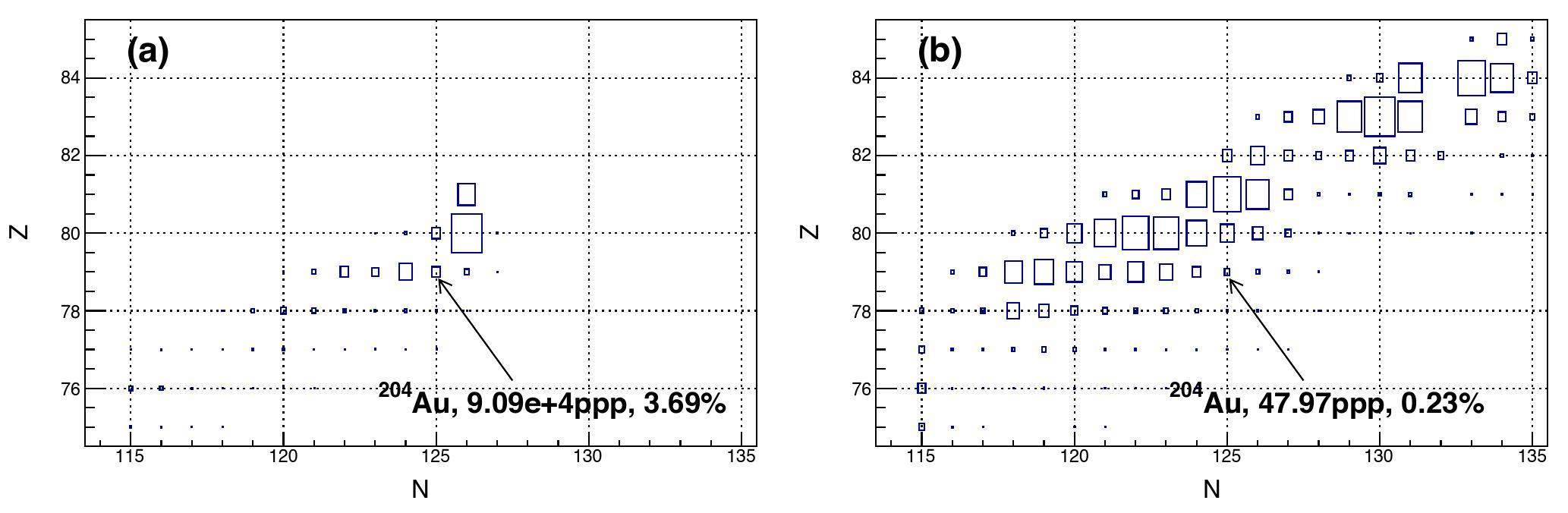
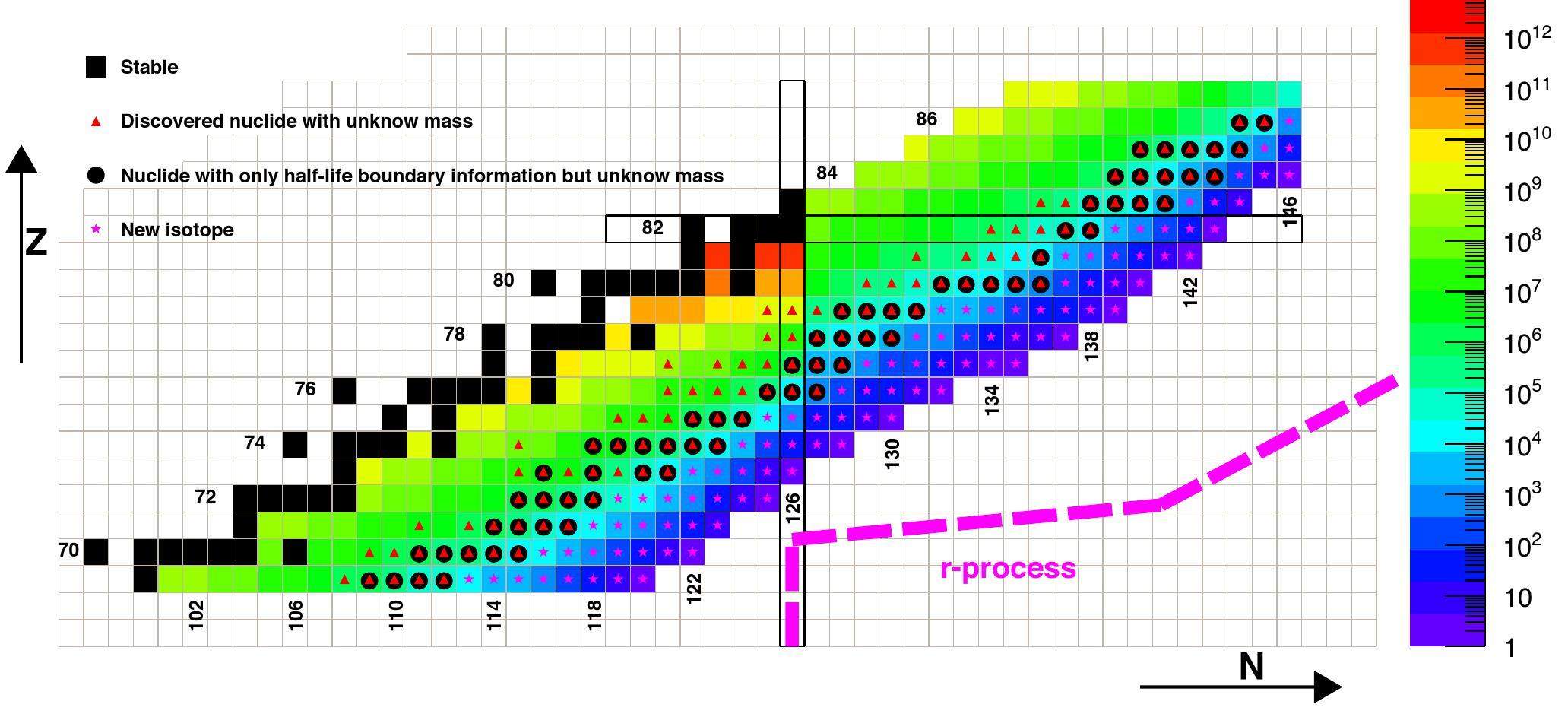
Using the calculated cross-sections and simulated transmissions, the yields of the neutron-rich nuclei around N=126 are estimated, as shown in Fig. 6. In the estimations, the primary beam, production target, and settings of the HFRS are similar to examples of the production and purification of ²⁰⁴Au ions. The production cross-sections were calculated using the FRACS formula. Based on the aforementioned simulation results, the transmission of fragments from the Pb and U fragmentation reactions was fixed at 7 % and 2 %, respectively. This figure presents the results of a 5-day experiment, showing the maximum yields of the fragments of interest produced through the fragmentation reactions of Pb or U. Many new neutron-rich nuclei approaching the r-process could be produced for the first time, along with a substantial yield of neutron-rich nuclei with unknown masses and lifetimes. This indicates that the HIAF-HFRS facility has great potential for research on the production and properties of neutron-rich nuclei around N=126.

Fig. 6Full-screen View

(Color online) Estimated yields of the neutron-rich nuclei around N=126 using the FRACS formula and the simulated transmissions. The maximum fragment yields produced by the fragmentation of Pb or U with a 5-day beam time are shown. The mass and lifetime information is extracted from NUBASE2020 [63]

3.3

Identification and mass measurement

Taking the production of ²⁰⁴Au ions by Pb fragmentation as an example, the particle identification and accuracy of the mass measurement using the Bρ –TOF method will be studied in this section.

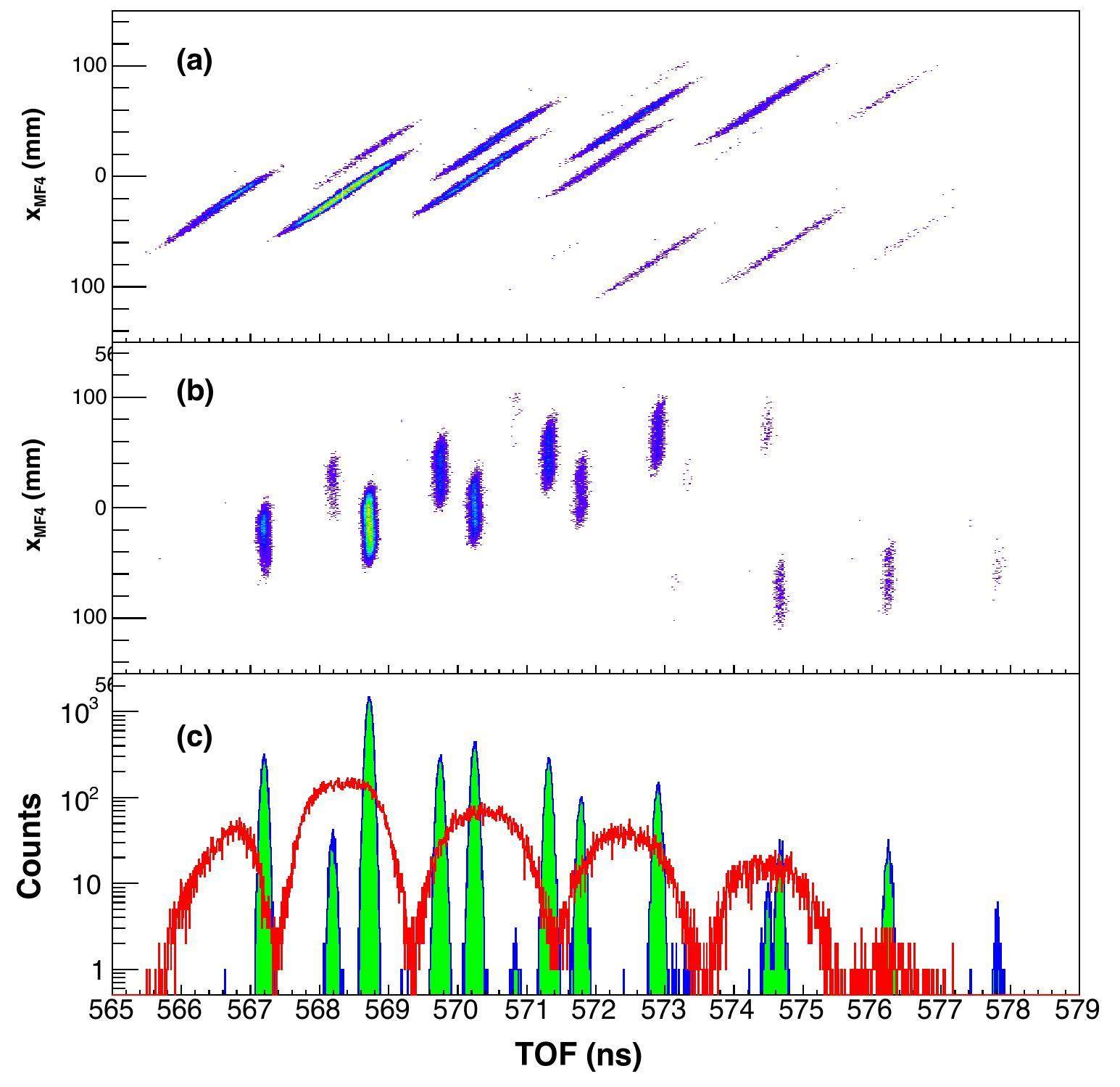
As mentioned above, the particle identification will be achieved using the Δ E–TOF–Bρ method. In the simulation, the influence of the material thickness of TOF and position detectors on ion transmission and identification was ignored. This is because they have a thinner thickness compared to the range of the fragments of interest. The thickness of the MUSIC energy-loss detector was equivalent to that of 300 μm-thick silicon. The time resolution (σ) of the TOF system was assumed to be 30 ps. The position resolution (σ) of the position detector in the dispersive plane and the energy resolution (σ) of the Δ E detector were set to 0.5 mm and 0.4 %, respectively. To obtain unambiguous particle identification, it is essential to correct the TOF values using the measured dispersive position information at the MF4 focal plane. This eliminates the magnetic rigidity dependence from the measured TOF spectra. A two-dimensional correlation between TOF and the horizontal position x in the MF4 dispersion plane for the Au isotopes is shown in Fig. 7(a). For all nuclides, the deviation between their TOF and the central time-of-flight TOF₀ can be corrected using a linear function of the dispersive position x: ${\text{TOF}}_0=\text{TOF}-kx\mathrm{,}$ (6) where k is the slope of the fitted linear function. The corrected TOF vs. x spectrum is shown in Fig. 7 (b)). The original and corrected TOF spectra of the Au isotopes are compared in Fig. 7(c)). It is evident that the corrected TOF has a better resolution, which is beneficial for particle identification.

Fig. 7Full-screen View

(Color online) (a) Two dimensional correlation between the TOF and the horizontal position x of the dispersion plane for Au isotopes. (b) Corrected TOF vs. x spectrum. (c) Corrected TOF spectra (filled histograms) compared with raw ones (histograms with red lines)

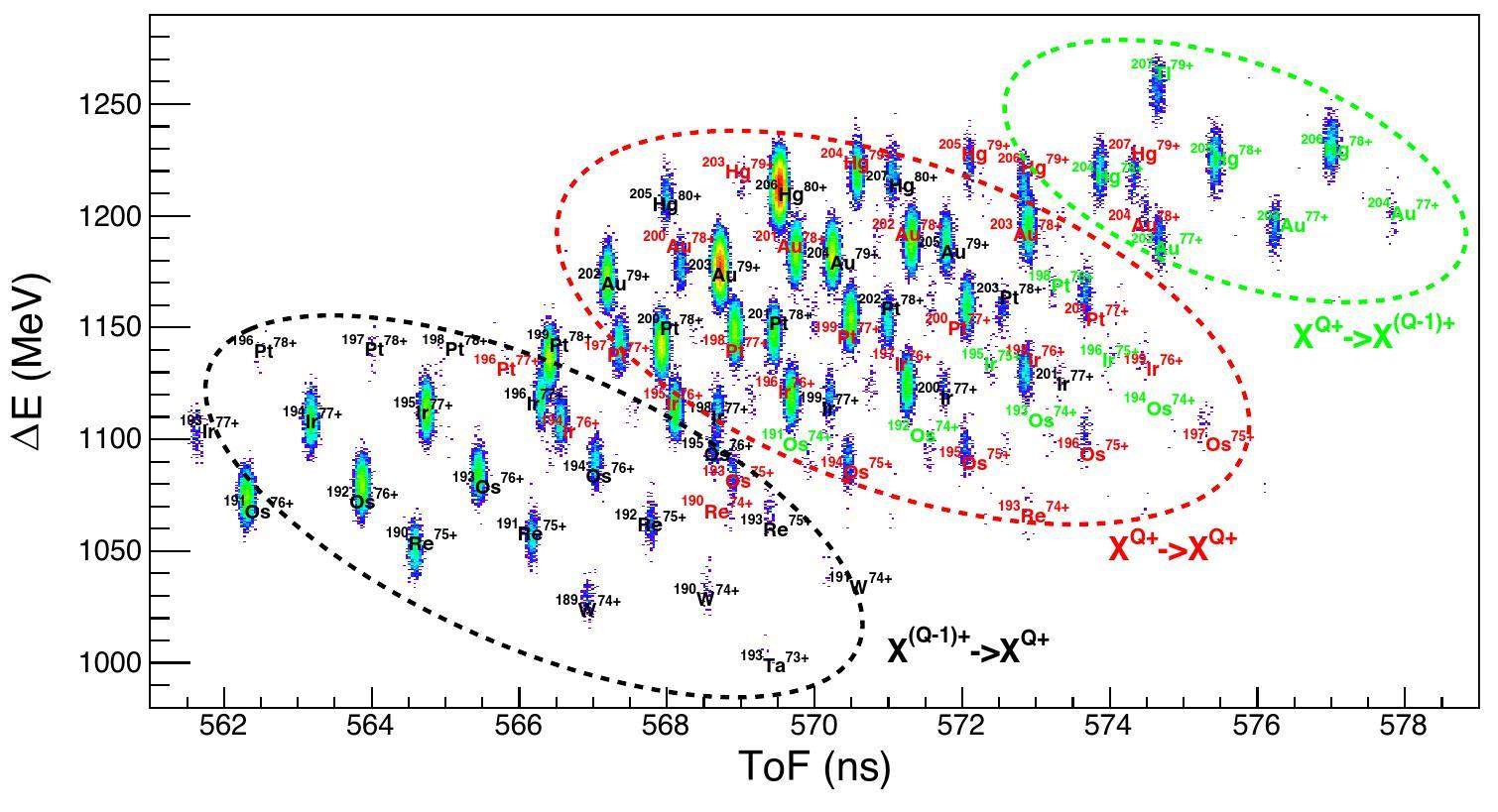
The two-dimensional correlation spectrum of the measured Δ E and corrected TOF can provide unambiguous particle identification, as shown in Fig. 8. The cocktails are unambiguously identified using an isomer-tagging method. In this experimental setting, the charge states between the fully stripped ions and helium-like ions are observed. As the fragments of interest are around $A=2.58\times Z$, the hydrogen-like ions ${}^A{Z}^{(Z-1)+}$ general appear between the fully stripped ions with ${}^{A+2}{Z}^{Z+}$ and ${}^{A+3}{Z}^{Z+}$, and the helium-like ions ${}^A{Z}^{(Z-2)+}$ appear between the ions with ${}^{A+5}{Z}^{Z+}$ and ${}^{A+6}{Z}^{Z+}$ in the TOF spectra. This rule is useful for identifying particles. In addition, the degrader installed on the PF2 dispersive plane changed the charge-state population of the fragments passing through it. The nuclides circled with a red dashed line remain unchanged in the charge-state before and after degrader. The nuclides stripped of one electron by the degrader fall into a circle with a black dashed line. Under the same magnetic rigidity, these nuclides exhibit higher velocities and shorter flight times. In contrast, the nuclides that capture an electron from the degrader have lower velocities and longer flight times, as indicated by the green dashed line in Fig. 8.

Fig. 8Full-screen View

(Color online) Two dimensional correlation spectrum of the measured Δ E and the corrected TOF. Fully stripped fragments, hydrogen-like fragments, and helium-like fragments are labeled with black fonts, red fonts, and green fonts, respectively. The black, red, and green circles indicate the isotopes stripped of one electron, the isotopes whose charge states are unchanged, and the isotopes that captured an electron at the PF2 degrader, respectively

Using the obtained particle identification spectra, we will study the mass measurement precision of the neutron-rich nuclei around N=126 using the Bρ–TOF method on the HFRS. The data analysis methodology is consistent with that described in Refs. [64, 65]. Typically, nuclei with known masses are used to calibrate the relationship between time-of-flight and mass-to-charge ratios. This can help remove many uncertainties in mass measurement experiments. Among the identified cocktails, ten fully stripped nuclides with well-known masses, according to the 2012 Atomic Mass Evaluation (AME2012) [66], were selected as calibrants. In addition, these chosen nuclides have only known isomers with excitation energies below 454 keV, which corresponds to the typical mass accuracy obtained using the Bρ -TOF technique. The calibrants and their atomic mass excess values with uncertainties are listed in the left-hand columns of Table 1. The right-hand columns of Table 1 list the nuclides to be measured and their mass excess values obtained from the literature [66].

Table 1Full-screen View

Nuclides and their atomic mass excess values with uncertainties used for the calibration and measurement [66]

Calibration nuclides			Nuclides to be measured
Isotope	AME2012 (keV)	σm (keV)	Isotope	AME2012 (keV)	σm (keV)
194Os	-32437.2	2.78	198Ir#	-25821#	196#
195Osm	-29511.6	60.55	200Ir#	-21611#	196#
196Os	-28278.8	10.06	201Ir#	-19897#	196#
196Irm	-29437.9	38.42	202Pt	-22692.1	25.15
197Irm	-28265.8	20.12	203Pt#	-19627#	196#
199Ir	-24400.2	41.06	203Au	-23143.5	3.08
199Ptm	-27390.4	2.22	204Au#	-20650#	200#
200Pt	-26600.9	20.12	205Au#	-18770#	196#
201Pt	-23740.9	50.1
202Au	-24353.0	23.29

Show more

Isotopes with known isomers with excitation energies below 454 keV are shown with ^m, and isotopes with estimated atom mass excess are labeled with ^#

The nuclear mass m can be determined from the corresponding atomic mass ma using the following formula: $m=m_{\text{a}}-Z{m}_{\text{e}}+B_{\text{e}}\left(Z\right)\mathrm{,}$ (7) where Z and m_e represent the nuclear charge number and the electron rest mass, respectively. $B_{\text{e}}\left(Z\right)$ denotes the total binding energy of extranuclear electrons. It is calculated using the following approximate formula [67]: $B_{\text{e}}\left(Z\right)=14.438Z^{2.39}+1.55468\times {10}^{-6}{Z}^{5.35}\left[\text{eV}\right]\mathrm{.}$ (8) From the corrected TOF spectra, a Gaussian fitting function was employed to extract the centroids and standard deviations of the TOFs for both calibration and measurement nuclides. Then, we can obtain the mass calibration function $f(\tau \mathrm{,}Z)$ according to the relationship between the time-of-flight centroids $\tau$ and mass-to-charge ratios m/q as follows: $f(\tau \mathrm{,}Z)=m/q=a_0+a_1\tau +a_2{\tau }^2+a_3\tau Z+a_{4}Z+a_5{Z}^2\mathrm{,}$ (9) where ai are the fit parameters. The terms related to Z must account for the impact of energy loss in the wedge degrader in the PF2 dispersive plane. The fit parameters in Eq. (9) were determined using an iterative ${\chi }^2$ minimization procedure: ${\chi }^2={\displaystyle \sum _{i=1}^n\frac{{\left[{\left(m/q\right)}_{i\mathrm{,}\text{AME}}-f\left({\tau }_i\mathrm{,}{Z}_i\right)\right]}^2}{{\left({\sigma }_{\text{AME}}\right)}_i^2+{\left({\sigma }_{\text{stat}}\right)}_i^2}},$ (10) where n is the number of the calibrants, ${\left(m/q\right)}_{i\mathrm{,}\text{AME}}$ is each calibration mass-to-charge ratio from AME2012 [66], ${\left({\sigma }_{\text{AME}}\right)}_i$ and ${\left({\sigma }_{\text{stat}}\right)}_i$ denote the uncertainty of the mass-to-charge ratio from the literature [66] and the statistical uncertainty, respectively. The statistical uncertainty was calculated based on the TOF measurement uncertainty: ${\left({\sigma }_{\text{stat}}\right)}_i^2=\frac{{\sigma }_{i\mathrm{,}\text{TOF}}^2}{N_i}{\left(a_1+2a_2\tau +a_{3}Z\right)}^2\mathrm{,}$ (11) where ${\sigma }_{i\mathrm{,}\text{TOF}}$ is the standard deviation of the TOF distribution and Ni is the statistical count for each calibration.

After obtaining the fit parameters, the masses of these measured nuclides were calculated from the corresponding time-of-flight centroids using Eq. (9) as follows: The total uncertainties in the mass results mainly included statistical, fitting, and systematic uncertainties. The statistical uncertainty can be estimated using Eq. (11). The fitting uncertainty σ_fit originates from the uncertainty in the calibration function parameters. This was calculated from the error propagation based on Eq. (9), ${\sigma }_{\text{fit}}^2={\displaystyle \sum _{j=0}^5{\displaystyle \sum _{i=0}^5\left[{\sigma }_{ij}^2\frac{\partial f\left(\tau \mathrm{,}Z\right)}{\partial a_j}\frac{\partial f\left(\tau \mathrm{,}Z\right)}{\partial a_i}\right]}}\mathrm{,}$ (12) where ${\sigma }_{ij}$ denotes the covariance of the fit parameters. We can perform this fit using the TMinuit class of the CERN root package [68], which provides an estimation of the covariance matrix. The systematic uncertainty σ_sys mainly originates from the velocity difference caused by the change in the charge-state in the wedge degrader and the method employed to correct TOF by the dispersive position. We can use the method of cross-validation of the calibration nuclides to evaluate the systematic errors. Assuming a total of n calibration nuclides, we determined the m/q value for each nuclide by calibrating the fitting function in Eq. (9) with the remaining $n-1$ nuclides. Then, the normalized chi-square value can be calculated as ${\chi }_{\text{norm}}^2=\frac{1}{n}{\displaystyle \sum _{i=1}^n\frac{{\left[{\left(m/q\right)}_{i\mathrm{,}\text{AME}}-{\left(m/q\right)}_{i\mathrm{,}\text{fit}}\right]}^2}{{\left({\sigma }_{\text{AME}}\right)}_i^2+{\left({\sigma }_{\text{stat}}\right)}_i^2+{\left({\sigma }_{\text{fit}}\right)}_i^2+{\sigma }_{\text{sys}}^2}}\mathrm{,}$ (13) The differences between the masses from the literature [66] and the values given by the fitting function as a function of the mass-to-charge ratio are shown in Fig. 9 for the calibration nuclides (circles) and measured nuclides (squares), the atomic mass excess results and the different contributions to the total uncertainties for both the calibration and measured nuclides are listed in Table 2. The statistical uncertainties were estimated using 5-day statistical counts with Eq. (11). The ²⁰¹Ir, ²⁰³Pt, and ²⁰⁵Au nuclei listed in Table 2 exhibit significant fitting uncertainties. This is because these nuclei have larger mass-to-charge ratios than the calibration nuclides, and their masses were extrapolated. Suppose more calibration nuclides are selected to cover the mass-to-charge ratios of the measured nucleus; smaller fitting uncertainties can be obtained. The systematic uncertainty was determined as 7.73 keV/q to achieve a normalized chi-square value of unity in Eq. (13). From Table 2, the total measurement uncertainties mainly originate from the system uncertainties. This is mainly caused by the TOF correction. Using more measurement information, such as the position and angle information at PF4 or MF6, may reduce system uncertainties. The total measurement uncertainty of the measured nuclei is better than that of 900 keV. This measurement accuracy meets the requirements of some physical studies, proving that the properties of some neutron-rich nuclei near N=126 can be studied using the HFRS separator.

Fig. 9Full-screen View

(Color online) Differences between the fit masses and the values from AME2012 as a function of the mass-to-charge ratio. The circles and squares represent the results of the calibration and measured nuclides, respectively. The error bars of the calibration nuclides include the uncertainty in the literature and the uncertainty in the total measurement. The uncertainty of the measured nuclides is only the total measurement uncertainty

Table 2Full-screen View

Nuclides and their atomic mass excess values with uncertainties obtained from the mass calibration function

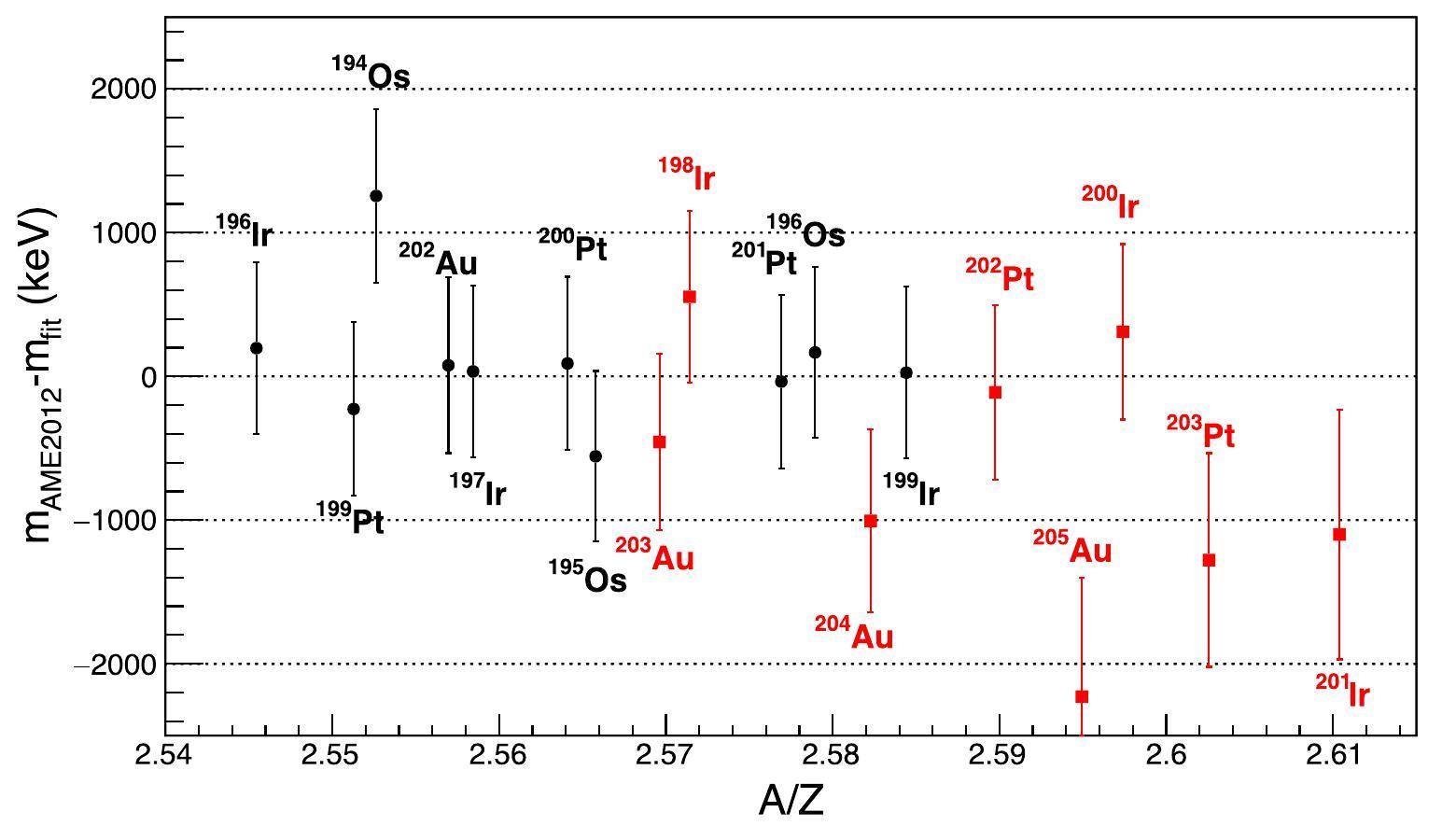
Isotope	mfit (keV)	σtotal (keV)	Uncertainties
			σstat (keV)	σfit (keV)	σsys (keV)
194Os	-33701.6	606.26	106.78	104.37	587.59
195Osm	-28961.5	593.94	77.02	39.7	587.59
196Os	-28447.8	595.61	91.99	32.14	587.59
196Irm	-29637.7	598.31	26.19	53.73	595.32
197Irm	-28296.1	595.85	22.64	10.88	595.32
199Ir	-24435.8	596.86	41.33	11.57	595.32
199Ptm	-27171.2	603.37	12.0	15.49	603.05
200Pt	-26692.6	603.15	8.94	6.25	603.05
201Pt	-23709.1	603.23	12.98	6.77	603.05
202Au	-24438.1	611.98	7.84	37.54	610.78
198Ir#	-26374.9	596.01	28.11	11.87	595.32
200Ir#	-21921.2	611.06	61.41	123.38	595.32
201Ir#	-18796.2	868.45	118.62	621.08	595.32
202Pt	-22580.8	608.4	19.88	78.02	603.05
203Pt#	-18348.8	743.61	35.16	433.65	603.05
203Au	-22687.2	613.34	3.65	55.82	610.78
204Au#	-19643.5	635.88	5.96	176.81	610.78
205Au#	-16541.0	827.99	10.64	558.92	610.78

Show more

Different contributions to the total uncertainties are shown. Isotopes with estimated atom mass excess in the literature [66] are labeled with ^#

Summary

The properties of N=126 neutron-rich nuclei play a crucial role in developing nuclear theories and understanding the r -process abundance peak around A=195. To produce these neutron-rich nuclei while measuring their mass and lifetime, an experimental scheme has been proposed based on the HIAF-HFRS facility, and the feasibility of this scheme was evaluated through simulations in this study.

In these studies, a high-resolution optical mode for the HFRS was developed. It has a large momentum dispersion of 12 cm/% at the MF4 dispersive plane, which is beneficial for improving the accuracy of magnetic rigidity measurements in Bρ -TOF mass measurement experiments. In this high-resolution optical mode, the yields of neutron-rich nuclei around N=126 produced from the ²⁰⁸Pb or ²³⁸U fragmentation reactions were estimated using the FRACS formula and simulated transmissions. The results show that many new neutron-rich nuclei approaching the r-process abundance peak around A=195 can be produced for the first time, and many nuclei with unknown masses and lifetimes can be produced with high statistics. Moreover, using the time-of-flight corrected by the measured dispersive position information and energy loss information, the cocktails produced from the ²⁰⁸Pb fragmentation can be unambiguously identified, and the masses of some neutron-rich nuclei around N=126 can be measured with an accuracy better than 900 keV using the Bρ -TOF technique. Using this new mass data combined with machine learning based on the Bayesian neural network, as described in Refs. [7, 8], the nuclear mass of this region can be accurately predicted, which is crucial for understanding the r-process abundance peak around A=195. These simulation results indicate that the HIAF-HFRS facility can provide an opportunity for the production and property research of neutron-rich nuclei around N=126.

Currently, the HIAF-HFRS facility is under construction. All devices, including magnets, vacuum, power supplies, targets, degraders, detectors, etc., are expected to be completed and tested by the end of 2024, after which they can be installed on-site. Meanwhile, some high-performance detectors for TOF and position measurements used in Bρ -TOF mass measurement experiments have been proposed. For example, a plastic scintillator detector coupled with multiple photomultiplier tube readouts and a diamond detector are being developed for time measurement, and a position-sensitive microchannel plate detector with a large active area is being developed for position measurement. These conditions may ensure the performance of future property research experiments of neutron-rich nuclei around N=126.