Introduction
In recent years, many theoretical and experimental works have focused on studying the reaction mechanism of weakly bound nuclei [1-13]. 6Li is commonly utilized in experiments because of its α+d cluster structure and low breakup threshold, resulting in complex reactions and diverse reaction mechanisms.
Because of the combined influence of Coulomb and nuclear interactions, 6Li might break up when approaching the target, giving rise to complete and incomplete fusion (CF and ICF) depending on whether all the projectile fragments are captured or not. Besides, a transfer reaction is a process involving the direct transfer of one or more nucleons between the projectile and target.
The investigation of the coupling between the transfer and fusion processes has been a hot topic in recent years with a series of related publications [14-24].
The one-neutron stripping process in 6Li+96Zr [14] and 6Li+89Y [15] has been investigated to analyze the influence of transfer reaction on fusion. In both studies, it was concluded that the one-neutron stripping cross section has the same magnitude as the CF cross section around the Coulomb barrier and drops more gradually than the CF cross section in the sub-barrier region. Similar results were obtained in several other experiments, for instance, in 6Li+198Pt [17], 7Li+198Pt [18],6,7Li+197Au [19], and 6,7Li+64Zn [20]. In the investigation of 9Be+169Tm,181Ta,187Re, Fang et al. [21] quantitatively studied the relationship between the ratio of transfer to fusion cross section with the incident beam energy. The result showed that the ratio attained a value of 10 when the beam energy was 10% lower than the barrier energy. Their research, along with the study in [25], has demonstrated that although the one-neutron transfer cross section holds significant importance in the sub-barrier region, its impact on the CF excitation function above the barrier is negligible.
The mechanism of (d,p) reactions, which is the most popular neutron-stripping reaction mechanism, is widely employed in the study of nuclear structure for the investigation of single-particle nature, spectroscopic factor, etc. [26-30]. For example, the (d,p) reaction was employed in 120, 124Sn [31, 32], 198Pt [33], and 96Zr [34] targets to investigate the nuclear structure of 121, 125Sn, 199Pt, and 97Zr. In contrast, the same one-neutron transfer channel has been studied using (6Li,5Li) reactions, such as 124Sn(6Li,5Li)125Sn [35], 198Pt(6Li,5Li)199Pt [17], 96Zr(6Li,5Li)97Zr [14],and 120Sn(6Li,5Li)121Sn [22] reactions. These investigations mainly concentrated on the reaction cross section and the effect of transfer on the CF cross section.
6Li is commonly recognized as a cluster structure of d+α. Assuming that α does not participate in the neutron transfer process, the (6Li,5Li), and (d,p) reactions are expected to have similar reaction mechanisms. Accordingly, when one finds discernible differences between two one-neutron transfer processes, such as the coupling between inelastic scattering and breakup, such investigations will shed light on the inner structure of the 6Li.
There are numerous researches on the level structure of 210Bi using (d,p) reaction [29, 30, 46-42], giving plenty of information on the different proton-neutron configurations; however, no information on the one-neutron stripping process in 6Li is available. In this work, the experimental result from the 6Li+209Bi reaction has been elucidated, emphasizing the comparison with the (d,p) reaction.
This paper is organized into different sections as follows. Section 2 introduces the experimental setup and experimental details. The data analysis and experimental results are presented in Sect. 3. Section 4 demonstrates the theoretical model and the theoretical calculation process.
In Sect. 5, we compare the CF cross section to the one-neutron transfer cross section and discuss the difference between the (6Li, 5Li), and (d,p) reactions. The summary is given in Sect. 6.
Experimental setup
To obtain the one-neutron transfer cross sections of weakly bound nuclei with heavy target nuclei, the experiment of 6Li+209Bi was performed at Legnaro National Laboratories (LNL), Italy. The profile of the experimental setup along the direction of incidence of the beam is shown in Fig. 1. A stable 6Li3+ beam with an average current intensity of 2.0 enA is produced by the Tandem-XTU accelerator. The 6Li beam energies are 28, 30, and 34 MeV, corresponding to 0.99, 1.06, and 1.21 times the height of the Coulomb barrier, respectively. A 550-μg/cm2 209Bi target backed with a 110-μg/cm2 12C foil is situated at the center of the detector array. The 12C foil is used to stop the residuals and eliminate or minimize the Doppler effect of the observed γ-ray.
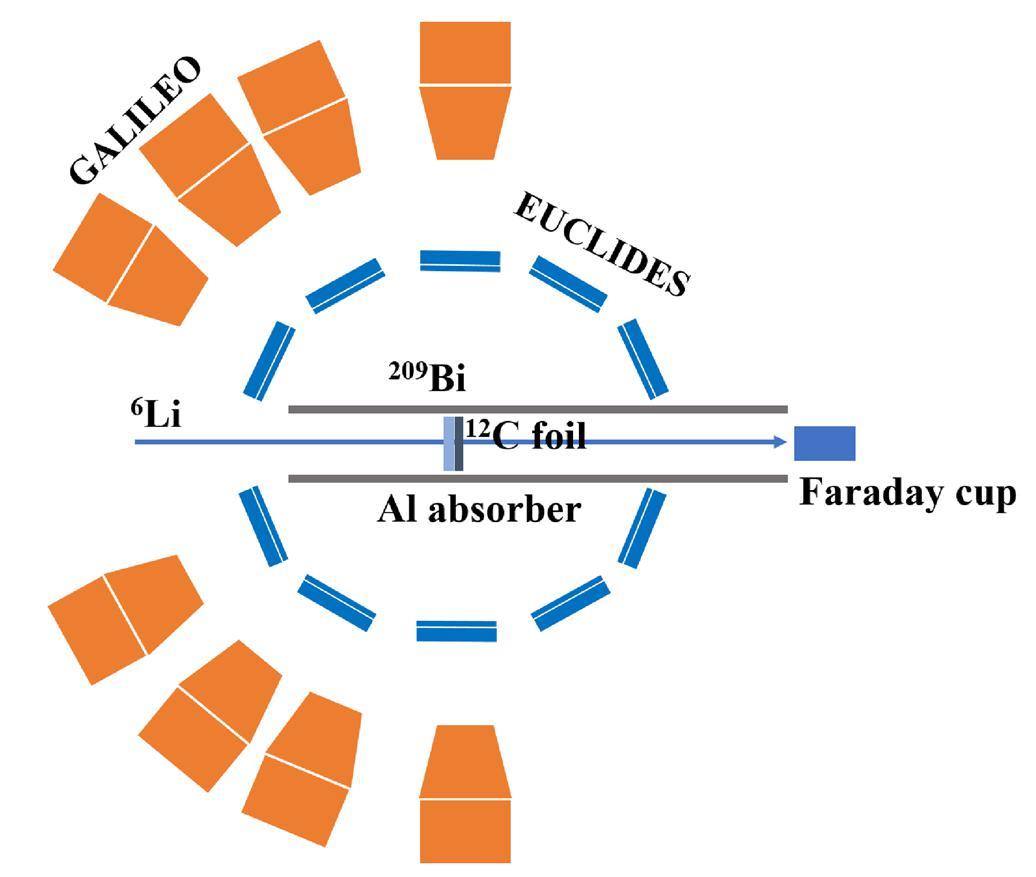
The GALILEO (Gamma detectors Array of Legnaro INFN Laboratories for nuclEar spectrOscopy) array was utilized to detect γ-rays emitted from various residuals. The GALILEO array is made up of 25 HPGe detectors spaced 235 mm apart from the target center and mounted on four support rings at different angles: 152° (5 detectors), 129° (5 detectors), 119° (5 detectors), and 90° (10 detectors). Additionally, each HPGe detector has an anti-Compton BGO crystal detector. The total measured full-energy-peak efficiency was 1.83% at 1408 keV. The energy resolution was 0.20% at 1408 keV transition of 152Eu calibration source (FWHM = 2.88 keV). In this experiment, γ ray energies detected by the GALILEO array range from 30 to 3000 keV.
At the center of the GALILEO array was the Si ball detection array known as EUCLIDES (EUroball Charged Light particle Identification DEtector Sphere). The 40 sets of 130- and 1000-μm-thick ΔE-E telescopes can perform charged particle discrimination.
To protect the Si detectors from the intense scattering particles, a cylindrical aluminum absorber of various thicknesses at different energies was placed in the EUCLIDES along the beam direction.
A Faraday cup (FC) was positioned 3 meters from the end of the beam to measure its intensity. The acquisition system in the experiment was an XDAQ-based, full digital acquisition system [43]. A more thorough explanation of the experimental setup is given in the references [44, 45].
Data analysis and results
In the 6Li+209Bi reaction, it is more challenging to evaporate charged particles than neutrons for a compound nucleus (CN). Thus, the CN of the CF process, 215Rn, mainly decays by evaporating neutrons to form other lighter Rn isotopes. Similarly, the products of α-ICF and d-ICF are mainly At and Po isotopes.
As a result, the 210Bi primarily originates from the one-neutron stripping process in this reaction system. This conclusion is also supported by the statistical evaporation code PACE4 [46].
The typical in-beam single-γ-ray spectrum is displayed in Fig. 2 (a) at Elab=30 MeVE. The γ transitions at 319.5 keV and 162.2 keV can be recognized clearly. Other rays in the spectrum are produced by 6Li reacting with the target 209Bi and the foil 12C, which include 212Rn, 210Po, 209Po, and 13C. Figures 2 (b) and (c) show the coincident spectra with a gate condition on the 319.5 and 162.2 keV transitions, respectively. The γ rays marked in the spectra can be found in the partial level scheme of 210Bi, as shown in Fig. 3. It should be mentioned here that all the levels belong to the identified multiplets organized by different proton-neutron configurations [47, 29] as shown in the same figure. This phenomenon implies that many excited states in 210Bi have been produced directly via the one-neutron stripping process. Because cross sections for high-lying levels are small, it is impossible to identify each one in the single γ-ray spectrum, and one can only obtain the cross section of the low-lying transitions, such as 319.5 and 162.2 keV γ rays.
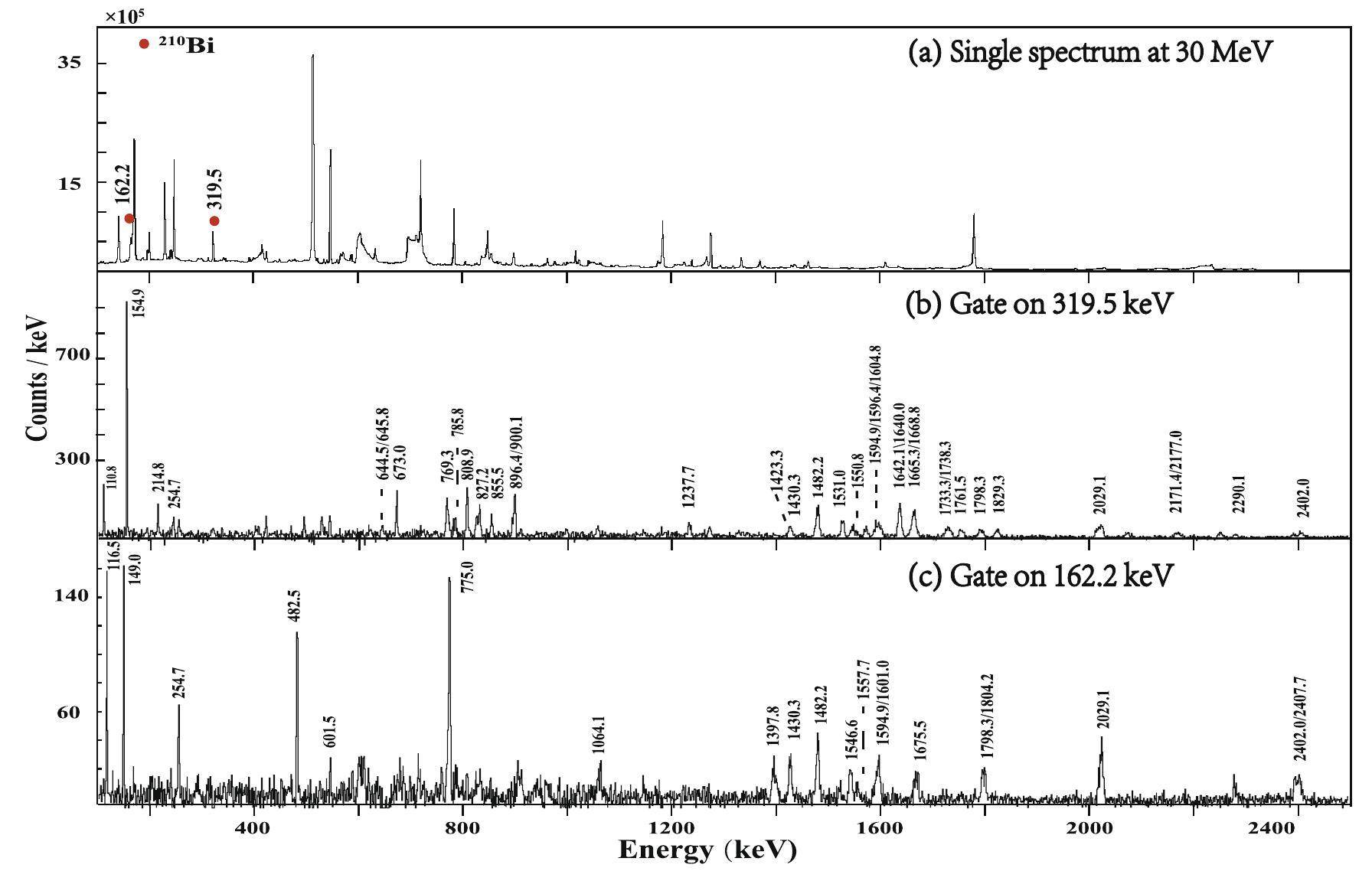
The half-life of 210Bi ground state is 5.01 days, and a long-lived isomer state also exists with a half-life of 3.04×106 years at 271.3 keV (9- state).
In the current experiment, we add the intensities of the 319.5 and 162.2 keV transitions as the one neutron stripping partial cross sections, as shown in Table 1.
| Residual channels | Transition | Eγ (keV) | Feeding state |
|---|---|---|---|
| 210Bi | 2-→ 1- | 319.5 | ground state |
| 7-→ 9- | 162.2 | long-lived isomer state |
In the current work, the cross section for the one-neutron-stripping reaction is obtained as follows:
The uncertainties for the deduced cross section include: (1) the statistical error in γ-rays yield; (2) the error in the efficiency calibration of the detector, which is approximately 3%; and(3) error in the target thickness. The overall error bars range from 5% at Ebeam=34 MeV to approximately 10% at Ebeam=28 MeV. The result is summarized in Table 2.
| E (MeV) | CSExp (mb) | CS1Theo (mb) | CS2Theo (mb) | CS3Theo (mb) | CS4Theo (mb) | CS5Theo (mb) |
|---|---|---|---|---|---|---|
| state of 209Bi | g.s+f7/2+i13/2 | g.s+f7/2+i13/2 | g.s | g.s | g.s+ f7/2 | |
| state of 5Li | g.s | g.s+ p1/2 | g.s | g.s+ p1/2 | g.s | |
| 28 | 16.41 ± 1.71 | 13.77 | 16.86 | 13.61 | 16.85 | 13.77 |
| 30 | 28.81 ± 1.53 | 26.70 | 35.84 | 26.74 | 34.77 | 26.70 |
| 34 | 79.23 ± 4.20 | 47.49 | 66.15 | 47.41 | 68.41 | 47.41 |
Theoretical analysis
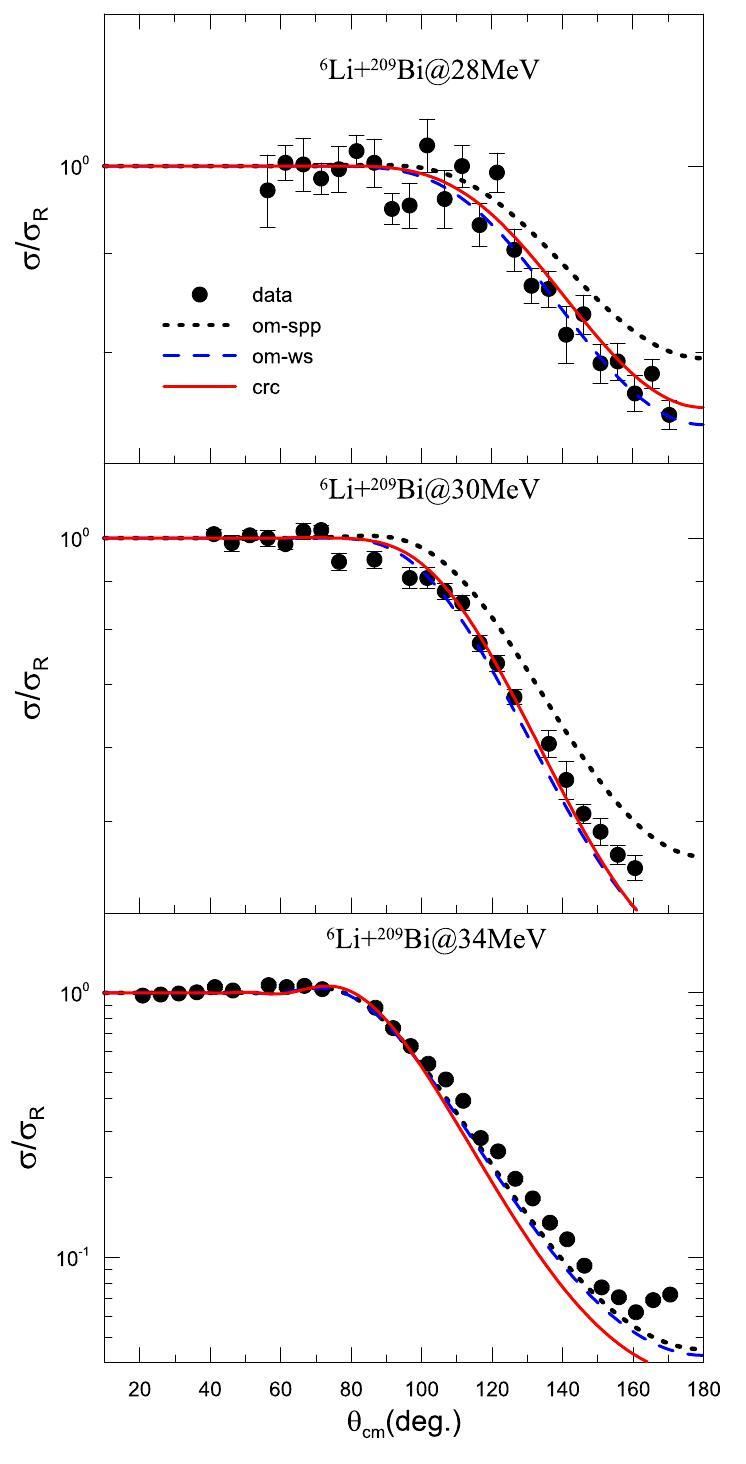
The theoretical one-neutron stripping cross sections for the 209Bi(6Li, 5Li)210Bi* reaction at 28, 30, and 34 MeV incident energies were obtained by performing coupled reaction channel (CRC) calculations using the Fresco code [48]. The optical potential used in the entrance partition (6Li+209Bi) can be obtained from the elastic scattering. The experimental data of the elastic scattering obtained from Ref. [49] were studied. First, the standard São Paulo double folding potential (SPP) [50] was used as an optical potential in the real and imaginary parts (U=(1.0+0.78i)VSPP) in the optical model (OM) calculation. As observed in Fig. 4, the elastic angular distributions are not well described when SPP is used as the potential (dotted line). This is understandable because the systematic is only valid when there is no relevant coupling to the elastic channels. In this case, the coupling to the breakup channel should at least affect the angular distributions of the elastic scattering. Nonetheless, when SPP is used in the real part, and the Woods–Saxon imaginary potential, used in Ref. [49], is employed in the OM calculation, the data description is better (dashed line). However, for the CRC calculation, the coupling of the inelastic scattering states of 209Bi and the transfer channel were explicitly included (red line). Therefore, it was necessary to reduce the depth of the imaginary potential to avoid double counting and consider the loss of flux to other channels. Thus, the depth of the imaginary part was reduced by 10 MeV in each energy, keeping the radius and diffusivity fixed. One can note that the inelastic scattering and transfer channels slightly influence the elastic scattering. For the energies of 28 and 30 MeV, the elastic distributions suffered a slight increase, while the cross section decreased for 34 MeV when compared with the results of the OM calculation, which considered only the ground states of each nucleus in the entrance partition. This behavior at the highest energy was anticipated (E>VB) because the couplings to breakup channels were not included. It is well known that these dynamic couplings produce repulsive polarization potentials that increase VB and hinder the CF fusion cross section, especially at energies above VB [5, 51, 52]. Consequently, the elastic scattering should increase with a decrease in fusion.
The single-particle wave functions were derived using Woods–Saxon potentials for the nuclear interactions in the intrinsic Hamiltonian. Standard reduced radius r0 = 1.25 fm and diffuseness a = 0.65 fm were used to generate the single-particle wave functions for the target and projectile nuclei. The potential depths were varied to fit the experimental one-neutron separation energies.
The coupling scheme for the current calculation is shown in Fig. 5, which depicts the rays cascading with the 319.5 or 162.2 keV transitions. Since the 209Bi had 83 protons and 126 neutrons, the last valence proton could occupy π (h9/2, f7/2, or i13/2) orbitals, giving rise to the configuration of the ground state and two lowest excited states in 209Bi [53]. Because of the fact that during the one-neutron stripping reaction, the valence neutron might be added to all the possible empty orbitals outside the N = 126 shell, including ν (g9/2, i11/2, j15/2, d5/2, s1/2, and g7/2), different multiplets with similar strengths would be produced. According to the aforementioned γ-γ coincidence analysis, even though low, almost all the multiplets (or part of the members) with valence proton on both π1h9/2 or 2f7/2 orbitals are clearly observed. Multiplets with protons on π1i13/2 orbital have also been found, but their existence is uncertain because of very weak intensity and the interference of the same energy γ rays. Therefore, the coupling of this orbit is indicated by dashed lines in Fig. 5, emphasizing its uncertainty. This is the coupling originating from the first and second excited states in 209Bi must be considered in the current calculation.
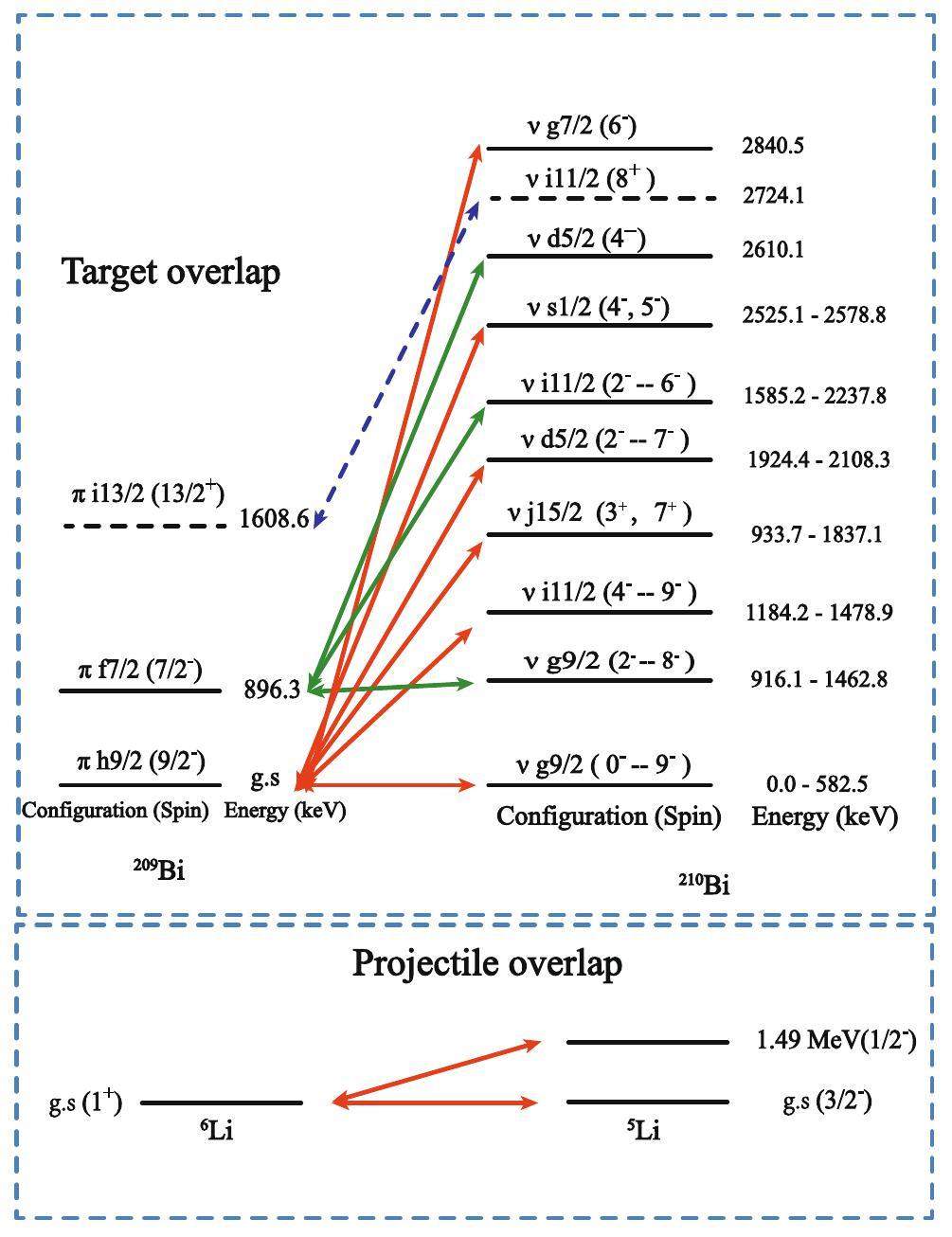
As a result, the levels whose decay transitions have a cascade relationship with the two observed γ rays up to approximately 3000 keV, corresponding to the (
The one-neutron spectroscopic amplitudes for target overlaps were derived from shell-model calculations using the NuShellX code [54]. The khpe effective phenomenological interaction [55, 56] was used to describe the structure of the target and the residual nucleus. The model space assumes 208Pb as a closed core with 1h9/2, 2f7/2, 2f5/2, 3p3/2, 3p1/2, and 1i13/2 orbitals as valence space for protons, and 1i11/2, 2g9/2, 2g7/2, 3d5/2, 3d3/2, 4s1/2, and 1j15/2 for neutrons. Because of our computational limitations in performing shell-model calculations, it was necessary to introduce some constraints to derive the amplitudes using these large valence spaces. Therefore, the last valence orbitals for protons and neutrons were constrained so that only two nucleons could occupy them.
The experimental measurements in this paper reported counts for two γ-rays: the 319.5 keV and 162.2 keV electromagnetic transitions in the residual nucleus 210Bi from the one-neutron stripping reaction. However, the cross sections were contributed by both the de-excitations from the highly excited states and the direct population of the
Discussion
In fact, 5Li is an unbound nucleus that decays in 4He + p. Concerning the
As shown in Table 2, when the spectroscopic amplitude of the projectile overlaps was set to 1.0, many calculations were carried out to evaluate the effects of the excited states of 209Bi and 5Li on the cross section. The first one considers only the ground state of 5Li (3/2-), and the results are designated as CS1, CS3, and CS5, respectively. Among these, CS1 considers the ground state as well as two excited states of 209Bi, CS5 considers both the ground state and the first excited state, and CS3 only considers the ground state. Furthermore, the first resonant state of 5Li (1/2-) is considered, and the results are labeled CS2 and CS4. Similarly, CS2 studies 209Bi’s ground state as well as two low excited states, but CS4 only considers the ground state. By comparing CS1 with CS2, the cross sections calculated considering the first resonance state of 5Li are approximately 22% (at 28 MeV)—39% (at 34 MeV) higher than that calculated when only considering the ground state of 5Li.
The results suggest that the first excited state of 5Li is critical in the actual one-neutron transfer mechanism. The underlying theory and physics should be explored further in future works.
When comparing the results of the experimental integral cross section and the theoretical calculation in CS2, which considers both the excited states of 209Bi and 5Li, the two cross sections are in good agreement when the beam energy is 28 MeV. At 30 MeV, the theoretical calculation overestimates the cross section, and at 34 MeV, the experimental results are higher than that of the theoretical calculation. The discrepancies between the calculated and experimental cross sections indicate that the refined spectroscopic amplitudes must be considered in further calculations to make the theoretical and experimental results match better.
When comparing CS1, CS3, and CS5, we can observe that the effect on the integrated cross section is not noticeable after accounting for the first and second excited states of 209Bi. This indicates that 209Bi was excited during the transfer reaction, but its effect on the transfer cross section was negligible.
It is known that the (d,p) reaction is frequently employed to investigate the single-particle nature of different states in the produced nucleus. Levels in 210Bi have been studied by the 209Bi(d,p)210Bi reaction at 19 MeV and the 209Bi(α,3He)210Bi reaction at 58 MeV [29]. In this study, the observed energy levels are interpreted as the multiplets formed by coupling a valence proton occupying the 1h9/2 orbital, with a neutron in either 2g9/2, 1i11/2, 1j15/2, 3d5/2, 4s1/2, 2g7/2, or 3d3/2 orbitals [47, 29]. Note here that the ground state in 209Bi has a spin-parity of 9/2-, being identified as a single-proton configuration (h9/2). This means the deuteron does not excite the target nucleus during the one-neutron stripping process, being suitable for the study of transferred momentum, spectroscopic factor, or other observables, which can reflect the single-particle nature of the produced levels in the existing channel. However, in the case of 6Li, in addition to π h9/2, the observed level scheme as shown in Fig. 3 also includes the excited states with valence protons in 2f7/2 and 1i13/2 orbitals. Thus, 6Li can significantly excite the 209Bi target during the one-neutron process.
In Fig. 6, the cross sections of the one-neutron stripping reaction and the CF [5] are compared in the 6Li+209Bi system.

When the beam energy decreases, the cross section of the one-neutron stripping process gradually exceeds that of the CF reaction, being quite similar to the case of 6Li+96Zr [14]. This behavior is commonly explained by the fact that the neutron transfer does not need to overcome the Coulomb barrier, being different from the CF process.
Meanwhile, the coupling between the neutron-stripping and the fusion process is still under investigation.
Summary
Experiments on the 6Li+209Bi reaction were performed on the GALILEO Array coupled with 4π Si-ball EUCLIDES at Legnaro National Laboratory to study the transfer of weakly bound nuclei on heavy target nuclei in the near-barrier energy region. The one-neutron stripping product 210Bi populates the excited state, and the de-excited rays are identified by using the γ- γ coincidence method. The yield of 210Bi is calculated via two rays, 319.5 keV and 162.2 keV, which are de-excited to the ground and the long-lived states, respectively.
The one-neutron stripping partial cross sections obtained at 28, 30, and 34 MeV are comparable to those obtained for CF. As incident energy decreases, the excitation function for the one-neutron transfer reaction decreases more slowly. It exceeds the fusion section at energies below the Coulomb barrier. This indicates that the one-neutron transfer reaction plays a more important role in the reaction systems involving weakly bound nuclei at energies around and below the Coulomb barrier.
The theoretical one-neutron transfer cross sections were obtained by performing CRC calculations. The cross sections calculated considering the first excited state of 5Li are approximately 20% to 40% larger than those calculated considering only the ground state of 5Li. Furthermore, in contrast to the (d,p) reaction, the valence proton of 209Bi is excited to the low-lying states in (6Li, 5Li) reaction, implying that the single-particle energy level of 210Bi cannot be studied using this reaction.
Recent developments in heavy-ion fusion reactions
. Rev. Mod. Phys. 86, 317-360 (2014). https://doi.org/10.1103/RevModPhys.86.317Coupled-channel effects in elastic scattering and near-barrier fusion induced by weakly bound nuclei and exotic halo nuclei
. Phys. Rev. C 75, 054605 (2007). https://doi.org/10.1103/PhysRevC.75.054605Fusion and breakup of weakly bound nuclei
. Phys. Rep. 424, 1-111 (2006). https://doi.org/10.1016/j.physrep.2005.10.006Recent developments in fusion and direct reactions with weakly bound nuclei
. Phys. Rep. 596, 1-86 (2015). https://doi.org/10.1016/j.physrep.2015.08.001Effect of breakup on the fusion of 6Li, 7Li, and 9Be with heavy nuclei
. Phys. Rev. C 70, 024606 (2004). https://doi.org/10.1103/PhysRevC.70.024606Elastic scattering and reactions of light exotic beams
. Prog. Part. Nucl. Phys. 63, 396-447 (2009). https://doi.org/10.1016/j.ppnp.2009.05.003Fusion and direct reactions of halo nuclei at energies around the coulomb barrier
. Prog. Part. Nucl. Phys. 59, 579-630 (2007). https://doi.org/10.1016/j.ppnp.2007.02.002Subbarrier Fusion Reactions and Many-Particle Quantum Tunneling
. Prog. Theor. Phys. 128, 1061-1106 (2012). https://doi.org/10.1143/PTP.128.1061Fusion induced by radioactive ion beams
. Int. J. Mod. Phys. E 14, 1121-1150 (2005).Fusion of the weakly bound projectile 9Be with 89Y
. Phys. Rev. C 82, 044608 (2010). https://doi.org/10.1103/PhysRevC.82.044608Resonant breakup of 6li by 209bi
. Phys. Lett. B 677, 139-144 (2009). https://doi.org/10.1016/j.physletb.2009.05.016Exploring fusion at extreme sub-barrier energies with weakly bound nuclei
. Phys. Rev. Lett. 103, 232702 (2009). https://doi.org/10.1103/PhysRevLett.103.232702Quasi-elastic scattering of the proton drip line nucleus 17f on 12c at 60 mev
. Eur. Phys. J. A 48, 65 (2012). https://doi.org/10.1140/epja/i2012-12065-xOne-neutron stripping processes to excited states of the 6Li+96Zr reaction at near-barrier energies
. Phys. Rev. C 93, 014621 (2016). https://doi.org/10.1103/PhysRevC.93.014621One-neutron stripping processes to excited states of 90Y* in the 89Y(6Li,5Li)90Y* reaction
. Phys. Rev. C 97, 014611 (2018). https://doi.org/10.1103/PhysRevC.97.014611One-neutron stripping from 9Be to 169Tm, 181Ta, and 187Re at near-barrier energies
. Phys. Rev. C 93, 034615 (2016). https://doi.org/10.1103/PhysRevC.93.034615Exploring fusion at extreme sub-barrier energies with weakly bound nuclei
. Phys. Rev. Lett. 103, 232702 (2009). https://doi.org/10.1103/PhysRevLett.103.232702Role of the cluster structure of 7Li in the dynamics of fragment capture
. Phys. Lett. B 718, 931-936 (2013). https://doi.org/10.1016/j.physletb.2012.11.064Fusion and quasi-elastic scattering in the 6,7Li+197Au systems
. Phys. Rev. C 89, 024607 (2014). https://doi.org/10.1103/PhysRevC.89.024607Heavy residue excitation functions for the collisions 6,7li+64zn near the coulomb barrier
. Phys. Rev. C 87, 064614 (2013). https://doi.org/10.1103/PhysRevC.87.064614Complete and incomplete fusion of 9Be+169Tm, 187Re at near-barrier energies
. Phys. Rev. C 91, 014608 (2015). https://doi.org/10.1103/PhysRevC.91.014608Breakup and n-transfer effects on the fusion reactions 6,7Li+120,119Sn around the coulomb barrier
. Phys. Rev. C 95, 034617 (2017). https://doi.org/10.1103/PhysRevC.95.034617Importance of the 1n-stripping process in the 6Li + 159Tb reaction
. Phys. Rev. C 88, 064603 (2013). https://doi.org/10.1103/PhysRevC.88.064603Disentangling reaction mechanisms for α production in the 6Li + 209Bi reaction
. Phys. Rev. C 85, 014612 (2012). https://doi.org/10.1103/PhysRevC.85.014612Transfer reactions as a doorway to fusion
. J. Phys. G: Nucl. Part. Phys. 23, 1315 (1997). https://doi.org/10.1088/0954-3899/23/10/020Theory of deuteron stripping and pick-up reactions for nuclear structure studies
. Prog. Part. Nucl. Phys. 111, 103738 (2020). https://doi.org/10.1016/j.ppnp.2019.103738On angular distributions from (d,p) and (d,n) nuclear reactions [2]
. Phys. Rev. 80, 1095-1096 (1950). https://doi.org/10.1103/PhysRev.80.1095.2Nucleon transfer reactions with radioactive beams
. J. Phys. G: Nucl. Part. Phys. 45, 033002 (2018). https://doi.org/10.1088/1361-6471/aaa2bfMultiplet structure of 210bi from the 209bi(d, p) and 209bi(α, 3he) reactions
. Nucl. Phys. A 186, 273-296 (1972). https://doi.org/10.1016/0375-9474(72)90046-2Shell-model structure of 210Bi: 209Bi(d, p) at 17 mev
. Phys. Rev. C 5, 568-578 (1972). https://doi.org/10.1103/PhysRevC.5.568Neutron shell structure in 125Sn by (d, p) and (α, 3He) reactions
. Phys. Rev. C 8, 729-736 (1973). https://doi.org/10.1103/PhysRevC.8.729States in 121Sn from the 120Sn(d, p)121Sn reaction at 17 mev
. Phys. Rev. C 12, 90-101 (1975). https://doi.org/10.1103/PhysRevC.12.90Single-nucleon-transfer tests of the u(612) supersymmetry in platinum isotopes
. Nucl. Phys. A 517, 1-26 (1990). https://doi.org/10.1016/0375-9474(90)90258-NNeutron shell structure in 93Zr, 95Zr, and 97Zr by (d, p) and (α, 3He) reactions
. Phys. Rev. C 7, 1509-1518 (1973). https://doi.org/10.1103/PhysRevC.7.1509Investigating neutron transfer in the 6Li+124Sn system
. Phys. Rev. C 107, 024602 (2023). https://doi.org/10.1103/PhysRevC.107.024602209Bi (d, p) 210Bi reaction at low bombarding energies and with high resolution
. Phys. Rev 128, 720 (1962).Decay modes and lifetimes of the levels in the πh92. vg92 multiplet in 210Bi
. Phys. Lett. B 35, 145-147 (1971).Low-lying configurations in 210Bi
. Phys. Rev. Lett. 26, 854 (1971).Magnetic moments of the 7- and 5-(πh 9/2, v g 9/2) states in 210Bi
. Phys. Rev. Lett. 29, 496 (1972).Gamma decay of excited states in 210Bi and an interpretation with the shell model
. Phys. Rev. C 7, 2137 (1973).Transition rates between two-body states in 206Tl, 208Bi, and 210Bi
. Phys. Rev. C 12, 1547 (1975).The γ-decay of two-particle states in 210bi
. Nucl. Phys. A 205, 145-167 (1973).Towards a homogeneous architecture for high-energy physics data acquisition systems
. Comput. Phys. Commun. 153, 155-163 (2003). https://doi.org/10.1016/S0010-4655(03)00161-9The galileo-ray array at the legnaro national laboratories
. Nucl. Instr. and Meth. Phys. Res. A 1015, 165753 (2021). https://doi.org/10.1016/j.nima.2021.165753The 4 π highly-efficient light-charged-particle detector euclides, installed at the galileo array for in-beam γ-ray spectroscopy
. Eur. Phys. J. A 55, 47 (2019). https://doi.org/10.1140/epja/i2019-12714-6Statistical model calculations in heavy ion reactions
. Phys. Rev. C 21, 230-236 (1980). https://doi.org/10.1103/PhysRevC.21.230Spectroscopy of the high-lying configurations in 210Bi
. Czech.J.Phys. B39, 22 (1989). https://doi.org/10.1007/BF01597435Coupled reaction channels calculations in nuclear physics
. Comput. Phys. Rep. 7, 167-212 (1988). https://doi.org/10.1016/0167-7977(88)90005-6Reaction mechanisms involving weakly bound 6Li and 209Bi at energies near the coulomb barrier
. Phys. Rev. C 83, 034616 (2011). https://doi.org/10.1103/PhysRevC.83.034616Nonlocal description of the nucleus-nucleus interaction
. Phys. Rev. Lett. 79, 5218-5221 (1997). https://doi.org/10.1103/PhysRevLett.79.5218Fusion processes in collisions of 6Li beams on heavy targets
. Phys. Rev. C 105, 054601 (2022).Continuum-continuum coupling and polarization potentials for weakly bound systems
. Phys. Rev. C 80, 047601 (2009).Structure of 209Bi deduced from the 208Pb(t, 2nγ) reaction
. Phys. Rev. C 27, 1431-1453 (1983). https://doi.org/10.1103/PhysRevC.27.1431NuShellX for Windows and Linux
, http://www.garsington.eclipse.co.uk/ (2024)Appraisal of the kuo-herling shell-model interaction and application to a=210–212 nuclei
. Phys. Rev. C 43, 602-617 (1991). https://doi.org/10.1103/PhysRevC.43.602Shell model calculations of two to four identical-“particle” systems near 208pb
. Nucl. Phys. A 247, 283-316 (1975). https://doi.org/10.1016/0375-9474(75)90637-5The authors declare that they have no competing interests.


