Introduction
The advancement of nuclear energy and its safe use can provide an impetus for human progress and support the production of high-end equipment, energy security, a reduction of climate change, and a shift to greener energy sources [1, 2]. Increasing the autonomous operation of nuclear power plants (NPPs) through digitalization and intellectualization is crucial for enhancing the efficiency and safety of nuclear energy, as well as for lowering operation and maintenance costs [3, 4]. The phrase "unmanned surveillance, few people on duty" describes the automation activities of NPPs in the future [5].
One of the pivotal technologies required to fulfill this desire is the prediction of key parameters in NPPs, especially under transient conditions, to perform timely decision-making and ensure early warning [6, 7]. The precise forecasting of key parameters in reactors is a well-established challenge. In recent years, considerable efforts have been made to predict various operating parameters in reactor transient conditions, including in-core power [8], outlet temperature [9], coolant leakage [10], and pressure [11]. Typical artificial intelligence (AI) models with multidimensional mappability, support vector regression (SVR), artificial neural networks (ANNs), and long short-term memory (LSTM) are frequently utilized in operating-parameter forecasting [12-14]. For example, Zeng et al. [15] combined SVR with particle filtering to predict the core power and coolant temperature of a reactor and achieved satisfactory accuracy for reactor reactivity insertion events. Lu et al. [16] developed an ANN-based model for forecasting the thermal-hydraulic parameters in a KLT-40S nuclear reactor under steady-state operation, and their results were in good agreement with the RELAP5 simulation.
For economic and security purposes, frequently conducting trials in real-world NPPs may trigger uncontrollable events and equipment damage. Therefore, obtaining a large number of transient samples is extremely challenging. A viable alternative for addressing the scarcity of real data is to apply numerical simulations to address class-imbalance problems [17]. For example, Xiang et al. [18] proposed a gear-oriented fault-detection method to enlarge fault samples by integrating a finite-element-method simulation and generative adversarial network, achieving satisfactory results. This idea is suitable for a mechanical system with a corresponding well-constructed simulation. Additionally, studies have utilized various programs that can perform system-level simulations (such as RELAP5 [19], TRACE [20], PCTRAN [21], CASMO5 [22], and PANGU [23]) to produce simulated data for AI-model training and verification based on nuclear-engineering experience and physical knowledge. Li et al. [24] conducted a study using data from the Qinshan 300 MWe NPP full-scope simulator. They combined an automated feed-forward neural network with optimization algorithms, which could effectively forecast the steam mass flow rate and water temperature during transient reactor operation for up to five seconds in advance. Tan et al. [25] established a mathematical model to prove the equivalence of simulated and operation data when the mean noise distribution is zero. This indicates that the simulated data can provide a supplemental dataset for the AI model in the initial training and theoretical analysis. Although various simulators have been designed to closely mimic the operations of actual reactors, the simulated and real data still exhibit certain domain discrepancies in terms of noise, numerical distributions, and dynamic characteristics for the following reasons:
(1) The mathematical models in simulators are simplified from real complex nuclear-power systems and cannot fully capture the nuanced physical processes.
(2) The operating parameters and states of simulators gradually differ from actual reactors, especially the changes in burnup caused by reactor-lifespan variation.
(3) In certain transient or extreme conditions, the dynamic response of simulators may marginally differ from the operations of actual reactors.
Even if real data accurately capture the intricate features of environmental interactions in NPPs, the difficulty of data collection leads to an inability to encompass all possible scenarios. Data derived from theoretical models and computational simulations of nuclear systems are readily available and inherently safer to obtain. Both the simulated and real data have unique state characteristics. Consequently, AI models trained solely on simulated or real data may be inaccurate and difficult to apply in NPPs with high safety and reliability standards [26]. Thus, investigating the transfer of prior knowledge from sufficiently simulated data to scarce actual data is essential for enhancing the precision of operating-parameter forecasts in NPPs.
However, this scheme raises an open issue: how well do simulated data generalize to real data? Transfer learning, a deep-learning technique that aims to leverage pre-existing knowledge to improve the performance in a new task or domain, has become a feasible solution [27]. Lin et al. [28] proposed a transfer-learning model using maximum mean discrepancy (MMD) and a convolutional neural network (CNN). The experimental results demonstrated that transferring prior diagnostic knowledge is conducive to expanding the scope of nuclear-accident diagnosis in NPPs. Domain adaptation, which is a subset of transfer learning, specifically focuses on addressing domain discrepancies between the source and target domains in scenarios of the same task [29]. For insufficiently learnable samples, numerous domain-adaptation methods have been developed to address situations in mechanical fault diagnosis [30], medical-image analysis [31], and robot control [32]. Xiang et al. [33] established a fault-diagnosis method using simulations to obtain sufficient faults and domain adaptation to transfer the simulated knowledge to a real-world diagnosis. This approach not only supplements scarce fault samples but also mitigates the gap between simulation and reality. Inspired by their work, domain adaptation theoretically has the potential to transfer knowledge from simulation to reality and learn the common feature subspace for parameter prediction, wherein simulated and real data are considered as the source and target domains, respectively. Thus, the effectiveness of domain-adaptation techniques in bridging the gap between simulation and reality should be investigated, particularly for accurately forecasting critical parameters in nuclear reactors.
Based on the aforementioned discussion, this study aims to devise a transferability architecture for forecasting operating parameters in nuclear reactors using a simulation-to-reality domain adaptation (SRDA) model. Specifically, the SRDA model comprises four components: a feature extractor, parameter predictor, domain discriminator, and multiple kernel maximum mean discrepancy (MK-MMD). The feature extractor, as the backbone network within the SRDA model, is established using transformers that can capture dynamic characteristics and temporal dependencies from simulated and real data. A parameter predictor containing an improved logarithmic loss function can perform precise forecasting tasks under distinct reactor power levels. The domain discriminator utilizes an adversarial strategy that forces the feature extractor to learn deep domain-invariant features. MK-MMD quantifies the discrepancies between simulated and real data through sophisticated high-dimensional mapping. The key contributions of this study are summarized as follows:
(1) Unlike conventional methods solely using simulated-data modeling, the simulation-to-reality transferability model is pioneered by a novel technique in the domain adaptation of computer vision to precisely forecast critical parameters in nuclear reactors.
(2) The transformer uses a multi-head attention mechanism and is embedded as a feature extractor in the SRDA framework to capture both dynamic characteristics and temporal dependencies from simulated and real data. The improved logarithmic loss function in the predictor is refined to adapt varied power levels in reactors.
(3) The SRDA framework is expertly developed to bridge the gap between the simulated and real data and harness the strengths of adversarial strategy (i.e., the extraction of deep domain-invariant features) with the MK-MMD (i.e., the minimization of domain-distribution discrepancies) simultaneously.
The remainder of this article is organized as follows. Section 2 analyzes the differences between the simulated and real data. Section 3 introduces the proposed SRDA framework in detail. In Sect. 4, we validate the precision and superiority of the proposed method through comparative experiments. Finally, Sect. 5 concludes the paper.
Preliminary analysis
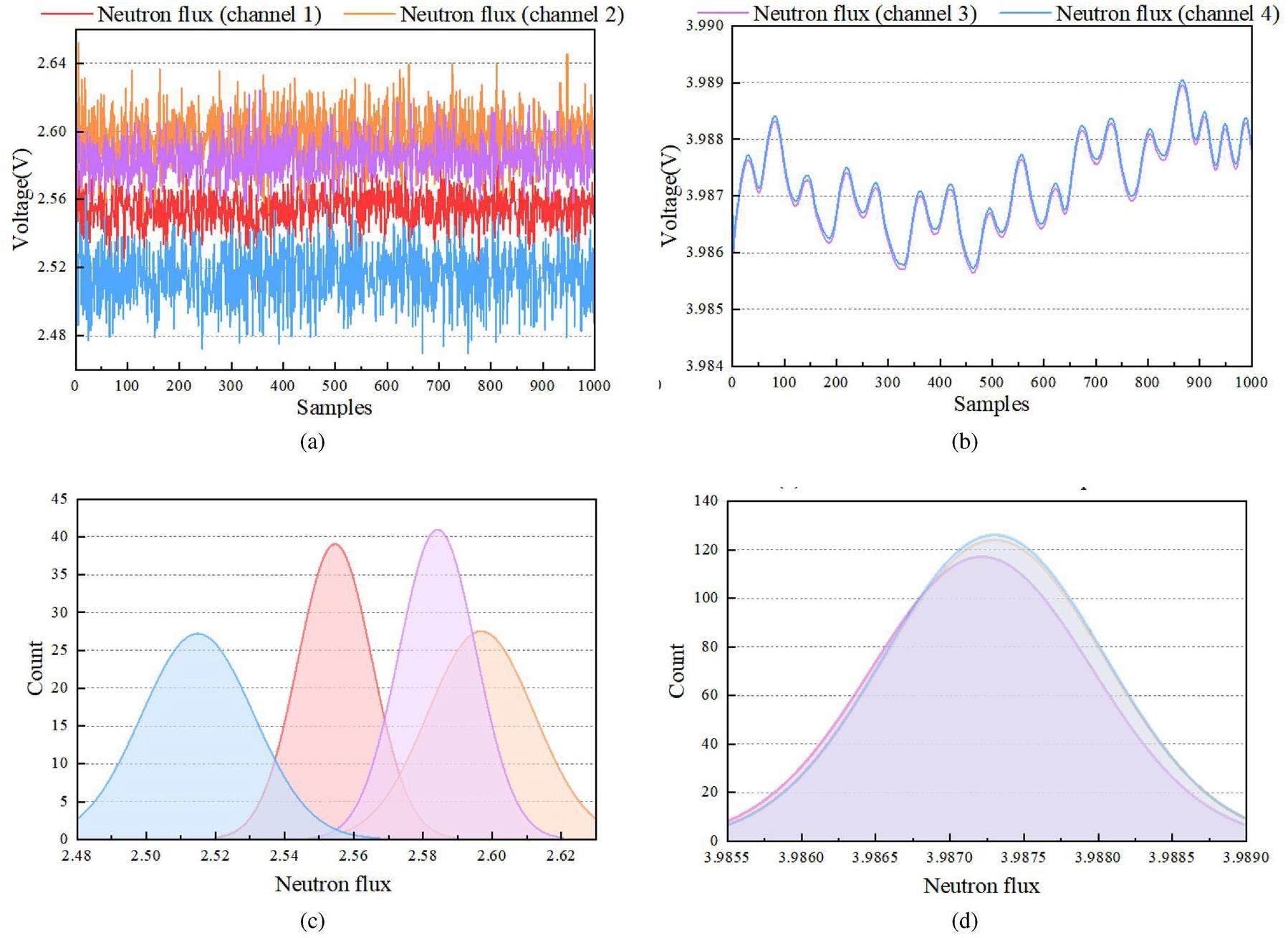
To visualize the differences between the simulated and real data, neutron fluxes at the same height in each of the four reactor channels are shown in Fig. 1. The four simulated curves of the height coincidence exhibited smooth tendencies over a narrower range, whereas the actual curves exhibited obvious noise over a wider range. Discrepancies arise primarily from model simplifications and potential errors in the parameter estimation. For example, in simulating reactor dynamics, certain assumptions must be made for computational feasibility, which can lead to deviations from the actual reactor responses. The dynamic characteristics of an NPP, such as its thermal-hydraulic behavior and neutron kinetics, were approximated in the simulations. However, these approximations can oversimplify real phenomena. In real-world reactors, neutron-flux signals are collected by ex-core detectors, whose signals are primarily induced by neutrons and gamma rays, along with a component of electrical noise [34]. In addition, burnup changes caused by reactor-lifespan variations cause the numerical distributions of the simulation and reality to shift progressively. These observations underscore the limitations of simulations and the complexities of real-world nuclear reactors, which further demonstrate the discrepancies in noise, numerical distributions, and dynamic characteristics between simulations and reality.
Methodology
Problem formulation
The operating-parameter data
Overview of SRDA
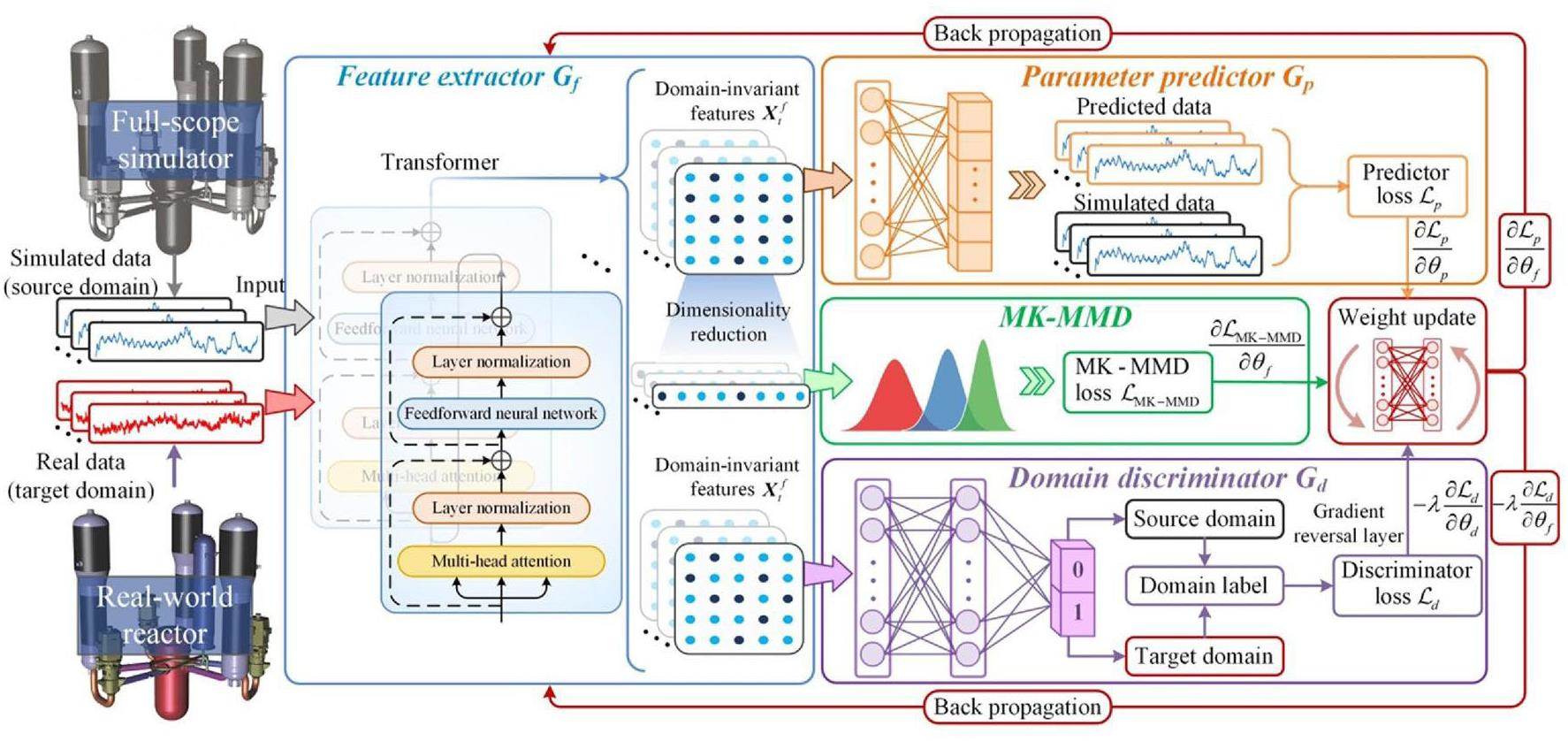
The proposed SRDA framework aims to predict real data in nuclear reactors precisely over time by learning and transferring prior knowledge from simulations to reality. As presented in Fig. 2, the architecture of SRDA resembles that of conventional neural networks and possesses two output modules instead of one. The SRDA model comprises four modules. The blue module is the feature extractor Gf and serves as the backbone network that directly affects the transfer effect. We use a transformer as the feature extractor, which is described in detail in Sect. 3.4. The orange module, representing the parameter predictor Gp, is constructed using an improved logarithmic loss, a fully connected (FC) layer, and a prediction output layer, which forecasts the future variation of operating parameters in the reactors. The purple module represents the domain discriminator Gd and comprises two FC layers and a classification output layer. The purpose of Gd is to classify the training data from each domain and establish an adversarial learning strategy with feature extractor Gf. In addition, the green module represents the multiple kernel maximum mean discrepancy (MK-MMD) used to estimate the discrepancies between the simulated and real reactor data after the feature extraction.
Principles of domain adversarial strategy
In the training phase, the samples Xt from
This framework mitigates domain differences and makes precise parameter predictions by jointly training Gf, Gp, and Gd. More specifically, training has two goals: (1) minimizing the prediction loss for Gp and (2) maximizing the domain loss for Gd simultaneously, such that the domain discriminator cannot distinguish the domain from which the obtained features originate [35]. Feature extractor Gf and domain discriminator Gd are trained adversarially to ensure that Gf maps the simulated and real data into a common subspace and generates domain-invariant features. Consequently, the training convergence learns deep domain-invariant features in the feature extractor, which refers to temporal dependencies or generic patterns that do not significantly change between the simulated and real data. To perform adversarial training, the feature extractor Gf and domain discriminator Gd are interconnected by a gradient-reversal layer to achieve optimal results. For efficient backpropagation, the trade-off loss function (
In the testing phase, the trained SRDA model utilizes a feature extractor (i.e., the transformer) to capture temporal characteristics from real data, which are then fed into the predictor to forecast the operating-parameter variations in a real-world reactor. The domain discriminator and MK-MMD modules are not involved in the testing phase because their purpose is solely to assist the feature extractor in learning domain-invariant features during training.
Principles of transformer
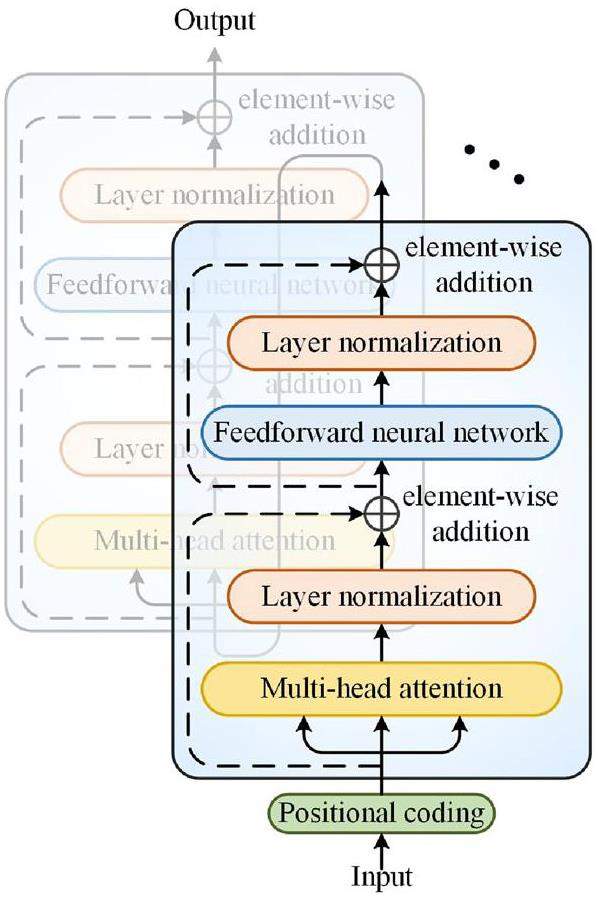
A transformer [36] has an excellent capacity for handling time series and is utilized as the feature extractor within the SRDA model. A standard transformer has a sequence-to-sequence structure that incorporates an encoder and a decoder. To capture the dynamic characteristics and temporal dependencies from the simulated and real data, the encoder in the transformer is utilized to map the inputs into a high-dimensional domain-invariant feature matrix.
As presented in Fig. 3, the encoder comprises positional coding, multi-head attention, layer normalization, and a feed-forward neural network. The positional information is calculated using sine and cosine functions [37]. Multi-head attention aims to capture the dynamic characteristics of special events that can enhance the sensitivity of the model to critical moments or transient scenarios in reactors. As shown in Fig. 4, multi-head attention, as the basic module in the transformer, first expands the input Xt into a new embedding
Embedding
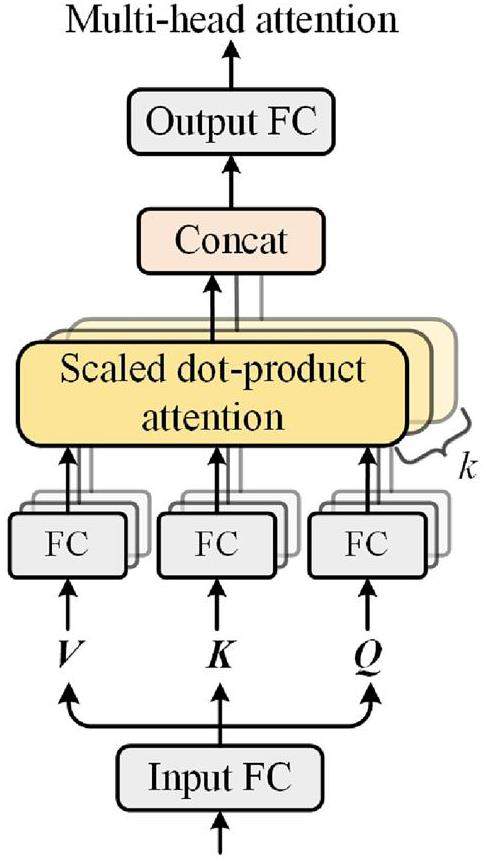
The scaled dot-product attention can calculate the correlation between Q and K to produce an attention map, which is employed as the weight of V; the calculation of which is described formulas follows:
The output of each head is concatenated and calculated using an output FC layer. This process can be simplified as follows:
The feed-forward neural network, consisting of two FC layers and a rectified linear unit activation function, primarily boosts the nonlinear fitting capability of feature extraction, which is utilized separately for each position.
Principles of MK-MMD
A standalone domain adversarial strategy may have suboptimal effects or instability in simulation-to-reality knowledge transfer. Combining the adversarial strategy with MK-MMD can compensate for these shortcomings while promoting the stability and robustness of the model. In the SRDA framework, the dimensionality of the feature matrix Xf obtained by the feature extractor is reduced to eigenvectors
Experiments
In this section, the proposed SRDA model is evaluated using two types of data (simulated and real), which are regarded as the source and target domains. Typical operating parameters are selected for forecasting, including twenty-four neutron fluxes (N1, …, N24) and six temperatures (T1, …, T6) at different locations in the reactor. Neutron fluxes and temperatures play critical roles in reactors, as they are essential for monitoring the power distributions and levels of the reactor. As presented in Fig. 5, the neutron fluxes are gathered by ex-core neutron detectors (i.e., uncompensated ion chambers) to generate channel currents at six distinct heights in the four channels. The currents are amplified and converted into voltage signals. The temperatures recorded by the resistance thermometers correspond to the inlet and outlet temperatures in the three primary loops.
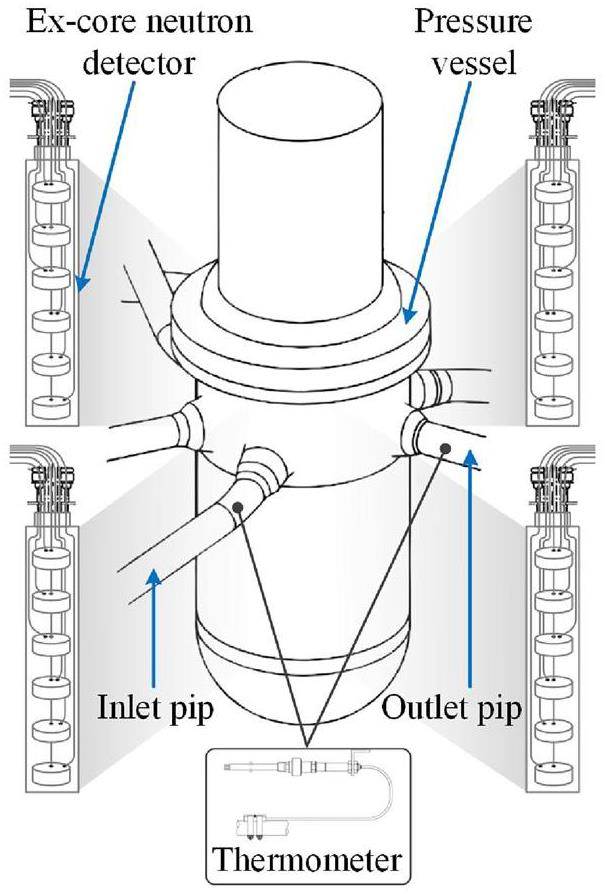
The simulated data with a one-second sampling interval are produced by the full-scope simulator of a pressurized water reactor (PWR), which is meticulously designed to match the actual control station of an NPP, ensuring that every component and system are precisely simulated. All critical nuclear-reactor systems such as the reactor core, cooling systems, control systems, and emergency-response systems are integrated into the simulator to provide a comprehensive simulation environment. To extract abundant information and transfer knowledge, a full-scope simulator produces various transitory data under varying power. The actual data originate from a real-world digital instrumentation and the control system in a PWR.
Nuclear reactors mostly operate in a steady state, owing to their operating characteristics. Transient operation rarely occurs, except when it is caused by external factors such as grid peaking, shutdowns, and faults. To demonstrate the reliability of the results, the target domain data contains two sets: 37,000 samples of shutdown data and 60,000 samples of power variation with one-second and ten-second sampling intervals, respectively. In the two transient scenarios, the control rods are manipulated to induce perturbations in the three-dimensional power distribution, which characterizes the different degrees of change in the reactor. In the joint training phase, the training set is composed of all source data and the first 5% of the target domain data (only steady-state operation). The remaining target-domain data are used as the test set. For the two test sets with different sampling intervals, the past 180 steps (3 and 30 min) of the historical data are applied to recursively predict the data of the next 60 steps (1 and 10 min, respectively).
Experimental setup
Examining the effects of various feature extractors on the SRDA model can provide valuable insights. Six representative deep-learning networks are applied to explore the generalizability of the proposed framework: autoencoder (AE), CNN, recurrent neural network (RNN), LSTM, gated recurrent unit (GRU), and temporal convolutional network (TCN). The key parameters of each model are listed in Tab. 1.
| Model | Parameter | Value |
|---|---|---|
| AE | Neurons of encoder | 64 |
| Neurons of decoder | 64 | |
| CNN | Number of filters | 32 |
| Filter size | 3 | |
| RNN | Bi-direction structure | True |
| Neurons of hidden layer | [32, 32] | |
| LSTM | Bi-direction structure | True |
| Neurons of hidden layer | [32, 32] | |
| GRU | Bi-direction structure | True |
| Neurons of hidden layer | [32, 32] | |
| TCN | Number of filters | 32 |
| Number of residual layer | 2 | |
| Filter size | 13 | |
| Dilated factor | [1, 2] |
In addition to comparing different feature extractors, the SRDA model is compared with six advanced domain-adaptation methods in parallel to prove its superiority. Owing to the limited domain-adaptation methods available for forecasting tasks, we modified the existing methods proposed for time-series or visual classification. Comparison methods include deep domain confusion (DDC) [39], correlation alignment via domain adaptation (CA-DA) [40], minimum discrepancy estimation for domain adaptation (MDE-DA) [41], a DIRT-T approach to domain-adversarial adaptation (DIRT-T) [42], an adaptive domain-adversarial neural network (ADANN) [43], and adversarial spectral-kernel matching for domain adaptation (ASKM-DA) [44]. The hyperparameters of the aforementioned approaches are rationally set in accordance with corresponding studies to ensure fairness. In the training phase, the learning rate and batch size in all models are critical parameters adjusted by grid optimization. For the proposed SRDA, the parameter settings are listed in Tab. 2. All the AI models are developed using PyTorch 2.0.1 in Python version 3.8.
| Module | Parameter | Value |
|---|---|---|
| SRDA (transferability framework) | Input length | 180 |
| Output length | 60 | |
| Neurons of predictor | [32, 64, 60] | |
| Neurons of discriminator | [32, 16, 16, 2] | |
| Number of kernels in MK-MMD | 5 | |
| Optimizer | Adam | |
| Epoch | 200 | |
| Learning rate | 0.001 | |
| Batch size | 32 | |
| Transformer (feature extractor) | Number of multi-head | 2 |
| Feature dimension | 32 | |
| Number of encoder layers | 4 | |
| Neurons of feedforward neural network | [32, 128, 32] | |
| Dropout | 0.1 |
Three precision metrics, namely the root mean square error (δRMSE), mean absolute error (δMAE), and symmetric mean absolute percentage error (δSMAPE), are adopted to evaluate the forecasting performance. The smaller the δRMSE, δMAE, and δSMAPE metrics, the higher the prediction accuracy. These can be calculated as follows:
Forecasting results
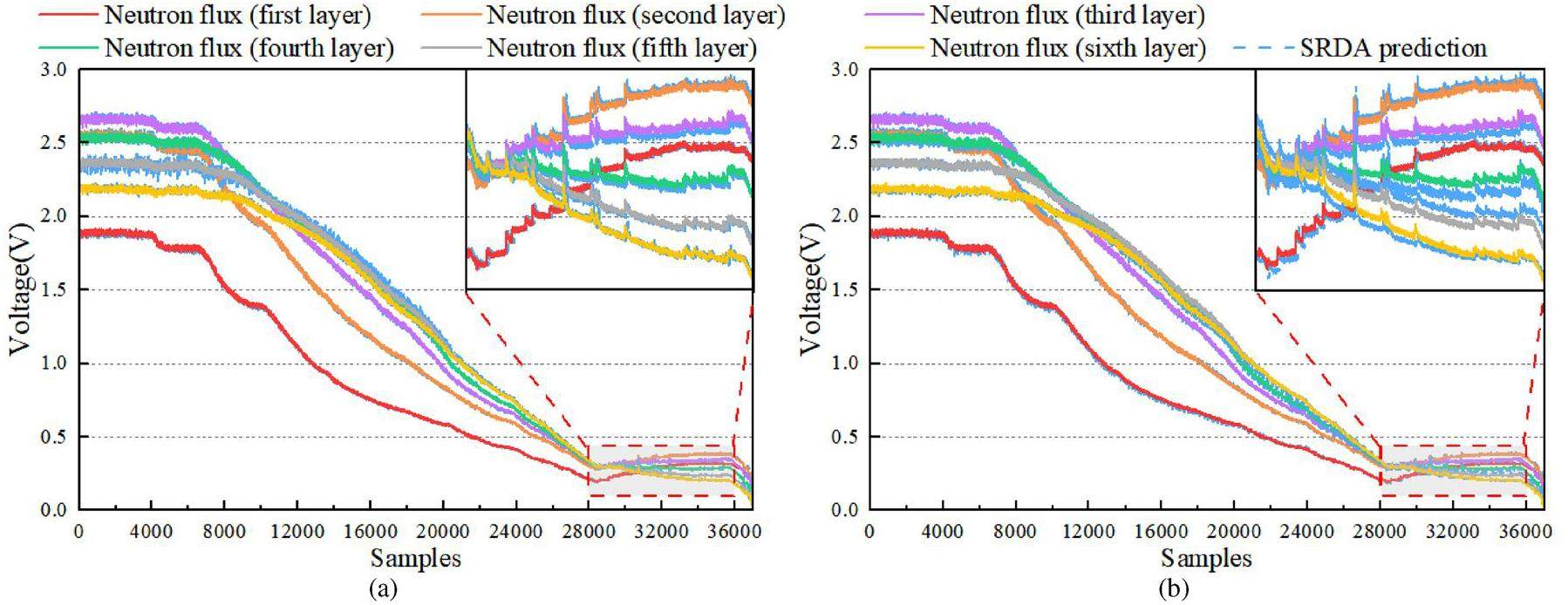
Experiments on forecasting tasks are conducted using source-only, target-only, and source-target models as baselines to validate the effectiveness of the proposed SRDA model for knowledge transfer from simulation to reality in nuclear reactors. The source-only model is trained exclusively on the source-domain training set and directly tested on the target-domain test set. Similarly, the target-only model is trained on the target-domain training set and directly tested on the target-domain test set. The source-target model is trained on the source-domain data using conventional transfer learning, and it fine-tunes the weights of its final layer on the target-domain data. Furthermore, a transformer and improved logarithmic loss are used to construct the three baselines mentioned above. Domain adaptation is not employed in this process. Forecasting of the neutron flux N1 and hot-leg temperature T1 are performed as examples. As shown in Fig. 6, the target-only model trained using the first 5% of the steady-operation data exhibits the largest predictive deviation. After learning a sufficient number of simulated samples, the trained source-only model can adapt to the basic variational trend of real neutron fluxes and temperatures, resulting in suboptimal effects attributable to the difference between the simulation and reality. Although the source-target model outperforms the above two models, it exhibits a certain deviation in the local area. Compared with the three baselines, the predictive trend obtained by the SRDA model with domain adaptation is generally closer to the real curves and free from the interference of operational noise in complex nuclear systems.

Table 3 provides the specific average and standard deviation of the errors (
| Forecasting target | Model | Shutdown | Power variation | ||||
|---|---|---|---|---|---|---|---|
| Neutron flux | Target-only | 0.902±0.688 | 0.903±0.689 | 61.549 ± 23.977 | 0.107±0.051 | 0.105±0.049 | 8.710±4.543 |
| Source-only | 0.034±0.011 | 0.041±0.011 | 6.615±1.639 | 0.035±0.014 | 0.036±0.014 | 3.083±1.733 | |
| Source-target | 0.028±0.005 | 0.030±0.005 | 5.587±1.277 | 0.026±0.035 | 0.027±0.035 | 2.192±3.081 | |
| SRDA* | 0.010±0.002 | 0.012±0.003 | 1.248±0.287 | 0.008±0.003 | 0.009±0.003 | 0.636±0.178 | |
| Temperature | Target-only | 4.918±4.379 | 4.914±4.377 | 1.653±1.482 | 1.246±1.092 | 1.252±1.096 | 0.393±0.331 |
| Source-only | 0.825±0.697 | 0.825±0.696 | 0.280±0.239 | 0.357±0.134 | 0.369±0.123 | 0.118±0.049 | |
| Source-target | 0.777±0.749 | 0.778±0.748 | 0.264±0.256 | 0.351±0.140 | 0.363±0.130 | 0.116±0.051 | |
| SRDA* | 0.113±0.079 | 0.118±0.085 | 0.037±0.026 | 0.223±0.111 | 0.231±0.110 | 0.073±0.038 | |
Forecasting comparison and analysis
Temporal feature extraction within the SRDA model is interlinked with the operating-parameter prediction performance. To analyze the impact of various feature extractors, experiments are conducted to replace the transformer in the SRDA framework with the six representative neural networks specified in Sect. 4.1: AE, CNN, RNN, LSTM, GRU, and TCN. As depicted in Fig. 7, the SRDA framework consistently achieves favorable outcomes across various feature extractors, demonstrating its broad versatility. However, different backbone networks moderately affect the prediction accuracy for neutron fluxes and temperatures during the shutdown and power-variation phases. Owing to the lack of inherent architecture in AE and CNN for recording temporal dependencies, the SRDA (AE) and SRDA (CNN) models exhibit insufficient feature-extraction capabilities. The SRDA (RNN) makes unstable predictions, as reflected in its δSMAPE, owing to the absence of effective memory mechanisms. The SRDA (LSTM) and SRDA (GRU) models incorporate memory cells and gating mechanisms to mitigate issues, such as vanishing gradients, thereby bolstering the temporal feature-extraction process. SRDA (TCN), which incorporates dilated causal convolutions with a larger receptive field to capture long-term characteristics, exhibits precision comparable to that of SRDA (Trans) and is a robust contender. The multi-head attention block of the proposed SRDA (Trans) allows it to capture both subtle long- and short-term dependencies, which makes it superior to other feature extractors in adapting to complex variations. The experimental results are demonstrated by the steady
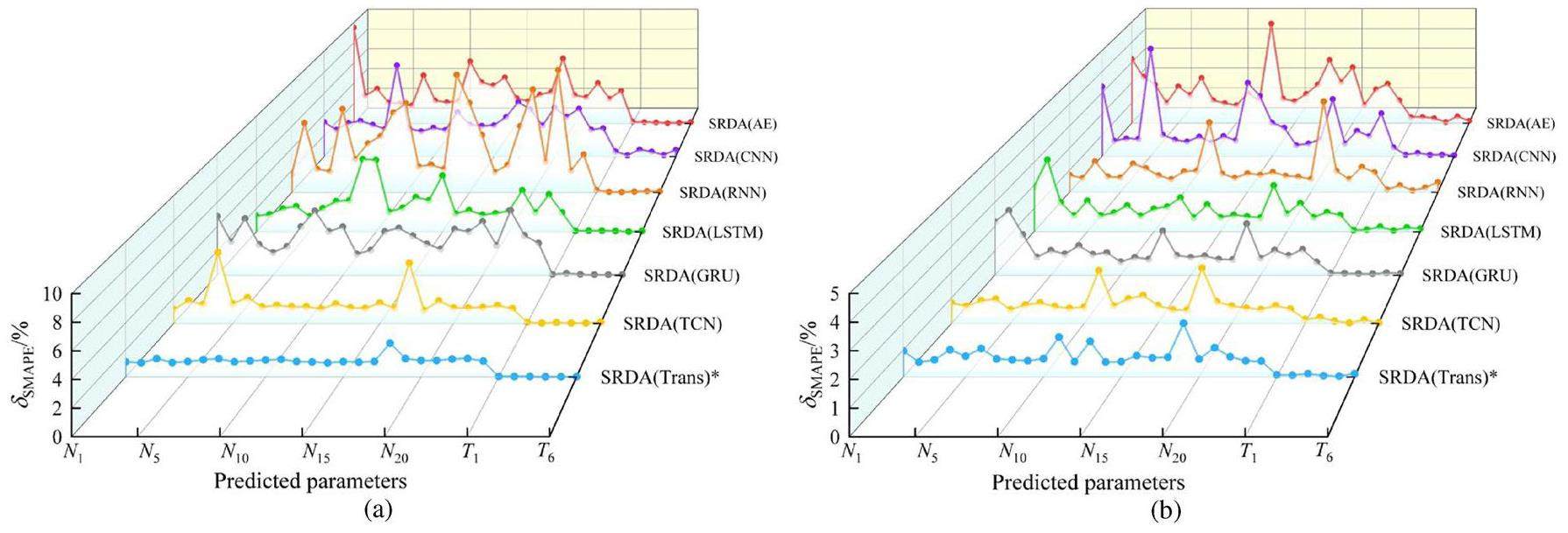
Table 4 presents a detailed comparison of the predictive precision across various feature extractors for the two test sets. In summary, the models intricately designed for time-series analysis, such as TCN and the transformer within the SRDA framework, possess advanced temporal feature-extraction capabilities. This facilitates more effective domain adaptation, resulting in enhanced predictive performance. Although SRDA (TCN) yields formidable and competitive results, SRDA (Trans) demonstrates unparalleled performance for both neutron fluxes and temperatures. For example, in inlet- and outlet-temperature prediction, compared with the average errors (
| Forecasting target | Feature extractor | Shutdown | Power variation | ||||
|---|---|---|---|---|---|---|---|
| Neutron flux | SRDA (AE) | 0.023±0.013 | 0.038±0.044 | 3.496±1.791 | 0.022±0.009 | 0.028±0.011 | 1.817±0.942 |
| SRDA (CNN) | 0.026±0.007 | 0.030±0.010 | 3.525±1.344 | 0.019±0.015 | 0.020±0.015 | 1.464±1.176 | |
| SRDA (RNN) | 0.044±0.035 | 0.048±0.036 | 4.902±3.013 | 0.014±0.012 | 0.015±0.013 | 1.077±0.829 | |
| SRDA (LSTM) | 0.021±0.013 | 0.024±0.015 | 2.563±1.410 | 0.014±0.008 | 0.015±0.008 | 1.076±0.589 | |
| SRDA (GRU) | 0.024±0.009 | 0.026±0.009 | 3.375±1.065 | 0.013±0.006 | 0.015±0.006 | 1.076±0.577 | |
| SRDA (TCN) | 0.010±0.003 | 0.013±0.003 | 1.365±0.280 | 0.009±0.002 | 0.010±0.003 | 0.686±0.198 | |
| SRDA (Trans)* | 0.010±0.002 | 0.012±0.003 | 1.248±0.287 | 0.008±0.003 | 0.009±0.003 | 0.636±0.178 | |
| Temperature | SRDA (AE) | 0.376±0.148 | 0.497±0.239 | 0.123±0.047 | 0.707±0.365 | 1.050±0.583 | 0.226±0.115 |
| SRDA (CNN) | 1.276±0.730 | 1.628±0.977 | 0.419±0.238 | 0.429±0.468 | 0.513±0.514 | 0.135±0.143 | |
| SRDA (RNN) | 0.300±0.195 | 0.339±0.264 | 0.098±0.062 | 1.074±0.982 | 1.120±0.981 | 0.345±0.305 | |
| SRDA (LSTM) | 0.241±0.094 | 0.252±0.093 | 0.079±0.030 | 0.379±0.197 | 0.397±0.206 | 0.122±0.063 | |
| SRDA (GRU) | 0.256±0.153 | 0.271±0.154 | 0.084±0.047 | 0.241±0.048 | 0.258±0.048 | 0.078±0.015 | |
| SRDA (TCN) | 0.177±0.131 | 0.181±0.133 | 0.058±0.043 | 0.254±0.179 | 0.270±0.180 | 0.083±0.056 | |
| SRDA (Trans)* | 0.113±0.079 | 0.118±0.085 | 0.037±0.026 | 0.223±0.111 | 0.231±0.110 | 0.073±0.038 | |
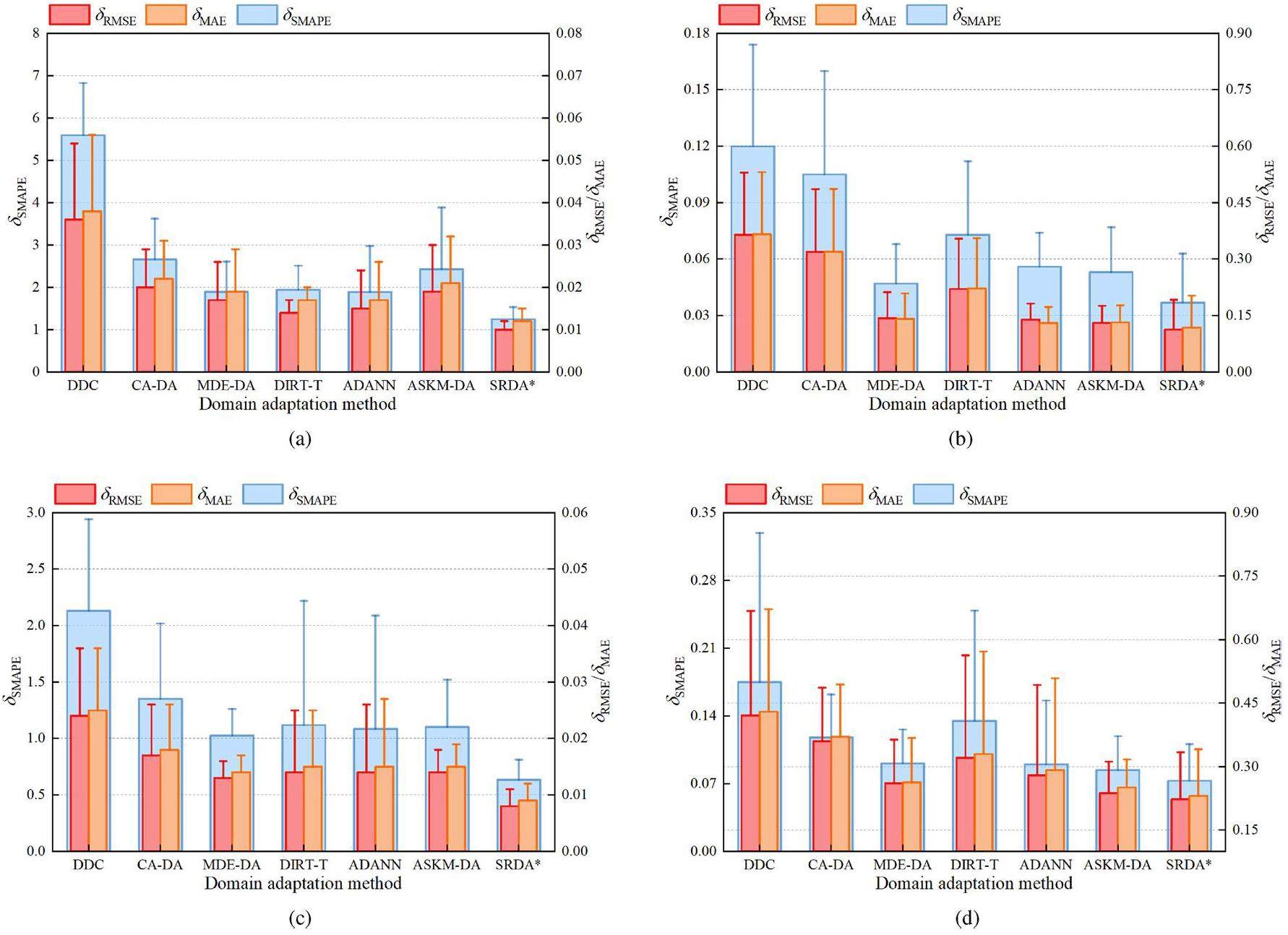
To demonstrate the knowledge-transfer superiority of the proposed method from simulation to reality, the SRDA model is compared with the six advanced domain-adaptation methods specified in Sect. 4.1, namely the DDC, CA-DA, MDE-DA, DIRT-T, ADANN, and ASKM-DA models. To ensure a fair evaluation, the transformer and improved logarithm losses are applied in the aforementioned methods. As presented in Fig. 8, the DDC and CA-DA models are statistic-based domain adaptations, and are designed to mitigate the distribution discrepancies between the simulated and real features. Their knowledge-transfer ability for neutron fluxes and temperatures during shutdown is inadequate, leading to larger errors. MDE-DA is a composite method that improves the predictive stability on the two test sets by fusing second-order statistics in CA-DA with MMD in DDC. With the incorporation of conditional entropy and a teacher model, the adversarial-based DIRT-T approach effectively forces the feature extractor to align domain-invariant features. This methodology demonstrates moderate performance in terms of inlet- and outlet-temperature predictions. In contrast, ADANN and ASKM-DA, specially designed for time-series-analysis tasks, exhibit more refined accuracy because of their marginally smaller errors compared to DIRT-T. Based on Fig. 8, adversarial-based methods tend to perform consistently better, thereby enhancing the generalization from simulation to reality. The finesse of the SRDA model involves adopting a domain adversarial strategy to extract deep domain-invariant features between the simulated and real data, in addition to utilizing MK-MMD to mitigate their distribution discrepancies. This dual approach guarantees that the model maintains the essential characteristics of the simulation while adjusting to the distribution and fluctuations that exist in a real-world reactor, which considerably improves its forecast precision.
Model interpretation
The proposed trade-off loss function includes the predictor
To present the transferability effect of the domain adaptation intuitively, feature distributions are visualized using t-distributed stochastic embedding (t-SNE). t-SNE is a nonlinear dimensionality-reduction algorithm that can transform a high-dimensional feature matrix into a two-dimensional eigenvector for visualization. As depicted in Fig. 10, the two domains are color-coded, with red denoting the simulated data and blue denoting the real data. In detail, Fig. 10a and c show the feature distributions without domain adaptation for both datasets. The features of the two domains only overlap locally, illustrating the similarities and discrepancies that commonly exist between simulation and reality. Thus, directly applying a model trained on simulated data to real data results in unsatisfactory forecasting results owing to a domain shift. In contrast, Fig. 10b and d show the feature distribution after the feature extraction in the SRDA model. Notably, after the domain adaptation, the distributions of the extracted features from the simulation and reality are uniformly mixed, illustrating that the SRDA model can mitigate the domain discrepancies effectively to enhance the operating-parameter prediction in reactors.

Conclusion
Simulators imperfectly emulate reality in NPPs due to their different actuation modes and system dynamics. This study aimed to mitigate the discrepancies in noise, numerical distributions, and dynamic characteristics between simulated and real data. A novel transferability framework, called the SRDA model, was proposed for forecasting critical parameters in nuclear reactors. The SRDA framework comprised a feature extractor, parameter predictor, domain discriminator, and MK-MMD. Relative to several advanced domain-adaptation methods, the results indicated that the SRDA model demonstrates superior knowledge transfer by leveraging ample simulated and finite real data. The transformer-based feature extractor adeptly captured the dynamic characteristics and temporal dependencies in transient conditions, such as reactor shutdown and power variation, as evidenced by comparisons with various feature extractors. The improved logarithmic loss within the predictor was conducive to enhancing forecasting precision at various power levels. Furthermore, the integration of the domain adversarial strategy and MK-MMD effectively adapted to the distributions and fluctuations in real-world reactors while retaining the essential characteristics in the simulation. Considering the significant impact of different feature extractors, the versatility of the SRDA model enables the substitution of backbone networks tailored to specific scenarios in NPPs, which is another intriguing problem.
Conceptual design and safety characteristics of a new multi-mission high flux research reactor
. Nucl. Sci. Tech. 34, 1-16 (2023). https://doi.org/10.1007/s41365-023-01191-6Is public service transportation increase environmental contamination in china? the role of nuclear energy consumption and technological change
. Energy 238, 929-962 (2022). https://doi.org/10.1016/j.energy.2021.121890Design of a supervisory control system for autonomous operation of advanced reactors
. Ann. Nucl. Energy 182, 1-14 (2023). https://doi.org/10.1016/j.anucene.2022.109593Twin model-based fault detection and tolerance approach for in-core self-powered neutron detectors
. Nucl. Sci. Tech. 34, 1-14 (2023). https://doi.org/10.1007/s41365-023-01276-2Fault prediction method for nuclear power machinery based on bayesian ppca recurrent neural network model
. Nucl. Sci. Tech. 31, 1-11 (2020). https://doi.org/10.1007/s41365-020-00792-9Comparative study of data-driven and model-driven approaches in prediction of nuclear power plants operating parameters
. Appl. Energ. 341, 1-14 (2023). https://doi.org/10.1016/j.apenergy.2023.121077Artificial neural network reconstructs core power distribution
. Nucl. Eng. Technol. 54, 617-626 (2022). https://doi.org/10.1016/j.net.2021.08.015Gradient descent-particle swarm optimization based deep neural network predictive control of pressurized water reactor power
. Prog. Nucl. Energ. 145, 1-10 (2022). https://doi.org/10.1016/j.pnucene.2021.104108Ensemble empirical mode decomposition and long short-term memory neural network for multi-step predictions of time series signals in nuclear power plants
. Appl. Energ. 283, 1-15 (2021). https://doi.org/10.1016/j.apenergy.2020.116346Neural-based time series forecasting of loss of coolant accidents in nuclear power plants
. Expert Syst. Appl. 160, 1-13 (2020). https://doi.org/10.1016/j.eswa.2020.113699Comparative study of application of different supervised learning methods in forecasting future states of npps operating parameters
. Ann. Nucl. Energy 132, 87-99 (2019). https://doi.org/10.1016/j.anucene.2019.04.031Application of artificial neural network for the critical flow prediction of discharge nozzle
. Nucl. Eng. Technol. 54, 834-841 (2022). https://doi.org/10.1016/j.net.2021.08.038Forecasting thermal parameters for ultra-high voltage transformers using long- and short-term time-series network with conditional mutual information
. IET Electr. Power Appl. 16, 548-564 (2022). https://doi.org/10.1049/elp2.12175Machine learning based system performance prediction model for reactor control
. Ann. Nucl. Energy 113, 270-278 (2018). https://doi.org/10.1016/j.anucene.2017.11.014Prediction method for thermal-hydraulic parameters of nuclear reactor system based on deep learning algorithm
. Appl. Therm. Eng. 196, 1-15 (2021). https://doi.org/10.1016/j.applthermaleng.2021.117272A novel personalized diagnosis methodology using numerical simulation and an intelligent method to detect faults in a shaft
. Appl. Sci-Basel 6, 1-19 (2016). https://doi.org/10.3390/app6120414Fault detection in gears using fault samples enlarged by a combination of numerical simulation and a generative adversarial network
. IEEE-ASME Transactions on Mechatronics 27, 3798-3805 (2022). https://doi.org/10.1109/TMECH.2021.3132459Online autonomous calibration of digital twins using machine learning with application to nuclear power plants
. Appl. Energ. 326, 1-14 (2022). https://doi.org/10.1016/j.apenergy.2022.119995The large-break loca uncertainty analysis in a vver-1000 reactor using trace and dakota
. Nucl. Eng. Des. 412, 1-15 (2023). https://doi.org/10.1016/j.nucengdes.2023.112459An open time-series simulated dataset covering various accidents for nuclear power plants
. Sci. Data 9, 714-766 (2022). https://doi.org/10.1038/s41597-022-01879-1Efficient predictor of pressurized water reactor safety parameters by topological information embedded convolutional neural network
. Ann. Nucl. Energy 192, 1-13 (2023). https://doi.org/10.1016/j.anucene.2023.110004Prediction calculations for the first criticality of the htr-pm using the pangu code
. Nucl. Sci. Tech. 32, 9-15 (2021). https://doi.org/10.1007/s41365-021-00936-5Research on short term prediction method of thermal hydraulic transient operation parameters based on automated deep learning
. Ann. Nucl. Energy 165, 1-15 (2022). https://doi.org/10.1016/j.anucene.2021.108777Equivalence analysis of simulation data and operation data of nuclear power plant based on machine learning
. Ann. Nucl. Energy 163, 1-12 (2021). https://doi.org/10.1016/j.anucene.2021.108507Artificial intelligence in nuclear industry: Chimera or solution
? J. Clean. Prod. 1–14 (2021). https://doi.org/10.1016/j.jclepro.2020.124022Federated transfer learning based cross-domain prediction for smart manufacturing
. IEEE Trans. Ind. Inf. 18, 4088-4096 (2022). https://doi.org/10.1109/TII.2021.3088057Transfer learning network for nuclear power plant fault diagnosis with unlabeled data under varying operating conditions
. Energy 254, 1-14 (2022). https://doi.org/10.1016/j.energy.2022.124358Deep unsupervised domain adaptation with time series sensor data: A survey
. Sensors-basel. 22, 1-29 (2022). https://doi.org/10.3390/s22155507Subdomain adaptation transfer learning network for fault diagnosis of roller bearings
. IEEE Trans. Ind. Electron. 69, 8430-8439 (2022). https://doi.org/10.1109/TIE.2021.3108726Domain adaptation for medical image analysis: a survey
. IEEE Trans. Biomed. Eng. 69, 1173-1185 (2022). https://doi.org/10.1109/TBME.2021.3117407Transferring policy of deep reinforcement learning from simulation to reality for robotics
. Nat. Mach. Intell. 4, 1077-1087 (2022). https://doi.org/10.1038/s42256-022-00573-6Machinery fault diagnosis based on domain adaptation to bridge the gap between simulation and measured signals
. IEEE Transactions on Instrumentation and Measurement 71, 1-9 (2022). https://doi.org/10.1109/TIM.2022.3180416Digitalization of the ex-core neutron flux monitoring system for apr1400 nuclear power plant
. Applied Sciences-Basel 10, 1-19 (2020). https://doi.org/10.3390/app10238331Adatime: a benchmarking suite for domain adaptation on time series data
. ACM Transactions on Knowledge Discovery From Data 17, 1-18 (2023).A transformer-based method of multienergy load forecasting in integrated energy system
. IEEE Trans. Smart Grid 13, 2703-2714 (2022). https://doi.org/10.1109/TSG.2022.3166600Attention is all you need
. 2017, pp. 6000–6010Learning transferable features with deep adaptation networks
. Vol. 1,Deep domain confusion: maximizing for domain invariance
. (2014). arXiv:1412.3474 http://arxiv.org/abs/1412.3474An adaptive adversarial domain adaptation approach for corn yield prediction
. Comput. Electron. Agr. 187, 1-10 (2021). https://doi.org/10.1016/j.compag.2021.106314Adversarial spectral kernel matching for unsupervised time series domain adaptation
.The authors declare that they have no competing interests.


