Introduction
The interaction between an ultra-intense short-pulse laser and solid targets can produce various charged particles, such as electrons [1], protons [2], and ions [3]. Because of the GV/m to TV/m acceleration gradient offered by the laser-induced charge separation field, 8 GeV energy electrons [4] and nearly 100 MeV protons [5] are accelerated within short distances. However, electromagnetic pulses (EMPs) of various frequencies are generated during the acceleration of charged particles, including radio frequency (RF) microwaves [6, 7], visible light [8], extreme ultraviolet (EUV) [9], X-rays [10], and γ-rays [11]. Among them, EMPs in the GHz domain with a strength of up to MV/m are induced within semiconductor devices, leading to equipment malfunctions, diagnostic damage, and pseudo-signal detection [12-15]. An in-depth understanding of the mechanisms and influencing factors of EMP radiation, strict control of the generation and propagation of harmful EMPs, and the design of effective EMP shielding systems are of great significance for the successful execution of experiments involving ultra-intense laser ablation.
Many studies have demonstrated that EMPs induced by the interaction of ultra-intense lasers with solid targets primarily involve the following physical processes [16-19]. Initially, the interaction of the laser with solid targets causes the electrons of the target to gain energy and subsequently escape to the vacuum, resulting in the accumulation of positive charges on the surface of the solid target, known as target polarization. Subsequently, the surface of the solid target develops a Coulomb potential, which causes sheath oscillations on the surface of the target and generates electromagnetic radiation. As a result of target polarization, a neutralization current flows through the target holder to the ground, thereby producing EMPs within the GHz frequency range. Several experimental and simulation studies have substantiated the presence of neutralization currents [20-24]. In addition, several other potential sources of EMPs have been proposed for the laser irradiation of solid targets, including charged layers owing to photoionization, wakefields of accelerated charges, and particles on surfaces [25].
Many previous studies have elucidated that the EMPs resulting from the laser ablation of solid targets are closely related to multiple factors, including laser parameters (laser energy [26, 27], pulse width [26-28], focus [26], and pre-pulse [26, 29-31]), target parameters (target size [27, 28, 32], material [33-37], thickness [37-39], and configuration [40-43]), and target holder parameters (target holder geometry [26, 44] and material [20, 26]).
Unlike with solid targets, short-pulse lasers interacting with gaseous-density plasma can excite periodic electronic oscillation structures through ponderomotive force, thereby generating plasma waves. Electrons that approach the phase velocity of the plasma wave and are in the accelerating phase can be trapped and accelerated by the plasma waves. This process is known as laser wakefield acceleration (LWFA) [45-47]. LWFA can generate electron energies in the GeV range, while the electron charge remains relatively low, typically ranging from pC to nC [48, 49].
However, when the density of the plasma increases to ωp > 1/τ, where τ is the duration of the laser pulse and ωp is the plasma frequency, as the laser intensity increases, plasma wave breaking destroys the periodic structure, and the ponderomotive force of the laser expulses electrons from the central regions to form a plasma channel. In this case, the electrons may undergo direct acceleration by the transverse laser field when their oscillation frequency within the field of the plasma channel is close to the Doppler-shifted laser frequency. In this scenario, direct laser acceleration (DLA) plays a significant role [50-52]. The electron energy produced by DLA is relatively low, typically ranging from tens to hundreds of MeV, but the electron charge can reach tens or even hundreds of nC [53, 54].
Many studies have comprehensively investigated the radiation produced by the laser-gas jet interactions, encompassing THz [55-57] and X-ray [58-60] radiation. However, previous studies related to laser-driven EMPs primarily focused on the characteristics of EMPs generated by a laser interacting with solid targets [61]. Few measurements are available regarding EMPs induced by the high-power laser ablation of gas jets. Previous studies have demonstrated that short-pulse laser-driven EMPs from an underdense gas jet target are weaker and much shorter in time duration than those from a solid plastic foil target [34]. However, to date, there is a scarcity of pertinent reports elucidating the sources and underlying mechanisms of EMPs resulting from laser interaction with gas jets, posing a challenge in effectively mitigating these EMPs. In this study, we measured and characterized EMPs using a petawatt laser to bombard nitrogen gas jets. By analyzing the results, the influence of laser energy and gas jet pressure on EMPs was investigated. Furthermore, a three-dimensional electromagnetic simulation model was developed. Based on the simulation results, we propose four potential sources of EMPs and further investigate the temporal, spectral, and spatial distribution characteristics of EMPs resulting from the laser irradiation of gas jets.
The experimental results will be helpful in elucidating the mechanisms of EMP generation during the laser ablation of gas jets and open a new avenue to achieve tuned EMPs. Additionally, they provide guidance for the future exploration of the potential applications of intense EMPs, such as high-power and short-pulse microwave sources [62], as well as non-destructive testing using electromagnetic waves [63].
Experimental setup
The EMPs were measured at the SILEX-II multi-petawatt laser facility located at the National Key Laboratory of Plasma Physics of China Academy of Engineering Physics [64]. A schematic of the experimental setup for the EMP detection is presented in Fig. 1.
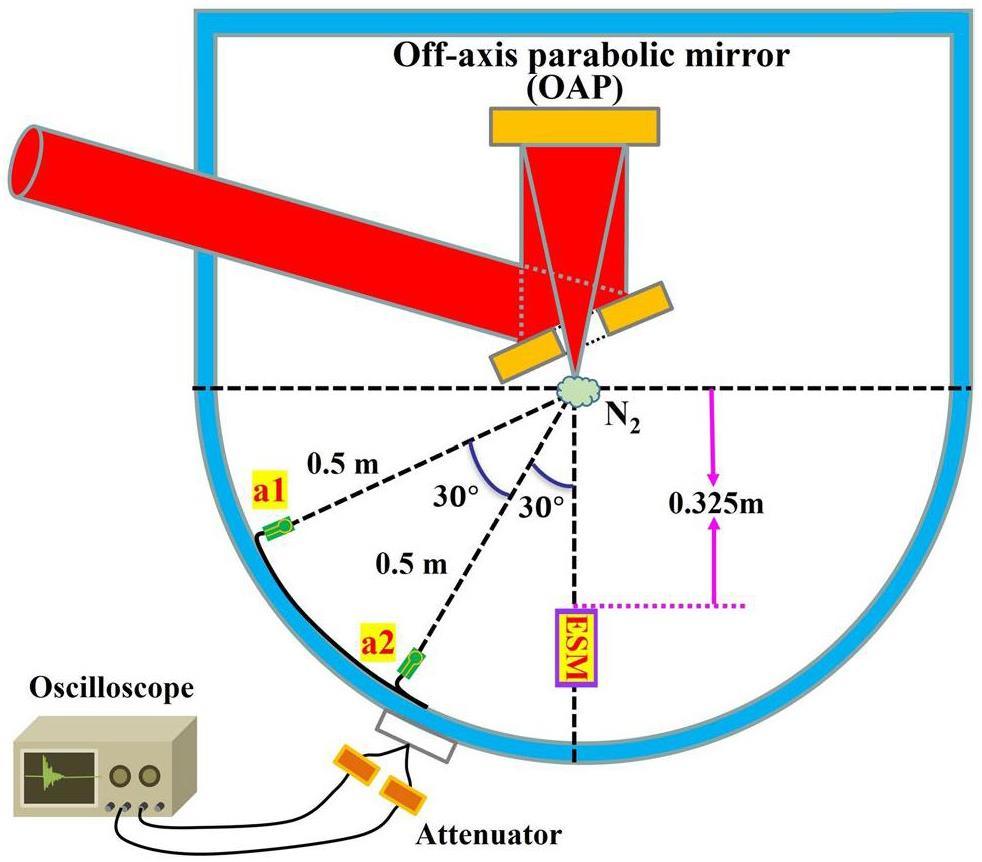
In this experiment, the length and width of the gas jet nozzle were 10 mm and 1 mm, respectively. The petawatt laser was perpendicularly incident onto the nitrogen gas jet, with a laser focus positioned 2 mm above the gas jet nozzle. In this study, we measured the EMPs induced by the laser ablation of nitrogen gas jets with four different gas jet pressures: 1, 1.5, 2.15, and 3.15 MPa. The corresponding electron densities for these gas jet pressures are 3.9×1019 cm-3, 5.6×1019 cm-3, 8.5×1019 cm-3, and 1.2×1020 cm-3, respectively. To investigate the spatial characteristics of EMPs inside the laser target chamber, two identical SG-IIIB01-2 small B-dot antennas labelled a1 and a2, with diameters of 10 mm, were mounted at 60° and 30° angles with respect to the direction of laser propagation and at a 0.5 m distance to the target chamber center (TCC) [65]. The antennas were connected through identical double-shielded RF coaxial cables to an oscilloscope with a 13 GHz analog bandwidth and 40 GS/s sampling rate, protected by a Faraday cage situated outside the target chamber. Suitable attenuators were added between the coaxial cable and oscilloscope to ensure that the signal was within the measuring range of the oscilloscope. To record the quantity and energy of the electrons emitted from the back of the nitrogen gas jet, a calibrated electron spectrometer with a magnetic field of 900 G was installed at 0° angle with respect to the direction of laser propagation, 0.325 m away from the nitrogen gas jet holder. In the electron spectrometer, an image plate (IP) records the deflection distance of electrons and quantifies them based on their corresponding energy levels.
In this experiment, the pulsed laser output energies of 16 to 48 J with a pulse width of 30 fs. The central wavelength of the main laser was
Results and discussion
EMPs versus laser energy and gas jet pressures
The maximum magnetic field
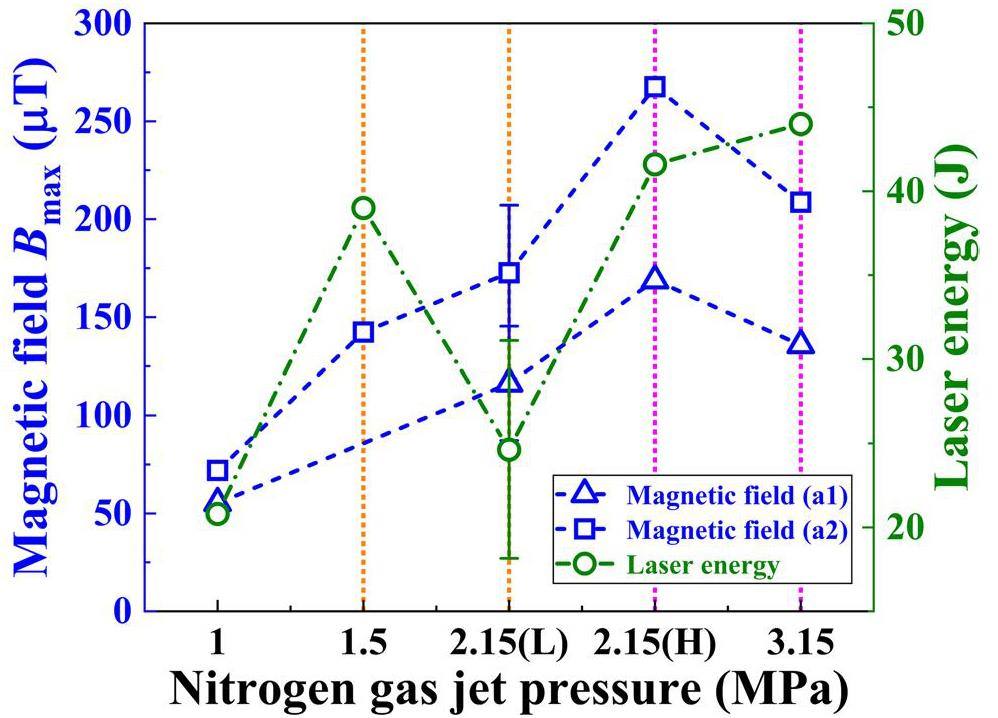
In Fig. 2, the maximum magnetic field Bmax clearly changes when the nitrogen gas jet pressure varies from 1 to 3.15 MPa. Under the same nitrogen gas jet pressure of 2.15 MPa, the maximum magnetic field increases as the laser energy increases. Furthermore, in the range of 1 to 2.15(L) MPa, the maximum magnetic field increases with an increase in the nitrogen gas jet pressure. However, despite the increase in laser energy and nitrogen gas jet pressure from 2.15(H) to 3.15 MPa, a significant decrease was observed in the maximum magnetic field, indicating a downward trend. Finally, under various nitrogen gas jet pressures, the maximum magnetic field at a2 (30° from the laser beam) is higher than that at a1 (60° from the laser beam). This finding is consistent with previous experimental results, which are mainly attributed to the fact that a larger quantity of higher-energy electrons is produced at a location closer to the laser propagation direction [68-70].
Temporal and spectral characteristics of EMPs
To further elucidate the characteristics of the EMP arising from the interaction between the laser and nitrogen gas jet at varying pressures, a Fast Fourier Transform (FFT) was performed on the time-domain EMP signals to obtain the frequency domain. The amplitudes were then squared to obtain the power density spectra for the four different nitrogen gas jet pressures. Figure 3 illustrates that EMP frequencies generated by laser interaction with nitrogen gas jets at 1 and 1.5 MPa pressure are primarily concentrated within the frequency range of 0 to 2 GHz, while the spectra predominantly extended to the range of 7 GHz for the pressures of 2.15 and 3.15 MPa.
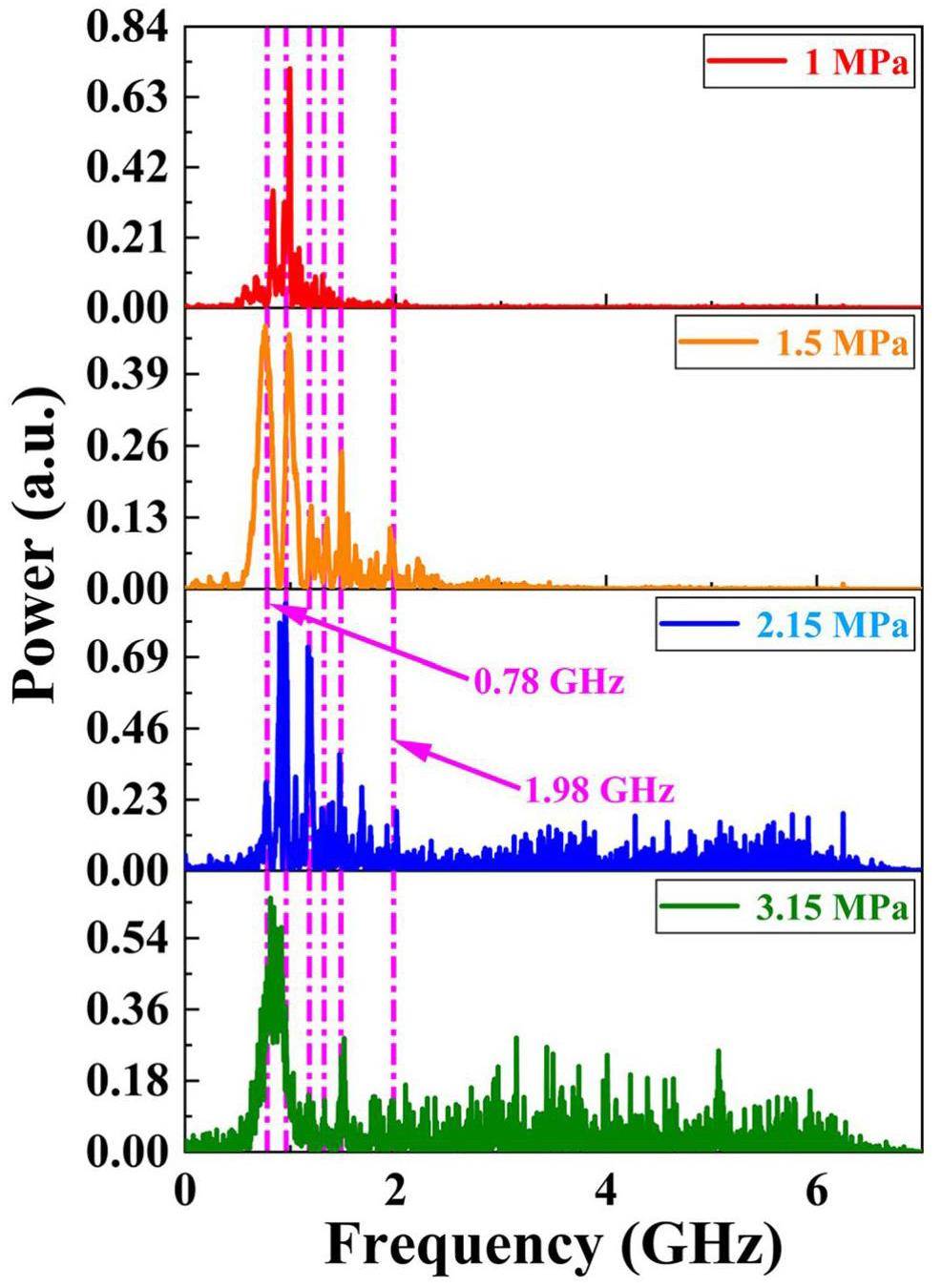
In Fig. 3, there are six superimposed peaks appearing at 0.78, 0.96, 1.18, 1.32, 1.48, and 1.98 GHz. These are primarily attributed to the eigenfrequency radiation, which depends on the structure of the experimental chamber [71]. For an ideal cuboid resonant cavity, the wavelength
The resonant frequency fr for the cuboid resonant cavity can be expressed as
As depicted in Fig. 4a, the SILEX-II target chamber appears as a composite structure composed of a cube with side lengths of 1.2 m and a semi-cylinder with a base diameter of 1.2 m and height of 1.2 m [64]. The SILEX-II target chamber can be regarded as being situated between two cuboid resonant cavities. For the first cuboid resonant cavity, the length is l=1.8 m, width is w=1.2 m, and height is h=1.2 m. The fundamental resonant frequency of the corresponding cuboid cavity is fr1=150.2 MHz. The second cuboid resonant cavity has a length of l=1.2 m, width of w=1.2 m, and height of h=1.2 m. The resonant frequency of the corresponding cuboid cavity is fr2=176.8 MHz. Therefore, the resonant frequency of the empty SILEX-II target chamber can be calculated within the range of 150.2 to 176.8 MHz.
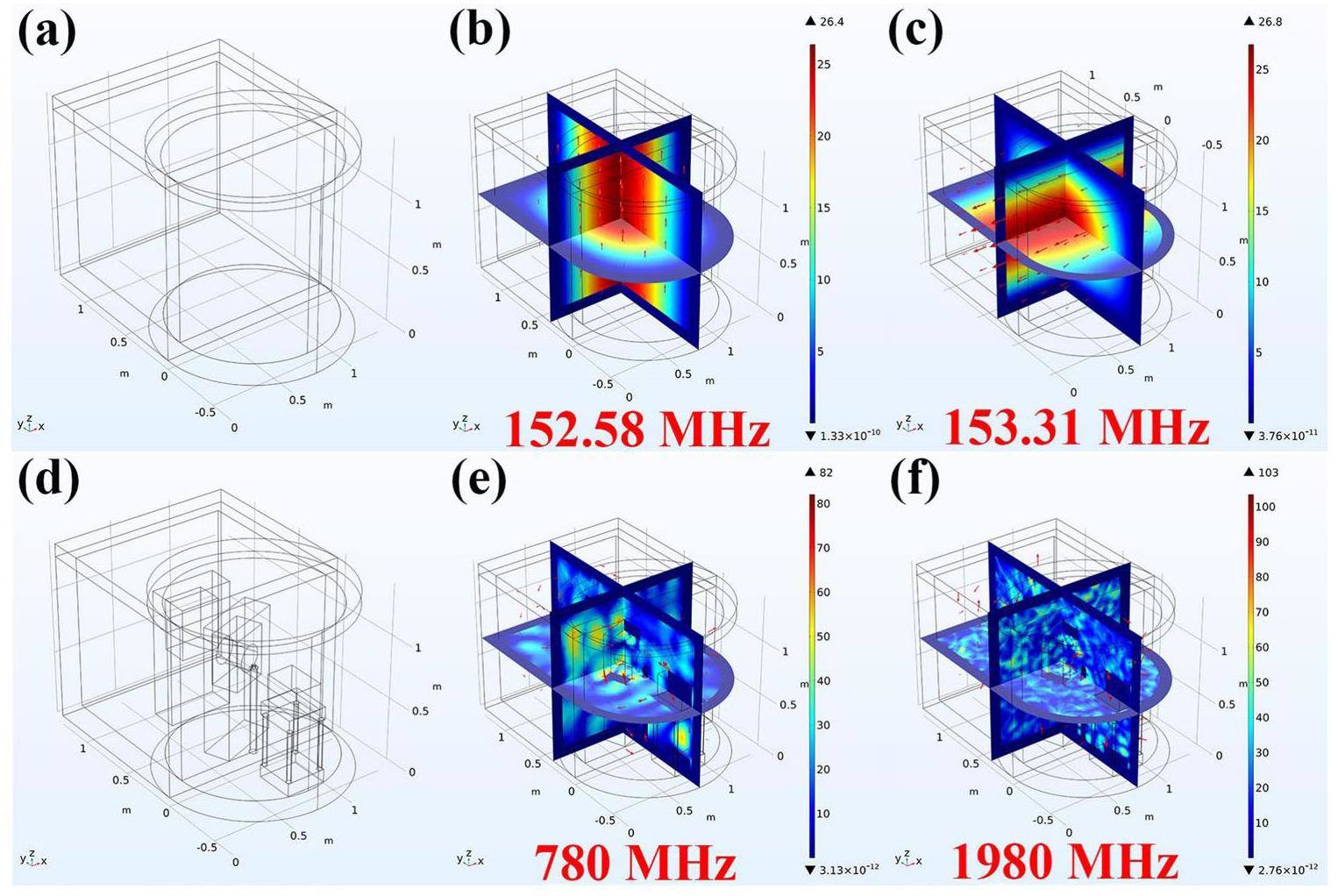
To elucidate the distribution of the electromagnetic field and eigenfrequencies in the actual SILEX-II target chamber, a simplified empty resonant cavity model of the SILEX-II target chamber was established using the COMSOL solver based on the finite element method [6, 73, 74]. Figure 4 shows the normalized electric fields associated with different modes inside the target chamber. As shown in Figs. 4b and 4c, there are two resonant frequencies: 152.58 and 153.31 MHz. These two typical resonant frequencies are significantly lower than those marked by the dashed magenta line in Fig. 3. This difference can primarily be attributed to the specific internal arrangements within the real target chamber [61, 72, 75, 76].
Considering the layout of the actual SILEX-II target chamber, multiple object models, as depicted in Fig. 4d, including mirror holders, the target holder, and electron spectrometers, were added to the COMSOL model, resulting in higher resonance frequencies. Figures 4e and 4f illustrate the two typical resonance frequencies of 780 and 1980 MHz, as also indicated in Fig. 3. The simulation results demonstrate an uneven distribution of the resonance frequencies, indicating certain variations in the resonance frequencies within different regions of the target chamber.
To obtain the temporal evolution of the spectra, a short-time Fourier transform (STFT) was applied to process the EMP signals [75]. The window width and overlap were set to 512 and 500, respectively. The results are presented in Fig. 5, where the main frequency band of the EMPs (0.6 to 0.96 GHz) appears from 0 to 5 ns.

Electron charge and temperature versus gas jet pressure
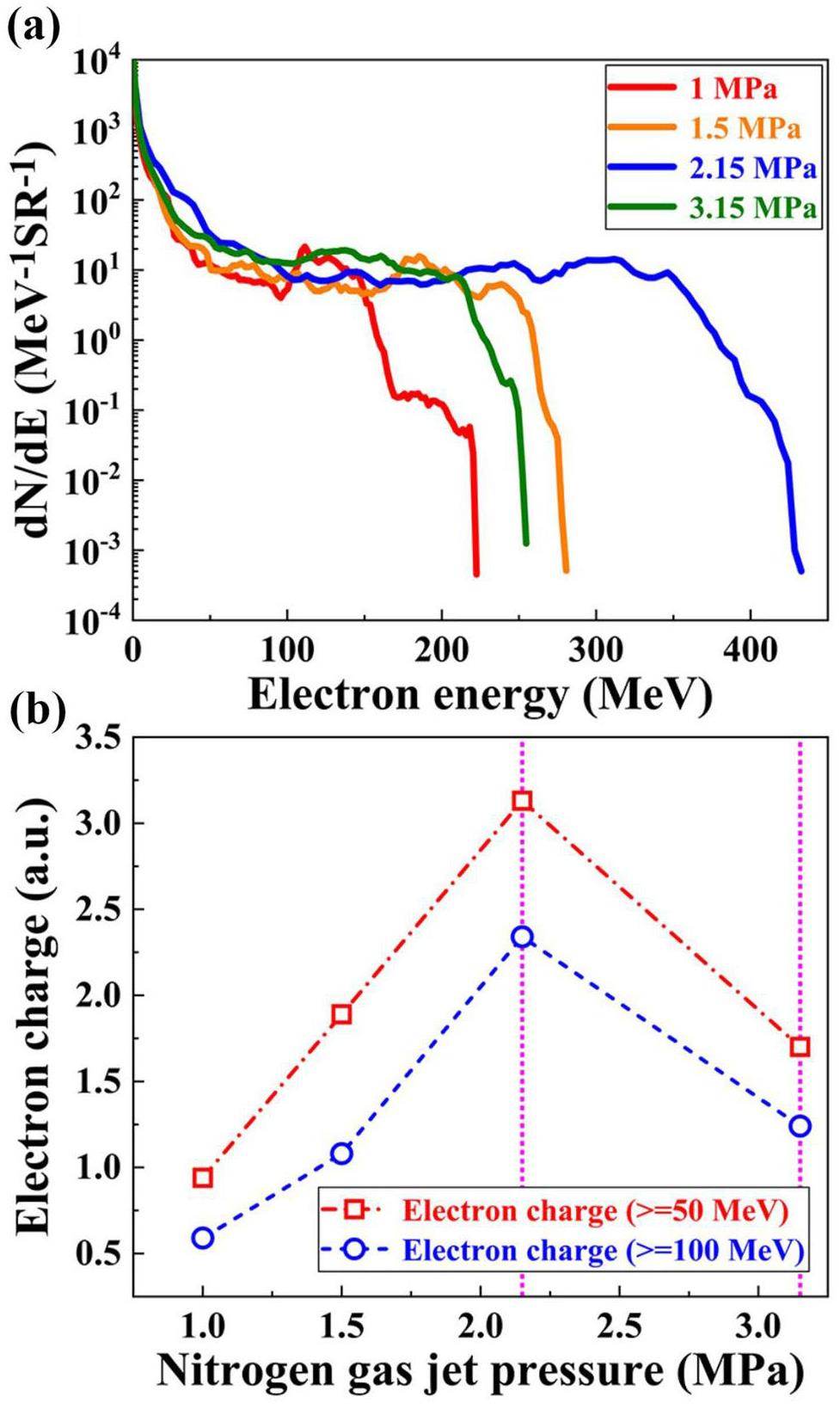
Figures 6a and 6b further illustrate the electron charge Qe and electron temperature Th generated by the petawatt laser irradiation of nitrogen gas jets with varying pressures during the experimental test. The experimental data of the electron energy spectra were fitted to a Maxwellian distribution with functional form
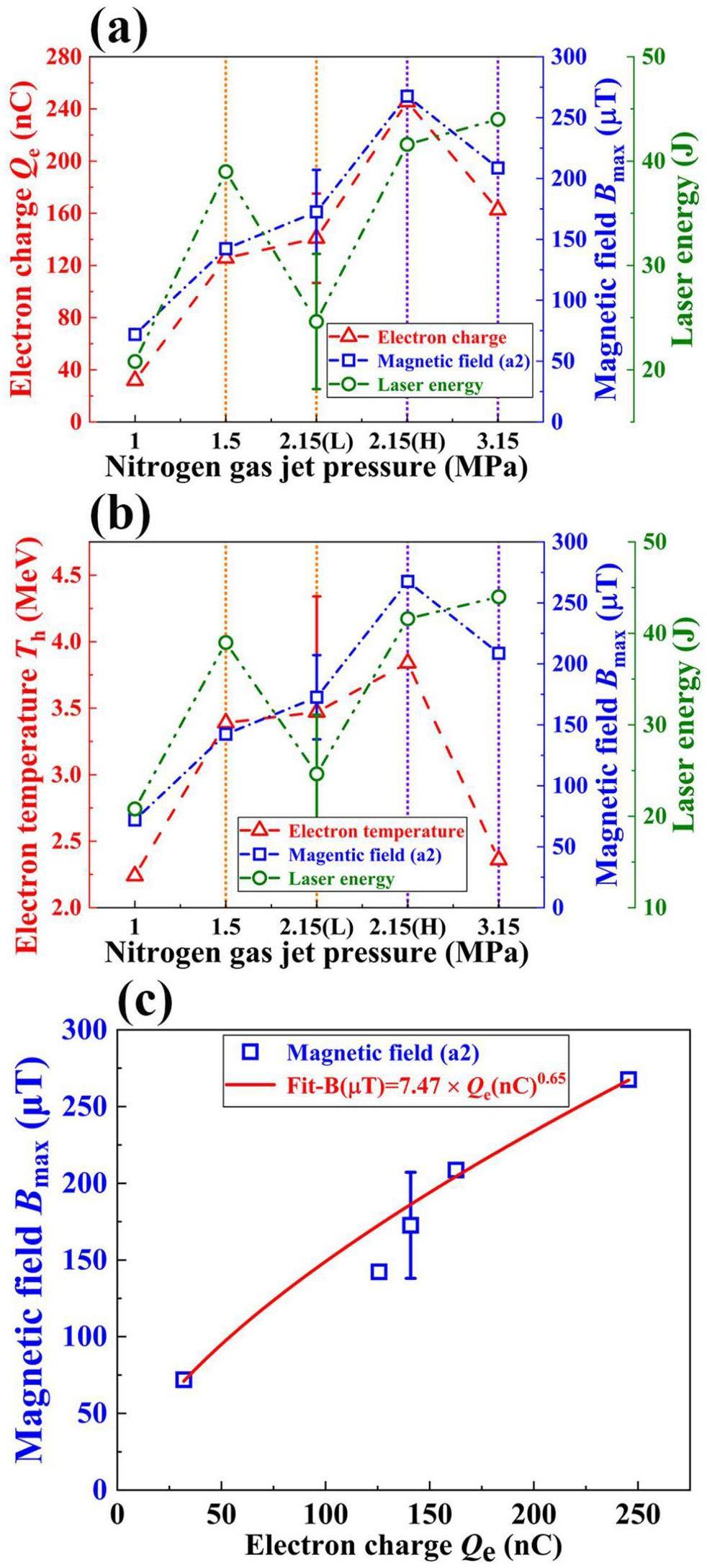
The maximum magnetic field Bmax and laser energy are also shown on the right axis of Fig. 6. The EMP signal and electron charge show a high degree of consistency, approximately following the trend
Simulation results and discussion
To further reveal the physical processes of petawatt laser ablation on nitrogen gas jets, the 2D PIC software EPOCH [78] was used. Considering that the width of the nitrogen gas jet nozzle employed in this experiment was 1 mm, the laser pulse was simulated to be incident directly onto a 1 mm-thick nitrogen gas jet. The laser pulse had a duration of 30 fs, diameter of 5 μm, and intensity of 5×1020 W/cm2. The central wavelength of the laser was 800 nm, which corresponded to a critical plasma density of nc=1.7×1021 cm-3.
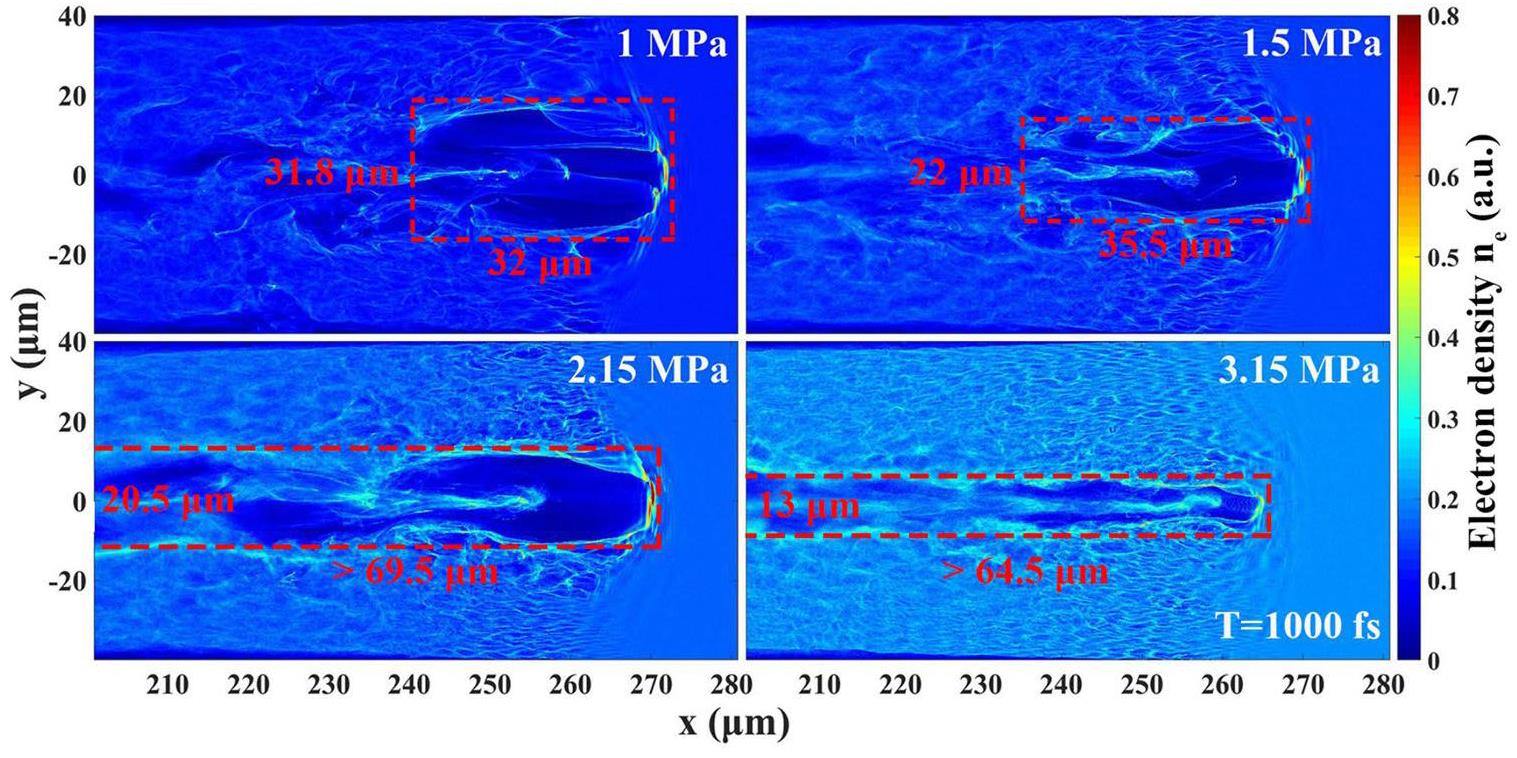
As shown in Fig. 7, the electrons generated by the petawatt laser ablation of the nitrogen gas jet are closely linked to the pressure (plasma density). When the nitrogen gas jet pressure increased from 1 to 2.15 MPa, the self-focusing effect was enhanced, and a larger portion of the laser energy was captured by the plasma channel. This led to an increase in the length of the plasma channel; consequently, the number and energy of electrons captured and accelerated by the plasma channel also increased. However, when the nitrogen gas jet pressure increased to 3.15 MPa, more laser energy was lost during electron heating at the channel boundary owing to ionization and ionization defocusing. This resulted in a decrease in the length and width of the plasma channel, thereby reducing the number and energy of electrons captured by the plasma channel [52, 79, 80].
The simulated electron energy spectra and electron charges are shown in Fig. 8. In the optimum case of 2.15 MPa, the quantity and energy of electrons that could be captured and accelerated by the plasma channel were the highest, which is consistent with the experimental results shown in Fig. 6.
Investigation of the generation and spatiotemporal characteristics of EMPs
When the nitrogen gas jet is bombarded by the laser pulse, the nitrogen atoms are ionized by the main laser pulse to form a plasma. The corresponding plasma frequency at position r and time t can be expressed as [81]
In this experiment, the plasma electron density exceeded 3.9×1019 cm-3; thus, the corresponding plasma frequency exceeded 56 THz. This is sufficient to suppress the electromagnetic waves in the GHz frequency range generated by electrons in the plasma channel [20, 25]. Therefore, the following investigations primarily focused on the EMPs generated after electrons escape from the gas target into the vacuum.
To further verify the correlation between the EMP intensity and the quantity and energy of electrons escaping from the gas target, we imported the parameters of the experimental electron beam into the 3D PIC simulation (coupled with a full EM solver) with the commercial code suite CST Particle Studio [25, 82]. The simulation model, as shown in Fig. 9a, is based on the actual target chamber model of SILEX-II. To decrease the computation time, we downsized the model by 10 times, including the target chamber, steel gas jet holder, and two steel conductors.
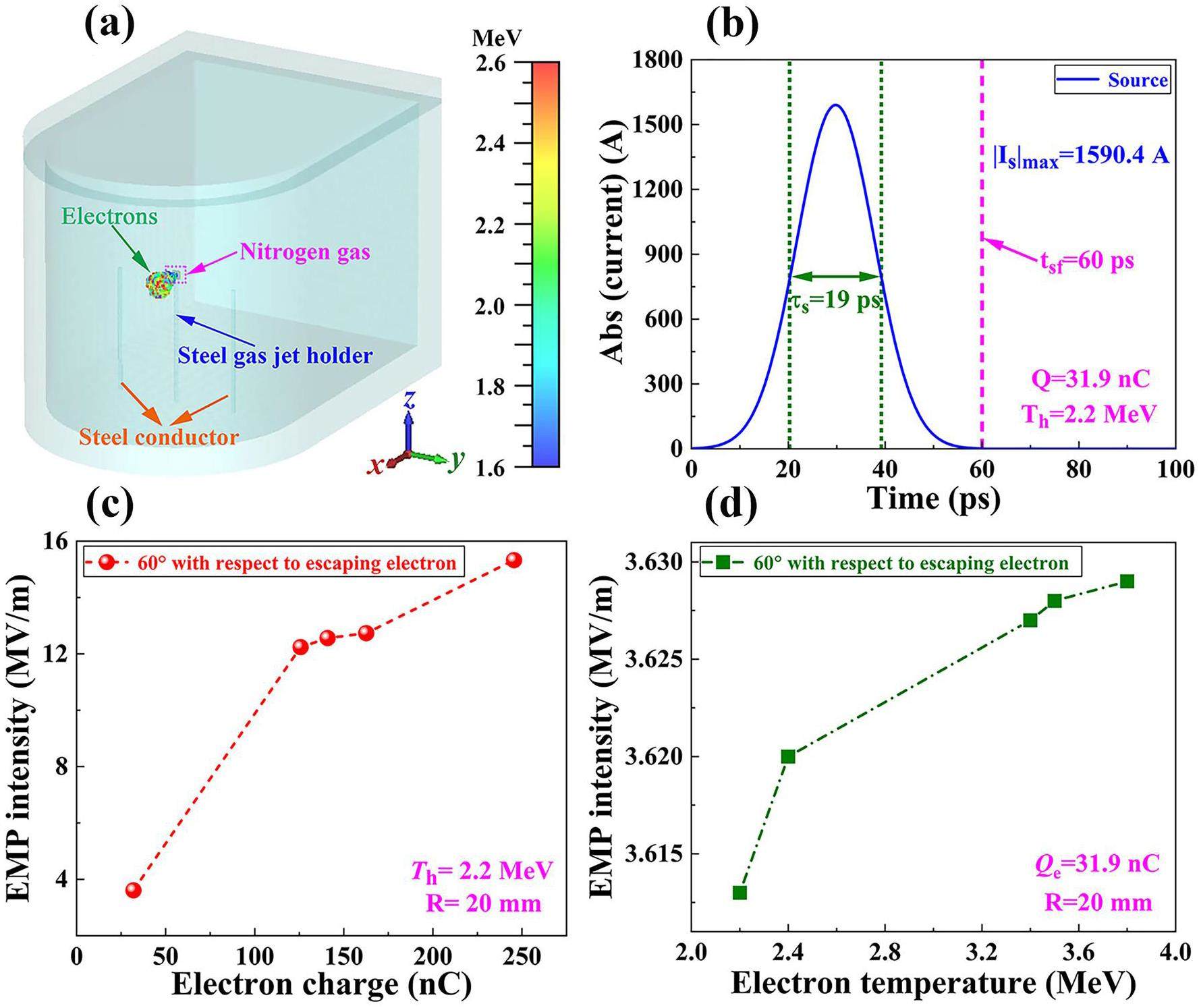
The target material consisted of nitrogen gas and had dimensions of X (1 mm) × Y (4 mm) × Z (4 mm). A cylindrical target holder with a diameter of 2 mm and height of 60 mm was employed instead of the gas jet holder. As shown in Fig. 9a, the gas jet holder material was set to conductor steel. Moreover, to investigate the impact of metallic conductors inside the target chamber on the generation and distribution of EMPs, two identical cylindrical steel conductors with a diameter of 2 mm and height of 60 mm were positioned 30 mm away from the gas jet holder. These steel conductors served as simplified substitutes for the diverse metallic conductors typically found in the target chamber. One electric field probe was positioned 20 mm behind the target at an angle of 60° relative to the direction of electron escape. The electrons were ejected from a circular ring with a diameter of 5 μm located at the center of the nitrogen gas target towards the vacuum. In the simulation, the time required for electrons to escape from the gas target and eventually reach the target chamber walls was several hundred picoseconds, which is much longer than the 30 fs width of the Gaussian laser pulses used in the experiment. If the duration of escaping electrons in the simulation was set too short, not only would the computational time increase but the detailed observation of the underlying physical processes would be hindered. Therefore, as shown in Fig. 9b, compared with the 30 fs Gaussian laser pulse used in the experiment, we increased the duration of the escaping electron pulse by approximately 1000 times, with a Gaussian width of approximately 19 ps and duration of approximately 60 ps.
The simulation results are shown in Fig. 9c. Based on our experimental results, the electron temperature was maintained at 2.2 MeV, while the electron charge was set to vary from 31.9 to 245.5 nC. The simulation results suggest that the EMP intensity is directly proportional to the number of electrons escaping from the nitrogen gas target. Moreover, a position closer to the direction of the electron escape exhibits stronger EMPs. In Fig. 9d, the electron charge ejected from the nitrogen gas target was set to 31.9 nC. The corresponding electron temperature ejected from the nitrogen gas target was varied from 2.2 to 3.8 MeV. The simulation results demonstrate that as the escaping electron temperature increases, the EMP intensity increases. However, compared with the electron charge, the impact of the electron temperature on the EMPs was relatively insignificant.
A preliminary exploration of the sources of EMPs induced by the interaction of the laser with gas jets was performed using 3D PIC simulation with the commercial code suite CST Particle Studio. The simulation model and parameter setup were as shown in Figs. 9a and 9b. The time required for the electron beam to reach the target chamber wall can be approximately calculated as
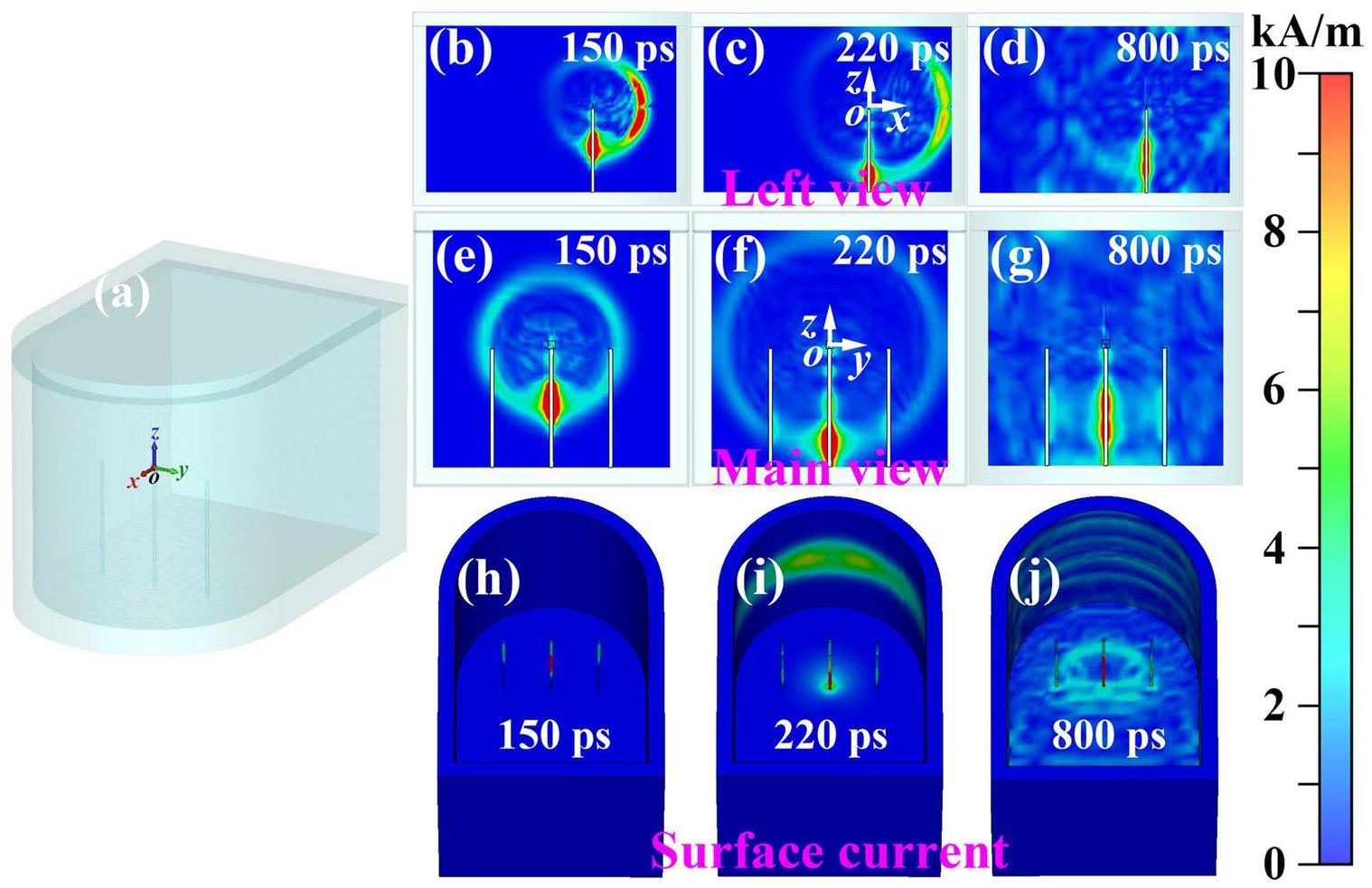
As shown in Figs. 10b, 10e, and 10h, at the time instance, due to the electron ejection, the nitrogen gas target becomes positively charged and a magnetic field envelops the path of electron transportation. The positively charged nitrogen gas target induces a charge displacement on the surface of the steel gas jet holder and then a neutralization current [83]. The neutralization current travels through the steel gas jet holder to the target chamber surface, while emitting intense EMPs into the vacuum. Furthermore, EMPs generated by the escaping electrons and neutralization currents reach the surrounding steel conductors, inducing currents on the surface of the steel conductors and producing EMPs. As shown in Figs. 10c, 10f, and 10i, at time instance t2=220 ps, the fastest electrons reach and accumulate on the target chamber wall. Consequently, surface currents develop and spread to other sections of the target chamber wall, leading to the emission of EMPs into the vacuum. As shown in Figs. 10d, 10g, and 10j, at time instance t2=800 ps, the current continuously oscillates on the gas jet holder, steel conductors, and target chamber wall, continuously radiating EMPs into the vacuum.
Based on the aforementioned CST PIC simulation, we propose multiple sources of EMPs that arise from the interaction between the laser and gas jet, as illustrated in Fig. 11.
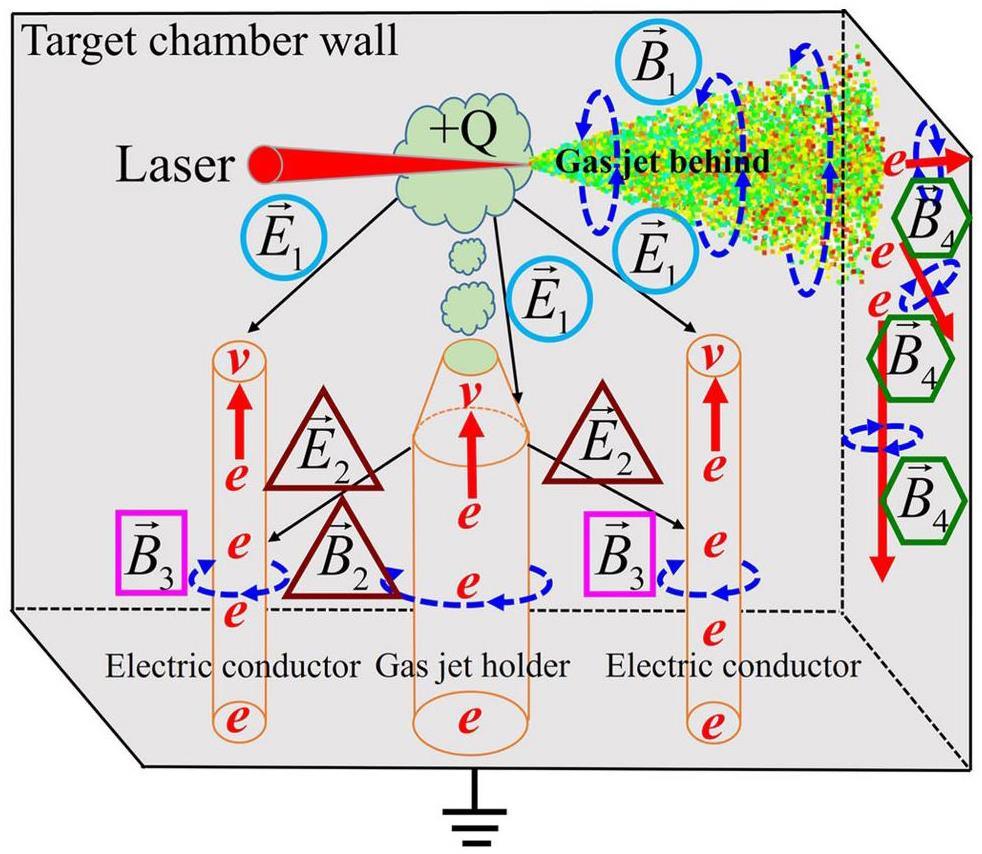
First, during the process of electrons escaping into the vacuum, transient currents are generated, and EMPs are produced around the transport path of the electrons.
Second, as some electrons escape from the gas target into the vacuum, the gas target becomes positively charged. A positively charged gas target induces displacement charges on the surface of the gas jet holder, generating neutralization currents and strong EMPs [83].
Third, the EMPs generated by the escaping electrons and neutralization currents induce transient currents on the surface of the surrounding metallic conductors inside the target chamber, generating EMPs.
Finally, the electrons escaping into the vacuum collide with the conductors and metallic target chamber wall along the transmission pathway, causing electrons to accumulate on the surface of the metallic conductors and metallic target chamber wall, resulting in transient currents and EMPs.
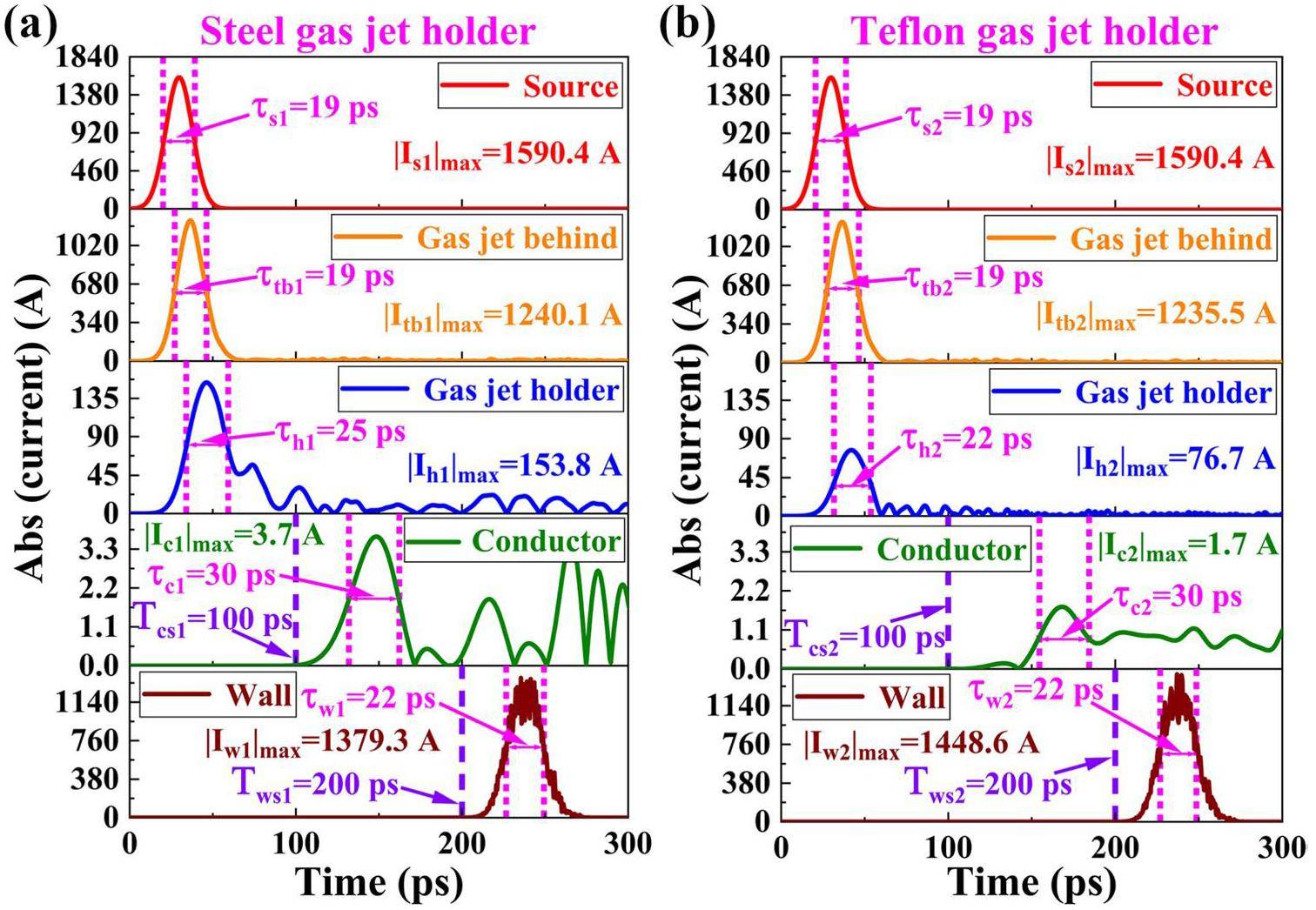
To further understand the temporal characteristics of EMPs from different sources, Fig. 12 presents the transient current waveforms at different positions during the simulation. Moreover, Fig. 12 shows the simulation results for the insulated Teflon gas jet holder. The following conclusions can be drawn from Fig. 12. First, in the time-domain profile, the transient currents at different locations exhibit a Gaussian distribution, and the width of the Gaussian pulse is approximately equal to the source current of the escaping electrons. Second, considering the start time of the transient current, when the electrons escape from the gas target, a transient current is generated behind the gas target and at the gas jet holder simultaneously. After 100 ps, EMPs generated by the escaping electrons and neutralization currents reach the steel conductor, inducing transient currents on the steel conductor. After 200 ps, the escaping electrons reach the target chamber wall, accumulate on it, and generate transient currents. Finally, compared with the steel gas jet holder, the Teflon-insulated gas jet holder can reduce the intensity of the neutralization and surface currents on the conductors.
According to the Biot-Savart law, the magnetic field
According to the relationship between electric field strength
Eq. (5) describes the electric field strength
The typical time-domain waveform of a Gaussian pulse can be expressed as
The Fourier transform of the time-domain Gaussian pulse also follows a Gaussian pulse distribution, which can be expressed as
According to Eqs. (7) and (8), the relationship between TFWHM and FFWHM can be expressed as
To study the spatial distribution of EMPs, electric field probes were placed at different angles, 20 mm away from the gas target. In addition, to avoid the influence of echo oscillations inside the target chamber, we only recorded the peak intensity of the first Gaussian pulse signal of the time-domain waveforms of EMPs in CST simulation. The simulation results are presented in Fig. 13.
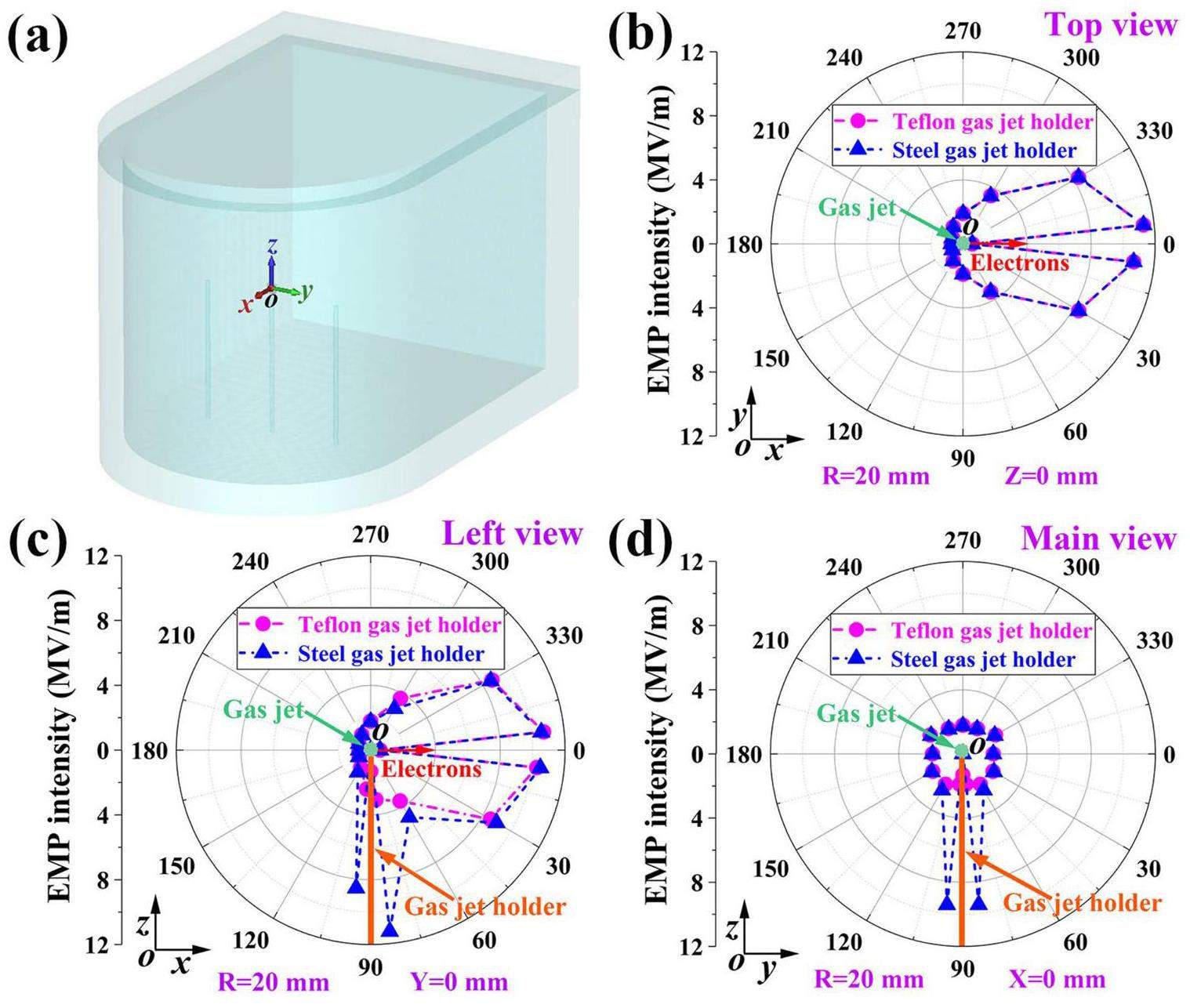
According to Eq. (5), the distribution of EMPs mainly depends on two factors. The EMP intensity is directly proportional to the transient current intensity I and inversely proportional to the distance r2 from the transient current. Figure 13 shows that the distribution of EMPs exhibits clear directionality, with EMPs mainly distributed around the escape path of electrons behind the gas target and gas jet holder. We preliminarily speculate that the EMPs generated by the gas target mainly originate from the electrons escaping from the gas target and neutralization current passing through the steel gas jet holder to the target chamber surface. Further experiments and simulations are required to validate the mechanism of EMP generation in gas targets. If confirmed, this conclusion will introduce novel strategies for shielding against EMPs induced by gas targets.
In addition, as shown in Figs. 12 and 13, compared with the steel gas jet holder, the Teflon-insulated gas jet holder can significantly reduce the neutralization current and indirectly decrease the EMP intensity driven by the neutralization current.
Conclusion
The characteristics of EMPs generated by the multi-petawatt laser ablation of nitrogen gas jets under varying pressure conditions were analyzed. The EMP amplitude could be tuned by manipulating the laser energy and nitrogen gas jet pressure (nitrogen gas density). The experimental results revealed that an increase in laser energy leads to a corresponding increase in the EMP amplitude while maintaining a constant nitrogen gas jet pressure. However, the EMP amplitude does not increase progressively as the nitrogen gas jet pressure increases from 1 to 3.15 MPa, with the peak amplitude observed at 2.15 MPa. The experimental and simulation results demonstrated that the nitrogen gas jet pressure affects the quantity and energy of electrons captured and accelerated by the plasma channel generated by the laser ablation of nitrogen gas jets, which indirectly affects the EMP amplitude. Through simulation and theory, we verified that the EMP amplitude is directly proportional to the energy and quantity of electrons escaping from the nitrogen gas jet. We also proposed several possible sources of EMPs resulting from the interaction between the laser and gas jets. The resulting conclusions will be beneficial for both shielding design and the generation of controllable EMP radiation during the intense laser bombardment of gas jets.
High energy electrons, nuclear phenomena and heating in petawatt laser-solid experiments
. Laser Part. Beams. 17, 773-783 (1999). https://doi.org/10.1017/S0263034699174238Intense High-Energy Proton Beams from Petawatt-Laser Irradiation of Solids
. Phys. Rev. Lett. 85, 2945-2948 (2000). https://doi.org/10.1103/PhysRevLett.85.2945Radiation-Pressure Acceleration of Ion Beams Driven by Circularly Polarized Laser Pulses
. Phys. Rev. Lett. 103,Petawatt Laser Guiding and Electron Beam Acceleration to 8 GeV in a Laser-Heated Capillary Discharge Waveguide
. Phys. Rev. Lett. 122,Laser-driven high-energy proton beams from cascaded acceleration regimes
. Nat. Phys. 20, 1211-1216 (2024). https://doi.org/10.1038/s41567-024-02505-0Measurement of the radiofrequency-microwave pulse produced in experiments of laser-plasma interaction in the ABC laser facility
. Physics Procedia. 62, 11-17 (2015). https://doi.org/10.1016/j.phpro.2015.02.004Multimillijoule coherent terahertz bursts from picosecond laser-irradiated metal foils
. Proceedings of the National Academy of Sciences of the United States of America. 116, 3994-3999 (2019). https://doi.org/10.1073/pnas.1815256116IR Laser Plasma Interaction with Glass
. American Journal of Applied Sciences. 4, 1009 (2007). https://doi.org/10.3844/ajassp.2007.1009.1015Time-resolved absolute measurements by electro-optic effect of giant electromagnetic pulses due to laser-plasma interaction in nanosecond regime
. Sci. Rep. 6, 1-8 (2016). https://doi.org/10.1038/srep27889Generation of hard X-rays using an ultrafast fiber laser system
. Opt. Express. 15, 13942-13948 (2007). https://doi.org/10.1364/OE.15.013942Photonuclear production of nuclear isomers using bremsstrahlung induced by laser-wakefield electrons
. Nucl. Sci. Tech. 34, 74 (2023). https://doi.org/10.1007/s41365-023-01219-xAssessment and Mitigation of Electromagnetic Pulse(EMP) Impacts at Short-pulse Laser Facilities
. J. Phys. Conf. Ser. 244,Generation of intense quasi-electrostatic fields due to deposition of particles accelerated by petawatt-range laser-matter interactions
. Sci. Rep. 9, 1-14 (2019). https://doi.org/10.1038/s41598-019-44937-2Development of gated fiber detectors for laser-induced strong electromagnetic pulse environments
. Nucl. Sci. Tech. 32, 58 (2021). https://doi.org/10.1007/s41365-021-00898-8Mitigation of electromagnetic pulses interfering with Thomson parabola ion spectrometers at XG-III laser facility
. Rev. Sci. Instrum. 95,Target charging in short-pulse-laser–plasma experiments
. Phys. Rev. E. 89,Dynamic model of target charging by short laser pulse interactions
. Phys. Rev. E. 92,Erratum: Physics of giant electromagnetic pulse generation in short-pulse laser experiments
. Phys. Rev. E. 97,Physics of giant electromagnetic pulse generation in short-pulse laser experiments
. Phys. Rev. E. 91,Mitigation of strong electromagnetic pulses on the LMJ-PETAL facility
. Phys. Rev. Res. 2,Measurement of the target current by inductive probe during laser interaction on terawatt laser system PALS
. Rev. Sci. Instrum. 85,Spectral and temporal characteristics of target current and electromagnetic pulse induced by nanosecond laser ablation
. Plasma. Phys. Control. Fusion. 59,Target current: a useful parameter for characterizing laser ablation
. Laser Part. Beams. 35, 170-176 (2017). https://doi.org/10.1017/S0263034617000040Target current: an appropriate parameter for characterizing the dynamics of laser-matter interaction
.Sources and space–time distribution of the electromagnetic pulses in experiments on inertial confinement fusion and laser–plasma acceleration
. Philos. Trans. Royal Soc. A. 379,EMP control and characterization on high-power laser systems
. High Power Laser Sci. Eng. 6,Simulation of electromagnetic pulses generated by escaped electrons in a high-power laser chamber
. Plasma Sci. Technol. 20,Enhancement of electromagnetic pulse emission from ultrashort laser pulse irradiated solid targets
.Plasma enhancement of femtosecond laser-induced electromagnetic pulses at metal and dielectric surfaces
. Opt. Eng. 53, 051515-051515 (2014). https://doi.org/10.1117/1.OE.53.5.051515Enhancing electromagnetic radiations by a pre-ablation laser during laser interaction with solid target
. Phys. Plasmas. 27,Effect of target size on electromagnetic pulses generation from laser radiation with targets
. Laser Phys. 29,Measurement of electromagnetic pulse in laser acceleration enhanced by near-critical density targets
. Phys. Plasmas. 31, (2024). https://doi.org/10.1063/5.0231143Demonstration of a low electromagnetic pulse laser-driven argon gas jet x-ray source
. Appl. Phys. Lett. 101,Spectral selective radio frequency emissions from laser induced breakdown of target materials
. Appl. Phys. Lett. 105,Generation and regulation of electromagnetic pulses generated by femtosecond lasers interacting with multitargets
. Nucl. Sci. Tech. 35, 10 (2024). https://doi.org/10.1007/s41365-024-01381-wAnalysis of electromagnetic pulses generated from ultrashort laser irradiating solid targets at CLAPA
. Chin. Phys. B. 31,Target charging during laser ablation of polyethylene
. Appl. Phys. A. 124, 138 (2018). https://doi.org/10.1007/s00339-018-1557-xElectromagnetic pulses produced by a picosecond laser interacting with solid targets
. Chin. Phys. B. 33,Generation and regulation of electromagnetic pulses induced by hybrid laser pulses interacting with solid targets
. Nucl. Fusion. 62,Spatial and temporal evolution of electromagnetic pulses generated at Shenguang-II series laser facilities
. Plasma Sci. Technol. 23,Electromagnetic radiations from laser interaction with gas-filled Hohlraum
. Laser Phys. Lett. 15,Intense Electromagnetic Pulses Generated From kJ-Laser Interacting With Hohlraum Targets
. IEEE Trans. Nucl. Sci. 69, 2027-2036 (2022). https://doi.org/10.1109/TNS.2022.3187569Electromagnetic pulse emission from target holders during short-pulse laser interactions
. Phys. Plasmas. 27,Monoenergetic beams of relativistic electrons from intense laser–plasma interactions
. Nature. 431, 535-538 (2004). https://doi.org/10.1038/nature02939High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding
. Nature. 431, 538-541 (2004). https://doi.org/10.1038/nature02900A laser–plasma accelerator producing monoenergetic electron beams
. Nature. 431, 541-544 (2004). https://doi.org/10.1038/nature02963Multi-GeV electron beams from capillary-discharge-guided subpetawatt laser pulses in the self-trapping regime
. Phys. Rev. Lett. 113,Quasi-monoenergetic laser-plasma acceleration of electrons to 2 GeV
. Nat. Commun. 4, 1988 (2013). https://doi.org/10.1038/ncomms2988Characteristics of betatron radiation from direct-laser-accelerated electrons
. Phys. Rev. E. 93,Particle acceleration in relativistic laser channels
. Phys. Plasmas. 6, 2847-2854 (1999). https://doi.org/10.1063/1.873242Multi-MeV electron beam generation by direct laser acceleration in high-density plasma channels
. Phys. Rev. Lett. 83, 4772 (1999). https://doi.org/10.1103/PhysRevLett.83.4772Surface waves and electron acceleration from high-power, kilojoule-class laser interactions with underdense plasma
. New J. Phys. 15,Electron acceleration in cavitated channels formed by a petawatt laser in low-density plasma
. Phys. Rev. Lett. 94,Observation of terahertz emission from a laser-plasma accelerated electron bunch crossing a plasma-vacuum boundary
. Phys. Rev. Lett. 91,Emission of electromagnetic pulses from laser wakefields through linear mode conversion
. Phys. Rev. Lett. 94,Millijoule Terahertz Radiation from Laser Wakefields in Nonuniform Plasmas
. Phys. Rev. Lett. 132,Circularly polarized x-ray generation from an ionization induced laser plasma electron accelerator
. Plasma. Phys. Control. Fusion. 62,Enhancement of laser-driven betatron radiation
. Opt. Eng. 54,Inverse Compton scattering x-ray source from laser electron accelerator in pure nitrogen with 15 TW laser pulses
. Plasma. Phys. Control. Fusion. 61,Laser produced electromagnetic pulses: generation, detection and mitigation
. High Power Laser Sci. Eng. 8,Review of high-power microwave source research
. Rev. Sci. Instrum. 68, 3945-3974 (1997). https://doi.org/10.1063/1.1148382Electromagnetic non-destructive evaluation techniques for the monitoring of water and chloride ingress into concrete: a comparative study
. Mater. Struct. 48, 369-386 (2015). https://doi.org/10.1617/s11527-013-0189-zCommissioning experiment of the high-contrast SILEX- multi-petawatt laser facility
. Matter Radiat. Extrem. 6,Characterization of electromagnetic pulses via arrays on ShenGuang-III laser facility laser
. Chinese Optics Letters. 14,Characterisation and Modelling of Ultrashort Laser-Driven electromagnetic pulses
. Sci. Rep. 10, 1-8 (2020). https://doi.org/10.1038/s41598-020-59882-8Gigahertz electromagnetic pulse emission from femtosecond relativistic laser-irradiated solid targets
. Opt. Express. 32, 2670-2678 (2024). https://doi.org/10.1364/OE.510468Analysis of electromagnetic pulses generation from laser coupling with polymer targets: Effect of metal content in target
. Matter Radiat. Extrem. 5,Collimated electron jets by intense laser-beam–plasma surface interaction under oblique incidence
. Phys. Rev. Lett. 82, 743 (1999). https://doi.org/10.1103/PhysRevLett.82.743Plasma jet formation and magnetic-field generation in the intense laser plasma under oblique incidence
. Phys. Plasmas. 6, 2855-2861 (1999). https://doi.org/10.1063/1.873243Spatial and temporal evolution of electromagnetic pulses from solid target irradiated with multi-hundred-terawatt laser pulse inside target chamber
. Plasma Sci. Technol. 26,Electromagnetic pulse generation within a petawatt laser target chamber
. Rev. Sci. Instrum. 75, 4225-4227 (2004). https://doi.org/10.1063/1.1787606EMP characterization at PALS on solid-target experiments
. Plasma. Phys. Control. Fusion. 60,Measurement of electromagnetic pulses generated during interactions of high power lasers with solid targets
. J. Instrum. 11,Experiments on electromagnetic pulse (EMP) generated by laser-plasma interact ion in nanosecond regime
.Basic features of electromagnetic pulse generated in a laser-target chamber at 3-TW laser facility PALS
. J. Phys. Conf. Ser. 508,Shaped liquid drops generate MeV temperature electron beams with millijoule class laser
. Communications Physics. 7, 85 (2024). https://doi.org/10.1038/s42005-024-01550-8Contemporary particle-in-cell approach to laser-plasma modelling
. Plasma. Phys. Control. Fusion. 57,Relativistic Magnetic Self-Channeling of Light in Near-Critical Plasma: Three-Dimensional Particle-in-Cell Simulation
. Phys. Rev. Lett. 76, 3975-3978 (1996). https://doi.org/10.1103/PhysRevLett.76.3975Onset of relativistic self-focusing in high density gas jet targets
. Phys. Rev. E. 56, 4615-4639 (1997). https://doi.org/10.1103/PhysRevE.56.4615Effect of expanding plasma on propagation of electromagnetic pulses by laser-plasma interaction
. Plasma. Phys. Control. Fusion. 62,Transient electromagnetic fields generated in experiments at the PHELIX laser facility
. High Power Laser Sci. Eng. 9,Electromagnetic pulse (EMP) radiation by laser interaction with a solid H2 ribbon
. Phys. Plasmas. 24,Biot-Savart-like law in electrostatics
. Eur. J. Phys. 22, 31 (2001). https://doi.org/10.1088/0143-0807/22/1/304Measurement of the electric field strength generated in the experimental chamber by 10 TW femtosecond laser pulse interaction with a solid target
. J. Instrum. 14,Xue-Qing Yan is an editorial board member for Nuclear Science and Techniques and was not involved in the editorial review, or the decision to publish this article. All authors declare that there are no competing interests.


