Introduction
Among the pressurized water reactors (PWRs) operating worldwide, Russian-type PWRs such as VVER-440 and VVER-1000 comprise hexagonal fuel assemblies. Liquid metal fast breeder reactors and very high-temperature reactors under the Next-Generation Nuclear Plant project also use hexagonal assemblies. In addition, these reactors are employed for broader applications in the nuclear industry, such as plutonium and hydrogen production; therefore, considerable improvements have been achieved in the underlying physics calculations of reactors with hexagonal geometry. In the early years, reactor physics calculations for a hexagonal geometry were performed using the finite difference method [1, 2]. In the 1990s, conformal mapping of a hexagon onto a rectangle were reported and codes based on conformal mapping, such as ANC-H [3] and PANTHER [4], were developed. Moreover, numerical methods based on the finite element method have been proposed to solve the neutron diffusion equation for hexagonal geometries [5-8]. The nodal methods developed in the mid-1970s were introduced to neutron diffusion calculations in hexagonal geometry, and nodal method codes such as DIF3D [9] were developed and applied. Owing to the geometrical complexity, it is difficult to solve nodal equations in hexagonal geometry using Cartesian coordinates; therefore, various approximation methods are applied. In the function expansion nodal method (FENM), the neutron flux within a node is expanded using polynomials or exponential functions [10-12]. This method has been used to solve multigroup neutron space-dependent kinetics equations in some studies [13-17]. In Cartesian geometry, nodal methods apply the transverse integration procedure (TIP) to the 3D neutron diffusion equation, resulting in three one-dimensional diffusion equations called transverse-integrated equations. When TIP is applied to a hexagonal geometry, singular (discontinuous) terms arise in the transverse leakage terms. Wagner [18] ignored these discontinuous terms in their solution and used lower-order polynomials to approximate the average source of a transverse-integrated equation. The use of the nodal Green’s function method (NGFM) allows for more accurate treatment of discontinuous terms that arise from the TIP. However, the accurate treatment of discontinuous terms was not implemented in earlier studies [19, 20]. The method presented in [21] improved the accuracy and fidelity of the code by adding the effect of discontinuous terms to the transverse integrated flux solution; however, the detailed description was limited to a two-dimensional geometry. In this paper, we propose a numerical model to solve the multigroup neutron diffusion equation in 3D hexagonal geometry using NGFM under the Neumann boundary condition. This model considers discontinuous terms in the solution of the 1D transverse integrated equation. By comparing this with the benchmark for the VVER-440 reactor, we demonstrate the accuracy of the proposed model.
Description of the method
The TIP for multigroup neutron diffusion equation in 3D hexagonal geometry
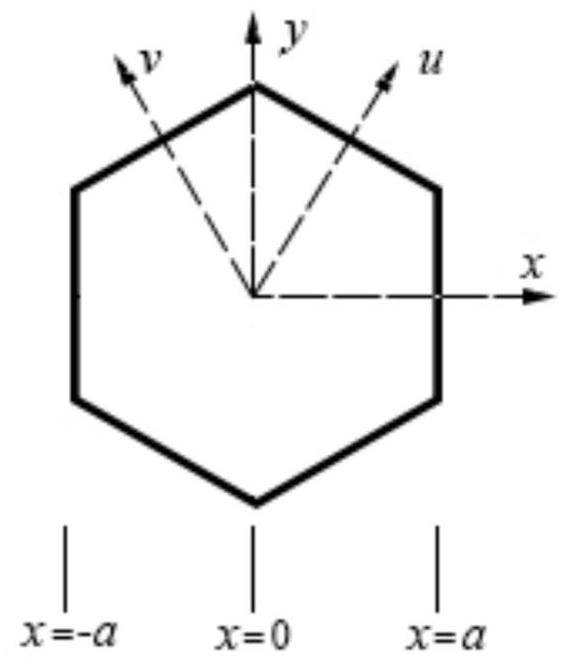
In 3D Cartesian coordinates (Fig. 1), the multigroup neutron diffusion equation within node k can be written as
In Eq. (3),
The transverse integration procedure for Eq. (1) leads to the following equation:
Similarly to Eq. (9), the transverse integrated equation along the z-direction is given by
Solution to the transverse integrated equation using Green’s function under the Neumann boundary condition
Equation (28) can be written as follows (the index g and k and the - symbol are omitted for convenience):
We denote the transverse leakage by the sum of the individual terms as follows:
Using the following linear approximations for
Substituting Eq. (38), Eq. (39) and (40) again into Eq. (41), the fourth, fifth, and sixth terms in right side of Eq. (41) become zero, and thus, the following equation for the transverse averaged flux is obtained:
Constitution of the closed system of equations
The transverse-averaged flux, source, and leakage terms are expanded using orthogonal polynomials:
From Eq. (45), the expansion coefficients in Eq. (43) are given by
The zeroth order moment of the transverse averaged flux equals the node-averaged flux, that is,
The transverse-averaged flux at the boundary
Using the continuity conditions of the transverse-averaged flux and the neutron current at the interfaces between adjacent nodes,
We substitute Eq. (43) into Eq. (42) and multiply both sides of Eq. (42) by ωm(x). Using
Note that the corner-point numbers in Eqs.(55) and (60) correspond to the calculation along the x-direction. The corner point numbers in the u- and ν-directions are smaller than one and two, respectively, compared to those in the x-direction; that is,
The nodal balance equation, net neutron current coupling equation in each coordinate direction, its boundary conditions, and equation for the expansion coefficients of the transverse averaged flux constitute a closed system of equations.
Numerical results
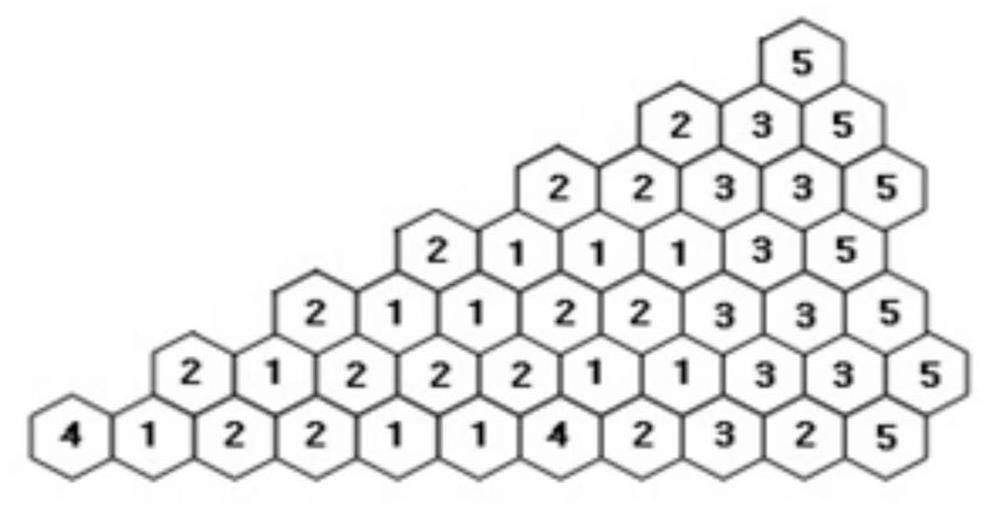
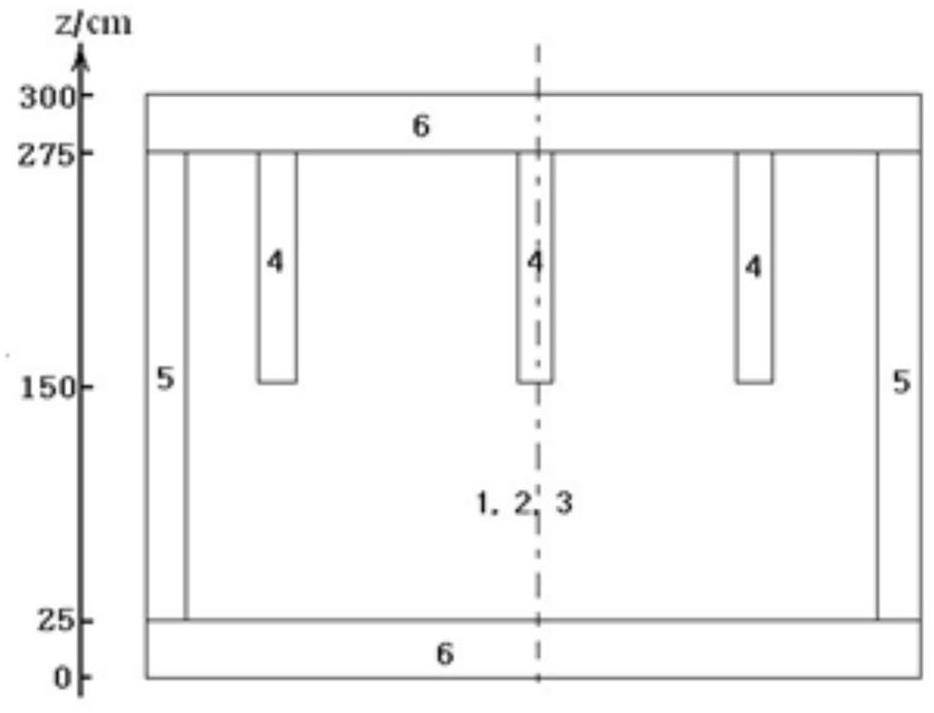
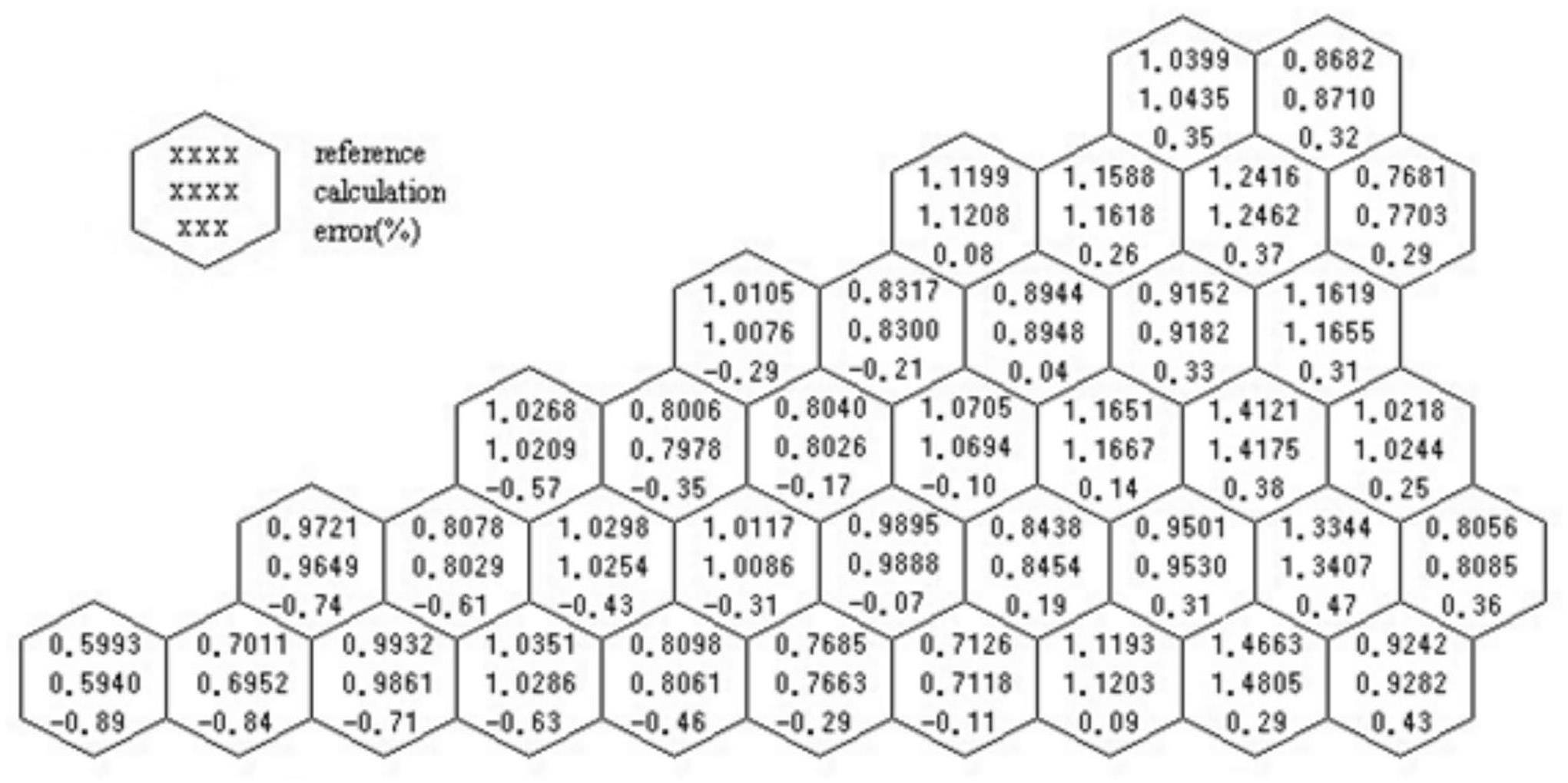
The three-dimensional VVER-440 benchmark [3] was used to test the proposed numerical method. The material layout of the core of the problem is shown in Figs. 2 and 3. The group constants of these materials are listed in Table 1. The numerical results of this problem are summarized in Table 2, where
| Material | D1 (cm) | D2 (cm) | Σr1 (cm-1) | Σa2 (cm-1) | νΣf1 (cm-1) | νΣf2 (cm-1) | Σ1→2 (cm-1) |
|---|---|---|---|---|---|---|---|
| 1 | 1.34660 | 0.37169 | 0.025255 | 0.064277 | 0.0044488 | 0.073753 | 0.016893 |
| 2 | 1.33770 | 0.36918 | 0.024709 | 0.079361 | 0.0055337 | 0.105810 | 0.015912 |
| 3 | 1.33220 | 0.36502 | 0.024350 | 0.10010 | 0.0070391 | 0.149640 | 0.014888 |
| 4 | 1.19530 | 0.19313 | 0.035636 | 0.13498 | 0.0 | 0.0 | 0.022264 |
| 5 | 1.44850 | 0.25176 | 0.033184 | 0.032839 | 0.0 | 0.0 | 0.032262 |
| 6 | 1.34130 | 0.24871 | 0.029301 | 0.064655 | 0.0 | 0.0 | 0.027148 |
| Method | Δkeff (%) | ΔPmax (%) | ΔPavg (%) |
|---|---|---|---|
| NGFM | 0.029 | 2.51 | 0.63 |
| FENM | 0.026 | 2.35 | 0.58 |
| AFEN | 0.030 | 3.20 | 0.73 |
| ANC-H | 0.025 | 1.28 | - |
Conclusion
A numerical model was proposed to solve the neutron diffusion equation in hexagonal-z geometry, and the discontinuous terms in the transverse leakage were explicitly considered in this model. The solution of 1D transverse integrated equation was expressed using the nodal Green’s function under the Neumann boundary condition. Using the quadratic polynomial expansion of the transverse averaged quantities, the net neutron current coupling equation and equation for the expansion coefficients of the transverse averaged neutron flux were obtained. We constructed a closed system of equations by deriving the equations corresponding to the boundary conditions. The numerical model proposed in this study was tested by comparison with the benchmark for the VVER-440 reactor, and the numerical results were in good agreement with the reference solutions.
Nuclear reactor core analysis code: CITATION. ORNL-TM-2496
(1971).Combination of finite-difference and finite-volume techniques in global reactor calculation
. Kerntechnik 57, 216-222 (1992). https://doi.org/10.1515/kern-1992-570406Conformal mapping and hexagonal nodal methods-II: implementation in the ANC-H code
. Nucl. Sci. Eng. 121, 210-225 (1995). https://doi.org/10.13182/nse95-a28559Comparison of PANTHER nodal solutions in hexagonal-z geometry
. Nucl. Sci. Eng. 121, 254-263 (1995). https://doi.org/10.13182/nse95-a28562CRONOS: a modular computational system for neutronic core calculations, IAEA-TECDOC–678
(1992)Application of a dual variational formulation to finite element reactor calculations
. Ann. Nucl. Energy 20, 823-845 (1993). https://doi.org/10.1016/0306-4549(93)90076-2High Order Finite Element Method for the Lambda modes problem on hexagonal geometry
. Ann. Nucl. Energy 36, 1450-1462 (2009). https://doi.org/10.1016/j.anucene.2009.07.003Fast solution of neutron transport SP3 equation by reduced basis finite element method
. Ann. Nucl. Energy 120, 707-714 (2018)..https://doi.org/10.1016/j.anucene.2018.06.042The DIF3D nodal neutronics option for two- and three-dimensional diffusion theory calculations in hexagonal geometry. ANL-83-1
(1983). https://doi.org/10.2172/6318594Two-dimensional intra-nodal flux expansion method for hexagonal geometry
. Nucl. Sci. Eng. 133, 201-212 (1999). https://doi.org/10.13182/NSE99-A2082Polynomial nodal method for solving neutron diffusion equations in hexagonal-z geometry
. Ann. Nucl. Energy 29, 1105-1117 (2002). https://doi.org/10.1016/S0306-4549(01)00083-4Flux expansion nodal method for solving multigroup neutron diffusion equations in hexagonal-z geometry
. Ann. Nucl. Energy 33, 370-376 (2006). https://doi.org/10.1016/j.anucene.2005.06.011The reactor dynamics code DYN3D and its trigonal-geometry nodal diffusion model
. Kerntechnik 78, 310-318 (2013). https://doi.org/10.3139/124.110382The HEXNEM3 nodal flux expansion method for the hexagonal geometry in the code DYN3D
. Ann. Nucl. Energy 116, 187-194 (2018). https://doi.org/10.1016/j.anucene.2018.02.037The numerical solution of space-dependent neutron kinetics equations in hexagonal-z geometry using Diagonally Implicit Runge-Kutta method
. Ann. Nucl. Energy 94, 150-154 (2016). https://doi.org/10.1016/j.anucene.2016.03.006The numerical solution of space-dependent neutron kinetics equations in hexagonal-z geometry using backward differentiation formula with adaptive step size
. Ann. Nucl. Energy 128, 203-208 (2019). https://doi.org/10.1016/j.anucene.2019.01.004A modal ACMFD formulation of the HEXNEM3 method for solving the time-dependent neutron diffusion equation
. Ann. Nucl. Energy 130, 331-337 (2019). https://doi.org/10.1016/j.anucene.2019.03.006Three-dimensional nodal diffusion and transport theory methods for hexagonal-z geometry
. Nucl. Sci. Eng. 103, 377 (1989). https://doi.org/10.13182/nse89-a23690Systematics of neutron diffusion modeling for neutron-optically thin, multiply-heterogeneous High Temperature Reactors. INL/EXT-09-16414
(2009)Developments in nodal reactor analysis for hexagonal geometry
. PhD ThesisNodal Green’s Function Method singular source term and burnable Poison treatment in hexagonal geometry. INL/EXT-09-16773
(2009) https://doi.org/10.2172/983357A nodal Green’s function method for multidimensional neutron diffusion calculations
. Nucl. Sci.Eng. 76, 218-231 (1980). https://doi.org/10.13182/NSE80-A19452Advanced nodal Green’s function method on Neumann boundary condition
. J. Sci. Technol. 38, 17-21 (1998).Coupled 3D neutron kinetics/thermal-hydraulics calculation of PWR core using nodal Green’s function method on Neumann boundary condition
. Prog. Nucl. Energy 123,DIF3D: A code to solve one-, two-, and three-dimensional finite-difference diffusion theory problems, ANL-82-64
(1984). https://doi.org/10.2172/7157044The authors declare that they have no competing interests.

