Introduction
Radiation detectors, which are often called special eyes for the visualization of high-energy rays (X/γ-rays), play critical roles in nuclear security and medical diagnosis [1-3]. At the core of these detectors are single crystals, which transform high-energy rays into photons or electron-hole pairs and substantially determine the performance of the detector devices [4-6]. Cadmium telluride (CdTe), a semiconductor with a large effective atomic mass and superior charge transport properties, is a leading material for room-temperature X-ray and gamma-ray detection via a direct detection mechanism [7-9]. The world's first commercial photon-counting computed tomography (CT) system, the NAEOTOM Alpha, was developed using CdTe radiation detectors by Siemens Healthineers. This system was authorized by the FDA (The United States Food and Drug Administration) as “the most significant technological advancement in the CT field in the past decade” [10]. In general, for an optimal CdTe crystal performance in detectors, both high resistivity (ρ≥109 Ω) and high charge mobility (μe ~ 103 cm2 V-1 s-1) are required [11, 12]. The high resistivity of these crystals is essential for minimizing the background signal from the thermally generated carriers, enabling high-voltage operation at room temperature [11]. Similarly, a high charge mobility is crucial for supporting highly efficient charge collection and achieving a decent energy resolution for detecting devices [12]. However, achieving detector-grade CdTe single crystals with both high resistivity and high mobility has been a challenge, primarily because of difficulties in controlling stoichiometry during the growth process.
The major challenge in controlling the stoichiometry arises from the high volatility of Cd under high-temperature conditions. Specifically, the crystallization of stoichiometric CdTe occurs at 1092 ℃, where the partial pressure of Cd is assumed to be 1.04 atm, whereas the partial pressure of Te is 2.8×10-3 atm, which is negligible compared with that of Cd [13]. Consequently, Cd made a dominant contribution to the inner pressure of the crucible. To ensure pressure tolerance of the crucible and prevent breakage during the crystal growth process, CdTe materials are typically prepared from Te-rich starting materials [14]. Moreover, even with a stoichiometric CdTe starting material, Cd tends to evaporate into the vapor space in the ampoule, resulting in a Te-rich melt [15]. During crystallization, excess Te segregates at the solid-liquid interface, forming Te clusters that accumulate near the interface owing to the high melt viscosity [15]. This process leads to constitutional supercooling, disrupting the stability of the liquid-solid interface, and causing the incorporation of Te droplets (inclusions) into the growing crystals [15]. Furthermore, the loss of Cd can result in a deficiency of Cd at the solid-liquid interface, introducing vacancy defects into the crystal matrix. In the context of CdTe crystals used for detectors, Te inclusions introduce nonuniform internal electric fields and electron cloud trapping, deteriorating the charge transport properties [16]. In addition, a high concentration of Cd vacancies can act as acceptors and unfavorable charge-trapping centers, compromising the resistive and charge-transport properties and limiting their application in detection.
Efforts to produce high-quality CdTe crystals with precise stoichiometry have led to various methods including the modified vertical Bridgman method (MVB), high-pressure Bridgman method (HPB), and traveling heater method (THM). Using the MVB technique for CdTe growth, Mochizuki et al. attempted to regulate the partial pressures by incorporating a Cd reservoir chamber [17]. Similarly, the HPB technique, which has been utilized for CdTe crystal growth, mitigates the loss of volatile Cd in CdTe by applying a high inert gas pressure during the growth process [18]. Additionally, THM, recognized as a Te solvent method and developed for the uniform growth of CdTe, offers advantages such as a low growth temperature and the purifying influence of the Te solvent zone. This method reduces the risk of ampoule breakage and facilitates the fabrication of high-purity CdTe with minimal Cd vacancies [19]. However, these methods typically involve relative mechanical motion between the heater and ampoule containing charged materials. Such mechanical motion can compromise the growth stability, leading to stoichiometry-correlated defects and a reduction in the yield of single crystals. By contrast, the vertical gradient freeze (VGF) method, which is a melt growth method, is modified using temperature-profile-programmed control of the furnace multizone instead of the mechanical movement of the ampoule or furnace [20]. VGF offers a higher growth rate than THM and ensures more stable conditions at the crystallization front by minimizing the thermal drift and temperature fluctuations [21]. Despite these advantages, Su et al. reported the growth of undoped CdTe using the VGF method, achieving a resistivity of 1×107 Ω at room temperature, which falls short of radiation applications [22].
Given the pivotal role that doping plays in regulating the carrier concentration and band structure in semiconductors, chlorine dopants are often favored for their function as donors in CdTe crystals [8]. Cl dopants compensate for existing defects, reduce trap centers, enhance charge-collection efficiency, and increase resistivity. In this context, Bugár et al. grew CdTe crystals using the VGF method with Cl dopants, achieving high resistivity for the as-grown CdTe crystals [23]. However, the detector performance was suboptimal, mainly attributed to large Te inclusions, necessitating a sophisticated two-step post-growth annealing treatment. The treatment involved an initial step involving post-growth annealing in Cd overpressure to eliminate large-sized Te inclusions in the CdTe crystals, followed by a second annealing step under Te overpressure to restore high resistivity after Cd vapor annealing. Unfortunately, the detection capability of CdTe crystals treated in this manner was worse than that of the as-grown samples. Thus, attempts to obtain CdTe single crystals with both high resistivity and charge transport properties through direct VGF growth or post-treatment require further study. Conversely, the introduction of an additional Cd reservoir during the VGF growth of cadmium zinc telluride (CZT) is an effective approach for reducing large Te inclusions, resulting in decent spectral performance [24]. Therefore, controlling the Cd vapor pressure during the VGF growth process of CdTe(Cl) could be the key to reducing large Te inclusions and enhancing detector performance.
In this study, we introduced an external Cd source to regulate the cadmium vapor pressure and incorporated Cl as a dopant during the VGF growth of CdTe to preserve the crystal stoichiometry and modulate its electrical properties. To evaluate the effectiveness of this approach, we conducted a comprehensive analysis of the properties of CdTe(Cl) crystals using various techniques, such as infrared transmittance spectroscopy, near-infrared transmission spectroscopy, and photoluminescence spectroscopy. Furthermore, we investigated the resistivity and charge transport properties of CdTe(Cl) crystals and successfully fabricated an alpha detector.
Results and discussion
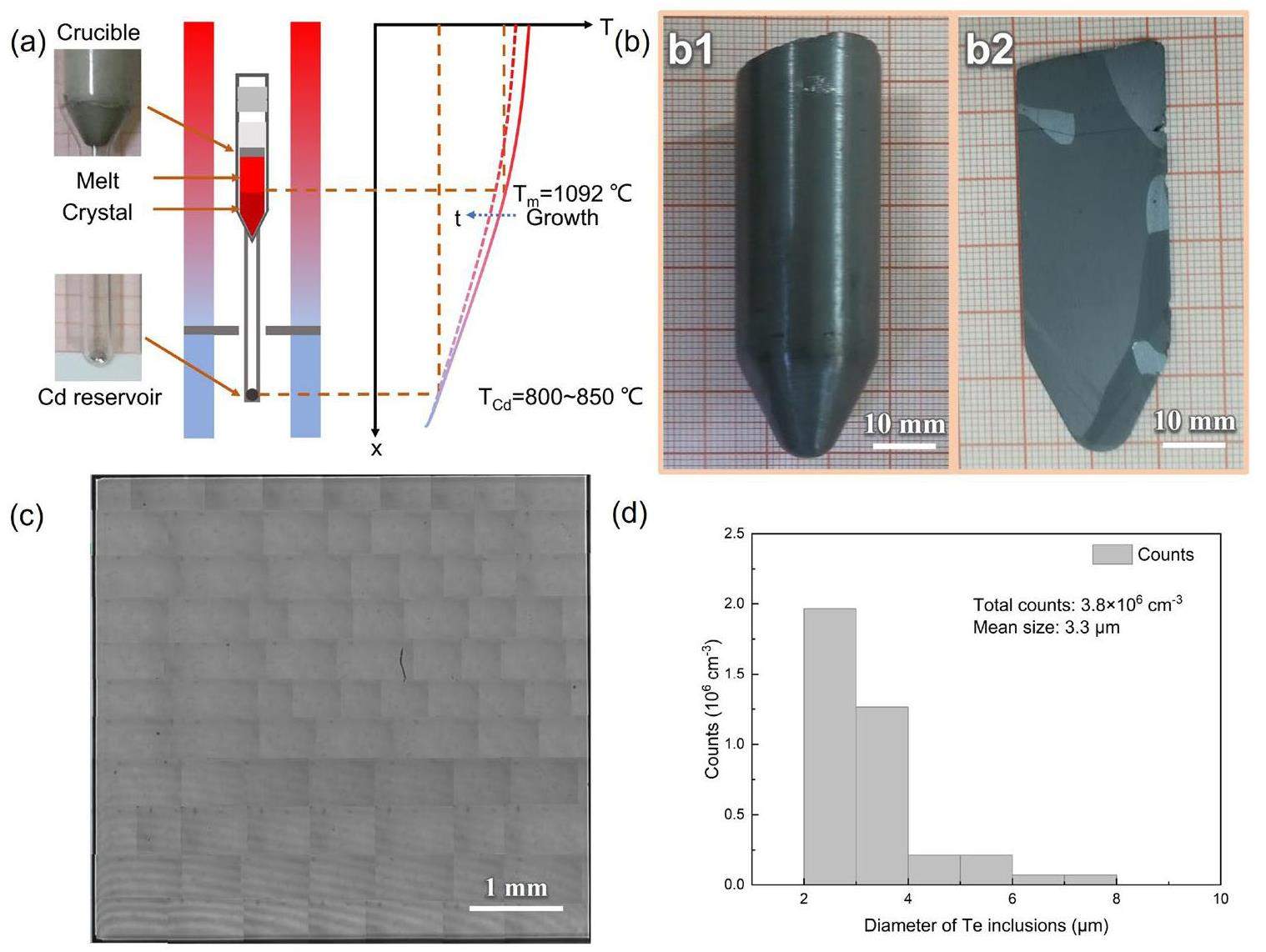
Figure 1a shows a schematic representation of the furnace/ampoule assembly, along with a typical gradient freeze-temperature program. The synthesized polycrystalline CdTe was loaded into a homemade crucible with an extension to house a Cd reservoir. Recognizing that the crystal quality can be improved by superheating [25], we performed a preheating process to increase the temperature of the ampoule to more than 20 ℃ above the melting point of CdTe before crystal growth. Consequently, the CdTe melt was heated to a superheating temperature to eliminate the need for the seed crystals. The growth process involved the electronic translation of the temperature gradient through the melt. To optimize the crystal growth, we employed low-temperature gradients (5 °C cm-1) and moderate growth rates (0.1 cm h-1) to reduce the thermal stress and minimize the dislocation density, which are critical factors for preventing constitutional supercooling effects. In addition, to ensure accurate stoichiometry in both the CdTe melt and solid, we meticulously programmed the temperature range between 800 ℃ and 850 ℃ of the Cd reservoir during solidification and cooling. Figure 1b shows a typical cross-sectional image of an as-grown CdTe(Cl) ingot with a diameter of 2.2 cm and length of 6 cm. This image shows that the ingot consists of several single-crystalline grains, including a large grain over 0.5 cm × 0.5 cm in size. Furthermore, the measured Cl concentration for CdTe(Cl) is 1.79×1018 cm-3. Te inclusions in the as-grown CdTe(Cl) crystals were assessed using IR transmission microscopy. As illustrated in Fig. 1c, the presence of Te inclusions in the sample decreased, and the average sizes of the Te inclusions were effectively reduced to below 5 μm, with an average density of ~ 3.8×106 cm-3 (Fig. 1(d)). These results indicate that the incorporation of large Te inclusions into the crystal was effectively suppressed by controlling the partial pressure of Cd in the growth ampoule.
We used an optical method to evaluate the obtained CdTe crystals. As illustrated in Fig. 2a, a high transmittance value of nearly 60% can be observed over a large wavelength shift range from 4000 cm-1 to 500 cm-1 at room temperature. Notably, the absorption behavior of a crystal plays a crucial role in determining its infrared transmittance characteristics, which are primarily driven by lattice absorption and free carrier absorption [26]. The lattice absorption is primarily influenced by the presence of Te inclusions, which can lead to lattice distortion and disrupt the periodic structure of the lattice [27]. In our CdTe crystals, which are characterized by the reduction of large Te inclusions, the impact of lattice absorption was negligible. Consequently, free-carrier absorption became the dominant mechanism responsible for absorption. The absorption coefficient α associated with the free-carrier absorption is directly proportional to the free-carrier density N [28]. Consequently, the significantly high transmittance observed for the CdTe(Cl) sample can be attributed to a reduction in free carrier density.
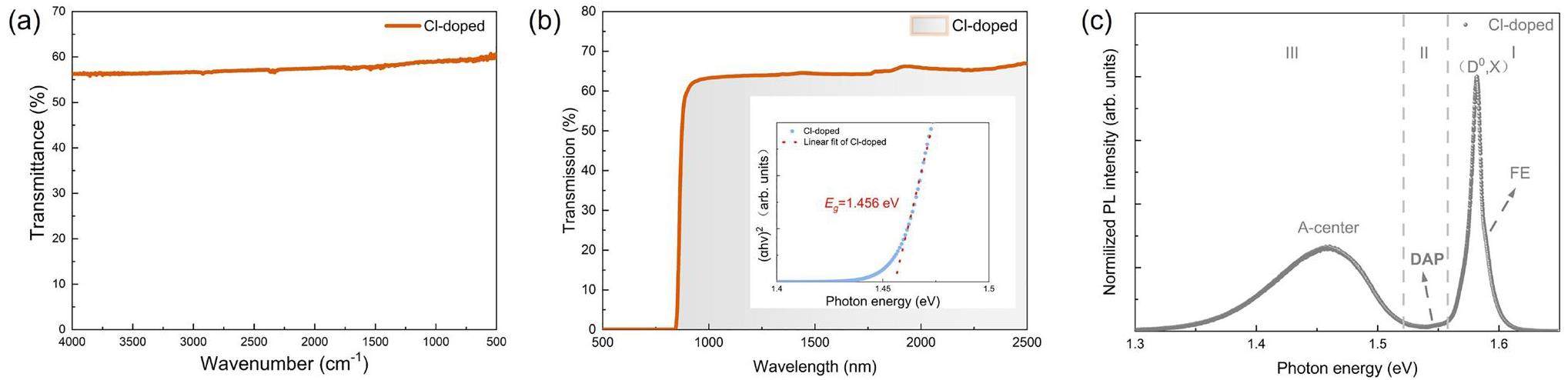
A typical UV-Vis-NIR transmittance spectrum of CdTe(Cl) crystals is presented in Fig. 2b. Significantly, within the wavelength range of 820 nm to 950 nm, a distinct exponential change in transmittance was observed. This observation enabled the calculation of the absorption coefficient α, thereby facilitating the determination of the bandgap (Eg) of CdTe crystals near the absorption cutoff. The inset of Fig. 2 (b) demonstrates the Eg calculations for direct transitions in CdTe by employing Eq. [27]:
Photoluminescence (PL) spectroscopy was conducted at a temperature lower than that of liquid nitrogen (N2) to investigate the specific defects in CdTe(Cl). The typical PL spectra shown in Fig. 2 (c) for the CdTe(Cl) samples reveal the presence of three distinct regions: (I) The first region, located around 1.58 eV, corresponds to excitonic recombination, specifically the near-band-edge shallow donor-bound exciton peak (D0, X) [29]. (2), and the second region, situated around 1.54 eV, corresponds to the Donor-Acceptor Pair recombination (DAP) region[29]. (3) The third region, approximately at 1.46 eV, is broad and recognized as the defect-related deep emission peak known as the A-center[30]. Region (1) features a Cl-related shallow donor-bound exciton peak (D0, X) (hν=1.582 eV) and the free exciton line (FE: hν=1.588 eV) positioned at the high energy side of (D0, X). The presence of free excitons indicates the high crystallinity of the CdTe(Cl) sample. The region (2), centered at approximately 1.54 eV, was initially associated with an acceptor-like structural defect caused by Cd vacancies or complexes comprising a Cd vacancy and two residual donors (VCd-2D)[29]. However, this emission nearly disappeared upon Cl doping, mirroring the PL spectrum of CdTe(Cl) grown using THM [30]. This suggests consumption of Cd vacancies owing to the formation of Cl-related complexes. Simultaneously, the intensity of the A center became more pronounced in the presence of Cl doping. According to experimental findings, this is primarily governed by the spontaneous formation of the acceptor complex (ClTe-VCd)-1. Consequently, a plausible defect reaction equation is formulated as follows:
The electrical properties were characterized using an I-V-test. As demonstrated in the I-V curve in Fig. 3a, the results align well with Ohmic law at a ±0.1 V bias and this data can be used to calculate the resistivity according to the equation:
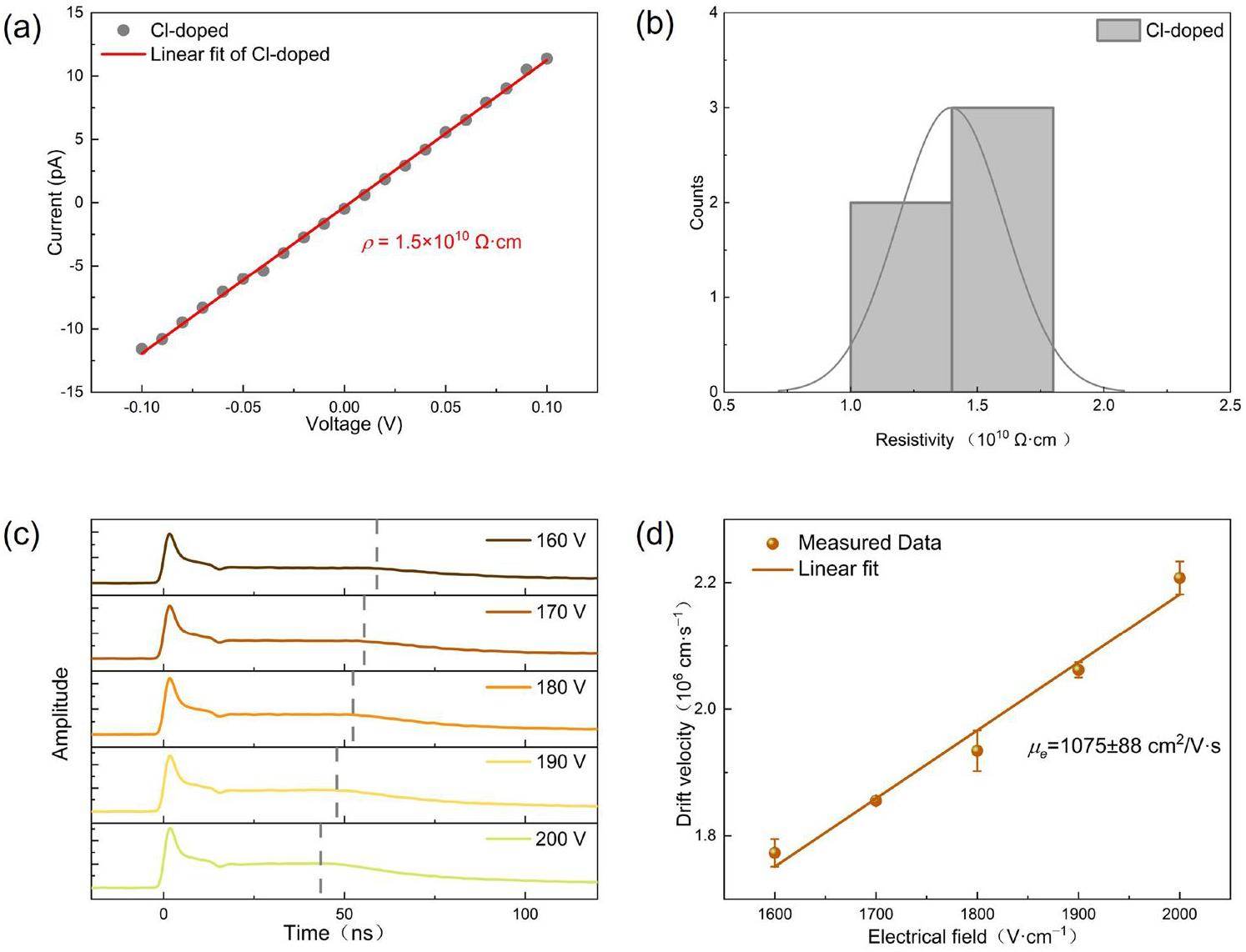
Additionally, electron mobility is a pivotal parameter that significantly influences the overall performance of the detector. To this end, a thorough investigation into the electron mobility of the CdTe(Cl) planar detector was conducted using the LBIC (Laser beam-induced current) technique. As shown in Fig. 3(c), the typical time-of-flight waveform transients of electrons captured by the CdTe(Cl) planar detector under various bias voltages. Initially, there is a region where the signal experiences a rapid reduction, which is attributed to fast surface recombination processes [31]. Subsequently, the transient current waveforms exhibit a plateau, and the separation between this plateau and the trailing edge of the transient current is identified as the transit time τr [31]. This critical point signified the arrival of electrons at the anode, as indicated by the dashed line in Fig. 3(c). The extended tail following the transit time is attributed to the gradual release of carriers from the traps. By measuring the transit time and assuming a constant average electric field, the drift mobility can be calculated using [31]:
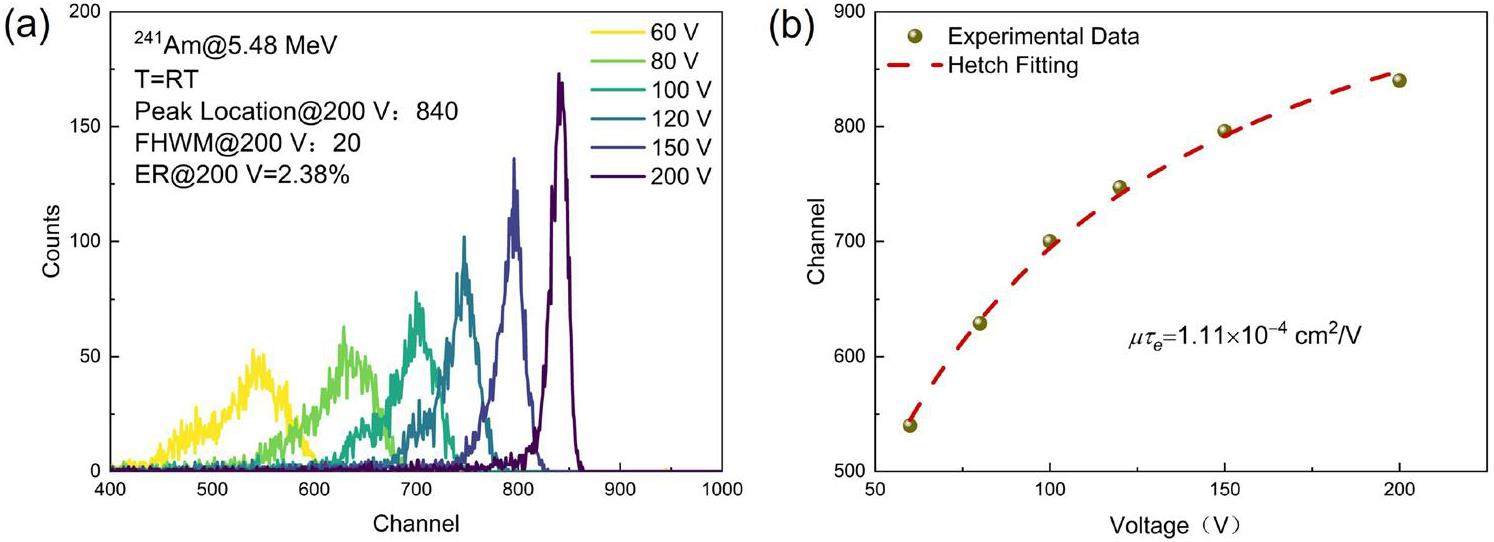
After the above characterizations, we used the obtained CdTe crystals to fabricate a planar radiation detector. As shown in Fig. 4(a), the spectra of the α particles (241Am@5.48 MeV) acquired using the Au/CdTe(Cl)/Au planar detector are shown at various bias voltages ranging from 60 V to 00 V. With an increase in the bias voltage, the centroid of the full-energy peak shifts toward higher channel numbers, with a preference for higher amplitudes. Importantly, the spectra at a reverse bias voltage (V=200 V) exhibit a symmetrical shape with prominent lines corresponding to the 5.48 MeV energies of the 241Am-α sources. Concurrently, the full width at half maximum (FWHM) value narrowed to approximately 20 channels around the full-energy peak channel (840) at 200 V, resulting in an energy resolution of 2.38%. Considering the shallow penetration depth of α particles, which is approximately 14 μm beneath the detector surface, the mobility-lifetime product μτ of the charge carriers can be estimated using the simplified Hecht equation for a single carrier[32]:
Finally, we achieved high-resistivity CdTe single crystals with exceptionally high electron mobilities via Cl doping. Increased electrical resistivity can lower leakage currents and improve the signal-to-noise ratio, which is crucial for detecting weak X-ray signals with high precision. The enhanced charge transport properties can contribute to a better charge collection efficiency, ultimately leading to improved energy resolution and sensitivity in X-ray detection applications. Typically, the resistivity of CdTe is approximately 109 Ω. For example, CdTe grown by THM through Acrorad Company, Ltd. exhibits a resistivity of approximately 6×109 Ω, exceeding the intrinsic value of CdTe (4×109 Ω) [33]. In our experiments, we obtained an even higher resistivity, primarily attributable to p-type conduction in high-resistivity CdTe crystals, which was heavily compensated for by Cl. The observed resistivity surpassed the intrinsic value of CdTe, owing to the increased contribution of holes, which possess significantly lower mobility than electrons, to the conductivity of the material [33]. Furthermore, we recorded a significant improvement in electron mobility, which is the highest value ever reported for VGF-grown CdTe(Cl) crystals. This value is in agreement with the 1100 cm2 V-1 s-1 achieved using THM-grown CdTe(Cl) crystals [34]. Achieving both high resistivity and high mobility in high-resistance CdTe devices is a considerable challenge. This necessitates the compensation of the intrinsic defects in the crystal through doping to achieve high resistivity. However, both intrinsic defects and introduced impurities can adversely affect carrier transport via scattering and trapping. Additionally, there is an ongoing debate within the scientific community regarding the attainment of high resistivity in CdTe crystals. While the deep donor model attributes high resistivity to Fermi level pinning by a deep donor level induced by native defects or extrinsic deep donors, the compensation model in CdTe(Cl), as proposed by Maohua Du et al., suggests that self-compensation between the shallow donor
Conclusion
In summary, we employed a vapor-pressure-controlled vertical-gradient freeze-growth method to produce CdTe(Cl) crystals, resulting in the reduction of large Te inclusions. Additionally, we conducted a comprehensive investigation of the properties of CdTe(Cl) crystals. We observed significant improvements in both the optical and electrical properties following Cl doping. Remarkably, high IR transmission of up to 60% was observed for the CdTe(Cl) sample. UV-vis-NIR analysis confirmed an energy bandgap value close to 1.456 eV for the CdTe(Cl) samples. Moreover, through PL spectroscopic analysis, we experimentally observed a dominant emission related to the A center (ClTe–VCd)-1 defect. This observation supports the notion of a self-compensation mechanism involving
Experimental Methods
The CdTe compound was synthesized in a custom-designed rocking furnace. To ensure purity, we selected 6N-grade cadmium and tellurium as raw materials. Furthermore, we incorporated 4N-grade ultradry CdCl2 salt as the dopant source. To grow the crystals, the initially synthesized CdTe was placed in a pyrolytic boron nitride (pBN) crucible, which was subsequently positioned inside a quartz ampoule. This quartz ampoule, featuring an extension containing a reservoir of Cd, was then evacuated to a pressure of 1×10-5 Pa and sealed under vacuum. The specific structures of the crystal growth ampoule and Cd reservoir are shown in Fig. 1(a). During the initial growth stages, the pBN crucible prevented the melt from falling into the Cd reservoir when the entire material was melted. Subsequently, a crystal growth process was conducted using a multizone vertical gradient freeze furnace equipped with Cd partial pressure control. We obtained a CdTe(Cl) ingot that was subsequently sliced into wafer forms using a diamond wire saw. We conducted glow discharge mass spectrometry (GDMS) to determine the ceCldopant concentration (GDMS) analysis. In addition, an infrared transmission microscope was used to examine the Te inclusions in the CdTe crystals.
The CdTe samples were polished and etched with bromine–methanol solution. To measure IR transmittance in the wavenumber range 4000 cm-1 - 500 cm-1, we employed an infrared spectrometer (Nicolet Nexus 670 spectrometer, Thermo Fisher Scientific, Waltham, MA, USA). UV–vis–NIR transmission spectra were acquired using a UV-3150 ultraviolet-visible/near-infrared spectrometer (Shimadzu, Japan). To measure the photoluminescence spectrum at low temperatures (77 K), a 532 nm laser beam was used as the excitation source to measure the PL spectrum at low temperatures (77 K). The signals emitted from the samples were collected using a Horiba Scientific Labram HR Evolution Raman spectrometer (Horiba Scientific).
The planar Au/CdTe(Cl)/Au detector, with dimensions of 0.7 cm×0.7 cm×0.2 cm, was fabricated by thermal evaporation of Au on the crystal surface. Subsequently, it was prepared for I-V testing using a semiconductor parameter analyzer (Agilent 4155C, Agilent, USA). Electron mobility was investigated using LBIC (laser beam-induced current) measurements. A pulse laser with a wavelength of 527 nm, pulse width of 893 ps, and 0.1 μJ/pulse was directed onto the cathode to generate electron–hole pairs, resulting in approximately 1012 photons per mm2 on the surface of A bias voltage was applied using a Keithley 6517 and the resulting current signals were recorded using a digital oscilloscope (LeCroy WaveRunner 610 Zi, 1 GHz, 20 GS/s) connected through a 50 Ω resistor.
To measure the response to α particles, the cathode was exposed to uncollimated 241Am@5.49 MeV radioactive sources, while being biased using an ORTEC 710 bias supply. The pulse shape information was amplified using an ORTEC 142 charge-sensitive preamplifier (CSP) and an ORTEC 570 shaping amplifier. Subsequently, the signals were analyzed using a standard Imdetek AMCA-01 multichannel analyzer (MCA) and processed using software to generate and display the response spectra. Measurements were conducted with a shaping time of 1 μs and collection time of 300 s in a dark environment at room temperature, with the pressure maintained below 10 Pa.
High-resolution pixelated CdZnTe detector prototype system for solar hard X-ray imager
. Nucl. Sci. Tech. 30, 42 (2019). https://doi.org/10.1007/s41365-019-0571-9Hformer: highly efficient vision transformer for low-dose CT denoising
. Nucl. Sci. Tech. 34, 61 (2023). https://doi.org/10.1007/s41365-023-01208-0Measurement of air kerma rate and ambient dose equivalent rate using the G(E) function with hemispherical CdZnTe detector
. Nucl. Sci. Tech. 29, 35 (2018). https://doi.org/10.1007/s41365-018-0375-3New flexible CsPbBr3-based scintillator for X-ray tomography
. Nucl. Sci. Tech. 33(8), 98 (2022). https://doi.org/10.1007/s41365-021-00952-yA characterization study on perovskite X-ray detector performance based on a digital radiography system
. Nucl. Sci. Tech. 34(5), 69 (2023). https://doi.org/10.1007/s41365-022-01099-8Advances in nuclear detection and readout techniques
. Nucl. Sci. Tech. 34, 205 (2023). https://doi.org/10.1007/s41365-023-01359-0Detecting ionizing radiation using halide perovskite semiconductors processed through solution and alternative methods
. Nat. Photonics 16(1), 14-26 (2022). https://doi.org/10.1038/s41566-021-00773-7Structural and electronic properties of CdTe:Cl from first-principles
. Mat. Chem. Phys. 143, 637-641 (2014). https://doi.org/10.1016/j.matchemphys.2013.09.046Research on optimal design of new neutron detector based on 6Li+ CdTe
. Nucl. Tech. 43(8), 74-79 (2020). https://doi.org/10.11889/j.0253-3219.2020.hjs.43.080401The Effect of Dopant Concentration and Annealing Treatments on N-type Iodine Doped CdTe
. J. Alloys Compd. 960,Large-area CdZnTe thick film based array X-ray detector
. Vacuum 183,Analysis on energy spectra for CdZnTe gamma ray detector
. J. Synth. Cryst. 10, 1883-1891 (2021). https://doi.org/10.3969/j.issn.1000-985X.2021.10.008The Hg-Cd-Zn-Te phase diagram
. J. Phase Equilib. 13, 476-496 (1992). https://doi.org/10.1007/BF02667355investigated the electrical property variations in undoped CdTe and ZnTe crystals grown under Te-rich conditions
. J. Alloys Compd. 612, 392-397 (2014). https://doi.org/10.1016/j.jallcom.2014.05.167Research progress on CdZnTe crystal growth for room temperature radiation detection applications
. J. Synth. Cryst. 49, 561-569 (2020). https://doi.org/10.3969/j.issn.1000-985X.2020.04.001Effects of Te inclusions on charge-carrier transport properties in CdZnTe radiation detectors
. Nucl. Instrum. Methods Phys. Res. B 343, 89-93 (2015). https://doi.org/10.1016/j.nimb.2014.11.050Melt growth of CdTe single crystals with controlled deviation from stoichiometry
. Mater. Lett. 6, 119-122 (1988). https://doi.org/10.1016/0167-577X(88)90022-6CdTe synthesis and crystal growth using the high-pressure Bridgman technique
. J. Cryst. Growth 534,Studies on the deep‐level defects in CdZnTe crystals grown by travelling heater method
. Phys. Status of Solidi A 214,Technology of 6-inch semi-insulating GaAs single crystals grown by VGF and VB Method
. Semicond. Technol. 45, 383-389 (2020). https://doi.org/10.13290/j.cnki.bdtjs.2020.05.009Evolution features and optimization of interface shape during CdZnTe crystal growth using Vertical Gradient Freeze (VGF) technique
. J. Cryst. Growth 627,Crystal growth and characterization of CdTe grown by vertical gradient freeze
. Mater. Sci. Eng., B 147, 35-42 (2008). https://doi.org/10.1016/j.mseb.2007.07.016Inclusions elimination and resistivity restoration of CdTe:Cl crystals by two-step annealing
. IEEE Trans. Nucl. Sci. 58, 1942-1948 (2011). https://doi.org/10.1109/TNS.2011.2167337Advances in the crystal growth of semi-insulating CdZnTe for radiation detector applications
. IEEE Trans. Nucl. Sci., 49, 2535-2540 (2002). https://doi.org/10.1109/TNS.2002.805236The correlation between superheating and supercooling in CdTe melts during unseeded bridgman growth
. J Cryst. Growth 128, 571-575 (1993). https://doi.org/10.1016/0022-0248(93)90577-TInfluence of surface preparation on CdZnTe nuclear radiation detectors
. Appl. Surf. Sci. 257, 8742-8746 (2011). https://doi.org/10.1016/j.apsusc.2011.04.097Effects of excess Te on optical and electrical properties of Cd1-xMgxTe single crystals grown by modified vertical Bridgman method
. CrystEngComm 25(9), 1446-1452 (2023). https://doi.org/10.1039/D3CE01484GCorrelation between the IR transmission spectra and the CdZnTe qualities
. Chin. Phys. Lett. 20, 1600 (2003). https://doi.org/10.1088/0256-307X/20/9/355The exciton and edge emissions in CdTe crystals
. Mater. Sci. Eng., B 52, 78-83 (1998). https://doi.org/10.1016/S0921-5107(97)00370-5Growth of high resistivity CdTe and (Cd, Zn) Te crystals
. Cryst. Res. Technol. 38, 588-597 (2003). https://doi.org/10.1002/crat.200390125Effect of de-trapping on carrier transport process in semi-insulating CdZnTe
. Chin. Phys. B 24,Material properties and device performance of CdSe radiation detectors
. Nucl. Instrum. Methods Phys. Res., Sect. A 959,Self-compensation limited conductivity of Cl-doped CdTe crystals
. Phys. Status Solidi. 11(9-10), 1519-1522 (2014). https://doi.org/10.1002/pssc.201300694Drift mobility and mobility-lifetime products in CdTe:Cl grown by the travelling heater method
. IEEE Trans. Nucl. Sci. 52, 3074-3078 (2005). https://doi.org/10.1109/TNS.2005.858575What causes high resistivity in CdTe
. New J. Phys. 14,Cl-doping of Te-rich CdTe: complex formation, self-compensation and self-purification from first principles
. AIP Adv. 5,Effect of deep level defects on CdZnTe detector internal electric field and device performance
. J. Appl. Phys. 130,The authors declare that they have no competing interests.


