Introduction

The synthesis of superheavy nuclei (SHN) is an important research topic in modern nuclear physics. With the use of ${}^{48}\text{Ca}$ beams and actinide targets, hot fusion reactions in neutron evaporation channels have been used to successfully synthesize SHN with charge numbers $Z=112-118$ [1-7]. Most microscopic–macroscopic models propose that element Fl ($Z=114$) has a closed proton shell [8-11]. Recent data from Ref. [12] underscores the significance of proton shell closures in the F1 nucleus. The first synthesis of Fl isotopes was accomplished in 1999 by the Dubna group through the reaction ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ at the Dubna gas-filled recoil separator (DGFRS). Two decay chains were observed by identifying ${}^{288}\text{Fl}$ and ${}^{289}\text{Fl}$ [13]. Subsequently, with higher projectile energies, the isotope ${}^{287}\text{Fl}$ was observed at an excitation energy of $E^{*}=53\text{MeV}$ with a corresponding maximum production cross-section of ${1.1}_{-0.9}^{+2.6}\text{pb}$ [14]. Later, other isotopes were also obtained through the reactions ${}^{48}\text{Ca}{+}^{242}\text{Pu}$, ${}^{48}\text{Ca}{+}^{240}\text{Pu}$ and ${}^{48}\text{Ca}{+}^{239}\text{Pu}$ [15-17]. Notably, recent investigations of the ${}^{48}\text{Ca}{+}^{242}\text{Pu}$ reaction have provided valuable data that contribute to constraining theoretical predictions [12, 18]. However, based on current experimental data, the structural properties of the Fl isotope chain are not well understood; thus, a significant amount of additional experimental data is required. In this letter, we show that new methods for synthesizing Fl isotopes should be investigated.

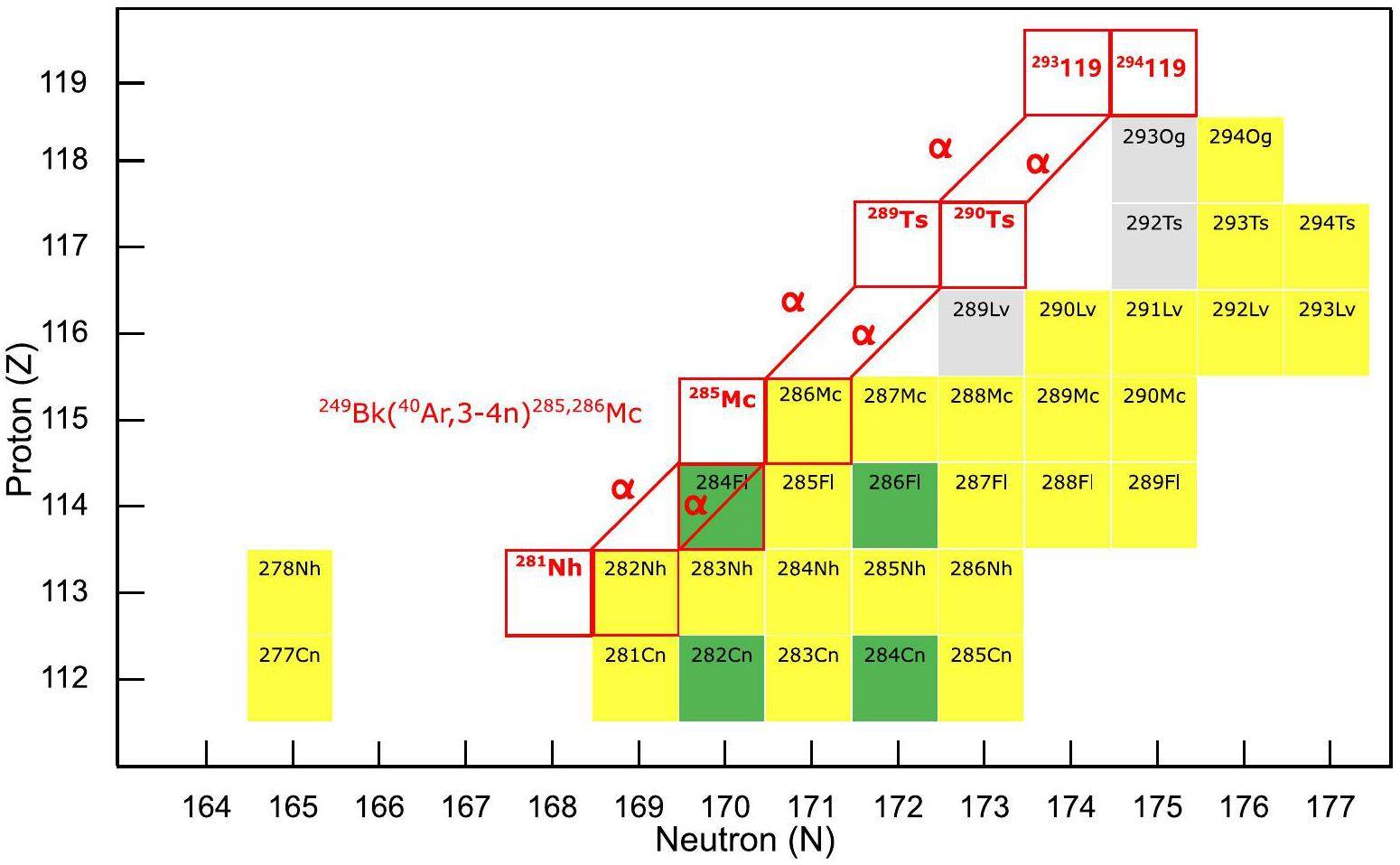
The synthesis of the new element with $Z=119$ and exploration of the limits of its existence pose challenges [19-29]. Recently, the reaction ${}^{54}\text{Cr}{+}^{243}\text{Am}$ was proposed as the most promising method for synthesizing the new element [30-32]. $\alpha$-decay is an important decay mode for SHN [33-35]. Experimentally, new elements and isotopes can be identified by observing the position-time correlated α-decay chains from an unknown parent nucleus to its known descendants [36-38]. Studying the isotopes along the α-decay chain of a new element is crucial for its identification. However, as shown in Fig. 1, some nuclides along the α-decay chain of the predicted synthesized nuclide ${}^{\mathrm{293,294}}119$ are undiscovered. Therefore, this paper proposes the use of ${}^{40}\text{Ar}$ as the projectile nucleus. This approach holds promise for synthesizing new nuclides along the alpha α-decay chain of the new element, thereby facilitating its identification.

Fig. 1Full-screen View

(Color online) α decay chain of the new element with Z = 119. The filled and open squares denote the known and predicted nuclei, respectively. Yellow and olive indicate the α decay and spontaneous fission, respectively. Gray represents unknown decay modes

In heavy-ion fusion reactions, the entire process of compound nucleus formation and decay is typically divided into three stages: the capture process, in which the colliding system overcomes the Coulomb barrier, the formation of the compound nucleus by surpassing the inner fusion barrier, and the de-excitation of the excited compound nucleus to counter fission. The evaporation residue cross-section is expressed as a sum over partial waves with angular momentum $J$ at the center-of-mass energy $E_{\text{c}\text{.m}\text{.}}$ [39-41], $\begin{array}{c}{\sigma }_{\text{ER}}\left(E_{\text{c}\text{.m}\text{.}}\right)=\frac{\pi {\hslash }^2}{2\mu E_{\text{c}\text{.m}\text{.}}}{\displaystyle \sum _{J=0}^{J_{\text{max}}}}\left(2J+1\right)T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)\times \\ P_{\text{CN}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)\times W_{\text{sur}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)\mathrm{.}\end{array}$ (1) Here, the transmission probability $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ is affected by the Coulomb barrier and the strong channel coupling with internal degrees of freedom. This coupling significantly enhances the capture cross-section by several orders of magnitude at sub-barrier energies [42]. When the capture cross-section is experimentally measured within a near-barrier energy range, the barrier height and barrier distribution function can be derived from the experimental data. Subsequently, $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ can be readily calculated or approximated. However, measuring the capture cross-section directly in the synthesis of superheavy elements is challenging, and it is typically inferred from the total yield of fission fragments. In such cases, $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ must be estimated using theoretical models that describe the initial stages of the reaction. $P_{\text{CN}}$ is the fusion probability. However, the fusion stage of this reaction has not been extensively studied. This is because, in light and medium nucleus fusion, the fissility of the compound nucleus is low, and the probability of forming a compound nucleus after overcoming the Coulomb barrier is close to 1 ($P_{\text{CN}}\approx 1$). However, during heavy nucleus fusion, the heavy system may reseparate into two fragments without forming a compound nucleus (quasifission). Thus, the value of $P_{\text{CN}}$ may be significantly less than 1, and an accurate calculation of $P_{\text{CN}}$ is challenging. The formation dynamics of SHN in massive fusion and multinucleon transfer reactions are complex and involve the interplay of numerous degrees of freedom, including radial elongation, mass or charge asymmetry, shape configuration, and relative motion energy [43-46]. Several models have been developed to describe fusion hindrance in massive systems, including macroscopic dynamical models [47], fusion-by-diffusion models [48], dynamical models based on Langevin-type equations [49], and dinuclear system (DNS) models [50, 51, 51, 52]. Currently, there is no consensus on the mechanism of compound nucleus formation, and quite different, occasionally opposite, physical models are used for its description. $W_{\text{sur}}$ is the survival probability, typically calculated using statistical models. In the calculation of $W_{\text{sur}}$, the fission barrier of the excited compound nucleus is the most important and ambiguous parameter, because theoretical estimates of the fission barrier in the SHN region are not yet reliable and exhibit significant differences among them [53].

Our aim is to theoretically analyze the three stages of fusion reactions to understand the factors influencing the evaporation residue cross-sections at each stage and explore the possibility of synthesizing key new isotopes using ${}^{40}\text{Ar}$ as the projectile nucleus. In Sect. 2, we introduce the theoretical framework. In Sect. 3, we analyze and discuss the results. In Sect. 4, we summarize our work.

Theoretical descriptions

The most widely used method for calculating the capture cross-section is the coupled-channel approach. The computer code CCFULL, which is based on the coupled-channel formalism, is used to perform these calculations (for a detailed description, see Ref. [54]). This involves numerically solving the following set of coupled-channel equations: $\begin{array}{l}\left[-\frac{{\hslash }^2}{2\mu }\frac{d^2}{d{r}^2}+\frac{J(J+1){\hslash }^2}{2\mu r^2}+V_N^{\left(0\right)}\left(r\right)+\frac{Z_P{Z}_T{e}^2}{r}+{ϵ}_n-E\right]\\ {\psi }_n\left(r\right)+{\displaystyle \sum _m}{V}_{nm}\left(r\right){\psi }_m\left(r\right)=\mathrm{0,}\end{array}$ (2) where $r$ represents the radial part of the relative motion coordinate, and $\mu$ denotes the reduced mass. The bombarding energy at the center of the mass frame is denoted by $E$, and ${ϵ}_n$ is the excitation energy of the $n$-th channel. The elements $V_{nm}$ are the matrix components of the coupling Hamiltonian, which includes both the Coulomb and nuclear terms in the collective model. These components are elaborated in the subsequent section. $V_N^{\left(0\right)}$ is the nuclear potential in the entrance channel.

However, for SHN, an empirical coupled-channel (ECC) method is typically used to calculate their capture cross-sections [55]. In this method, the transmission probability $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ can be calculated using the Hill–Wheeler formula [56], which approximates the radial variation in the Coulomb barrier between the colliding nuclei in a parabolic form. Considering the multidimensional character of a realistic barrier, we may introduce the barrier distribution function $f(B)$ to determine its total transmission probability [57], $\begin{array}{l}T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)={\displaystyle \int }f\left(B\right)\\ \times \frac{1}{1+\exp \left(\frac{2\pi }{\hslash \omega \left(l\right)}\left[B+\frac{{\hslash }^2}{2\mu R_B^2\left(l\right)}l\left(l+1\right)-E\right]\right)}dB\mathrm{.}\end{array}$ (3) In this context, $\hslash {\omega }_B$ indicates the width of the parabolic barrier, and $R_B$ defines its position. $f(B)$ represents the empirical dynamical barrier distribution function, which, under Gaussian approximation, can be expressed as $f\left(B\right)=\{\begin{array}{ll}\frac{1}{N}\exp \left[-{\left(\frac{B-B_{\text{m}}}{{\text{Δ}}_1}\right)}^2\right]\hfill & B<B_{\text{m}}\hfill \\ \frac{1}{N}\exp \left[-{\left(\frac{B-B_{\text{m}}}{{\text{Δ}}_2}\right)}^2\right]\hfill & B>B_{\text{m}}\mathrm{,}\hfill \end{array}$ (4) Here, $B_{\text{m}}=\frac{B_s+B_0}{2}$, $B_0$ is the height of the Coulomb barrier in the waist-to-waist orientation, $B_s$ is the minimum height of the Coulomb barrier with variance of dynamical deformation, and N is the normalization constant. ${\text{Δ}}_2=\left(B_0-B_s\right)/2$. the value of ${\text{Δ}}_1$ is typically 2-4 MeV less than that of ${\text{Δ}}_2$.

In the DNS model framework, $P_{\text{CN}}$ is obtained by numerically solving a set of master equations, where the neutron and proton numbers of the projectile-like fragment are considered as variables, along with the corresponding potential energy surface variables [58]. The time evolution of the distribution probability function, $P\left(Z_1\mathrm{,}{N}_1\mathrm{,}{E}_1\mathrm{,}t\right)$, which describes the probability at time $t$ of finding $Z_1$ protons and $N_1$ neutrons in fragment 1 with excitation energy $E_1$, is obtained using the following master equation: $\begin{array}{l}\frac{dP\left(Z_1\mathrm{,}{N}_1\mathrm{,}{E}_1\mathrm{,}t\right)}{dt}=\\ {\displaystyle \sum _{{Z^{\prime }}_1}}{W}_{Z_1\mathrm{,}{N}_1;{Z^{\prime }}_1\mathrm{,}{N}_1}\left(t\right)\times [d_{Z_1\mathrm{,}{N}_1}P\left({Z^{\prime }}_1\mathrm{,}{N}_1\mathrm{,}{E}_1\mathrm{,}t\right)\\ -d_{{Z^{\prime }}_1\mathrm{,}{N}_1}P\left(Z_1\mathrm{,}{N}_1\mathrm{,}{E}_1\mathrm{,}t\right)]\\ +{\displaystyle \sum _{{N^{\prime }}_1}}{W}_{Z_1\mathrm{,}{N}_1;Z_1\mathrm{,}{N^{\prime }}_1}\left(t\right)\times [d_{Z_1\mathrm{,}{N}_1}P\left(Z_1\mathrm{,}{N^{\prime }}_1\mathrm{,}{E}_1\mathrm{,}t\right)\\ -d_{Z_1\mathrm{,}{N^{\prime }}_1}P\left(Z_1\mathrm{,}{N}_1\mathrm{,}{E}_1\mathrm{,}t\right)]\\ -\left\{{\text{Λ}}^{\text{qf}}\left[\text{Θ}\left(t\right)\right]+{\text{Λ}}^{\text{fs}}\left[\text{Θ}\left(t\right)\right]\right\}P\left(Z_1\mathrm{,}{N}_1\mathrm{,}{E}_1\mathrm{,}t\right)\mathrm{.}\end{array}$ (5) Here, $W_{Z_1\mathrm{,}{N}_1;{Z^{\prime }}_1\mathrm{,}{N}_1}$ is the mean transition probability from the channel $\left(Z_1\mathrm{,}{N}_1\right)$ to $\left({Z^{\prime }}_1\mathrm{,}{N}_1\right)$, and $d_{N_1\mathrm{,}{Z}_1}$ denotes the microscopic dimension corresponding to macroscopic state $\left(Z_1\mathrm{,}{N}_1\right)$. All possible proton and neutron numbers of fragment 1 are considered in the sum, but only one nucleon transfer is considered in the model $\left({N^{\prime }}_1=N_1\pm \mathrm{1,}{Z^{\prime }}_1=Z_1\pm 1\right)$. The quasifission rate ${\text{Λ}}^{\text{qf}}$ and fission rate ${\text{Λ}}^{\text{fs}}$ are estimated using the one-dimensional Kramers’ formula, and the potential energy surface of the DNS in the fusion process is defined as $\begin{array}{l}U\left(Z_1\mathrm{,}{N}_1\mathrm{,}{Z}_2\mathrm{,}{N}_2\mathrm{,}R\right)=E_{\text{B}}\left(Z_1\mathrm{,}{N}_1\right)+E_{\text{B}}\left(Z_2\mathrm{,}{N}_2\right)\\ -E_{\text{B}}(Z_{\text{CN}}\mathrm{,}{N}_{\text{CN}})+V_{\text{C}}\left(R\right)+V_{\text{N}}\left(R\right)\mathrm{,}\end{array}$ (6) where $Z_{\mathrm{1,2}}$ and $N_{\mathrm{1,2}}$ denote the proton and neutron numbers of the two fragments, respectively. $E_{\text{B}}\left(Z_i\mathrm{,}{N}_i\right)$ and $E_{\text{B}}\left(Z_{\text{CN}}\mathrm{,}{N}_{\text{CN}}\right)$ are the binding energies of the fragment $\left(Z_i\mathrm{,}{N}_i\right)$ and the compound nucleus, respectively. We utilize the Coulomb potential $V_{\text{C}}\left(R\right)$ and nuclear potential $V_{\text{N}}\left(R\right)$ mentioned in Ref. [59]. $W_{\text{sur}}$ is calculated using a statistical model: $\begin{array}{l}{W}_{\text{sur}}\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}x\mathrm{,}J\right)=P\left(E_{\text{CN}}^{*}\mathrm{,}x\mathrm{,}J\right){\displaystyle \prod _{i=1}^x}{\left[\frac{{\text{Γ}}_n}{{\text{Γ}}_{\text{n}}+{\text{Γ}}_{\text{f}}}\right]}_i\mathrm{,}\hfill \end{array}$ (7) where $E_{\text{CN}}^{*}$ represents the excitation energy of the compound nuclei, $P\left(E_{\text{CN}}^{*}\mathrm{,}x\mathrm{,}J\right)$ denotes the probability of emitting x neutrons, and ${\text{Γ}}_{\text{n}}$ and ${\text{Γ}}_{\text{f}}$ represent the partial wave decay widths of the evaporating neutron and fission, respectively.

Results and discussion

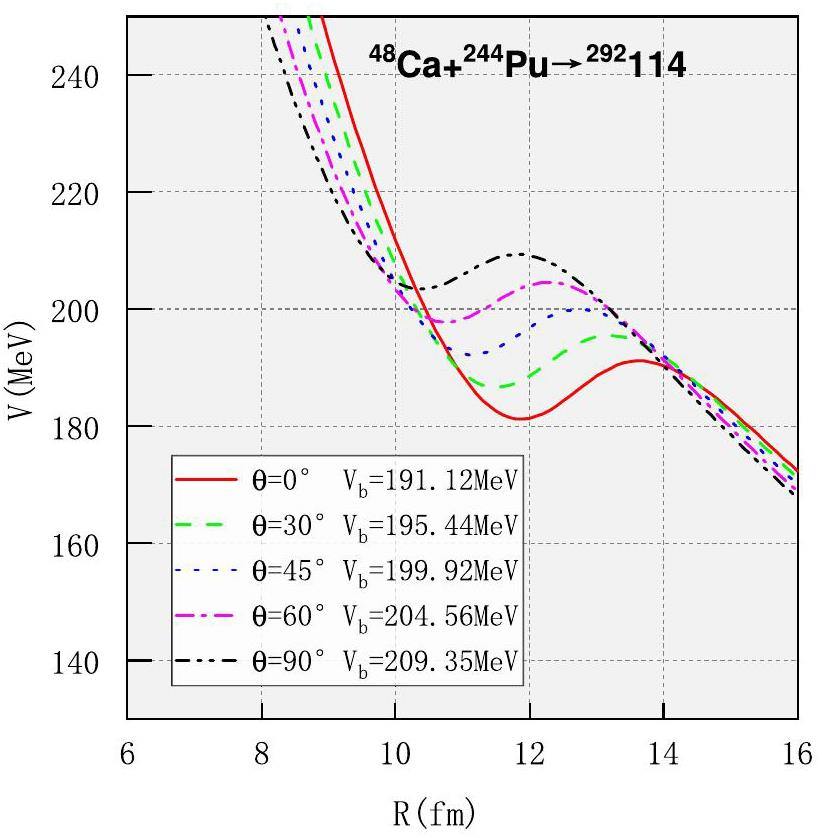
In Fig. 2, we show the dependence of the barrier height on the collision orientation with static deformation in the ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ reaction. The quadrupole deformation parameter is obtained from Ref. [8]. As ${}^{48}\text{Ca}$ is a spherical nucleus, we vary only the orientation $\theta$ of ${}^{244}\text{Pu}$. We can observe that the Coulomb barrier height differs by 18.23 MeV between the pole-to-pole collisions ($\theta {=0}^{\circ }$) and waist-to-waist collisions ($\theta {=90}^{\circ }$). This indicates that the collision orientation has a significant impact on the capture cross-section. In the synthesis of SHN, not only the static deformation of the nuclei but also the significant dynamic deformations caused by nucleus–nucleus interactions should be considered.

Fig. 2Full-screen View

(Color online) Dependence of the nucleus–nucleus interaction potential on collision direction in the ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ reaction

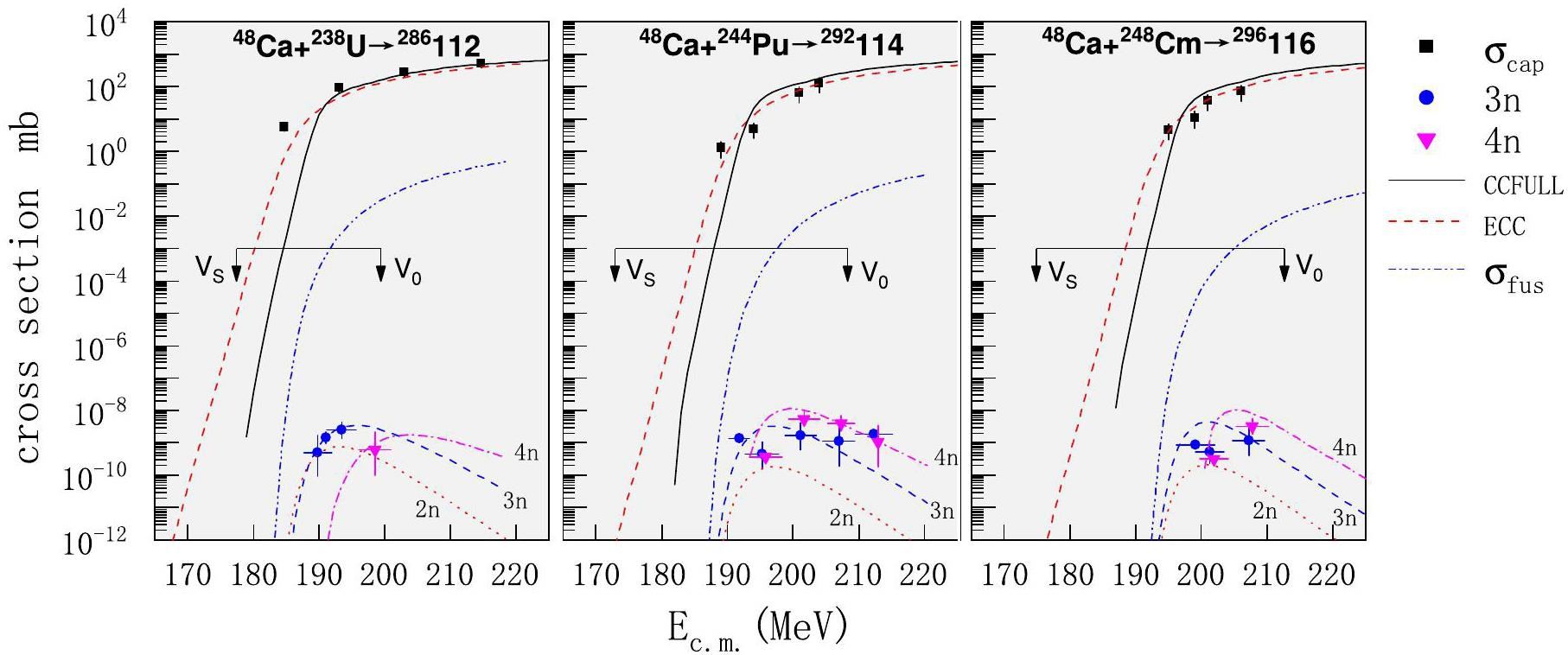
In Fig. 3, we present the capture and evaporation residue cross-sections for three reactions involved in the synthesis of SHN. The position $V_0$ represents the height of the Coulomb barrier in the waist-to-waist direction. The position $V_s$ represents the height of the minimum barrier that changes with dynamic deformation (the position of the Coulomb barrier at the saddle point). The difference $V_0-V_s$ increases with increasing masses of the interacting nuclei. We can also observe that the ECC model, compared with CCFULL, describes the capture cross-sections of the reactions for synthesizing SHN very well, including the sub-barrier energy region. This is because, for SHN (low-energy vibrational excitations), a realistic nucleus–nucleus interaction can result in very large dynamic deformations. Thus, a large number of coupling channels must be considered, which significantly complicates the microscopic calculation of $T\left(E_{\text{c}\text{.m}\text{.}}\mathrm{,}J\right)$ and renders it unreliable. In this case, CCFULL calculations cannot reproduce the experimental capture cross-sections at sub-barrier energies. Additionally, we have provided the fusion cross-sections ${\sigma }_{\text{fus}}\left({\sigma }_{\text{fus}}={\sigma }_{\text{cap}}\times P_{\text{CN}}\right)$ for these three reactions and calculated the evaporation residue cross-sections. The results show that the calculated evaporation residue cross-sections reproduce the experimental data very well.

Fig. 3Full-screen View

(Color online) Capture cross-section ${\sigma }_{\text{cap}}$, fusion cross-section ${\sigma }_{\text{fus}}$ and evaporation residue cross-sections in the 2n, 3n, and 4n channels. Experimental data for the capture cross-section are taken from Ref. [60], and experimental data for the evaporation residue cross-sections in the xn channels are obtained from Ref. [14, 17, 61, 62]. Positions of the Coulomb barrier at waist-to-waist collision (V₀) and at the saddle point (VS) are shown by the arrows

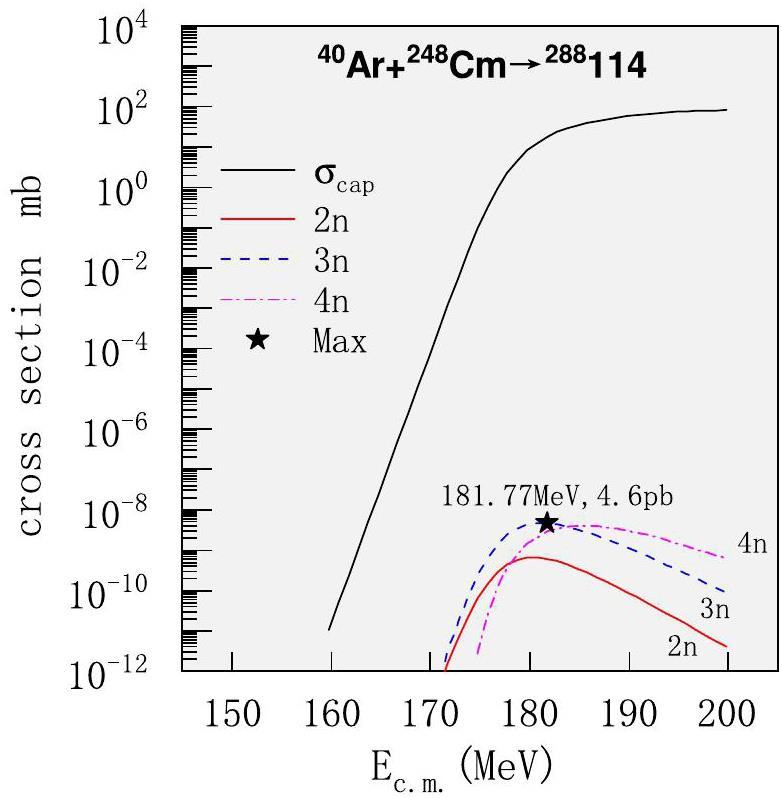
Based on the theoretical description of SHN synthesis, we conducted research on the synthesis of key superheavy isotopes. Figure 4 shows the capture and evaporation residue cross-sections for the $Z=114$ isotope, which is predicted to have a proton magic number, synthesized using ${}^{40}\text{Ar}$ as the projectile nucleus. As shown, the maximum evaporation residue cross-section of the reaction ${}^{40}\text{Ar}{+}^{248}\text{Cm}$ appears in the $3n$ channel, with a maximum evaporation residue cross-section of 4.6 pb, corresponding to an incident energy of 181.77 MeV. Additionally, the maximum evaporation residue cross-section in the $4n$ channel closely matches that in the $3n$ channel, which is slightly below the maximum observed in the $3n$ channel. Experimental fusion reactions with ${}^{48}\text{Ca}$ as the projectile nucleus yield a maximum cross-section of 5 pb for the synthesis of the $Z=114$ isotope [14]. Thus, using ${}^{40}\text{Ar}$ as the projectile nucleus to synthesize the $Z=114$ isotope not only reduces the advantages of reducing experimental costs and requires lower incident energy, but the maximum evaporation residue cross-section is also comparable to that induced by the ${}^{48}\text{Ca}$ fusion reaction.

Fig. 4Full-screen View

(Color online) Capture cross-section ${\sigma }_{\text{cap}}$ and evaporation residue cross-sections in the $2n$, $3n$, and $4n$ channels in the ${}^{40}\text{Ar}{+}^{248}\text{Cm}$ reaction. The maximum evaporation residue cross-section is marked with a pentagram

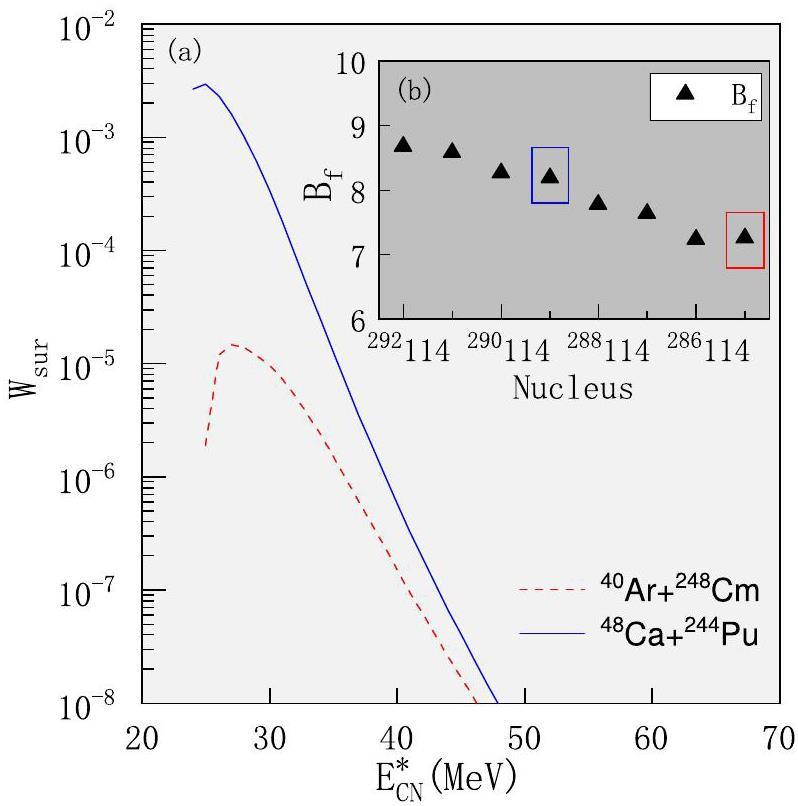
To gain deeper insight into the physical mechanisms behind the synthesis of SHN using ${}^{40}\text{Ar}$ and ${}^{48}\text{Ca}$, we analyze $P_{\text{CN}}$ using the DNS model. The advantage of the DNS model is that it can naturally explain the existence of an inner fusion barrier when forming a compound nucleus and includes the competitive processes of fusion and quasifission during the evolution of the dinuclear system towards the compound nucleus. In Fig. 5(a), we show the $P_{\text{CN}}$ for the synthesis of the $Z=114$ isotope induced by ${}^{48}\text{Ca}$ and ${}^{40}\text{Ar}$. We can observe that $P_{\text{CN}}$ induced by ${}^{40}\text{Ar}$ is an order of magnitude higher than that induced by ${}^{48}\text{Ca}$. Figs. 5(b) and 5(c) show the driving potentials and inner fusion barrier heights of the reactions ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ and ${}^{40}\text{Ar}{+}^{248}\text{Cm}$, respectively. Their inner fusion barrier heights are 9.15 and 7.56 MeV, respectively. The larger the inner fusion barrier, the more difficult it is for the dinuclear system to evolve into a compound nucleus. Conversely, the smaller the inner fusion barrier, the easier the dinuclear system evolves into a compound nucleus. Thus, the reason for the higher $P_{\text{CN}}$ of the reaction ${}^{40}\text{Ar}{+}^{248}\text{Cm}$ is the greater mass asymmetry of the reaction system, which results in a lower inner fusion barrier.

Fig. 5Full-screen View

(Color online) (a) $P_{\text{CN}}$ for ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ and ${}^{40}\text{Ar}{+}^{248}\text{Cm}$. (b) Driving potentials for the reaction ${}^{48}\text{Ca}{+}^{244}\text{Pu}$, with arrows indicating the entrance channel position. (c) Driving potentials for the reaction ${}^{40}\text{Ar}{+}^{248}\text{Cm}$, with arrows indicating the entrance channel position

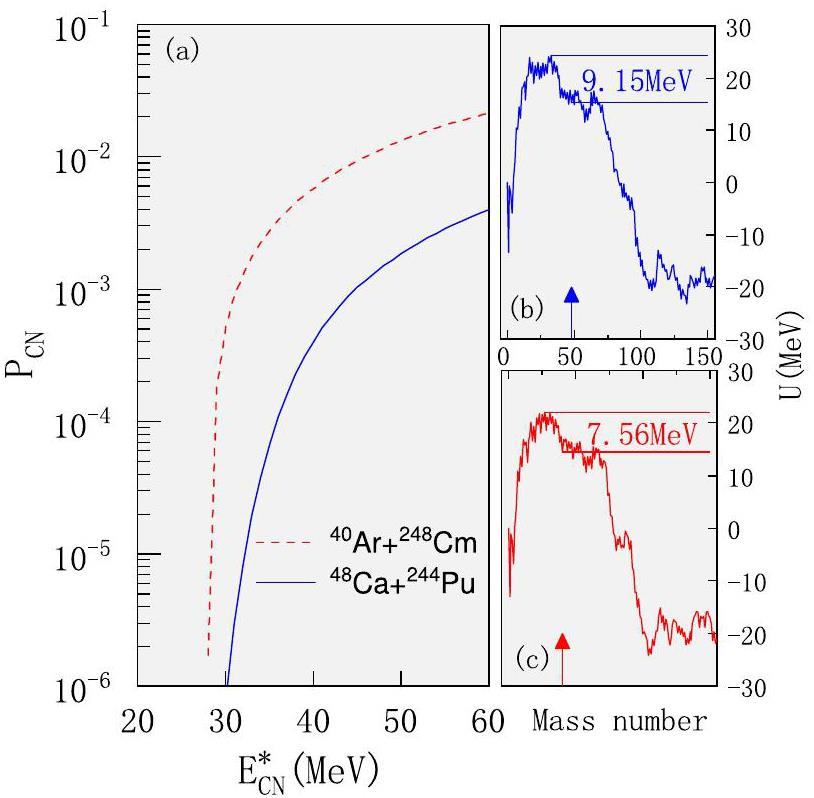
We also analyzed $W_{\text{sur}}$ in the 3n channel for the two aforementioned reactions. In Fig. 6(a), we can observe a higher $W_{\text{sur}}$ for the ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ reaction system. For reaction ${}^{48}\text{Ca}{+}^{244}\text{Pu}$, after the formation of the compound nucleus ${}^{292}\text{114}$, three neutrons evaporate, resulting in the nucleus ${}^{289}\text{114}$. Similarly, for the reaction ${}^{40}\text{Ar}{+}^{248}\text{Cm}$, the compound nucleus ${}^{288}\text{114}$ undergoes evaporation of three neutrons, yielding the nucleus ${}^{285}\text{114}$. In other words, the $Z=114$ isotope synthesized using the ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ reaction is relatively neutron-rich. In Fig. 6(b), we depict the fission barrier heights along the $Z=114$ isotope chain, marking the positions of nuclei ${}^{289}\text{114}$ and ${}^{285}\text{114}$. The fission barrier height difference between ${}^{289}\text{114}$ and ${}^{285}\text{114}$ is about 1 MeV. This 1 MeV difference in the fission barrier height translates to an approximate order of magnitude difference in the survival probabilities; hence, the survival probability for the ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ reaction system is higher.

Fig. 6Full-screen View

(Color online) (a) $W_{\text{sur}}$ in the $3n$ channel for synthesizing a SHN with $Z=114$ using the reaction systems ${}^{48}\text{Ca}{+}^{244}\text{Pu}$ and ${}^{40}\text{Ar}{+}^{248}\text{Cm}$. (b) Fission barrier heights for the isotopic chain with $Z=114$ [8]

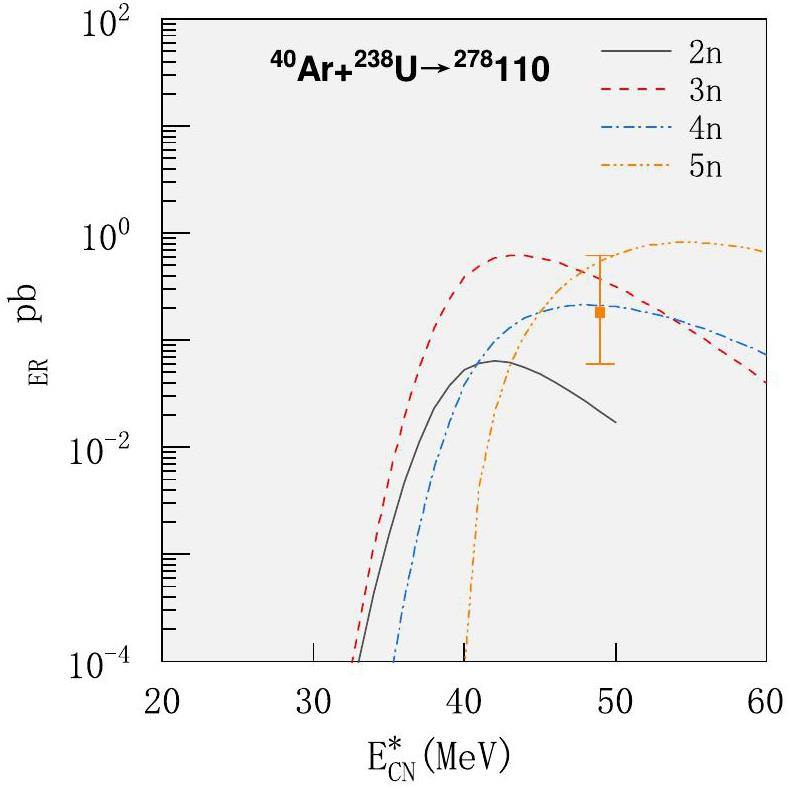
The Ds isotopes in the reaction ${}^{40}\text{Ar}{+}^{238}\text{U}$ were measured by Dubna [63]. The cross-section of the 5n evaporation channel of the reaction at $E^{*}=49\text{MeV}$ is ${0.18}_{-0.12}^{+0.44}\text{pb}$. In Fig. 7, we show our calculation results for the 2n, 3n, 4n, and 5n evaporation channels. In the 5n evaporation channel, our results match the experimental data within the error range. In the calculations of this reaction, we used the fission barrier from Ref. [64].

Fig. 7Full-screen View

(Color online) Evaporation residue cross-sections in the 2n, 3n, 4n, and 5n channels for reaction ${}^{40}\text{Ar}{+}^{238}\text{U}$. Experimental data for the evaporation residue cross-section in the 5n channel are obtained from Ref. [63]

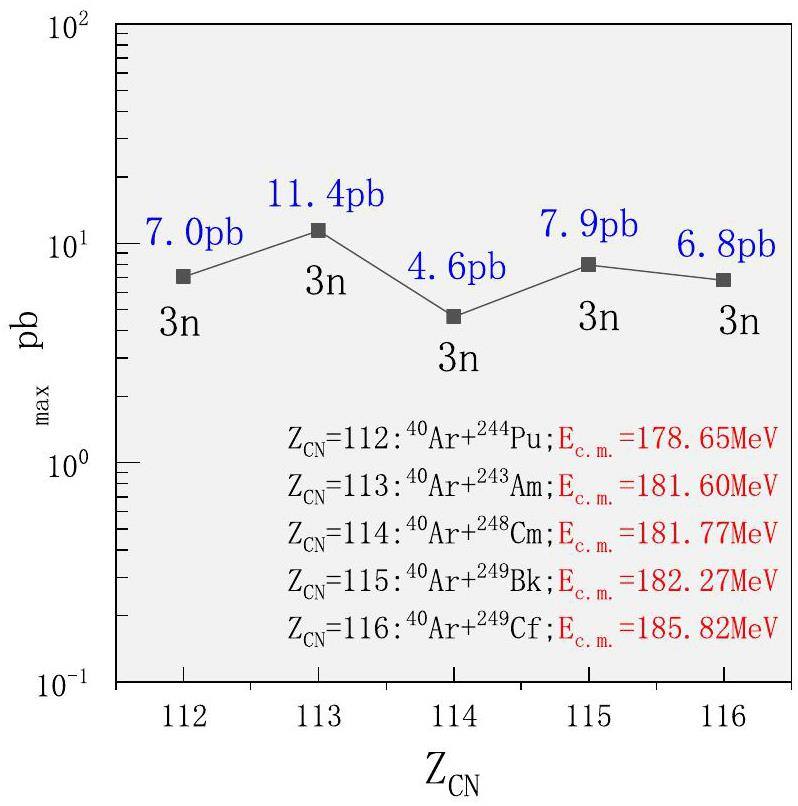
In Fig. 8, we present the maximum evaporation residue cross-sections for synthesizing SHN with $Z=112-116$ using ${}^{40}\text{Ar}$ as the projectile nucleus, along with the corresponding neutron evaporation channels and incident energies. The maximum evaporation cross-sections for these reactions occur in the 3n channel, and the maximum evaporation residue cross-sections are all in the pb range. Such cross-sections are similar in magnitude to those produced by fusion reactions induced by ${}^{48}\text{Ca}$, suggesting the potential of using ${}^{40}\text{Ar}$ as a projectile nucleus for synthesizing SHN. Most importantly, the reaction ${}^{40}\text{Ar}{+}^{249}\text{Bk}$ in the 3n channel can synthesize a crucial new isotope ${}^{286}\text{115}$, which is part of the alpha decay chain of the new element $Z=119$. The predicted maximum cross-section for this reaction is 7.9 pb. Thus, before attempting to synthesize the new element $Z=119$, we recommend experimentally synthesizing ${}^{286}\text{115}$ via the ${}^{40}\text{Ar}{+}^{249}\text{Bk}$ reaction facilitate the identification of the new element.

Fig. 8Full-screen View

(Color online) Maximum evaporation residue cross-sections for synthesizing SHN with $Z=112-116$ using ${}^{40}\text{Ar}$, along with the corresponding neutron evaporation channels and incident energies

Summary

For the capture process, the ECC method effectively describes the experimental capture cross-sections in the fusion reactions for synthesizing SHN, including the sub-barrier energy region. The dynamics of the fusion process remain unclear, and certain critical parameters of the survival process, such as the fission barrier height, are uncertain. This necessitates extensive experimental and theoretical research. In this study, we conducted a systematic investigation of the synthesis of SHN Z=112 to Z=116 using ⁴⁰Ar as the projectile, employing available experimental data and relatively accurate theoretical methods. This study indicated that ⁴⁰Ar can be used as a projectile to synthesize Z=114 isotopes, enabling us to investigate the stability of nuclei predicted to possess the proton magic number Z=114. Additionally, ⁴⁰Ar can be used as a projectile to synthesize the key nucleus ²⁸⁶115, which lies on the α-decay chain of the new element Z=119, aiding in the identification of the new element. We hope that this paper provides valuable insights for future experiments using ⁴⁰Ar as a projectile to synthesize crucial superheavy nuclei.