AMPT model

The AMPT hybrid dynamic model [47, 48], which includes both partonic and hadronic scattering, has been used extensively to study various key features of HICs, such as hadron production [49, 50], collectivity [51-54] and phase transitions [55]. In recent years, this model has been extended to small systems, such as pp and p–Pb collisions [45]. AMPT consists of four key components to simulate the collision process: the initial conditions generated using the Heavy Ion Jet Interaction Generator (HIJING) model [56, 57]; the partonic interactions described by Zhang’s Parton Cascade (ZPC) model [58]; the hadronization process, which occurs through either Lund string fragmentation or a coalescence model; and the hadronic rescatterings modeled by A Relativistic Transport (ART) model [59]. The model has two versions: (1) the string-melting version, in which a partonic phase is generated from excited strings in the HIJING model and a simple quark coalescence model combines partons into hadrons, and (2) the default version, which proceeds only through a pure hadron gas phase.

This work is based on the AMPT with the string-melting configuration, incorporating subnucleon geometry when sampling the initial transverse positions of parton sources before converting them into constituent quarks (denoted by “3 quarks”). This special tuning method introduced in Ref. [44] can successfully reproduce the spectra and elliptic flows of the identified hadrons in pp collisions at TeV scale. Details of the initial partonic distribution are presented in Sec. 3. To illustrate the effects of the parton rescattering process, the value of ${\sigma }_{\text{p}}$ in the ZPC was set to 1.5 mb and 10 mb, where 1.5 mb is typically applied to larger systems [60].

The high-multiplicity events in the AMPT were selected based on the number of charged particles in the pseudorapidity regions -3.7<η<-1.7 and 2.8<η<5.1 corresponding to the acceptance of the ALICE V0 detector. Additionally, an average multiplicity of approximately 30 charged particles was considered in the pseudorapidity interval |η|<0.5, following the event classification scheme used in ALICE pp collisions [61]. Using the particle selection criteria from the ALICE measurements [17], charged pions were selected in the pseudorapidity range |η|<0.8 within the transverse momentum (p_T) range of 0.14-4.0 GeV/c.

The correlation function and emission source

The correlation function is expressed in Eq. (1). In this study, assuming that the emission source was identical in all spatial directions, a single scalar k^* was considered instead of the general three-dimensional k*. The source function $S\left(r^{*}\right)$ describes the probability of producing two particles at a relative distance r^* and is commonly modeled using a Gaussian profile: $S\left(r^{*}\right)=\frac{1}{{\left(2\pi R_{ab}^2\right)}^{3/2}}\exp \left(-\frac{r^{*2}}{2R_{ab}^2}\right)\mathrm{.}$ (2) Here, Rab represents the general expression for the two-particle source radius of the $a-b$ pair. For identical particle pairs ($a=b$), this is simplified to $R_{aa}=\sqrt{2}{R}_a$. Note that r^* denotes the relative distance between the particles in specific pairs, whereas R typically represents the variance in the distribution, reflecting the overall characteristics of the r^* distribution contributed by many pairs. A two-component source consisting of a core from primary particles and a halo formed by resonance decay has been used to describe the Bose–Einstein correlations between identical pions in HICs [62]. This study follows the same nomenclature. In additional, this “resonance halo,” arising from short-lived, strongly decaying resonances ($c\tau \le 5\text{ fm}$), significantly increases the source size by introducing exponential tails to the source function of p-p and $\pi -\pi$, as observed in recent pp collisions measurements [17, 18]. R_core represents the core Gaussian source radius, and R_eff represents the effective Gaussian source radii that contain the resonance effect. For the previous measurements in [7], R_inv can also be used to determine the source radius of identical pairs, called the single-particle source radius, which is the same as Ra. In this study, the observed core source radius $\pi -\pi$ is expressed as R_core, where $R_{\text{core}}=R_{\pi }=R_{\pi \pi }/\sqrt{2}$. Previous studies [63-65] did not explicitly account for the effects of resonances; instead, they used a Cauchy/exponential-type source parameterization [66], $S\left(r^{*}\right)=\frac{1}{{\pi }^2}\frac{R_{\exp }}{{\left(R_{\exp }^2+r^{*2}\right)}^2}\mathrm{,}$ (3) where the Cauchy source size is denoted by $R_{\exp }$. In the absence of angular dependence, the probability of emitting two particles at a given r^* can be obtained by a simple integration over the solid angle $S_{4\pi }\left(r^{*}\right)=4\pi r^{*2}S\left(r^{*}\right)$. From a different perspective, Hanbury-Brown–Twiss (HBT) interferometry measurements [67, 68] indicate that the shape of the correlation function obtained in a longitudinally comoving system (LCMS) is different in the R_long, R_side, and R_out directions.

However, for simplicity, the results of this study were based on the isotropic Gaussian source shown in Equation 2. Because of the fundamental assumptions in the Lednický parameterization [5], the effective range expansion of the scattering amplitude is not valid for small systems, particularly pp collisions [69]. Therefore, the two-particle wave function is obtained using the “Correlation Analysis Tool using the Schrödinger Equation” (CATS) framework [70], which numerically solves the Schrödinger equation for a configurable interaction potential. In this study, the phase space of the charged particles (positions and momenta) is provided by the AMPT model, whereas the CATS framework is used to accurately account for the FSI of the pairs to construct the $\pi -\pi$ correlation function.

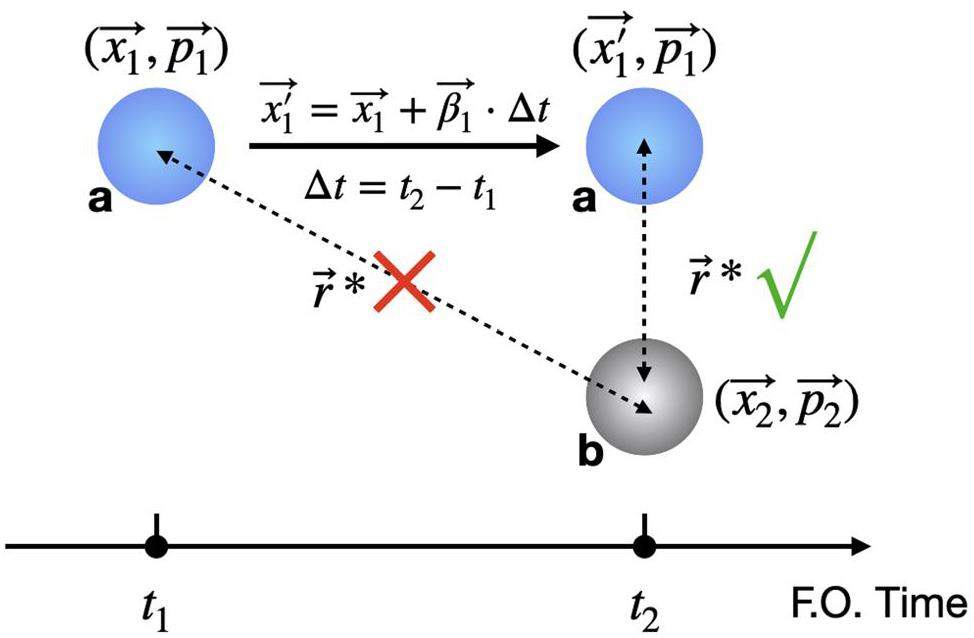
With a time step of 0.2 fm/c in the AMPT computational framework, the particle generated earlier must propagate along its momentum for the time difference between the pair to satisfy the equal emission time condition, as illustrated in Fig. 1. Consider a pair of particles labeled a and b. The particle a, represented as a blue disk, is emitted at freeze-out (F.O.) time t₁ with position and momentum $\left({\overrightarrow{x}}_1\mathrm{,}{\overrightarrow{p}}_1\right)$, earlier than the particle b, represented as a gray disk, which is emitted at time t₂ with $\left({\overrightarrow{x}}_2\mathrm{,}{\overrightarrow{p}}_2\right)$. Under equal emission time conditions, the particle a must propagate over a certain distance $\text{Δ}{\overrightarrow{x}}_1={\overrightarrow{\beta }}_1\cdot \left(t_2-t_1\right)$ along the direction of its velocity ${\overrightarrow{\beta }}_1$. The distance of the pair r^* is then calculated using $\left({\overrightarrow{x}}_1^{\text{'}}\mathrm{,}{\overrightarrow{p}}_1\right)$ and $\left({\overrightarrow{x}}_2\mathrm{,}{\overrightarrow{p}}_2\right)$, where ${\overrightarrow{x}}_1^{\text{'}}={\overrightarrow{x}}_1+\text{Δ}{\overrightarrow{x}}_1$. In this model, no difference is expected between π⁺ and π^-. Therefore, in the following text, the term $\pi -\pi$ refers to a combination of ${\pi }^{+}-{\pi }^{+}$ and ${\pi }^{-}-{\pi }^{-}$ pairs.

Fig. 1Full-screen View

(Color online) Illustration of the modification of the coordinate ${\overrightarrow{x}}_1$ to ${{\overrightarrow{x}}^{\prime }}_1$ for particle a (blue disk), which is generated at time t₁, due to the different freeze-out time compared to particle b (gray disk), generated at time t₂, in pairing the two particles based on the AMPT framework. The coordinate system is defined by the rest frame of the two particles and is consistent with Eq. (1), where ${\overrightarrow{r}}^{*}$ represents their relative distance (dash-dotted lines)

Effect of initial partonic distribution

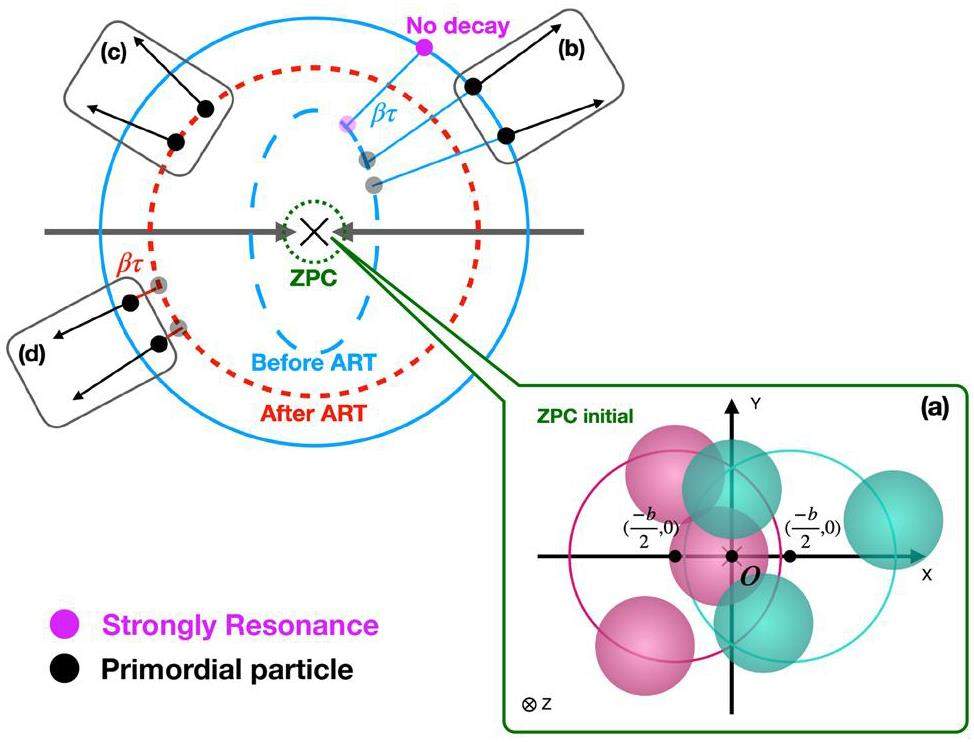
The initial partonic distribution during the ZPC stage played a crucial role in determining the source function. To investigate this effect, three initial partonic patterns were considered, as shown in panel (a) of Fig. 2. Partons can be generated from (1) the overlapping area of the quarks (colored disks) inside the protons [44], mimicking the constituent-quark scenario, and (2) three fixed black points along the impact parameter direction b, corresponding to the centers of two colliding protons and the center of the impact parameter. In the model coordinate system, these are located at $x=-b/2$, $x=b/2$ and x=0. This is the intrinsic setting of AMPT, although it may not be entirely realistic; and (3) the geometrical center of the event (x=0), which serves as a reference for cross-checking the extreme case. These three settings are labeled as “3 quarks,” “Normal,” and “Point-like,” respectively, in this work.

Fig. 2Full-screen View

(Color online) Schematic view of the AMPT evolution from the space-time perspective. (a) illustrates the initial partonic distribution. (b) and (d) depict the core source radii for a pair of primordial hadrons, boosted before and after the ART stage, respectively, with an emission time parameter τ and each particle’s velocity $\overrightarrow{\beta }$. (c) is the same as (d) but with τ=0. The figure is inspired by [43]

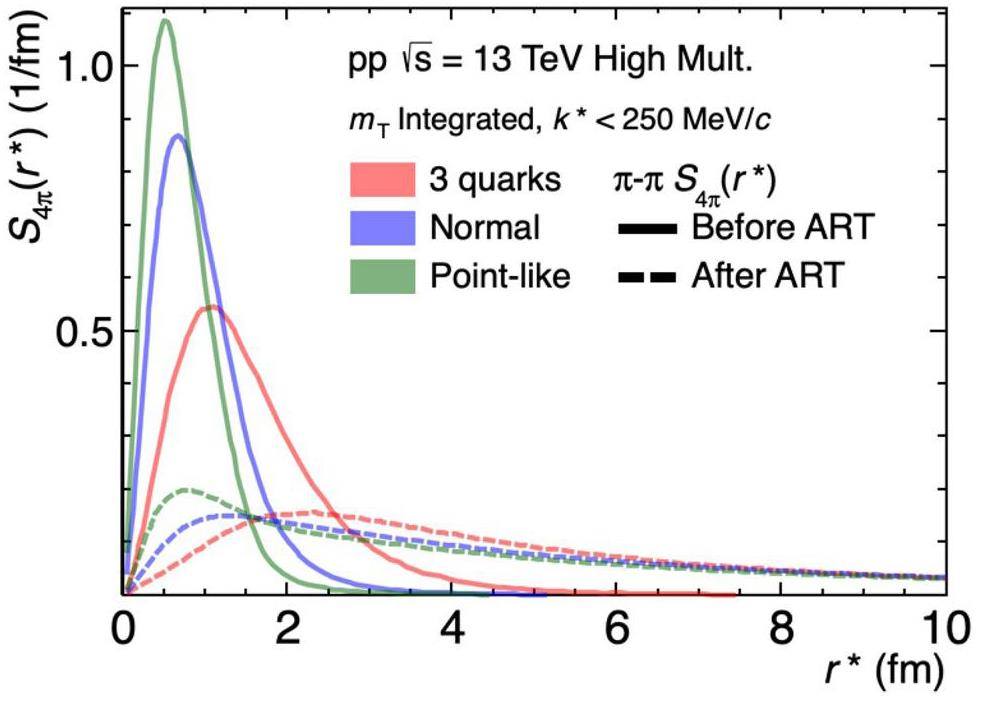
In Fig. 3, the m_T integrated source functions of the $\pi -\pi$ pairs in femtoscopy region (k^* < 250 MeV/c) for the three initial configurations are represented. The results before and after ART are represented by solid and dashed lines, respectively. Because the coalescence mechanism from partons to hadrons is identical for any initial partonic configuration, discrepancies in the source function before the ART stage can arise only from differences in the initial partonic distribution. The mean relative distance $\langle r^{*}\rangle$ of the source function is a convenient variable for comparing the different distributions. Qualitative observations of the source function shape show that, before the ART stage, the source aligns with a Gaussian with $R_{\pi }\approx 0.65\text{ fm}$, 0.41 fm, and 0.33 fm and $\langle r^{*}\rangle \approx 1.58\text{ fm}$, 0.98 fm, and 0.77 fm for three initial patterns, respectively. In contrast, after the ART stage, the source matches a Cauchy with $R_{\exp }\approx 2.22\text{ fm}$, 2.13 fm, and 1.93 fm and $\langle r^{*}\rangle \approx 4.15\text{ fm}$, 3.94 fm, and 3.60 fm. As mentioned in Sect. 2, the Cauchy source is considered an effective representation of the genuine source, with its exponential tail primarily originating from the resonances, as investigated in the following sections. In the “3 quarks” model, hadrons can only be generated from the overlap region of the binary constituent quark, as shown in sub-panel (a) of Fig. 2. This overlap has the potential to contribute to a more widely dispersed distribution in the coordinate space compared with the other two initial distributions, resulting in a broader source function.

Fig. 3Full-screen View

(Color online) $\pi -\pi$ source functions before and after the ART stage from three initial partonic distributions. See the text for details

Fitting source function in different k_T intervals

The correlation function is commonly divided into m_T intervals to ensure a consistent number of pairs in the femtoscopic signal region (e.g., k^* < 250 MeV/c). Here, the $\pi -\pi$ source function in the AMPT is also divided into different k_T (m_T) intervals, following Ref. [17], with k_T ranges 0.15-0.3, 0.3-0.5, 0.5-0.7, 0.7-0.9, and 0.9-1.5 GeV/c. The general explanation for the m_T-scaling observed in several different experiments [7, 17, 18] and simulations [19, 20, 43] is that a higher m_T corresponds to earlier particle generation, leading to a smaller source radius. Conversely, as m_T decreases, low-momentum particles are more likely to be produced in a more homogeneous region [1], thereby contributing to a larger source. In Fig. 4, the source functions for the two example k_T intervals are represented by red and blue lines, respectively, with the before- and after-ART stages shown by solid crosses and circles, respectively.

Fig. 4Full-screen View

(Color online) Source function in the $k_{\text{T}}\in [\mathrm{0.15,0.3})$ and $[\mathrm{0.9,1.5})$ GeV/c intervals before- and after-ART stages within the “3 quarks” AMPT model. Fitting with Gaussian and Cauchy functions are represented by solid and dashed lines, respectively. The shaded bands are the core radii from Ref. [17]

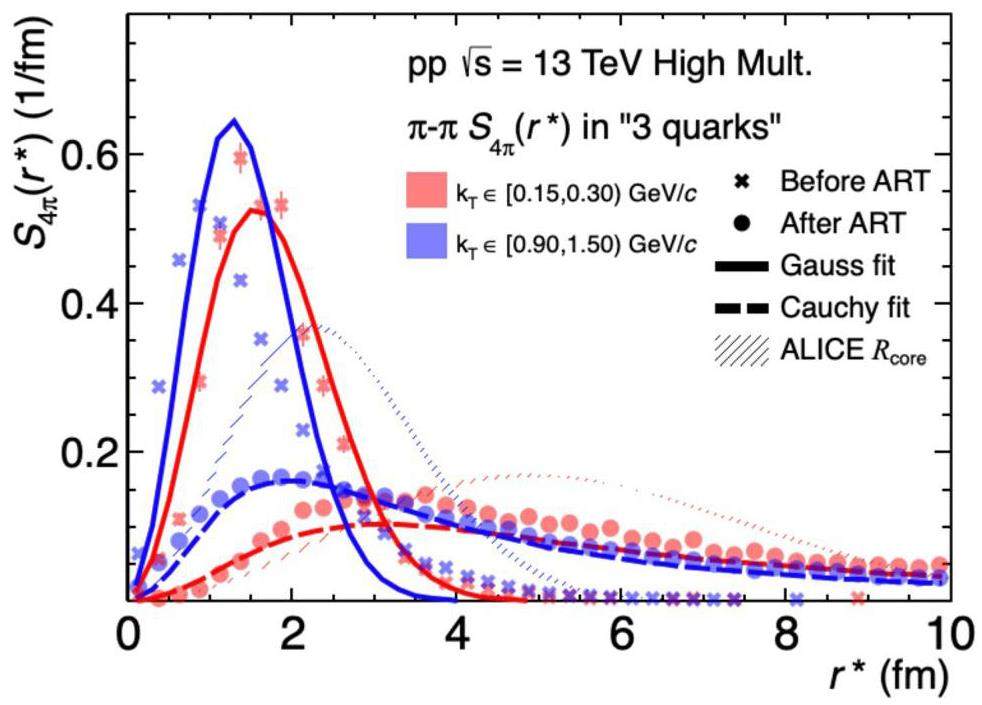
Gaussian and Cauchy source functions were used to fit the source distributions before and after the ART stage at two k_T intervals, represented by the solid and dashed lines, respectively. This fitting yields the radii $R_{\pi }=0.78\text{ fm}$ and 0.63 fm and $R_{\exp }=3.09\text{ fm}$ and 1.96 fm, respectively. The experimental measurements with the corresponding core radii $R_{\text{core}}=2.46\pm 0.028\text{ fm}$ and $1.13\pm 0.015\text{ fm}$ are shown in the shaded boxes. According to Fig. 1 of Ref. [17], strong resonances only reduce the height of the peak in the source function and do not affect its position. It can be inferred that the core source radius obtained in the “3 quarks” scenario after the ART stage is smaller than the corresponding core source extracted from experimental data within the given k_T interval. Therefore, as illustrated in Fig. 3, the “3 quarks” scenario already provides the largest size among the three configurations, the “Normal” and “Point-like” scenarios are too small to adequately describe the data. The effect of resonances on the source function is explained below.

$\pi -\pi$ correlation functions

To understand the impact of the source on the final correlation function, the simulation results are presented for three different initial partonic distributions before and after the ART stage using the aforementioned source functions and the accurate two-particle wave function from CATS [70]. The results are presented in Fig. 5 and Fig. 6 correspond to two examples k_T-intervals.

Fig. 5Full-screen View

(Color online) $\pi -\pi$ correlation function in the k_T interval 0.15–0.30 GeV/c before and after the ART stages for three initial partonic distributions in the AMPT+CATS framework [70]

Fig. 6Full-screen View

(Color online) Same as Fig. 5, but for another k_T interval 0.90–1.50 GeV/c

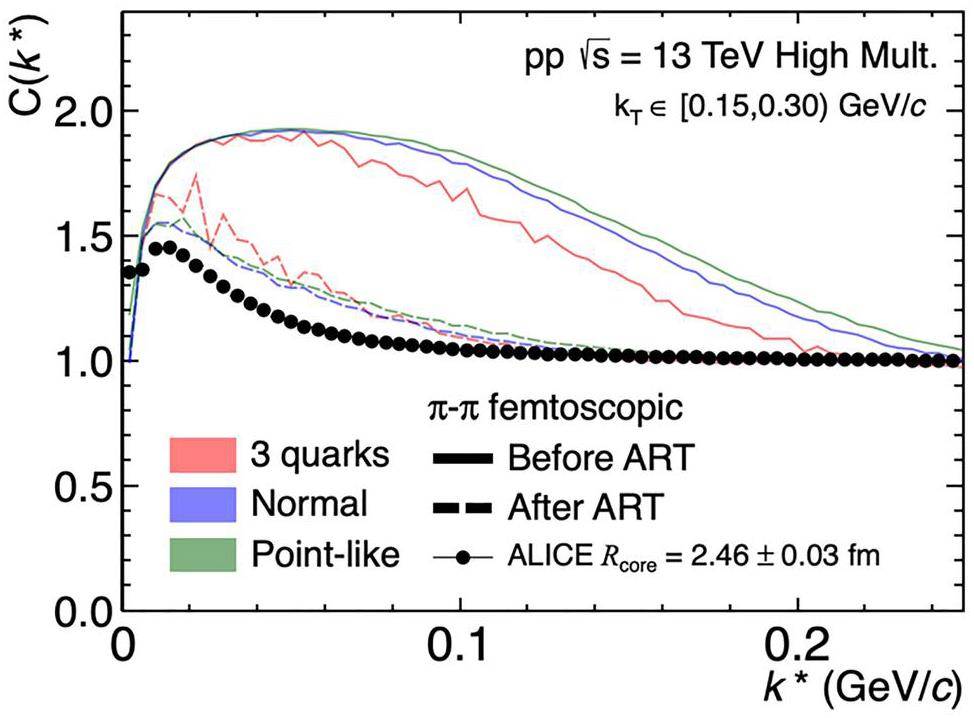
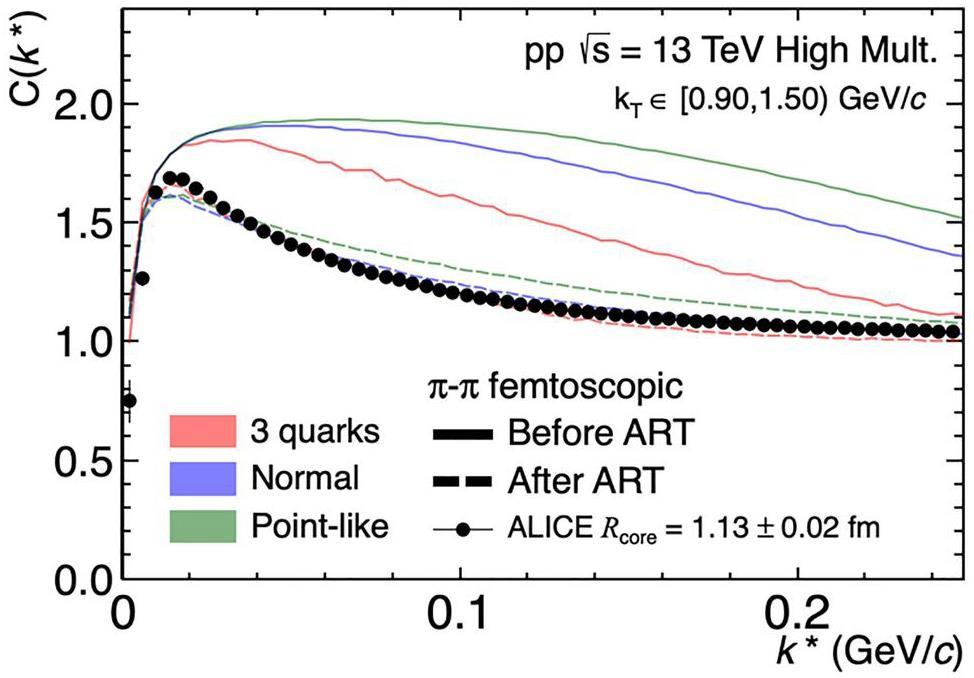
It can be observed that the correlation functions after the ART stage approximate the experimental data to a certain extent. By contrast, because the source distribution before the ART stage was concentrated in the small $r^{*}$ region, the strength of the correlation function was higher than that observed in the experimental measurements. Considering only quantum statistical effects, the correlation function for two identical particles is given in Ref. [71] by $C\left(k^{*}\right)=1\pm \exp \left(-k^{*2}{R}^2\right)$, where the ±sign corresponds to the Bose–Einstein and Fermi–Dirac statistics. In this formula, the maximum value of the correlation function $C\left(k^{*}\right)$ equals 2 at $k^{*}=0$, and decreases to 1 as $k^{*}$ increases. However, because of the influence of long-range Coulomb interactions, the correlation function is significantly distorted for $k^{*}<50$ MeV/c. For a large $k^{*}$, the correlation function approaches unity, and the rate of decrease is primarily determined by the shape of the source distribution. If the source is concentrated in the small $r^{*}$ region, the correlation function decreases more slowly with $k^{*}$. Conversely, if the source is more widely distributed, the larger $r^{*}$ regions, where the interactions are weaker, contribute more, leading to a larger dilution of the signal. It can also be observed that deviations in $C\left(k^{*}\right)$ between the three initial partonic conditions occur only at high $k^{*}$ before ART, and are negligible at low $k^{*}$ and after ART. This indicates that unlike azimuthal observables such as v₂ calculated in Refs. [44-46], $C\left(k^{*}\right)$ are less sensitive to initial geometrical conditions.

Impact of parton scattering cross section on the source function

In addition to the initial position of the parton, the parton scattering cross section σρ, which reflects the probability of two partons interacting, also affects the source and final correlation functions, as previously discussed in Ref. [38]. In Fig. 7, the source function for the “3 quarks” scenario is presented for σρ = 1.5 mb and 10 mb. It was observed that σρ significantly affected the source function before the ART stage. The results were similar for the other two initial partonic distributions. As σρ increases, the probability of two-parton interactions increases, leading to a more dispersed parton and hadron distribution and, consequently, a wider source function. However, the results after the ART are almost unaffected by σρ, indicating that the hadronic process plays a decisive role. Most of the initial effects were smeared or masked by hadronic scattering and resonance decay, which are discussed in the following section.

Fig. 7Full-screen View

(Color online) Source function for two-parton scattering cross-sections, σρ = 1.5 mb and 10 mb, before and after the ART stage in the “3 quarks” scenario

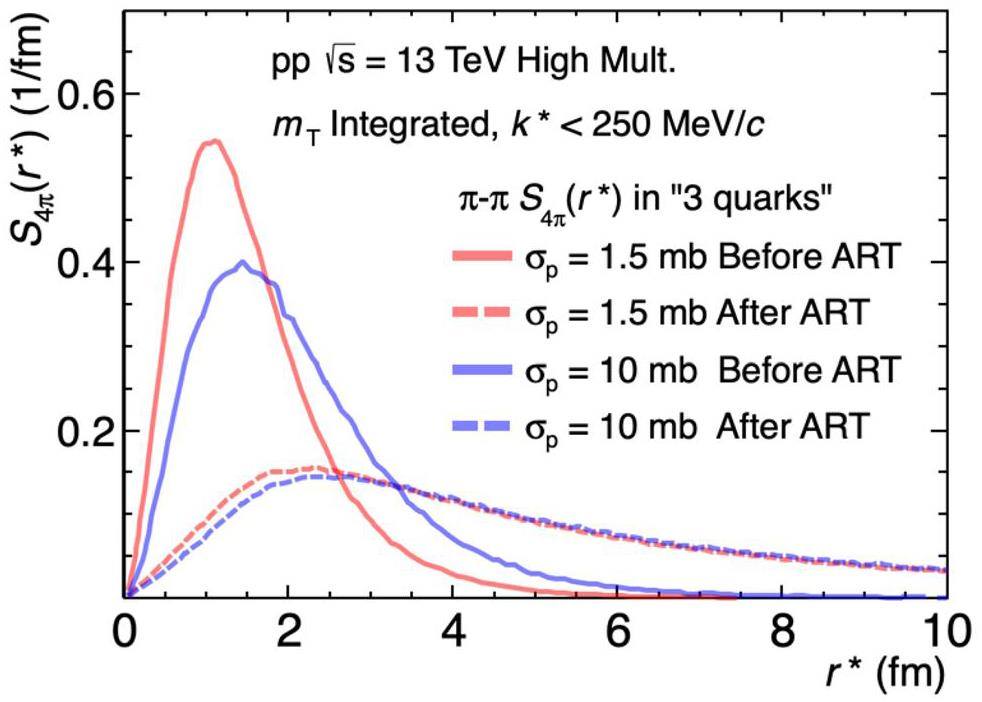
Impact of resonance and hadronic scattering on the source function

The hadronic interaction in AMPT and ART is dominated by two mechanisms: short-lived strongly decaying resonances and hadronic rescattering, including both elastic and inelastic processes. In Fig. 8 compared to the case where rescattering is turned off, the r^* distribution is wider when rescattering is on for all three initial conditions. This agrees with the expectation that the generated hadrons undergo adequate hadronic scattering, causing the entire system to expand outward. The long tail persists even when rescattering is off, suggesting a contribution from resonance decay.

Fig. 8Full-screen View

(Color online) Source function, with and without hadronic rescattering, after the ART stage for three initial partonic distributions

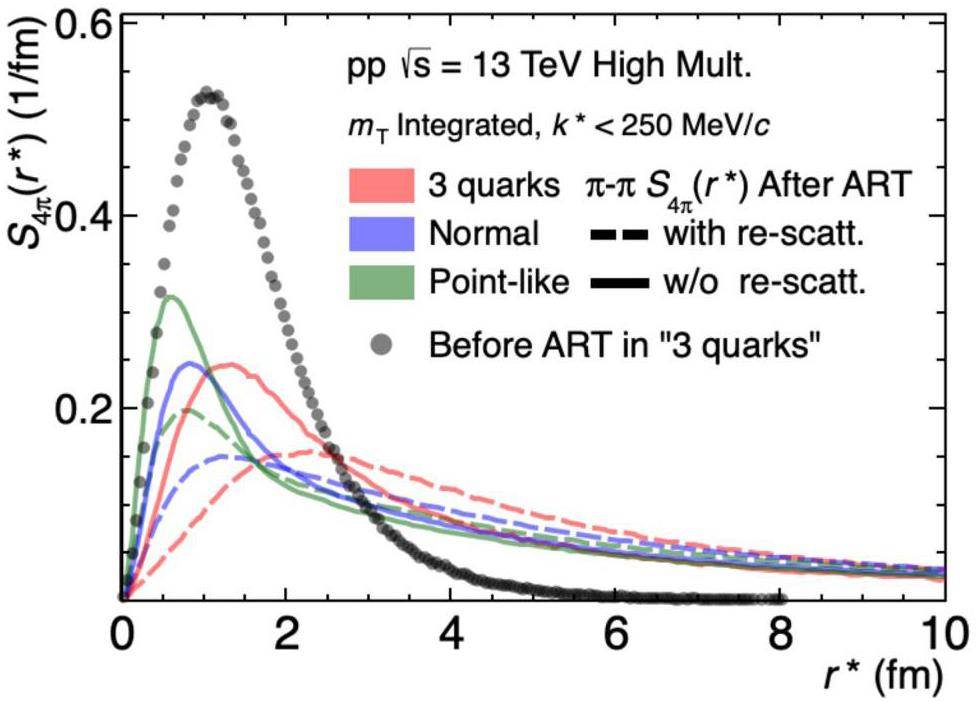
As mentioned in Sect. 2, the source function has two main components: primordial particles produced in collisions, which are well described by a Gaussian distribution with width $R_{\text{core}}$ (the core part), and a non-Gaussian contribution, represented by an exponential tail, mainly arising from short-lived resonances. A previous study showed that the Statistical Hadronization Model (SHM) [23] combined with EPOS [28] can accurately reproduce the tail part measured in ALICE [17, 18]. Using this approach, the core of the source was separated from the “resonance halo”.

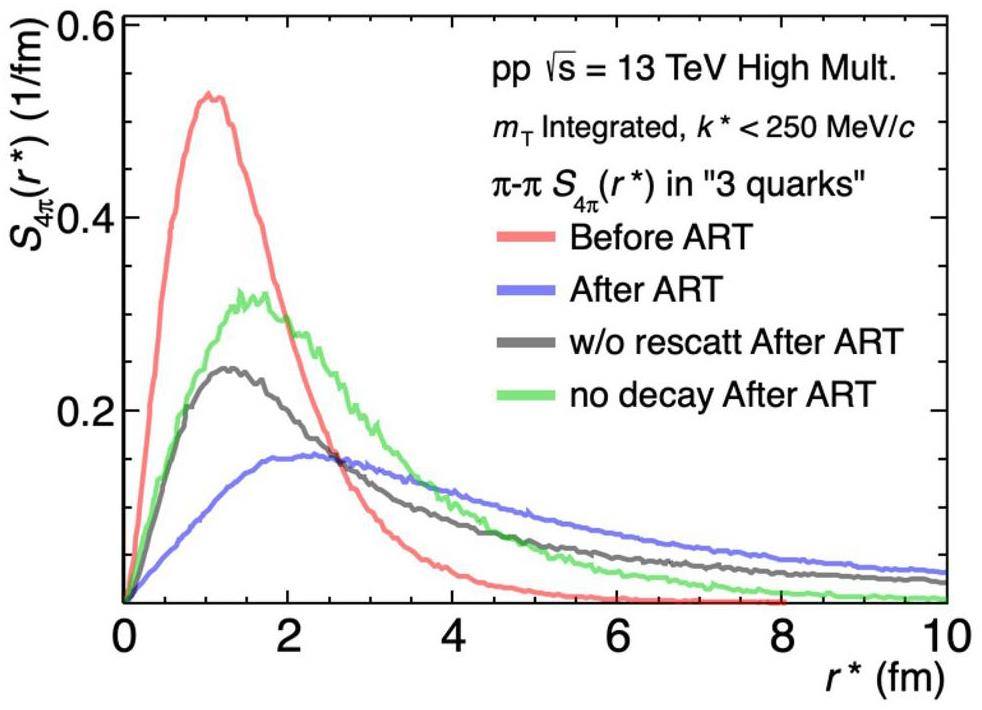
In the SHM calculation, only the decay products of short-lived resonances that contributed at least 1% were considered. As shown in Tab. 1, 28% of the charged pions are primordial, whereas 72% originate from resonance. However, in AMPT, several decay channels are not included, leading to a different fraction compared to the SHM calculation. There are ongoing efforts to incorporate production and annihilation channels into the ART stage [72], and a more thorough description of the resonances remains to be explored. Despite the differences in the resonance components and fractions, the qualitative impact of FSIs on the source is shown in Fig. 9. Four scenarios were investigated: before ART, after ART, after ART without the rescattering process, and after ART without resonance decay but with hadronic rescattering. The total ART contribution (blue) can be decomposed into the resonance (black) and hadronic rescattering (green) components. When no resonances contribute to the pions (green), the tail of the relative source function is significantly shorter than that of the gray function, which extends up to 30 fm.

Fig. 9Full-screen View

(Color online) Source functions at four scenarios in the “3 quarks” AMPT. The black and green lines represent the results after ART, with the black line indicating no hadronic rescattering but including resonance decay, and the green line indicating no resonance decay but including hadronic rescattering. See the text for details

Final source function and -scaling

In principle, the standard method for subtracting the resonance contribution from the total source function and extracting R_core follows Eq. (4) in Ref. [18], which employs Gaussian fitting of $S_{\text{total}}\left(r^{*}\right)$ to decompose the primordial and resonance components. However, the applicability of this approach to the AMPT framework remains to be determined.

In the present study, we employed an alternative method. A schematic representation of the space-time dynamics is shown in Fig 2. Collisions with a given initial distribution (panel a) first proceed through the ZPC stage (green dashed circles). After the coalescence process, hadrons are formed (blue dashed circles), representing the stage before ART. To understand the core source function, the default resonance decays in the ART are fully turned off, and their contributions are excluded, matching the original definition of the core source and scenario described in Ref. [43]. Subsequently, the emission time parameter τ is introduced. The generated hadrons are forced to travel along their original momentum directions for τ fm/c without any hadronic interactions, resulting in an increase in the core source radii by $\overrightarrow{\beta }\tau$ fm ($\overrightarrow{\beta }$ is the particle velocity) in the spatial coordinates (panel b). For comparison, the default ART process, including hadronic interactions (red dashed circle), was also studied with a possible boost, where τ can be zero (panel c) or nonzero (panel d).

Figure 10 shows the r^* distribution (dots) and fitting results using Gaussians (lines) in the k_T interval of 0.15–0.3 GeV/c. The emission time parameter τ=1.5 fm/c was computed using the weighted abundances and lifetimes of the resonances considered in Ref. [17]. As expected, the average radius after ART (red) was larger than that before ART (blue). The fittings worked approximately despite minor inaccuracies. Notably, the results after ART were highly compatible with the ALICE results [17], indicating the validity of the model.

Fig. 10Full-screen View

(Color online) Fitting results for the r^* distribution in the $k_{\text{T}}\in [\mathrm{0.15,0.3}]$. The blue and red markers represent results before and after the ART stage, respectively, with τ = 1.5 fm/c. The shadow band represents the source distribution extracted by ALICE [17]

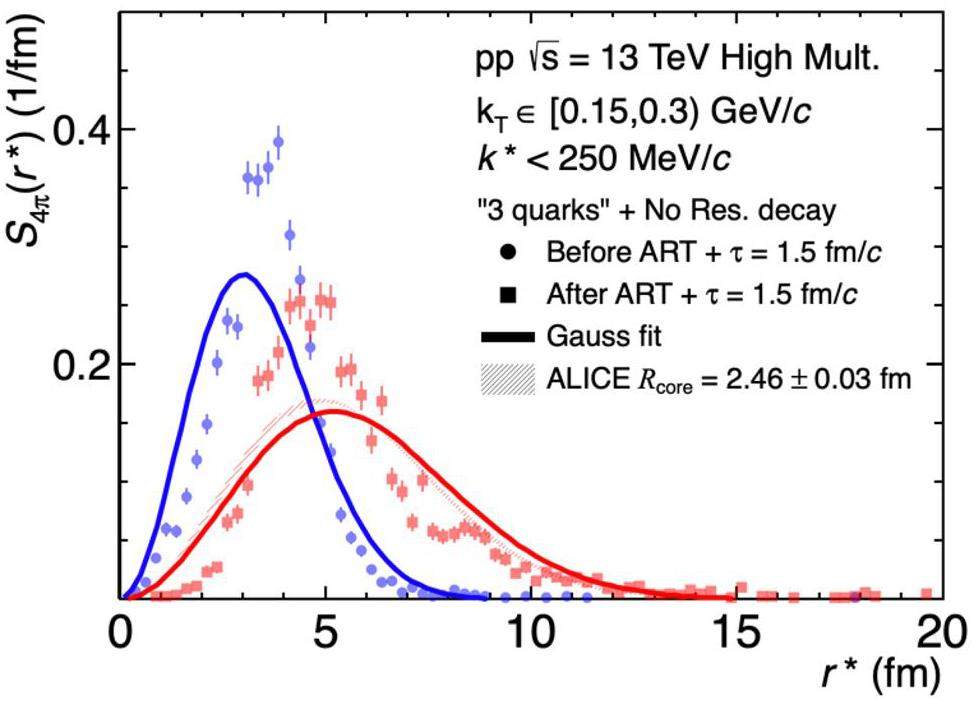
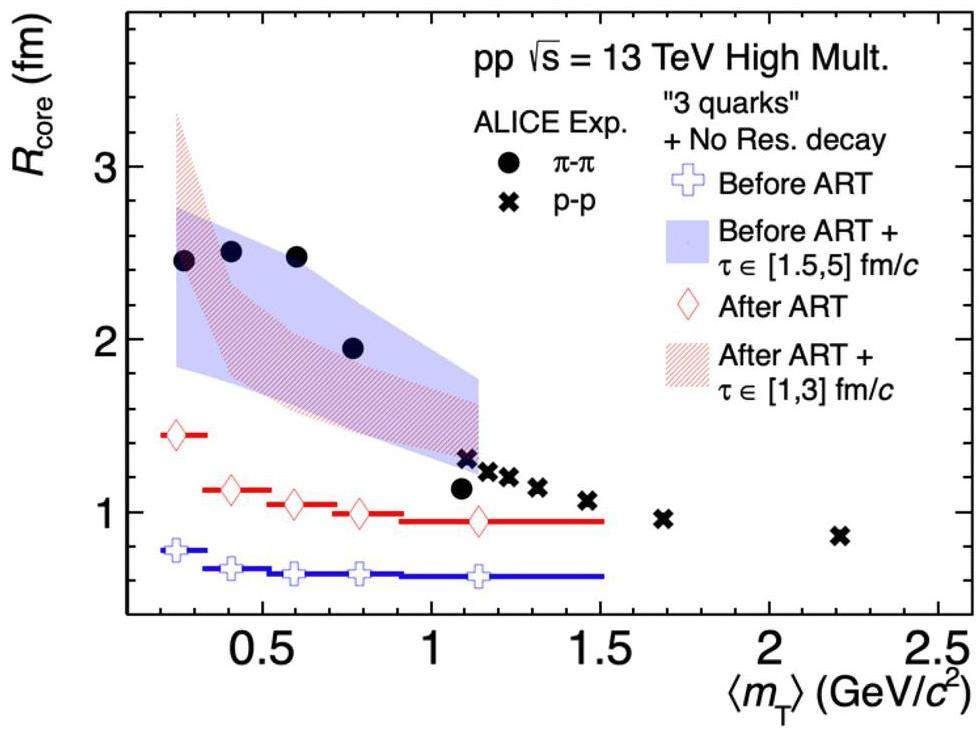
Based on the fitting results, the R_core values in each k_T interval are extracted for four different scenarios: (i) before ART without further boost, (ii) before ART with a boost of $\tau \in [\mathrm{1.5,5}]$ fm/c, (iii) after ART without boost, and (iv) after ART with a boost of $\tau \in [\mathrm{1,3}]$ fm/c. In (ii), the upper limit originates from the general assumption that resonances with $c{\tau }_{\text{res}}>5\text{ fm}$ are long-lived, whereas in (iv), the τ values are deliberately reduced to approximately match the results of (ii). Figure 11 shows the m_T-scaling behavior of the m_T. All four cases are in line with the expectation that the source radii decrease as m_T increases, roughly following the power-law relationship [17]: $R_{\text{core}}=a+b\cdot {\langle m_{\text{T}}\rangle }^c$. This can be understood in terms of collectivity generated during the partonic stage. Compared with the ALICE measurements (solid dots), the original AMPT sources (i) and (iii) without additional boosting were systematically smaller, whereas the modified cases of (ii) and (iv) were in good agreement with the data in the low m_T ranges. Note that the ALICE results also exhibit a plateau at m_T <0.5 GeV/c², which can be interpreted as a limitation on the system size in pp collisions. However, this feature was not observed in AMPT, which instead followed a power-law increasing trend. Generally, AMPT provides a good environment to reveal the mechanisms behind the system size and -scaling; however, further investigation is required to understand the detailed behaviors.

Fig. 11Full-screen View

(Color online) -scaling behavior of R_core in AMPT is shown for four emission scenarios (see the text for details) and is compared with the ALICE results (solid markers)