Semi-Analytical BIXS X-ray Spectrum

A large dataset of BIXS spectra is required to train the ANN, including the X-ray spectra induced by electrons from β decays of tritium in the sample, corresponding tritium depth profiles, and sample thicknesses. In this study, the semi-analytical model developed in Ref. [16] for calculating the X-ray spectrum of tritium-containing sample was employed to generate the dataset. The experimental setup of the BIXS, based on a silicon drift detector (SDD), is shown in Figure 1 and identical to the setup described in detail in [16]. A 5.01 μm-thick aluminum film was used as the β-ray stopping layer, and tritium-containing samples (i.e., zirconium films in this study) were supported by 1 mm-thick molybdenum substrates.

Fig. 1Full-screen View

The geometrical model for the BIXS setup

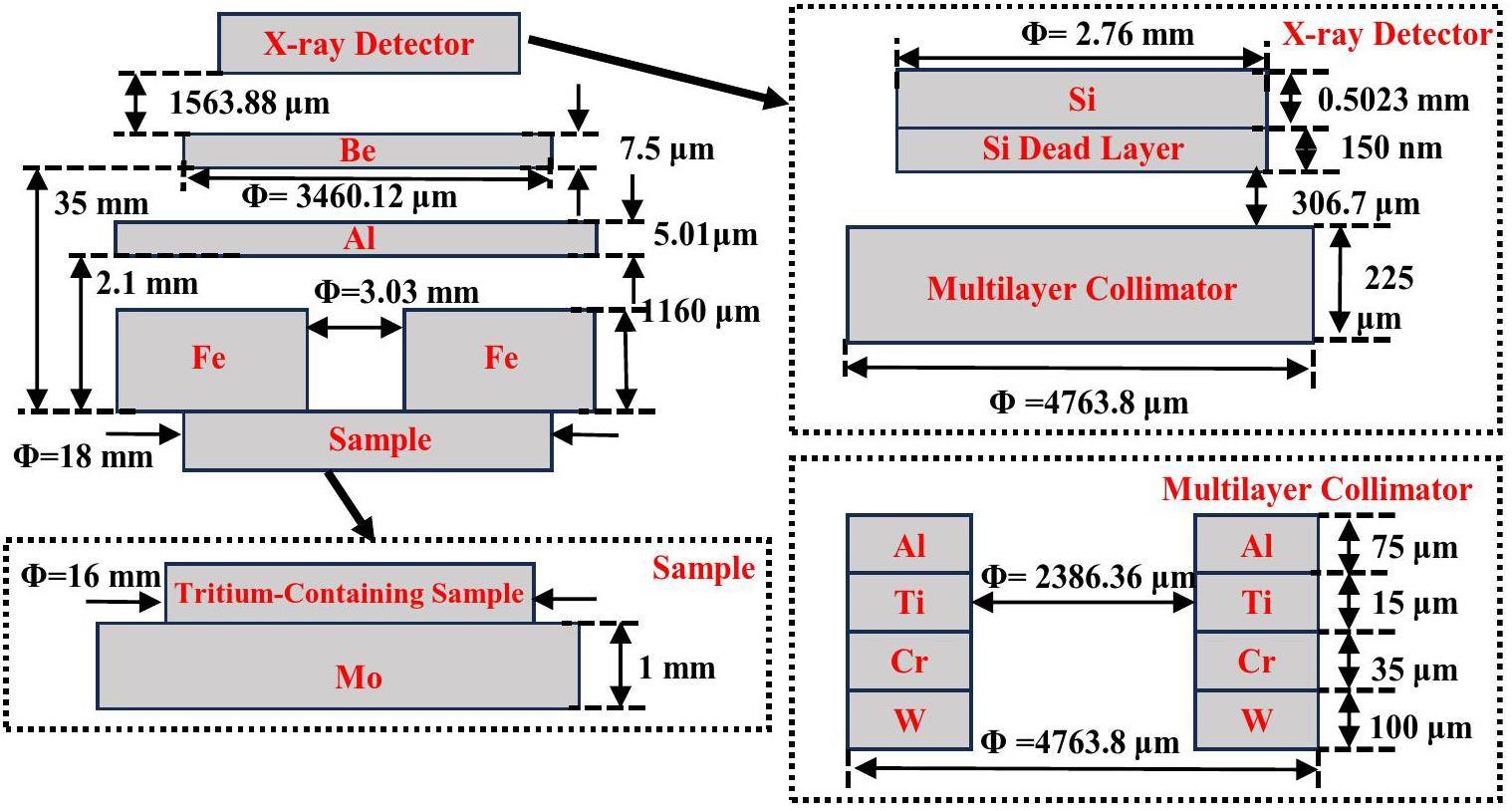
To calculate the X-ray spectrum of the tritium-containing sample using the semi-analytical model, internal bremsstrahlung (IB), external bremsstrahlung (EB), and characteristic X-rays were considered. The detailed calculation process is described in Refs. [16], and a brief description is provided here. The total X-ray fluence, which is the differential in the photon energy k per β electron from tritium decay per solid angle, can be expressed by the following formula [16]: $\begin{array}{c}{N}^{\text{TOT}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)=H\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma }\right)\times \\ (N^{\text{CH}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)+\\ N^{\text{IB}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)+N^{\text{EB}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right))\mathrm{,}\end{array}$ (1) where $N^{\text{CH}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)$, $N^{\text{EB}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)$, and $N^{\text{IB}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)$ represent the corresponding fluences of the characteristic X-rays, EB photons, and IB photons, respectively, and $H\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma }\right)$ is the attenuation of X-rays in the filters (i.e., the Be window and Si dead layer). Z is the atomic number, ${\widehat{\text{Ω}}}_{\gamma }$ is the emission direction of the photons. The depth distributions of characteristic X-rays in materials were simulated using the modified MC PENEPMA code [41] and used to calculate the $N^{\text{CH}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)$. The electron distributions in materials, including both energy and angular distributions, were simulated with the modified MC PENELOPE code [13] and used to calculate the $N^{\text{EB}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)$, which can be determined as follows [16]: $\begin{array}{ll}{N}^{\text{EB}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)\hfill & \hfill \\ \hfill & =n{\displaystyle {\int }_0^{Dz}}\text{d}s{\displaystyle {\int }_k^{E_{\text{max}}}}\text{d}E{\displaystyle \int }\hfill \\ \hfill & \text{d}{\widehat{\text{Ω}}}_{\text{e}}{N}^{\text{e}}\left(Dz\mathrm{,}E\mathrm{,}{\widehat{\text{Ω}}}_{\text{e}};Z\right)\hfill \\ \hfill & \times \frac{{\text{d}}^2{\sigma }_{\text{br}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma }\cdot {\widehat{\text{Ω}}}_{\text{e}};Z\mathrm{,}E\right)}{\text{d}k\text{d}{\widehat{\text{Ω}}}_{\gamma }}f\left(Dz\mathrm{,}k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)\mathrm{,}\hfill \end{array}$ (2) where E_max is the maximum kinetic energy of electrons from tritium β-decay, $N^{\text{e}}\left(Dz\mathrm{,}E\mathrm{,}{\widehat{\text{Ω}}}_{\text{e}};Z\right)$ is the electron distributions in materials with energy E moving in the direction ${\widehat{\text{Ω}}}_e$ at depth Dz generated by an electron from tritium β-decay, n is the atomic or molecular density with a unit of number of atoms or molecules per cubic centimeter, $f\left(Dz\mathrm{,}k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)$ is the self-absorption of the target, $\frac{{\text{d}}^2{\sigma }_{\text{br}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma }\cdot {\widehat{\text{Ω}}}_e;Z\mathrm{,}E\right)}{\text{d}k\text{d}{\widehat{\text{Ω}}}_{\gamma }}$ is the double differential bremsstrahlung cross sections [42, 43]: $\begin{array}{l}\frac{{\text{d}}^2{\sigma }_{\text{br}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma }\cdot {\widehat{\text{Ω}}}_{\text{e}};Z\mathrm{,}E\right)}{\text{d}k\text{d}{\widehat{\text{Ω}}}_{\gamma }}=\chi \frac{Z^2}{{\beta }_1^2}\frac{1}{k}S\\ =\chi \frac{Z^2}{\left(1-\frac{1}{{\left(1+\frac{E}{m_{\text{e}}{c}^2}\right)}^2}\right)}\frac{1}{k}S\mathrm{,}\end{array}$ (3) where $m_{\text{e}}{c}^2$ is the electron rest energy, S is the shape function of the bremsstrahlung angular distribution, the Kissel-Quarles-Pratt (KQP) [44] theory was used in this work, and χ is the scaled cross-section differential in k. The other symbols have the same definitions as those in Eqs. 1 and 2. The Knipp-Uhlenbeck-Bloch (KUB) model proposed by Knipp and Uhlenbeck [45] and Bloch [46] was used to calculate $N^{\text{IB}}\left(k\mathrm{,}{\widehat{\text{Ω}}}_{\gamma };Z\right)$. Each X-ray spectrum consists of 200 energy bins at interval of 0.093 keV.

Construction of BP Network Dataset

A total of 420 tritium-containing zirconium samples of different thicknesses and tritium-to-zirconium ratios were used to generate a dataset of tritium β-decay X-ray spectra. The zirconium thicknesses before absorbing tritium ranged between 3 μm and 5 μm, with the assumption that tritium was uniformly distributed throughout the sample. The zirconium thickness was divided into 21 groups with an interval of 0.1 μm, whereas the tritium-to-zirconium ratio ranged from 0.1 to 2, divided into 20 groups with an interval of 0.1. The time required by the semi-analytical method to obtain a tritium β-decay X-ray spectrum for each combination of sample thickness and tritium-to-zirconium ratio was approximately 1 h [16]. Thus, the total time required to obtain 420 X-ray spectra is approximately 19 d [16]. From Ref. [16], it is noted that the semi-analytical X-ray spectra were expressed in unit of “counts per keV per β decay”. To ensure consistency between the semi-analytical and experimental spectra, the unit of the semi-analytical spectra was converted to the unit of the experimental spectra, that is, counts per keV per second, based on the number of tritium atom decays, N_T, within a unit time t: $\begin{array}{l}{N}_{\text{T}}=N_{\text{Zr}}\times R\times \left(1-\exp \left(-\frac{\ln 2\times t}{T}\right)\right)\mathrm{,}\hfill \end{array}$ (4) where N_Zr is the number of zirconium atoms, R is the tritium-to-zirconium ratio, and T is the half-life of tritium (approximately 12.25 years.) The semi-analytical X-ray spectra were convoluted using the Gaussian response function of the SDD [47]. The full width at half maximum (FWHM) of the SDD in the BIXS experimental setup was 185 eV at 5.89 keV, as measured using a standard Fe-55 radioactive source: $\begin{array}{l}FWHM=\sqrt{8WFE\ln 2+\text{Δ}{E}_{\text{elec}}^2}=2\sqrt{2\ln 2}\sigma \mathrm{,}\hfill \end{array}$ (5) where W is the average energy for electron-hole creation (3.62 eV), F is Fano factor (0.12), E is the X-ray energy, $\text{Δ}{E}_{\text{elec}}$ is the electronic noise (141.55 eV), and σ is the standard deviation of the Gaussian distribution. Figure 2 shows the semi-analytical tritium β decay X-ray spectra before and after convolution for a sample with a zirconium thickness of 3 μm and a tritium-to-zirconium ratio of 0.1.

Fig. 2Full-screen View

Tritium semi-analytical β-decay X-ray spectrum before and after convolution for a sample with a zirconium thickness of 3 μm and a tritium-to-zirconium ratio of 0.1. Bremsstrahlung and Al K, Zr L, and Fe K represent the bremsstrahlung plus Al K-shell characteristic X-ray, Zr L-shell characteristic X-ray, and Fe K-shell characteristic X-ray, respectively

Construction of BP Network

Figure 3 illustrates the structure of a back propagation (BP) network designed to predict the zirconium thickness and tritium-to-zirconium ratio. The structure consists of three layers: input, hidden, and output layers. The number of hidden layers shown in this figure differs from that of the optimized configuration adopted for our application. Only the energy region of the X-ray spectrum between 1 keV and 15 keV was used to train the BP neural network to avoid noise in the low-energy region and poor statistics in the high-energy region of the experimental X-ray spectrum. The input layer consisted of 150 neurons, corresponding to 150 energy bins of the tritium β decay X-ray spectrum in the 1 keV–15 keV range. The output layer contains two neurons that represent the zirconium thickness and tritium-to-zirconium ratio. To enhance the accuracy and computational efficiency of the neural network model, a scaling transformation of the input and output data were performed [26], and the β-decay X-ray spectra were treated as follows: $\begin{array}{l}C1(k)=\frac{{{\displaystyle \log }}_{10}\left(C(k)\right)}{10}\mathrm{,}\hfill \end{array}$ (6) where $C(k)$ and $C1(k)$ are the photon counts with energy k before and after processing, respectively. The thickness of zirconium was divided by 10 and the tritium-to-zirconium ratio was normalized as follows: $\begin{array}{l}{N}_{\text{in}}=\frac{N_{\text{i}}-N_{\text{min}}}{N_{\text{max}}-N_{\text{min}}}\mathrm{,}\hfill \end{array}$ (7) where N_i and N_in are the actual and scaled tritium-to-zirconium ratios, respectively. N_min is the minimum tritium-to-zirconium ratio (e.g., 0.1) and N_max is the maximum tritium-to-zirconium ratio (e.g., 2.0).

Fig. 3Full-screen View

The structure of BP network used to predict the zirconium thickness and tritium-to-zirconium ratio

The network was implemented and trained in Python 3.7 using the PyTorch library [48], with the error back-propagation algorithm employed for training. The mean squared error (MSE) [49] was used as the loss function, which was commonly used in regression tasks. It is calculated by summing the squared differences between the predicted and true values. $\begin{array}{l}MSE=\frac{1}{m}{\displaystyle \sum _{i=1}^m}{\left(y_i-{\widehat{y}}_i\right)}^2\mathrm{,}\hfill \end{array}$ (8) where yi and ${\widehat{y}}_i$ represent the true and predicted values, respectively, and m is the number of yi. With the same learning rate, the AdamW optimizer [50] consistently demonstrated faster convergence and smaller test errors. Currently, AdamW has been widely adopted and selected as the optimization algorithm for the BIXS neural network structure. The training process was repeated five times, resulting in five individual ANNs to evaluate the precision in terms of reproducibility. This yielded the MSE values for the two ANN outputs (tritium-to-zirconium ratio and zirconium thickness). The training and testing datasets were randomly split in a ratio of 0.8:0.2. The training process was performed iteratively to optimize network parameters, such as weights and biases, allowing for accurate pattern recognition and feature extraction. An iteration is referred to as an “epoch”, indicating that the neural network processes the entire training dataset once. The number of epochs was set to 10,000.

Optimization of BP Network Structure

To select the optimal network structure, the numbers of hidden layers and neurons were optimized. To achieve nonlinear transformations, the ReLU activation function [51] was used for all the hidden layers. Table 1 shows the MSEs as functions of the numbers of hidden layers and neurons. From the results in Table 1, it can be observed that when the number of neurons exceeds 10, the MSEs tend to decrease as the number of hidden layers and neurons increases. When the number of hidden layers was between 2 and 10, and the number of neurons was between 30 and 150, the MSEs of the neural network for predicting the zirconium target thickness and tritium-to-zirconium ratio became small, ranging from approximately 5.99E-6 to 7.75E-5.

To simplify the neural-network structure while maintaining a low MSE, we selected a relatively simple five-layer neural network with three hidden layers, each containing 150 neurons. The total MSEs for the training and testing datasets were 1.02×10^-5 and 1.00×10^-5, respectively. The mean relative errors (MREs) [52] for the zirconium thickness and tritium-to-zirconium ratio in the training dataset of the neural network were 0.56% and 0.42%, respectively, whereas those in the test dataset, the MREs were 0.59% and 0.38%, respectively. The MRE [52] was calculated as follows: $\begin{array}{l}MRE=\frac{1}{m}{\displaystyle \sum _{i=1}^m}\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|\mathrm{,}\hfill \end{array}$ (9) where the definitions of yi, ${\widehat{y}}_i$ and m are identical to those in 8.

Optimization of Activation Functions

In this study, the activation functions used in the hidden layers were optimized. To simplify the optimization process, the same activation function (i.e., ReLU [51], sigmoid [53], or tanh [54]) was applied to all the hidden layers. Table 2 shows the MSEs of the BP network for different activation functions in the hidden layers. It can be observed that the MSEs vary with the choice of activation function. We selected the activation function that resulted in the best MSE, i.e., the ReLU function. The MSEs for the training and test datasets are 1.02×10^-5 and 1.00×10^-5, respectively.

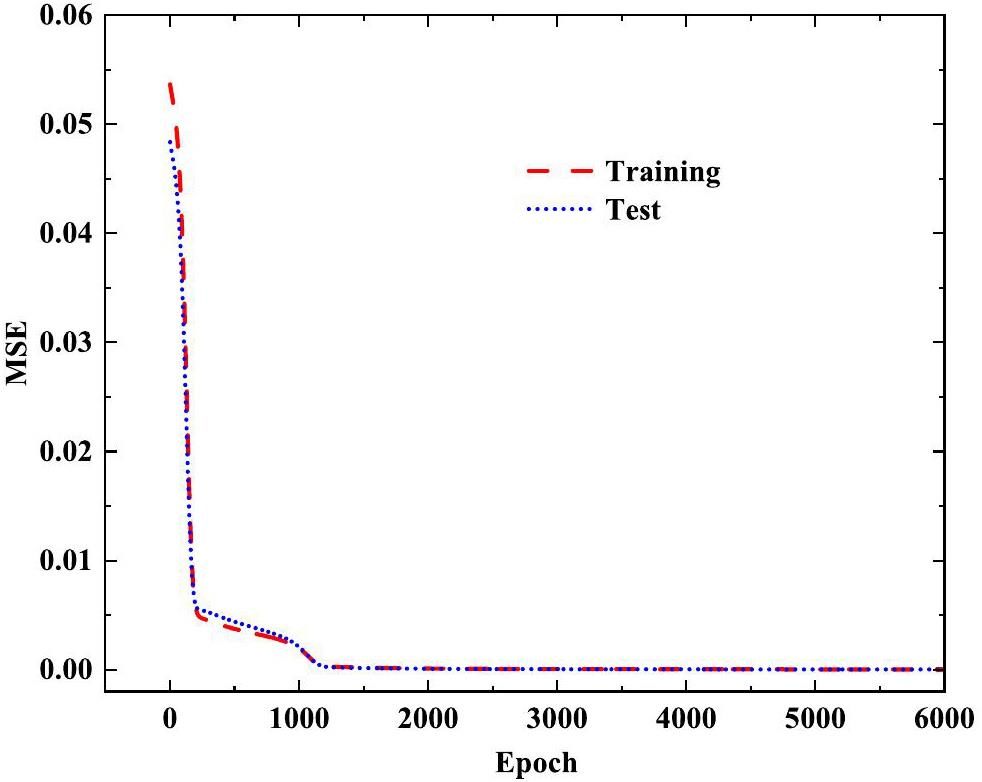
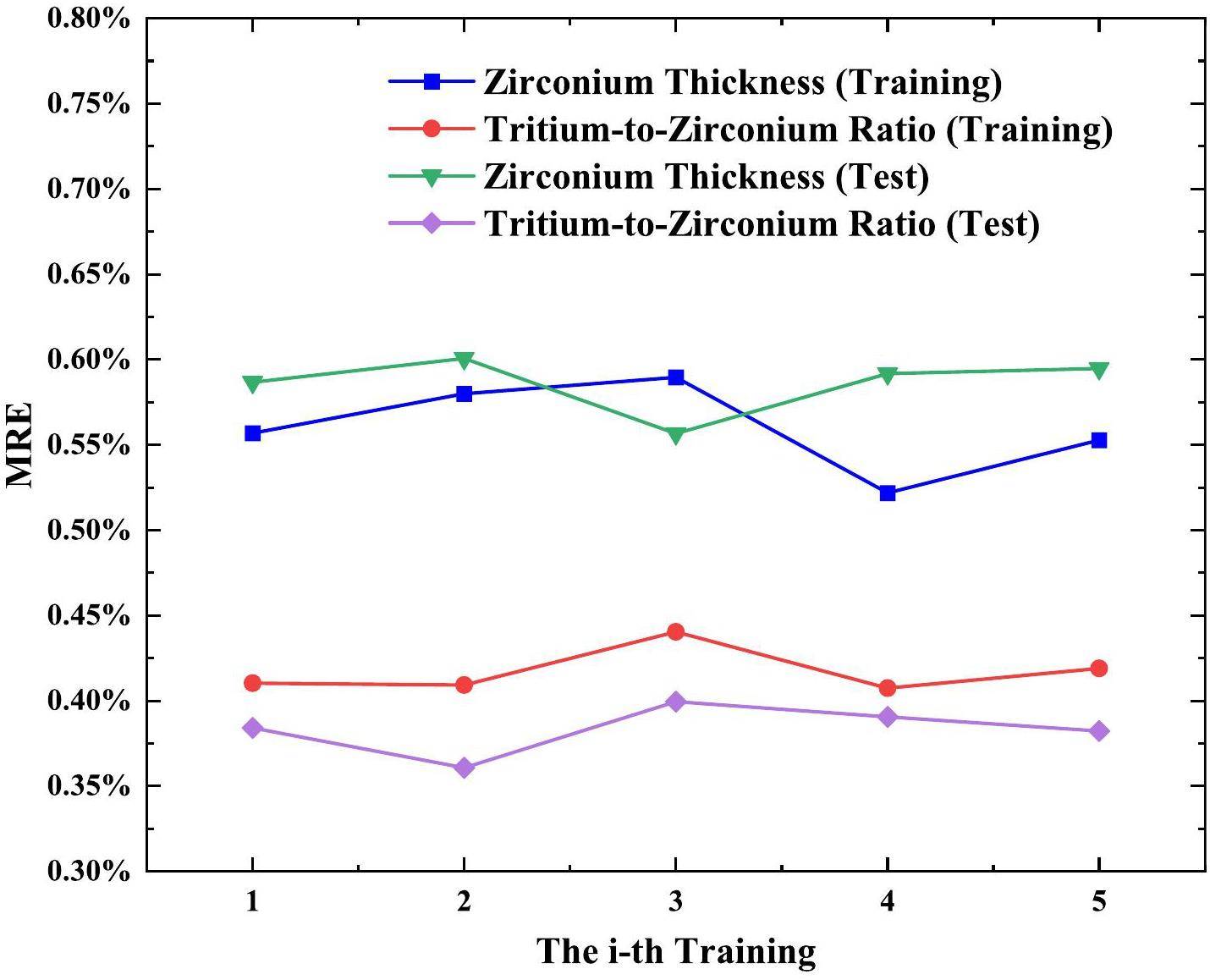
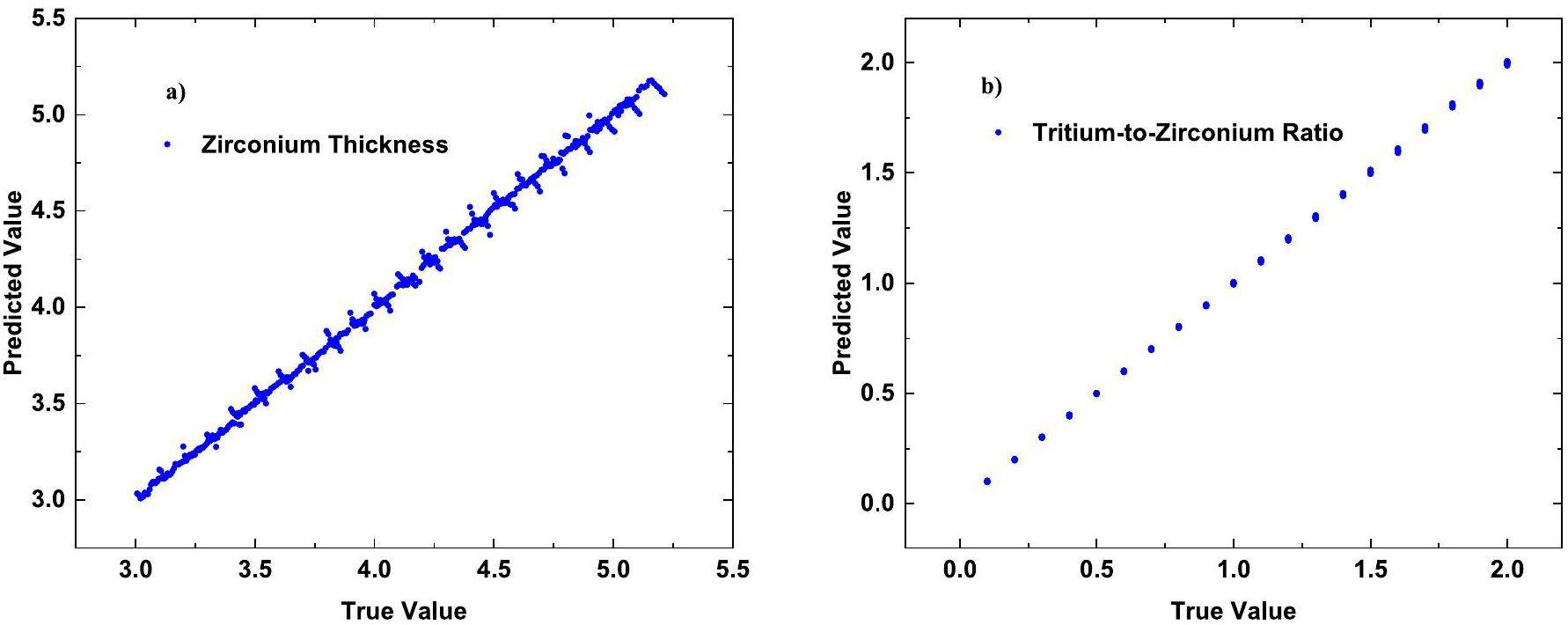
Figure 4 presents the MSEs of the BP network for both the training and test datasets as a function of the number of epochs. It can be observed that the BIXS neural network converged rapidly, with sufficient convergence achieved within 2000 iterations. Moreover, the MSEs for both datasets exhibited minimal divergence as the number of epochs increased, indicating that overfitting did not occur during training. Figure 5 presents the MREs of the training dataset and test dataset for each training period. For the tritium-to-zirconium ratio and zirconium thickness, the MRE differences obtained from each training were considerably small, indicating the good stability of the system. Figure 6 shows a comparison between the true and predicted values for the zirconium thickness and tritium-to-zirconium ratio for all 420 sets of data. Excellent predictions were obtained with the true and predicted values in close agreement. The MREs for the 420 datasets used to train and test the BP network are listed in Table 3.

Fig. 4Full-screen View

The MSEs of the BP network for both the training and test datasets as a function of the number of epochs

Fig. 5Full-screen View

The MREs of the training dataset and the test dataset in each repeated training

Fig. 6Full-screen View

Comparison between the true and predicted values of a) zirconium thickness and b) tritium-to-zirconium ratio for all 420 sets of data

Effect of Statistical Uncertainty

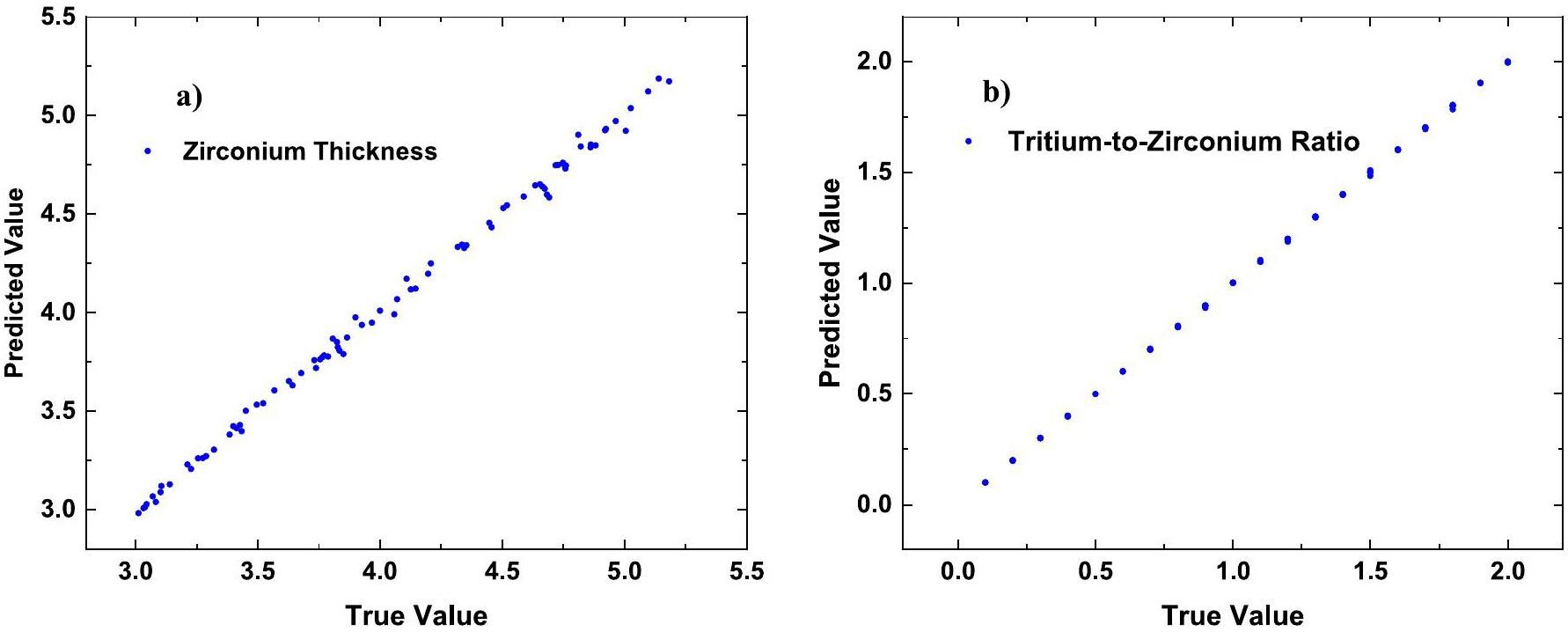
The experimental BIXS X-ray spectrum may exhibit varying degrees of statistical uncertainty, which can affect the prediction accuracy. To assess the effect of statistical uncertainty, the uncertainties ranging from 0.5% to 3% were randomly with Gaussian distribution added to the 84 sets of test data of X-ray spectra, which were randomly selected from the 420 data, as described in the section “C. Construction of BP network”. Figure 7 compares the true and predicted values for the 84 sets of test data without statistical uncertainty. It can be observed that the true and predicted results are in close agreement. Table 4 lists the MREs for 84 sets of test data under different levels of uncertainty. The results demonstrate that uncertainty can affect the accuracy of neural network predictions to some extent. Generally, the greater the uncertainty, the larger the relative error in the prediction result. When the statistical uncertainty of the test set is 3%, the neural network maintains higher prediction accuracy for both zirconium thickness and the tritium-to-zirconium ratio, with average relative errors of 2.14% and 1.98%, respectively.

Fig. 7Full-screen View

Comparison between the true and predicted values of a) zirconium thickness and b) tritium-to-zirconium ratio for the 84 sets of test data without statistical uncertainty

Generalizability of BP Network

Additional 22 sets of data, with the zirconium thicknesses outside the BP network training range from 3 μm to 5 μm, were used to preliminarily test the generalization ability of the BP neural network (i.e., the capability of extrapolation). The zirconium thicknesses and tritium-to-zirconium ratios for the 22 datasets are listed in Table 5, and the MREs of the predicted results are listed in Table 6. From Table 6, it can be observed that the BP neural network demonstrates good prediction capability, even for the dataset outside the training range. For the 22 sets of data, the MREs of the predicted zirconium thicknesses and tritium-to-zirconium ratios are 7.61% and 9.33%, respectively. For a dataset outside the training parameter range, the prediction accuracy of the neural network decreases, which is consistent with the conclusion in Ref. [27].

Application of BIXS BP Neural Network

3.5.1

Sample

Two tritium-containing samples were prepared, labeled No. 26 and No. 42, in which zirconium films were deposited onto smooth molybdenum substrates (approximately 1 mm thick) using the electron beam evaporation technique. The processes for preparing the tritium-containing samples are the same as those described in Refs.[15, 55].

The thicknesses of the zirconium films and the tritium depth profiles of samples 26 and 42 were measured using the elastic backscattering spectrometry (EBS) method. The EBS experiment was conducted using a 3 MV tandetron accelerator at Sichuan University [56]. The incident proton energy was 3 MeV with a current intensity of approximately 2 nA. The proton beams impacted the sample surface vertically, and a Si detector (ORTEC U-012-050-100) was placed at 165° with respect to the proton beam direction. The experimental details are presented in Refs.[15].

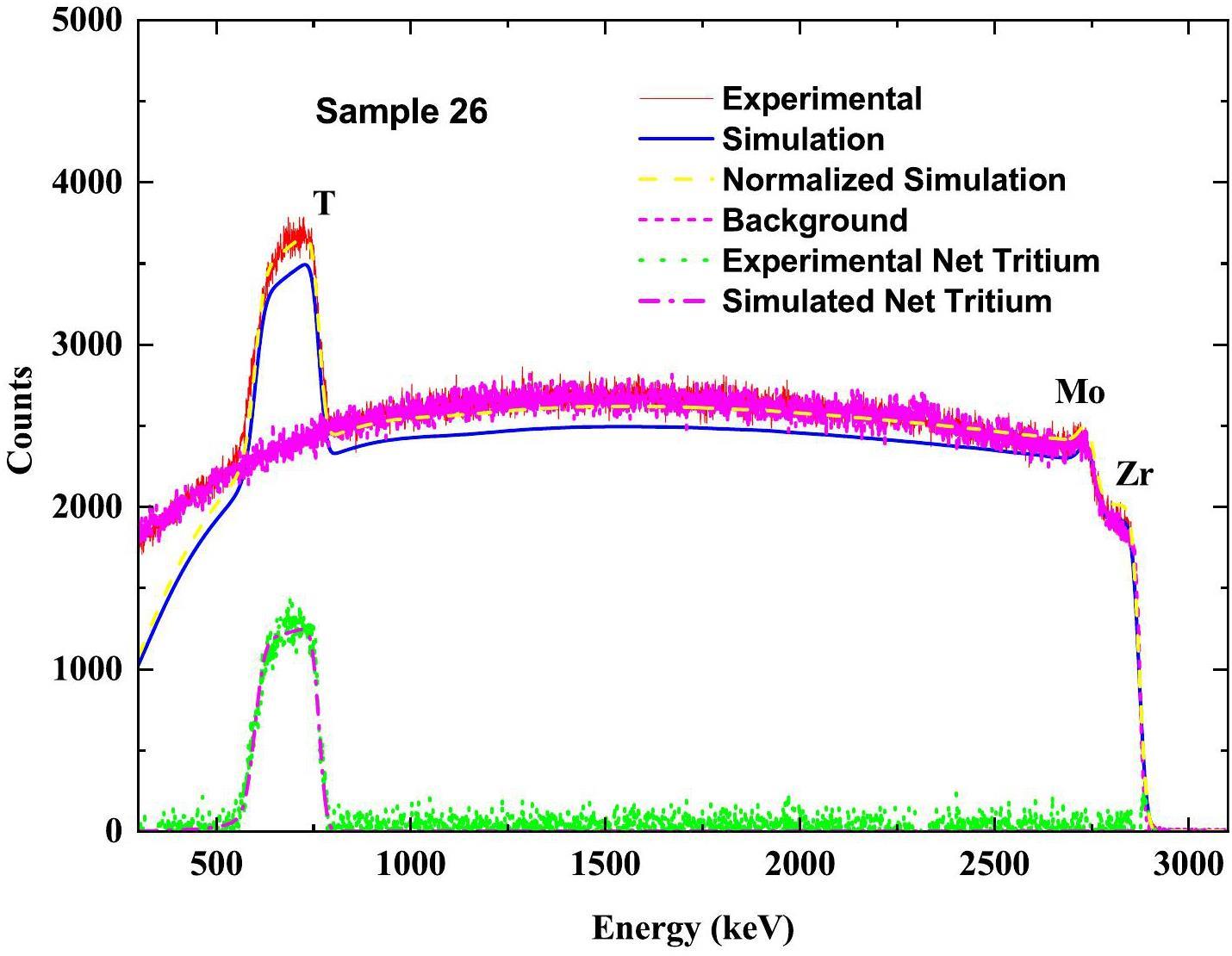
The experimental spectra of the EBS were analyzed using the SIMNRA program [57] with the same processes as in Refs.[14, 15] The parameters used in SIMNRA were consistent with those in Ref. [15]. The uncertainties for the tritium contents and zirconium thicknesses obtained using the EBS were approximately 11.7% and 5%, respectively, mainly arising from uncertainties in the proton elastic scattering cross-section data, stopping power, and statistical uncertainties [14, 15]. For example, Figure 8 shows the EBS experimental spectrum and SIMNRA simulation for sample 26, where the tritium distribution in the SIMNRA simulation was assumed to be uniform. The background spectrum was obtained by measuring a hydrogen-containing Zr film sample with a Mo substrate, whose geometric dimensions and hydrogen isotope-zirconium ratio were approximately the same as those of samples 26 and 42; the EBS experimental conditions were the same. The experimental net tritium spectrum was obtained by deducting the background spectrum from the experimental spectrum of the tritium-containing samples. The measured results are summarized in Table 7. The EBS results indicate that the tritium distributions for samples 26 and 42 were uniform.

Fig. 8Full-screen View

The experimental spectrum of EBS and the SIMNRA simulation for sample 26. The normalized simulation spectrum represents the simulation spectrum that was normalized to the experimental tritium counts (see the text for other details)

Table 7Full-screen View

Results of zirconium thickness and tritium-to-zirconium ratio obtained by EBS and BP-Network

Samples	Parameters	EBS	BP-Network
26	Zirconium thickness (μm)	1.64	1.60
	Tritium-to-Zirconium ratio	1.87	1.83
42	Zirconium thickness (μm)	1.72	1.63
	Tritium-to-Zirconium ratio	1.87	1.89

Show more

3.5.2

Predictions of BP Network

The experimental BIXS spectra of samples 26 and 42 were obtained using the same experimental setup as in Refs.[14, 15] and corrected for the signal pile-up effect by using Monte Carlo method [15], as shown in Figure 9. Corrections for the pile-up effect were less than 1%. The trained BP neural network was used to analyze the experimental BIXS spectra after correcting for the intrinsic detection efficiency of the SDD. The predicted values of the zirconium thicknesses and tritium-to-zirconium ratios are listed in Table 7. The predicted tritium-to-zirconium ratios have been converted to the tritium-to-zirconium ratios on the day of the EBS experiment.

Fig. 9Full-screen View

The experimental BIXS spectra for samples 26 and 42, which were corrected for the signal pile-up effect by employing Monte Carlo method

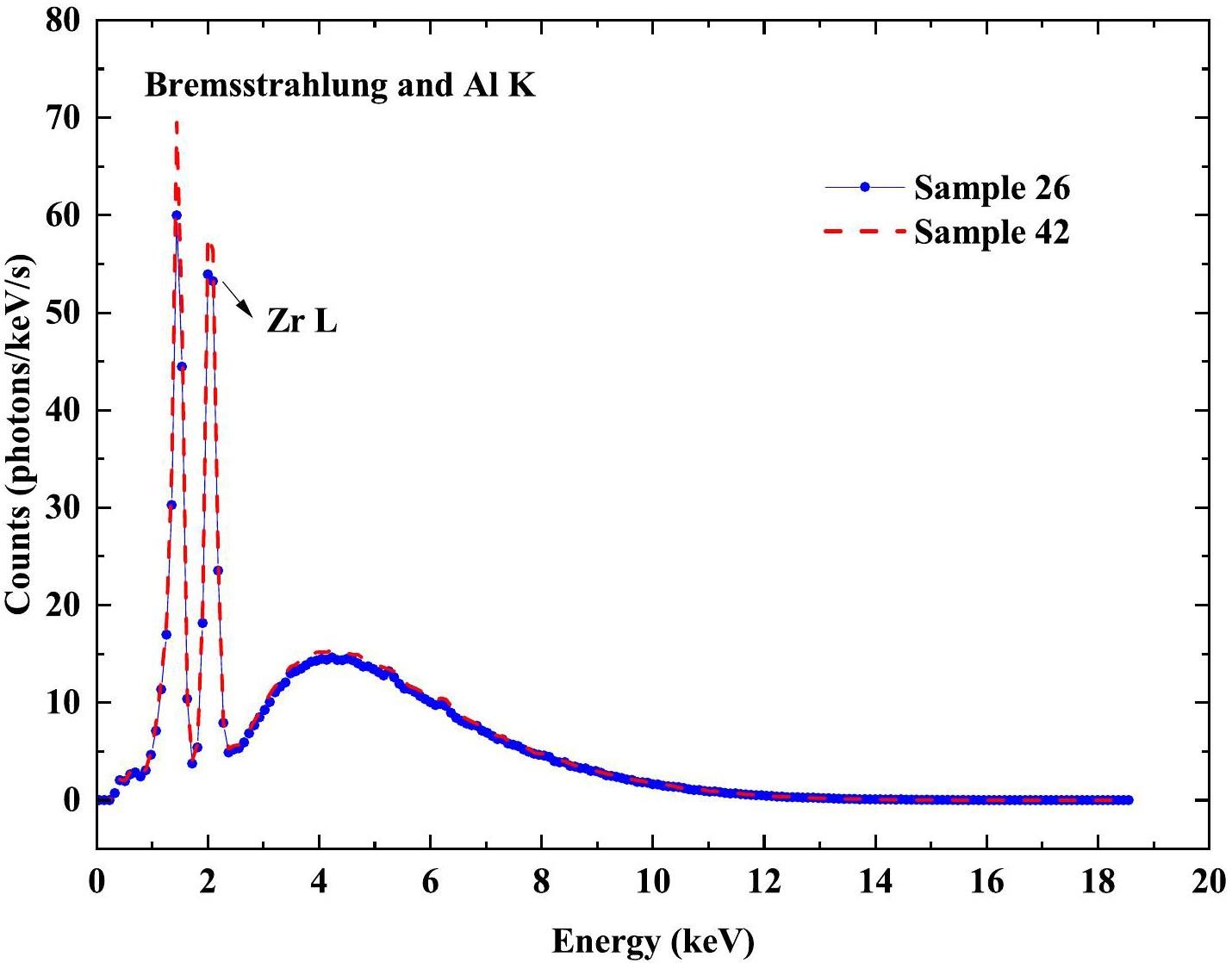
For sample 26, the predicted zirconium thickness is 1.60 μm, which deviates by 2.43% from the EBS result, whereas for sample 42, the predicted zirconium thickness is 1.63 μm, showing a 5.23% difference compared to the EBS result. The predicted tritium-to-zirconium ratios for samples 26 and 42 are 1.83 and 1.89, with the relative deviations of 2.14% and 1.07% relative to the EBS results, respectively.

Considering that the predicted values from the BP neural network are consistent with the measured results from the EBS within experimental uncertainties, we can conclude that the BP neural network can be used to predict the thicknesses and tritium contents simultaneously with higher accuracy for thin solid tritium-containing samples with substrates and uniform tritium distribution. Previously, we employed the MC BIXS method for tritium analysis, which required prior information about the sample thickness, and its accuracy was affected by the reconstruction algorithm [9, 14, 15, 58, 59]. However, the present BIXS BP neural network approach overcomes the difficulties inherent in traditional regularization BIXS analysis methods.