Production characteristics of light nuclei, hypertritons, and Ω-hypernuclei in Pb+Pb collisions at sNN=5.02 TeV

NUCLEAR PHYSICS AND INTERDISCIPLINARY RESEARCH

Production characteristics of light nuclei, hypertritons, and Ω-hypernuclei in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV

Rui-Qin Wang ，

Xin-Lei Hou，

Yan-Hao Li，

Jun Song，

Feng-Lan Shao

Nuclear Science and Techniques

Vol.36, No.10

Article number 185

Published in print Oct 2025

Available online 18 Jul 2025

DOI：10.1007/s41365-025-01750-z

CSTR：32136.14.NST.2025.10185

10000

This study aims to investigate the production of light nuclei, hypertritons, and Ω-hypernuclei in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV using a modified analytical nucleon coalescence model with hyperons. To this end, the momentum distributions of two bodies coalescing into dibaryon states and of three bodies coalescing into tribaryon states are derived. Available data on coalescence factors B₂ and B₃, transverse momentum spectra, averaged transverse momenta, yield rapidity densities, and yield ratios of the deuteron, antihelium-3, antitriton, and hypertriton measured by the ALICE collaboration are explained. Productions of different species of Ω-hypernuclei H(pΩ^-), H(nΩ^-), and H(pnΩ^-) are predicted. Particularly, the production correlations of different light (hyper-)nuclei are studied, and two groups of interesting observables—the averaged transverse momentum ratios of light (hyper-)nuclei to protons (hyperons) and their corresponding yield ratios—are studied. The averaged transverse momentum ratio group exhibits a reverse hierarchy of the nucleus size, and the yield raito group is sensitive to the nucleus production mechanism as well as the size of the nucleus.

Light nucleus productionHypernucleus productionCoalescence modelRelativistic heavy ion collision

Introduction

In ultra-relativistic heavy ion collisions, light nuclei and hypernuclei such as deuteron (d), helium-3 (³He), triton (t), and hypertriton ( $_{Λ}^{3} H$ ) are produced as a special group of observables [1-5]. These groups comprise composite clusters, and their production mechanism is still debated [6-8]. Production mechanisms of such composite objects face many fundamental issues in relativistic heavy ion community; e.g., the hadronization mechanism [9], hadronic rescattering effect [10], structure of the quantum chromodynamics phase diagram [11-15], local baryon-strangeness correlation [16, 17], system freeze-out characteristics [18-20], hyperon–nucleon interaction [21, 22], and search for more hadronic molecular states [23, 24].

The production mechanisms of light nuclei and hypernuclei in ultra-relativistic heavy ion collisions have attracted considerable attention in experimental [25-28] and theoritical [29-32] research in the last few decades. The STAR experiment at the BNL Relativistic Heavy Ion Collider (RHIC) and the ALICE experiment at the CERN Large Hadron Collider (LHC) have been conducted to measure light nuclei [33-37] and hypernuclei [38-40]. Theoretical research has considered two popular production mechanisms, the thermal production mechanism [41-45] and the coalescence mechanism [46-50], which have been proven to be successful in describing the formation of such composite objects.

The coalescence mechanism, assuming light nuclei and hypernuclei are produced by the coalescence of the adjacent nucleons and hyperons in the phase space, exhibits certain unique characteristics such as the mass number scaling property [51-53] and nontrivial coalescence factor behavior [54-57]. To understand the extent to which these characteristics depend on the particular coalescence models used in obtaining these characteristics, we have developed an analytical model for describing the productions of different species of light nuclei, as reported in our previous works [58-61]. We applied the developed analytical nucleon coalescence model to Au+Au collisions at the RHIC to successfully explain the energy-dependent behaviors of d, t, ³He, and ⁴He [58, 59]. We also applied the model to pp, p+Pb, and Pb+Pb collisions at the LHC to understand different behaviors of coalescence factors B₂ and B₃ [60] from small to large collision systems, and a series of concise production correlations of d, ³He, and t [61] were presented.

Recently, the ALICE collaboration published the most precise measurements of d, ³He, t, and especially $_{Λ}^{3} H$ in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV to date [62-64]. In this study, we extend the coalescence model considering the coordinate–momentum correlation [61] to include the hyperon coalescence besides the nucleon coalescence and apply it to simultaneously study the productions of light nuclei, $_{Λ}^{3} H$ , and Ω-hypernuclei. This study primarily aims to present a comprehensive overview of the latest data published in Pb+Pb collisions with the highest collision energy. The study also aims to explain the production characteristics, specifically, the production correlations of light nuclei and hypernuclei originating from the coalescence. We propose two groups of interesting observables–the averaged transverse momentum ratios and centrality-dependent yield ratios of light nuclei to protons and hypernuclei to hyperons. These ratios tend to offset the differences in the primordial p, Λ, and Ω^-, making them potent to reveal the existence of a universal production mechanism for different species of nuclei in light and strange sectors. These ratios are found to exhibit certain relationships, which are considerably different from those observed in the thermal production mechanism.

The remainder of this manuscript is organized as follows. Section 2 introduces the coalescence model and presents the formulae of the momentum distributions of two baryons coalescing into dibaryon states and three baryons coalescing into tribaryon states. Section 3 presents the behaviors of B₂ and B₃ evaluated as functions of the collision centrality and the transverse momentum per nucleon. Furthermore, the transverse momentum (p_T) spectra, averaged transverse momenta $〈 p_{T} 〉$ , yield rapidity densities dN/dy, and yield ratios of d, $^{3} \bar{He}$ , and $\bar{t}$ are presented. Section 4 presents the results of the $_{Λ}^{3} H$ and Ω-hypernuclei. Specifically, the averaged transverse momentum ratios $\frac{{〈 p_{T} 〉}_{d}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{H (p Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ , $\frac{{〈 p_{T} 〉}_{H (n Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ , $\frac{{〈 p_{T} 〉}_{t}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{^{3} He}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{_{Λ}^{3} H}}{{〈 p_{T} 〉}_{Λ}}$ , $\frac{{〈 p_{T} 〉}_{H (pn Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ , and centrality-dependent behaviors of yield ratios $\frac{d}{p}$ , $\frac{H (p Ω^{-})}{Ω^{-}}$ , $\frac{H (n Ω^{-})}{Ω^{-}}$ , $\frac{t}{p}$ , $\frac{^{3} He}{p}$ , $\frac{_{Λ}^{3} H}{Λ}$ , and $\frac{H (pn Ω^{-})}{Ω^{-}}$ are evaluated. Finally, Section 5 presents the conclusions drawn from the study findings.

Coalescence model

This section presents the extension of the analytical nucleon coalescence model developed in our previous work [61] to include the hyperon coalescence. The current model executes the coalescence process on an equivalent kinetic freeze-out surface formed from different times. To realize the analytical and intuitive insights, we eliminate the systematic time-evolution execution and utilize the finite emission duration in an effective volume. First, the formalism of two baryons coalescing into d-like dibaryon states is explained. Subsequently, an analytical expression of three baryons coalescing into ³He, t, and their partners in the strange sector is presented.

2.1

Formalism of two bodies coalescing into dibaryon states

Starting with a hadronic system produced at the final stage of the evolution of high-energy collisions, we consider that the dibaryon state H_j is formed via the coalescence of two baryons h₁ and h₂. We use $f_{H_{j}} (p)$ to denote the three-dimensional momentum distribution of the produced H_j, as follows: $\begin{matrix} f_{H_{j}} (p) = \int d x_{1} d x_{2} d p_{1} d p_{2} f_{h_{1} h_{2}} (x_{1}, x_{2}; p_{1}, p_{2}) \\ \times R_{H_{j}} (x_{1}, x_{2}; p_{1}, p_{2}, p) . \end{matrix}$ (1) Here, $f_{h_{1} h_{2}} (x_{1}, x_{2}; p_{1}, p_{2})$ is the two-baryon joint coordinate–momentum distribution; and $R_{H_{j}} (x_{1}, x_{2}; p_{1}, p_{2}, p)$ is the kernel function of the H_j. Hereinafter, we use bold symbols to denote three-dimensional coordinates and momentum vectors.

In terms of the normalized joint coordinate–momentum distribution denoted by the superscript ‘(n)’, we have $\begin{matrix} f_{H_{j}} (p) = N_{h_{1} h_{2}} \int d x_{1} d x_{2} d p_{1} d p_{2} f_{h_{1} h_{2}}^{(n)} (x_{1}, x_{2}; p_{1}, p_{2}) \\ \times R_{H_{j}} (x_{1}, x_{2}; p_{1}, p_{2}, p) . \end{matrix}$ (2) Here, $N_{h_{1} h_{2}} = N_{h_{1}} N_{h_{2}}$ is the number of all possible h₁h₂-pairs in the considered hadronic system, and $N_{h_{i}} (i = 1,2)$ is the number of the baryons hi.

The kernel function $R_{H_{j}} (x_{1}, x_{2}; p_{1}, p_{2}, p)$ denotes the probability density for h₁, h₂ with momenta p₁ and p₂ at x₁ and x₂ to combine into an H_j of momentum p. It carries the kinetic and dynamical information of h₁ and h₂ combining into H_j, and its precise expression should be constrained by laws such as the momentum conservation and constraints due to intrinsic quantum numbers; e.g., spin [58-61]. To consider these constraints explicitly, we rewrite the kernel function in the following form: $\begin{matrix} R_{H_{j}} (x_{1}, x_{2}; p_{1}, p_{2}, p) = g_{H_{j}} R_{H_{j}}^{(x, p)} (x_{1}, x_{2}; p_{1}, p_{2}) \\ \times δ (\sum_{i = 1}^{2} p_{i} - p) . \end{matrix}$ (3) The spin degeneracy factor $g_{H_{j}} = (2 J_{H_{j}} + 1) / [\prod_{i = 1}^{2} (2 J_{h_{i}} + 1)]$ , where $J_{H_{j}}$ is the spin of the produced H_j and $J_{h_{i}}$ is that of the primordial baryon hi. The Dirac δ function guarantees momentum conservation in the coalescence process. The remaining $R_{H_{j}}^{(x, p)} (x_{1}, x_{2}; p_{1}, p_{2})$ can be solved using the Wigner transformation as the H_j wave function is given. Considering the wave function of a spherical harmonic oscillator is particularly tractable and useful for analytical insights, therefore, we adopt this profile as reported in Refs. [65-67] and have $R_{H_{j}}^{(x, p)} (x_{1}, x_{2}; p_{1}, p_{2}) = 8 e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ^{2}}} e^{- \frac{2 σ^{2} {(m_{2} {p^{'}}_{1} - m_{1} {p^{'}}_{2})}^{2}}{{(m_{1} + m_{2})}^{2}}} .$ (4) The superscript ‘′’ in the coordinate or momentum variables denotes the baryon coordinate or momentum in the rest frame of h₁h₂-pair, respectively. Moreover, m₁ and m₂ represent the mass of h₁ and that of h₂, respectively. The width parameter $σ = \sqrt{\frac{2 {(m_{1} + m_{2})}^{2}}{3 (m_{1}^{2} + m_{2}^{2})}} R_{H_{j}}$ , where $R_{H_{j}}$ is the root-mean-square radius of the H_j.

Substituting Eqs. (3) and (4) into Eq. (2), we have $\begin{matrix} f_{H_{j}} (p) = N_{h_{1} h_{2}} g_{H_{j}} \int d x_{1} d x_{2} d p_{1} d p_{2} f_{h_{1} h_{2}}^{(n)} (x_{1}, x_{2}; p_{1}, p_{2}) \\ \times 8 e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ^{2}}} e^{- \frac{2 σ^{2} {(m_{2} {p^{'}}_{1} - m_{1} {p^{'}}_{2})}^{2}}{{(m_{1} + m_{2})}^{2}}} δ (\sum_{i = 1}^{2} p_{i} - p) . \end{matrix}$ (5) This is the general formalism of the H_j production via the coalescence of two baryons h₁ and h₂.

Notably, the root-mean-square radius $R_{H_{j}}$ of the dibaryon state H_j is always about or larger than 2 fm, and σ is considerably larger than $R_{H_{j}}$ . Thus, the Gaussian width in the momentum-dependent part of the kernel function in Eq. (5) has a small value, about or smaller than 0.1 GeV/c. Therefore, we approximate the Gaussian form of the momentum-dependent kernel function to be a δ function as follows: $e^{- \frac{{({p^{'}}_{1} - \frac{m_{1}}{m_{2}} {p^{'}}_{2})}^{2}}{{(1 + \frac{m_{1}}{m_{2}})}^{2} / (2 σ^{2})}} \approx {[\frac{\sqrt{π}}{\sqrt{2} σ} (1 + \frac{m_{1}}{m_{2}})]}^{3} δ ({p^{'}}_{1} - \frac{m_{1}}{m_{2}} {p^{'}}_{2}) .$ (6) The robustness of the δ function approximation has been checked at the outset of the analytical coalescence model in our previous work [60]. Substituting Eq. (6) into Eq. (5) and integrating p₁ and p₂, we obtain $\begin{array}{l} f_{H_{j}} (p) = N_{h_{1} h_{2}} g_{H_{j}} \int d x_{1} d x_{2} d p_{1} d p_{2} \\ f_{h_{1} h_{2}}^{(n)} (x_{1}, x_{2}; p_{1}, p_{2}) 8 e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ^{2}}} {(\frac{\sqrt{π}}{\sqrt{2} σ})}^{3} {(1 + \frac{m_{1}}{m_{2}})}^{3} \\ \times δ ({p^{'}}_{1} - \frac{m_{1}}{m_{2}} {p^{'}}_{2}) δ (\sum_{i = 1}^{2} p_{i} - p) \\ = N_{h_{1} h_{2}} g_{H_{j}} \int d x_{1} d x_{2} d p_{1} d p_{2} f_{h_{1} h_{2}}^{(n)} (x_{1}, x_{2}; p_{1}, p_{2}) \\ \times 8 e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ^{2}}} {(\frac{\sqrt{π}}{\sqrt{2} σ})}^{3} {(1 + \frac{m_{1}}{m_{2}})}^{3} γ δ (p_{1} - \frac{m_{1}}{m_{2}} p_{2}) \\ \times δ (\sum_{i = 1}^{2} p_{i} - p) \\ = N_{h_{1} h_{2}} g_{H_{j}} γ {(\frac{\sqrt{π}}{\sqrt{2} σ})}^{3} \times 8 \int d x_{1} d x_{2} \\ f_{h_{1} h_{2}}^{(n)} (x_{1}, x_{2}; \frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ^{2}}} . \end{array}$ (7) Here, γ denotes the Lorentz contraction factor corresponding to the three-dimensional velocity β of the center-of-mass frame of the h₁h₂-pair in the laboratory frame, and the momentum transformation parallel to β is ${p^{'}}_{1 / /} - \frac{m_{1}}{m_{2}} {p^{'}}_{2 / /} = \frac{1}{γ} (p_{1 / /} - \frac{m_{1}}{m_{2}} p_{2 / /})$ and that perpendicular to β is invariant.

Changing coordinate variables in Eq. (7) to $X = \frac{\sqrt{2} (m_{1} x_{1} + m_{2} x_{2})}{m_{1} + m_{2}}$ and $r = \frac{x_{1} - x_{2}}{\sqrt{2}}$ gives $\begin{matrix} f_{H_{j}} (p) = N_{h_{1} h_{2}} g_{H_{j}} γ {(\frac{\sqrt{π}}{\sqrt{2} σ})}^{3} \\ \times 8 \int d X d r f_{h_{1} h_{2}}^{(n)} (X, r; \frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) e^{- \frac{{r^{'}}^{2}}{σ^{2}}} . \end{matrix}$ (8) Considering the strong interaction and coalescence to be local, we neglect the effect of collective motion on the center of mass coordinate and assume it is factorized as $\begin{array}{l} f_{h_{1} h_{2}}^{(n)} (X, r; \frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) = f_{h_{1} h_{2}}^{(n)} (X) \\ \times f_{h_{1} h_{2}}^{(n)} (r; \frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) . \end{array}$ (9) Substituting Eq. (9) into Eq. (8), we have $\begin{matrix} f_{H_{j}} (p) = N_{h_{1} h_{2}} g_{H_{j}} γ {(\frac{\sqrt{π}}{\sqrt{2} σ})}^{3} \\ \times 8 \int d r f_{h_{1} h_{2}}^{(n)} (r; \frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) e^{- \frac{{r^{'}}^{2}}{σ^{2}}} . \end{matrix}$ (10) We adopt the frequently-used Gaussian form for the relative coordinate distribution, as reported in Refs. [68-70], as follows: $\begin{array}{l} f_{h_{1} h_{2}}^{(n)} (r; \frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) = \frac{1}{{[π C_{0} R_{f}^{2} (p)]}^{3 / 2}} \\ \times e^{- \frac{r^{2}}{C_{0} R_{f}^{2} (p)}} f_{h_{1} h_{2}}^{(n)} (\frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) . \end{array}$ (11) Here, $R_{f} (p)$ is the effective radius of the hadronic source system at the H_j freeze-out, and C₀ is introduced to make r²/C₀ to be the square of one-half of the relative position and is equal to 2 [68-70]. Similarly, $R_{f} (p)$ is the Hanbury–Brown–Twiss (HBT) interferometry radius, which can be extracted from the two-particle femtoscopic correlations [69, 70].

With instantaneous coalescence in the rest frame of the h₁h₂-pair, i.e., Δt’=0, we get the coordinate transformation $r = r' + (γ - 1) \frac{r' \cdot β}{β^{2}} β .$ (12) The instantaneous coalescence is a basic assumption in coalescence-like models, wherein the overlap of the nucleus Wigner phase–space density with the constituent phase–space distributions is adopted [65]. Considering the coalescence criterion judging in the rest frame is more general than in the laboratory frame, we choose the instantaneous coalescence in the rest frame of the h₁h₂-pair, as reported in Refs. [71, 65]. Substituting Eq. (11) into Eq. (10) and using Eq. (12) to integrate from the relative coordinate variable, we obtain $\begin{matrix} f_{H_{j}} (p) = \frac{8 π^{3 / 2} g_{H_{j}} γ}{2^{3 / 2} [C_{0} R_{f}^{2} (p) + σ^{2}] \sqrt{C_{0} {[R_{f} (p) / γ]}^{2} + σ^{2}}} \\ \times f_{h_{1} h_{2}} (\frac{m_{1} p}{m_{1} + m_{2}}, \frac{m_{2} p}{m_{1} + m_{2}}) . \end{matrix}$ (13) Ignoring the correlations between h₁ and h₂, we obtain the three-dimensional momentum distribution of the H_j as $\begin{matrix} f_{H_{j}} (p) = \frac{8 π^{3 / 2} g_{H_{j}} γ}{2^{3 / 2} [C_{0} R_{f}^{2} (p) + σ^{2}] \sqrt{C_{0} {[R_{f} (p) / γ]}^{2} + σ^{2}}} \\ \times f_{h_{1}} (\frac{m_{1} p}{m_{1} + m_{2}}) f_{h_{2}} (\frac{m_{2} p}{m_{1} + m_{2}}) . \end{matrix}$ (14) Denoting the Lorentz invariant momentum distribution $E \frac{d^{3} N}{d p^{3}} = \frac{d^{2} N}{2 π p_{T} d p_{T} d y}$ with f^(inv), we finally get $\begin{matrix} f_{H_{j}}^{(inv)} (p_{T}, y) = \frac{8 π^{3 / 2} g_{H_{j}}}{2^{3 / 2} [C_{0} R_{f}^{2} (p_{T}, y) + σ^{2}] \sqrt{C_{0} \frac{R_{f}^{2} (p_{T}, y)}{γ^{2}} + σ^{2}}} \\ \times \frac{m_{H_{j}}}{m_{1} m_{2}} f_{h_{1}}^{(inv)} (\frac{m_{1} p_{T}}{m_{1} + m_{2}}, y) f_{h_{2}}^{(inv)} (\frac{m_{2} p_{T}}{m_{1} + m_{2}}, y), \end{matrix}$ (15) where y is the longitudinal rapidity and $m_{H_{j}}$ is the mass of H_j.

2.2

Formalism of three bodies coalescing into tribaryon states

For tribaryon state H_j formed via the coalescence of three baryons h₁, h₂, and h₃, the momentum distribution $f_{H_{j}} (p)$ is $\begin{matrix} f_{H_{j}} (p) = N_{h_{1} h_{2} h_{3}} \int d x_{1} d x_{2} d x_{3} d p_{1} d p_{2} d p_{3} f_{h_{1} h_{2} h_{3}}^{(n)} \\ (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}) R_{H_{j}} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}, p) . \end{matrix}$ (16) Here, $N_{h_{1} h_{2} h_{3}}$ is the number of all possible h₁h₂h₃-clusters and equals to $N_{h_{1}} N_{h_{2}} N_{h_{3}}, N_{h_{1}} (N_{h_{1}} - 1) N_{h_{3}}$ for $h_{1} \neq h_{2} \neq h_{3}$ , and $h_{1} = h_{2} \neq h_{3}$ . Moreover, $f_{h_{1} h_{2} h_{3}}^{(n)} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3})$ is the normalized three-baryon joint coordinate–momentum distribution, and $R_{H_{j}} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}, p)$ is the kernel function.

The kernel function can be modified as $\begin{array}{l} R_{H_{j}} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}, p) \\ = g_{H_{j}} R_{H_{j}}^{(x, p)} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}) δ (\sum_{i = 1}^{3} p_{i} - p) . \end{array}$ (17) The spin degeneracy factor $g_{H_{j}} = (2 J_{H_{j}} + 1) / [\prod_{i = 1}^{3} (2 J_{h_{i}} + 1)]$ . The Dirac δ function guarantees momentum conservation. Solving from the Wigner transformation [65-67], $R_{H_{j}}^{(x, p)} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3})$ is $\begin{matrix} R_{H_{j}}^{(x, p)} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}) \\ =^{82} e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ_{1}^{2}}} e^{- \frac{2 {(\frac{m_{1} {x^{'}}_{1}}{m_{1} + m_{2}} + \frac{m_{2} {x^{'}}_{2}}{m_{1} + m_{2}} - {x^{'}}_{3})}^{2}}{3 σ_{2}^{2}}} e^{- \frac{2 σ_{1}^{2} {(m_{2} {p^{'}}_{1} - m_{1} {p^{'}}_{2})}^{2}}{{(m_{1} + m_{2})}^{2}}} \\ e^{- \frac{3 σ_{2}^{2} {[m_{3} {p^{'}}_{1} + m_{3} {p^{'}}_{2} - (m_{1} + m_{2}) {p^{'}}_{3}]}^{2}}{2 {(m_{1} + m_{2} + m_{3})}^{2}}} . \end{matrix}$ (18) Here, the superscript ‘′' denotes the baryon coordinate or momentum in the rest frame of the h₁h₂h₃-cluster. The width parameter $σ_{1} = \sqrt{\frac{m_{3} (m_{1} + m_{2}) (m_{1} + m_{2} + m_{3})}{m_{1} m_{2} (m_{1} + m_{2}) + m_{2} m_{3} (m_{2} + m_{3}) + m_{3} m_{1} (m_{3} + m_{1})}} R_{H_{j}}$ , and $σ_{2} = \sqrt{\frac{4 m_{1} m_{2} {(m_{1} + m_{2} + m_{3})}^{2}}{3 (m_{1} + m_{2}) [m_{1} m_{2} (m_{1} + m_{2}) + m_{2} m_{3} (m_{2} + m_{3}) + m_{3} m_{1} (m_{3} + m_{1})]}} R_{H_{j}}$ , where $R_{H_{j}}$ is the root-mean-square radius of the H_j. Substituting Eqs. (17) and (18) into Eq. (16), we obtain $\begin{array}{l} f_{H_{j}} (p) =^{82} N_{h_{1} h_{2} h_{3}} g_{H_{j}} \\ \int d x_{1} d x_{2} d x_{3} d p_{1} d p_{2} d p_{3} e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ_{1}^{2}}} e^{- \frac{2 {(\frac{m_{1} {x^{'}}_{1}}{m_{1} + m_{2}} + \frac{m_{2} {x^{'}}_{2}}{m_{1} + m_{2}} - {x^{'}}_{3})}^{2}}{3 σ_{2}^{2}}} \\ f_{h_{1} h_{2} h_{3}}^{(n)} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}) \\ \times e^{- \frac{2 σ_{1}^{2} {(m_{2} {p^{'}}_{1} - m_{1} {p^{'}}_{2})}^{2}}{{(m_{1} + m_{2})}^{2}}} \\ e^{- \frac{3 σ_{2}^{2} {[m_{3} {p^{'}}_{1} + m_{3} {p^{'}}_{2} - (m_{1} + m_{2}) {p^{'}}_{3}]}^{2}}{2 {(m_{1} + m_{2} + m_{3})}^{2}}} δ (\sum_{i = 1}^{3} p_{i} - p) . \end{array}$ (19) Approximating the Gaussian form of the momentum-dependent kernel function to be a δ function and integrating p₁, p₂, and p₃ from Eq. (19), we obtain $\begin{array}{l} f_{H_{j}} (p) =^{82} N_{h_{1} h_{2} h_{3}} g_{H_{j}} \\ \int d x_{1} d x_{2} d x_{3} d p_{1} d p_{2} d p_{3} f_{h_{1} h_{2} h_{3}}^{(n)} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}) \\ e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ_{1}^{2}}} \\ e^{- \frac{2 {(\frac{m_{1} {x^{'}}_{1}}{m_{1} + m_{2}} + \frac{m_{2} {x^{'}}_{2}}{m_{1} + m_{2}} - {x^{'}}_{3})}^{2}}{3 σ_{2}^{2}}} \\ \times {(\frac{\sqrt{π}}{\sqrt{2} σ_{1}})}^{3} {(1 + \frac{m_{1}}{m_{2}})}^{3} \\ δ ({p^{'}}_{1} - \frac{m_{1}}{m_{2}} {p^{'}}_{2}) {(\frac{\sqrt{2 π}}{\sqrt{3} σ_{2}})}^{3} {(1 + \frac{m_{1}}{m_{3}} + \frac{m_{2}}{m_{3}})}^{3} \\ δ ({p^{'}}_{1} + {p^{'}}_{2} - \frac{m_{1} + m_{2}}{m_{3}} {p^{'}}_{3}) δ (\sum_{i = 1}^{3} p_{i} - p) \\ =^{82} N_{h_{1} h_{2} h_{3}} g_{H_{j}} \\ \int d x_{1} d x_{2} d x_{3} d p_{1} d p_{2} d p_{3} f_{h_{1} h_{2} h_{3}}^{(n)} (x_{1}, x_{2}, x_{3}; p_{1}, p_{2}, p_{3}) \\ e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ_{1}^{2}}} e^{- \frac{2 {(\frac{m_{1} {x^{'}}_{1}}{m_{1} + m_{2}} + \frac{m_{2} {x^{'}}_{2}}{m_{1} + m_{2}} - x'_{3})}^{2}}{3 σ_{2}^{2}}} \\ \times {(\frac{\sqrt{π}}{\sqrt{2} σ_{1}})}^{3} {(1 + \frac{m_{1}}{m_{2}})}^{3} γ δ (p_{1} - \frac{m_{1}}{m_{2}} p_{2}) {(\frac{\sqrt{2 π}}{\sqrt{3} σ_{2}})}^{3} \\ {(1 + \frac{m_{1}}{m_{3}} + \frac{m_{2}}{m_{3}})}^{3} \\ γ δ (p_{1} + p_{2} - \frac{m_{1} + m_{2}}{m_{3}} p_{3}) δ (\sum_{i = 1}^{3} p_{i} - p) \\ =^{82} N_{h_{1} h_{2} h_{3}} g_{H_{j}} γ^{2} {(\frac{π}{\sqrt{3} σ_{1} σ_{2}})}^{3} \\ \int d x_{1} d x_{2} d x_{3} f_{h_{1} h_{2} h_{3}}^{(n)} (x_{1}, x_{2}, x_{3}; \frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \\ \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) \\ \times e^{- \frac{{({x^{'}}_{1} - {x^{'}}_{2})}^{2}}{2 σ_{1}^{2}}} e^{- \frac{2 {(\frac{m_{1} {x^{'}}_{1}}{m_{1} + m_{2}} + \frac{m_{2} {x^{'}}_{2}}{m_{1} + m_{2}} - {x^{'}}_{3})}^{2}}{3 σ_{2}^{2}}} . \end{array}$ (20) Changing coordinate variables in Eq. (20) to $Y = (m_{1} x_{1} + m_{2} x_{2} + m_{3} x_{3}) / (m_{1} + m_{2} + m_{3})$ , $r_{1} = (x_{1} - x_{2}) / \sqrt{2}$ and $r_{2} = \sqrt{\frac{2}{3}} (\frac{m_{1} x_{1}}{m_{1} + m_{2}} + \frac{m_{2} x_{2}}{m_{1} + m_{2}} - x_{3})$ , as reported in Refs. [65-67], we get $\begin{matrix} f_{H_{j}} (p) =^{82} N_{h_{1} h_{2} h_{3}} g_{H_{j}} γ^{2} {(\frac{π}{\sqrt{3} σ_{1} σ_{2}})}^{3} \\ \times \int 3^{3 / 2} d Y d r_{1} d r_{2} f_{h_{1} h_{2} h_{3}}^{(n)} \\ (Y, r_{1}, r_{2}; \frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) e^{- \frac{{r^{'}}_{1}^{2}}{σ_{1}^{2}}} e^{- \frac{{r^{'}}_{2}^{2}}{σ_{2}^{2}}} . \end{matrix}$ (21) Assuming the center of mass coordinate in the joint distribution to be factorized gives $\begin{matrix} 3 3 / 2 f_{h_{1} h_{2} h_{3}}^{(n)} \\ (Y, r_{1}, r_{2}; \frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) \\ = f_{h_{1} h_{2} h_{3}}^{(n)} (Y) f_{h_{1} h_{2} h_{3}}^{(n)} (r_{1}, r_{2}; \frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \\ \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) . \end{matrix}$ (22) Substituting Eq. (22) into Eq. (21), we get $\begin{array}{l} f_{H_{j}} (p) =^{82} N_{h_{1} h_{2} h_{3}} g_{H_{j}} γ^{2} {(\frac{π}{\sqrt{3} σ_{1} σ_{2}})}^{3} \\ \int d r_{1} d r_{2} f_{h_{1} h_{2} h_{3}}^{(n)} \\ (r_{1}, r_{2}; \frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) \\ \times e^{- \frac{{r^{'}}_{1}^{2}}{σ_{1}^{2}}} e^{- \frac{{r^{'}}_{2}^{2}}{σ_{2}^{2}}} . \end{array}$ (23) Adopting the Gaussian forms for the relative coordinate distributions [60, 68-70], we get $\begin{array}{l} f_{h_{1} h_{2} h_{3}}^{(n)} (r_{1}, r_{2}; \frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \\ \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) \\ = \frac{1}{{[π C_{1} R_{f}^{2} (p)]}^{3 / 2}} e^{- \frac{r_{1}^{2}}{C_{1} R_{f}^{2} (p)}} \frac{1}{{[π C_{2} R_{f}^{2} (p)]}^{3 / 2}} e^{- \frac{r_{2}^{2}}{C_{2} R_{f}^{2} (p)}} f_{h_{1} h_{2} h_{3}}^{(n)} \\ (\frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) . \end{array}$ (24) Comparing the relationships of r₁ and r₂ with x₁, x₂, and x₃ to that of r with x₁ and x₂ presented in Sect. 2.1, we observe that C₁ is equal to C₀ and C₂ is $4 C_{0} / 3$ [60, 68-70]. Substituting Eq. (24) into Eq. (23) and considering the coordinate Lorentz transformation, we integrate from the relative coordinate variables and obtain $\begin{matrix} f_{H_{j}} (p) = \frac{8^{2} π^{3} g_{H_{j}} γ^{2}}{3^{3 / 2} [C_{1} R_{f}^{2} (p) + σ_{1}^{2}] \sqrt{C_{1} {[R_{f} (p) / γ]}^{2} + σ_{1}^{2}} [C_{2} R_{f}^{2} (p) + σ_{2}^{2}] \sqrt{C_{2} {[R_{f} (p) / γ]}^{2} + σ_{2}^{2}}} \\ \times f_{h_{1} h_{2} h_{3}} (\frac{m_{1} p}{m_{1} + m_{2} + m_{3}}, \\ \frac{m_{2} p}{m_{1} + m_{2} + m_{3}}, \frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) . \end{matrix}$ (25) Ignoring the correlations between h₁, h₂, and h₃, we get the three-dimensional momentum distribution of H_j as $\begin{matrix} f_{H_{j}} (p) = \frac{8^{2} π^{3} g_{H_{j}} γ^{2}}{3^{3 / 2} [C_{1} R_{f}^{2} (p) + σ_{1}^{2}] \sqrt{C_{1} {[R_{f} (p) / γ]}^{2} + σ_{1}^{2}} [C_{2} R_{f}^{2} (p) + σ_{2}^{2}] \sqrt{C_{2} {[R_{f} (p) / γ]}^{2} + σ_{2}^{2}}} \\ \times f_{h_{1}} (\frac{m_{1} p}{m_{1} + m_{2} + m_{3}}) f_{h_{2}} (\frac{m_{2} p}{m_{1} + m_{2} + m_{3}}) \\ f_{h_{3}} (\frac{m_{3} p}{m_{1} + m_{2} + m_{3}}) . \end{matrix}$ (26) Finally, the Lorentz invariant momentum distribution can be expressed as $\begin{matrix} f_{H_{j}}^{(inv)} (p_{T}, y) = \frac{8^{2} π^{3} g_{H_{j}}}{3^{3 / 2} [C_{1} R_{f}^{2} (p_{T}, y) + σ_{1}^{2}] \sqrt{C_{1} {[R_{f} (p_{T}, y) / γ]}^{2} + σ_{1}^{2}} [C_{2} R_{f}^{2} (p_{T}, y) + σ_{2}^{2}] \sqrt{C_{2} {[R_{f} (p_{T}, y) / γ]}^{2} + σ_{2}^{2}}} \\ \times \frac{m_{H_{j}}}{m_{1} m_{2} m_{3}} f_{h_{1}}^{(inv)} (\frac{m_{1} p_{T}}{m_{1} + m_{2} + m_{3}}, y) f_{h_{2}}^{(inv)} (\frac{m_{2} p_{T}}{m_{1} + m_{2} + m_{3}}, y) f_{h_{3}}^{(inv)} (\frac{m_{3} p_{T}}{m_{1} + m_{2} + m_{3}}, y) . \end{matrix}$ (27) In summary, Eqs. (15) and (27) give the following: (i) the relationships of dibaryon states and tribaryon states with primordial baryons in momentum space in a laboratory frame, (ii) effects of different factors on dibaryon or tribaryon production; e.g., the whole hadronic system scale and the size of the formed composite object. These equations can be directly used to calculate the production of light nuclei, hypernuclei, and even other hadronic molecular states. Moreover, they can be conveniently used to investigate production correlations of different species of composite objects. As the formulae for the antiparticles are the same as those for the dibaryon and tribaryon states, we have not derived them here to eliminate duplication. Their applications at midrapidity (i.e., y = 0) in heavy ion collisions at the LHC are presented in the following sections.

Results of light nuclei

This section presents the use of the coalescence model to study productions of d, $^{3} \bar{He}$ and $\bar{t}$ at midrapidity in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. First, we calculate the coalescence factors B₂ and B₃ and discuss their centrality and p_T-dependent behaviors. Subsequently, we compute the p_T spectra of d, $^{3} \bar{He}$ , and $\bar{t}$ . Finally, we calculate the averaged transverse momenta $〈 p_{T} 〉$ , the yield rapidity densities dN/dy, and the yield ratios of different light nuclei.

3.1

Coalescence factor of light nuclei

The coalescence factor BA is defined as $B_{A} (p_{T}) = \frac{f_{d,^{3} He, t}^{(inv)} (p_{T})}{{[f_{p}^{(inv)} (\frac{p_{T}}{A})]}^{Z} {[f_{n}^{(inv)} (\frac{p_{T}}{A})]}^{A - Z}},$ (28) where A is the mass number and Z is the charge of the light nuclei. It is a unique link between the formed light nuclei and the primordial nucleons. Several studies have investigated BA using different coalescence models [72-75]. From Eqs. (15) and (27), we get d, ³He, and t, as follows: $B_{2} (p_{T}) = \frac{m_{d} g_{d} {(\sqrt{2 π})}^{3}}{m_{p} m_{n} [C_{0} R_{f}^{2} (p_{T}) + σ_{d}^{2}] \sqrt{C_{0} {[\frac{R_{f} (p_{T})}{γ}]}^{2} + σ_{d}^{2}}},$ (29) $\begin{matrix} B_{3} (p_{T}) = \frac{64 π^{3} g_{^{3} He}}{3^{\frac{3}{2}} [C_{1} R_{f}^{2} (p_{T}) + σ_{^{3} He}^{2}] \sqrt{C_{1} {[\frac{R_{f} (p_{T})}{γ}]}^{2} + σ_{^{3} He}^{2}}} \\ \times \frac{m_{^{3} He}}{m_{p}^{2} m_{n} [C_{2} R_{f}^{2} (p_{T}) + σ_{^{3} He}^{2}] \sqrt{C_{2} {[\frac{R_{f} (p_{T})}{γ}]}^{2} + σ_{^{3} He}^{2}}}, \end{matrix}$ (30) $\begin{matrix} B_{3} (p_{T}) = \frac{64 π^{3} g_{t}}{3^{\frac{3}{2}} [C_{1} R_{f}^{2} (p_{T}) + σ_{t}^{2}] \sqrt{C_{1} {[\frac{R_{f} (p_{T})}{γ}]}^{2} + σ_{t}^{2}}} \\ \times \frac{m_{t}}{m_{p} m_{n}^{2} [C_{2} R_{f}^{2} (p_{T}) + σ_{t}^{2}] \sqrt{C_{2} {[\frac{R_{f} (p_{T})}{γ}]}^{2} + σ_{t}^{2}}} . \end{matrix}$ (31) Here, $σ_{d} = \sqrt{\frac{4}{3}} R_{d}$ , and the root-mean-square radius of the deuteron R_d=2.1421 fm [76]. Moreover, $σ_{^{3} He} = R_{^{3} He} = 1.9661$ fm, $σ_{t} = R_{t} = 1.7591$ fm [76], $m_{p, n}$ denotes the nucleon mass, and $m_{d,^{3} He, t}$ denotes the mass of the d, ³He, or t, respectively.

To further compute B₂ and B₃, the specific form of R_f(p_T) is necessary. Similar to Ref. [61], the dependence of R_f(p_T) on centrality and p_T is considered to factorize into a linear dependence on the cube root of the pseudorapidity density of charged particles ${(d N_{ch} / d η)}^{1 / 3}$ and a power-law dependence on the transverse mass of the formed light nucleus [70]. Therefore, we get $R_{f} (p_{T}) = a \times {(d N_{ch} / d η)}^{\frac{1}{3}} \times {(\sqrt{p_{T}^{2} + m_{d,^{3} He, t}^{2}})}^{b},$ (32) where a and b are the free parameters, and their values in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV are (0.70,-0.31) for d and (0.66,-0.31) for ³He and t, determined by reproducing the experimental data of p_T spectra of d and ³He in the most central 0–5% centrality. Here, b is set to be centrality independent and is consistent with that in hydrodynamics [78] and that in STAR measurements of two-pion interferometry in central and semi-central Au+Au collisions [79]. Moreover, a is set to be centrality-independent, the same as that in our previous work [61].

We used the data of dN_ch/dη reported in Ref. [80] to evaluate R_f(p_T) and computed the coalescence factors B₂ and B₃. Figure 1 shows B₂ of d as a function of the transverse momentum scaled by the mass number p_T/2 in different centralities in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Symbols with error bars represent experimental data [77], and solid lines represent theoretical results of the coalescence model. As observed from Fig. 1, from central to peripheral collisions, B₂ exhibits an increasing trend owing to the decreasing scale of the created hadronic system. For a certain centrality, B₂ increases as a function of p_T/2. This increased behavior results, on the one hand, from the Lorentz contraction factor γ, which has been studied in Ref. [60]. On the other hand, it results from the decreasing R_f with increasing p_T. The increase in the experimental data as a function of p_T/2 from central to peripheral collisions can be quantitatively described by the coalescence model.

Fig. 1

(Color online) B₂ of d as a function of p_T/2 in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Symbols with error bars represent experimental data [77], and solid lines represent theoretical results

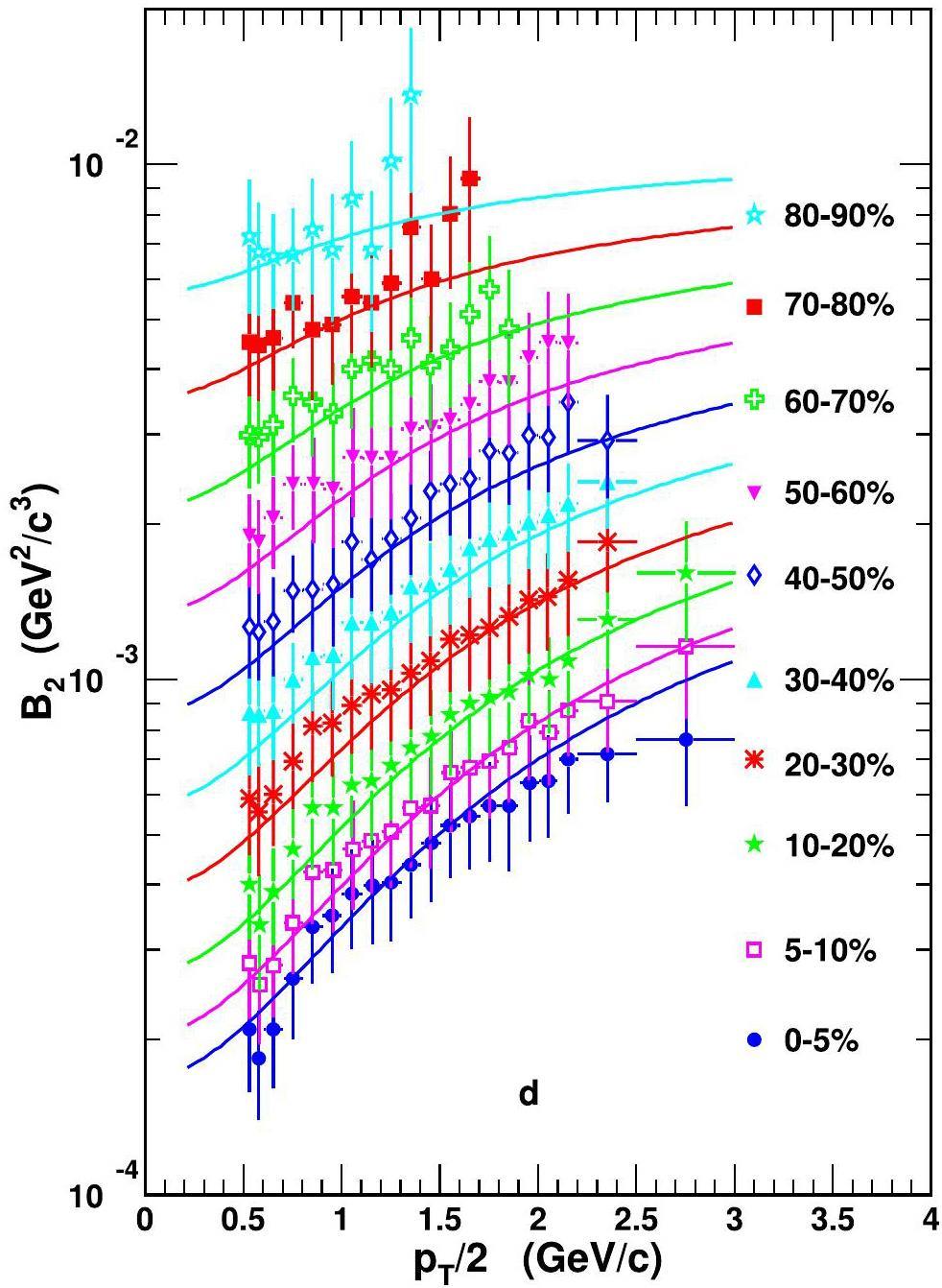
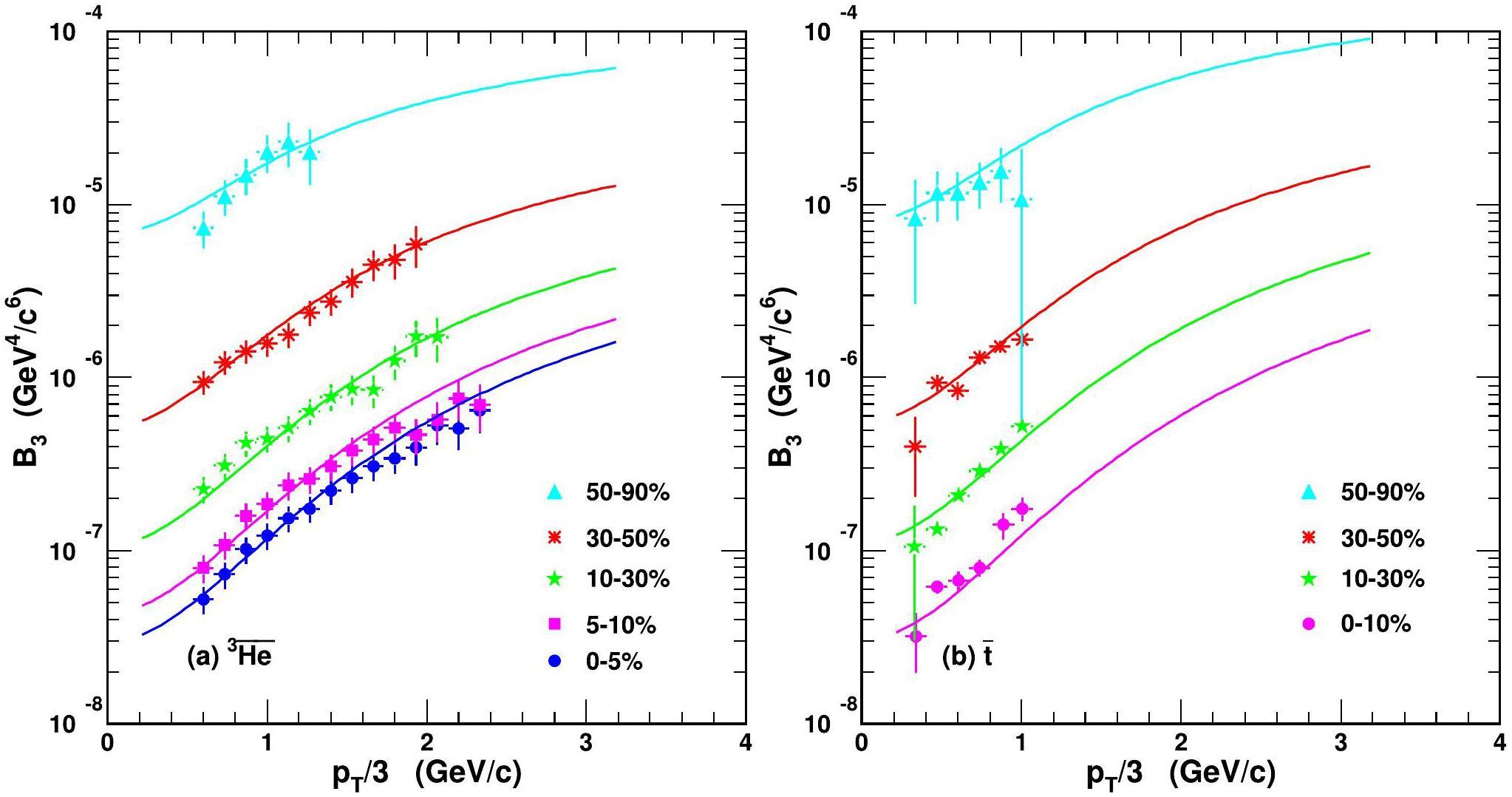
Figure 2 shows B₃ of $^{3} \bar{He}$ and that of $\bar{t}$ as a function of p_T/3 in different centralities in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Symbols with error bars represent experimental data [62], and solid lines represent theoretical results. Similar to B₂, the experimental data of B₃ exhibit an increasing trend as a function of p_T/3 and is reproduced well by the coalescence model from central to peripheral collisions. Figures 1 and 2 show that the centrality and p_T-dependent behaviors of B₂ and B₃ are simultaneously explained by the coalescence model. The results extracted for R_f(p_T) can provide quantitative references for future measurements of HBT interferometry radius from the two-nucleon correlations. Through the light nucleus production, we provide an alternative way to obtain the HBT interferometry radius of the hadronic source system.

Fig. 2

(Color online) B₃ of (a)

^{3} \bar{He}

and (b)

\bar{t}

as a function of p_T/3 in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Symbols with error bars represent experimental data [62], and solid lines represent theoretical results

3.2

p_T spectra of light nuclei

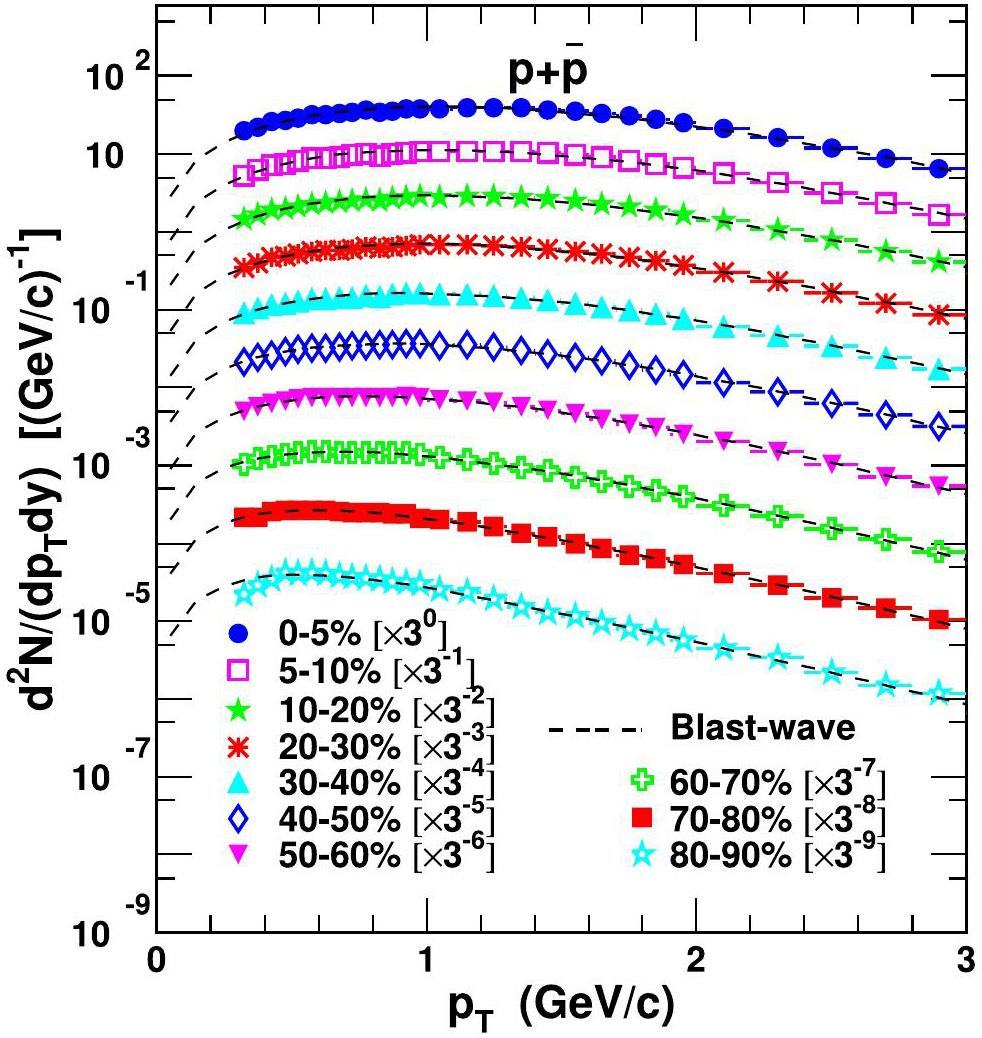
The p_T spectra of primordial nucleons are necessary inputs for computing p_T distributions of light nuclei in the coalescence model. Here, we used the blast-wave model to get p_T distribution functions of primordial protons by fitting the experimental data of prompt (anti)protons, as reported in Ref. [80]. The blast-wave function [81] is given as $\begin{array}{l} \frac{d^{2} N}{2 π p_{T} d p_{T} d y} \propto \\ \int_{0}^{R} r d r m_{T} I_{0} (\frac{p_{T} \sinh ρ}{T_{kin}}) K_{1} (\frac{m_{T} \cosh ρ}{T_{kin}}), \end{array}$ (33) where r is the radial distance in the transverse plane and R is the fireball radius. Moreover, I₀ and K₁ are the modified Bessel functions, and the velocity profile $ρ = \tanh^{- 1} β_{T} = \tanh^{- 1} [β_{s} {(\frac{r}{R})}^{n}]$ . The kinetic freeze-out temperature T_kin, the averaged radial expansion velocity $〈 β_{T} 〉$ , and n are fit parameters. Their values can be found in Ref. [80].

Figure 3 shows the p_T spectra of prompt protons plus antiprotons in different centralities in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Symbols with error bars represent experimental data [80], and dashed lines represent the results of the blast-wave model. The p_T spectra in different centralities are scaled by different factors for clarity, as shown in the Fig. 3. For the primordial neutrons, we adopted the same p_T spectra as those of primordial protons, as we focused on light nucleus production at midrapidity at high LHC energy, that the isospin symmetry was well satisfied.

Fig. 3

(Color online) p_T spectra of prompt protons plus antiprotons in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Symbols with error bars represent experimental data [80], and dashed lines represent the results of the blast-wave model

First, the p_T spectra of deuterons in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV in 0–5%, 5–10%, 10–20%, 20–30%, 30–40%, 40–50%, 50–60%, 60–70%, 70–80%, and 80–90% centralities were determined. Different solid lines scaled by different factors for clarity in Fig. 4 represent our theoretical results. Symbols with error bars represent the experimental data from the ALICE collaboration [62]. Subsequently, the p_T spectra of $^{3} \bar{He}$ and $\bar{t}$ in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV in different centralities were computed. Different solid lines in Fig. 5 represent our theoretical results, which agree with the available data denoted by the filled symbols [62]. As observed from Figs. 4 and 5, nucleon coalescence is the dominant mechanism for light nucleus production in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. More precise measurements for $^{3} \bar{He}$ and $\bar{t}$ in a wide p_T range in the future can help test the coalescence mechanism further, specifically in peripheral Pb+Pb collisions.

Fig. 4

(Color online) p_T spectra of deuterons in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Symbols with error bars represent experimental data [77], and solid lines represent the theoretical results

Fig. 5

(Color online) p_T spectra of (a)

^{3} \bar{He}

and (b)

\bar{t}

in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Filled symbols with error bars represent experimental data [62], and solid lines represent theoretical results

3.3

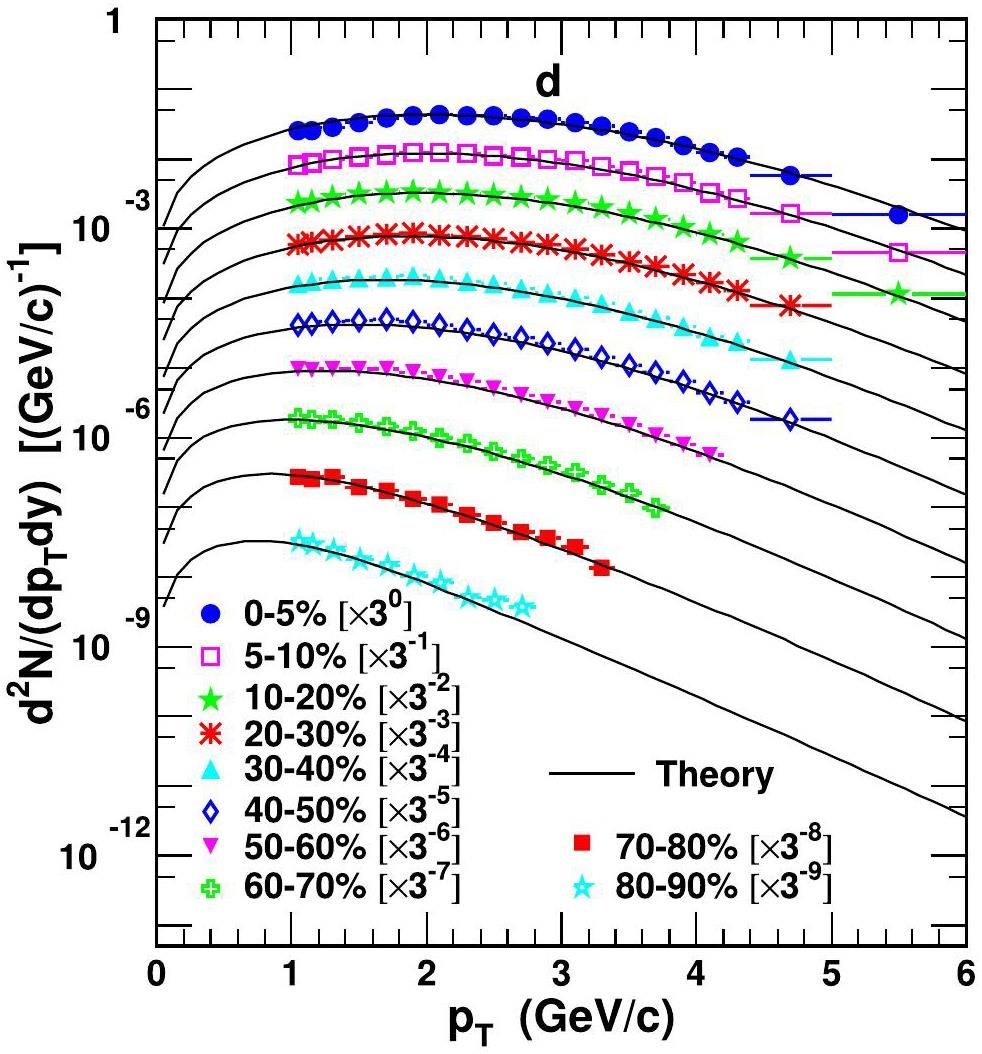
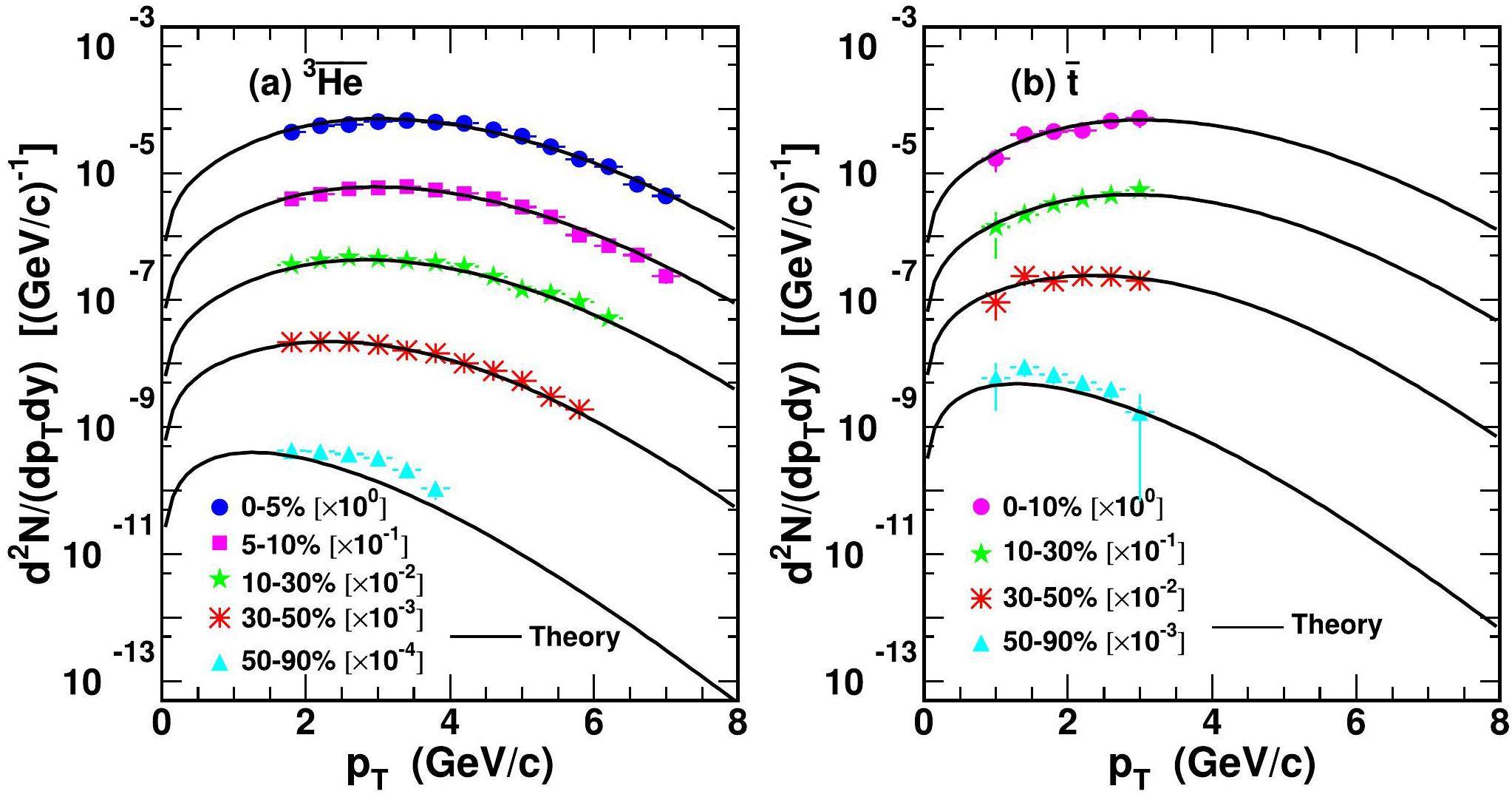
Averaged transverse momenta and yield rapidity densities of light nuclei

The averaged transverse momenta $〈 p_{T} 〉$ and yield rapidity densities dN/dy of d, $^{3} \bar{He}$ , and $\bar{t}$ are examined. Our theoretical results are presented in the fourth and sixth columns in Table 1. Experimental data presented in the third and fifth columns are obtained from Refs. [62, 77]. A decreasing trend for $〈 p_{T} 〉$ and dN/dy from central to peripheral collisions is observed. This is because in collisions that are more central, more energy is deposited in the midrapidity region, and collective evolution exists for longer. Theoretical results for d, $^{3} \bar{He}$ , and $\bar{t}$ are consistent with the corresponding data within the experimental uncertainties, except for a very little underestimation for dN/dy of $\bar{t}$ in a peripheral 50–90% collision. Such underestimation needs to be confirmed using precise data from future research.

Averaged transverse momenta

〈 p_{T} 〉

and yield rapidity densities dN/dy of d,

^{3} \bar{He}

, and

\bar{t}

in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Experimental data in the third and fifth columns are obtained from Refs. [62, 77]. Theoretical results are presented in the fourth and sixth columns

	Centrality	$〈 p_{T} 〉$ (GeV/c)		dN/dy
	Centrality	Data	Theory	Data	Theory
d	0–5%	2.45±0.00±0.09	2.37	(1.19±0.00±0.21)×10^-1	1.22×10^-1
	5–10%	2.41±0.01±0.10	2.33	(1.04±0.00±0.19)×10^-1	1.01×10^-1
	10–20%	2.34±0.00±0.11	2.28	(8.42±0.02±1.50)×10^-2	7.86×10^-2
	20–30%	2.21±0.00±0.12	2.18	(6.16±0.02±1.10)×10^-2	5.58×10^-2
	30–40%	2.05±0.00±0.12	2.04	(4.25±0.01±0.75)×10^-2	3.82×10^-2
	40–50%	1.88±0.01±0.12	1.87	(2.73±0.01±0.48)×10^-2	2.46×10^-2
	50–60%	1.70±0.01±0.11	1.66	(1.62±0.01±0.28)×10^-2	1.47×10^-2
	60–70%	1.46±0.01±0.12	1.45	(8.35±0.14±1.43)×10^-3	7.58×10^-3
	70–80%	1.27±0.02±0.11	1.25	(3.52±0.06±0.63)×10^-3	3.22×10^-3
	80–90%	1.09±0.02±0.40	1.10	(1.13±0.03±0.23)×10^-3	0.925×10^-3
$^{3} \bar{He}$	0–5%	3.465±0.013±0.154±0.144	3.26	(24.70±0.28±2.29±0.30)×10^-5	25.6×10^-5
	5–10%	3.368±0.014±0.141±0.132	3.21	(20.87±0.26±1.95±0.43)×10^-5	21.4×10^-5
	10–30%	3.237±0.021±0.157±0.150	3.08	(15.94±0.31±1.53±0.34)×10^-5	14.8×10^-5
	30–50%	2.658±0.016±0.084±0.049	2.64	(7.56±0.13±0.70±0.10)×10^-5	7.16×10^-5
	50–90%	2.057±0.023±0.090±0.027	1.77	(1.19±0.08±0.16±0.14)×10^-5	0.931×10^-5
$\bar{t}$	0–10%	3.368±0.241±0.060	3.27	(24.45±1.75±2.71)×10^-5	24.6×10^-5
	10–30%	3.015±0.286±0.040	3.11	(14.19±1.35±1.29)×10^-5	15.9×10^-5
	30–50%	2.524±0.593±0.180	2.68	(7.24±1.70±0.65)×10^-5	7.97×10^-5
	50–90%	1.636±0.226±0.040	1.80	(1.66±0.23±0.16)×10^-5	1.14×10^-5

3.4

Yield ratios of light nuclei

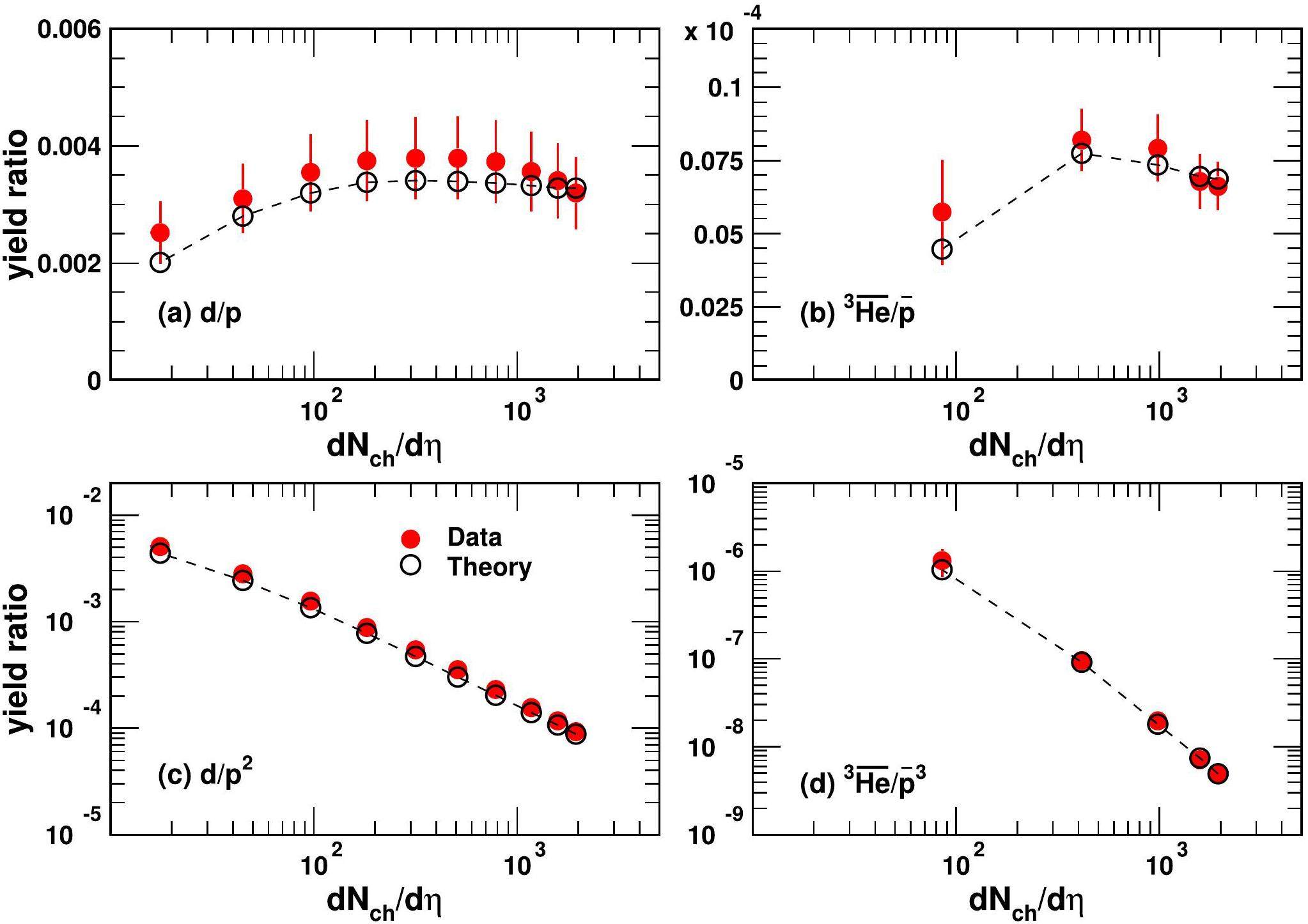
Yield ratios carry information on the intrinsic production correlations of different light nuclei and are predicted to exhibit nontrivial behaviors [61]. This subsection presents the centrality dependence of different yield ratios, such as d/p, $^{3} \bar{He} / \bar{p}$ , d/p², $^{3} \bar{He} / {\bar{p}}^{3}$ , and $\bar{t} /^{3} \bar{He}$ .

Figure 6(a) and (b) show the dN_ch/dη dependence of d/p and $^{3} \bar{He} / \bar{p}$ in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Filled circles with error bars represent experimental data [82], and open circles connected with dashed lines to guide the eye represent the theoretical results. From Eq. (15), we approximately obtain the p_T-integrated yield ratio as $\begin{matrix} \frac{d}{p} \propto \frac{N_{p}}{{〈 R_{f} 〉}^{3} (C_{0} + \frac{σ_{d}^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{\frac{C_{0}}{{〈 γ 〉}^{2}} + \frac{σ_{d}^{2}}{{〈 R_{f} 〉}^{2}}}} \\ = \frac{N_{p}}{{〈 R_{f} 〉}^{3} / 〈 γ 〉} \times \frac{1}{(C_{0} + \frac{σ_{d}^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{C_{0} + \frac{σ_{d}^{2}}{{〈 R_{f} 〉}^{2} / {〈 γ 〉}^{2}}}}, \end{matrix}$ (34) where the angle brackets denote the averaged values. Equation (34) implies that the behavior of d/p is determined by two factors—one is the nucleon number density $\frac{N_{p}}{{〈 R_{f} 〉}^{3} / 〈 γ 〉}$ , and the other is the suppression effect from the relative size of the d to the hadronic source system $\frac{σ_{d}}{〈 R_{f} 〉}$ . Similar case holds for $^{3} \bar{He} / \bar{p}$ . The nucleon number density decreases, specifically from semi-central to central collisions [80], thereby decreasing d/p and $^{3} \bar{He} / \bar{p}$ with increasing dN_ch/dη. The relative size $\frac{σ_{d}}{〈 R_{f} 〉}$ decreases and its suppression effect becomes weak in large hadronic systems, thereby increasing d/p and $^{3} \bar{He} / \bar{p}$ with increasing dN_ch/dη [83]. For significantly high dN_ch/dη area values, the difference in the suppression extents in different centralities becomes insignificant, and the decreasing nucleon number density dominates the decreasing behavior of d/p and $^{3} \bar{He} / \bar{p}$ . For low dN_ch/dη area values, different suppression extents of the relative size in different centralities increase d/p and $^{3} \bar{He} / \bar{p}$ as a function of dN_ch/dη. The final conjunct result from the nucleon number density and the suppression effect first increases d/p and $^{3} \bar{He} / \bar{p}$ from peripheral to semi-central collisions and then decreases them from semi-central to central collisions, as shown in Fig. 6(a) and (b).

Fig. 6

(Color online) Yield ratios (a) d/p, (b)

^{3} \bar{He} / \bar{p}

, (c) d/p², and (d)

^{3} \bar{He} / {\bar{p}}^{3}

as a function of dN_ch/dη in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Filled circles with error bars represent experimental data [62, 77], and open circles connected with dashed lines to guide the eye represent the theoretical results

Figure 6(c) and (d) show d/p² and $^{3} \bar{He} / {\bar{p}}^{3}$ as a function of dN_ch/dη in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Filled circles with error bars represent experimental data [82]. Open circles connected with dashed lines to guide the eye represent the theoretical results. Evidently, both graphs exhibit explicit decreasing trends with the increasing dN_ch/dη and are very different from the previous trends observed for d/p and $^{3} \bar{He} / p$ . As d/p² and $^{3} \bar{He} / {\bar{p}}^{3}$ represent the probability of any pn-pair coalescing into a deuteron and that of any $\bar{p} \bar{p} \bar{n}$ -cluster coalescing into a $^{3} \bar{He}$ , respectively, it is more difficult for any pn-pair or $\bar{p} \bar{p} \bar{n}$ -cluster to recombine into a deuteron or $^{3} \bar{He}$ in the larger hadronic system produced in a more central collision.

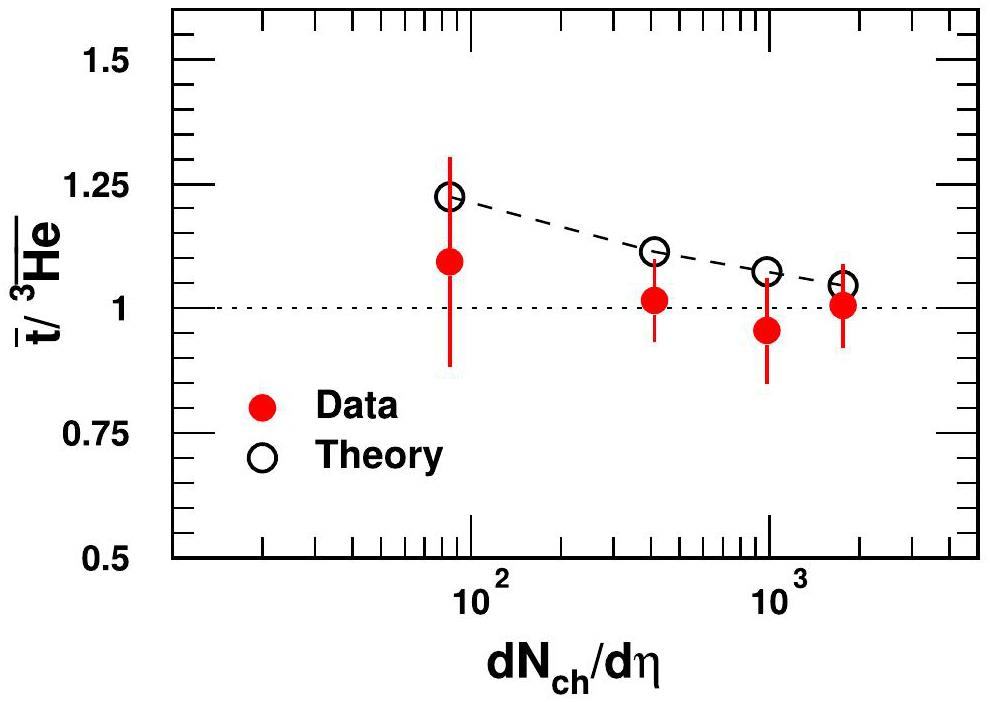
Therefore, a yield ratio t/³He is proposed as a valuable probe to distinguish the thermal and coalescence productions for light nuclei [61]. In the coalescence framework, the ratio is always greater than one and approaches one at large R_f values, where the suppression effect from the nucleus size can be ignored. The smaller the $R_{f}$ value, the higher the deviation of $t /^{3} He$ from one. The same case holds for $\bar{t} /^{3} \bar{He}$ . Figure 7 shows $\bar{t} /^{3} \bar{He}$ as a function of p_T in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV in different centralities 0–10%, 10–30%, 30–50% and 50–90%. Filled circles with error bars represent experimental data [62], and solid lines represent the theoretical results. A reference line of one is plotted as a dotted line. With the increasing p_T, R_f decreases; consequently, our theoretical results increase. However, this trend is different from that observed in the thermal model, where the expectation for this ratio is one [43]. The trend of the data in 0–10%, 10–30%, and 30–50% centralities is increasing, but a final conclusion is hard to make owing to the limited p_T range and the large error bars. Data in the peripheral 50–90% centrality seem to decrease, but further, more precise measurements are needed to confirm this trend. More precise data must be obtained in the future to further distinguish the production mechanisms of $^{3} \bar{He}$ and $\bar{t}$ .

Fig. 7

(Color online) Yield ratio

\bar{t} /^{3} \bar{He}

as a function of p_T in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Filled circles with error bars represent experimental data [62], and solid lines represent the theoretical results

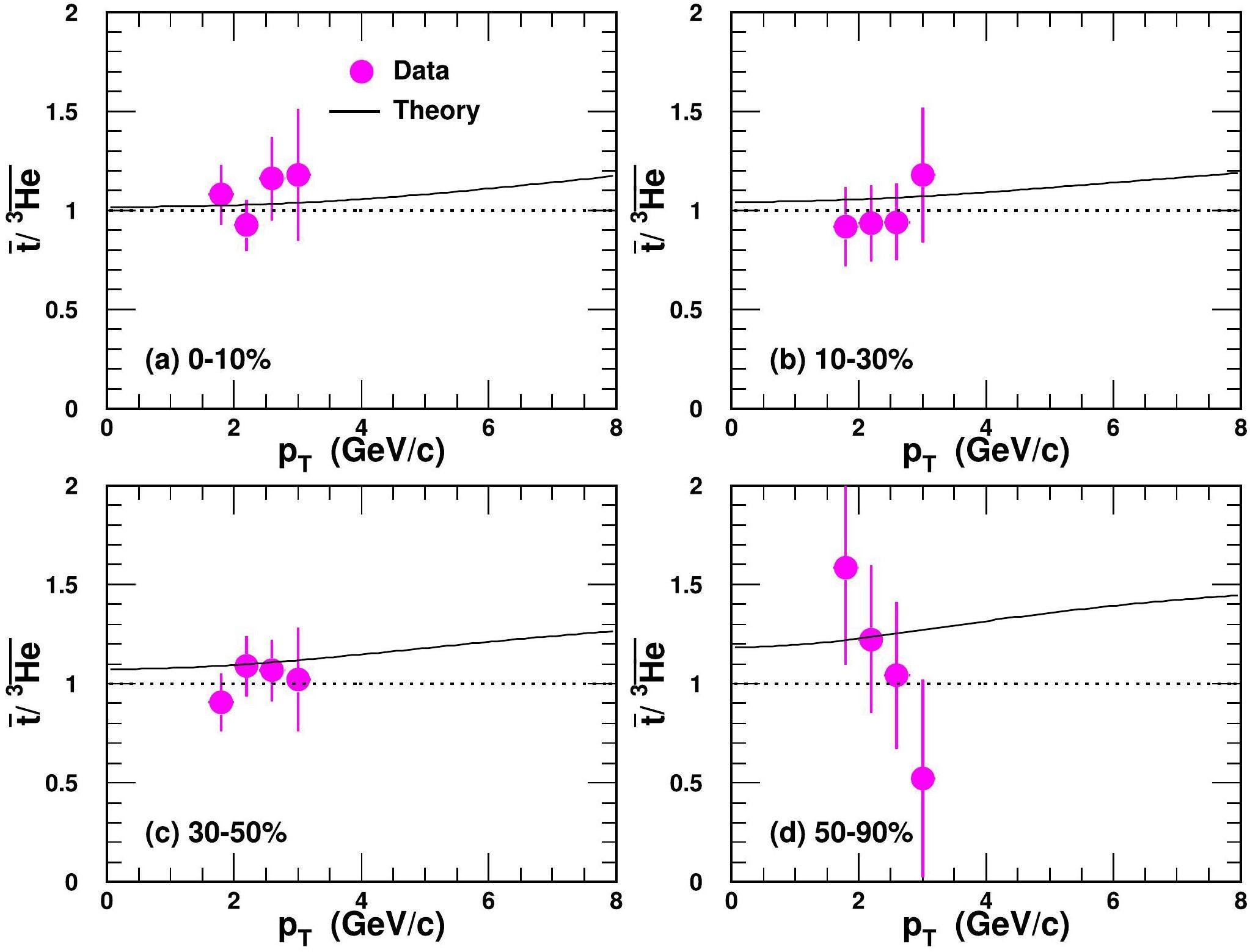
The p_T-integrated yield ratio $\bar{t} /^{3} \bar{He}$ as a function of dN_ch/dη is shown in Fig. 8. Filled circles with error bars represent experimental data [62], and open circles connected with the dashed line to guide the eye represent the theoretical results. A reference line of one is also plotted as a dotted line. Here, $\bar{t} /^{3} \bar{He}$ exhibits a decreasing trend. This is because of the larger dN_ch/dη values, i.e., the larger R_f values decreases $\bar{t} /^{3} \bar{He}$ to be closer to one. Theoretical results of $\bar{t} /^{3} \bar{He}$ in the coalescence model show a non-flat behavior as a function of dN_ch/dη. This is due to the different relative production suppression between $^{3} \bar{He}$ and $\bar{t}$ from their own sizes at different hadronic system scales.

Fig. 8

(Color online) Yield ratio

\bar{t} /^{3} \bar{He}

as a function of dN_ch/dη in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Filled circles with error bars represent experimental data [62], and open circles connected with dashed lines to guide the eye represent the theoretical results

Results of hypertriton and Ω-hypernuclei

This section presents the use of the coalescence model presented in Sect. 2 to study the production of the hypertriton $_{Λ}^{3} H$ and Ω-hypernuclei. Results of the p_T spectra, the averaged p_T, and the yield rapidity densities of $_{Λ}^{3} H$ are presented. Predictions of different Ω-hypernuclei, H(pΩ^-), H(nΩ^-), and H(pnΩ^-) are reported. We propose two groups of observables, both of which exhibit novel behaviors. One group refers to the averaged transverse momentum ratios of light nuclei to the proton and hypernuclei to hyperons. The other is the centrality-dependent yield ratios of light (hyper-)nuclei to the proton (hyperons).

4.1

p_T spectra of Λ and Ω^- hyperons

The p_T spectra of Λ and Ω^- hyperons are necessary for computing p_T distributions of $_{Λ}^{3} H$ and Ω-hypernuclei. We use the blast-wave model to get p_T distribution functions by fitting the experimental data of Λ and Ω^- in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV in 0–10%, 10–30%, and 30–50% centralities [84]. They are shown in Fig. 9. Filled symbols with error bars represent experimental data [84], and dashed lines represent the results of the blast-wave model. Values of the blast-wave fit parameters for Λ and Ω^- are listed in Table 2. The p_T spectra in 0–10%, 10–30%, and 30-50% centralities are scaled by 2⁰, 2^-1, and 2^-2, respectively, for clarity in the figure. We have also studied the p_T spectra of Λ and Ω^- hyperons with the Quark Combination Model developed by the Shandong group (SDQCM) in another work [85], where the results are consistent with the blast-wave model results at low and intermediate p_T regions. Thus, we adopted these Λ and Ω^- hyperons in Fig. 9 to compute productions of the $_{Λ}^{3} H$ and Ω-hypernuclei. The values of parameters a and b in R_f(p_T) for H(pΩ^-) and H(nΩ^-) are the same as those for the deuteron, and those for $_{Λ}^{3} H$ and H(pnΩ^-) are the same as the values for ³He. Thus, our calculated results for the $_{Λ}^{3} H$ and Ω-hypernuclei are parameter-free, and they are more potent for further testing of the coalescence mechanism in describing the production of nuclei with strangeness flavor quantum number.

Fig. 9

(Color online) p_T spectra of (a) Λ and (b) Ω^- in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Symbols with error bars represent experimental data [84], and dashed lines represent the results of the blast-wave model

Values of parameters in the blast-wave model for Λ and Ω^- in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV

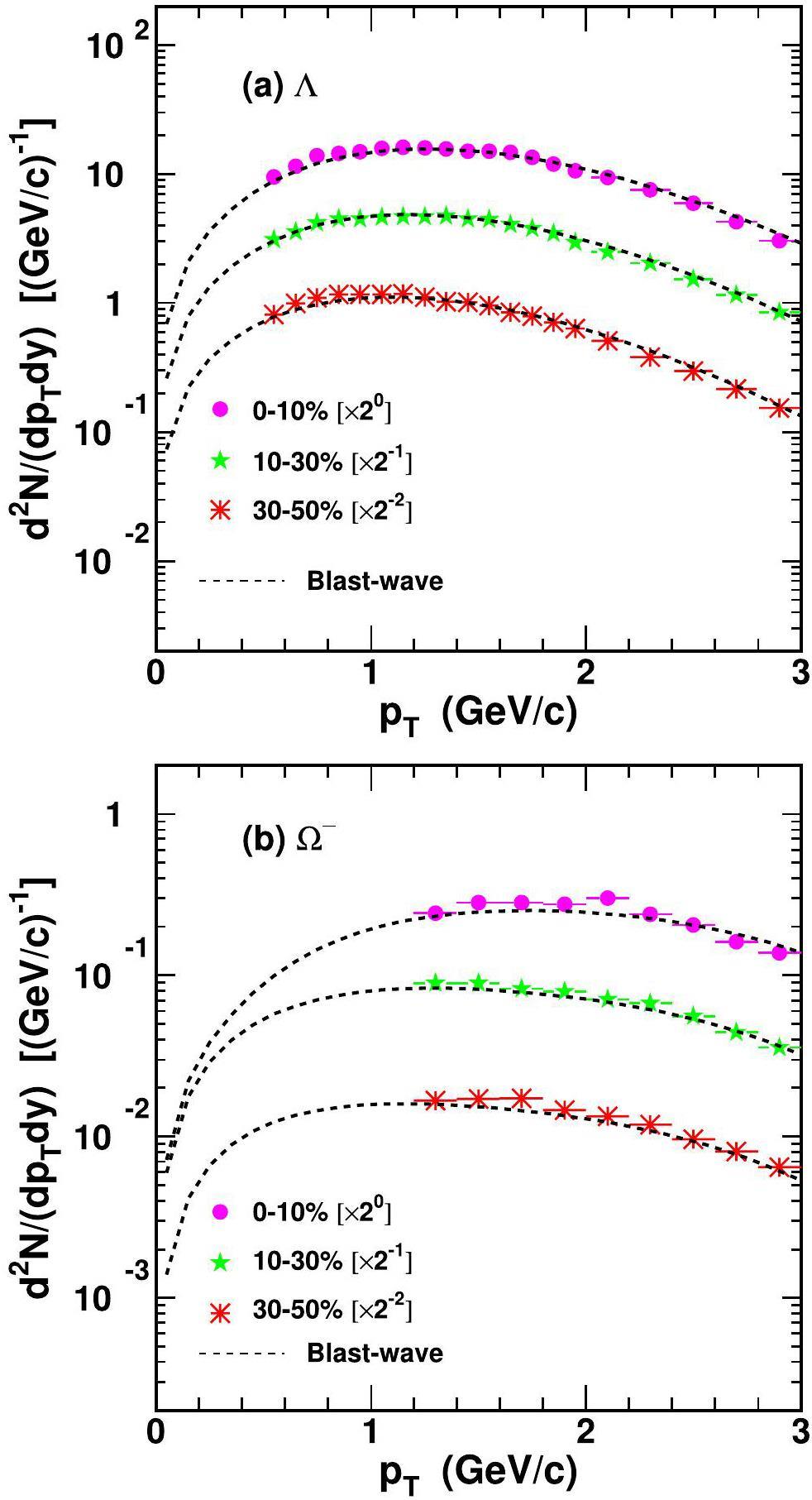
	Centrality	T_kin (GeV)	$〈 β_{T} 〉$	n
Λ	0–10%	0.090	0.670	0.64
	10–30%	0.092	0.648	0.70
	30–50%	0.095	0.622	0.78
$Ω^{-}$	0–10%	0.095	0.627	0.78
	10–30%	0.097	0.569	1.05
	30–50%	0.100	0.549	1.15

4.2

Results of the $_{Λ}^{3} H$

Based on Eq. (27), we compute the production of the $_{Λ}^{3} H$ . Considering that the experimental measurements of the $_{Λ}^{3} H$ suggest a halo structure with a d core encircled by a Λ, we first use $σ_{1} = \sqrt{\frac{2 {(m_{p} + m_{n})}^{2}}{3 (m_{p}^{2} + m_{n}^{2})}} R_{d}$ and $σ_{2} = \sqrt{\frac{2 {(m_{d} + m_{Λ})}^{2}}{9 (m_{d}^{2} + m_{Λ}^{2})}} r_{Λ d}$ . The $Λ - d$ distance $r_{Λ d}$ is evaluated via $r_{Λ d} = \sqrt{ℏ^{2} / (4 μ B_{Λ})}$ [86], where μ is the reduced mass, and the binding energy B_Λ is adopted to be the latest and most precise measurement reported to date 102 keV [63]. We also considered a spherical shape for the $_{Λ}^{3} H$ to execute the calculation to evaluate the influence of the shape on its production. In this case, $σ_{1} = \sqrt{\frac{m_{Λ} (m_{p} + m_{n}) (m_{p} + m_{n} + m_{Λ})}{m_{p} m_{n} (m_{p} + m_{n}) + m_{n} m_{Λ} (m_{n} + m_{Λ}) + m_{Λ} m_{p} (m_{Λ} + m_{p})}} R_{_{Λ}^{3} H}$ , σ₂ $= \sqrt{\frac{4 m_{p} m_{n} {(m_{p} + m_{n} + m_{Λ})}^{2}}{3 (m_{p} + m_{n}) [m_{p} m_{n} (m_{p} + m_{n}) + m_{n} m_{Λ} (m_{n} + m_{Λ}) + m_{Λ} m_{p} (m_{Λ} + m_{p})]}} R_{_{Λ}^{3} H}$ , where the root-mean-square radius $R_{_{Λ}^{3} H}$ is adopted to be 4.9 fm [2]. Figure 10 shows the p_T spectra of the $_{Λ}^{3} H$ in 0–10%, 10–30%, and 30–50% centralities in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Filled symbols with error bars represent the experimental data [64]. Solid lines represent the theoretical results of the coalescence model with the halo structure, and dashed lines represent the results for the model with the spherical shape. The p_T spectra in different centralities are scaled by different factors for clarity, as shown in the figure. As observed from Fig. 10, a weak difference exists in the theoretical results of the p_T spectra between the halo structure and the spherical shape, and the latter gives a little softer p_T spectra. The results with a halo structure approach the available data better, for amplitude and shape. This is also observed in the averaged transverse momenta $〈 p_{T} 〉$ results and yield rapidity densities dN/dy of $_{Λ}^{3} H$ .

Fig. 10

(Color online) p_T spectra of the

_{Λ}^{3} H

in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Filled symbols with error bars represent the experimental data [64]. The solid and dashed lines represent the theoretical results with a halo structure and a spherical shape, respectively

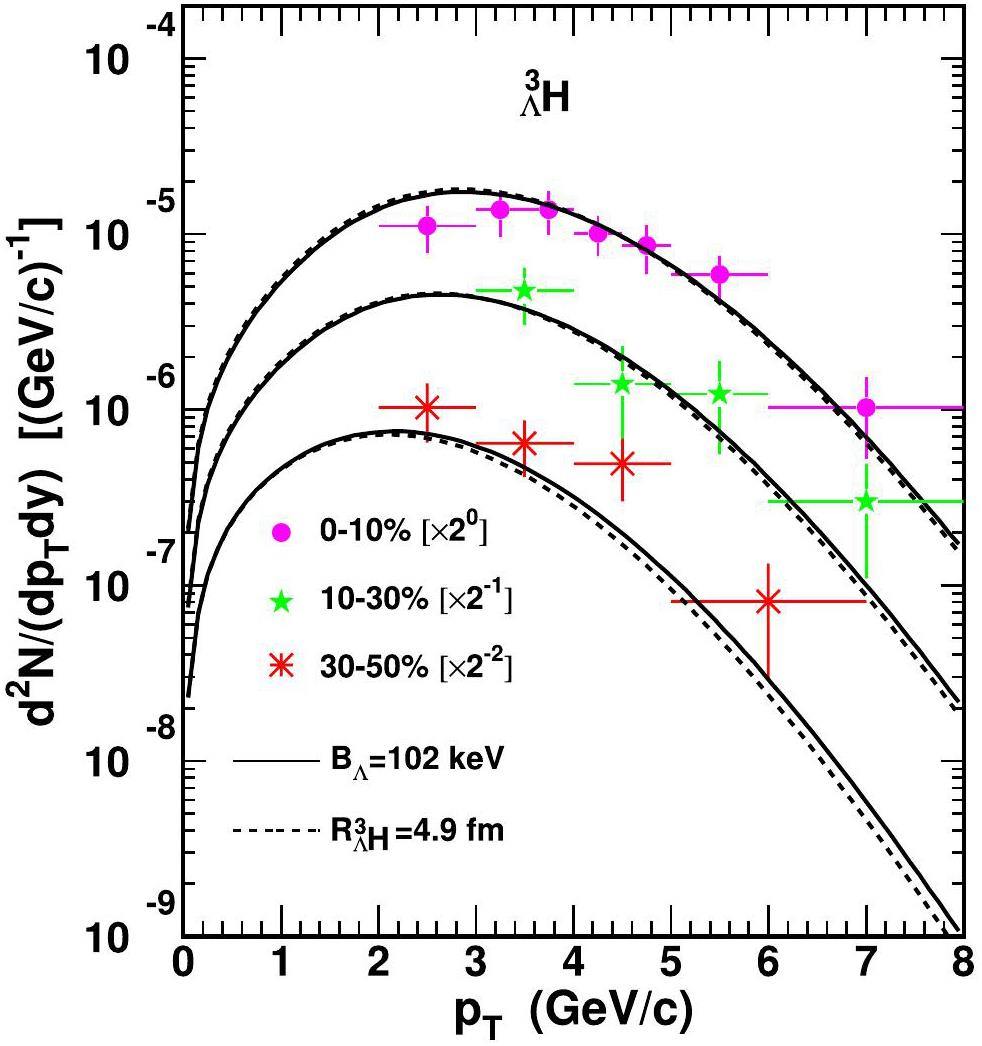
Table 3 presents $〈 p_{T} 〉$ and dN/dy of $_{Λ}^{3} H$ in different centralities in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Experimental data in the seventh column are obtained from Ref. [64]. Theory-4.9 in the third and eighth columns denotes the theoretical results for the model with a spherical shape at $R_{_{Λ}^{3} H} = 4.9$ fm. Theory-102 in the fourth and ninth columns represents the theoretical results at B_Λ=102 keV. Theory-148 in the fifth and tenth columns represents the theoretical results at a word averaged value of B_Λ=148 keV [63]. We also present the theoretical results at B_Λ=410 keV measured by the STAR collaboration [38] in the sixth and eleventh columns. Clear decreasing trends for $〈 p_{T} 〉$ and dN/dy from central to semi-central collisions are observed. This is the same as the results for light nuclei; this is because, in more central collisions, more energy is deposited in the midrapidity region, and collective evolution exists for longer. For the halo structure, with the increase of the B_Λ, the size of the $_{Λ}^{3} H$ decreases, and the suppression effect from the $_{Λ}^{3} H$ size becomes relatively weak. This leads to an increase of dN/dy with the increasing B_Λ. Besides dN/dy, such production suppression effect also affects the p_T distribution [61, 87]. This is because the suppression effect becomes stronger with a larger nucleus size in a smaller system. Recalling that R_f(p_T) decreases with p_T, the $_{Λ}^{3} H$ production is more suppressed in larger p_T areas in the case of larger $_{Λ}^{3} H$ size. Hence, $〈 p_{T} 〉$ follows a decreasing trend with the decreasing B_Λ, as listed in Table 3. This is why the $〈 p_{T} 〉$ of $_{Λ}^{3} H$ is even smaller than that of the triton, whereas the $〈 p_{T} 〉$ of Λ is larger than that of the nucleon.

Averaged transverse momenta

〈 p_{T} 〉

and yield rapidity densities dN/dy of

_{Λ}^{3} H

in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Experimental data in the seventh column are obtained from Ref. [64]. Theory-4.9 denotes the theoretical results for the model with a spherical shape at

R_{_{Λ}^{3} H} = 4.9

fm. Theory-102, Theory-148, and Theory-410 denote the theoretical results for the model with a halo structure at B_Λ=102, 148, and 410 keV, respectively

	Centrality	$〈 p_{T} 〉$ (GeV/c)				$d N / d y (\times 10^{- 5})$
	Centrality	Theory-4.9	Theory-102	Theory-148	Theory-410	Data	Theory-4.9	Theory-102	Theory-148	Theory-410
$_{Λ}^{3} H$	0–10%	3.16	3.19	3.24	3.37	4.83±0.23±0.57	6.09	5.96	7.75	12.7
	10–30%	2.90	2.94	2.99	3.11	2.62±0.25±0.40	2.98	2.99	4.07	7.44
	30–50%	2.46	2.52	2.55	2.65	1.27±0.10±0.14	0.875	0.932	1.35	2.94

Owing to its small binding energy compared to other light (hyper-)nuclei, the $_{Λ}^{3} H$ has a very loosely-bound structure and a relatively large size. It would be easily destroyed after its formation from freezeout nucleons and Λ’s. As a result, the $_{Λ}^{3} H$ is more likely to be produced later than the kinetic freezeout time for the hadronic matter. In Ref. [88], the dependence of the yield of the $_{Λ}^{3} H$ on its freezeout time has been studied, and found that the dependence is very weak. This suggests that $_{Λ}^{3} H$ abundance is essentially determined when nucleons and Λ’s freeze out from the system. So our coalescence calculations based on the same kinetic freezeout with light nuclei can still reasonably describe the experimental data of $_{Λ}^{3} H$ .

4.3

Predictions of Ω-hypernuclei

The nucleon-Ω> dibaryon in the S-wave and spin-2 channel is an interesting candidate for the deuteron-like state [89, 90]. The HAL QCD collaboration has reported the root-mean-square radius of H(pΩ^-) is about 3.24 fm and that of H(nΩ^-) is 3.77 fm [91]. According to Eq. (15), we study their productions, where the spin degeneracy factor $g_{H (p Ω^{-})} = g_{H (n Ω^{-})} = 5 / 8$ . Fig. 11 shows predictions for their p_T spectra in 0-10%, 10-30%, and 30-50% centralities with solid, dashed, and dash-dotted lines, respectively, in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Different lines are scaled by different factors for clarity, as shown in the figure.

Fig. 11

(Color online) Predictions of the p_T spectra of (a) H(pΩ^-) and (b) H(nΩ^-) in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV

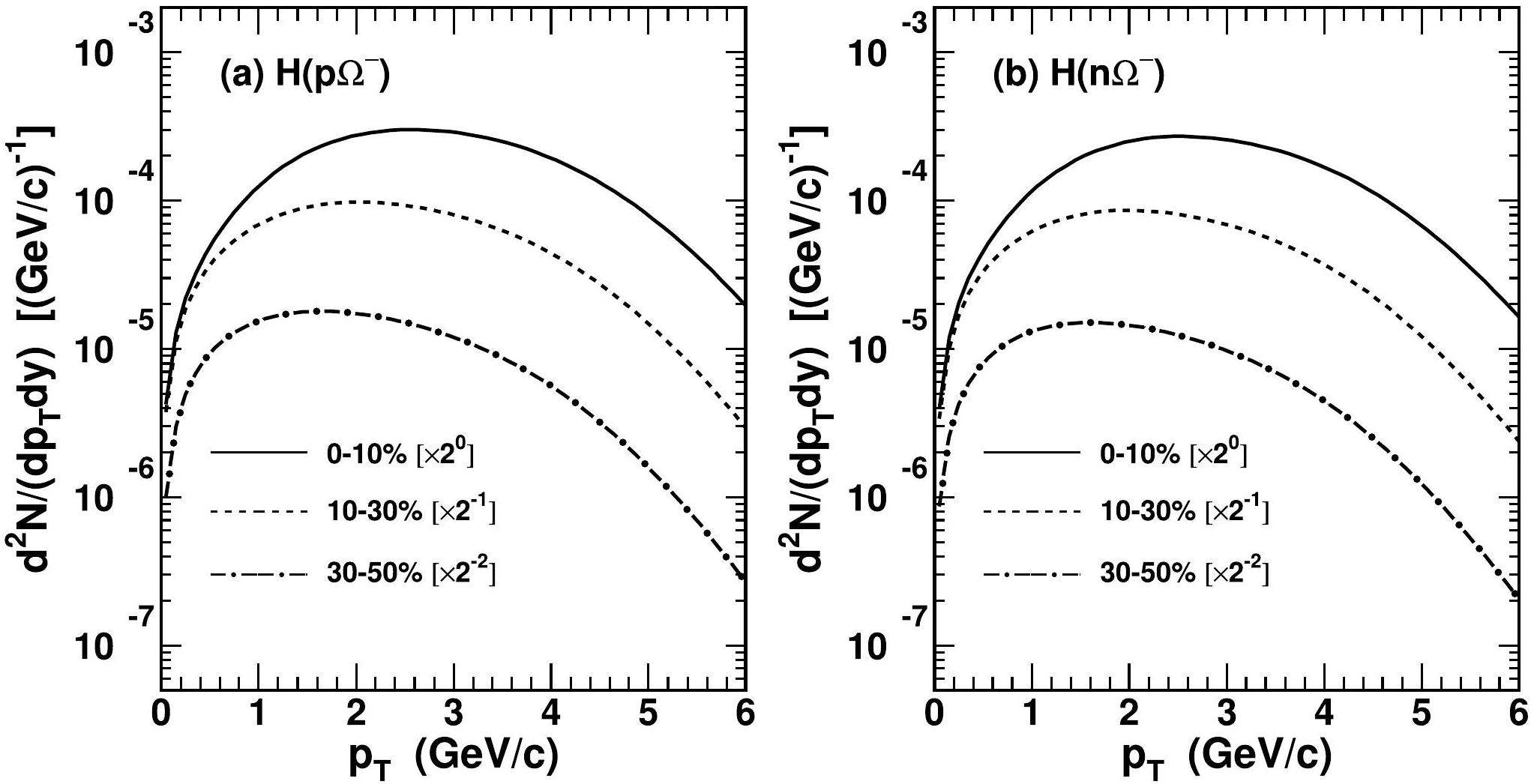
Table 4 presents predictions of the averaged transverse momenta $〈 p_{T} 〉$ and yield rapidity densities dN/dy of H(pΩ^-) and H(nΩ^-). Both of them decrease from central to semi-central collisions, similar to light nuclei and the $_{Λ}^{3} H$ . The slightly lower results of H(nΩ^-) than H(pΩ^-) come from its slightly larger size.

Predictions of averaged transverse momenta

〈 p_{T} 〉

and yield rapidity densities dN/dy of H(pΩ^-) and H(nΩ^-) in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV

	Centrality	$〈 p_{T} 〉$ (GeV/c)	$d N / d y (\times 10^{- 4})$
H(pΩ^-)	0–10%	2.84	9.80
	10–30%	2.44	6.27
	30–50%	2.18	2.16
H(nΩ^-)	0–10%	2.81	8.75
	10–30%	2.41	5.46
	30–50%	2.15	1.79

The H(pnΩ^-) with maximal spin- $\frac{5}{2}$ is proposed to be one of the most promising partners of the t and $_{Λ}^{3} H$ with multi-strangeness flavor quantum number [92]. With Eq. (27), we study its production and the spin degeneracy factor $g_{H (pn Ω^{-})} = 3 / 8$ . As its root-mean-square radius $R_{H (pn Ω^{-})}$ is undetermined, we adopt 1.5, 2.0, and 2.5 fm to execute calculations, respectively. Figure 12 shows predictions of the p_T spectra in 0–10%, 10–30% and 30–50% centralities in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Solid, dashed, and dash-dotted lines denote results with $R_{H (pn Ω^{-})} = 1.5$ , 2.0, and 2.5 fm, respectively, which are scaled by different factors for clarity as shown in the figure. Table 5 presents predictions of the averaged transverse momenta $〈 p_{T} 〉$ and yield rapidity densities dN/dy of H(pnΩ^-). Theory-1.5, Theory-2.0, and Theory-2.5 denote the theoretical results at $R_{H (pn Ω^{-})} = 1.5$ , 2.0, and 2.5 fm, respectively.

Fig. 12

(Color online) Predictions of the p_T spectra of H(pnΩ^-) in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV

Predictions of averaged transverse momenta

〈 p_{T} 〉

and yield rapidity densities dN/dy of H(pnΩ^-) in different centralities in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Theory-1.5, Theory-2.0, and Theory-2.5 denote the theoretical results at

R_{H (pn Ω^{-})} = 1.5

, 2.0, and 2.5 fm, respectively

	Centrality	$〈 p_{T} 〉$ (GeV/c)			$d N / d y (\times 10^{- 6})$
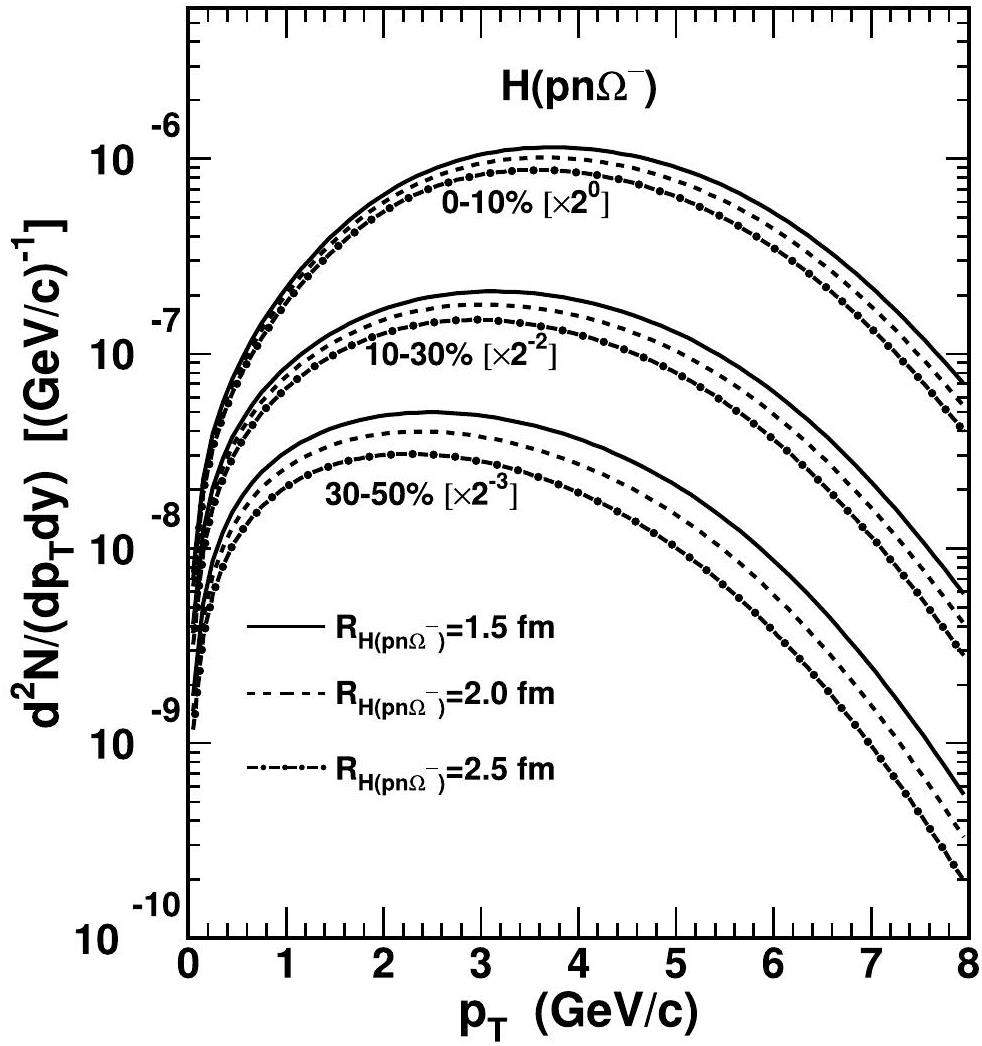
	Centrality	Theory-1.5	Theory-2.0	Theory-2.5	Theory-1.5	Theory-2.0	Theory-2.5
H(pnΩ^-)	0–10%	3.94	3.88	3.82	4.77	4.17	3.56
	10–30%	3.44	3.36	3.29	3.50	2.95	2.41
	30–50%	2.98	2.89	2.81	1.60	1.24	0.92

Our predictions in the central collisions for H(pΩ^-) and H(nΩ^-) are of the same magnitude as those with BLWC and AMPTC models in Ref. [93], and those for H(pnΩ^-) are of the same magnitude as reported in Ref. [94]. Our predictions in other centralities provide more detailed references for centrality-dependent measurements of these Ω-hypernuclei in future LHC experiments.

4.4

Averaged transverse momentum ratios and yield ratios

Based on the results of light nuclei and hypernuclei presented above, we study two groups of interesting observables as powerful probes for the production correlations of different species of nuclei. One group refers to the $〈 p_{T} 〉$ ratios of light nuclei to the proton and hypernuclei to hyperons. The other is their centrality-dependent yield ratios.

Figure 13(a) and (b) show the $〈 p_{T} 〉$ ratios of dibaryon states to baryons and those of tribaryon states to baryons, i.e., $\frac{{〈 p_{T} 〉}_{d}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{H (p Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ , $\frac{{〈 p_{T} 〉}_{H (n Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ , $\frac{{〈 p_{T} 〉}_{t}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{^{3} He}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{_{Λ}^{3} H}}{{〈 p_{T} 〉}_{Λ}}$ and $\frac{{〈 p_{T} 〉}_{H (pn Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ . Open symbols connected by dashed lines to guide the eye represent the theoretical results of the coalescence model. All these $〈 p_{T} 〉$ ratios increase as a function of dN_ch/dη owing to the stronger collective flow in more central collisions. More interestingly, these $〈 p_{T} 〉$ ratios of light nuclei to nucleons and hypernuclei to hyperons happen to offset the $〈 p_{T} 〉$ differences of p, Λ, and Ω^-. This makes them more powerful in bringing the characteristics resulting from the production mechanism to light. Both dibaryon-to-baryon and tribaryon-to-baryon $〈 p_{T} 〉$ ratios exhibit a reverse hierarchy of the nucleus sizes at any centrality, i.e., $\frac{{〈 p_{T} 〉}_{d}}{{〈 p_{T} 〉}_{p}} > \frac{{〈 p_{T} 〉}_{H (p Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}} > \frac{{〈 p_{T} 〉}_{H (n Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ as $R_{d} < R_{H (p Ω^{-})} < R_{H (n Ω^{-})}$ , and $\frac{{〈 p_{T} 〉}_{t}}{{〈 p_{T} 〉}_{p}} > \frac{{〈 p_{T} 〉}_{^{3} He}}{{〈 p_{T} 〉}_{p}} > \frac{{〈 p_{T} 〉}_{H (p n Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}} > \frac{{〈 p_{T} 〉}_{_{Λ}^{3} H}}{{〈 p_{T} 〉}_{Λ}}$ as $R_{t} < R_{^{3} He} < R_{H (pn Ω^{-})} < R_{_{Λ}^{3} H}$ . Here, we consider results of H(pnΩ^-) at $R_{H (pn Ω^{-})} = 2$ fm for exhibition, and those at $R_{H (pn Ω^{-})} = 1.5$ , 2.5 fm give the same conclusion, a reverse hierarchy of the nucleus size. Such reverse hierarchy comes from stronger production suppression for light (hyper-) nuclei with larger sizes in higher p_T regions. This production property is considerably different from the thermal model in which these ratios are approximately equal to each other [43].

Fig. 13

(Color online) The

〈 p_{T} 〉

ratios of (a) dibaryon states to baryons, (b) tribaryon states to baryons, and the yield ratios of (c) dibaryon states to baryons, (d) tribaryon states to baryons as a function of dN_ch/dη in Pb+Pb collisions at

\sqrt{s_{NN}} = 5.02

TeV. Different open symbols connected with dashed lines to guide the eye are the theoretical results

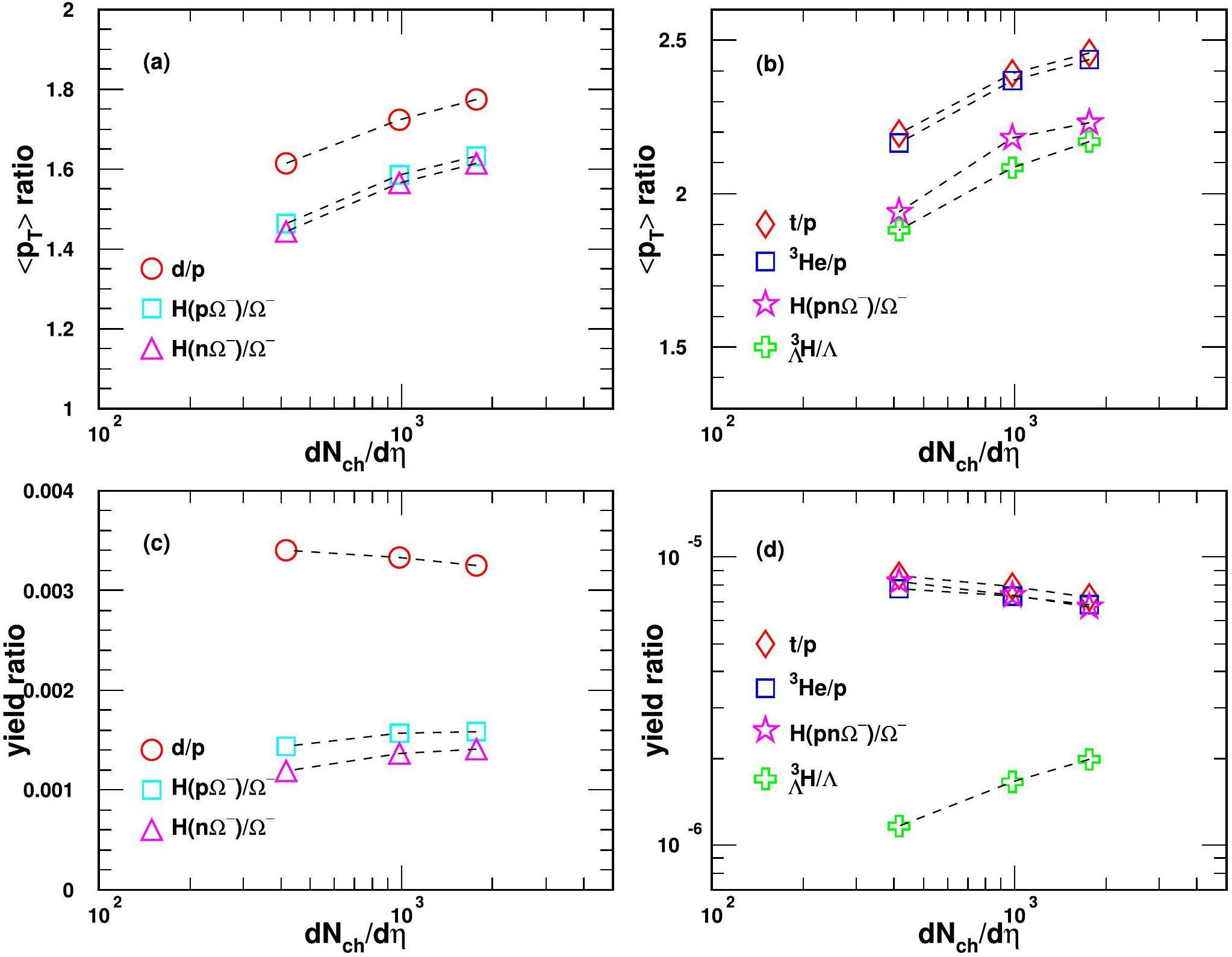
Figure 13(c) and (d) show yield ratios of dibaryon states to baryons and those of tribaryon states to baryons. Open symbols connected with dashed lines to guide the eye represent the theoretical results of the coalescence model. Some of these ratios such as d/p, t/p, ³He/p and H(pnΩ^-)/Ω^- decrease while the others H(pΩ^-)/Ω^-, $H (n Ω^{-}) / Ω^{-}$ and $_{Λ}^{3} H / Λ$ increase as a function of dN_ch/dη.

From Eqs. (15) and (27), similar as Eq. (34), we approximately have $\begin{array}{l} \frac{d}{p} \sim \frac{H (p Ω^{-})}{Ω^{-}} \sim \frac{H (n Ω^{-})}{Ω^{-}} \\ \propto \frac{N_{p}}{{〈 R_{f} 〉}^{3} (C_{0} + \frac{σ^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{\frac{C_{0}}{{〈 γ 〉}^{2}} + \frac{σ^{2}}{{〈 R_{f} 〉}^{2}}}} \\ = \frac{N_{p}}{{〈 R_{f} 〉}^{3} / 〈 γ 〉} \times \frac{1}{(C_{0} + \frac{σ^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{C_{0} + \frac{σ^{2}}{{〈 R_{f} 〉}^{2} / {〈 γ 〉}^{2}}}}, \end{array}$ (35) and $\begin{array}{l} \frac{t}{p} \sim \frac{^{3} He}{p} \sim \frac{_{Λ}^{3} H}{Λ} \sim \frac{H (p n Ω^{-})}{Ω^{-}} \\ \propto \frac{N_{p}^{2}}{{〈 R_{f} 〉}^{6} (C_{0} + \frac{σ_{1}^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{\frac{C_{0}}{{〈 γ 〉}^{2}} + \frac{σ_{1}^{2}}{{〈 R_{f} 〉}^{2}}}} \\ \times \frac{1}{(\frac{4 C_{0}}{3} + \frac{σ_{2}^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{\frac{4 C_{0}}{3 {〈 γ 〉}^{2}} + \frac{σ_{2}^{2}}{{〈 R_{f} 〉}^{2}}}} \\ = {(\frac{N_{p}}{{〈 R_{f} 〉}^{3} / 〈 γ 〉})}^{2} \frac{1}{(C_{0} + \frac{σ_{1}^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{C_{0} + \frac{σ_{1}^{2}}{{〈 R_{f} 〉}^{2} / {〈 γ 〉}^{2}}}} \\ \times \frac{1}{(\frac{4 C_{0}}{3} + \frac{σ_{2}^{2}}{{〈 R_{f} 〉}^{2}}) \sqrt{\frac{4 C_{0}}{3} + \frac{σ_{2}^{2}}{{〈 R_{f} 〉}^{2} / {〈 γ 〉}^{2}}}} . \end{array}$ (36) Eqs. (35) and (36) show that behaviors of these two-particle yield ratios closely relate with the nucleon number density $\frac{N_{p}}{{〈 R_{f} 〉}^{3} / 〈 γ 〉}$ and the production suppression effect items of the relative size of nuclei to hadronic source systems $\frac{σ}{〈 R_{f} 〉}$ , $\frac{σ_{1}}{〈 R_{f} 〉}$ and $\frac{σ_{2}}{〈 R_{f} 〉}$ .

For the limit case of the nuclei with considerably small (negligible) sizes compared to the hadronic system scale, the dN_ch/dη-dependent behaviors of their yield ratios to baryons are completely determined by the nucleon number density. For the general case, the item $\frac{σ_{i}}{〈 R_{f} 〉}$ suppresses these ratios, and such suppression becomes weaker in larger hadronic systems. This makes these yield ratios increase from peripheral to central collisions, i.e., with the increasing dN_ch/dη. The larger the nucleus size, the stronger the increase as a function of $d N_{ch} / d η$ . The nucleon density decreases with increasing $d N_{ch} / d η$ [80], which makes these ratios decrease. As the root-mean-square radii of d, t, $^{3} He$ , and H(pnΩ^-) are approximately equal or smaller than 2 fm, the decreasing nucleon density dominates the behaviors of their yield ratios to baryons. But for H(pΩ^-), H(nΩ^-) and $_{Λ}^{3} H$ , their root-mean-square radii are larger than 3 fm, the production suppression effect from their sizes becomes dominant, which leads their yield ratios to baryons increase as a function of dN_ch/dη. Such different centrality-dependent behaviors can help justify the sizes of more light nuclei and hypernuclei in future experiments.

Summary

This study extended the analytical coalescence model previously developed for the productions of light nuclei to include the hyperon coalescence to simultaneously study the production characteristics of d, $^{3} \bar{He}$ , $\bar{t}$ , $_{Λ}^{3} H$ , and Ω-hypernuclei. To this end, the formulae of momentum distributions of two baryons coalescing into dibaryon states and three baryons coalescing into tribaryon states were derived. The relationships of dibaryon states and tribaryon states with primordial baryons in momentum space in the laboratory frame were presented, and the effects of the hadronic system scale and the nucleus’s size on the nucleus production were demonstrated.

The extended coalescence model was applied to Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV. Available data on B₂ and B₃, p_T spectra, averaged transverse momenta, and yield rapidity densities of the d, $^{3} \bar{He}$ , $\bar{t}$ , and $_{Λ}^{3} H$ measured by the ALICE collaboration were explained. Moreover, the p_T spectra, averaged transverse momenta, and yield rapidity densities of different Ω-hypernuclei, e.g., H(pΩ^-), H(nΩ^-), and H(pnΩ^-), were predicted for future experimental measurements.

Notably, this study presented two groups of novel observables. One referred to the averaged transverse momentum ratios $\frac{{〈 p_{T} 〉}_{d}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{H (p Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ , $\frac{{〈 p_{T} 〉}_{H (n Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ , $\frac{{〈 p_{T} 〉}_{t}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{^{3} He}}{{〈 p_{T} 〉}_{p}}$ , $\frac{{〈 p_{T} 〉}_{_{Λ}^{3} H}}{{〈 p_{T} 〉}_{Λ}}$ , and $\frac{{〈 p_{T} 〉}_{H (pn Ω^{-})}}{{〈 p_{T} 〉}_{Ω^{-}}}$ . These ratios exhibited a reverse hierarchy according to the sizes of the nuclei themselves at any collision centrality. The other group of observables involved the centrality-dependent yield ratios $\frac{d}{p}$ , $\frac{H (p Ω^{-})}{Ω^{-}}$ , $\frac{H (n Ω^{-})}{Ω^{-}}$ , $\frac{t}{p}$ , $\frac{^{3} He}{p}$ , $\frac{_{Λ}^{3} H}{Λ}$ , and $\frac{H (pn Ω^{-})}{Ω^{-}}$ . Some of these yield ratios $\frac{d}{p}$ , $\frac{t}{p}$ , $\frac{^{3} He}{p}$ , and $\frac{H (pn Ω^{-})}{Ω^{-}}$ decreased while the others $\frac{H (p Ω^{-})}{Ω^{-}}$ , $\frac{H (n Ω^{-})}{Ω^{-}}$ , and $\frac{_{Λ}^{3} H}{Λ}$ increased as a function of dN_ch/dη. Such different trends were caused by different production suppression degrees from the nucleus sizes. The behaviors of these two groups of ratios in the coalescence mechanism were different from the thermal model. Therefore, these are powerful observables for probing the production mechanism of light (hyper-)nuclei and can reveal the production mechanisms of different types of nuclei in the coalescence framework.

References

J. Chen, D. Keane, Y.G. Ma et al.,

Antinuclei in Heavy-Ion Collisions

. Phys. Rept. 760, 1-39 (2018). arXiv:1808.09619, https://doi.org/10.1016/j.physrep.2018.07.002

Production characteristics of light nuclei, hypertritons, and Ω-hypernuclei in Pb+Pb collisions at sNN=5.02 TeV

Introduction

Coalescence model

Formalism of two bodies coalescing into dibaryon states

Formalism of three bodies coalescing into tribaryon states

Results of light nuclei

Coalescence factor of light nuclei

pT spectra of light nuclei

Averaged transverse momenta and yield rapidity densities of light nuclei

Yield ratios of light nuclei

Results of hypertriton and Ω-hypernuclei

pT spectra of Λ and Ω- hyperons

Results of the Λ3H

Predictions of Ω-hypernuclei

Averaged transverse momentum ratios and yield ratios

Summary

Production characteristics of light nuclei, hypertritons, and Ω-hypernuclei in Pb+Pb collisions at $\sqrt{s_{NN}} = 5.02$ TeV

p_T spectra of light nuclei

p_T spectra of Λ and Ω^- hyperons

Results of the $_{Λ}^{3} H$