Introduction

Since the identification of the first Λ hyperfragment in an emulsion exposed to cosmic rays in 1952 [1], Λ hypernuclei have been intensively studied, both experimentally [2-9] and theoretically [10-16]. Recent studies have mainly focused on hyperon-nucleon (YN) interactions [16-25], hypernuclear structure [15, 24, 26-31], and hypernuclear decay [7, 32-38] and so on. understanding the internal structure and YN interactions is a challenging goal in nuclear physics.

A single-Λ hypernucleus, which consists of a normal core nucleus and a Λ hyperon, provides a unique environment for investigating ΛN interactions. The degree of freedom of strangeness liberates the Λ hyperon from the constraints of the nuclear Pauli exclusion principle, allowing it to penetrate deeply into the nucleus and alter the core structure as an impurity. Therefore, the presence of impurity effects in the Λ hypernuclear system is crucial for illuminating nuclear features that might remain obscure in normal nuclei, including both the structure and interactions.

With the emergence of new and improved experimental facilities, the measurement of Λ hypernuclear binding energies spans a broad mass range from light to heavy with high resolution. These advancements not only enhance our understanding of Λ hypernuclear properties compared to previous studies but also pose challenges to the development and refinement of theoretical approaches in hypernuclear structures. To comprehensively describe these crucial nuclear properties, various types of ΛN interactions have been introduced and discussed. These include the Skyrme types [39-47], relativistic types [48-54], Nijmegen soft-core (NSC) types [55-57], Nijmegen extended-soft-core (ESC) types [13, 18, 21, 58-60] and chiral effective field theory ($\chi \text{EFT}$) types [22, 25, 61-63]. By using effective Λ-nucleon interactions, Λ hypernuclei have been comprehensively characterized within various nuclear models, including the anti-symmetrized molecular dynamics model [30, 64-67], shell model [15, 68, 69], and mean field model [12, 31, 51-54, 70-78].

Over the past decades, two types of ΛN interactions have been proposed and adopted in the Skyrme-Hartree-Fock (SHF) model. The first type, derived from Brueckner-Hartree-Fock (BHF) calculations of hypernuclear matter, has a more microscopic basis. The second type is phenomenological Skyrme-type interactions, which are determined by fitting the experimental binding energies of Λ hypernuclei. Microscopic interactions originate from deeper physical principles (e.g., explicit momentum/density dependence). However, owing to the limited experimental data on Λ hypernuclei at present, microscopic interactions do not describe Λ hypernuclei very well. In contrast, phenomenological Skyrme-type interactions, which are determined by fitting the experimental binding energies of Λ hypernuclei, can better predict the ground-state properties of the hypernuclei.

Although Skyrme interactions provide a good description of hypernuclei, there are still some details that require improvement. For the Skyrme interaction, the parameter sets are RAY12 [39, 40], YBZ1 [42], SKSH2 [43], HPΛ2 [45], and SLL4 [47]. Different interactions were obtained by fitting different ground-state or excited-state energies of Λ hypernuclei. Moreover, different three-body interactions were considered in different Skyrme interactions. The Skyrme interaction with three-body interaction derived from the G-matrix can provide a good description of Λ hypernuclei ranging from light mass to heavy mass, such as SLL4 and HPΛ2. However, the Skyrme interaction with three-body interaction derived from the ΛNN contact force, like RAY12, YBZ1, and SKSH2, cannot provide a global description. A noticeable feature in the calculated results with the ΛNN contact force is that the parameters fitted to the binding energies of light-mass Λ hypernuclei, such as RAY12, YBZ1, and SKSH2, clearly fail to predict the experimental results for heavy-mass hypernuclei. Moreover, the calculated binding energies of heavy-mass Λ hypernuclei are smaller than the experimental values [77]. This underbinding shows that the ΛN potential depth is not sufficiently deep in heavy-mass Λ hypernuclei. This phenomenon is found not only in Skyrme interactions but also in other types of hyperon-nucleon interactions. For microscopic interactions, the calculated binding energies with the NSC89 interaction were smaller than the experimental results for heavy Λ hypernuclei [26]. The NSC97f interaction gives good results for heavy Λ hypernuclei, but its prediction for light Λ hypernuclei is approximately 2 MeV higher [26]. For the optical potential, the experimental binding energies of heavy Λ hypernuclei are larger than those calculated with the interaction obtained by fitting the 1s and 1p states of ${}_{\text{Λ}}^{16}\text{N}$ [14]. Notably, the behavior of light-mass hypernuclei with symmetric nuclear matter core nuclei differs from that of heavy-mass hypernuclei with asymmetric nuclear matter core nuclei. This highlights the significant impact of isospin of the core nuclei on binding energy calculations.

In previous Skyrme-type interactions, only the simplest form of the contact ΛNN three-body interaction was considered [79]. However, an important feature of the ΛNN interaction is its proportionality to the isospin factor ${\tau }_1\cdot {\tau }_2$ for the two nucleons involved [80]. Because of the isospin factor, ΛNN interaction between ’core’ nucleons and ’excess’ neutrons is suppressed when excess neutrons occupy shell-model orbits higher than those occupied by protons [14, 81]. By adding excess neutron, the influence of the isospin factor can be considered in the three-body interaction of Skyrme-type interactions. The three-body ΛNN interaction usually contributes significantly to the repulsion of Nv forces, although there is no assurance that the three-body ΛNN interaction is universally repulsive. Therefore, the repulsive ΛNN interaction decreases owing to neutron excess, which is expected to solve the underbinding in heavy-mass Λ hypernuclei.

In the optical potential methodology [14, 81], the effects of neutron excess, considered using a more phenomenological approach, are discussed to address the underbinding issue in heavy-mass Λ hypernuclei. Deformation is a fundamental property of hypernuclei and has a significant impact on the B_Λ and other properties, especially for Λ states above the 1s state; therefore, it cannot be ignored. Furthermore, the pairing force is crucial in the calculation of nuclear properties [82]. In this study, the impact of neutron excess on deformed Λ hypernuclei is discussed in the framework of the SHF method with pairing force, which deals with the Bardeen-Cooper-Schrieffer (BCS) approximation.

The remainder of this paper is organized as follows: In Sect. 2, the theoretical method and interaction are briefly described. In Sect. 3, we discuss the binding energies of Λ hypernuclei and present the Λ single-particle potential along with the changes in the density distributions due to neutron excess. Finally, a summary is given in Sect. 4.

Theoretical descriptions

In the SHF approach, the total energy of a hypernucleus is given by [40, 83-87] $E={\displaystyle \int }{d}^{3}r\epsilon (r)\mathrm{,}$ (1) where the energy-density functional is $\epsilon ={\epsilon }_N\left[{\rho }_{\text{n}}\mathrm{,}{\rho }_{\text{p}}\mathrm{,}{\tau }_{\text{n}}\mathrm{,}{\tau }_{\text{p}}\mathrm{,}{J}_{\text{n}}\mathrm{,}{J}_{\text{p}}\right]+{\epsilon }_{\text{Λ}}\left[{\rho }_{\text{n}}\mathrm{,}{\rho }_{\text{p}}\mathrm{,}{\rho }_{\text{Λ}}\mathrm{,}{\tau }_{\text{Λ}}\mathrm{,}{J}_N\mathrm{,}{J}_{\text{Λ}}\right]\mathrm{,}$ (2) with εN and ${\epsilon }_{\text{Λ}}$ as the contributions from NN and ΛN interactions, respectively. For the nucleonic functional εN, we used the standard Skyrme force SLy4 [88]. The one-body density ρq, kinetic density τq, and s.o. current $J_q$ are $\left({\rho }_q\mathrm{,}{\tau }_q\mathrm{,}{J}_q\right)={\displaystyle \sum _{k=1}^{N_q}}{n}_q^k\left[\left|{\varphi }_q^k{|}^2\mathrm{,}\right|\nabla {\varphi }_q^k{|}^2\mathrm{,}{\varphi }_q^k{}^{*}\left(\nabla {\varphi }_q^k\times \sigma \right)/i\right]\mathrm{,}$ (3) where ${\varphi }_q^k\left(k=\mathrm{1,}\cdots N_q\right)$ are the s.p. wave functions of the k-th occupied states for the different particles $q=n\mathrm{,}p\mathrm{,}\text{Λ}$. The occupation probabilities $n_q^k$ were calculated by considering pairing within a BCS approximation for nucleons only. The pairing interaction between nucleons is considered as a density-dependent δ force [82, 89]: $V_q\left(r_1\mathrm{,}{r}_2\right)={V^{\prime }}_q\left[1-\frac{{\rho }_N\left(\left(r_1+r_2\right)/2\right)}{0.16{\text{fm}}^{-3}}\right]\delta \left(r_1-r_2\right)\mathrm{,}$ (4) where pairing strengths ${V^{\prime }}_p={V^{\prime }}_n=-410$ MeVfm³ are used for light-mass nuclei [90], and ${V^{\prime }}_p=-1146$ MeV fm³, ${V^{\prime }}_n=-999$ MeV fm³ for medium-mass and heavy-mass nuclei [85]. A smooth energy cutoff was employed in the BCS calculations [91]. In the case of an odd number of nucleons, the orbit occupied by the unpaired nucleon is blocked, as described in Ref. [92].

Through the variation in the total energy, Eq. (1), one derives the SHF Schödinger equation for both nucleons and hyperons: $\left[-\nabla \cdot \frac{1}{2m_q^{*}\left(r\right)}\nabla +V_q\left(r\right)-i{W}_q\left(r\right)\cdot (\nabla \times \sigma )\right]{\varphi }_q^k\left(r\right)=e_q^k{\varphi }_q^k\left(r\right),$ (5) where $V_q\left(r\right)$ is the central part of the mean field depending on the density and $W_q\left(r\right)$ is the s.o. interaction part [83, 89].

For the Skyrme-type interactions, ${\epsilon }_{\text{Λ}}$ is given as [40, 42, 44, 46, 47] $\begin{array}{c}{\epsilon }_{\text{Λ}}=\frac{{\tau }_{\text{Λ}}}{2m_{\text{Λ}}}+a_0{\rho }_{\text{Λ}}{\rho }_N+a_3{\rho }_{\text{Λ}}{\rho }_N^{1+\alpha }+{a^{\prime }}_3{\rho }_{\text{Λ}}\left({\rho }_N^2+2{\rho }_n{\rho }_p\right)\\ +a_1\left({\rho }_{\text{Λ}}{\tau }_N+{\rho }_N{\tau }_{\text{Λ}}\right)-a_2\left({\rho }_{\text{Λ}}\text{Δ}{\rho }_N+{\rho }_N\text{Δ}{\rho }_{\text{Λ}}\right)/2\\ -a_4\left({\rho }_{\text{Λ}}\nabla \cdot J_N+{\rho }_N\nabla \cdot J_{\text{Λ}}\right)\mathrm{,}\end{array}$ (6) where the last term is the s.o. part, which was adjusted to reproduce the observed s.o. splitting of ${}_{\text{Λ}}^{13}\text{C}$ in our approach [31, 93, 94]. Previous studies [31] have shown that the effect of this term is small (0.1 MeV), which is ignored in this work. Two alternative parametrizations of nonlinear effects are indicated, that is, the first one a₃ motivated by a G-matrix [41, 45, 95] and the second one a_3’ derived from a ΛNN contact force [39, 40]. In symmetric matter the two choices are equivalent when $a_3\equiv \frac{3}{2}{a^{\prime }}_3$ and α=1 [46].

Then one obtains the corresponding SHF mean fields: $\begin{array}{c}{V}_{\text{Λ}}=a_0{\rho }_N+a_1{\tau }_N-a_2\text{Δ}{\rho }_N\\ +a_3{\rho }_N^{1+\alpha }+{a^{\prime }}_3\left({\rho }_N^2+2{\rho }_n{\rho }_p\right)\mathrm{,}\end{array}$ (7) $\begin{array}{c}{V}_n^{\left(\text{Λ}\right)}=a_0{\rho }_{\text{Λ}}+a_1{\tau }_{\text{Λ}}-a_2\text{Δ}{\rho }_{\text{Λ}}\\ +a_3\left(1+\alpha \right){\rho }_{\text{Λ}}{\rho }_N^{\alpha }+2{a^{\prime }}_3{\rho }_{\text{Λ}}\left(2{\rho }_N-{\rho }_n\right)\mathrm{.}\end{array}$ (8) $\begin{array}{c}{V}_p^{\left(\text{Λ}\right)}=a_0{\rho }_{\text{Λ}}+a_1{\tau }_{\text{Λ}}-a_2\text{Δ}{\rho }_{\text{Λ}}\\ +a_3\left(1+\alpha \right){\rho }_{\text{Λ}}{\rho }_N^{\alpha }+2{a^{\prime }}_3{\rho }_{\text{Λ}}\left(2{\rho }_N-{\rho }_p\right)\mathrm{.}\end{array}$ (9) In the previous Skyrme interactions [79], only the simplest form of the three-body interaction was considered, which is given by $t_{123}=\delta \left({\text{r}}_1-{\text{r}}_2\right)\delta \left({\text{r}}_3-{\text{r}}_1\right)t_3\mathrm{.}$ (10) The three-body interaction is only related to the coordinates of the hyperons and nucleons. However, an important feature of the ΛNN interaction is its proportionality to the isospin factor ${\tau }_1\cdot {\tau }_2$ for the two nucleons involved [80]. Expanding the isospin operator in terms of raising and lowering operators within the matrix elements, we obtain $\begin{array}{ll}{\displaystyle \sum _{ijk}}\langle ijk\left|{\tau }_i\cdot {\tau }_j\right|ijk\rangle =\hfill & {\displaystyle \sum _{\begin{array}{c}i\in \text{ core}\\ j\in \text{ valence}\text{excess}\end{array}}}\langle i\left|{\tau }_{iz}\right|i\rangle \langle j\left|{\tau }_{jz}\right|j\rangle \hfill \\ \hfill & +{\displaystyle \sum _{ij\in \text{others}}}\langle ij\left|{\tau }_{iz}{\tau }_{jz}\right|ij\rangle \hfill \\ \hfill & +{\displaystyle \sum _{ij}}\langle ij\left|\frac{\left({\tau }_{i+}{\tau }_{j-}+{\tau }_{i-}{\tau }_{j+}\right)}{2}\right|ij\rangle ，\hfill \end{array}$ (11) where i and j are the indices of the nucleons and k is the index of the Λ hyperon. ‘core’ refers to the isospin T=0 part of nuclei while ‘valence excess’ refers to the part of nuclei where excess neutrons occupy shell-model orbits higher than those occupied by protons. For each j, ${\displaystyle \sum _{i\in \text{core}}}\langle i\left|{\tau }_{iz}\right|i\rangle =0$ since the isospin of the ‘core’ is zero. Therefore, the first term in Eqs. (11) vanishes: The third term in Eq. (11) is the exchange partner of such matrix elements that renormalize the two-body ΛN interaction [80]. Thus, the ΛNN interaction between ‘core’ nucleons and ‘excess’ neutrons is expected to be suppressed when the excess neutrons occupy shell-model orbits higher than those occupied by protons [14, 81]. By introducing excess neutrons, the effect of the isospin factor can be incorporated into the three-body interactions of the Skyrme-type interactions.

When excess neutrons occupy shell-model orbits that are higher than those occupied by protons, ρN is separated as: ${\rho }_N\left(r\right)={\rho }^{\text{c}}\left(r\right)+{\rho }^{\text{v}}\left(r\right)={\rho }_{\text{n}}^{\text{c}}\left(r\right)+{\rho }_{\text{p}}^{\text{c}}\left(r\right)+{\rho }_{\text{n}}^{\text{v}}\left(r\right),$ (12) where ρ^c refers to the Z protons plus the Z neutrons occupying the same nuclear ‘core’ orbits, and ρ^v refers to the (N-Z) excess neutrons associated with the nuclear periphery [14, 81]. By deleting the cross term ${\rho }^{\text{c}}{\rho }^{\text{v}}$ to account for the neutron excess [14, 80, 81], Eq. (6) and Eq. (7) can be rewritten as $\begin{array}{ll}{\epsilon }_{\text{Λ}}=\hfill & \frac{{\tau }_{\text{Λ}}}{2m_{\text{Λ}}}+a_0{\rho }_{\text{Λ}}{\rho }_N+{a^{\prime }}_3{\rho }_{\text{Λ}}\left[2{\left({\rho }^{\text{c}}\right)}^2+2{\left({\rho }^{\text{v}}\right)}^2-{\rho }_n^2-{\rho }_p^2\right]\hfill \\ \hfill & +a_1\left({\rho }_{\text{Λ}}{\tau }_N+{\rho }_N{\tau }_{\text{Λ}}\right)-\frac{a_2}{2}\left({\rho }_{\text{Λ}}\text{Δ}{\rho }_N+{\rho }_N\text{Δ}{\rho }_{\text{Λ}}\right)\hfill \\ \hfill & -a_4\left({\rho }_{\text{Λ}}\nabla \cdot J_N+{\rho }_N\nabla \cdot J_{\text{Λ}}\right)\mathrm{,}\hfill \end{array}$ (13) $\begin{array}{ll}{V}_{\text{Λ}}=\hfill & a_0{\rho }_N+a_1{\tau }_N-a_2\text{Δ}{\rho }_N\hfill \\ \hfill & +{a^{\prime }}_3\left[2{\left({\rho }^{\text{c}}\right)}^2+2{\left({\rho }^{\text{v}}\right)}^2-{\rho }_n^2-{\rho }_p^2\right]\mathrm{.}\hfill \end{array}$ (14) We will keep Eqs. (8) and (9) are unchanged for the HF calculations because there is no cross term ${\rho }^c{\rho }^v$ in these equations.

In the present calculations, the deformed SHF Schrödinger equation was solved in cylindrical coordinates (r,z), under the assumption of axial symmetry of the mean fields. When compared with experimental deformations derived from the quadrupole moment Qp, we employ the definition $\beta =\frac{\sqrt{5\pi }}{3}\frac{Q_p}{Z{R}_0^2}$ (15) with $R_0\equiv 1.2A^{1/3}\text{fm}$ [87, 90, 96-98].

Results and discussion

In order to study the influence of neutron excess on Skyrme-type interaction RAY12, YBZ1 and SKSH2, we calculated the binding energies of Λ hypernuclei: ${}_{\text{Λ}}^{12}\text{B}$, ${}_{\text{Λ}}^{12}\text{C}$, ${}_{\text{Λ}}^{13}\text{C}$, ${}_{\text{Λ}}^{16}\text{N}$, ${}_{\text{Λ}}^{16}\text{O}$, ${}_{\text{Λ}}^{28}\text{Si}$, ${}_{\text{Λ}}^{32}\text{S}$, ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$ and ${}_{\text{Λ}}^{208}\text{Pb}$.

Figure 1 shows the binding energies for the 1s and 1p states calculated with and without neutron excess compared to the experimental data. The red triangles show the results without neutron excess, blue squares show the results with neutron excess, and black circles show the experimental results from Ref. [99]. To better present the results of ${}_{\text{Λ}}^{12}\text{B}$, ${}_{\text{Λ}}^{12}\text{C}$, ${}_{\text{Λ}}^{16}\text{N}$ and ${}_{\text{Λ}}^{16}\text{O}$, the results for ${}_{\text{Λ}}^{12}\text{C}$ and ${}_{\text{Λ}}^{16}\text{O}$ are displayed in the inset plots. It should be noted that not all hypernuclei in the figure contain excess neutrons. The results show that the highest neutrons occupy the shell-model orbit, which is lower than that of the highest protons in ${}_{\text{Λ}}^{12}\text{C}$, ${}_{\text{Λ}}^{16}\text{O}$, ${}_{\text{Λ}}^{28}\text{Si}$ and ${}_{\text{Λ}}^{32}\text{S}$, while the highest neutrons occupy the same shell-model orbit as the highest protons in ${}_{\text{Λ}}^{13}\text{C}$. Therefore, the results for ${}_{\text{Λ}}^{12}\text{C}$, ${}_{\text{Λ}}^{13}\text{C}$, ${}_{\text{Λ}}^{16}\text{O}$, ${}_{\text{Λ}}^{28}\text{Si}$ and ${}_{\text{Λ}}^{32}\text{S}$ remain unchanged regardless of the presence of neutron excess.

Fig. 1Full-screen View

(Color online) The binding energies (in MeV) of Λ 1s and 1p states of ${}_{\text{Λ}}^{12}\text{B}$, ${}_{\text{Λ}}^{12}\text{C}$, ${}_{\text{Λ}}^{13}\text{C}$, ${}_{\text{Λ}}^{16}\text{N}$, ${}_{\text{Λ}}^{16}\text{O}$, ${}_{\text{Λ}}^{28}\text{Si}$, ${}_{\text{Λ}}^{32}\text{S}$, ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$ and ${}_{\text{Λ}}^{208}\text{Pb}$ as calculated with and without neutron excess in Skyrme-type interaction RAY12, YBZ1 and SKSH2 compared with experimental data. The red triangles represent the results without neutron excess, the blue squares represent the results with neutron excess, and the black circles represent the experimental results including uncertainties from Ref. [99]. To enhance the visualization of the results for ${}_{\text{Λ}}^{12}\text{B}$, ${}_{\text{Λ}}^{12}\text{C}$, ${}_{\text{Λ}}^{16}\text{N}$ and ${}_{\text{Λ}}^{16}\text{N}$, the results for ${}_{\text{Λ}}^{12}\text{C}$ and ${}_{\text{Λ}}^{16}\text{O}$ are presented in inset plots

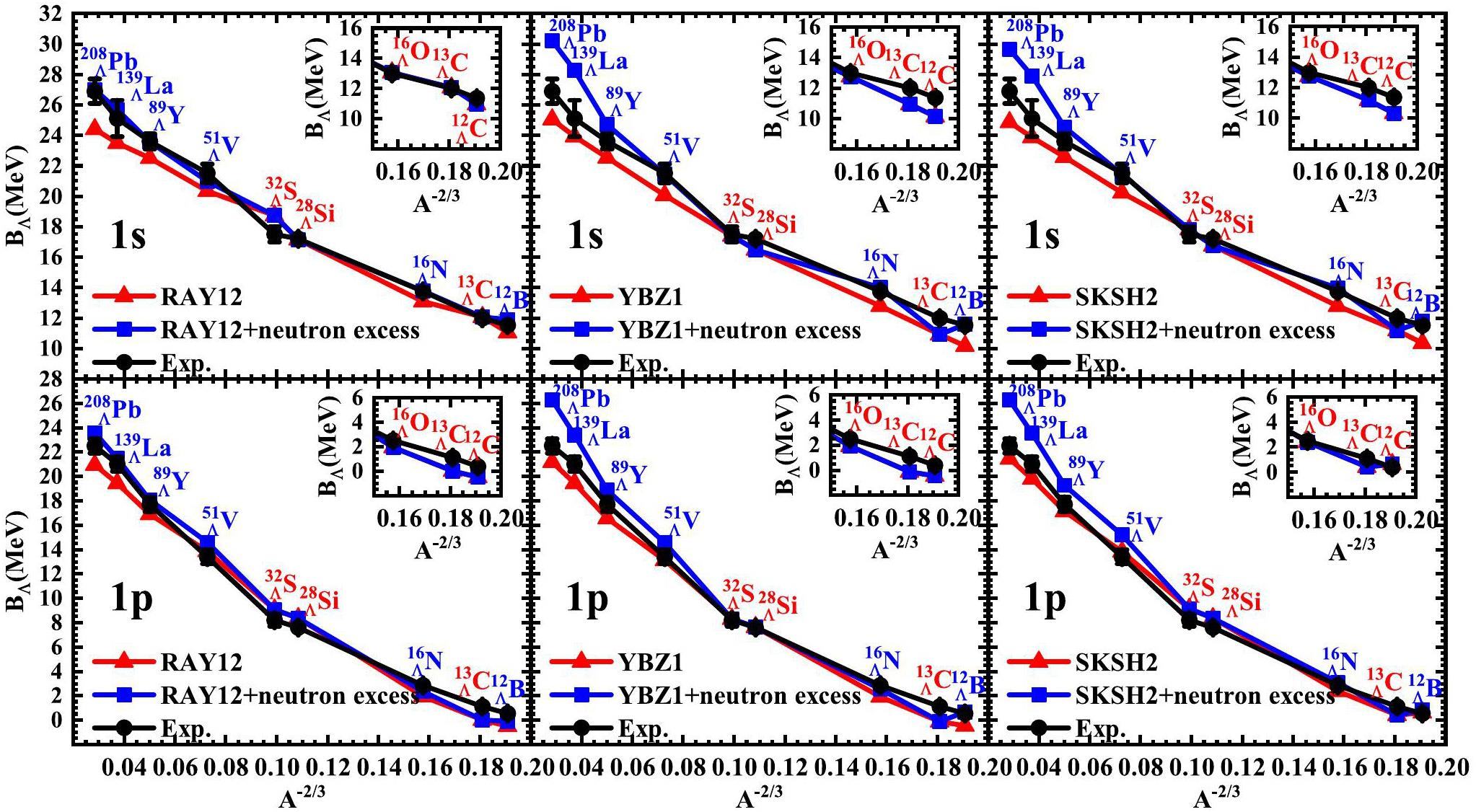
It is clearly seen that the binding energies calculated using the Skyrme-type interactions RAY12, YBZ1 and SKSH2 failed to predict the experimental results in the heavy-mass hypernuclei. Moreover, the calculated binding energies in the heavy-mass Λ hypernuclei were smaller than the experimental values. This underbinding shows that the ΛN potential depth is not sufficiently deep in heavy-mass Λ hypernuclei. The reason for this phenomenon is that the parameter are fitted to the binding energies of the light-mass Λ hypernuclei. Therefore, the calculated results from the interaction exhibited poor agreement with the experimental values in the heavy-mass region. It is evident that the behavior of light-mass hypernuclei with symmetric nuclear matter core nuclei differs from that of heavy-mass hypernuclei with asymmetric nuclear matter core nuclei. Therefore, the influence of the isospin of the core nuclei on the binding energy calculations is significant. The ΛNN three-body is related to the isospin factor ${\tau }_1\cdot {\tau }_2$ for the two nucleons involved [80]. The neutron excess reflects the influence of the isospin of core nuclei.

In Fig. 1, it is clear that the neutron excess slightly changes the binding energies of light-mass Λ hypernuclei with excess neutrons because excess neutrons are small in the light mass. Most importantly, neutron excess significantly increases the binding energies of heavy-mass Λ hypernuclei, because hypernuclei with heavy mass often have more excess neutrons. For the Skyrme-type interactions RAY12, YBZ1, and SKSH2, the interactions with neutron excess lead to better agreement with the experimental results of ${}_{\text{Λ}}^{12}\text{B}$ and ${}_{\text{Λ}}^{16}\text{N}$. For the Skyrme-type interactions YBZ1 and SKSH2, although the interaction with neutron excess leads to increased binding energies, the calculated results do not agree with the experimental results for heavy hypernuclei. For the interaction YBZ1, $a_{3^{\prime }}$ was determined by assuming $500$ MeV⋅fm⁶ and calculating the binding energies of ${}_{\text{Λ}}^{13}\text{C}$, ${}_{\text{Λ}}^{16}\text{O}$, ${}_{\text{Λ}}^{28}\text{Si}$, ${}_{\text{Λ}}^{40}\text{Ca}$, ${}_{\text{Λ}}^{51}\text{V}$, and ${}_{\text{Λ}}^{89}\text{Y}$, which yielded good results, thereby confirming that $a_{3^{\prime }}$ was 500 MeV⋅fm⁶ [42]. The interaction SKSH2 is fitted to binding energies of ${}_{{\text{Λ}}_{1s}}^{12}\text{C}$, ${}_{{\text{Λ}}_{1s}}^{13}\text{C}$, ${}_{{\text{Λ}}_{1p}}^{13}\text{C}$, ${}_{{\text{Λ}}_{1s}}^{16}\text{O}$, ${}_{{\text{Λ}}_{1p}}^{16}\text{O}$, ${}_{{\text{Λ}}_{1s}}^{28}\text{Si}$, ${}_{{\text{Λ}}_{1p}}^{28}\text{Si}$, ${}_{{\text{Λ}}_{1s}}^{40}\text{Ca}$, ${}_{{\text{Λ}}_{1p}}^{40}\text{Ca}$, ${}_{{\text{Λ}}_{1d}}^{40}\text{Ca}$, ${}_{{\text{Λ}}_{1s}}^{51}\text{V}$, ${}_{{\text{Λ}}_{1p}}^{51}\text{V}$, ${}_{{\text{Λ}}_{1d}}^{51}\text{V}$, ${}_{{\text{Λ}}_{1s}}^{89}\text{Y}$, ${}_{{\text{Λ}}_{1p}}^{89}\text{Y}$, ${}_{{\text{Λ}}_{1d}}^{89}\text{Y}$, ${}_{{\text{Λ}}_{1f}}^{89}\text{Y}$ [43]. The two interactions, YBZ1 and SKSH2, were fitted to heavy-mass hypernuclei with asymmetric nuclear matter cores. The influence of asymmetric nuclear matter on the interaction parameters was relatively large. Therefore, these two interactions with neutron excess lead to the overbinding of hypernuclei. Compared to the interactions of YBZ1 and SKSH2, RAY12 is more suitable for studying this problem. The interaction of RAY12 was obtained without fitting heavy-mass hypernuclei with an asymmetric nuclear matter core. For Λ in 1s states, the calculated binding energies using RAY12 with neutron excess are in good agreement with the experimental data, especially for heavy hypernuclei, compared to those without neutron excess. For Λ in 1p states, it appears to work well, as shown by the significant improvement in the binding energies calculated using RAY12 with neutron excess for ${}_{\text{Λ}}^{12}\text{B}$, ${}_{\text{Λ}}^{16}\text{N}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$ and ${}_{\text{Λ}}^{208}\text{Pb}$.

To check the overall description using RAY12 for all 11 hypernuclei, we calculate and list in Table 1 the average deviation ${\overline{\chi }}^2$ and the root mean square deviation Δ, $\begin{array}{c}{\overline{\chi }}^2=\frac{1}{N}{\displaystyle \sum _i^N}{\left(\frac{B_{\text{Λ}\mathrm{,}i}^{\text{exp}\text{.}}-B_{\text{Λ}\mathrm{,}i}^{\text{cal}\text{.}}}{\text{Δ}{B}_{\text{Λ}\mathrm{,}i}^{\text{exp}\text{.}}}\right)}^2\mathrm{,}\\ \text{Δ}=\sqrt{\frac{1}{N}{\displaystyle \sum _i^N}{\left(B_{\text{Λ}\mathrm{,}i}^{\text{exp}\text{.}}-B_{\text{Λ}\mathrm{,}i}^{\text{cal}\text{.}}\right)}^2}\mathrm{,}\end{array}$ (16) with N=22. From Table 1, it can be seen that the average deviation ${\overline{\chi }}^2$ and root mean square deviation Δ of the binding energies for Λ 1s and 1p states in the selected hypernuclei are shown for different Skyrme-type interactions. SLL4 is a recently developed ΛN Skyrme-type interaction that effectively describes hypernuclei across the entire periodic table using a single set of four parameters [46, 47]. By analyzing the ${\overline{\chi }}^2$ and Δ, it is evident that the inclusion of neutron excess improves the ability of RAY12 to describe the binding energies of hypernuclei. The key point to emphasize is that all the calculations were conducted without adjusting any parameters. Compared with SLL4, RAY12, which incorporates neutron excess, shows a smaller ${\overline{\chi }}^2$ and a similar Δ, while requiring fewer parameters. Therefore, with RAY12 plus neutron excess, the calculated binding energies of Λ 1s and 1p states are very close to the experimental values, indicating reasonably good agreement. This demonstrates the importance of neutron excess when excess neutrons occupy shell-model orbits that are higher than those occupied by protons.

Table 2 lists the quadrupole deformation parameters β and the binding energies of the Λ 1s and 1p states for various hypernuclei, comparing deformed results with their spherical counterparts (values in brackets). The data reveals that deformation has a significant impact on the binding energy, particularly for hypernuclei in the 1p_Λ state. For instance, for ${}_{{\text{Λ}}_p}^{16}\text{N}$ and ${}_{{\text{Λ}}_p}^{16}\text{O}$, the binding energies differ noticeably between deformed and spherical calculations, with the deformed values being closer to experimental data. Conversely, the 1s_Λ state shows minimal differences, as the wave function of hyperon tends to be spherical in this state. These results show the necessity of considering deformation effects.

Figure 2 shows the Λ single-particle potential as a function of the radial distance $r$ (fm) in the $z=0$ plane for hypernuclei ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$, and ${}_{\text{Λ}}^{208}\text{Pb}$. The red curves represent calculations without neutron excess (NE), whereas the blue curves represent neutron excess. Solid lines denote the total ΛN interactions, dashed lines indicate the two-body ΛN interactions, and dot-dashed lines indicate three-body ΛNN interactions. The neutron excess has almost no effect on the two-body ΛN interaction, but it effectively reduces the repulsive three-body ΛN interaction, thereby increasing the total ΛN interaction. Therefore, the hyperons are bound more deeply. The Λ-nuclear potential depth at zero momentum, $V_{\text{Λ}}\left(0\right)$, is -29.7 MeV, closely matching the -28 MeV depth derived from the simple Woods-Saxon (WS) attractive potential in Ref. [41].

Fig. 2Full-screen View

(Color online) Two-body, three-body and total ΛN interactions as functions of the radial distance $r$ in the $z=0$ plane in ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$ and ${}_{\text{Λ}}^{208}\text{Pb}$ calculated using RAY12 with and without neutron excess. The red curves correspond to calculations without neutron excess (NE), while the blue curves account for neutron excess. Solid lines represent the total ΛN interactions, dashed lines illustrate the two-body ΛN interactions, and dot-dashed lines depict the three-body ΛNN interactions

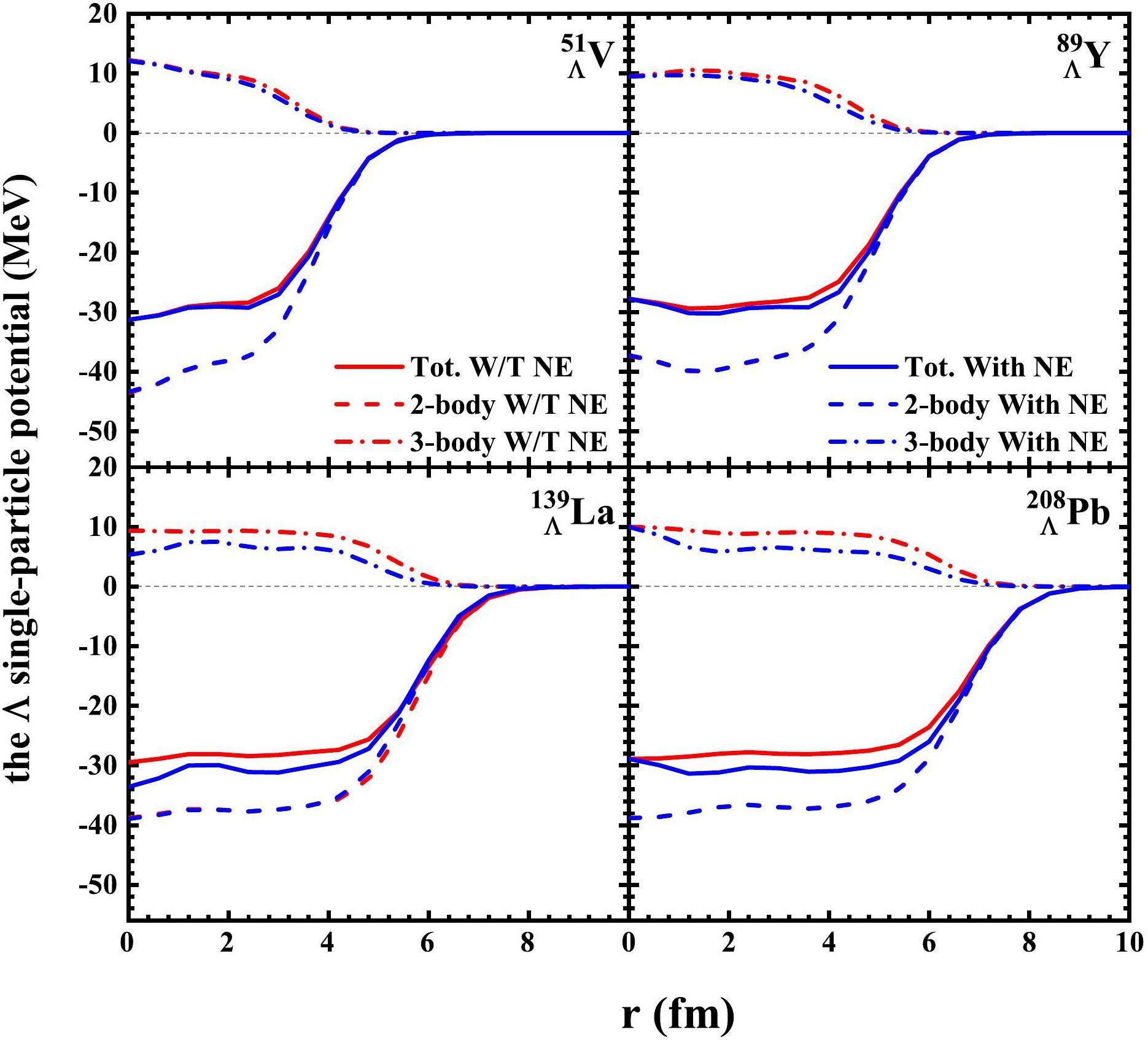
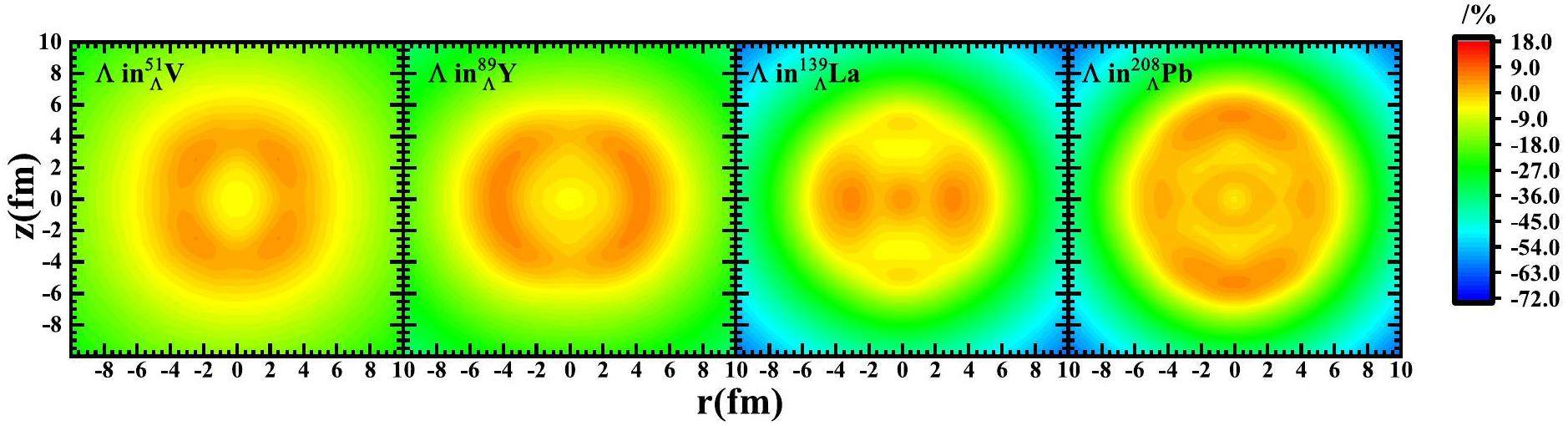
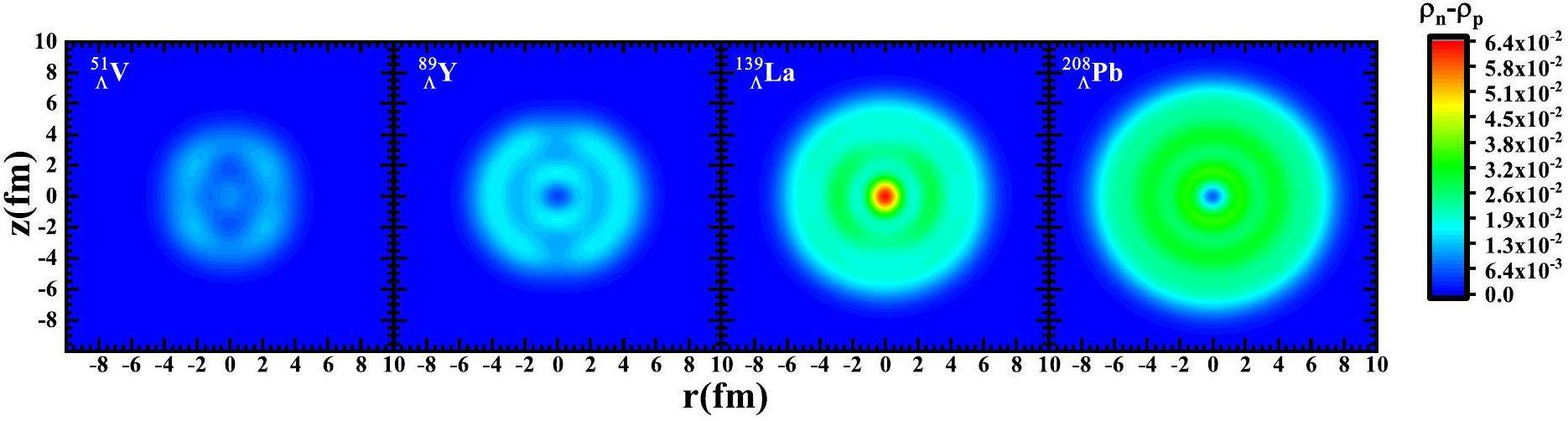
Figure 3 shows the rate of change in the hyperon density in the r-z plane due to neutron excess for four hypernuclei ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$, and ${}_{\text{Λ}}^{208}\text{Pb}$. The rate of change in the hyperon density δ_Λ is given as $\begin{array}{ll}{\delta }_{\text{Λ}}\hfill & \equiv \frac{{\rho }_{\text{Λ}}\left(\text{RAY12}+\text{neutron}\text{excess}\right)-{\rho }_{\text{Λ}}\left(\text{RAY12}\right)}{{\rho }_{\text{Λ}}\left(\text{RAY12}\right)}\mathrm{.}\hfill \end{array}$ (17) The color scale represents the percentage change, with red and yellow indicating positive changes and green and blue showing negative changes. Neutron excess significantly affects the hyperon density distribution but has a minor impact on the core nucleus density distribution. Neutron excess leads to an increase in the central density of the hyperon and a decrease in the outer density, resulting in a decrease in the radius of the hyperon. Figure 4 illustrates the difference between neutron density and proton density, ρ_n-ρ_p, in the (r,z) plane for the hypernuclei ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$, and ${}_{\text{Λ}}^{208}\text{Pb}$, respectively, calculated by the RAY12 interaction. From Fig. 3 and Fig. 4, we find very similar shapes of δ_Λ and ρ_n-ρ_p for ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$, and ${}_{\text{Λ}}^{208}\text{Pb}$. This indicates that the effect of neutron excess is more significant in regions where the neutron density differs greatly from the proton density.

Fig. 3Full-screen View

(Color online) The changing rate of hyperon density δ_Λ, Eq. (16), in the (r,z) plane, for ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$ and ${}_{\text{Λ}}^{208}\text{Pb}$, obtained with the RAY12 interaction

Fig. 4Full-screen View

(Color online) The difference between neutron density and proton density ${\rho }_n-{\rho }_p$, in the (r,z) plane, for ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$ and ${}_{\text{Λ}}^{208}\text{Pb}$, obtained with the RAY12 interaction

Summary

The effects of neutron excess on the Λ hypernuclei were studied by using the deformed SHF model in this work. Suppressing the ΛNN interaction between ‘core’ nucleons and ‘excess’ neutrons addresses underbinding in heavy-mass Λ hypernuclei. The microscopic mechanism can be explained as follows: the neutron excess decreases the repulsive ΛNN interaction, which can prevent this issue and be directly observed from the depth variation of the hyperon potential.

In addition, to quantitatively assess the impact of neutron excess, the binding energies of 1s and 1p Λ states for ${}_{\text{Λ}}^{12}\text{B}$, ${}_{\text{Λ}}^{12}\text{C}$, ${}_{\text{Λ}}^{13}\text{C}$, ${}_{\text{Λ}}^{16}\text{N}$, ${}_{\text{Λ}}^{16}\text{O}$, ${}_{\text{Λ}}^{28}\text{Si}$, ${}_{\text{Λ}}^{32}\text{S}$, ${}_{\text{Λ}}^{51}\text{V}$, ${}_{\text{Λ}}^{89}\text{Y}$, ${}_{\text{Λ}}^{139}\text{La}$ and ${}_{\text{Λ}}^{208}\text{Pb}$ were compared with those without the effect. Neutron excess significantly increases the B_Λ for heavy hypernuclei but has a less pronounced impact on light hypernuclei. In particular, for RAY12, good agreement was reached in this model between the calculated values and their corresponding experimental values considering the neutron excess effect.

By incorporating the isospin for the two nucleons into the three-body ΛNN interaction, a better prediction of the hypernuclear structure can be achieved. In the future, corrections for neutron excess will be introduced into the calculations of multi-Λ hypernuclei and Ξ hypernuclei (S=2).