General overview
Scientific objectives
The high-brightness frontier is one of the three major frontiers in contemporary international particle physics research and holds an indispensable position. Current high-brightness, cutting-edge experimental facilities collectively address key scientific problems and are both competitive and complementary. Operational and on-construction facilities include LHC/LHCb at CERN, SuperKEKB/Belle II at KEK, BEPCII/BESIII at IHEP, FAIR/PANDA at GSI, and CEBAF/GlueX at JLab.
LHCb and Belle II primarily focus on B physics, producing large samples of hadrons containing bottom quarks, while also yielding significant numbers of charm hadrons and tau leptons. PANDA and GlueX—based on proton-antiproton annihilation using an antiproton beam on a fixed target and high-energy photoproduction using polarized photons on a proton target, respectively—also encompass the tau-charm energy region. The BESIII experiment has concentrated on charm hadron and tau lepton physics; however, the current BEPCII accelerator cannot be upgraded to meet the demands of particle physics research in the next 20–30 years. Over the past decade, Chinese scientists have actively developed a new-generation tau-charm facility—known as the Super Tau-Charm Facility (STCF)—and are striving to launch it as a major national science infrastructure project during the period of the 15th Five-Year Plan. The goal of this facility is to sustain China’s global leadership in tau-charm physics established over the past three decades. In addition to China, Russia is also pursuing a similar initiative, known as the SCTF project.
The STCF aims to collect a substantial and unique dataset in the tau-charm energy region, with an expected integrated luminosity of approximately 1 ab-1 per year. The primary physics goals include:
Studies of CP Violation and New Sources of CPV
Charge-Parity (CP) violation is a key component in explaining the matter–antimatter asymmetry in the universe. STCF will produce billions of quantum-entangled pairs of neutral D mesons, tau leptons, and hyperons, offering a unique environment for precision CPV studies. In particular, hyperon CP violation searches at STCF are expected to reach world-leading sensitivity (better than 10-4), which is sufficient for testing Standard Model (SM) predictions.
Hadron Spectroscopy and Exotic States
Just as spectroscopy is central to atomic and molecular physics, hadron spectroscopy plays a crucial role in understanding quantum chromodynamics (QCD) confinement. STCF will yield trillions of (charmonium-like) quark-antiquark states, enabling precise studies of the light hadron spectrum, charmonium-like structures, and the systematics of exotic hadrons.
Nucleon Structure and Formation
Probing the internal structure of nucleons is essential for uncovering the properties of matter and QCD confinement. STCF will perform threshold scans of baryonic final states to measure nucleon electromagnetic form factors, baryon decay constants, and strong phases, with at least an order-of-magnitude improvement over existing measurements.
Precision Measurements of Fundamental Parameters and Searches for New Physics
STCF will significantly improve the precision of fundamental quantities such as the tau lepton mass, strong phases in neutral D meson decays, and the magnetic dipole moments of baryons and leptons. The sensitivity to potential new physics will be enhanced by up to two orders of magnitude compared to current limits.
Accelerator design objectives
The STCF accelerator complex is designed to fulfill the above physics goals through high-luminosity operation in the center-of-mass energy range of 2.0–7.0 GeV. The baseline accelerator design targets include:
· Beam energy range for both electrons and positrons: Tunable from 1.0 to 3.5 GeV per beam (2.0 to 7.0 GeV in c.m. energy)
· Luminosity: ≥ 5 × 1034cm-2s-1 at 2.0 GeV beam energy
· Operational mode: Top-up (constant current) injection mode
· Future upgrade potential: Design provisions for future luminosity enhancement and other possibilities such as polarized beam and monochrmonization
Accelerator conceptual scheme
The core design objective of a new-generation electron–positron collider is to largely increase luminosity. Compared to the currently operating BEPCII, STCF should enhance luminosity by approximately two orders of magnitude, which requires both new design concepts and advanced technologies. Since around 2010, the international community has converged on a set of key features for the so-called third-generation e+e- colliders: a large crossing angle, a crab-waist collision scheme, an extremely small vertical beta function (
To meet the physics requirements of a center-of-mass energy ranging from 2 to 7 GeV and luminosity greater than 5 × 1034cm-2s-1 at the optimized energy of 4 GeV STCF will adopt the most advanced designs and techniques for third-generation e+e– colliders. These include a double-ring configuration with separate storage rings for electrons and positrons with sufficient circumferences of above 800 m, a large Piwinski angle (total crossing angle of 60 mrad) and a crab-waist collision scheme, high stored beam currents (≈2 A), low emittance (horizontal emittance of approximately 5 nm·rad, with transverse coupling below 1%), and extremely small
In the crab-waist scheme, sextupole magnets near the IP rotate the beam-waist orientation, which, combined with strong focusing optics, significantly reduces the dynamic and momentum acceptances of the ring. This not only complicates beam injection but also leads to an extremely short beam lifetime (<300 s), primarily limited by Touschek scattering. This beam lifetime is far shorter than in other electron storage rings (colliders and synchrotron radiation light sources) and imposes significant challenges on both collider ring physics design and technical design.
In addition, STCF is designed to operate in a top-up mode, requiring frequent beam injection to maintain a quasi-constant current. The very short beam lifetime in the collider rings poses great beam injection and injector design challenges. Currently, two injection schemes for the collider rings are under parallel development: a conventional off-axis injection scheme and a state-of-the-art bunch swap-out injection scheme. They require very different bunch charges for beam injection: approximately 1 and 8 nC for the off-axis and swap-out injection schemes. Accordingly, the injector should be designed to follow the injection schemes.
STCF adopts an injector scheme with a full-energy linac, namely the linacs will accelerate both the electron and positron beams to the injection energy of the collider rings, from 1.0 to 3.5 GeV, according to the collider operation energy. This scheme is adopted to realize frequent beam injections in the collider rings. While an electron beam that is pre-accelerated in the linac can be injected into the collider electron ring, the positron beam is first produced by a high-energy and high-current electron beam. As a secondary particle, the positron exhibits low collection efficiency and poor beam quality. The most challenging aspects of the injector design are associated with the positron beam. Different injector designs have been proposed for the off-axis and swap-out injection schemes in the collider rings:
· Off-Axis Injection Scheme: In this scheme, each injection introduces a single electron/positron bunch with a charge of ≤ 1.5 nC using traditional methods. The electron beam is generated by a photocathode (PC) radio frequency (RF) electron gun that provides good beam quality and is directly accelerated to the injection energy. The positron beam is generated using a high-charge, high-energy electron beam on a positron production target. Here, the electron beam is from a thermionic-cathode (TC) RF electron gun and accelerated to 1.5 GeV. These positrons are collected, accelerated to 1.0 GeV, damped in a damping ring (DR), and reaccelerated to the required injection energy (see Fig. 1, top).
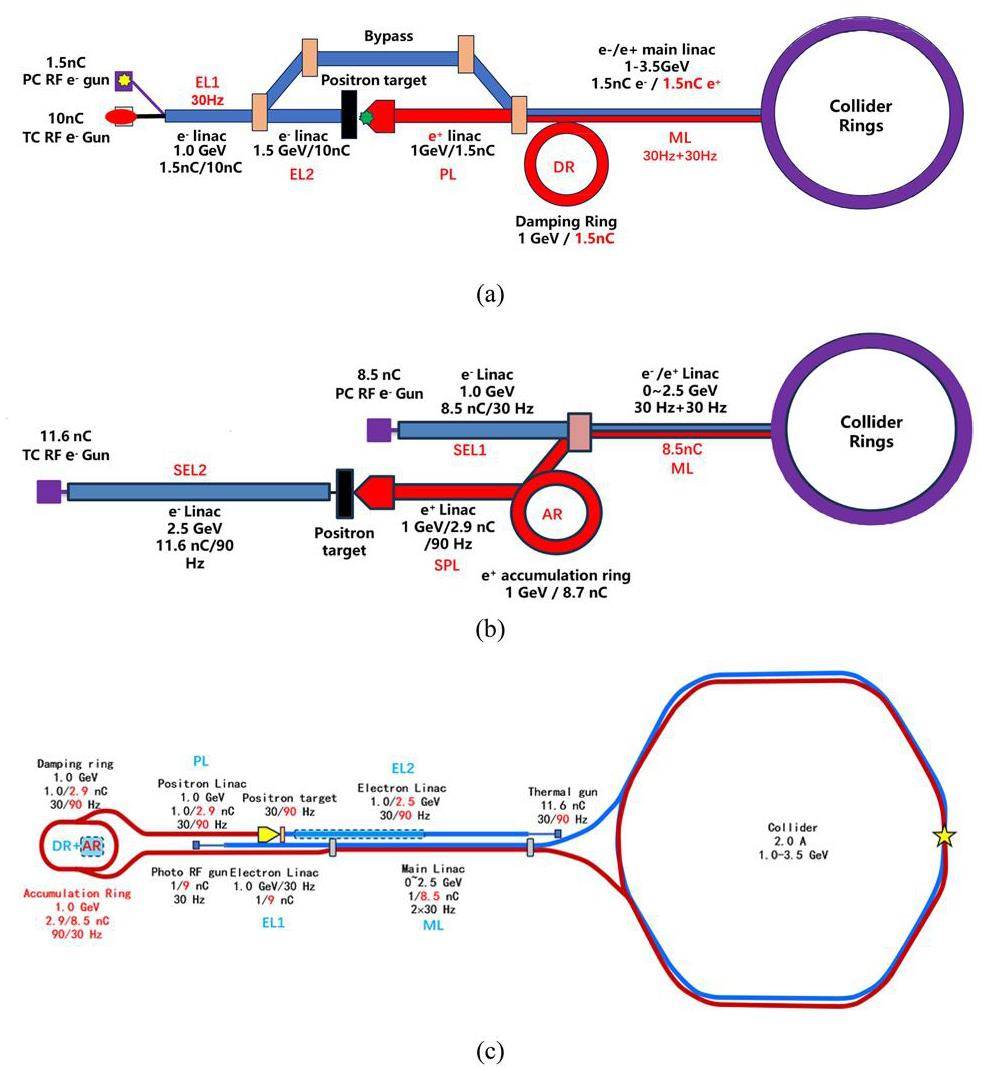
· Bunch Swap-out Injection Scheme: In this scheme, at each injection, a high-charge (8.5 nC) bunch is required for both electrons and positrons. The electron beam for direct injection into the collider electron ring is still generated by a PC gun, but with a higher bunch charge of 8.5 nC. The electron beam that produces positrons is also generated from a thermionic gun, but with an even higher bunch charge of 11.6 nC and accelerated to 2.5 GeV with a high repetition rate of 90 Hz. Subsequently, the positrons are collected, captured, accelerated to 1 GeV, and accumulated in an accumulation ring with strong damping to achieve low emittance before acceleration in the main linac (ML) and final injection into the collider positron ring (see Fig. 1, middle).
Regardless of whether the off-axis injection or swap-out injection is used, the ML should accelerate both the electron and positron beams alternately at a maximum of 30 Hz each. It will be capable of adjusting the energy of both electron and positron beams across the 1.0–3.5 GeV range according to the operating energy of the collider rings.
Based on feasibility studies, a compatible injector scheme (see Fig. 1, bottom) has been proposed. With this scheme, the linac tunnel hosts two linacs in two opposite directions. The off-axis injection mode is chosen as the baseline scheme since it is a mature and cheaper solution. The electron beam energy that drives the positron target is reduced to 1 GeV, which produces positron bunches with a charge of 1 nC. The bunch charges for both electrons and positrons for the injection into the collider rings are 1 nC. However, if the future study and operation find that the bunch swap-out injection mode is required to address challenges related to the strong coupling between the injected beam and beam–beam effect, the injector can be straightforwardly upgraded to the full bunch swap-out injection mode by increasing the drive electron beam energy to 2.5 GeV and the repetition rate to 90 Hz. The positron bunch charge is accumulated to 8.5 nC by adding an accumulation ring to the DR to form a dual-ring damping system in the same tunnel.
Key physics design challenges and technologies
As a new-generation electron–positron collider, the STCF accelerator complex not only adopts advanced design concepts but also requires the development of new accelerator physics methodologies and enabling novel accelerator technologies. Based on preliminary studies and international collaborations, several critical areas that require state-of-the-art design techniques and technological innovations, or significantly evolved existing methods, to meet the stringent specifications of the construction and operation of the STCF have been identified.
Collider ring physics design
The most challenging aspect of the collider ring design lies in the interaction region (IR). On one hand, ultra-strong focusing is required to achieve extremely small vertical beta functions (
This design complexity is shared across multiple third-generation e+e- collider projects worldwide, each facing varying degrees of difficulty. The SuperKEKB, the only third-generation collider currently in operation, has also struggled to reach its design beam parameters. There is a growing international consensus that new-generation colliders must comprehensively and simultaneously address a wide set of interdependent physics mechanisms, such as strong nonlinearities, Touschek effects, collective instabilities, beam–beam interactions, injection dynamics, machine errors, beam collimation, and radiation damping, through an integrated design approach. Traditionally, these physical mechanisms are studied independently. Existing simulation tools must therefore be upgraded to accommodate such complex, multi-physics studies.
Injector physics design
To accommodate the wide operational energy range (1–3.5 GeV) and short beam lifetime of the collider rings—particularly under the bunch swap-out injection scheme—the injector system must deliver electron and positron beams with the following characteristics: variable energy (1–3.5 GeV), high repetition rate (≈30 Hz), low emittance (<30 nm·rad), and high bunch charge (8.5 nC). Meeting these requirements poses significant challenges in the injector design. These challenges include how to optimize the linac design to minimize emittance growth and energy spread when accelerating high-charge electron bunches from a thermionic gun, how to design a positron production and accumulation chain—including target, capture optics, damping, and acceleration—to yield high-quality positron bunches with sufficient charge and low emittance, and how to suppress emittance degradation in beam transport lines to realize high-intensity electron and positron bunches during injection.
Key technologies
While most of the technical systems of the STCF accelerator will adopt mature and proven accelerator technologies wherever possible to ensure feasible and timely construction, several key technologies—though having a certain development base or being under development—remain immature and must be developed or advanced in significant undertakings to meet the facility’s performance goals and ensure technological advancement. The project team is actively organizing vigorous research and development (R&D) efforts in these areas, aiming for critical breakthroughs in the coming years to ensure the implementation of the engineering construction. In parallel, backup solutions to those key technologies are being prepared to guarantee the timely advancement of the construction project and compliance with final performance specifications, even if the R&D of the key technologies experiences delays or setbacks.
The key enabling technologies required for the STCF accelerator include:
Twin-Aperture Superconducting Magnets for the IR: These include the final focus quadrupoles as well as integrated corrector coils, higher-order field coils, anti-solenoids, and compensation solenoids.
Collider Ring RF Systems: Room-temperature cavities designed to support high circulating currents (≈2 A), with deep higher-order mode (HOM) suppression, high-power RF couplers, and stable low-level RF (LLRF) controls.
Beam Diagnostics and Feedback Systems: Fast-response, low-noise feedback systems and high-precision 3D bunch profiling instrumentation.
Other Advanced Accelerator Technologies: Ultra-fast kicker magnets with pulse bottom widths smaller than 6 ns; ultra-high vacuum systems with low impedance, capable of operating under very intense synchrotron radiation; high bunch-charge (>8 nC) PC electron guns; high-power positron production targets; klystrons and accelerating structures operating at up to a 90 Hz repetition rate; and complex mechanical systems for the MDI (Machine–Detector Interface) region, etc.
Collider ring accelerator physics
Collision scheme and global parameters
The core objective of designing an electron–positron collider is to maximize luminosity. The luminosity, L, can be expressed as follows [1]:
According to the scientific objectives of the STCF [2], which demand a center-of-mass energy range of 2–7 GeV and a design luminosity not lower than 0.5 × 1035cm-2s-1 at the optimized energy point of 4 GeV, the STCF accelerator will adopt the most advanced third-generation design philosophy for circular e+e- colliders. Specifically, it will follow the double-ring scheme of second-generation colliders and incorporate a large crossing angle with the crab-waist collision scheme [3].
This collision scheme is characterized by a flat beam profile at the IP, with extreme vertical compression (on the order of hundreds of nanometers) and significant horizontal compression (on the order of tens of microns). Due to the large crossing angle, the overlap region of the two bunches at the IP is very small, which permits the use of relatively long bunch lengths without experiencing severe luminosity degradation from the hourglass effect.
To mitigate the transverse and transverse-longitudinal coupling instabilities induced by the large crossing angle, crab sextuples are placed at specific phase advance locations on either side of the IP. These magnets couple the horizontal and vertical motions of the bunches such that the vertical focus of particles becomes correlated with their horizontal position, and all vertical foci fall along the optical axis of the opposing bunch—this is the so-called crab-waist collision scheme. Figure 2 illustrates the principle of the crab-waist collision scheme [3].
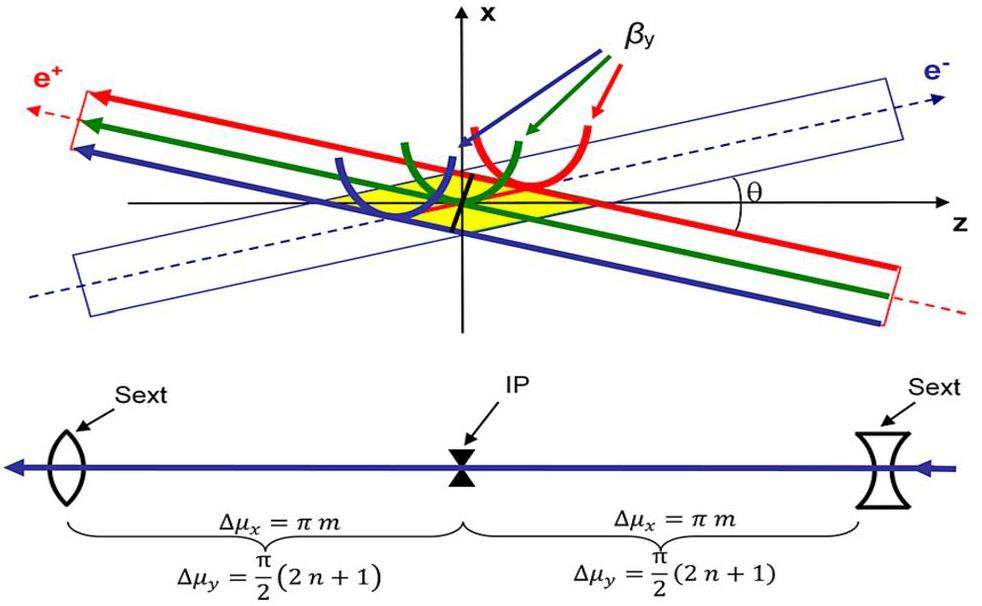
In addition, further measures to improve the luminosity of the STCF include achieving an ultra-small
The crab-waist collision scheme requires strong coupling between the X/Y directions of the bunches near the IP via crab sextupoles. Combined with strong focusing at the IP, this significantly reduces the dynamic and momentum apertures of the collider rings. In addition to instigating serious beam injection challenges, it can cause a very short Touschek lifetime under high bunch currents and low emittances—for example, less than 300 s, which is significantly shorter than that of other circular electron accelerators. Such a short Touschek lifetime increases the difficulty of designing and constructing the injector, as it would require significantly higher injection repetition rates, and causes severe beam loss during injection, which in turn negatively impacts the experimental background. Balancing high-luminosity collisions with beam dynamics, lifetime, and stability is one of the major challenges of the physical design of the collider rings [4]. The physical design of the STCF collider rings must balance design goals and these critical parameters.
Based on the analysis of the collision scheme proposed for the STCF, the selection of key parameters for the collider rings must be guided by detailed physics studies and iterative coordination with major hardware system designs while referencing results from other third-generation e+e- colliders and synchrotron light sources. Factors that must be considered for several key parameter choices are summarized below:
· Beam energy range: 1.0–3.5 GeV, with an optimized energy point at 2 GeV, as determined by the overarching scientific goals of the project.
· Luminosity: ≥ 0.5 × 1035cm-2s-1 @ 2 GeV beam energy, also defined by the project’s scientific objectives. At the lower and upper ends of the energy range, lower luminosity is permitted but must not decrease by more than one order of magnitude.
· Ring circumference: 800–1000 m based on international experience and with future expansion allowances. A longer circumference provides space for an ideal IR design and accommodates components that occupy long straight sections—such as damping wigglers (DWs), collimators, injection/extraction elements, and RF cavities. It also reserves space for future upgrades involving polarized beams (e.g., spin rotators or Siberian snakes (SSs)). However, excessively increasing the circumference should be avoided to contain construction costs.
· Circulating current: ≈2 A @ 2 GeV based on international experience and preliminary STCF studies. High current is essential for achieving high luminosity; however, further increases will severely shorten the Touschek lifetime. At lower energies, Touschek effects are more pronounced, and moderate reductions in beam current and luminosity are acceptable. At higher energies, synchrotron radiation power may impose additional constraints on the beam current.
·
· Transverse emittance: Horizontal emittance is approximately 5 nm·rad at 2 GeV, which is comparable to third-generation synchrotron light sources. The transverse coupling is limited to 1%, corresponding to a vertical emittance of approximately 50 pm·rad, sufficient to achieve a vertical beam size of approximately 100 nm at the IP. Emittance is allowed to vary within a reasonable range at other energies (lower at low energies, higher at high energies). At 1 GeV and 1.5 GeV, the coupling ratio remains at 1%; at 3.5 GeV, it is set to 0.5%. At low energy, vertical dispersion can be increased to boost vertical emittance and thereby improve Touschek lifetime.
As the optimization of the collider ring physics design progresses, the overall parameter table for the collider rings will also be periodically updated. Table 1 shows the latest version of the current global design parameters.
| Parameter | Value | |||
|---|---|---|---|---|
| Beam energy, E (GeV) | 2 | 1 | 1.5 | 3.5 |
| Circumference, C (m) | 860.321 | |||
| Crossing angle, 2θ (mrad) | 60 | |||
| L* (m) | 0.9 | |||
| Relativistic factor, γ | 3913.9 | 1956.9 | 2935.4 | 6849.3 |
| Revolution period, T0 (μs) | 2.87 | |||
| Revolution frequency, f0 (kHz) | 348.47 | |||
| Ratio, |
1% | 15% | 10% | 0.5% |
| Horizontal emittance (SR/DW, IBS), εx (nm) | 8.79/4.63 | 2.20/5.42 | 4.94/3.82 | 26.9/26.91 |
| Vertical emittance (SR/DW, IBS), εy (pm) | 87.9/46.3 | 330/813 | 494/382 | 134.5/134.55 |
| β functions at IP, βx/βy (mm) | 60/0.8 | |||
| Beam size at IP, σx/σy (μm) | 16.67/0.19 | 18.03/0.81 | 15.14/0.55 | 40.18/0.33 |
| Betatron tunes, νx/νy | 30.54/34.58 | 30.555/34.57 | ||
| Momentum compaction factor, αp (×10-4) | 13.49 | 12.63 | 13.24 | 13.73 |
| Energy spread (SR/DW, IBS), σe (×10-4) | 5.72/7.82 | 2.86/6.18 | 4.29/6.93 | 10.01/10.02 |
| Beam current, I (A) | 2 | 1.1 | 1.7 | 2 |
| Bunch filling factor | 48% | |||
| Number of bunches, nb | 688 | |||
| Bunch spacing, τb (ns) | 4 | |||
| Single bunch current, Ib (mA) | 2.91 | 1.6 | 2.47 | 2.91 |
| Particles per bunch, Nb (×1010) | 5.20 | 2.86 | 4.42 | 5.20 |
| Total particles per beam (×1013) | 3.58 | 1.97 | 3.05 | 3.58 |
| Charge per bunch (nC) | 8.34 | 4.59 | 7.09 | 8.34 |
| Energy loss per turn (SR/Total), U0_sr (keV) | 159/543 | 10/106 | 50/267 | 1494/1494 |
| Synchrotron radiation power loss per beam (SR/Total), PSR (MW) | 0.32/1.09 | 0.01/0.12 | 0.085/0.453 | 2.988/2.988 |
| Damping times, τx/τy/τz (ms) | 21/21/11 | 54/54/27 | 32/32/16 | 14/14/6.7 |
| RF Frequency, fRF (MHz) | 499.7 | |||
| Harmonic number, h | 1434 | |||
| RF voltage, VRF (MV) | 2.5 | 0.75 | 1.2 | 6 |
| Longitudinal phase, Фs (deg) | 167 | 172 | 167 | 166 |
| Synchrotron tune, νz | 0.0194 | 0.0146 | 0.0154 | 0.0228 |
| Natural bunch length, σz (mm) | 7.21 | 6.62 | 7.89 | 8.26 |
| Bunch length (0.1 Ω, IBS), σz_ibs (mm) | 8.7 | 9.46 | 10.01 | 8.79 |
| RF energy acceptance, (ΔE/E)max (%) | 1.68 | 1.44 | 1.35 | 1.88 |
| Piwinski angle, ФPiw (rad) | 15.66 | 15.74 | 19.84 | 6.56 |
| Beam–beam parameters, ξx/ξy | 0.005/0.095 | 0.005/0.023 | 0.004/0.033 | 0.003/0.032 |
| Hourglass factor, Fh | 0.915 | 0.905 | 0.927 | 0.750 |
| Luminosity, L (cm-2s-1) | 9.42×1034 | 6.19×1033 | 2.09×1034 | 4.48×1034 |
| Touschek lifetime (SAD/Elegant) (s) | 252/304 | 195/264 | 215/294 | 5400/3479 |
Lattice design
Baseline scheme (Two-fold symmetry)
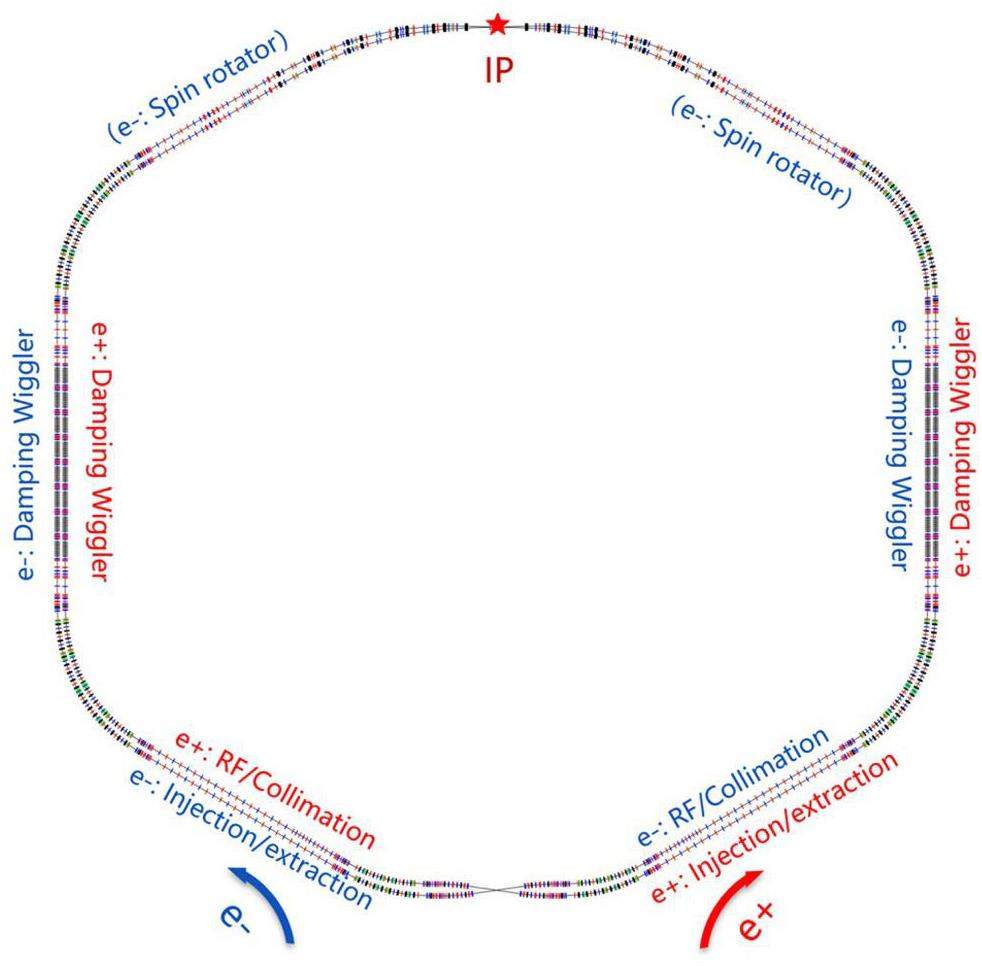
The STCF collider rings adopt a double-ring layout, consisting of an electron ring and a positron ring. Both rings lie in the same horizontal plane and intersect at the IP in the collision region and the crossing point in the region opposite the IP. The layout is symmetric along the line connecting these two points. Each collider ring features a two-fold symmetric structure. Owing to the crossing geometry of the double-ring configuration, the drift sections in the arc regions on opposite sides of the same ring differ slightly in length, forming inner and outer rings with an approximate spacing of 2 m. Space is reserved on both sides of the IR for the future installation of spin rotators to enable beam polarization upgrades.
Each ring consists of one collision region, four large arc sections (each bending by 60°), two small arc sections (each bending by 30°), one crossing region, and several straight sections. The straight sections serve different functions, including beam injection and extraction, housing DWs, beam collimation, accommodating RF cavities, and matching the working point. The total circumference of the ring is 860.321 m.
The main features of this lattice design include:
· A symmetric lattice layout that preserves the option of upgrading to a second IP;
· Flexibility in the type and length of DWs—currently adopting a well-established room-temperature DW scheme, with adjustments in the DW section not affecting the rest of the layout;
· A relatively small injection deflection angle where both electron and positron beams require a 60° bend to enter the collider rings;
· Reserved space for future upgrades, such as spin rotators required in potential beam polarization;
· A medium-scale arc section with a maximum arc bending of 60°, which improves local chromaticity correction and allows for the better optimization of the dynamic and momentum apertures.
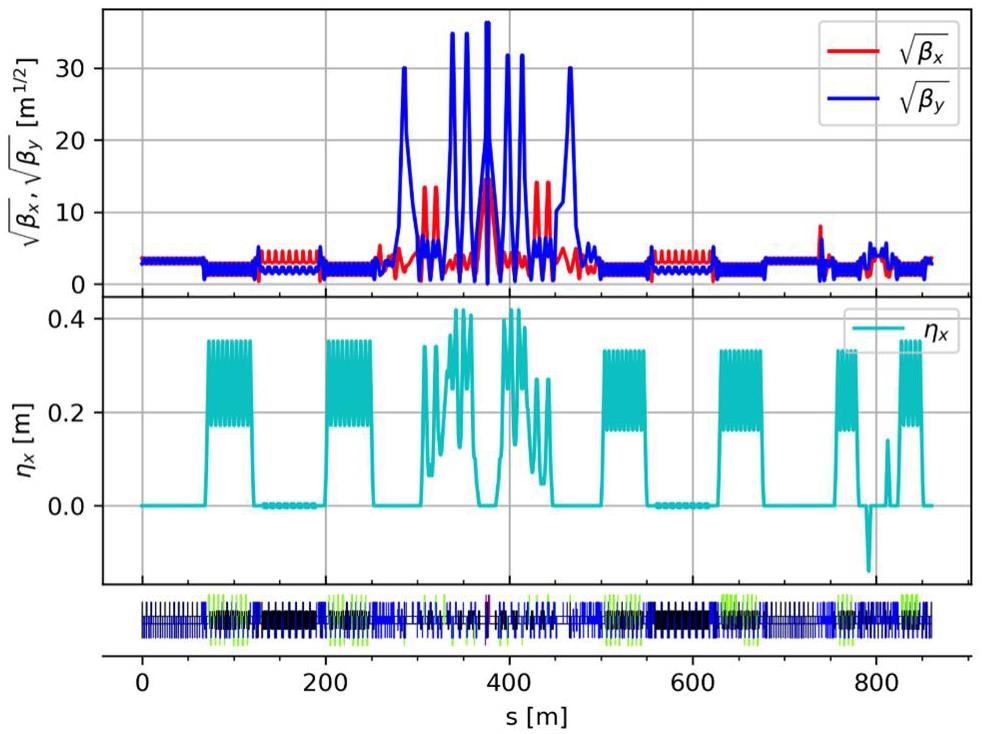
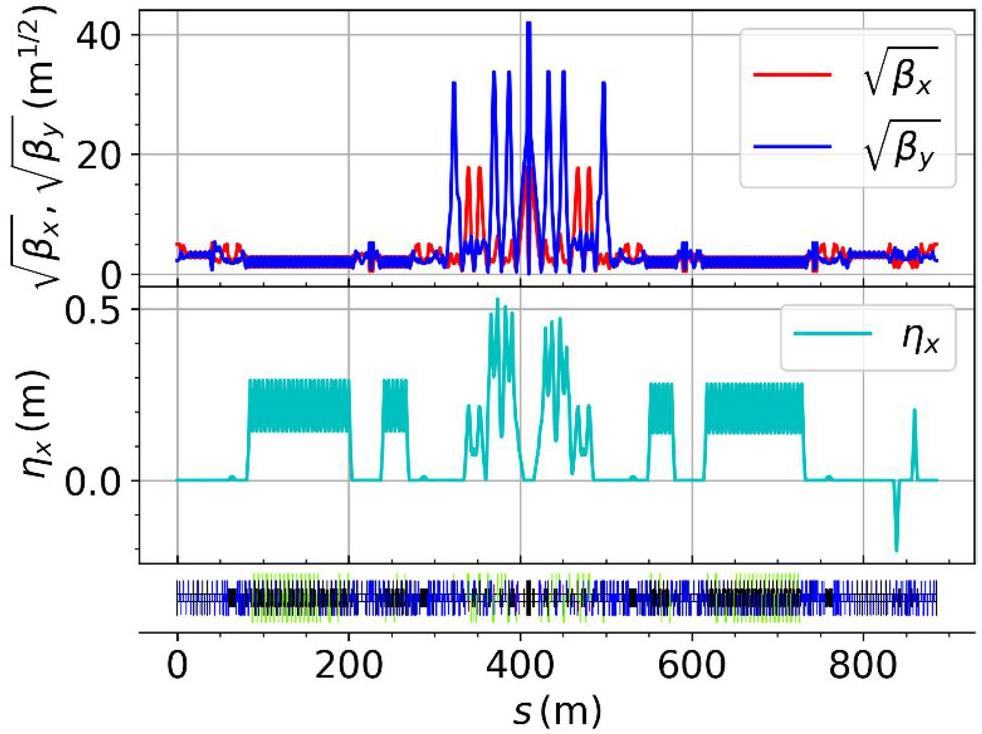
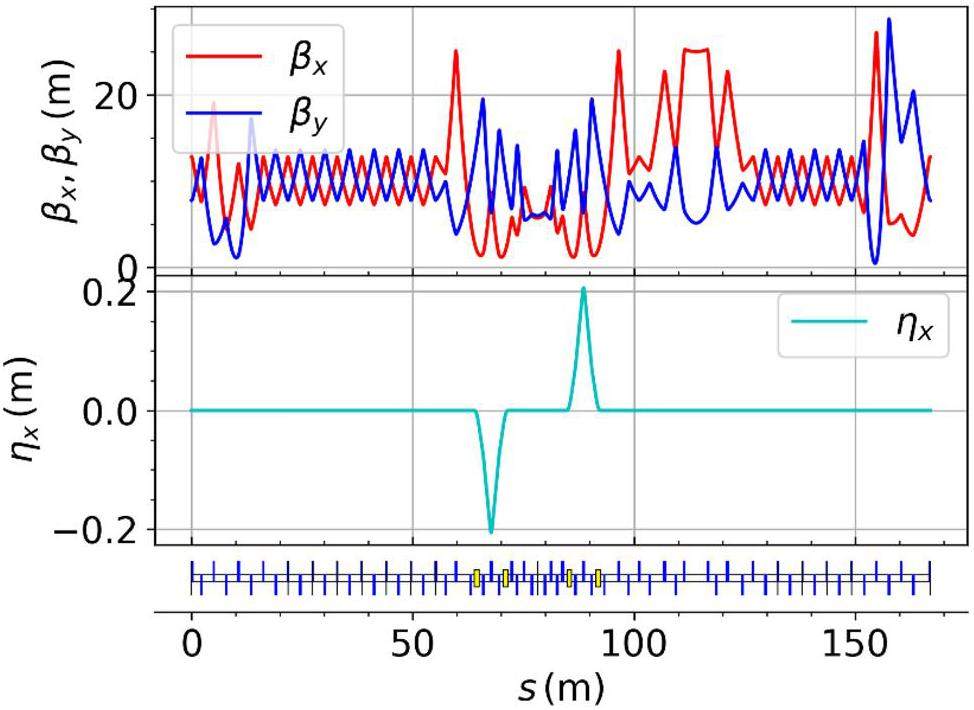
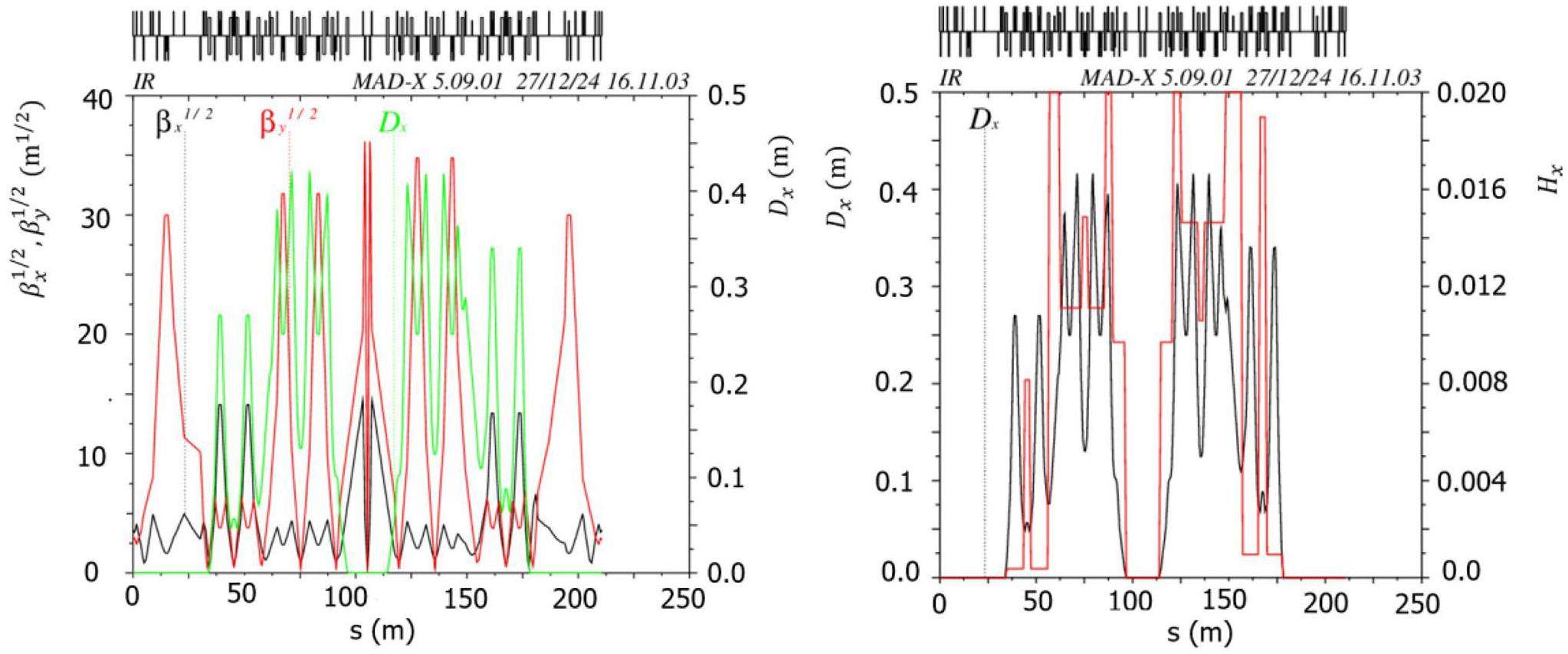
Figure 3 shows the layout of the collider rings, and Fig. 4 presents the optical functions. This section introduces the optical design of the arcs, straight sections, and crossing region in the two-fold symmetric lattice; the design of the IR optics is presented in Sect. 2.2.3.
Arc optics design
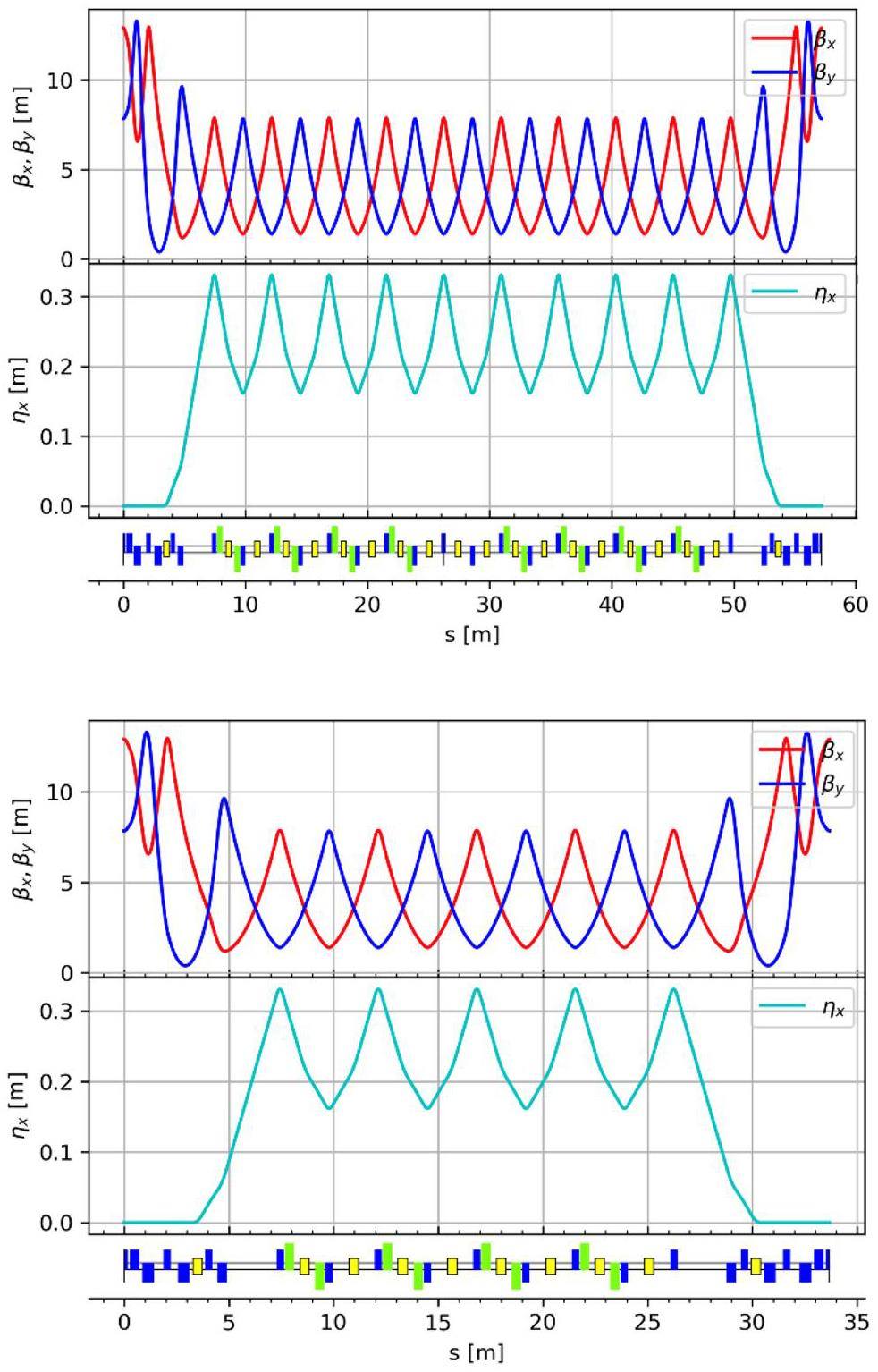
The large and small arc sections adopt the same standard FODO cell design. Each FODO cell is 4.7 m in length, providing a bending angle of 6°, a phase advance of 90°, and a momentum compaction factor of 4.9 × 10-3. Each cell includes four 0.8 m drift sections for hosting sextupole magnets and beam collimators. Figure 5 shows the optical functions of a FODO cell. The ends of each arc section contain dispersion suppressor sections and optics matching sections. The large arc section consists of 9 FODO cells plus the dispersion suppression and matching sections, totaling 57.184 m in length and providing a total bending angle of 60°; the small arc section contains 4 FODO cells plus the dispersion suppression and matching sections, with a total length of 33.684 m and a bending angle of 30°.
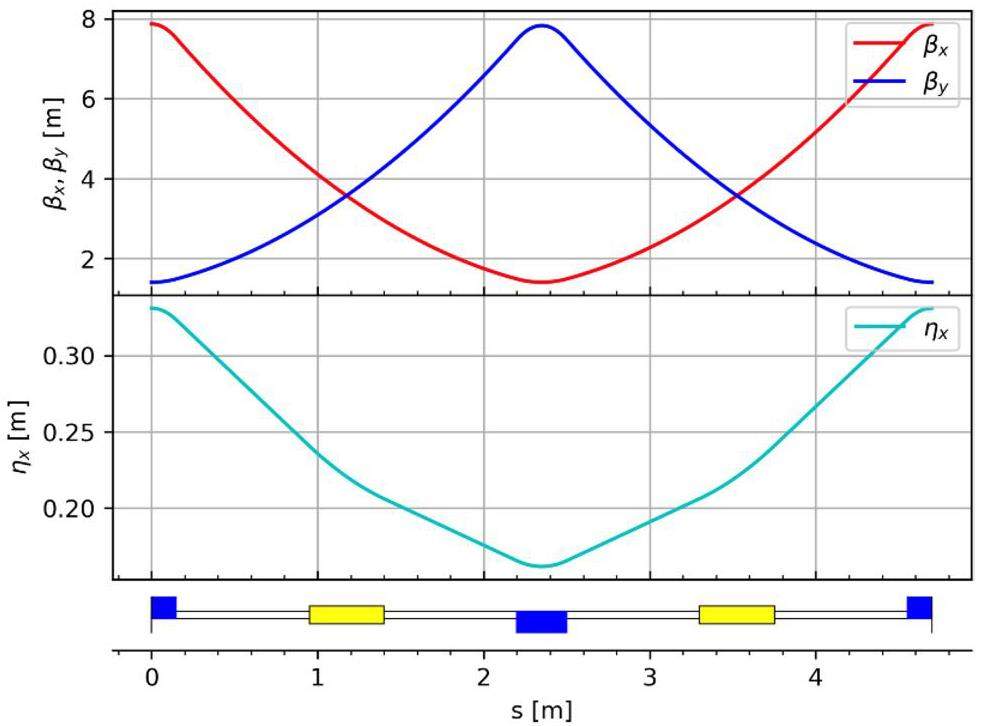
Chromaticity correction and nonlinear optimization in the arc sections are achieved using sextupole magnets. These sextupoles are placed in pairs with a phase advance of 180°, satisfying the −I transformation condition, which effectively cancels first-order geometric resonance terms. The large arc section contains 8 groups of sextupoles (4 defocusing sextupole (SD) pairs + 4 focusing sextupole (SF) pairs), and the small arc section contains 4 groups (2 SD pairs + 2 SF pairs). The field strength of each group of sextupole magnets can be adjusted independently. Figures 6 show the optical functions of the large and small arc sections.
Crossing region optics
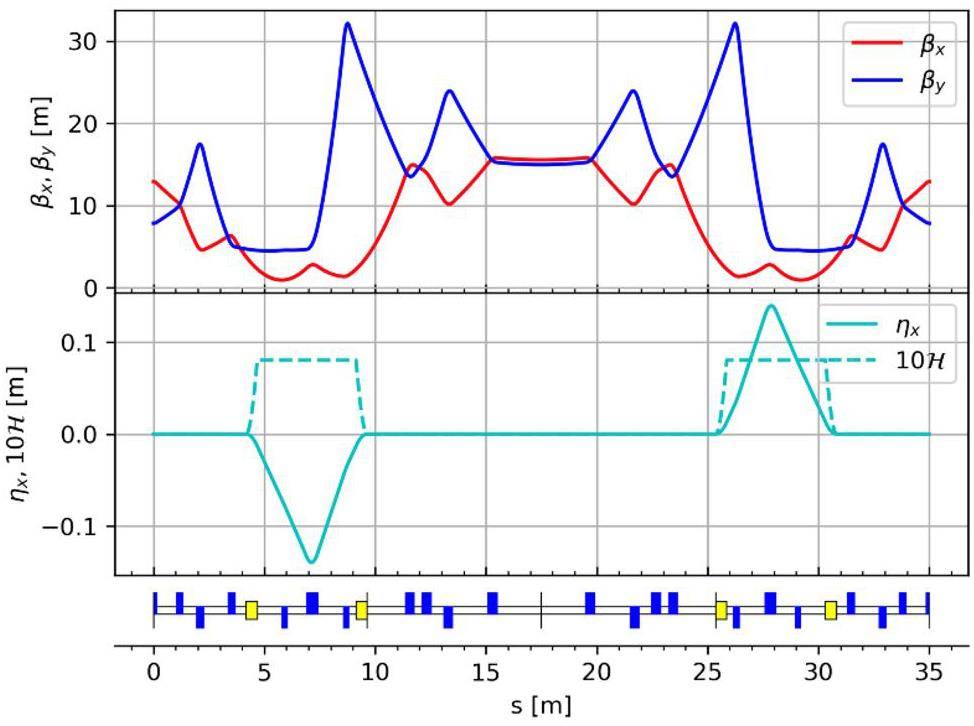
The crossing region employs two groups of dipole magnets to achieve the crossing and separation of the two beamlines. To achieve achromaticity, a triplet structure with a phase advance of π is used between the dipole magnets in each set. Additionally, two doublet structures are placed in the middle of the crossing region. To reduce the collision probabilities at the crossing point, the β functions in this section are designed to be relatively large, resulting in correspondingly larger beam sizes. The total length of the crossing region is 35 m, and the separation distance between the two rings ranges is approximately 2 m. Figure 7 shows the optical functions of the crossing region.
General straight section optics
In addition to generally designed straight sections that are only for connecting the arc sections, most of the straight sections in the collider rings are dedicated segments, such as the injection and extraction section, the DW sections, the RF section, and the beam collimation section, depending on their specific functions. Here, it describes only the design of the general straight section.
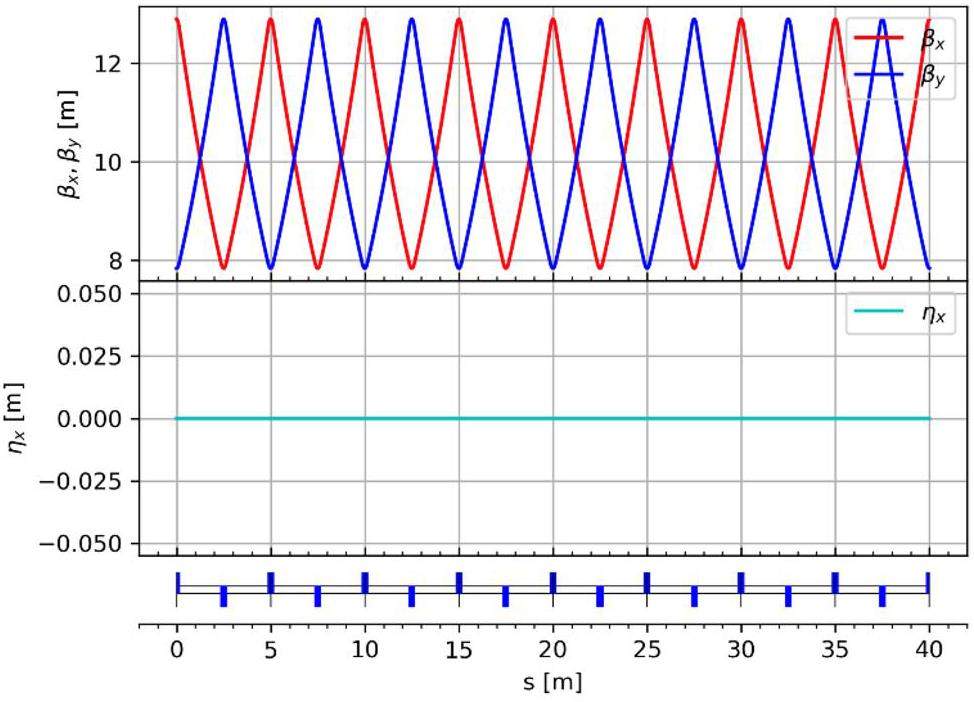
The general straight section adopts a standard FODO structure. Each FODO cell is 5 m long with a phase advance of 30° and contains two drift spaces that are 2.2 m long. Figure 8 shows the optical functions of the general straight section consisting of eight FODO cells.
Damping wiggler section optics
Each of the STCF collider rings includes two DW sections, which are used to reduce the damping time and adjust the beam emittance at different beam energies. Each DW section contains eight DWs that are 4.8 m long. To ensure the relatively gentle variation of the β-function within the wigglers, the lattice design incorporates a specially optimized structure for the wiggler sections.
A triplet configuration is chosen as the primary lattice structure for this section because of its flexibility. This configuration allows for long drift spaces to accommodate the wigglers while ensuring slow variation of the β-function at the wiggler locations. Since commonly used lattice design codes such as MADX and SAD do not include built-in DW models, the typical approach is to model the wigglers using a series of bending magnets and drift spaces that achieve equivalent radiation damping effects. Figure 9 shows the lattice functions of two focusing cells and the long drift section within the DW region.
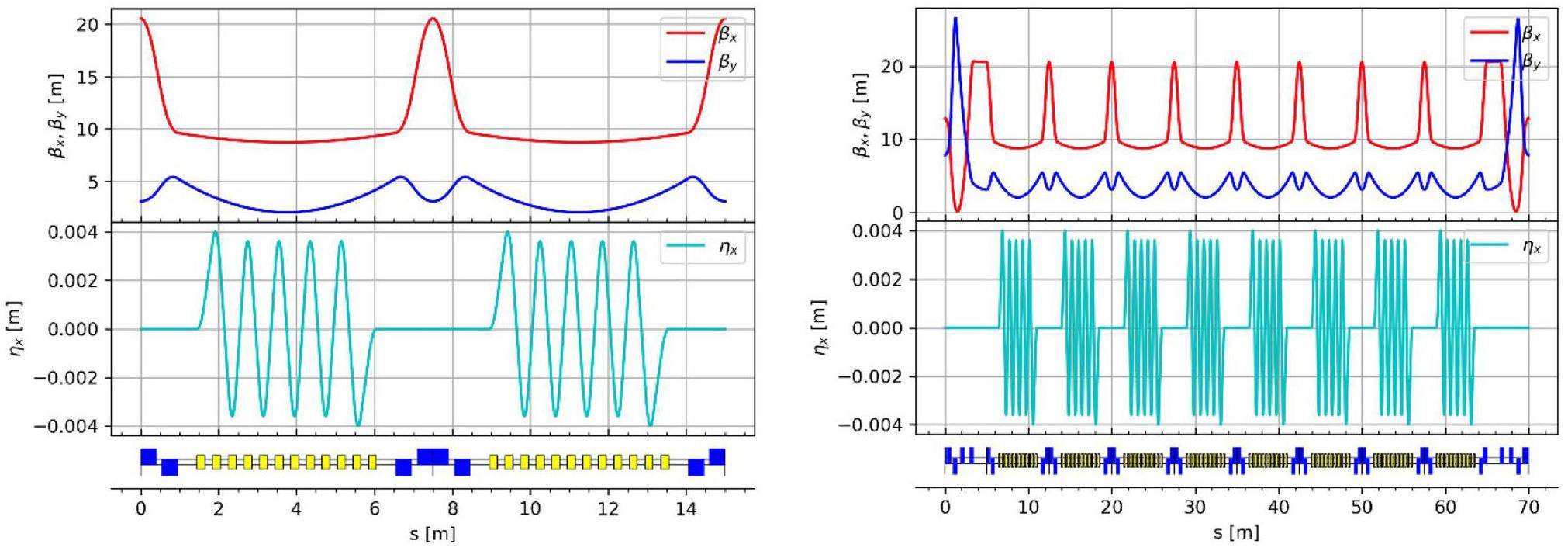
Because DWs influence the optical functions of the lattice, it is necessary to place several quadrupole magnets at both ends of each DW section. These are used to compensate for the optical distortions introduced by the wigglers and to match the Twiss parameters at the transition to adjacent straight sections. Table 2 lists the key parameters of the lattice design for the DW section.
| Parameter | Value |
|---|---|
| Total wiggler section length (m) | 2 × 70 |
| Triplet unit length (m) | 7.5 |
| Wiggler unit length (m) | 4.8 |
| Number of wigglers per ring | 16 |
| Average β-functions at wiggler, βx/βy (m) | 5.08/3.78 |
Scheme II (Single-fold symmetry)
In conjunction with developing the above scheme, we have also studied an alternative scheme called Scheme II. This scheme has a reserved space for the installation of SSs and a multifunctional long straight section.
The electron ring of this scheme has four arc sections, three SSs, four DWs, one IR, and one multifunctional section. The geometric layout of the dual ring and distribution of different units are shown in Fig. 10. This layout is realized by employing dipole magnets with different bending angles on both sides of the IR and arc dipole magnets with a bending radius difference of 2.14 m between the inner and outer half-rings.
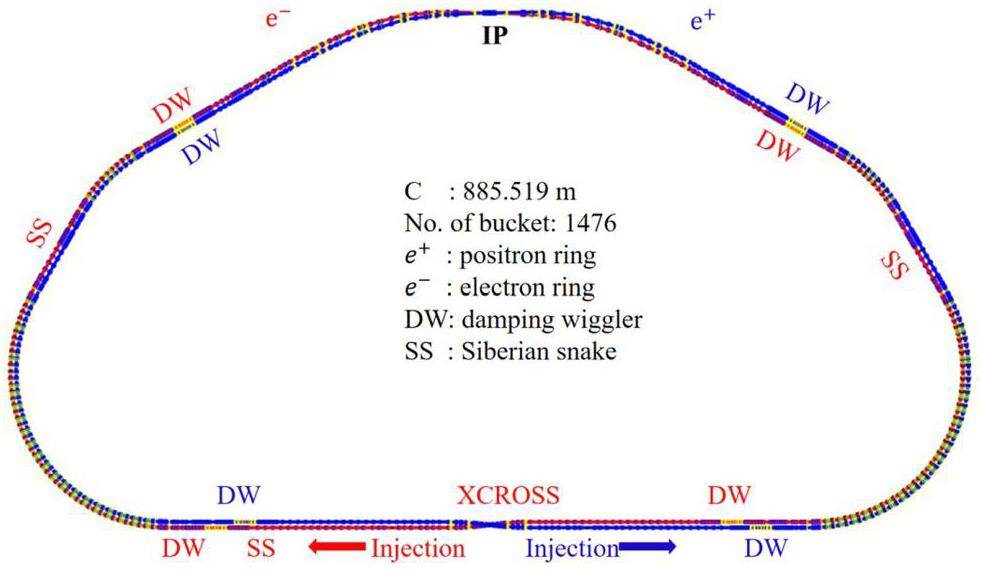
Figure 11 illustrates the full-ring lattice and its linear optical functions. Table 3 presents the main collider ring parameters of Scheme II considering intra-beam scattering (IBS), synchrotron radiation, and DWs. These parameters are for the optimal energy of 2 GeV.
| Parameter | Value |
|---|---|
| Optimal beam energy, E (GeV) | 2 |
| Circumference, C (m) | 885.519 |
| Crossing angle, |
60 |
| Revolution period, |
2.953 |
| Horizontal/Vertical emittance, |
6.368 / 0.0318 |
| Coupling factor, K | 0.5% |
| β-functions at IP, |
40 / 0.6 |
| Beam sizes at IP, |
15.96 / 0.138 |
| Betatron tunes, |
33.554 / 33.571 |
| Momentum compaction factor, |
12.433 ×10-4 |
| Energy spread, |
9.908 ×10-4 |
| Beam current, I (A) | 2 |
| Number of bunches, |
738 |
| Particles per bunch, |
5.00 ×1010 |
| Bunch charge (nC) | 8.0 |
| SR energy loss, |
383.77 |
| Damping times, |
30.77 / 30.77 / 15.39 |
| RF frequency, |
499.7 |
| Harmonic number, h | 1476 |
| RF voltage, |
2 |
| Longitudinal tune, |
0.0169 |
| Bunch length, |
10.25 |
| RF acceptance, |
1.58 |
| Piwinski angle, |
19.26 |
| Beam–beam parameters, |
0.0024/0.081 |
| Hourglass factor, |
0.8804 |
| Peak luminosity, L (cm-2 s-1) | 1.03 × 1035 |
| Touschek lifetime, |
>250 |
IR optics–scheme II
The IR adopts the crab-waist collision scheme, and its lattice structure is similar to that in Scheme I (see Sect. 2.2.3). The linear optics system of the right half (the left half has the same functional partitioning but with different parameters) consists sequentially of the final telescope (FT), the local chromaticity correction system (LCCS), the crab sextupole (CS) section, and the Matching Transport (MT) section, covering a total bending angle of 60°. At the IP, the β functions are
In addition to sextupoles for correcting first- and third-order chromaticities [5], the IR is also equipped with weak sextupole magnets [6] to optimize nonlinear performance. The geometric layout of the IR is shown in Fig. 12, and its linear optics functions are shown in Fig. 13.

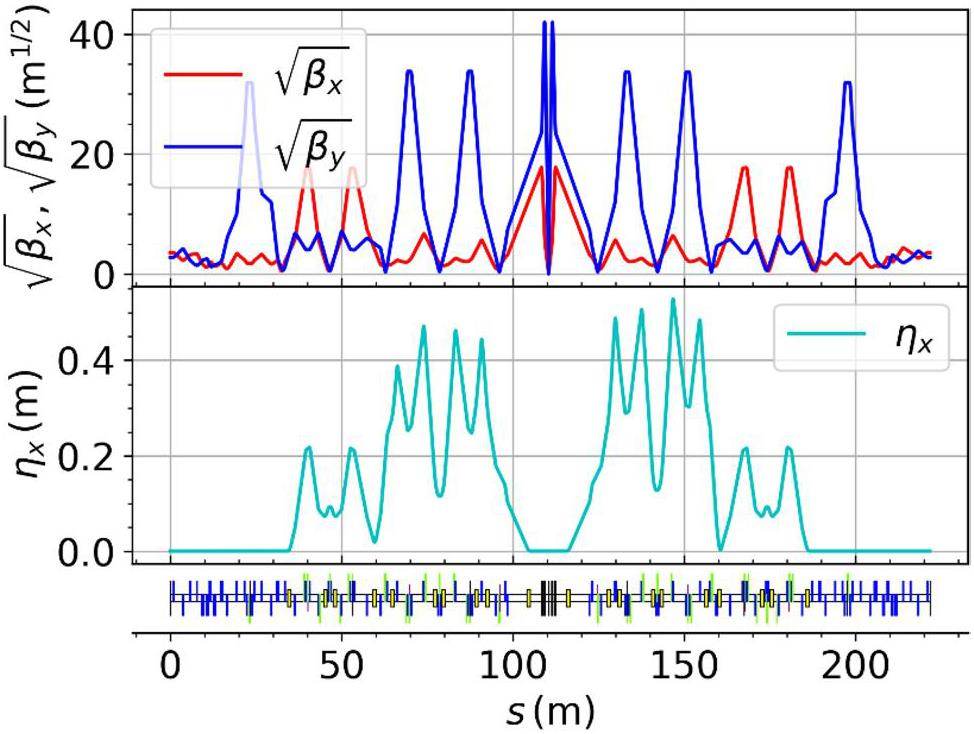
Arc optics–scheme II
To implement the dual-ring layout, the arc sections are divided into inner and outer arcs, each consisting of a long arc section with a 120° bend and a short arc section with a 30° bend. Both are constructed using FODO structures with horizontal and vertical phase advances of 90° and a bending angle of 5°. In the FODO structures of the inner and outer arcs, the bending magnets have a curvature radius difference of 2.14 m, while the quadrupoles, sextupoles, and drift sections have equal lengths.
Figure 14 shows the lattice functions of the long and short arc sections in the outer half-ring. In the short arc, non-interleaved sextupole pairs with a –I transfer are used for chromaticity correction. In the FODO cells of the long arc, a focusing sextupole follows each focusing quadrupole, and a defocusing sextupole follows each defocusing quadrupole. A sequence of four identical FODO structures forms one HOA (Higher-Order Achromat) unit, effectively canceling the first- and second-order geometric driving terms [7].
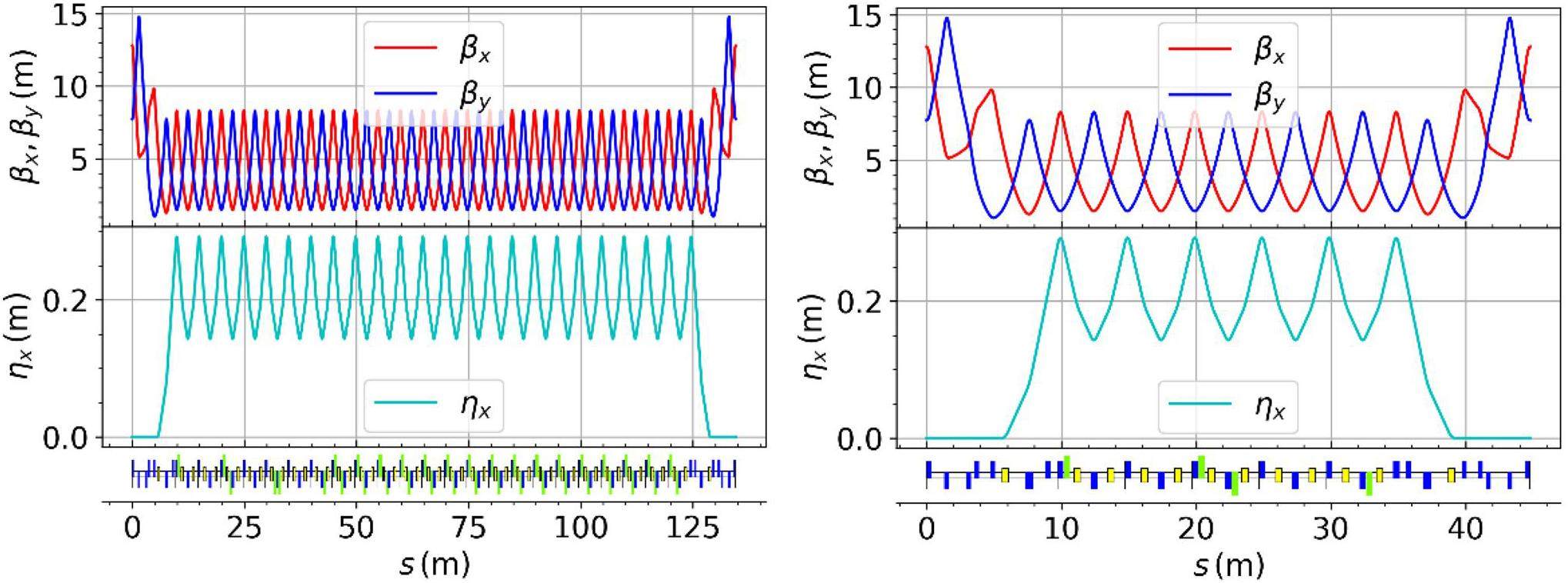
Straight section optics–scheme II
The straight sections include medium straight sections dedicated to the installation of SSs and DWs, as well as the multifunctional region for hosting the injection system, RF cavities, dual-ring crossing, and phase adjustment. Their corresponding linear optical functions are shown in Figs. 15 and 16.
SS refers to the space reserved for Siberian Snakes, which has an azimuthal angle of 120° between each pair. To regulate the damping time, two DWs are installed in both the inner and outer half-rings. Each wiggler is positioned at the center of its respective DW section, where a non-zero dispersion function is present. The dispersion function can be tuned by adjusting the magnetic field strength of the bending magnets, which enables control over the damping time and emittance. Six quadrupole magnets are arranged to ensure that the working point remains constant with varying wiggler field strength.
Dynamic aperture and Touschek lifetime–Scheme II
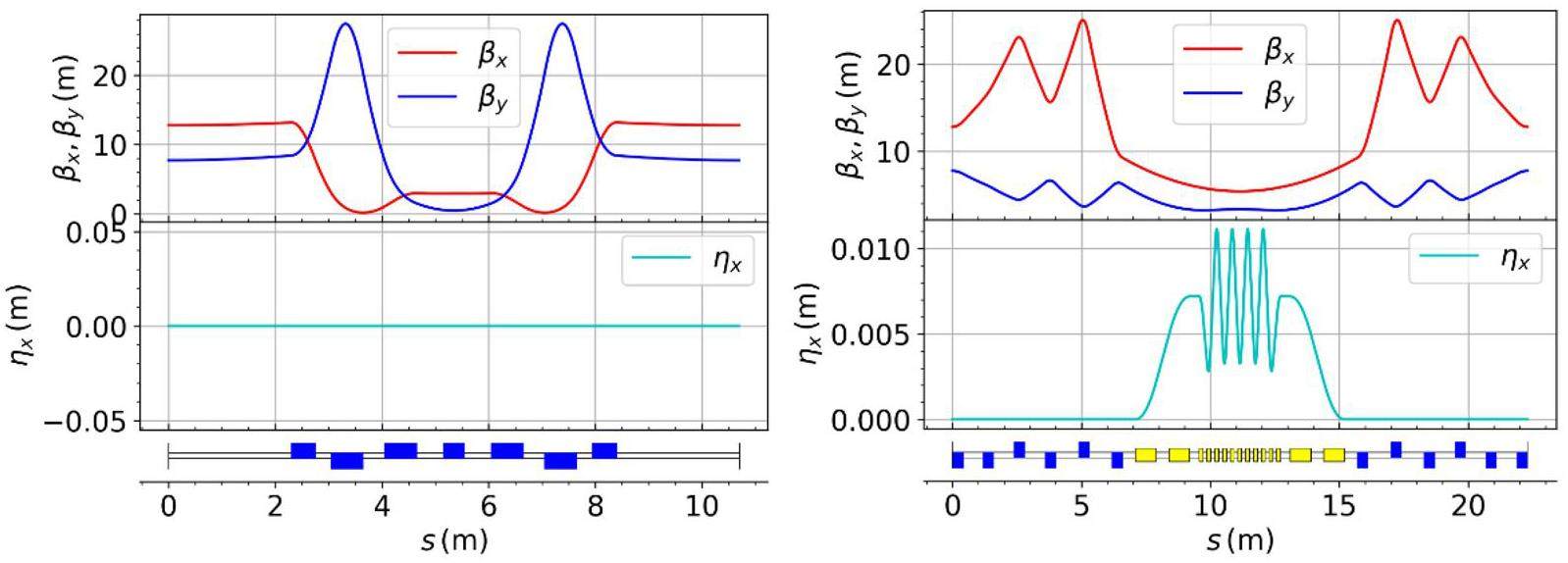
Placing phase tuners and sextupoles at the IP mirror position [8] enables the independent optimization of second- and third-order chromaticity, the W-function, and momentum acceptance. This optimization results in a large off-momentum dynamic aperture and momentum aperture. At a design luminosity of 1.03×1035 cm-2s-1
Interaction region optics design
The key objective of the lattice design of the STCF IR is compressing the β function at the IP to enhance luminosity while maintaining sufficient momentum acceptance and dynamic aperture for an adequate Touschek lifetime. This requires the careful optimization of both the linear lattice and nonlinear optics corrections in the IR. The fundamental design principle is to coordinate the linear optics with the phase advances required for nonlinear cancellation and the minimization of the effects of nonlinear sextupole fields.
Following the design philosophy of other new-generation electron–positron colliders [1, 4, 10–12], the STCF IR lattice adopts the modular structure illustrated in Fig. 18. It consists of a final focusing telescope (FFT) that minimizes the β functions at the IP, a matching section (MCY) between the FFT and the vertical chromatic correction section (CCY), local vertical/horizontal chromaticity correction sections (CCY/CCX), a matching section (YMX) from the CCY to the CCX, a dispersion suppressor (XMC), a CS section, and an MS connecting the IR to the long straight section. The linear optics functions of the STCF IR are shown in Fig. 19.

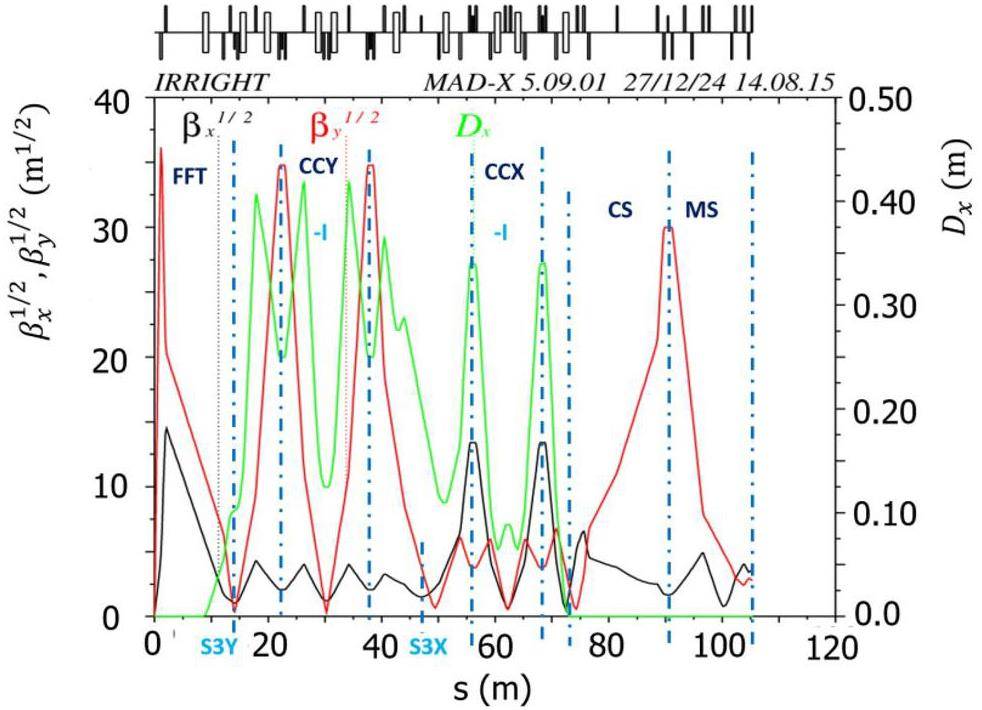
The FFT section adopts a focusing structure composed of two groups of quadrupole magnets: one superconducting and one room-temperature. The superconducting quadrupole doublet is used to achieve an extremely low
A bending magnet (B0) is inserted into the FFT to generate the dispersion required for local chromaticity correction. Given its proximity to the IP, the strength of this bending magnet should remain minimal to reduce the amount of synchrotron radiation background entering the detector.
The MCY section adopts a FODO-like cell starting with a defocusing quadrupole, making
The local vertical chromaticity correction section (CCY) must implement –I transformation between sextupole pairs to cancel their nonlinearities. This can be realized using two center-symmetric FODO cells with horizontal and vertical phase advances of π/2. Two identical dipole magnets, B3 and B4, are used to create symmetric dispersion.
The YMX section converts the β-function condition of
The local horizontal chromaticity correction section (CCX) is designed similarly to the CCY section, requiring a –I transfer transformation between sextupole pairs to cancel nonlinearities. Two identical dipole magnets, B7 and B8, are used to form symmetric dispersion. The XMC section cancels dispersion in the collision region, ensuring zero dispersion at the crab sextupoles.
The CS section consists of six quadrupole magnets satisfying the phase advance constraint between the crab sextupole and the IP and the alpha function constraint at the crab sextupole:
The dipole magnets in the IR have a total bending angle of 60°, and they are 1 m long. Apart from B0, which has a fixed bending angle of 1°, the strength of all dipoles must be chosen to adjust the dispersion function and keep the dispersion invariant
Transverse beam dynamics
The design goal of the transverse beam dynamics in the collider rings is achieving a sufficiently large dynamic aperture and momentum acceptance to ensure high injection efficiency and long beam lifetime.
In the arc sections of the collider rings, strong quadrupole focusing is required to realize a low emittance that is comparable to that of third-generation synchrotron light sources. A non-interleaved sextupole configuration was initially used to correct chromaticity in the arcs; however, owing to the limited number of sextupole pairs, the required sextupole strength was relatively high, resulting in significant nonlinear effects. Therefore, based on the concept of second-order achromats proposed by K.L. Brown [13], an interleaved –I transformation scheme was adopted for placing sextupoles in the arcs. This configuration cancels the first-order geometric terms generated by the sextupoles, although it cannot cancel higher-order geometric terms. Nevertheless, the use of more sextupole pairs allows for lower individual magnet strengths, leading to weaker residual higher-order terms. The increased number of sextupoles also aids in the global nonlinear optimization of the collider rings.
However, the dynamic aperture and momentum acceptance of the collider rings are primarily limited by the IR, which produces most of the ring’s nonlinearities [16, 17]:
· The IR must incorporate ultra-strong FF quadrupoles in a compact space to achieve extremely small
· The crab-waist mechanism imposes strict requirements on the phase advance between the crab sextupoles and the IP. Any lattice nonlinearity or imperfection can disrupt these phase constraints.
· Using compensation solenoids to cancel the detector solenoid field directly affects IR performance. For instance, solenoid and quadrupole field overlaps must be avoided, as they increase vertical emittance.
All of these nonlinear and high-order effects degrade the dynamic and momentum apertures of the collider rings, severely reducing beam injection efficiency and beam lifetime.
The IR optimization goal is to maximally compensate for the nonlinearities between the crab sextupole pairs. To achieve this, local horizontal and vertical chromatic sextupole pairs in the IR are designed to satisfy the –I transfer condition, which allows for the correction of first-order chromaticity while minimizing the nonlinear effects they introduce. The phase advance between the chromatic sextupoles and the FF quadrupoles is finely tuned to correct second-order chromaticity and the Montague function at the crab sextupole locations. Sextupoles are placed at the first and second IP mirror points to correct third-order chromaticity [6]. Since the β-functions at these mirror points are small, the geometric aberrations they contribute are relatively minor.
Since the STCF collider rings have numerous components and effects that create significant nonlinearities—such as the fringe fields of the FF quadrupoles, higher-order kinematic terms in IP drifts, chromatic sextupoles, and crab sextupoles—comprehensively analyzing these nonlinearities becomes intractable. Consequently, deriving the dynamic aperture through traditional analytical or perturbative methods is impractical.
Instead, a common approach is to first construct simplified models to individually assess the influence of each nonlinear or high-order effect and propose targeted optimization strategies. Subsequently, professional software tools such as MADX, SAD, and Elegant are employed to perform 4D/5D/6D tracking and optimize the dynamic aperture.
To optimize the dynamic aperture and momentum acceptance, advanced techniques such as multi-objective optimization algorithms are used for the global nonlinear optimization of the collider rings, where the crab sextupoles are always enabled during the process. A total of 48 chromatic sextupole pairs per ring are used as optimization variables (6 in the IR and 40 in the arcs). First, a program called PAMKIT [8], developed by members of this project, is employed in conjunction with intelligent multi-objective optimization algorithms to optimize sextupole strengths. First-order chromaticity and key resonance driving terms are used as constraints, while the dynamic and momentum apertures are treated as direct optimization objectives to determine the best sextupole configuration.
Subsequently, the software SAD is used to precisely evaluate the dynamic aperture of the collider rings because it accurately models the nonlinear effects mentioned above and has been successfully applied to KEKB and SuperKEKB. In SAD, six-dimensional canonical variables (x, px, y, py, z, and δ) describe particle motion, where px and py are normalized transverse canonical momenta with respect to the design momentum p0 and δ is the relative momentum deviation. Tracking simulations include longitudinal oscillations, synchrotron radiation in all magnets, high-order kinematic effects, finite-length effects of sextupoles, and crab sextupoles. Quantum excitation and Maxwellian fringe fields in quadrupoles are disabled. The number of tracked turns corresponds to one synchrotron radiation damping time.
After optimization, the dynamic apertures with the crab sextupoles turned off and on are shown in Fig. 21. As the figure shows, when the crab sextupoles are turned off, the horizontal dynamic aperture reaches nearly
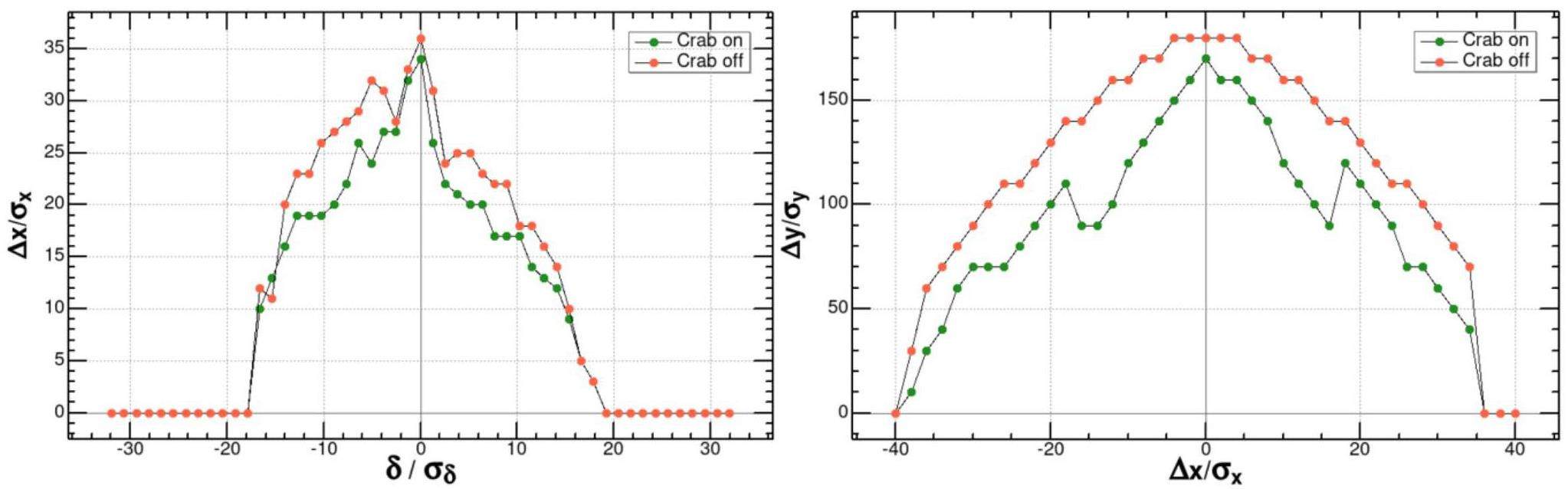
Fringe fields are present in all magnets and create nonlinearities that contribute to the reduction of the dynamic aperture. Analyzing the influence of Maxwellian fringe fields in dipole, quadrupole, and sextupole magnets using SAD showed that the fringe fields of the superconducting FF quadrupole magnets are dominant. Its effect on the dynamic aperture is shown in Fig. 23.
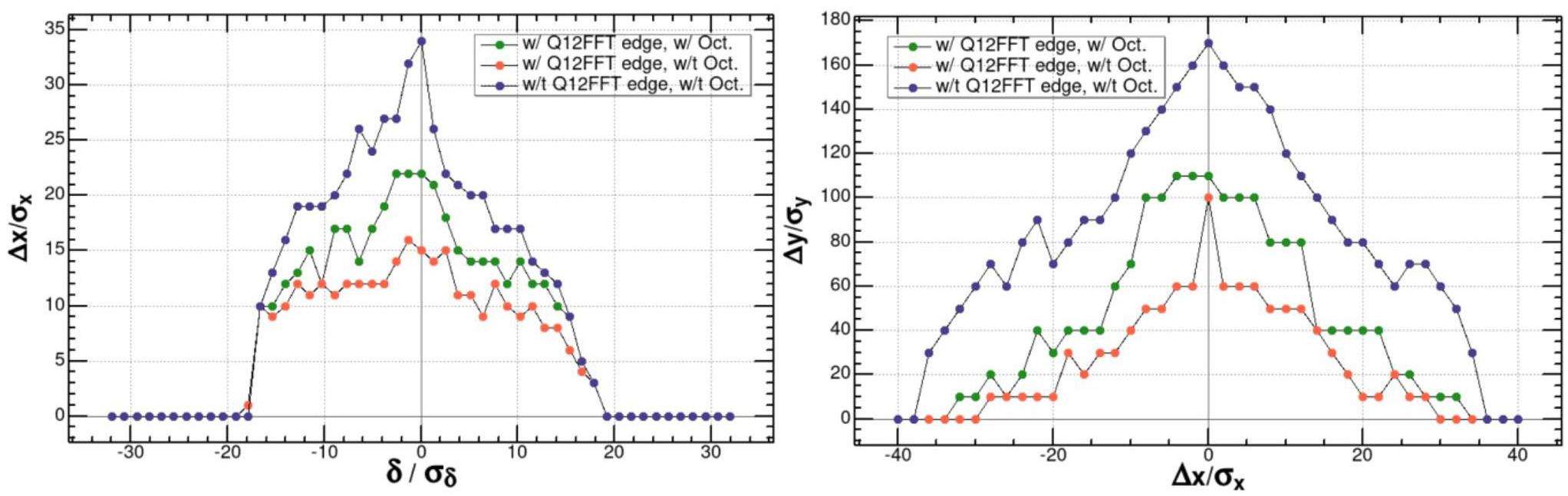
The second term in the Hamiltonian of the quadrupole fringe field resembles the form of the Hamiltonian of a thin octupole magnet. Therefore, octupole coils can be installed outside the FF quadrupole magnets to compensate for the fringe field effects of the FF quadrupoles. Figure 23 shows that the off-momentum and on-momentum dynamic apertures for the cases with and without the FF quadrupole fringe fields and with and without octupole compensation. All the cases have the crab sextupole switched on. The dynamic aperture with the FF quadrupole fringe fields decreases significantly compared to the case without the fringe fields; however, it can recover to some extent with the compensation of additional octupole coils. The optimization of the octupole coils remains ongoing to further recover the dynamic aperture.
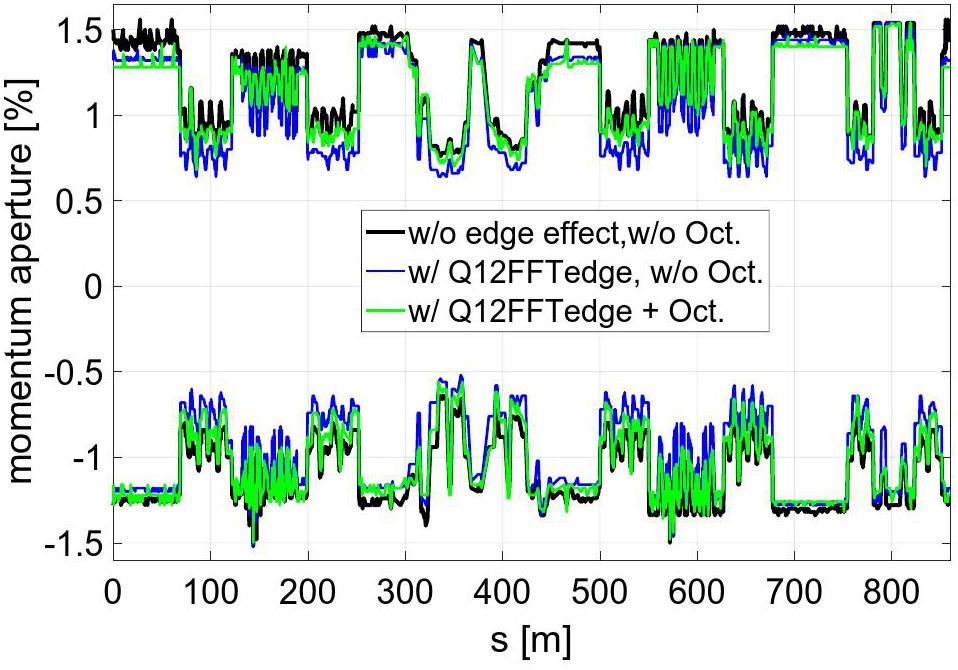
To further analyze dynamic aperture limitations, the Elegant program was utilized to track the local momentum acceptance (LMA) profiles around the entire ring with and without the FF quadrupole fringe fields and with and without octupole compensation. The results, as depicted in Fig. 24, indicate that the integration of the FF quadrupole fringe fields significantly degrades the LMA performance compared to the idealized fringe-field-free scenario. With octupole compensation, the LMA demonstrates remarkable recovery. The minimum LMAs under positive and negative momentum deviation are approximately 0.7% and 0.6%, respectively. The IR (between 300 m and 450 m in the figure) remains the critical bottleneck for the ring’s global momentum acceptance.
The solenoid field of the detector contributes to the vertical emittance growth in two main ways: the longitudinal Bz field directly induces horizontal x-y coupling, while the fringe radial field Bz introduces vertical dispersion. Consequently, careful compensation is required. The general principles for compensation are as follows: (1) the integral of the longitudinal Bz field must be zero; (2) within the region of the superconducting quadrupole magnets, the Bz field must vanish; (3) the integral of the radial fringe field of the solenoid should be maximally compensated. The focusing effect of the solenoid on the IR optics can be compensated by adjusting the strength of the FF quadruples. Preliminary studies show that the dynamic aperture can be fully recovered when the detector solenoid field is perfectly compensated.
At the beam energy of 2 GeV and peak luminosity of 1 × 1035 cm-2s-1 (with crab sextupoles activated), simulations using SAD and Elegant programs yield Touschek lifetimes of 325 s and 304 s, respectively, when the fringe field effects are neglected. Both values meet the design goal of exceeding 200 s lifetime at the target luminosity of 5 × 1034 cm-2s-1. When incorporating FF quadrupole fringe field effects, which typically introduce nonlinear distortions that reduce dynamic aperture, the uncompensated Touschek lifetime drops to approximately 150 s. However, after implementing compensation with octupoles, the lifetime recovers to approximately 250 s, maintaining compliance with the 200 s operational requirement.
To further improve the Touschek lifetime, additional nonlinear optimization strategies are required to enlarge the LMA. These include further optimization of nonlinearities in the collision region, the adoption of new nonlinear optimization strategies (such as those based on resonance driving terms and their fluctuations), and the inclusion of phase advances between different regions (such as between the IR and arc sections or between adjacent arc sections) as tuning variables.
Longitudinal beam dynamics
Challenges of longitudinal beam dynamics of electron storage rings with ampere-order target beam currents, such as the STCF collider rings, stem from longitudinal coupled-bunch instabilities due to the fundamental and parasitic modes of RF cavities [18]. The RF cavity scheme must meet both specific voltage and power requirements and effectively suppress these coupled-bunch instabilities. STCF is designed to adopt 500 MHz TM020-type room-temperature main RF cavities. Compared to conventional TM010 cavities, TM020 cavities feature relatively higher quality factors (Q) and lower R/Q values. Therefore, for the same cavity voltage and power requirements, the total R/Q can be reduced by approximately half [19], effectively mitigating coupled-bunch instabilities driven by the fundamental mode. This makes it feasible to suppress such instabilities through relatively simple means, avoiding overly complex LLRF feedback system designs.
Table 4 presents the longitudinal beam dynamics parameters and corresponding RF parameters of STCF at three beam energies. For beams of 1 GeV & 1.1 A, 2 GeV & 2 A, and 3.5 GeV & 2 A, 2, 6, and 15 cavities, respectively, are required to meet both voltage and power demands, with some safety margins. Table 5 lists the fundamental mode parameters of the STCF TM020 cavity. These parameters are primarily used to evaluate the coupled-bunch instabilities induced by the accelerating mode.
| Parameter | Value | ||
|---|---|---|---|
| Beam energy, E (GeV) | 2 | 1 | 3.5 |
| Momentum compaction factor, αp (×10-4) | 13.49 | 12.63 | 13.73 |
| Energy spread, σe (×10-4) | 7.8 | 6.18 | 10.02 |
| Beam current, I (A) | 2 | 1.1 | 2 |
| Bunch filling factor | 48% | ||
| Energy loss per turn, U0_sr (keV) | 543 | 106 | 1494 |
| Power loss per turn, P (kW) | 1086 | 117 | 2988 |
| Longitudinal damping time, τz (ms) | 10.57 | 27.07 | 6.72 |
| RF frequency, fRF (MHz) | 499.7 | ||
| Harmonic number, h | 1434 | ||
| Total RF voltage, VR (MV) | 2.5 | 1 | 7.5 |
| Number of RF cavities | 5 | 2 | 15 |
| Voltage per cavity (kV) | 500 | ||
| Power per cavity (kW) | 217 | 58.5 | 199.2 |
| Coupling factor | 4.71 | 2.33 | 5.5 |
| Detuning frequency (kHz) | –64.1 | –57.6 | –99.0 |
| Parameter | Value |
|---|---|
| Frequency (MHz) | 499.7 |
| R/Q=V2/(2P) | 47.5 |
| Q0 | 60,000 |
| R (MΩ) | 2.85 |
| QL (βopt=5.5) | 9230 |
TM020 accelerating mode stability analysis
To analyze coupled-bunch instabilities due to the fundamental modes of RF cavities, the influence of low-level feedback must be considered since it modifies the impedance experienced by the beam [20]. Two common methods are used for evaluation: analytical calculations based on closed-loop cavity impedance and particle tracking simulations [21]. For the LLRF feedback, we only consider PI (proportional-integral) feedback based on I/Q signals. The closed-loop impedance of the cavity can be expressed as:
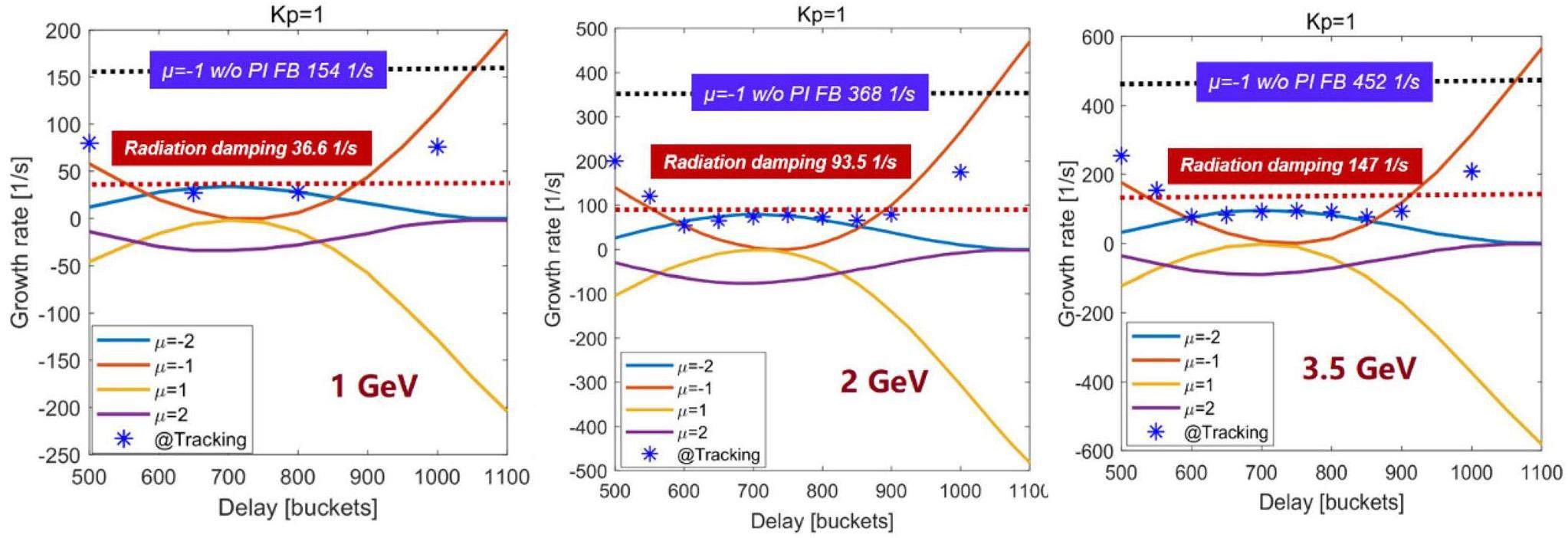
For STCF, by setting the appropriate proportional gain and delay time of the PI feedback, the –1 mode can be effectively suppressed and the –2 mode can be maintained below the threshold determined by synchrotron radiation damping, thus avoiding instabilities caused by the fundamental mode. Using the 2 GeV & 2 A beam case as an example, Fig. 25 shows the growth rates of major low-order modes obtained by both analytical and particle tracking methods for various proportional gains and delay times. Without PI feedback, the –1 mode has a growth rate of 368 s-1, which is much higher than the damping rate of 93.5 s-1. When
TM020 parasitic mode stability analysis
In the TM020 cavity, the TM020 mode is the accelerating mode, and modes with frequencies higher or lower than its nominal frequency are referred to as higher-order and lower-order modes, respectively. Both types can cause significant coupled-bunch instabilities. For simplicity, we refer to both as parasitic modes. To mitigate these instabilities, the cavity design must incorporate features that significantly suppress these parasitic modes. Assuming that beam spectral lines coincide with the resonance frequencies of parasitic modes, the associated coupled-bunch instability growth rate is typically calculated as
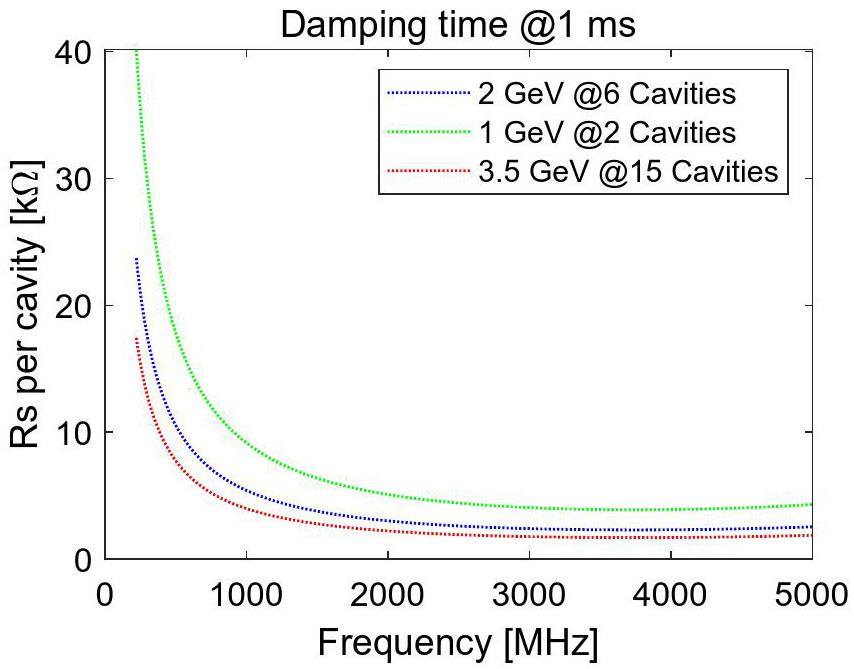
STCF has a synchrotron oscillation period less than 0.2 ms. Assuming that the longitudinal bunch-by-bunch feedback system has a conservative damping time of 1 ms, the impedance thresholds of parasitic modes are shown in Fig. 26. The threshold is lowest for 3.5 GeV because it uses the most cavities and assumes that all HOMs are aligned. Regardless, the lowest single-cavity threshold is 1.7 kΩ at 3.75 GHz, which is achievable for TM020 cavities.
Transient beam loading effects
The 5% empty buckets reserved to suppress ion trapping introduce transient beam loading effects [22], resulting in bunch-to-bunch variations in synchronous phase and bunch length. Tracking simulations of this effect show the resulting distributions of bunch centers and lengths, as illustrated in Fig. 27. The effect on bunch length is minimal (within ± 1 ps), and variations in the bunch center remain within ± 20 ps, suggesting that the impact on luminosity is negligible.
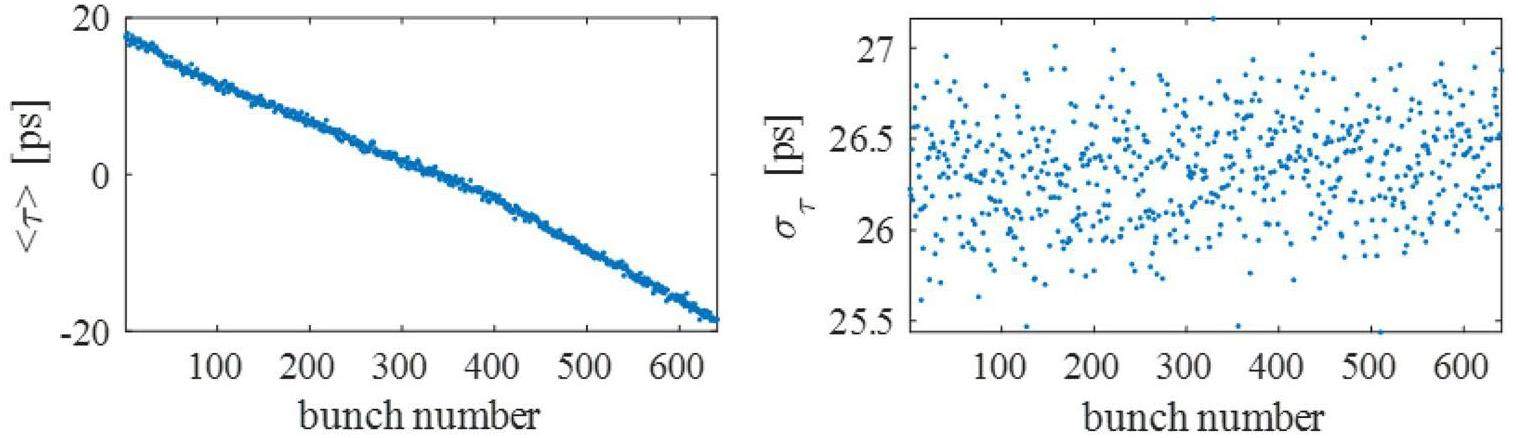
STCF is designed to use the TM020-type room-temperature RF cavity scheme. Owing to its relatively low R/Q, complex feedback schemes (e.g., one-turn delay feedback and direct feedback) such as those adopted by the PEP-II collider are not necessary. The stability of the fundamental mode can be maintained by choosing the appropriate PI feedback gain and delay parameters, thereby significantly simplifying the LLRF system. Radiation damping alone is insufficient for damping coupled bunch instabilities caused by parasitic modes; a longitudinal bunch-by-bunch feedback system providing at least 1 ms of damping is required. From the perspective of the RF cavity design, suppressing parasitic modes below the instability threshold under such damping conditions is entirely achievable.
Beam–beam interaction and luminosity optimization
For a crab-waist scheme collider using flat beams (with transverse beam sizes at the IP satisfying
The luminosity can also be written as [24]
Based on operational experience, the vertical beam–beam parameter
Beam–beam interaction is a key factor in determining collider luminosity, beam stability, and beam lifetime. In third-generation high-luminosity colliders using the crab-waist scheme, where the beam current is high and emittance is small, the beam–beam effects are especially prominent. Experience from colliders such as DAFNE and SuperKEKB, as well as numerous theoretical and numerical studies, has shown that beam–beam effects are significantly coupled to other processes, such as lattice nonlinearities and impedance, which limits overall machine performance. Therefore, the severity of beam–beam interactions depends jointly on key beam parameters and the machine operating mode and must be optimized carefully to enhance performance. In addition to qualitative theoretical analysis, the detailed impact of beam–beam interactions on accelerator performance is mainly assessed through simulations. Weak-strong simulations require fewer computational resources and are suited for the wide exploration of the beam parameter space, such as tune, Twiss parameters at the IP, and machine tolerance to imperfections, serving as a foundation for strong–strong simulations. Strong–strong simulations, which are more computationally intensive, are used for localized studies of the beam parameter space and to evaluate beam stability. Weak-strong simulations mainly address incoherent collective effects, whereas strong–strong simulations focus on coherent instabilities involving both beams.
Simulation results and analysis
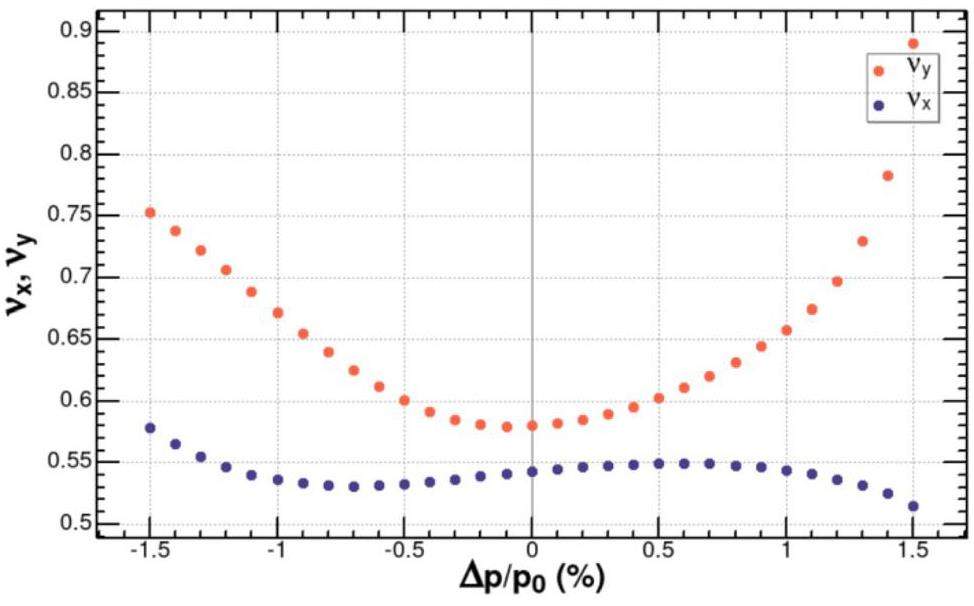
The working point in e+e- storage ring colliders is typically optimized near half-integer values to achieve maximum luminosity. The precise fractional tune values are optimized using beam–beam simulations. Figure 28 shows the luminosity versus working point calculated using the BBWS code for fractional tunes above the half-integer (beam energy is 2 GeV; other parameters refer to Table 1). Comparing the simulations with and without the crab-waist scheme reveals that the crab-waist can effectively suppress nonlinear betatron resonances induced by beam–beam effects, thus enlarging the high-luminosity region in the tune space.
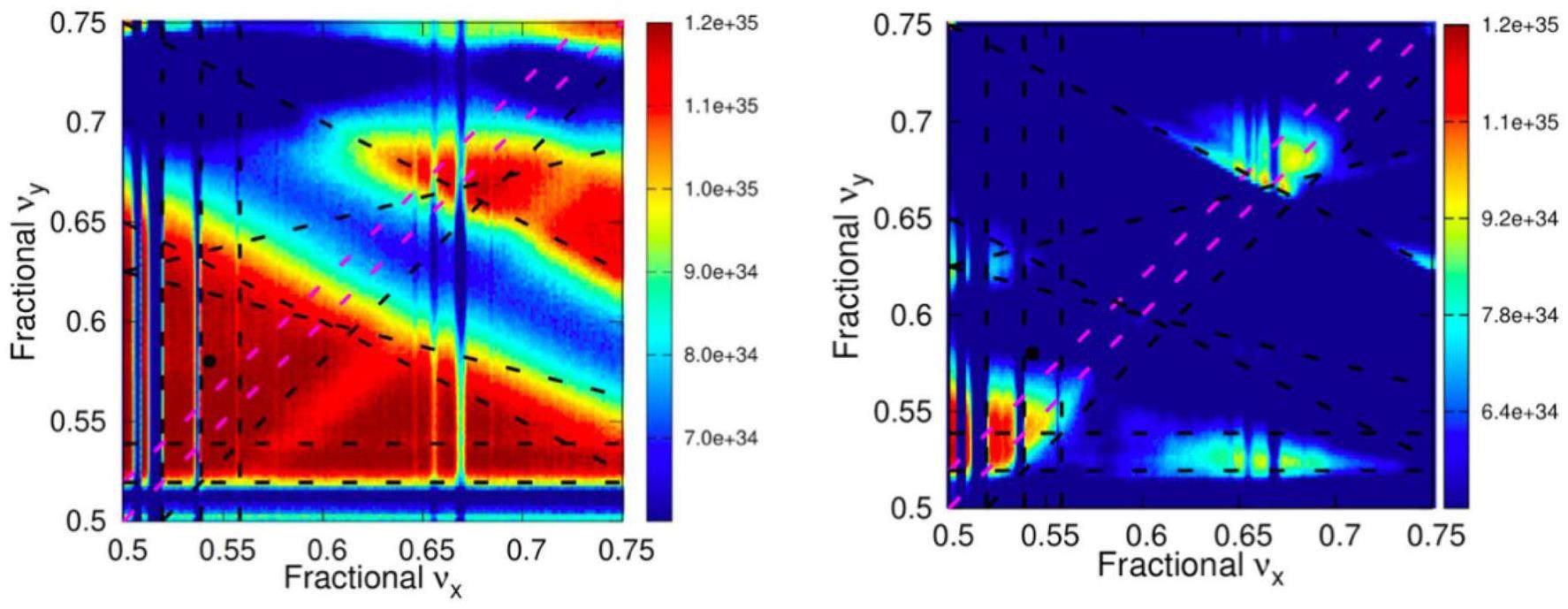
However, Figure 28 also shows that the crab-waist scheme cannot suppress synchro-betatron resonances induced by beam–beam interactions. Similar to SuperKEKB, STCF chooses a relatively large synchrotron tune
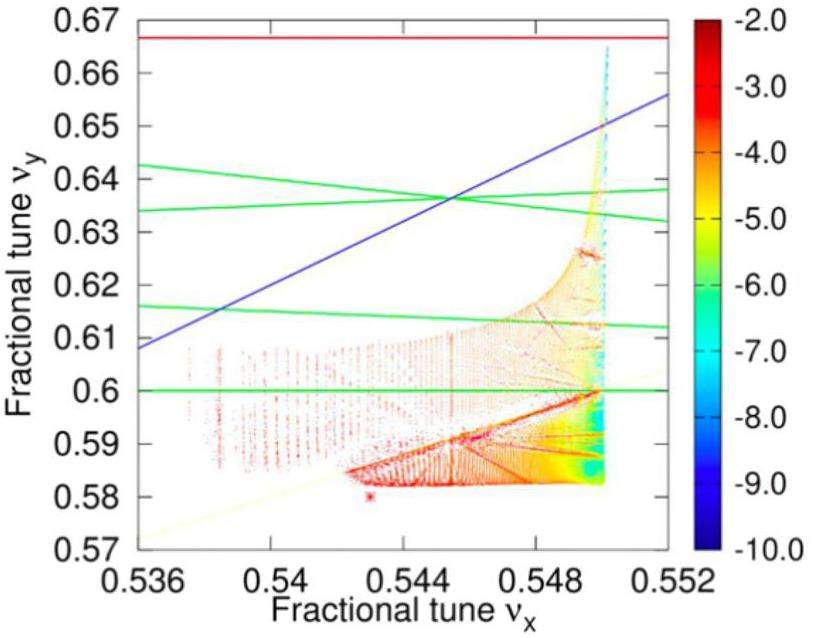
Coherent X-Z instabilities are evaluated using strong–strong beam–beam simulations. Figure 30 shows the results of scanning the horizontal tune (with vertical fractional tune fixed at 0.58) using the BBWS and BBSS codes. The results indicate that a horizontal tune near 0.543 avoids coherent X-Z instability. The strong–strong simulations suggest that the range of horizontal tune values for achieving high luminosity is narrow and can be widened by increasing the synchrotron tune
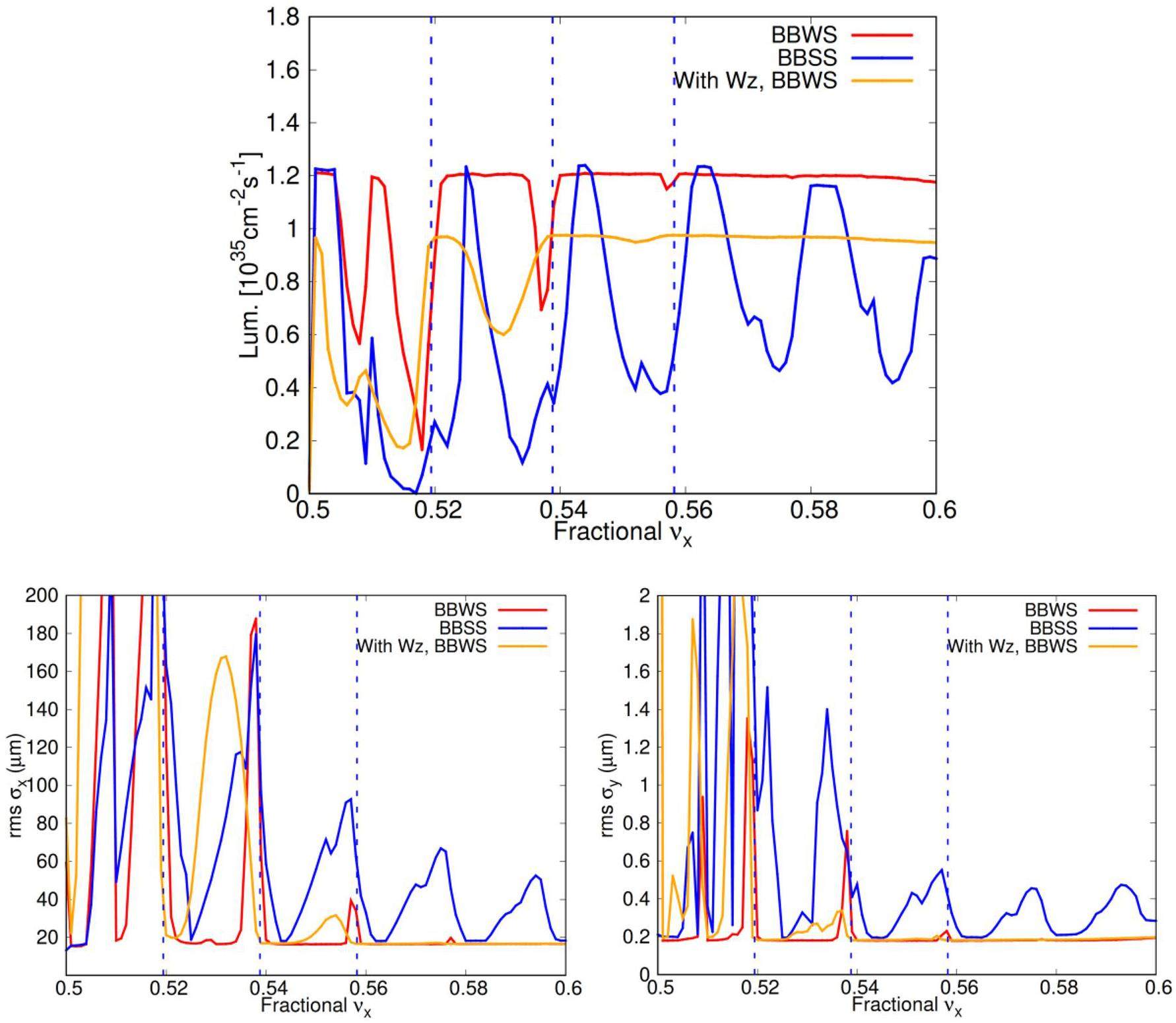
Fixing the horizontal fractional tune at 0.543, vertical tune scans were performed using BBSS. Figure 31 shows that the vertical fractional tune should be greater than 0.56 and that luminosity and transverse beam sizes are relatively insensitive to vertical tune within this range.
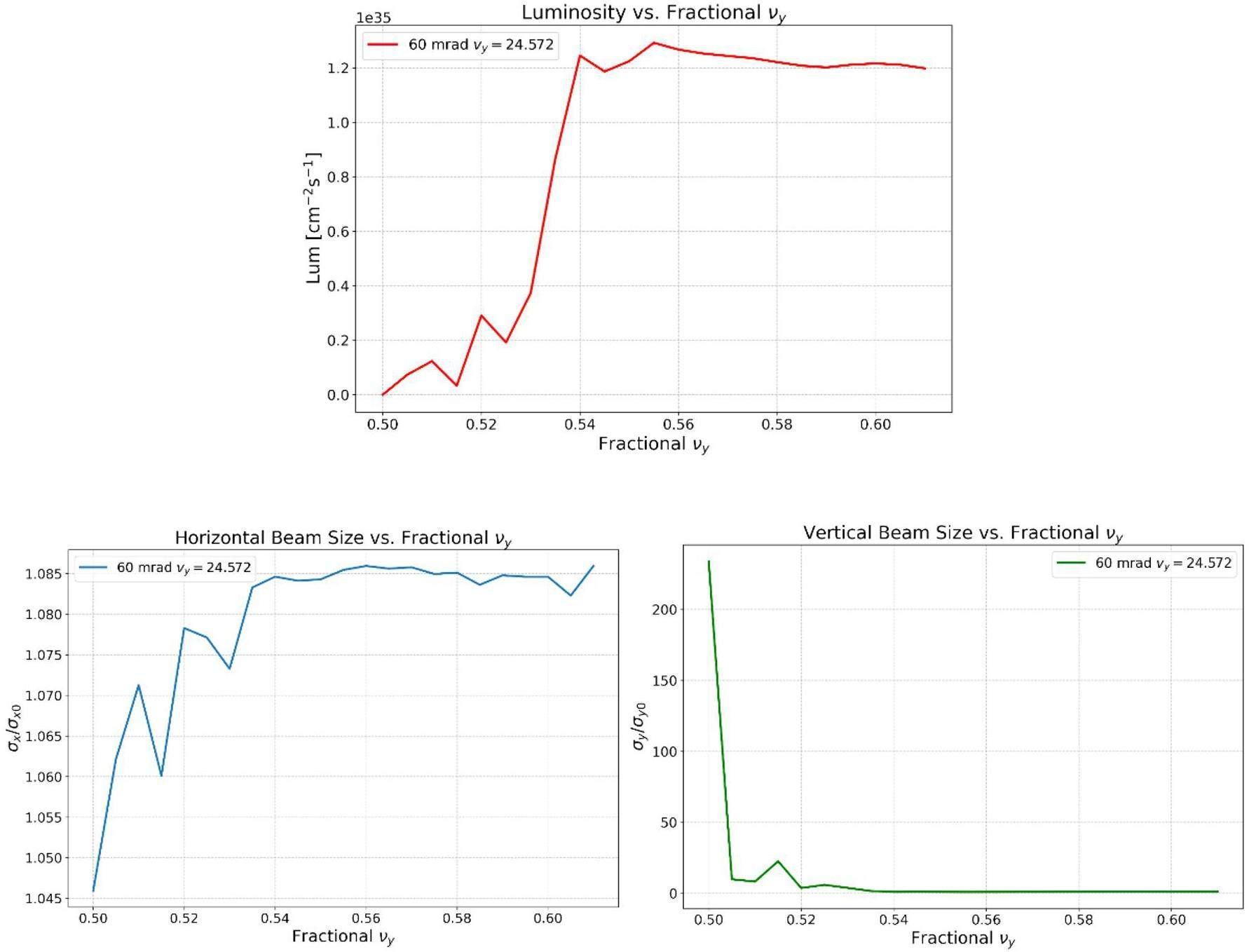
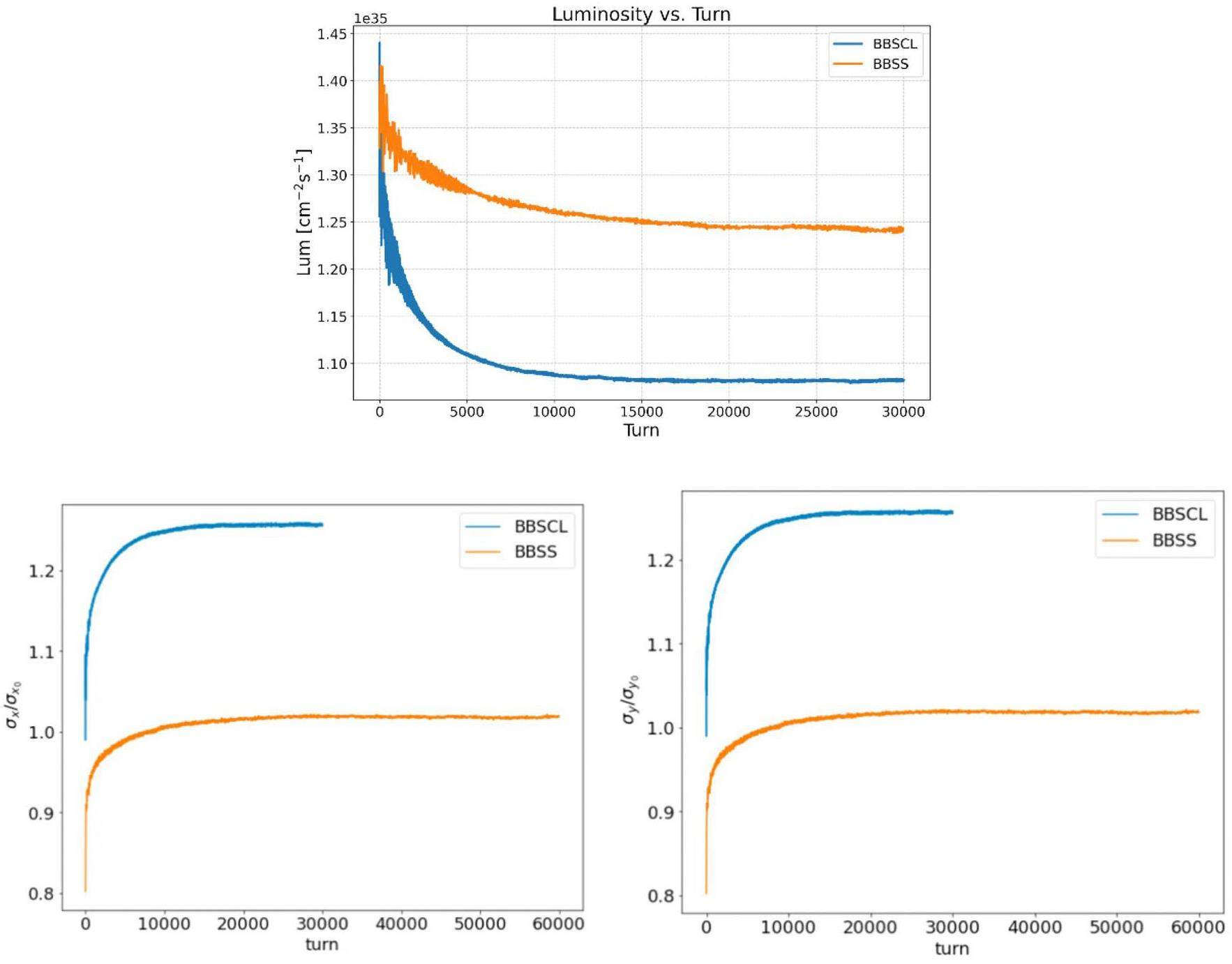
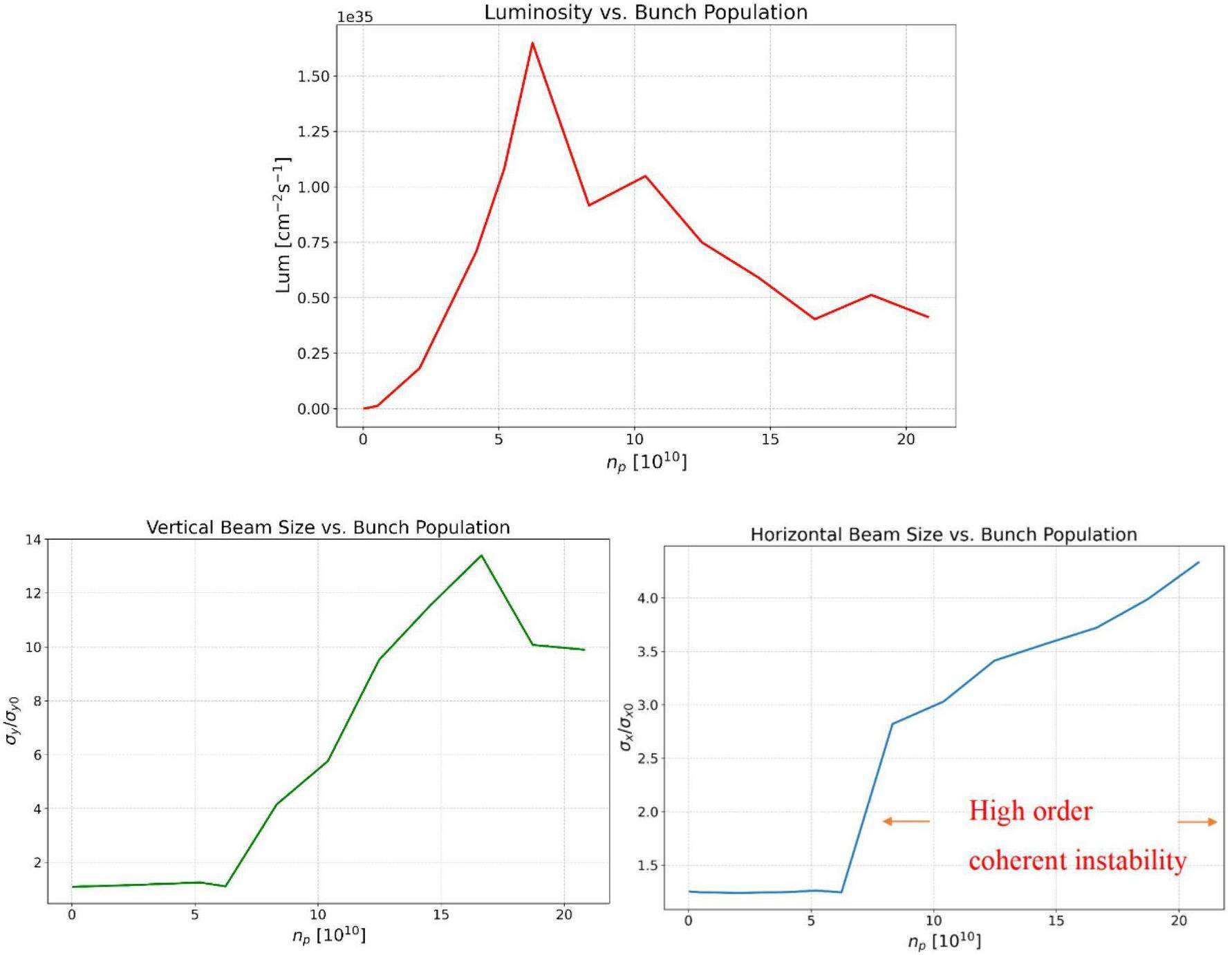
Simulations considering lattice nonlinearities (for details of lattice design, see Sect. 2.2) were performed using the BBSCL code and compared with the BBSS results. As shown in Fig. 32, coupling between lattice nonlinearities and beam–beam effects affects luminosity, with the extent depending on specific lattice design details. This highlights the need for deeper lattice nonlinearity studies and optimization. Additionally, BBSCL was used to scan the single-bunch current with the lattice included. Figure 33 shows that coherent instability occurs when Np exceeds 6.2×1010, above the nominal value of 5.2×1010.
Coupled effects of multiple physical mechanisms
The coupling of multiple physical mechanisms is particularly pronounced in colliders employing the crab-waist collision scheme, which significantly increases the complexity of machine design and the difficulty of achieving high-luminosity operation. In addition to the previously discussed couplings between beam–beam interactions, lattice nonlinearities, and impedance effects, several other factors warrant further investigation.
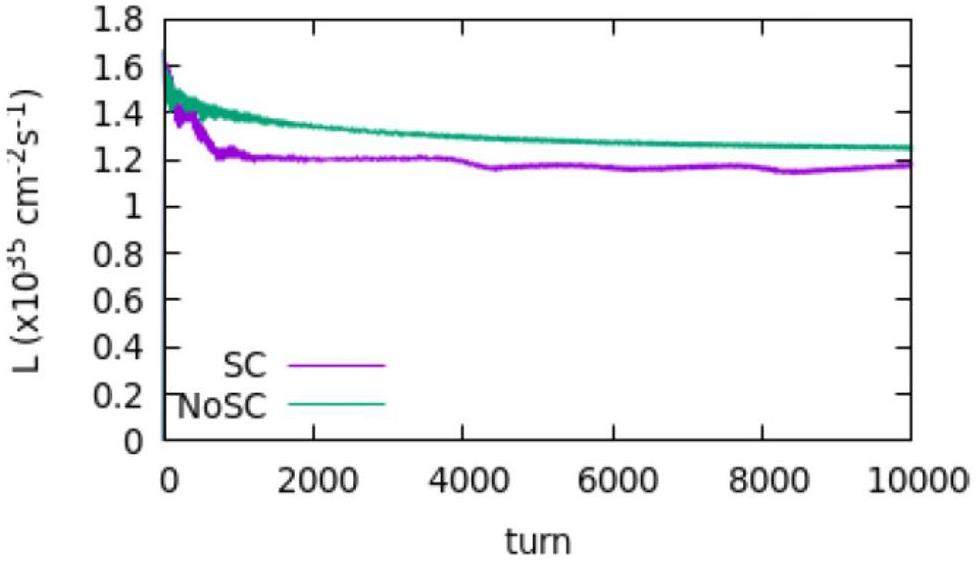
· Space charge (SC) effects: Under high-current conditions, the Coulomb field generated by the beam has a non-negligible influence on particle motion. According to the latest STCF lattice design and beam parameters, SC effects induce vertical and horizontal tune shifts of approximately −0.043 and –0.0027 (see Fig. 34), which are opposite the shift caused by beam–beam interactions. As this effect is distributed along the entire ring and influenced by the alternating-gradient focusing structure, its overall impact cannot be simply canceled by beam–beam tune shifts and thus cannot be directly utilized to enhance luminosity. Beyond simplified particle tracking models, a more comprehensive assessment requires full-ring tracking simulations incorporating the actual lattice structure. These simulations are being actively performed using the BBSCL code with full-lattice and SC effects. A preliminary luminosity result under the design beam parameters is shown in Fig. 35. Analysis of the simulation data reveals a notable luminosity degradation and is attributed to a weak coherent X-Z instability. This instability is primarily associated with the horizontal tune shift induced by SC (its absolute value is comparable with the horizontal beam–beam tune shift), rather than the vertical component. The horizontal tune shift moves the beams closer to the broad resonance peaks of the coherent X-Z instability, as illustrated in Fig. 30 under current machine conditions.
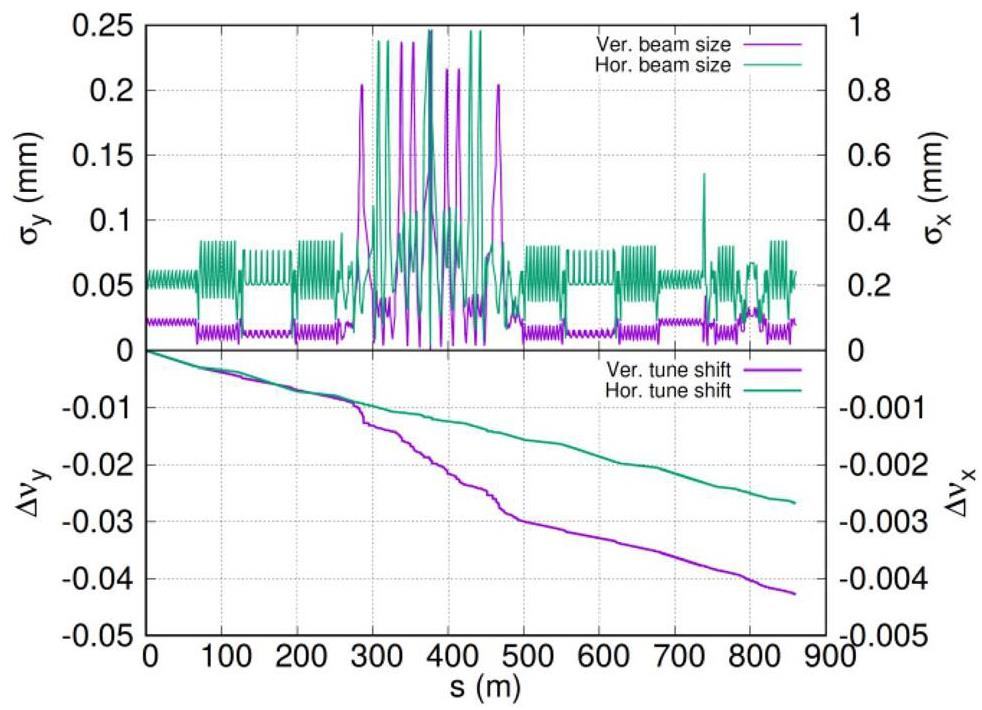
· Impedance effects: In addition to the longitudinal impedance effects discussed earlier, transverse impedance can also couple with beam–beam interactions and induce coherent mode-coupling instabilities. These instabilities are closely related to the vertical tune and thereby constrain the accessible working point space. A comprehensive impedance budget for STCF is currently under development. The combined impact of impedance and beam–beam interactions will be systematically investigated in future studies.
· Imperfections in the IP optics: These include non-zero coupling and dispersion at the IP, phase deviations between the IP and the crab-waist sextupoles, and orbit errors at both the IP and sextupole locations. Such imperfections can undermine the effectiveness of the crab-waist mechanism and consequently degrade the achievable luminosity.
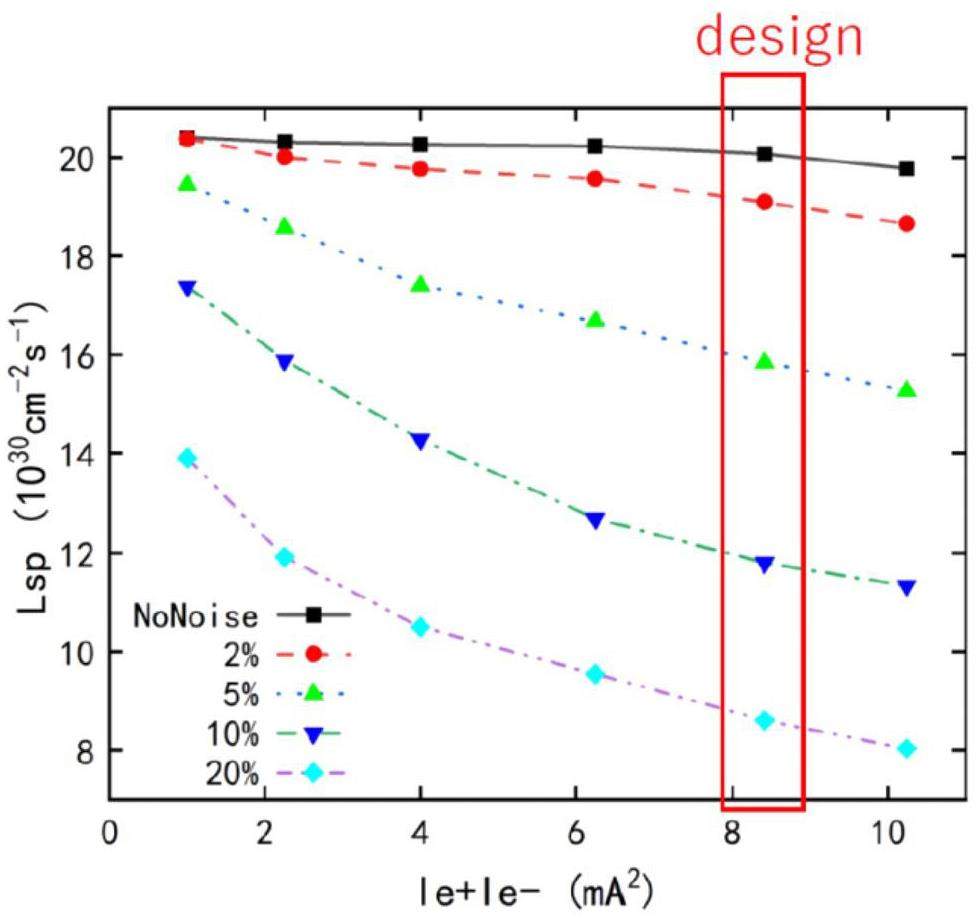
· Noise in the bunch-by-bunch feedback system: Under high-current operating conditions, the machine’s reliance on the feedback system for suppressing coherent instabilities increases significantly. However, because of the extremely small transverse beam sizes at the IP, noise in the feedback system may excite beam motion and contribute to luminosity degradation. To evaluate this effect, simulations using the BBSS code were performed, incorporating turn-by-turn noise modeled as vertical collision offsets at the IP with a standard deviation of
· Other collective effects: Phenomena such as electron clouds and ion trapping may also pose potential performance limitations for the machine.
Recently, GPU-accelerated codes (e.g., BBSCL at KEK, APES-T at IHEP, and Xsuite at CERN) have enabled more efficient simulations of coupled multi-physics effects. In the future, further STCF beam–beam studies will rely heavily on these advanced tools.
Impedance and beam collective effects
Collective effects
Beam collective effects encompass various phenomena correlated with beam current. On one hand, they can degrade beam quality, including by increasing emittance and energy spread; on the other hand, they can cause various instabilities that limit beam current and consequently reduce collision luminosity. Therefore, carefully studying the influence of these collective effects is essential. The types of beam collective effects are diverse and include intra-beam scattering (IBS) and Touschek scattering, which are both intra-scattering effects within the beam; various instabilities induced by the coupling of the beam with the impedance of the vacuum chamber environment, such as longitudinal microwave instabilities, transverse single-bunch instabilities, and coupled-bunch instabilities; and instabilities caused by residual gas molecules, ions, and electron clouds within the vacuum chamber. To meet the high-luminosity requirements of a collider, it is necessary to reduce the beta function
Impedance-driven single-bunch collective effects
Single-bunch collective effects [28] are predominantly governed by the broadband impedance of the storage ring (from flanges, BPMs, bellows, collimators, etc.) and include bunch lengthening, microwave instabilities, and transverse mode coupling instability (TMCI).
To suppress these effects, strict control of broadband impedance is required. During engineering implementation, this requires optimization of the vacuum chamber structure through streamlining geometry and minimizing discontinuities, combined with rigorous quality control in fabrication to mitigate impedance contributions—particularly from crucial vacuum components. Additionally, avoiding structures that could trap HOMs is crucial because they can lead to parasitic energy loss, local heating of vacuum chambers, and coupled-bunch instabilities.
When the single-bunch current remains below the microwave instability threshold, bunch lengthening is dominated by potential well distortion and can be described by
Microwave instability, a typical longitudinal single-bunch instability, arises when the current exceeds a certain threshold. While it does not cause particle loss, it degrades luminosity by amplifying the energy spread and elongating the bunch length. A conservative threshold estimate is provided by the Keil–Schnell–Boussard criterion
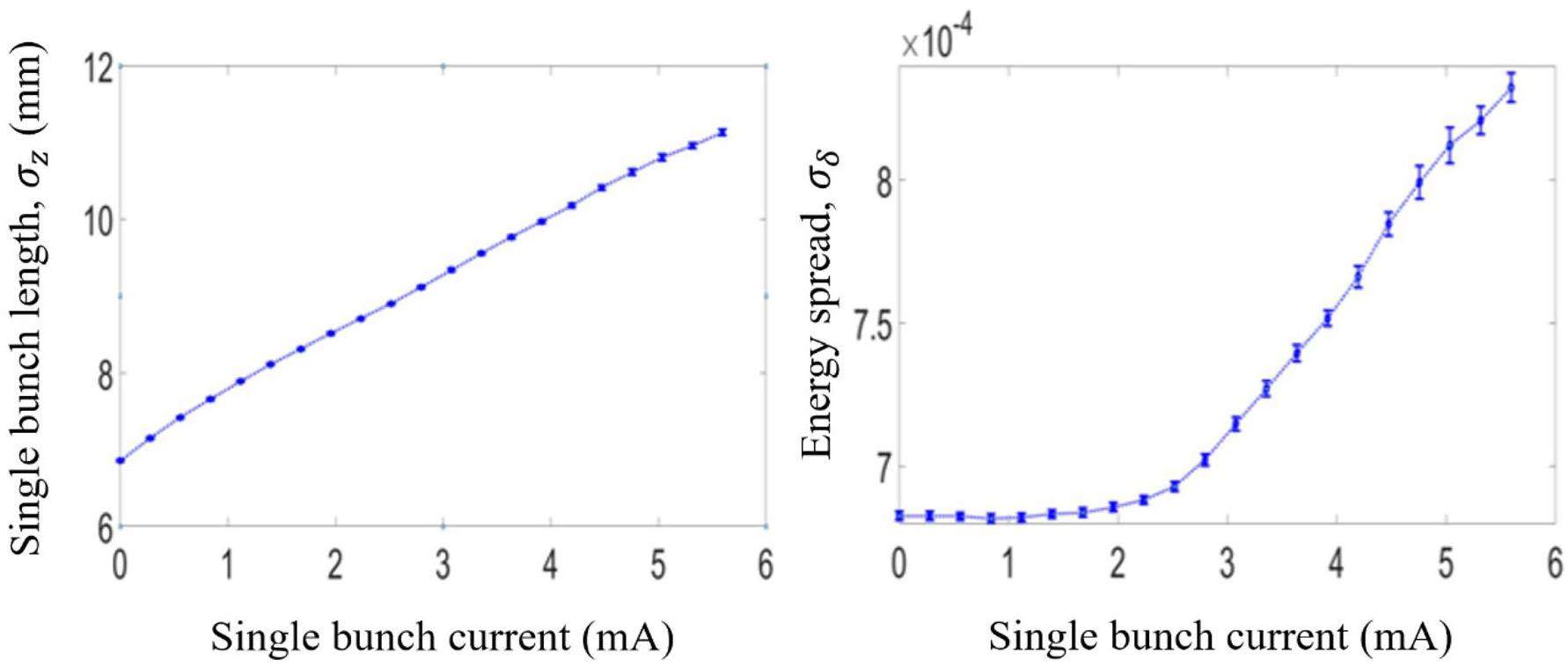
Simulations reveal that the microwave instability threshold is approximately 2 mA, which is smaller than the STCF’s target single-bunch current (2.8 mA). This proximity indicates potential operational risks. Increasing the momentum compaction factor
Coherent synchrotron radiation (CSR) and coherent wiggler radiation (CWR) [29] can also drive microwave instability. Assuming a wiggler vacuum chamber with a gap height of 35 mm, a peak field of 1.6 T, a single wiggler length of 4.8 m, and a period length of 0.6 m, the simulations employing CSR impedance models obtained using the CSRZ code and macro-particle tracking yield a single-bunch instability threshold of approximately 0.6 mA at a beam energy of 1 GeV; however, the instability is weaker at 2 GeV with a threshold of 3 mA. Strategies to enhance the current threshold at 1 GeV include modifying the wiggler period and optimizing the vacuum chamber geometry. The lattice could also be further optimized by increasing
Head–tail instability and TMCI are critical transverse single-bunch instabilities. Negative natural chromaticity can trigger the zero-mode head–tail instability, which is conventionally suppressed by using sextupoles to correct chromaticity to positive values. While positive chromaticity may excite higher-order head–tail modes, the mode tends to grow slowly and can be suppressed by radiation damping and transverse feedback systems. At zero chromaticity, increasing the beam current shifts the 0 mode toward the −1 mode, and after the threshold is crossed, the merging of the two modes triggers bunch instability, which is the strongest TMCI; hence, it is also called the strong head–tail instability. Once it occurs, the TMCI develops very fast and results in the rapid growth of transverse oscillations and particle loss. Thus, this instability must be strictly avoided.
Here, we only discuss the TMCI threshold under resistive wall impedance, assuming zero chromaticity, which is estimated using
To suppress the TMCI, the chromaticity can be corrected to positive values to help damp the head–tail zero-mode; however, this creates the risk of exciting higher-order head–tail modes. Nonetheless, these HOMs grow slowly and can be effectively suppressed by enhancing radiation damping through damping wigglers and implementing a transverse bunch-by-bunch feedback system, thereby raising the single-bunch transverse instability threshold current. In addition, the nonlinear collimation technique being developed at SuperKEKB—designed to mitigate impedance effects—may offer further benefits. Its potential application to STCF will be explored.
Impedance-related coupled-bunch instability
This analysis focuses on long-range wakefield effects, including narrowband impedance from RF cavities or vacuum structures and low-frequency resistive wall impedance. Instabilities induced by the RF cavity modes have already been discussed in Sect. 2.4 and will not be repeated here. Geometric narrowband impedances, which can trap resonant modes, should be minimized through the optimization of the geometric structures of the devices.
Resistive wall instability is mainly due to the strong transverse impedance near zero frequency. These long-range wakefields can cause transverse coupled-bunch instability. For Gaussian beams, the instability growth rate is governed by [30]
Here, the mode frequency is given by
Assuming a uniform aluminum beam pipe with a radius of 25 mm for the full ring circumference, Eq. (14) predicts an instability growth rate of 1.6 ms–1 at zero chromaticity. Although modern bunch-by-bunch feedback techniques can achieve damping times of approximately 100 μs or better, the SuperKEKB experience [31] shows that the noise of the feedback system has an important impact on the luminosity stability. A slower feedback system combined with other measures, such as correcting chromaticity to positive values to reduce the growth rate, is being considered. With these measures, STCF is expected to manage this instability effectively.
Beam lifetime
The Touschek scattering effect is the dominant factor limiting the beam lifetime in the collider rings. It refers to large-angle Coulomb scattering between two electrons or positrons within a bunch, where, during collisions, one particle transfers its transverse momentum to the longitudinal momentum of another particle. This interaction makes it possible for some particles to exceed the energy acceptance and be lost. From the local momentum aperture (LMA) shown in Fig. 24, the calculated beam lifetime at 2 GeV is approximately 252 s.
Residual gas scattering includes elastic scattering and inelastic scattering. Elastic scattering leads to transverse oscillations, and the particle will be lost if its amplitude exceeds the dynamic aperture. Inelastic scattering causes the deceleration and energy deviation of the particle, and it will also lead to a loss if it is beyond the momentum acceptance. Based on the SuperKEKB experience, elastic scattering is the dominant factor for vacuum-related beam losses in this collider ring type.
Assuming all residual gas molecules are CO, the vacuum-limited lifetime is
Ion effects and electron cloud effects
Ion instabilities originate from the interaction between the electron beam and their trapped ions. The ions are generated from the ionization of residual gas in the vacuum and desorption from the vacuum wall. In modern electron storage rings, ultra-high vacuum systems can provide a pressure lower than 10–7 Pa and can generally minimize these effects. When designing the bunch filling scheme, large gaps are typically introduced between bunch trains to help suppress ion instabilities. In addition, transverse bunch-by-bunch feedback systems can effectively suppress fast ion–induced oscillations. Transient fast ion instabilities may still occur during early machine operation under poor vacuum conditions but will diminish as the vacuum improves.
In the positron ring, synchrotron radiation photons strike the vacuum chamber wall and release photoelectrons. These photoelectrons are accelerated by the positron beam and can be multiplied by multiple reflections between the walls. The electrons captured by the positron beam form the so-called electron cloud [32]. The electron cloud interacts with the positron bunches and can couple the motions of successive positron bunches and cause both coupled-bunch instability and single-bunch head–tail instability. Using the PEI and PyECLOUD codes for simulations, at 2 GeV and with an average chamber diameter of 50 mm and a secondary electron yield (SEY) of 1.3, the cloud density near the beam is
Beam injection and extraction
The primary objective of the beam injection design for the collider rings is to inject positron/electron beams from the upstream injector into the collider rings with maximum efficiency. This ensures high integrated luminosity, minimizes disturbances to the circulating beam during injection, and reduces injection-related beam loss and its impact on detector background. The primary goal of the beam extraction design is to extract the high-energy, high-charge positron/electron bunch trains from the ring efficiently and transport them to the beam dump.
Several injection methods are used or studied for electron storage rings, including conventional off-axis injection (with variations), longitudinal injection, and swap-out injection. Since the momentum aperture of the STCF collider lattice design is small and STCF is not suitable for using an RF frequency lower than 500 MHz, increasing the bucket length, longitudinal injection, and off-momentum injection are not good options. Currently, considering the design of the upstream injector and the overall cost of the accelerator, STCF will adopt a compatible injection scheme combining off-axis injection and bunch swap-out injection. The off-axis injection scheme [33] is chosen as the baseline and will be employed in the construction. Different off-axis injection methods, such as employing bump kickers, nonlinear kickers, and anti-septum, are under investigation. Only the injection method employing bump kickers is described here. Thus, the injection system consists of a septum magnet and bump magnets. The injected and circulating beams are transversely separated. Under the action of the bump magnets, the closed orbit of the circulating beam moves closer to the septum magnet, and after one or several turns—once the injected beam falls within the collider ring acceptance—it returns to the pipe center. Eventually, the injected beam merges with the circulating beam via synchrotron radiation damping. This scheme is mature and imposes relatively low requirements on the rise time of the injection elements but requires a large dynamic aperture.
In the future, based on need, the system can be upgraded to a bunch swap-out injection scheme [34], while using the same injection section. With this scheme, circulating bunches are one-to-one replaced with newly injected bunches using ultra-fast pulsed kicker magnets. This scheme requires less dynamic aperture in the horizontal plane but imposes strict constraints on the kicker pulse width—it must be less than twice the minimum bunch spacing. Additionally, injecting high-charge positron bunches places stringent requirements on the repetition rate of the upstream injector. To facilitate future upgrades, the quadrupole magnets in the injection section will be laid out in a uniform design, requiring only the replacement of kicker components for the transition. Hardware parameters will be selected accordingly, and the injection process will be validated through tracking simulations.
The extraction system design for the collider rings also includes two operational scenarios. During bunch swap-outs, small angular deviations induced by ultra-fast pulsed kicker magnets are used, and the downstream septum magnet deflects the target bunch out of the ring. This method places stringent performance requirements on the ultra-fast kickers, similar to those in injection, requiring a pulse with a full width shorter than 6 ns. For beam dumping, the different kickers must have a rise time shorter than the gap between bunch trains and a flat-top width longer than the revolution period, enabling the extraction of whole bunches in one turn.
The luminosity fluctuation requirement forms the basis of the beam injection design. For example, assuming a 7% degradation in single-bunch luminosity and a typical beam lifetime of 250 s, the physical requirements for beam injection in the off-axis and swap-out injection schemes are summarized in Table 6. The goal of the injection design is to meet the parameters provided in Table 6, particularly the injection efficiency.
| Injection Scheme | Off-axis injection | Swap-out injection |
|---|---|---|
| Collider ring circumference (m) | 860.321 | 860.321 |
| Bunch spacing (ns) | 4 | 4 |
| Min. single-bunch luminosity/Peak | 93% | 93% |
| Beam lifetime (s) | ≈250 | ≈250 |
| Time to complete full ring injection (s) | 18.14 | 18.14 |
| Circulating bunch charge (nC) | 8.34 | 8.34 |
| Circulating beam emittance (rms) (nm·rad) | 4.16 (0.5% coupling) | 4.16 (0.5% coupling) |
| Injected bunch charge (nC) | 1.0* | 8.5 |
| Charge to refill/replace (nC) | 0.6 | 8.34 |
| Injected beam emittance (rms) (nm·rad) | H < 6; V < 2 | H < 30; V < 10 |
| Injection efficiency | > 60% | > 98% |
Off-axis injection
The key to off-axis injection design is to use local orbit bumps to steer the injected beam into the ring acceptance while minimizing its transverse offset from the central orbit and reducing beam losses at the septum magnet [35]. First, the optics of the injection section must be configured with large β functions to reduce the impact of septum thickness and closed-orbit errors on injection efficiency. Second, the beam clearance aperture must be optimized to balance dynamic aperture and beam losses—a clearance that is too large requires an excessively large dynamic aperture, while one that is too small causes significant beam loss. Lastly, the local bump orbit must be designed with appropriate bump height and angle so that the injected beam exits the septum magnet as close as possible to the pipe center, without excessive loss of the injected beam, while also controlling the influence of the stray magnetic field of the septum magnet to the circulating beam.
The off-axis injection system in the STCF collider rings consists of three components: quadrupoles for optics matching, bump magnets to form the local orbit, and septum magnets for large-angle bending of the injected beam. Table 7 lists the key parameters. Figure 38 shows a schematic of the off-axis injection scheme, while Fig. 39 presents the layout and optics of the injection section, located in one of the 20 m-long straight sections of the collider rings, where 10 quadrupoles are installed for optics matching. Figure 40 illustrates the local bump orbit formed by four bump magnets. Each magnet provides a maximum bending angle of less than 3.5 mrad and can be adjusted independently to vary the orbit height and angle.
| Parameter | Value |
|---|---|
| Circulating beam clearance (mm) | 1.68 (4.5σ) |
| Injected beam clearance (mm) | 1.18 (4.5σ) |
| βx at injection point (inner/outer ring) (m) | 33.34 / 11.53 |
| Injection angle (mrad) | –2.45 |
| Orbit bump height at injection point (mm) | 3.86 |
| Orbit bump angle at injection point (mrad) | –2.50 |
| Position after bump recedes (mm) | 4.36 |
| Bump duration (turns) | 1 |
| Bump magnet length (mm) | 350 |
| Max bump magnet deflection angle (mrad) | < 3.5 |
| Bump magnet field strength (Gs) | < 1167 |
| Thin septum height (mm) | 5.54 |
| Thin septum thickness (mm) | 1.0 |
| Thin septum length (mechanical/effective) (m) | 0.65 / 0.6 |
| Thin septum field strength (Gs) | 5500 |
| Thin septum deflection angle (mrad) | 28 |
| Thick septum thickness (mm) | 2.0 |
| Thick septum length (mechanical/effective) (m) | 1.7 / 1.3 |
| Thick septum field strength (Gs) | 9900 |
| Thick septum deflection angle (mrad) | 110 |
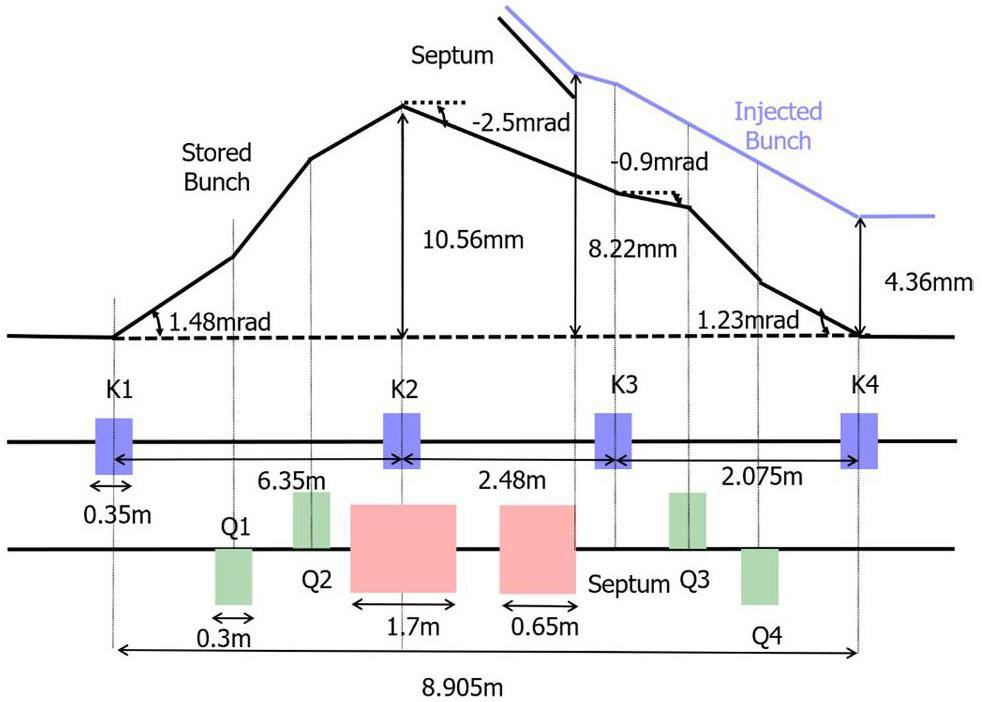
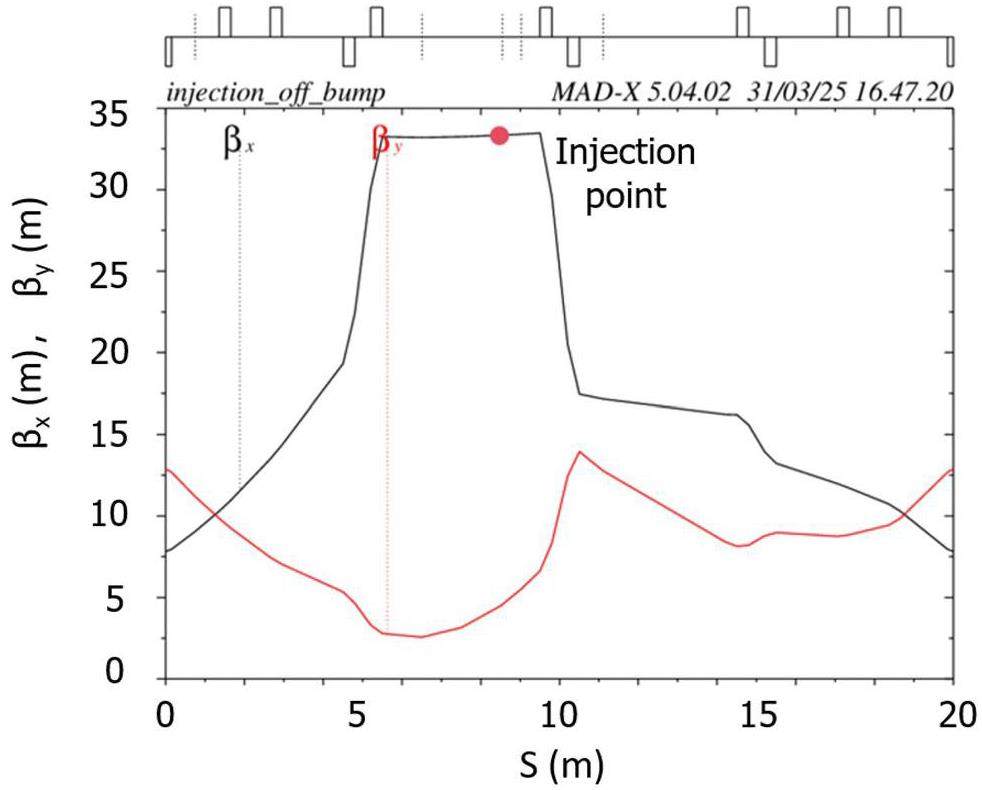
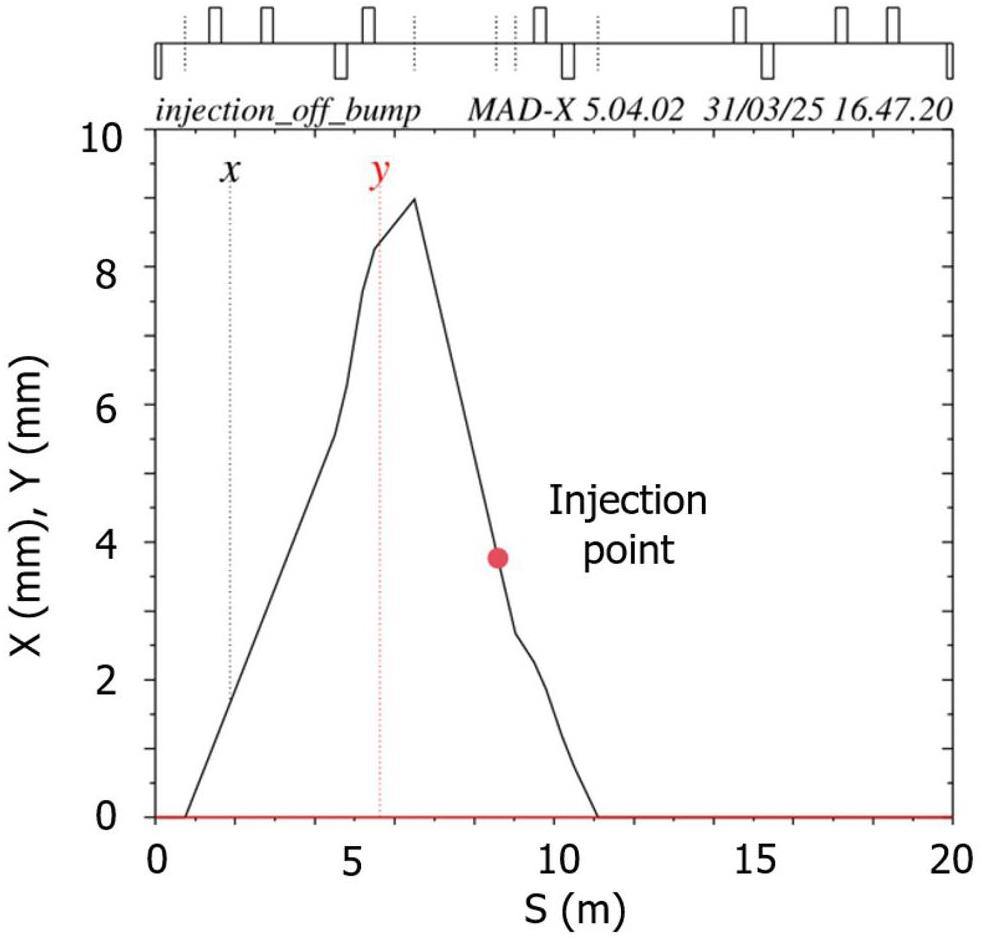
Figure 41 shows the evolution of the horizontal geometric emittance (phase-space area) of the injected bunch over five damping times, simulated with Elegant. Initially, the filamentation of the injected bunch dominates emittance growth. Then, synchrotron radiation exponentially damps the off-axis oscillation of the injected beam. After five damping times, the emittance decreases by more than an order of magnitude, fully merging with the stored bunch and reaching an equilibrium emittance of approximately 4.17 nm·rad. Considering the physical aperture of the septum and the dynamic aperture of the collider rings, the final injection efficiency reaches approximately 90%, meeting the design goals. Injection simulations with all realistic errors, which ensure that the injection physics design is robust, are ongoing. More simulations with all error types, including the combined beam–beam effect for merging bunches, will also be performed.
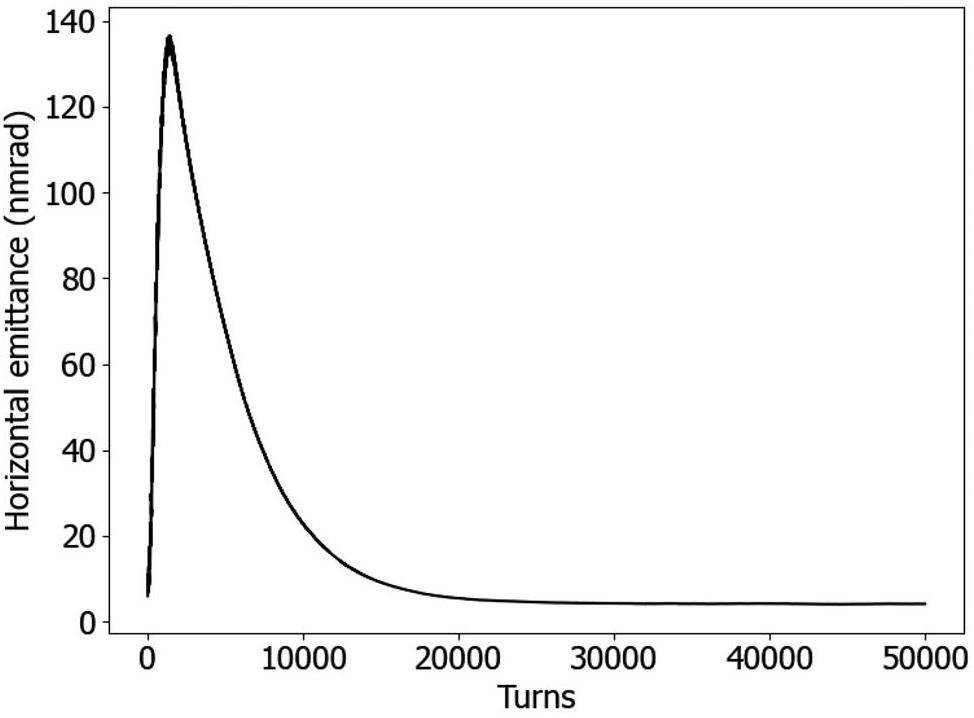
Bunch swap-out injection
The key to the physics design of the bunch swap-out injection scheme is arranging the components in a geometrically rational layout so that the injected bunch enters the closed orbit of the collider rings accurately, thereby minimizing disturbance to the stored beam and reducing the required deflection angle of the kicker magnets [36]. The STCF bunch swap-out injection system primarily consists of a septum magnet for large-angle deflection and a set of ultra-fast horizontal kicker magnets. The septum magnet design is identical to that used in the off-axis injection scheme. The kicker system consists of five identical modules spanning a 1.9 m drift.
Table 8 lists the relevant design parameters. Figure 42 shows a schematic of the injection system, while Fig. 43 presents the layout and optics of the injection section. This section, shared with the off-axis injection scheme, spans 20 m and incorporates ten quadrupoles. To accommodate the deflection angle and the good-field region of the kicker magnets, approximately 6 m of drift space is reserved for the injected beam to travel from the septum magnet to the kickers. Figure 44 illustrates the beam trajectory and envelope in this region.
| Parameter | Value |
|---|---|
| Kicker magnet length (mm) | 300 |
| Kicker magnet deflection angle (mrad) | 0.5 |
| Kicker plate gap (mm) | 12 |
| Number of modules | 5 |
| Rise / Flat-top / Fall time (ns) | 2 / 2 / 2 |
| Good field region (mm) | ±5 |
| Injection point position at kicker entry (mm) | 2.45 |
| Voltage amplitude (kV) | > 17.5 |
| Injection repetition rate (Hz) | 30 |
| Thin septum height (mm) | 5.54 |
| Thin septum thickness (mm) | 1.0 |
| Thin septum magnet length (Mechanical/Effective) (m) | 0.65 / 0.6 |
| Thin septum magnet field strength (Gs) | 5500 |
| Thin septum magnet deflection angle (mrad) | 28 |
| Thick septum thickness (mm) | 2.0 |
| Thick septum magnet length (Mechanical/Effective) (m) | 1.7 / 1.3 |
| Thick septum magnet field strength (Gs) | 9900 |
| Thick septum magnet deflection angle (mrad) | 110 |
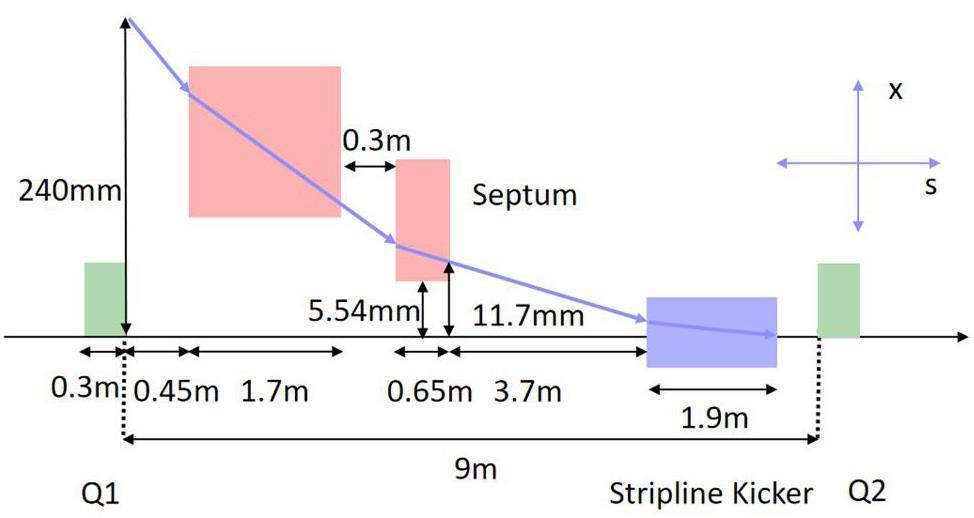
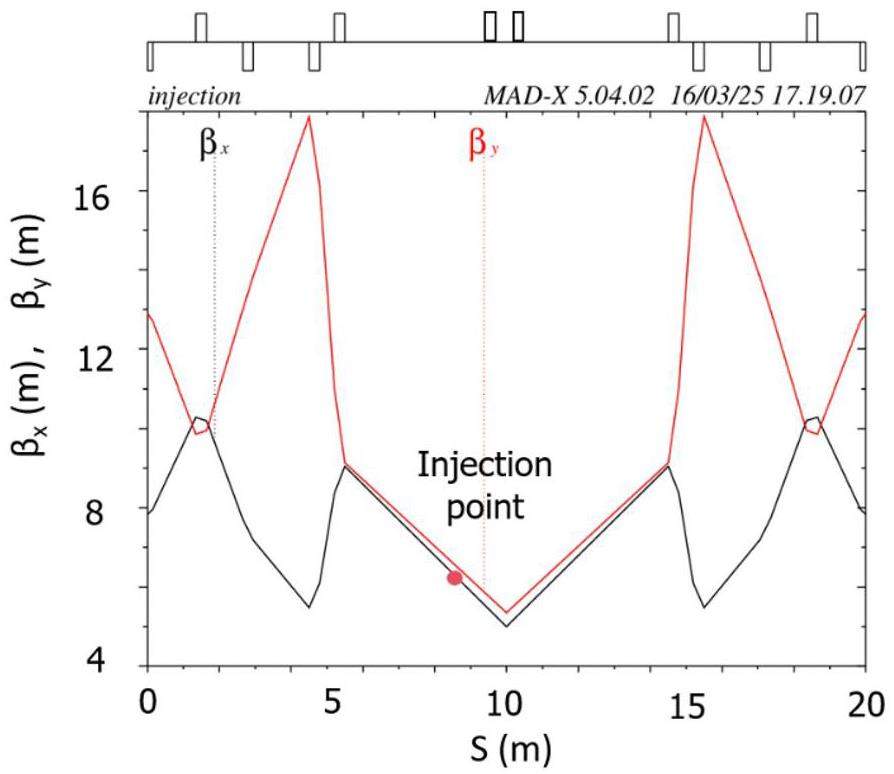
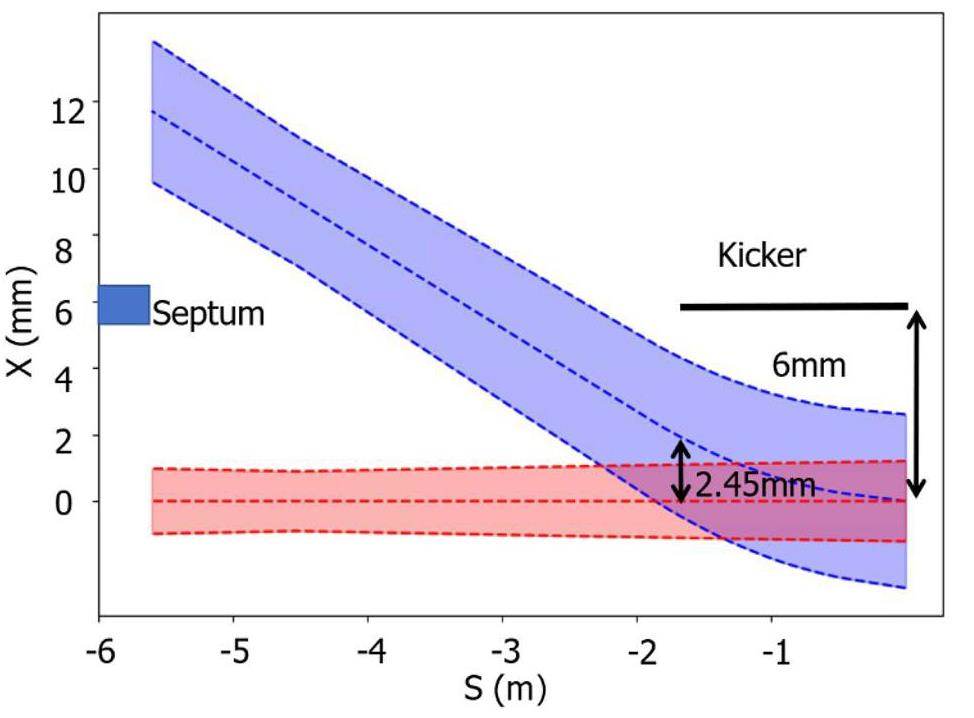
In the bunch swap-out injection scheme, the injected bunch has a relatively large emittance owing to the high bunch charge from the injector. A key factor for injection efficiency and final luminosity is whether the injected beam can avoid significant losses during the first few turns and then be damped by synchrotron radiation to the equilibrium emittance of the collider rings. Figure 45 shows the evolution of the horizontal beam emittance over five damping times, as simulated with the Elegant tracking code. After five damping times, the emittance converges to approximately 4.20 nm·rad, and the injection efficiency exceeds 98%, just meeting the basic physical design requirements. In future upgrades, smaller injection emittance will be adopted to further reduce the loss rate.
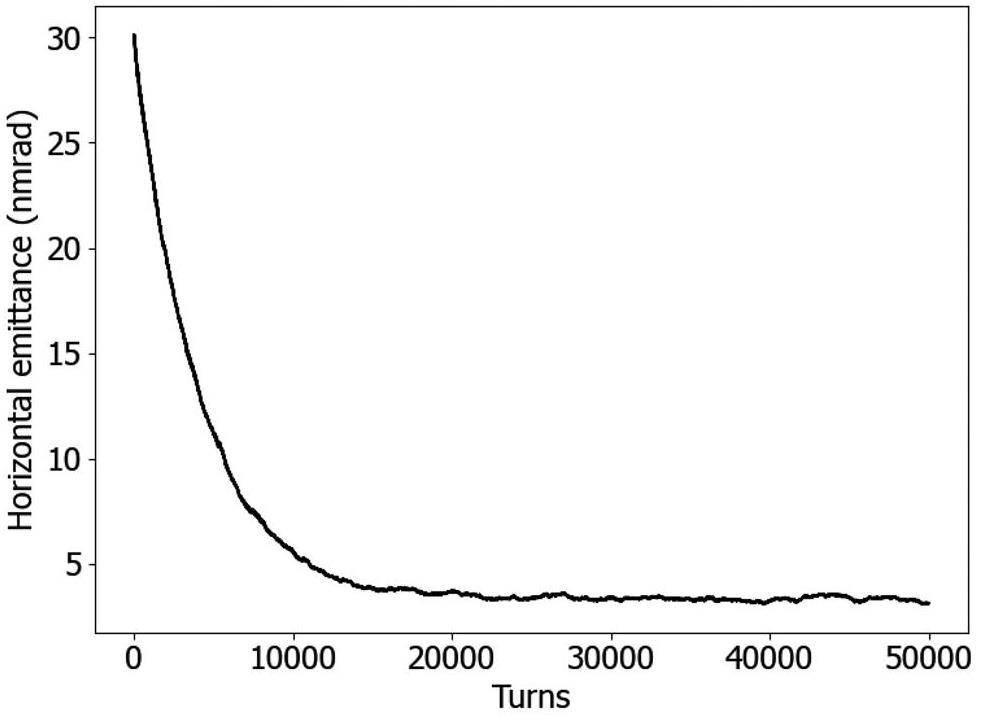
Beam dumping and extraction
Beam extraction can be considered as the reverse process of bunch swap-out injection and is realized using a set of pulsed kicker magnets and a downstream septum magnet. STCF requires two extraction systems to fulfill the following two beam extraction functions:
The first is during normal operation under the bunch swap-out injection scheme. Ultra-fast kicker magnets deflect the bunch to move it away from the equilibrium orbit, and the downstream septum magnet subsequently extracts it from the ring. One bunch is extracted every 33.3 ms to enable on-axis replacement. The hardware requirements are identical to those for swap-out injection, as shown in Table 8. The extraction section layout is also similar to that in Fig. 43, with the exception of having the septum magnet placed downstream in the beam direction. The main requirement for the extraction system in this case is minimizing circulating beam disturbances caused by the kicker magnets.
The second is for beam dumping during machine protection or experimental shutdown. This requires kicker magnets with a rise time shorter than the bunch train spacing and a flat-top width longer than the revolution period for the entire ring to be emptied in a single extraction. This process does not affect luminosity or experiments, and the design is relatively straightforward, with ample reference designs available. Therefore, this is not a technical challenge for the STCF beam injection/extraction design. However, considering the large stored beam energy in the collider rings, minimizing beam loss during extraction is critical. Additionally, kicker magnets with both short rise time and long flat-top width present certain technical challenges. A dedicated beam dump will be located outside the tunnel to receive the high-energy, high-charge (approximately 5.7 μC) dumped beam. Figure 46 shows the beam orbits in the two extraction modes.
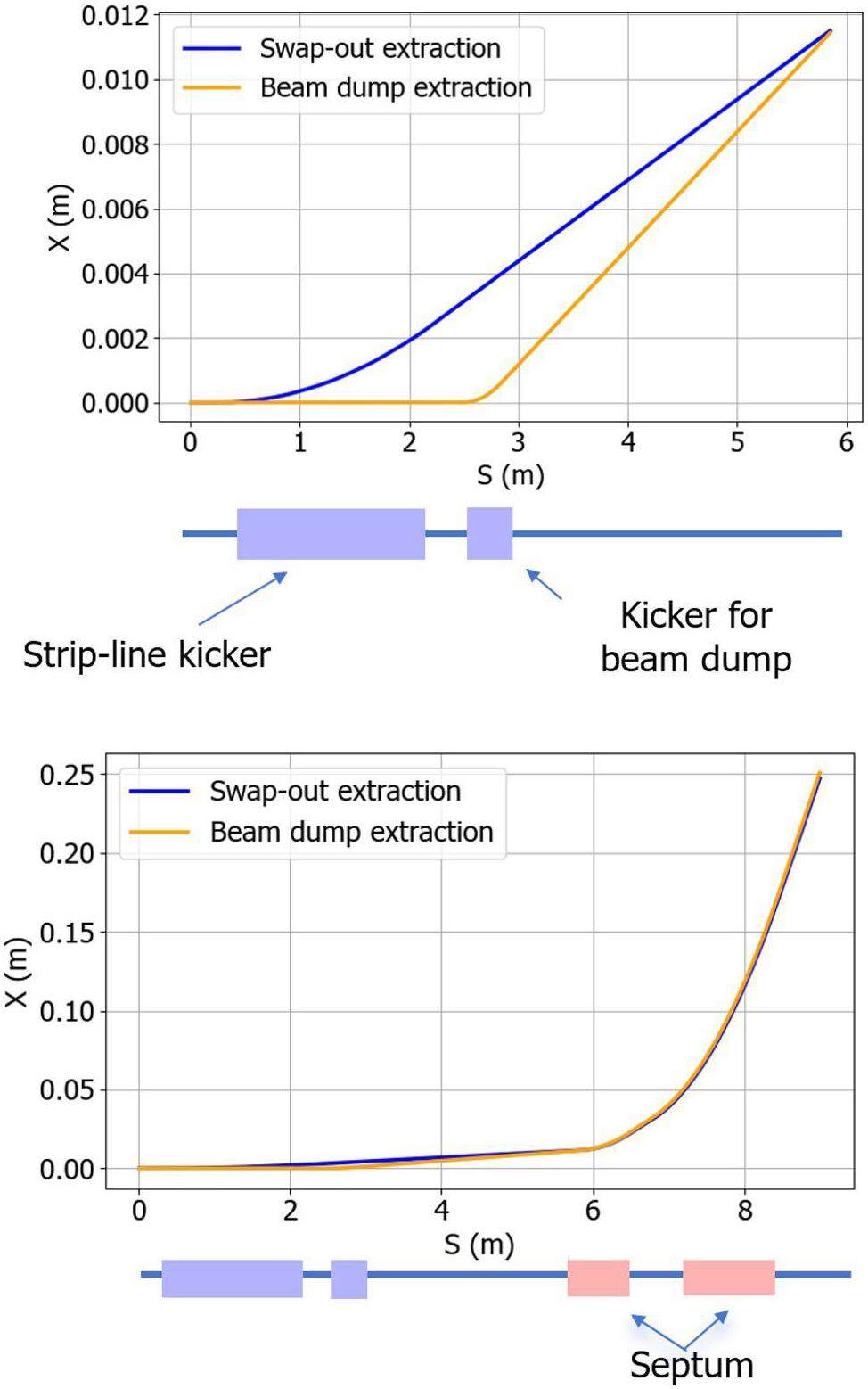
The off-axis injection scheme, widely used in positron/electron storage rings over the past decades, has proven effective and reliable in numerous experiments. Hence, adopting the septum-and-bump-based off-axis injection as the baseline scheme for STCF is feasible.
The bunch swap-out injection scheme, which is considered ideal for some fourth-generation light sources and new-generation e+e− colliders, has gained much attention in recent years. Its main challenge lies in developing kicker magnets with ultra-short pulses and ultra-fast rise times. Preliminary numerical simulations confirm the feasibility of this scheme, with injection efficiency reaching up to 98%. Therefore, the bunch swap-out injection scheme—based on fast pulsed kickers and septum magnets—will serve as an upgrading path for STCF. The bunch swap-out injection scheme is generally compatible with the off-axis scheme, especially in terms of injector requirements. Hence, adopting the off-axis method at the initial stages of development is advisable. After upgrading to the bunch swap-out injection scheme, the off-axis injection may still serve as a commissioning and operational fallback, ensuring the feasibility of maintaining peak luminosity via the top-up injection mode at STCF.
Error analysis and correction
During actual operation, the collider rings inevitably deviate from the ideal design model due to various errors, including alignment deviations caused by magnet installation and field errors from magnet manufacturing. These errors are primary contributors to closed orbit distortion, optical function perturbations, and transverse coupling. They significantly impact crucial machine performance metrics such as beam size, dynamic aperture, beam lifetime, and collision luminosity, and also affect the complexity of commissioning and operation of the collider rings. To assess the robustness of the magnetic focusing structure of the collider rings and to restore their nonlinear dynamic performance and luminosity, this section defines static error tolerances. Based on these tolerances, the error sensitivity of the collider ring lattice is analyzed, and corresponding corrections are applied to the orbit and optical functions.
Following the error settings of similar international facilities such as SuperKEKB [37], CEPC [12], and FCC-ee [38], the reference error levels are set as follows: magnet alignment error of 50 μm, angular misalignment of 0.1 mrad, and main field error of 0.02%. Under these assumptions, simulations of the closed orbit survival ratio of the STCF collider rings were performed to evaluate its error tolerance, as shown in the left panel of Fig. 47, where the horizontal axis indicates the scaling factor of the error relative to the reference level. At the reference error level, the closed orbit survival ratio is approximately 25.2%; when the error level is doubled, the survival ratio drops sharply to only 1.7%.
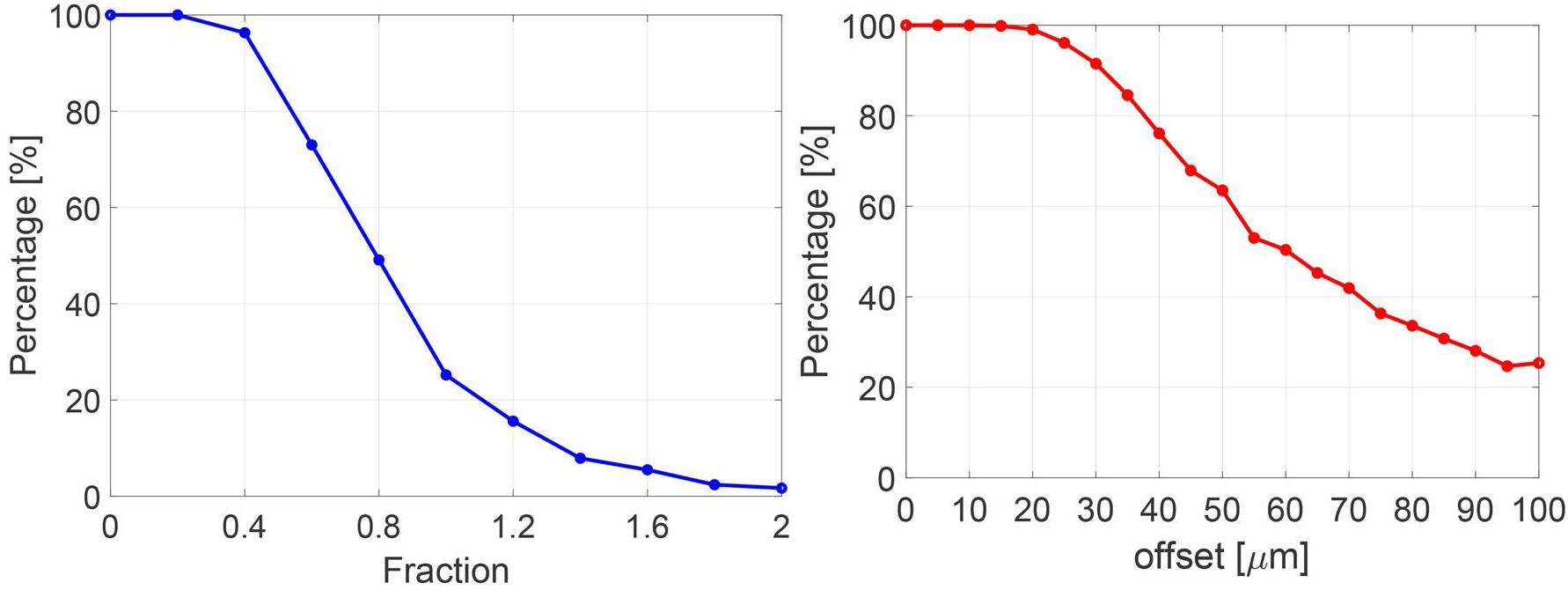
Further investigation of individual error sources reveals that transverse misalignment of quadrupole magnets has the greatest impact on the orbit survival ratio, particularly in the vertical direction. Among all quadrupoles, those in the FFT region near the IP are the most sensitive and therefore require higher alignment precision. The right panel of Fig. 47 illustrates the effect on the orbit survival ratio when different alignment errors are introduced only to the doublet quadrupoles on both sides of the IP. The results show a noticeable drop in the survival ratio when the alignment error exceeds 20–30 μm. To mitigate orbit distortion and suppress luminosity loss, the misalignments of the final doublet quadrupoles should be controlled within 30 μm. In addition, due to the high strength of sextupole magnets, their misalignments strongly affect the orbit, optics, and coupling. Accordingly, the STCF collider ring design incorporates movers for the sextupole magnets to achieve alignment precision at the 10 μm level. Considering both the STCF design requirements and practical engineering constraints, Table 9 summarizes the reference error values used in the current error analysis of the collider rings. The error levels are truncated at 3σ.
| Component | Horizontal (μm) | Vertical (μm) | Longitudinal (μm) | Rotation (mrad) | Main field Error |
|---|---|---|---|---|---|
| Dipole magnet | 100 | 100 | 100 | 0.1 | 0.02% |
| Quadrupole magnet | 50 | 50 | 100 | 0.1 | 0.02% |
| FFT doublet | 30 | 30 | 100 | 0.1 | 0.02% |
| Arc/IR sextupole | 50 / 30 | 50 / 30 | 100 | 0.1 | 0.02% |
Under ideal conditions, particles in the collider rings undergo β oscillations around the ideal closed orbit. However, field errors in dipole magnets and alignment errors in quadrupole magnets distort the closed orbit, with the distortion magnitude determined by the size and distribution of the errors and by the β value at the observation point. Such distortions degrade the dynamic aperture and alter the beam spot size and position, particularly near the IP, where orbit offsets and beam size growth reduce luminosity. Correction is therefore essential. Simulation results indicate that to limit luminosity loss to below 10%, horizontal and vertical orbit deviations at the IP must not exceed 12σx and 0.65σy, respectively, where σₓ and σy are the nominal beam sizes at the IP. Field errors in quadrupole magnets, alignment errors in sextupoles, and magnet rotation errors can also perturb optical functions. Calculations show that to maintain luminosity loss within 10%, the increase in βy at the IP must remain below 30%, whereas βx is more tolerant. Rotational errors in dipoles and quadrupoles can induce transverse coupling and vertical dispersion; to keep luminosity loss under 10%, the vertical dispersion at the IP must be restricted to less than 0.1 mm. These effects not only reduce luminosity but also degrade nonlinear beam dynamics, lower injection efficiency, and shorten beam lifetime. Effective measures are thus necessary for correction and recovery.
To prevent the significant degradation of nonlinear dynamics and luminosity, effective error correction and compensation strategies must be implemented. The static error correction process for the STCF collider rings mainly includes the following steps: (1) first-turn trajectory correction, (2) closed orbit and dispersion correction, and (3) optical function and coupling correction. These steps are typically iterated until the required physical conditions are met. The correction system consists primarily of beam position monitors (BPMs), orbit correctors, and skew quadrupole magnets, with the layout guided by the following principles:
· A BPM is installed next to each quadrupole magnet and some sextupoles to monitor the local closed orbit and facilitate beam-based alignment (BBA) and mitigate β-beating caused by sextupole feed-down effects. A pair of BPMs is also installed near the IP to better correct the local orbit.
· A horizontal corrector magnet is placed next to each focusing quadrupole, and a vertical corrector is placed next to each defocusing quadrupole. These positions correspond to high β values, enhancing correction efficiency and reducing the corrector strength. Additional independent correctors are installed near the IP to further improve orbit correction.
· Skew quadrupole coils are mounted on all sextupoles. Additional independent skew quadrupoles are placed near the IP and in certain straight sections.
The correction system layout for a single ring of STCF includes 405 BPMs, 287 horizontal correctors, 254 vertical correctors, and 102 skew quadrupoles.
During machine commissioning, the primary requirement is to achieve first-turn beam accumulation. Using 100 random seeds of error distributions, first-turn trajectories are corrected using the SVD method and trajectory response matrix. For n correctors and m BPMs, the corrector strength is given by
The pseudoinverse
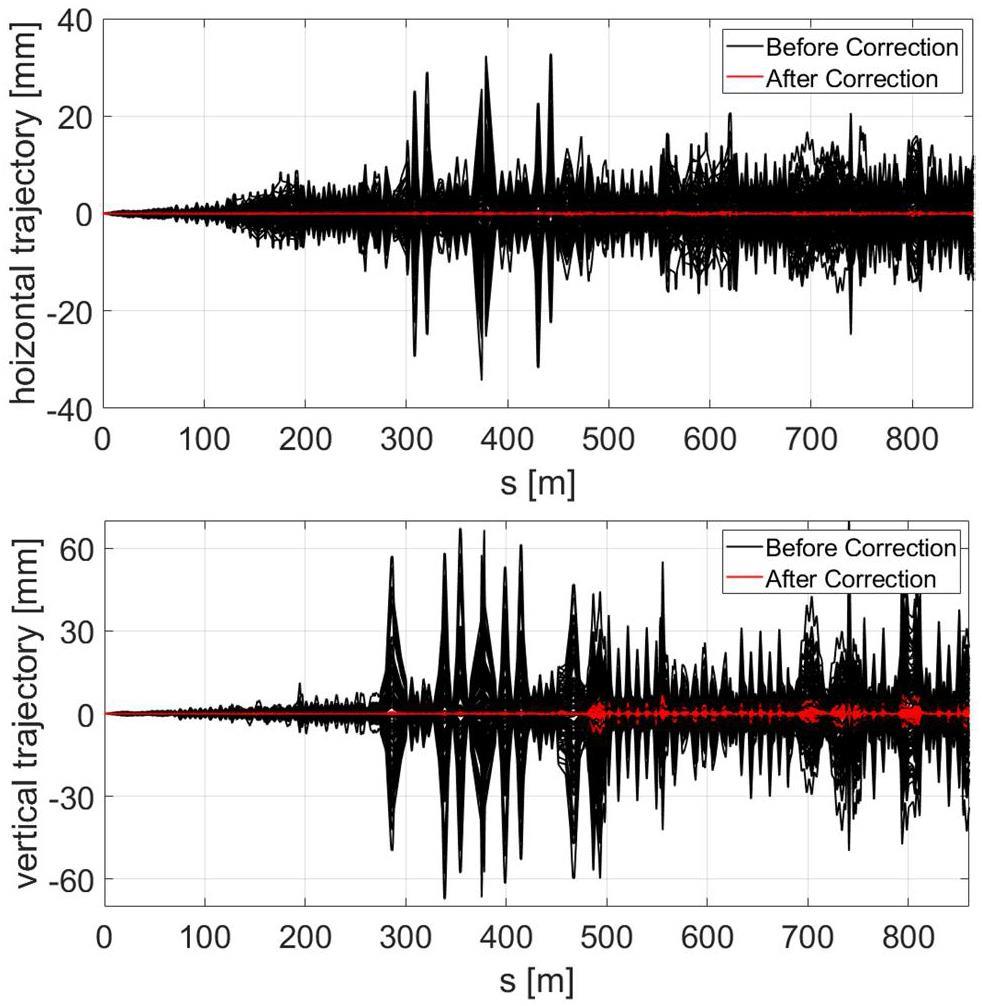
After successful first-turn accumulation and achieving a closed orbit, the dispersion free steering (DFS) method [39] is used to further correct the closed orbit and dispersion function. The corrector magnet strengths are still used as the tuning variables. Based on the orbit and dispersion response matrices, the goal is to minimize orbit and dispersion deviations. The corrector strengths Θ are calculated using the following equation:
Here, R is the response matrix, and d is the deviation of orbit and dispersion at the BPMs:
The orbit and dispersion at the IP are critical for achieving design luminosity and must be corrected to minimal levels. A weighted SVD method [40] is applied to solve for the corrector strengths. The orbit and dispersion deviations at the BPMs on both sides of the IP are multiplied by a weighting factor w, and the corresponding rows in the response matrix are also scaled by w. The corrector strengths are then computed as
To improve correction performance and control the magnitude of the corrector strengths, multiple iterative corrections of the closed orbit and dispersion functions are required, together with optimization of the number of singular values used in the SVD. The weighting factor w influences the correction results: larger w values enhance correction at the IP but may degrade orbit and dispersion performance elsewhere. A value of w = 1000 is selected to balance global and local correction performance.
Figure 49 shows the orbit distortion after DFS correction. The maximum horizontal and vertical orbit distortions across the entire ring remain within 400 μm, with rms values below 50 μm. Notably, orbit distortions at the IP before and after correction are analyzed in Fig. 50. Following weighted DFS correction, the orbit distortion at the IP is reduced by 2–3 orders of magnitude, reaching the tens-of-nanometers scale—sufficiently low to avoid any noticeable impact on luminosity. Figure 51 presents the dispersion function distortion before and after DFS correction. The correction substantially reduces both horizontal and vertical dispersion distortions. After correction, the rms dispersion function across the full ring is approximately 0.25 mm, while the rms values at the IP are approximately 0.4 μm (horizontal) and 0.5 μm (vertical). Figure 52 shows the required strengths of the corrector magnets during DFS correction. The maximum corrector kick angles are approximately 0.3 mrad in both planes, with rms values of approximately 32 μrad, all well within feasible technical limits.
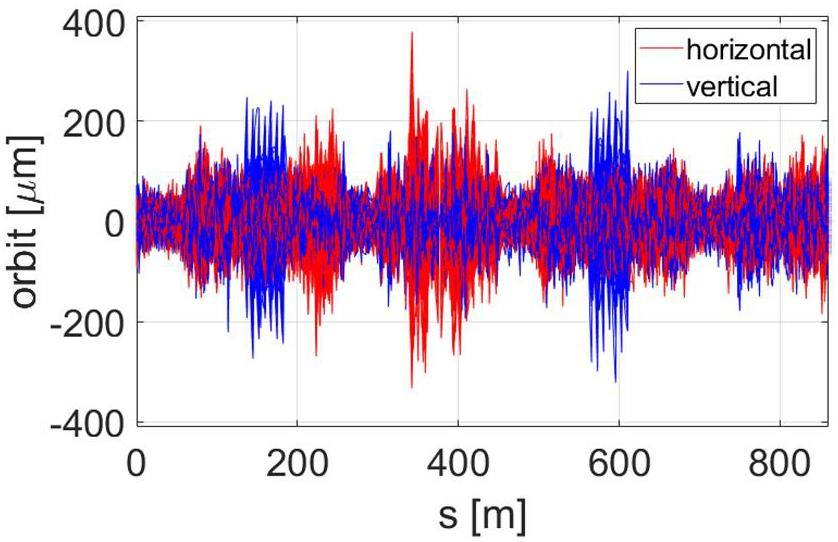
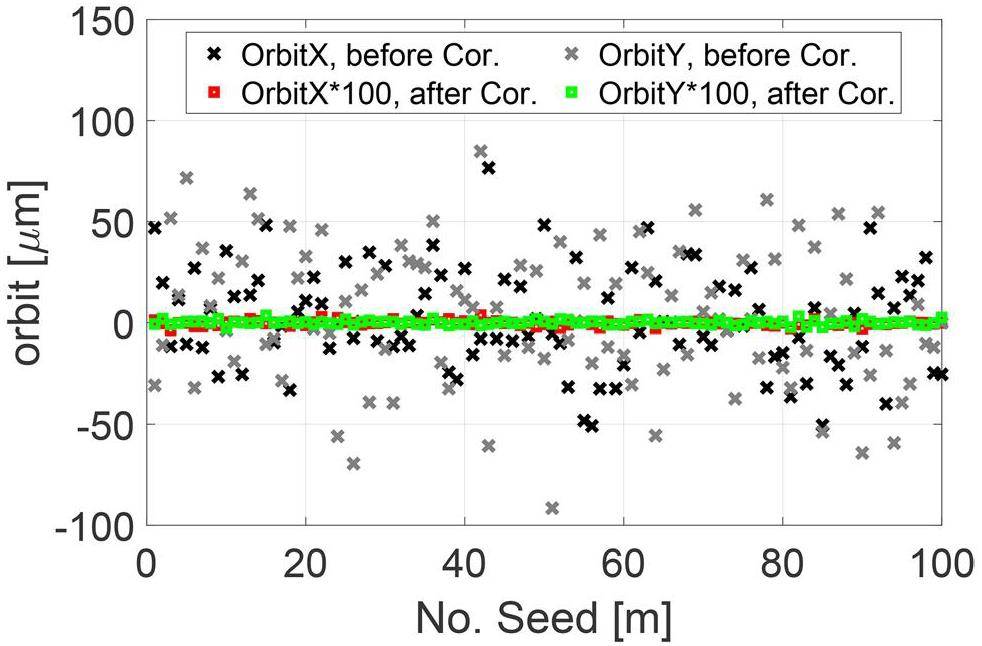
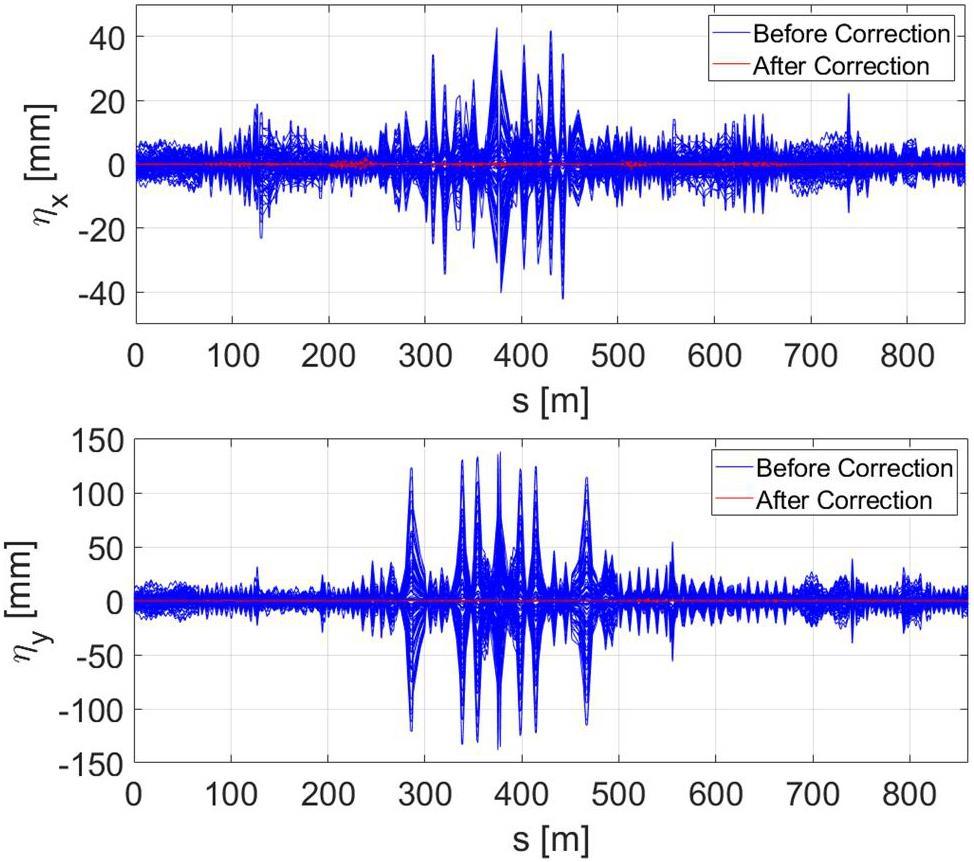
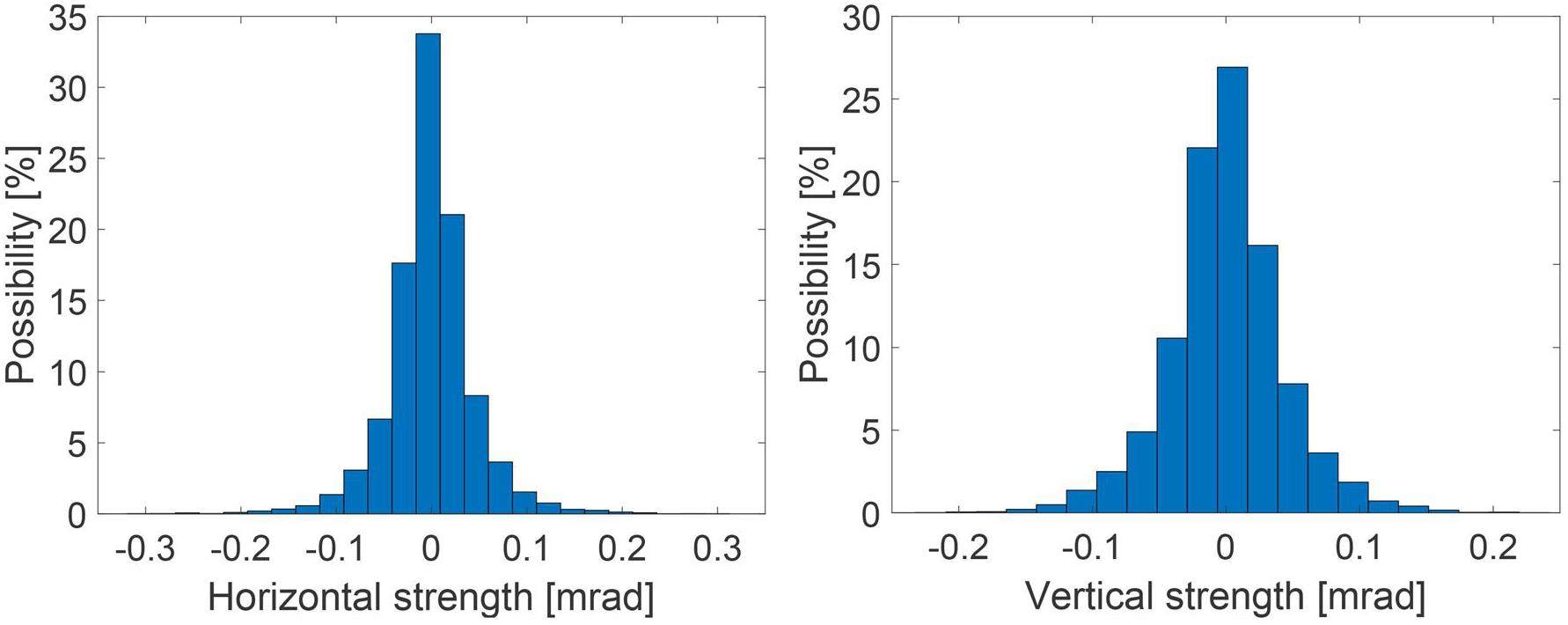
While DFS effectively restores the closed orbit and dispersion functions, it does not recover the beam emittance, β-functions, or tune. At this stage, approximately 25% of the seeds fail to yield stable optical function solutions.
To further restore beam emittance, tune, and dynamic aperture, the LOCO method [40] is employed for optical function correction. Skew quadrupole magnets are also used to correct transverse coupling and vertical dispersion. Figure 53 presents the statistical distribution of horizontal and vertical β-beating rms values before and after correction. Most seeds achieve good optical function correction, with β-beating rms values not exceeding 1% outside the IP region. However, βy distortion at the IP remains large, with rms and maximum values of approximately 9% and 40%, respectively, leading to luminosity losses of approximately 3% and 13%, respectively. To recover the luminosity, the strengths of quadrupoles on both sides of the IP are changed to rematch the optical functions to restore βy at the IP to near-design values. βx distortion is very small and has a negligible impact on luminosity.
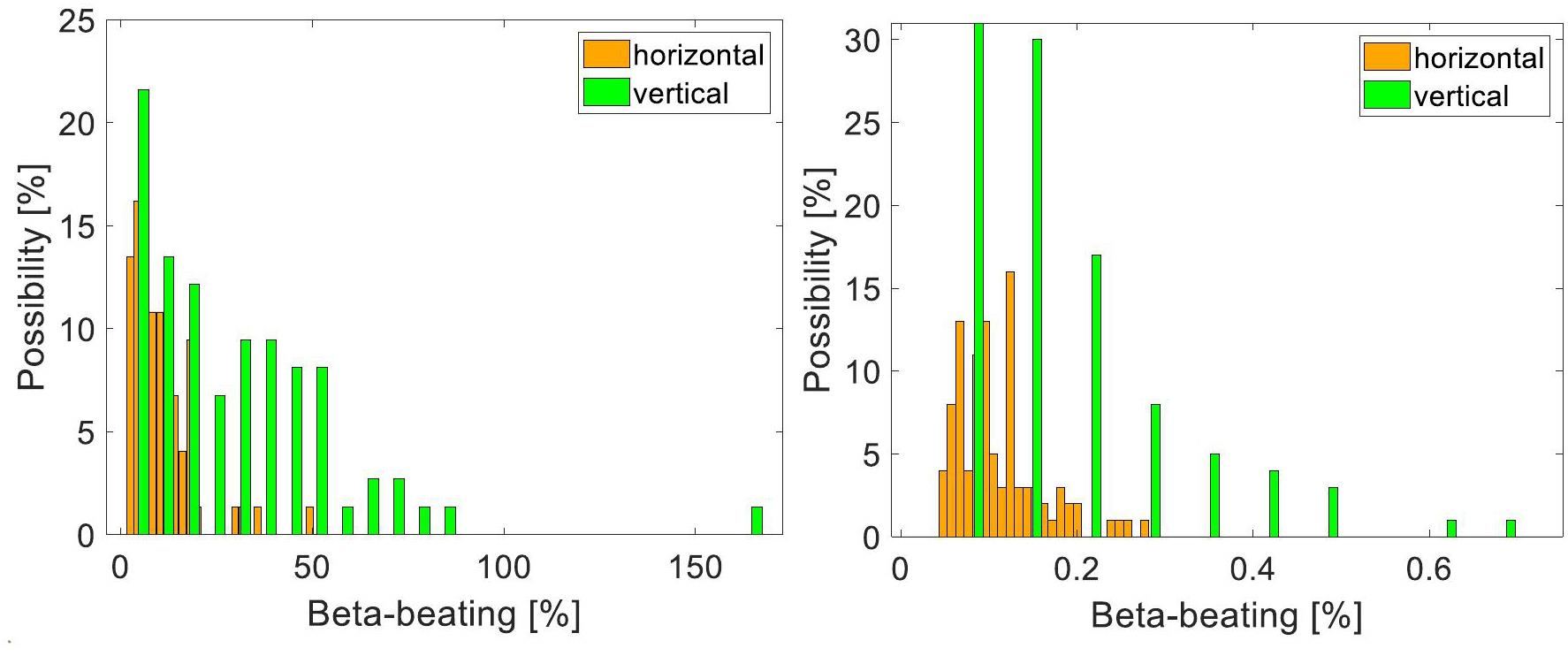
After correction, the horizontal and vertical dispersion function rms values are under 0.5 mm and 0.2 mm, respectively, with maximum deviations not exceeding 5 mm. Since weighting was not applied at the IP during this stage, vertical dispersion at the IP increases, with rms and maximum values reaching approximately 15 μm and 46 μm, respectively—leading to luminosity losses of approximately 1% and 3%, respectively. Future iterations may apply additional weighting to reduce vertical dispersion at the IP. Horizontal dispersion distortion has a negligible effect on luminosity.
Figure 54 shows the statistical distribution of transverse coupling ratios before and after correction. Before correction, the transverse coupling ratio is very large, and the resulting vertical emittance would notably reduce luminosity. After correction, the emittance coupling ratio is reduced to less than 0.1%, ensuring minimal luminosity loss due to vertical emittance growth. During correction, the variation in quadrupole strengths remains below 3%, and the maximum strength of skew quadrupole magnets is approximately 0.3 T/m, which is technically feasible.
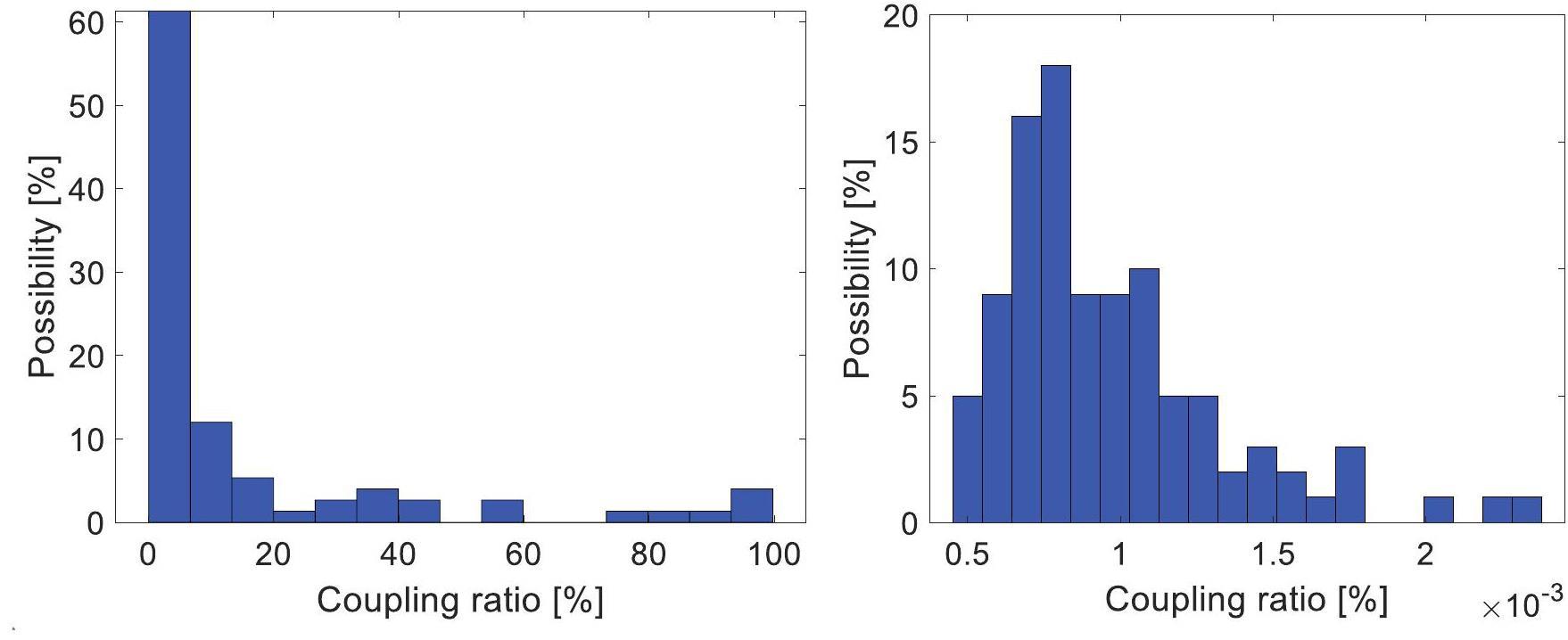
After orbit, optical function, and coupling corrections, the dynamic aperture and momentum aperture of the collider rings are significantly restored. Figure 55 illustrates the dynamic and momentum apertures with the edge effect considered after correction, indicating that the dynamic aperture has recovered to near-ideal lattice levels. Momentum aperture is also well restored, with Touschek lifetime degradation due to current error sources estimated at less than 30%. The multipole field errors of the magnets will further affect the nonlinear dynamics. Simulation results show that the multipole fields of the doublet quadrupoles on both sides of the IP have the most significant impact on the dynamic and momentum apertures. To mitigate these effects, the higher-order fields of these four quadrupoles should not exceed 2×10–4, while those in other magnets should be maintained below 5×10–4. This ensures that the reduction of dynamic aperture and Touschek lifetime remains within 10%.
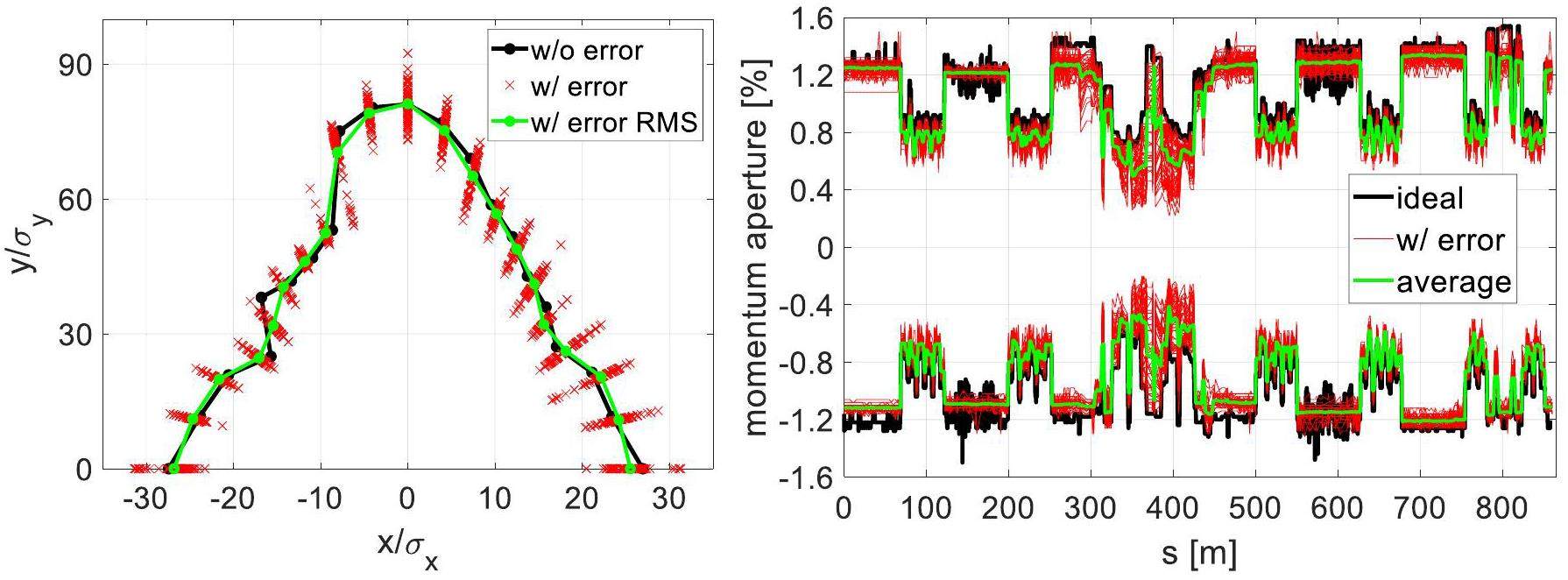
Beam collimation
Various beam loss mechanisms occur in the collider rings, including Touschek scattering, beam–beam scattering, and beam–gas scattering, all of which constrain the beam lifetime [41]. At STCF, Touschek scattering is particularly critical, reducing the particle lifetime to approximately 200 s. Consequently, an advanced beam collimation system is necessary to mitigate particle losses.
The primary functions of beam collimators in the collider rings are as follows: controlling experimental backgrounds in the IR, preventing uncontrolled particles from damaging accelerator components, and localizing beam losses to designated areas equipped with additional shielding, thereby reducing radiation dose in the tunnel and easing the shielding requirements for the tunnel walls [42].
Collimation efficiency is defined as the ratio of particles intercepted by the collimators (or their surroundings) to the total number of particles lost within a specific section of the collider rings. The design target is a collimation efficiency exceeding 90% outside the IR and over 80% within it.
Another requirement for the beam collimation system is to minimize impedance, with the collimators contributing no more than 50% of the total ring impedance.
Beam collimation methods
Beam loss mechanisms
During normal operation, multiple physical mechanisms contribute to beam losses in the collider rings, including Touschek scattering, beam instabilities, injection losses, beam–gas scattering in vacuum, and beam–beam scattering at the IP [41]. At STCF, the dominant sources of beam loss are estimated to be Touschek loss, beam–gas scattering in vacuum, and beam–beam scattering. The current estimated STCF beam lifetime is approximately 200 s, with a total circulating particle count (corresponding to a stored current of 2 A in top-up mode) of approximately 3.6×1013 e+/e-. This corresponds to a loss rate of roughly 1.8×1011 e+/e- per second. These losses exhibit no obvious time structure. Preliminary analyses of the major loss mechanisms are summarized below:
Injection loss: If STCF adopts an off-axis injection scheme, with an injection efficiency exceeding 90%, the resulting beam loss rate is approximately 1.8×1010 e+/e- per second. For a bunch swap-out injection scheme, injection losses are negligible. Injection-related losses are time-structured, occurring shortly after each injection (at 30 Hz or every 33 ms for both positron and electron rings), typically within 1 ms.
Touschek loss: This is expected to be the dominant beam loss mechanism at STCF, originating from intra-bunch scattering [41] and the very small momentum aperture of the collider rings. The most critical momentum-aperture limitations occur in the IR (particularly in regions of high dispersion) and in the arc sections. A large number of collimators are therefore placed in these regions to suppress losses both in the IR and elsewhere in the ring. Touschek-induced losses are random and lack a characteristic time structure.
Beam–beam scattering [43]: Excluding physics processes that produce detectable events, beam–beam scattering leads to two types of losses: instantaneous losses, which increase background at the IP, and emittance growth, which causes additional beam loss due to the limited dynamic and momentum apertures of the rings. These losses are random in time, although coupling between off-axis injection damping and beam–beam interactions may introduce some time structure.
Collective instability loss: These are unpredictable and may occur sporadically. If frequent, such losses would limit the maximum achievable beam current and luminosity until additional mitigation measures are implemented. They tend to be distributed around the entire ring and place significant demands on the collimation system. These losses are spontaneous and not time-predictable.
Beam-gas scattering loss [44]: Scattering of beam particles and residual gas molecules in the vacuum causes both direct particle losses (e.g., scattered particles lost within a few turns) and emittance growth (which can be mitigated by radiation damping). Outside the IR, such losses should be well controlled by a carefully designed vacuum system. However, in and near the IR—particularly inside the spectrometer—vacuum conditions are degraded due to limited space for pumps, resulting in relatively high local beam loss rates. These losses contribute directly to experimental background and must therefore be suppressed. While they are generally continuous, sudden vacuum degradation at specific locations can occasionally cause loss spikes.
Collimator layout design
STCF is designed to implement a more comprehensive beam collimation system than previous electron–positron colliders owing to two factors: first, STFC collider rings have an exceptionally short beam lifetime, representing an unprecedented challenge. Second, since the STCF will be constructed from scratch and is not an upgraded facility, it has the flexibility for optimum collimator placement. This design approach can better suppress backgrounds in the IR and enhance the management of the collider tunnel radiation dose distribution.
The beam collimators of the STCF collider rings fall into three categories: arc collimators, mainly responsible for cleaning particles from Touschek scattering; IR collimators, responsible for preventing off-momentum particles (including those from vacuum scattering) from entering the IR and collimating Touschek-scattered particles within it; and straight-section collimators, responsible for removing large emittance particles using nonlinear collimation methods (i.e., nonlinear lattice designs), thereby reducing the burden on the IR collimators.
Arc Collimators: Previous electron–positron colliders had relatively long beam lifetimes and therefore did not require complex collimation systems. For example, BEPC/BEPCII employed relatively few collimators [45], while KEKB and PEP-II implemented more [46], and SuperKEKB further increased the number, though space limitations restricted placement to one half-arc in each of the positron and electron rings [47]. As a new facility, STCF offers greater flexibility for favorable collimator placement. Because Touschek scattering is nearly uniformly distributed throughout the ring and represents a major source of beam loss due to the short Touschek lifetime, collimators are planned for all arc regions, including those near the IP (e.g., the small arcs). They will be located at positions with large dispersion and large beta functions, with the expectation that the majority of beam losses at STCF will be intercepted by these arc collimators.
IR Collimators: Dedicated optimization is required to control experimental backgrounds. At SuperKEKB, IR collimators carried an excessive burden [48]; STCF aims to alleviate this through a more comprehensive global collimation design. Further improvements will also be made in collimator materials and structural design to enhance both performance and effectiveness.
Straight-Section Collimators: While straight-section collimators are critical in hadron colliders, they are typically considered less important in electron colliders. However, SuperKEKB proposed a nonlinear beam collimation method [49] to reduce the load on IR collimators, and STCF is particularly well suited to implement this strategy due to its advantageous spatial layout. Each STCF collider ring (e+ and e-) will include a dedicated nonlinear collimation section within the long straight segments. These collimators are designed to remove particles with large transverse emittance using relatively wide gaps, thereby avoiding excessive coupling impedance. In addition to leveraging large beta functions, nonlinear elements such as sextupoles or octupoles will be introduced to distort the beam in phase space and enhance collimation efficiency—an approach referred to as nonlinear collimation.
Calculation and simulation results
Beam loss simulation from Touschek scattering
Owing to the very short Touschek lifetime, beam losses during routine STCF collider operation are primarily caused by the Touschek scattering effect. To better collimate Touschek-induced losses, the beam loss distribution in the absence of collimators was first evaluated. The vacuum pipe geometry was modeled as follows: a radius of 15 mm at the IP and the first quadrupole magnets on either side, expanding uniformly through one drift section to 25 mm at the second quadrupole, and then further increasing uniformly to 33.5 mm in the main IR. For the remainder of the ring, a constant vacuum pipe radius of 26 mm was assumed.
Under the condition of a single-bunch charge of 8 nC and a transverse coupling ratio of 0.5%, the distribution of beam losses due to Touschek scattering—assuming scattering points at every quadrupole magnet—was simulated using the Accelerator Toolbox (AT). The result is shown in Fig. 56. Analysis indicates that approximately 58.2% of the lost particles are absorbed in the IR (between 370 m and 380 m), 11.2% in the CCX section preceding the IR (300–320 m), and 13.4% near the CS section upstream of the IR (270–290 m). Most losses occur in the horizontal plane; however, vertical losses are also observed in the crab sextupole region, where βy is large. In the IR, losses primarily arise in the transition drifts where the pipe aperture changes, within 10 m of the IP, where β-functions are large and complex and the aperture is relatively narrow.
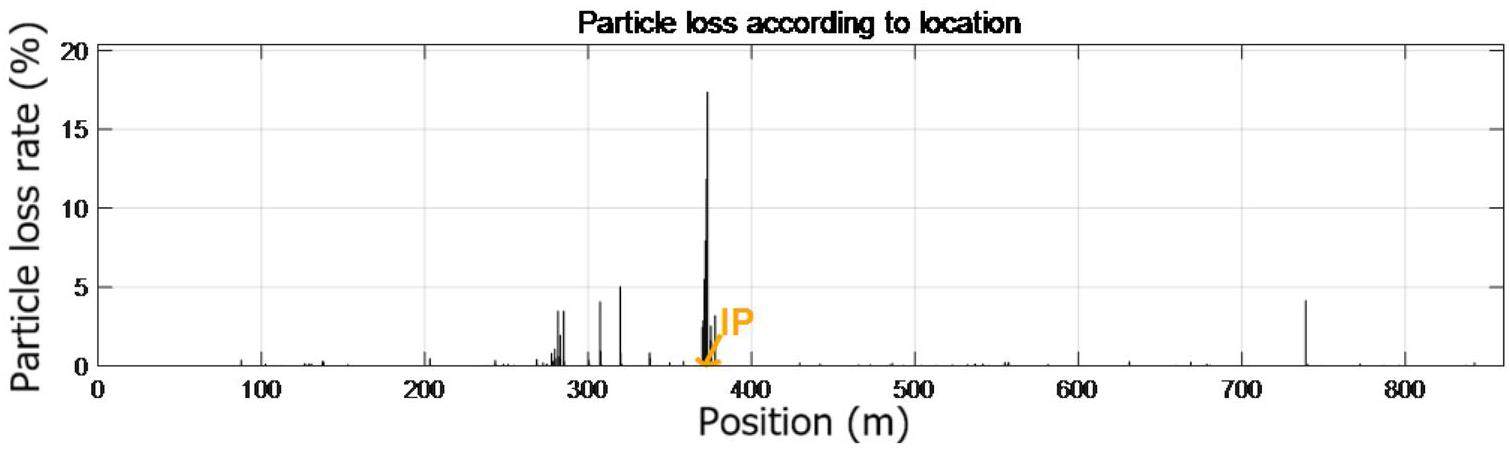
Based on the loss distribution, global optical function map, and betatron function distortions of off-momentum particles, a layout of 11 horizontal collimators (HCs) and 6 vertical collimators (VCs) was determined through iterative simulation and optimization. The final configuration is shown in Fig. 57. After collimator placement, the Touschek-induced loss distribution is presented in Fig. 58. The simulations indicate that the current configuration achieves a collimation efficiency of approximately 97.3%. Within ±20 m of the IP, residual beam losses are approximately 1.36%, occurring primarily in the transition region upstream of QF1. As shown in Fig. 58, HCs in the CCY section (HC5, HC6) and at locations with large horizontal β-function distortions (HC1) effectively intercept horizontally scattered particles. Similarly, VCs (VC1, VC2) placed in high-βy regions upstream of the IR efficiently intercept vertically scattered particles.
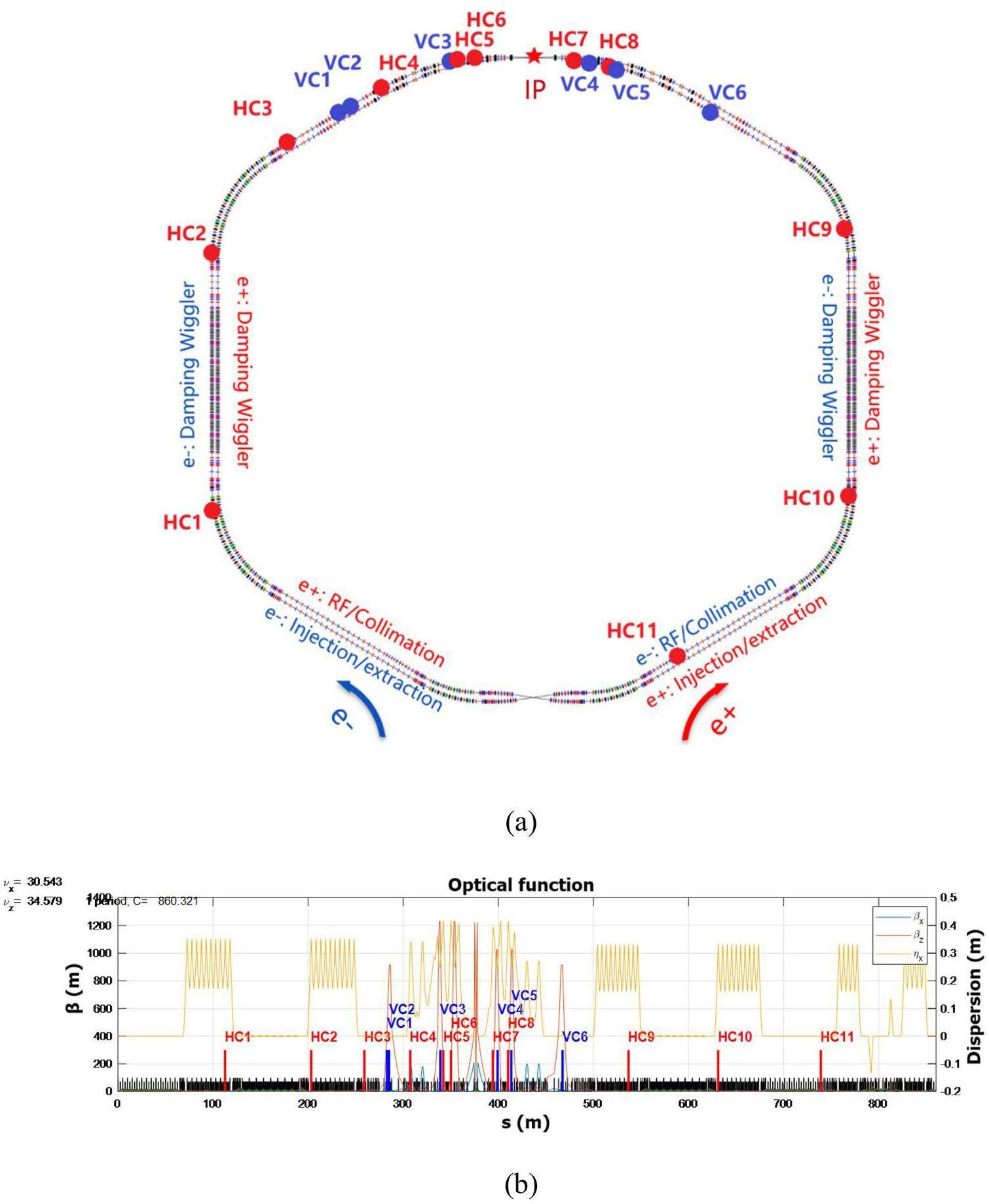
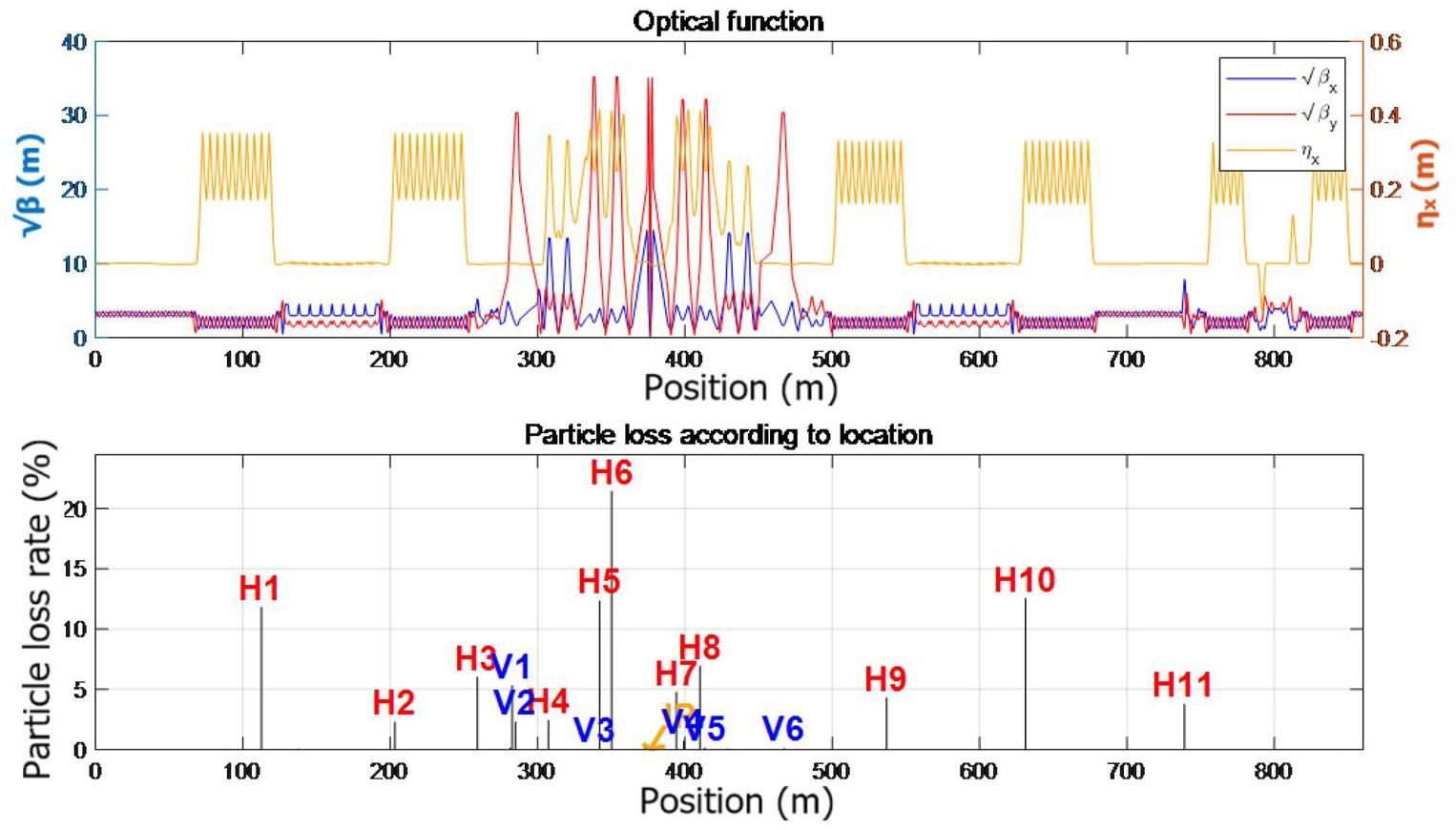
When additional loss mechanisms such as injection losses, beam–gas scattering, and beam–beam collisions at the IP are included in the simulations, a greater number of collimators will be required. A nonlinear collimation system, as discussed above, is also foreseen to reduce the impedance contribution from collimators with very small gaps.
Preliminary simulation of lost beam on collimators
When lost beam particles strike a collimator, they interact with its material, and the nature of this interaction varies with the choice of target material, affecting the ability to stop particles, the deposition of energy, and the production of secondary particles. Table 10 summarizes the relevant properties of several commonly used collimator materials.
| Material | Density (g/cm3) | Specific heat capacity (kJ/(kg·K)) | Thermal conductivity (W/(m·K)) | Melting point (K) |
|---|---|---|---|---|
| Tungsten (W) | 19.3 | 0.132 | 173 | 3695 |
| Tantalum (Ta) | 16.69 | 0.14 | 57 | 3017 |
| Copper (Cu) | 8.96 | 0.385 | 400 | 1358 |
| Aluminum (Al) | 2.7 | 0.88 | 190 | 933 |
| Graphite (C) | 2.26 | 0.709 | 120 | 3915 |
Considering both thermal performance and electrical conductivity, copper has been preliminarily selected as the primary material for the STCF collimators. Given the relatively wide operating beam energy range of STCF (1–3.5 GeV), ongoing studies are evaluating whether an absorbing-type or scattering-type collimator structure is more suitable.
Conclusions and analysis
The current collimator layout at STCF effectively reduces backgrounds in the IR while maintaining a reasonable loss distribution throughout the ring. Energy deposition from Touschek-induced losses appears relatively modest and is not expected to induce severe thermal effects at this stage. As the lattice design evolves, the collimator layout will be updated accordingly, and simulation models will be refined for improved accuracy. Future simulations will also incorporate additional beam loss mechanisms.
Synchrotron radiation damping
Requirements of the collider rings for radiation damping
The collider rings are subject to significant synchrotron radiation effects. These effects lead to the loss of beam energy, impose heavy thermal loads, and contribute adversely to experimental backgrounds. In addition, synchrotron radiation exerts a damping effect on the circulating beams, reducing transverse and longitudinal emittances. This damping effect is beneficial and crucial for beam injection, harmful collective effect suppression, and luminosity enhancement. Concurrently, the quantum excitation effect, also originating from synchrotron radiation, introduces randomness and competes with the damping. Hence, the horizontal emittance and energy spread eventually reach an equilibrium determined by the lattice design and beam energy.
The STCF collider rings are high-current, low-emittance electron and positron storage rings designed to operate over a wide energy range. Synchrotron radiation damping from the lattice alone is insufficient to achieve the required short damping times, low horizontal emittance, and relatively high energy spread, particularly at lower beam energies. To meet these requirements, additional DWs will be installed in the dedicated long straight sections to enhance the overall damping effect.
The design targets for radiation damping in the collider rings are as follows: at the optimal energy point (2 GeV), the damping time should be less than 30 ms, the horizontal emittance should be approximately 5 nm·rad, and the energy spread should not be less than 6×10-4. At other operating energies, these parameters may vary slightly but must remain within acceptable limits.
Mechanism of synchrotron radiation damping
Synchrotron radiation is emitted as a continuous spectrum of electromagnetic waves in the tangential direction when high-speed charged particles traverse curved trajectories in magnetic fields. In the STCF collider rings, synchrotron radiation is primarily produced by the dipole bending magnets and DWs. The dipole magnets provide approximately uniform vertical magnetic fields, and electrons emit radiation as they bend in these fields. The wiggler magnets consist of alternating-polarity dipole magnets arranged periodically and perpendicular to the central plane of the beam. As electrons pass through this alternating field, their trajectories oscillate, producing synchrotron radiation.
The radiated energy
In the collider rings, the higher energy of the electron and positron beams causes more synchrotron radiation energy loss and increases particle damping. The damping rates are different for different directions (horizontal, vertical, and longitudinal), as shown in Eq. (28), where
The radiation damping effect reduces both the horizontal and vertical emittance, while the quantum excitation during the radiation process slightly increases horizontal emittance. When quantum excitation and damping reach dynamic equilibrium in the horizontal plane, the horizontal equilibrium emittance is given by Eq. (29), where
The beam energy spread
Compared to the previous generation of colliders, the collider rings of the STCF have a significantly shorter beam lifetime, which necessitates frequent beam injections and a damping time of ≤ 30 ms. At lower energy (1 GeV), the radiation damping time is excessively long, necessitating the use of wiggler magnets to enhance damping and reduce the damping time. At higher energy (3.5 GeV), synchrotron radiation also affects the equilibrium emittance and energy spread of the stored beam; the introduction of wiggler magnets can also help tune these critical beam parameters.
Damping wiggler parameter design
Total effective length and peak magnetic field
For the optimized 2-GeV energy point, the transverse plane damping time of the collider rings must be shorter than 30 ms. At the beam energy of 1 GeV, the radiation damping contribution of the lattice is much smaller, and the required damping time should be less than 50 ms. Additional damping will originate from the DWs. By scanning the peak magnetic field strength
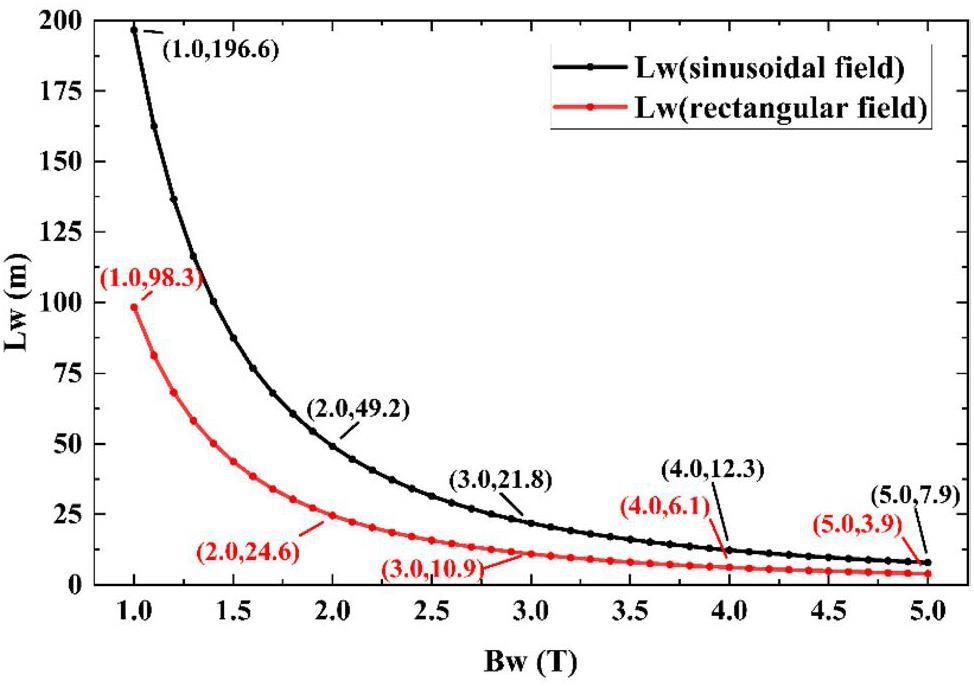
Insertion magnet technologies currently used in accelerators can generally be classified into three types: room-temperature magnets, cryogenic permanent magnets, and superconducting magnets [53]. Typical magnetic field strengths are 1–1.5 T for room-temperature magnets, 1.5–2 T for cryogenic permanent magnets [54, 55], and 3–5 T or higher for superconducting magnets.
Among these, superconducting wigglers are the most complex and expensive. Moreover, for a given damping time, increasing the field strength from 3 T to 5 T provides only marginal reductions in the required total effective length. Since the STCF collider rings are designed to operate over a wide energy range (1–3.5 GeV), the wigglers must provide sufficient flexibility and tunability. Permanent magnets allow limited field adjustment through mechanical gap control, whereas room-temperature magnets offer broader and more convenient tunability via coil excitation current.
For these reasons, STCF has adopted room-temperature wigglers. Taking into account cost, technical complexity, and the overall ring layout, a peak field of
Selection of wiggler period length
Wiggler magnets are composed of a series of periodic dipole magnets. The period length
Table 11 shows damping times across the 1–3.5 GeV energy range with and without wigglers (with
| Energy | No. wiggler | Sinusoidal field | Rectangular field |
|---|---|---|---|
| 1 GeV | 586.6 | 43 | 22.3 |
| 1.5 GeV | 173.8 | 26 | 14.2 |
| 2 GeV | 73.3 | 17.6 | 10.0 |
| 3.5 GeV | 13.7 | 6.7 | 4.5 |
Wiggler end field configuration
The wiggler end field is crucial for ensuring that the beam trajectory returns to its original transverse position and angle. Ideally, the integral and double integral of the wiggler magnetic field should be zero, which requires special end pole shaping [7].
A simple method uses weakened end poles at both wiggler ends with a symmetric field arrangement, i.e., an odd number (2N+1) of poles, where the end pole integral is half that of the central poles. This arrangement ensures that both the beam position and angle are restored after it passes through the wiggler, but the center axis of the oscillatory trajectory inside the wiggler remains offset.
To ensure that the trajectory oscillates around the zero axis within the wiggler, each end has two weakened end poles. For 2N poles, the field pattern is {+1/4, –3/4, +1, –1, ... +1, –1, +3/4, –1/4}, and for 2N+1 poles, {+1/4, –3/4, +1, –1, ..., +1, –3/4, +1/4}. This configuration also relaxes the requirement for a high quality field region in the horizontal direction.
Impact of damping wigglers on beam parameters
Based on the current design parameters—room-temperature magnets with a peak field of
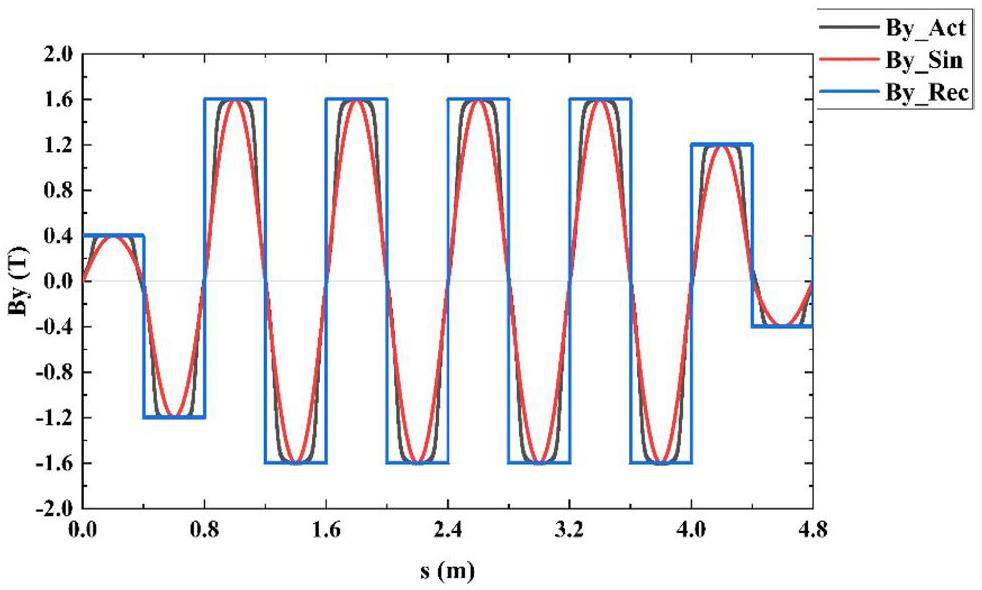
To accommodate the broad energy range of the STCF, the wigglers must support variable settings to satisfy beam dynamics requirements—including damping time, horizontal emittance, and energy spread—across different operational energies. Because sinusoidal and rectangular wiggler fields produce different damping effects, and the actual field lies between these extremes, Table 12 presents simulation results for damping time, horizontal emittance, and energy spread at four beam energies (1.0, 1.5, 2.0, and 3.5 GeV) for the cases of no wigglers, sinusoidal wigglers, rectangular wigglers, and realistic wigglers.
| E (GeV) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Sinusoidal field | 1.0 | 1.6 | 586.2 | 54.5 | 2.4 | 0.7 | 0.29 | 0.52 |
| 1.5 | 1.6 | 173.8 | 32.6 | 5.4 | 1.7 | 0.43 | 0.62 | |
| 2.0 | 1.6 | 73.3 | 21.3 | 9.7 | 3.6 | 0.57 | 0.71 | |
| 3.5 | 1.6 | 13.7 | 7.6 | 29.7 | 17.3 | 1.00 | 1.00 | |
| Realistic field | 1.0 | 1.6 | 586.2 | 42.4 | 2.4 | 0.9 | 0.29 | 0.55 |
| 1.5 | 1.6 | 173.8 | 25.9 | 5.4 | 1.8 | 0.43 | 0.66 | |
| 2.0 | 1.6 | 73.3 | 17.4 | 9.7 | 3.5 | 0.57 | 0.75 | |
| 3.5 | 1.6 | 13.7 | 6.7 | 29.7 | 15.9 | 1.00 | 1.03 | |
| Rectangular field | 1.0 | 1.6 | 586.2 | 28.6 | 2.4 | 1.3 | 0.29 | 0.57 |
| 1.5 | 1.6 | 173.8 | 18.0 | 5.4 | 2.2 | 0.43 | 0.69 | |
| 2.0 | 1.6 | 73.3 | 12.5 | 9.7 | 3.6 | 0.57 | 0.79 | |
| 3.5 | 1.6 | 13.7 | 5.3 | 29.7 | 14.0 | 1.00 | 1.06 |
The results indicate that adding wigglers reduces the damping time and increases the energy spread in all cases, with rectangular fields producing stronger effects than sinusoidal fields, and realistic fields falling in between. This trend is consistent across all considered beam energies.
Wiggler radiation generates substantial synchrotron light. At 2 GeV and 2 A, a single wiggler produces 64 kW of synchrotron radiation power. One straight section containing 8 wigglers emits a total of 512 kW. Figure 61 shows the power distribution of this radiation at the downstream end. To manage it, photon masks must be installed along the beamline to prevent direct strikes on the vacuum chamber. The remaining radiation can be extracted near the first bending magnet in the downstream arc and absorbed by a high-power photon absorber. In the future, synchrotron light from the outer ring could also be extracted for high-flux applications.
Evaluation of the effects of damping wigglers on linear lattice and nonlinear beam dynamics
Impact on linear lattice
Wiggler magnets with vertical dipole fields (By) exert additional vertical focusing forces on the beam. These forces can modify the lattice's optical functions and working point. The magnitude of this perturbation is proportional to
Impact on nonlinear beam dynamics
Wiggler magnets also affect the nonlinear beam dynamics of the lattice, primarily due to the roll-off effect in the magnetic field—that is, the non-uniformity of By in the horizontal and vertical directions [57]. The perturbations exerted on the beam in the horizontal and vertical directions are proportional to
When the wiggler’s good field region is sufficiently wide and the field quality is high, these high-order components remain small, minimizing their impact on nonlinear beam dynamics. Therefore, the design and fabrication of wiggler magnets must ensure a large, good field region and high magnetic field uniformity.
Physics design related to MDI
MDI design requirements
The Machine Detector Interface (MDI) is the region connecting the collider rings to the detector spectrometer, playing a critical role in both routine accelerator operation and physics data collection. Since both beams must pass through the detector center and collide at the IP, and a tightly focused beam spot is required to achieve high luminosity using superconducting quadrupole magnets, the inner detector components must be positioned very close to the IP. This results in extremely constrained space for accelerator components. For a third-generation e+/e– collider such as STCF, MDI design is particularly complex due to ultra-high luminosity, a large crossing angle, strong focusing, and short beam lifetime—all of which must be addressed.
The accelerator IR involves multiple technical systems, including lattice and beam dynamics design (accounting for nonlinear effects, chromaticity correction, beam–beam interactions, collective effects, etc.), superconducting magnets and cryostats, beam diagnostics, vacuum systems, mechanical structures, collimation, and alignment. On the detector side, MDI-related systems include background simulation and shielding, spatial arrangement of inner detectors and electronics, luminosity monitoring, and feedback. Coordinated study between the accelerator and detector teams is therefore essential, with the design objective of ensuring spatial compatibility between accelerator and detector systems, enabling the accelerator to achieve its target luminosity and stable operation while minimizing background levels for collision experiments.
Impact of interaction region design on MDI
The lattice design of the IR determines the layout and longitudinal allocation of accelerator components within the MDI. To maximize the solid angle for physics measurements, the detector imposes stringent constraints on the transverse space available to accelerator elements. Figure 62 shows the layout of the STCF MDI, illustrating the preliminary positions and dimensions of components within ±3.5 m of the IP, including detector boundaries, central beam pipe, vacuum pipe structures, superconducting magnets and cryostats, beam diagnostics components, and mechanical supports. Spatially, the detector requires that all accelerator components within the IR be confined to a conical region with a 15° opening angle centered on the IP.
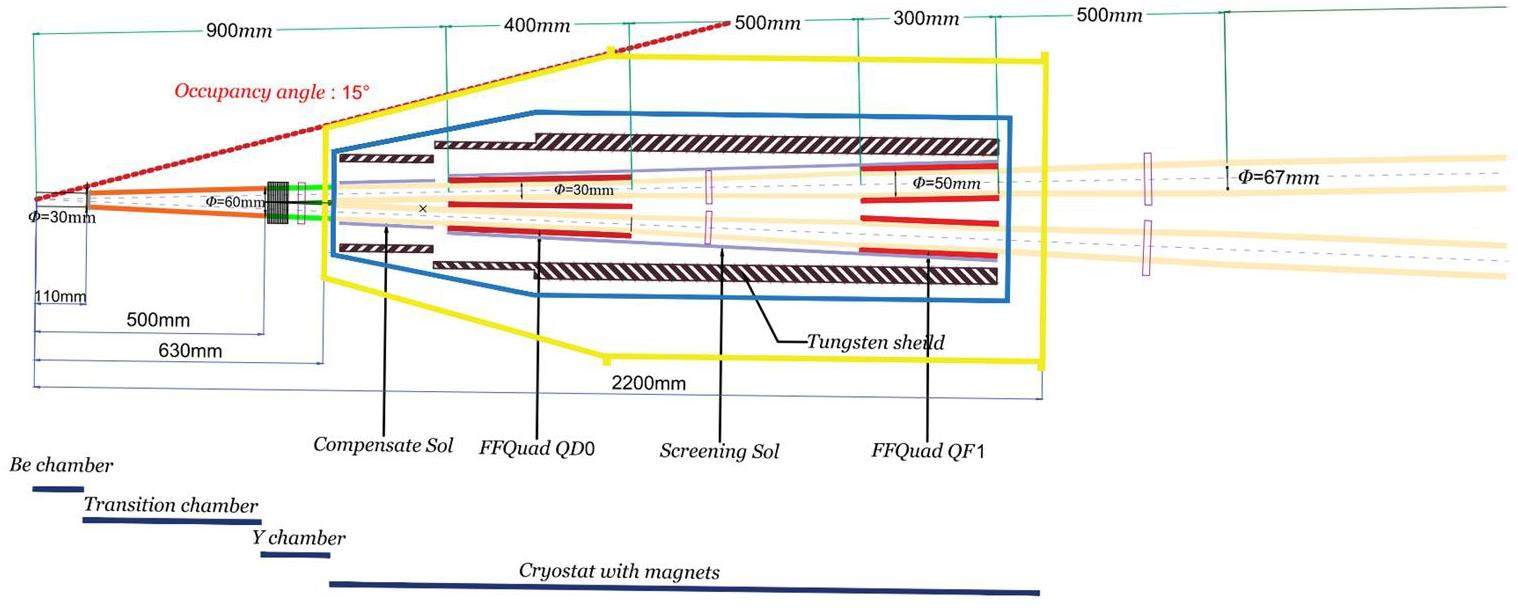
The cryostat houses compensating solenoids, two superconducting quadrupoles, several correctors, and a shielding solenoid. The compensating solenoid upstream of the superconducting quadrupoles and closest to the IP cancels the integrated longitudinal magnetic field of the detector solenoid. The shielding solenoid, wound around the superconducting quadrupoles, ensures that
The central beam pipe consists of the IP pipe and a transition pipe. The IP pipe is made of beryllium, with its inner wall coated in gold to shield against synchrotron radiation and reduce impedance, and has a diameter of 30 mm. The transition pipe expands longitudinally from 110 mm to 500 mm, transitioning from a 30 mm round pipe to a racetrack-shaped cross-section measuring 60 mm wide and 30 mm high. At the Y-chamber—remote vacuum connector (RVC)—the beam pipe splits into two 30 mm diameter channels up to the end of QD0, then transitions over 0.5 m to a 50 mm diameter at the entrance of QF1, and finally increases within 0.5 m to 67 mm. The design of the transition from the dual-aperture region in the superconducting magnets to the single-aperture central beam pipe prioritizes the minimization of impedance.
The upstream bending magnet B0 is a primary source of synchrotron radiation entering the MDI. In the lattice design, this magnet is deliberately positioned away from the IP (approximately 8.5 m) and set to a relatively weak bending angle of only 1°. Synchrotron radiation distributions were analyzed for electron/positron beams entering the IP from both the outer and inner rings, as shown in Fig. 63. The directly irradiated regions are marked in yellow, and only the case of the positron beam is illustrated for simplicity. Table 13 lists the synchrotron radiation power deposited in various MDI regions. For beams entering from the outer ring, radiation does not directly strike the central beryllium pipe, which occurs for beams entering from the inner ring. Hence, the preferred configuration has the beams entering the IP from the outer ring.
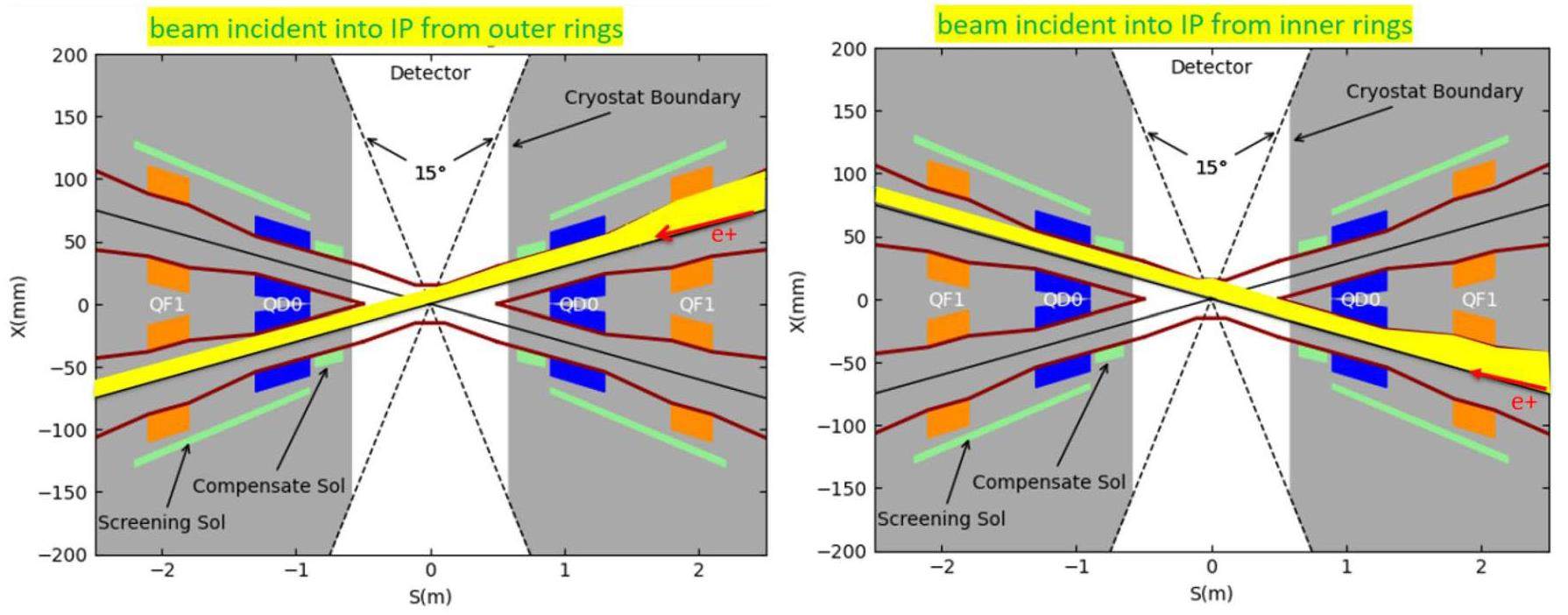
| Synchrotron power (W) | B0 | Central Be pipe | Conical transition pipe | Y-section pipe | Cryostat |
|---|---|---|---|---|---|
| Outer ring @ 2 GeV | 137.2 | 0 | 3.64 | 0.43 | 17.8 |
| Outer ring @ 3.5 GeV | 1287.3 | 0 | 34.1 | 4.02 | 167.2 |
| Inner ring @ 2 GeV | 137.2 | 4.02 | 0 | 0.27 | 17.7 |
| Inner ring @ 3.5 GeV | 1287.3 | 37.7 | 0 | 2.5 | 165.7 |
The definition of beam stay-clear regions in the IR is a critical factor for MDI magnet design. In second-generation e+/e- colliders, such as PEP-II and BEPCII, the stay-clear region is typically defined as 15–20 times the beam envelope σₓ/σᵧ plus 1–2 mm to account for orbit deviations. For newer-generation colliders, including SuperKEKB, SuperB, and FCC-ee, the extremely small beam sizes at the IP require strict control of orbit deviations near superconducting quadrupoles (less than 100 µm); consequently, the stay-clear region is defined without including orbit deviations. CEPC adopts the same definition as BEPCII.
Here, both interpretations are provided. Figure 64 shows the beam stay-clear boundaries at 2 GeV and 3.5 GeV. The magenta and green dashed lines represent the stay-clear boundaries for the positron and electron beams, respectively. At 2 GeV, the horizontal stay-clear region is defined as 22σₓ + 2 mm (or 24σₓ), and the vertical as 22σy + 2 mm (or 26σy). At 3.5 GeV, due to the larger beam emittance, the stay-clear region is reduced to 9.5σₓ + 2 mm (or 10.5σₓ) for the horizontal region and 9.5σy + 2 mm (or 11.5σy) for the vertical region. In these calculations, the horizontal emittance εₓ is taken as 5 nm at 2 GeV and 27 nm at 3.5 GeV, with the vertical emittance assumed to be 5% of εₓ, i.e., εy = 0.05εₓ. The small beam stay-clear regions at 3.5 GeV can be enlarged by increasing
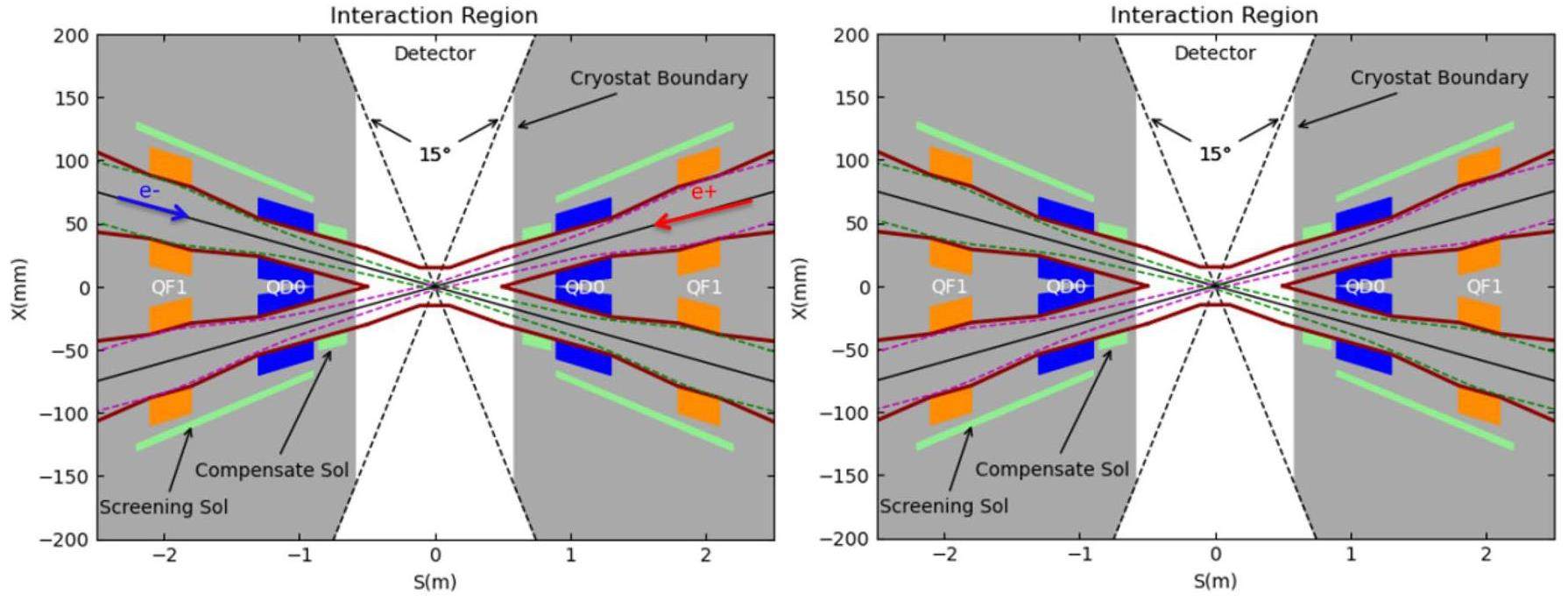
| Superconducting magnet | Distance from IP (m) | Beam stay-clear region 2×(22σx,y + 2) (mm) | e+/e- beam center separation (mm) | Good field region H/V (mm) | Field gradient (T/m) | Beam pipe inner radius (mm) | Effective length (m) |
|---|---|---|---|---|---|---|---|
| QD0 | 0.9–1.3 | Entrance: 15.2 / 24.5 | 54 | 24.6 × 27.3 | 50 | 15 | 0.4 |
| Middle: 18.7 / 27.3 | 66 | ||||||
| Exit: 24.6 / 26.3 | 78 | ||||||
| QF1 | 1.8–2.1 | Entrance: 43.2 / 19.2 | 108 | 48.3 × 19.2 | 40 | 25 | 0.3 |
| Middle: 47.3 / 17.6 | 117 | ||||||
| Exit: 48.3 / 17.0 | 126 |
Beam loss and experimental background simulation
The primary sources of experimental background in the IR are non-collisional beam losses, Bhabha scattering, synchrotron radiation effects, and beam-induced bremsstrahlung. In a low-energy e+e- collider such as STCF, the latter two contribute less significantly, with beam loss and Bhabha scattering being the dominant factors. Bhabha scattering is an inherent process accompanying collisions and is essentially unavoidable. While beam loss is also inevitable, its impact on experimental backgrounds can be mitigated through appropriate measures.
As a newly constructed accelerator, STCF aims to minimize beam loss in the IR by employing collimators at strategic locations in the collider rings to intercept particles from Touschek scattering and the transverse beam halo, as described in the beam collimation section. Synchrotron radiation primarily contributes to the thermal load on the beam pipe in the IR; however, its effect on experimental backgrounds—particularly from high-energy X-ray components—must also be considered. Beam-induced bremsstrahlung can influence background levels, especially when operating at the high-energy end near 3.5 GeV, providing another rationale for maintaining ultra-high vacuum conditions in the IR.
With the exception of the central beam pipe section—particularly the beryllium IP pipe, which serves as the passage for reaction products entering the detector and therefore cannot be shielded—all other beam pipe sections and components are equipped with shielding absorbers. These are designed to reduce the likelihood that secondary particles from upstream beam collimators, vacuum-induced bremsstrahlung, or synchrotron radiation reach the detector or superconducting magnet coils, while minimizing the impedance introduced by the shielding structures.
Simulation studies of collision-induced backgrounds are ongoing. Preliminary results indicate that the background levels remain within controllable limits.
Considerations for future polarized beams
The design of polarized beams involves two key considerations: achieving longitudinal polarization at the IP and satisfying the spin matching condition to mitigate depolarization effects. Longitudinal polarization at the IP can be realized either by implementing SSs in the ring or by installing spin rotators at suitable locations near the IP [58, 59]. To reduce depolarization, the spin tune should be kept as far as possible from integer resonances—ideally near a half-integer. This can be achieved by using a Siberian snake to fix the spin tune at an integer value or by employing a spin rotator to slightly adjust the beam energy so that the fractional part of a×γ equals 0.5, where a is the anomalous magnetic moment (a=0.00115965218).
At STCF, the preferred approach is to use spin rotators to achieve both longitudinal polarization and spin matching. This method offers greater flexibility in the collider ring lattice design, without requiring dedicated structures to accommodate SSs, and allows the use of a two-fold symmetric lattice layout. Furthermore, since STCF plans to adopt a bunch swap-out injection scheme and the beam lifetime is approximately 200 s, the requirement on depolarization time is relatively relaxed, making the spin rotator approach sufficient to achieve the desired polarization and depolarization suppression. However, it remains unclear whether the present lattice is fully compatible with polarized beam operation, and further detailed studies are required. In Phase I of STCF, polarized beams will not be implemented; only space for polarization components will be reserved in the lattice design.
Injector accelerator physics
Introduction to the injector design
Design requirements and specifications
As an integral part of the STCF accelerator complex, the injector is a sophisticated accelerator system. Its primary role is providing high-quality, full-energy electron and positron beams for injection into the collider rings, serving as a key component for realizing high luminosity at the STCF. The collider rings operate in the top-up mode, and currently, the beam injection design considers two schemes: off-axis injection and bunch swap-out injection.
The off-axis injection scheme aims to replenish particle losses during collider operation. In this approach, the electron beam is accelerated and transported directly to the collider electron ring via a linac and beamline. For positrons, the beam produced by the high bunch-charge electron beam onto a target is accelerated to 1 GeV and damped in a DR. Next, it is further accelerated through the ML and transported into the collider positron ring. In contrast, the bunch swap-out injection scheme sequentially replaces bunches whose charge has dropped below a certain threshold with injected high-charge bunches in both rings. In this scheme, high-charge electron bunches are directly supplied by the electron gun and accelerated for on-axis injection into the collider electron ring. For positrons, bunch charge accumulation in an accumulator ring is necessary due to the relatively low conversion efficiency from electrons to positrons. Following accumulation, the bunches undergo emittance damping and acceleration before on-axis injection into the collider positron ring. Bunches scheduled for replacement must be extracted in advance to accommodate incoming injections.
After comparison and evaluation, an injector scheme compatible with both off-axis and swap-out injection is proposed. This allows initial implementation with off-axis injection to control construction costs, while remaining for a swap-out injection upgrade when needed.
Although the two injection schemes impose different design requirements on the injector, their primary objective is the same: to maintain approximately 95% of the nominal electron and positron beam currents (2 A) in the collider rings, assuming a minimum beam lifetime of 200 s. The off-axis injection scheme places higher demands on beam quality, such as emittance and energy spread, whereas the swap-out scheme requires higher bunch charge and an increased repetition rate for part of the injector linac. Key injector design parameters are summarized in Table 15. The extremely short beam lifetime at STCF presents substantial challenges for both beam injection into the collider rings and the overall design and construction of the injector.
| Parameter | Off-axis injection | Swap-out injection |
|---|---|---|
| Electron gun type | Photo-/thermionic cathode | Thermionic/PITZ cathode |
| Linac RF frequency (MHz) | 2998.2 | 2998.2 |
| Bunch charge into collider (nC) | 1.5 | 8.5 |
| Injection energy/nominal energy (GeV) | 1.0–3.5 / 2.0 | 1.0–3.5 / 2.0 |
| Injected electron bunch geometric emittance (X/Y, nm·rad) | ≤6/2 | ≤30/15 |
| Injected positron bunch geometric emittance (X/Y, nm·rad) | ≤6/2 | ≤30/15 |
| Injected bunch energy spread (rms, %) | ≤0.1 | ≤0.5 |
| Injected bunch length (rms, mm) | <7 | <7 |
| Repetition rate (electron, Hz) | 30 | 30 |
| Repetition rate (positron, Hz) | 30 | 30 |
| Positron damping/accumulation ring | Damping ring | Accumulator ring |
| Bunch charge at ring entrance (nC) | 1.5 | 2.9 |
| Entrance emittance (X/Y, nm·rad) | ≤1400 | ≤1400 |
| Entrance energy spread (rms, %) | ≤0.1 | ≤0.3 |
| Exit emittance (X/Y, nm·rad) | ≤11 / 0.2 | ≤30 / 5.2 |
| Ring RF frequency (MHz) | 499.7 | 499.7 |
| Number of bunches in ring | 5 | 5 |
Traditional off-axis injection offers higher beam utilization, lower bunch charge per injection, and reduced frequency requirements for the injector linac, making it relatively straightforward to implement. However, the larger beam loss associated with off-axis injection introduces significant experimental background and can induce emittance growth through coupling with beam–beam effects.
To mitigate these issues, the swap-out injection scheme is under study. This approach allows, in principle, higher injection efficiency for individual bunches and can suppress experimental background arising from injection losses. However, if the extracted bunches are not reused—as in the present design—beam utilization is reduced. In addition, the large bunch charge imposes challenges for emittance control, positron bunch charge accumulation, and achieving small vertical emittance in the injector design.
The swap-out injection scheme requires beamlines and accelerator components with larger physical apertures while maintaining strictly controlled emittance growth. It also necessitates pre-extraction of the bunches to be replaced before injection, adding complexity to the extraction system, which in traditional operation only needs to remove the entire beam for machine protection, and requires a more sophisticated beam dump. Reuse of the spent high-charge bunches for other applications could mitigate beam utilization issues. A notable advantage of this scheme is that an injector designed for swap-out injection can also support off-axis injection with relatively minor modifications.
In the conceptual design phase, injector physics designs for both off-axis and swap-out injection schemes have been developed, and a compatible injector design accommodating both approaches is currently under study.
Given the wide operating energy range and the very short beam lifetime of the collider rings—particularly under swap-out injection—the injector must deliver electron and positron beams with variable energy (1–3.5 GeV), high repetition rate (30–90 Hz), low emittance (<30 nm·rad), and high bunch charge (8.5 nC) for swap-out injection. These requirements pose substantial challenges for the injector design, including:
· Electron and positron linacs: Three-stage linacs are required for both injection schemes (Fig. 65). The low-energy sections must accommodate large bunch charges while controlling emittance growth. Positron linacs (PL and SPL) must handle larger positron emittance. The maximum linac repetition rate is expected to reach 90–100 Hz.

· Positron generation, capture, and pre-acceleration: All schemes employ conventional target-based positron production. Key tasks include efficient generation, collection, and pre-acceleration of positrons, incorporating adiabatic matching, e+/e− separation, and longitudinal compression, necessitating detailed tracking simulations.
· Damping and accumulator rings: The damping ring (DR) reduces positron emittance via synchrotron radiation. In the swap-out scheme, the accumulator ring (AR) simultaneously accumulates and damps positrons to satisfy the collider’s bunch charge and emittance requirements. In the hybrid scheme, both the DR and AR are used sequentially.
· ML: Accelerates 1 GeV e+/e− bunches to 1–3.5 GeV for injection into the collider rings, operating alternately at 30 Hz for the electron and positron beams.
· Beam transport lines: Include the bypass beam line (for off-axis injection only), injection and extraction lines for the DR and AR, and transport lines from the ML to the collider rings. The physics design emphasizes beam matching, emittance preservation, and high transmission efficiency.
A detailed description of the compatible injector scheme is provided in Sect. 3.6.
Overview of the design schemes
Schematic layouts of both the collider ring injection schemes, which are based on the physics design requirements and injector specifications and reference similar international accelerator layouts, are shown in Fig. 1.
The linac system for each of the two injection schemes incorporates two electron sources—one corresponding to a low-emittance electron gun for direct injection into the collider electron ring and the other to a high-charge electron gun for positron production via target bombardment. For the off-axis injection scheme, the low-emittance electron source is a PC RF gun producing 1.5 nC, and the high-charge electron source is a TC RF gun producing 10 nC. For the swap-out injection scheme, the electron sources comprise a TC gun (8.5 nC) or an L-band PITZ PC gun (8.5 nC), along with an 11.6 nC TC gun. Different bunching schemes are used for beams from different types of electron guns: a chicane scheme is applied for beams from the RF PC guns, while for all three TC guns, a subharmonic buncher (SHB) and a fundamental harmonic buncher system are adopted.
In the off-axis injection scheme (Fig. 1a), electrons from the two sources pass through respective bunching sections (BSs) and pre-injector sections (PISs) for bunching and initial acceleration. They are then merged at 200 MeV at the entrance of the first ML section (EL1), which accelerates the beam to 1.0 GeV. From there, the beam from the RF PC gun is delivered via a bypass line to the positron/electron ML and accelerated to the injection energy required by the collider rings. The 10 nC electron beam from the thermionic gun is further accelerated to 1.5 GeV by a second linac section (EL2) before striking a tungsten target to produce positrons. The resulting positrons are collected to form a bunch charge of 1.5 nC and pre-accelerated to 200 MeV. In the main accelerator section of the positron linac (PL), the positrons are accelerated to 1.0 GeV and injected into a DR for emittance reduction. The DR uses a single-turn (on-axis) injection scheme, storing five bunches simultaneously. Each bunch undergoes damping from an initial emittance of 1400 nm·rad to below 11 nm·rad. The extraction repetition rate of the DR matches the injection of the collider rings. The damped positron bunches are then transported to the ML and accelerated to the injection energy of the collider rings.
In the swap-out injection scheme (Fig. 1b), 8.5 nC electron beams from a thermionic or PITZ L-band PC gun are bunched in Bunching Section 1 (BS1) and accelerated to 1.0 GeV in the linac section SEL1. They are then accelerated by the ML to the collider ring injection energy. The electron beam from the 11.6 nC thermionic is bunched in BS2, then accelerated to 2.5 GeV in SEL2 before striking a tungsten target to generate positrons. A positron beam with a bunch charge of 2.9 nC is collected and pre-accelerated to 200 MeV, then accelerated to 1.0 GeV in the PL. These positrons are injected into an accumulator ring (AR) for bunch charge accumulation and emittance damping. The AR uses a multi-turn off-axis injection scheme, sequentially filling all stored bunches and allowing sufficient damping time before extraction. The injection repetition rate is a multiple of the extraction repetition rate, which is determined by the accumulation ratio. Once the accumulation and damping are complete, positron bunches are extracted and accelerated by ML to the required energy for injection into the collider rings.
Swap-out injection requires high bunch charges and stringent control of beam quality for both electron and positron beams. Due to the positron production mechanism, the international standard employs a high-charge electron beam to bombard a production target. Considering the sensitivity of cost to electron beam energy and the technical limits on bunch charge from the electron gun and linac, a positron AR is adopted instead of a DR for off-axis injection. This AR, combined with a higher repetition rate and modest beam energy for the driving electron linac, allows accumulation of positron bunch charge through multiple injections while simultaneously damping transverse and longitudinal emittance.
For electrons, considering technological maturity and cost considerations, direct injection of high-quality, high-charge bunches into the collider electron ring is explored to replace degraded bunches. The main challenges remain achieving high bunch charge and low beam emittance. Two feasible approaches are considered: (1) Conventional thermionic guns: Capable of generating bunches exceeding 8.5 nC. This method is technically reliable and does not require a high-power laser system; however, the relatively large emittance from the gun may necessitate beam scraping prior to injection to meet emittance requirements. (2) L-band PC guns: Capable of generating high-charge (>8.5 nC), high-quality electron bunches. While technically promising, this approach imposes strict demands on the driver laser, the high-vacuum environment, and the lifetime of the semiconductor PC, particularly when operating at high repetition rates, and still requires engineering validation.
Despite differences in injector physics design corresponding to the two collider ring injection schemes, they share common requirements: strict control of beam emittance during acceleration, high positron capture efficiency, optimized design of the positron damping and accumulator rings, and optimized injection transport lines. The following sections present the physics design details for each scheme, demonstrating how the required bunch charge and beam quality are achieved.
Injector physics design for off-axis injection
Electron source and low-energy acceleration section
Based on electron charge requirements for direct collider electron ring injection and bombardment-based positron production, two electron guns are used to generate bunches with different charges. Consequently, the system is divided into a photocathode low-energy section and a thermionic cathode low-energy section. At the exit of the two low-energy sections, the beams from both electron guns are merged into the first main acceleration section through a combining segment. The layout of the dual-gun low-energy section is shown in Fig. 65.
Photocathode low-energy section
The electron beam quality (e.g., emittance, current, bunch length, etc.) of the low-energy section is crucial in determining the final beam quality injected into the collider electron ring. To maximize the injector beam quality, a well-established S-band 2998 MHz PC RF gun, which has already been tested at major international and Chinese accelerator facilities, is adopted for the STCF. This gun can deliver high beam quality that meets the stringent requirements of the STCF. The basic configuration of this section is shown in Fig. 66.

The gun operates at a cathode gradient exceeding 100 MV/m and delivers a beam energy of approximately 4 MeV at its exit. The beam is then accelerated to 120 MeV using two S-band accelerating structures, L0 and L1. The next stage, L2, consists of two additional S-band structures powered by a shared RF source with an energy doubler, which accelerates the beam to over 200 MeV while imparting an energy chirp. This is followed by an X-band accelerating structure serving as a linearizer and a chicane acting as a magnetic bunch compressor, which reduces the bunch length to below 1 ps (equivalent to 1° RF phase at S-band frequency). A Ti:sapphire mode-locked laser system, synchronization control system, and various power supplies are also required.
Compared with a conventional low-energy section based on a thermionic cathode, a key challenge for the photocathode scheme is maintaining low emittance at high bunch charge. Typically, an external solenoid is used to focus the beam after the RF gun. Following a drift section, the linear space-charge effects can be partially compensated, mitigating emittance growth. According to the design requirements, the photocathode low-energy section must deliver bunches with a charge greater than 1.5 nC and a bunch length shorter than 1 ps to maintain low energy spread in the subsequent linac sections for direct and efficient injection into the collider electron ring. Therefore, a global optimization of the parameters for the low-energy section is necessary.
The electron beam properties are mainly influenced by the following four components:
1. Accelerating structures provide energy gain and longitudinal focusing.
2. Focusing elements (e.g., solenoids) compensate for transverse emittance and provide transverse focusing to confine the beam size.
3. Laser profile on the photocathode. The transverse and longitudinal distributions of the drive laser affect space charge forces and nonlinearities.
4. Photocathode material. Its thermal emittance directly impacts the beam brightness.
Given the complex interplay among these parameters and the spatial constraints of the injector, manual tuning or scan-based optimization is inefficient. Instead, multi-objective optimization algorithms, such as genetic algorithms, are employed and integrated with ASTRA beam dynamics simulations. Realistic 3D electromagnetic field maps of the components are used in the simulations to accurately represent their performance.
The optimization targets the bunch length and transverse emittance at the exit of the second S-band linac section. Three types of laser profiles are considered (see Table 16).
| Case | Transverse laser profile | Longitudinal laser profile |
|---|---|---|
| Case 1 | Truncated Gaussian | Gaussian |
| Case 2 | Truncated Gaussian | Flat-top |
| Case 3 | Uniform | Flat-top |
Charge values of 1, 1.5, and 2 nC are studied. The results show that the transverse beam quality is relatively insensitive to the transverse laser shape; therefore, a truncated Gaussian profile is used to minimize energy losses associated with laser shaping. In contrast, a flat-top longitudinal laser profile significantly improves the emittance. Consequently, a flat-top longitudinal and truncated Gaussian transverse laser profile is selected. Based on the optimization results and spatial constraints, the entrance to the first accelerating structure is positioned 1.5 m from the cathode, the second structure at 5.02 m, and the center of the second solenoid at 2.0 m.
Simulation results at the exit of the two S-band sections, including the phase space, current, and energy spectrum, are shown in Fig. 67.
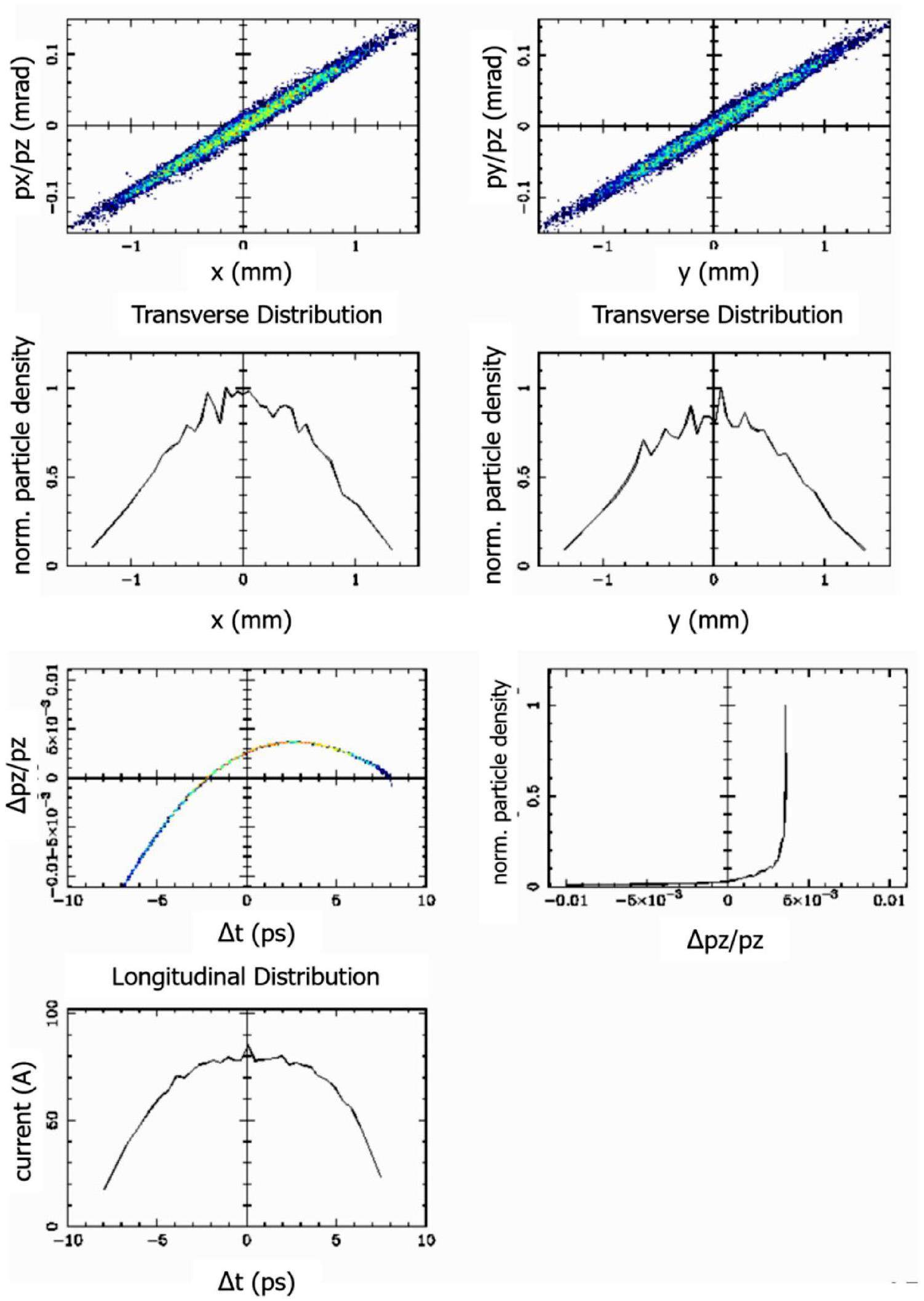
In the L2 section, the RF phase is before the peak, which induces an energy chirp. The third and fourth S-band structures generate the chirp, while an X-band linearizer and a chicane (providing negative R56) compress the bunch length to ≈1 ps at ≈200 MeV. At this point, both emittance and energy spread are optimized (<0.1%). With this setup, normalized emittance at 1.5 nC remains below 2 mm·mrad for all studied laser distributions. Figure 68 shows the final transverse and longitudinal beam distributions.
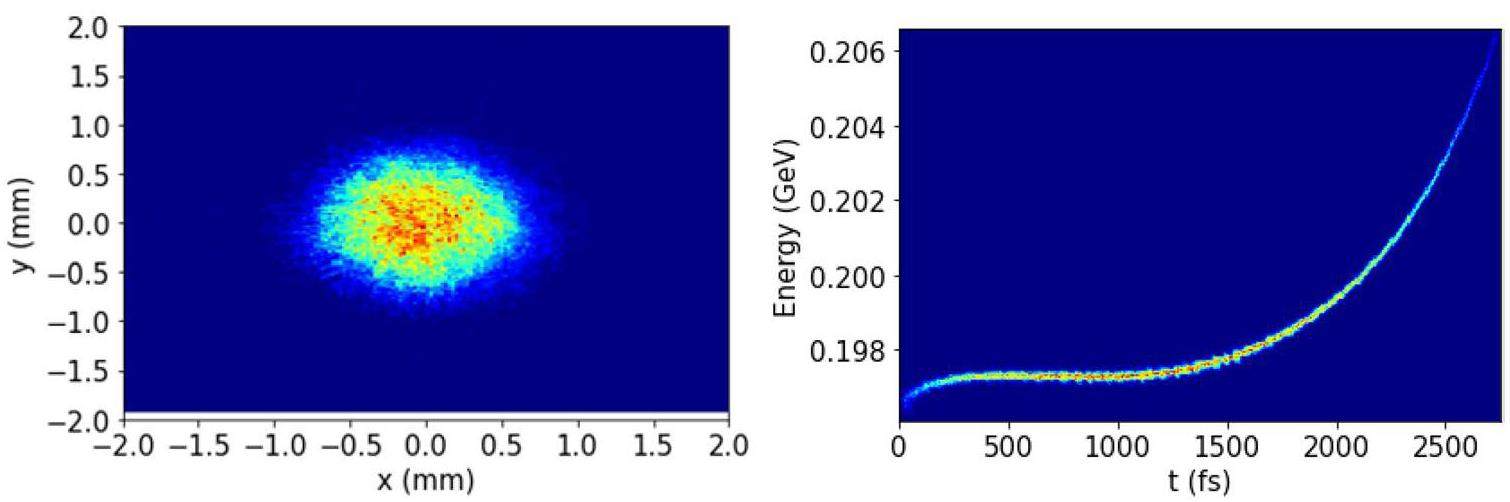
Thermionic cathode low-energy section
Bunching Section
The BS primarily consists of an electron gun and a bunching system. The section primarily longitudinally compresses the low-energy electron beam from the gun to achieve a short bunch length (5–10 ps). This bunch length is achieved while maintaining an appropriate capture efficiency, adequate transverse phase space, and high-quality emittance to satisfy the requirements for further acceleration in the linac’s high-energy section. To deliver a high-charge, high-energy electron beam for tungsten-based positron generation, we employ a thermionic cathode electron gun that can produce a bunch with a full width at half maximum (FWHM) greater than 1 ns. Considering capture losses, the total charge at the source should exceed 11 nC. The bunching system is immediately downstream from the electron gun. It has two SHBs, one S-band fundamental buncher, and an S-band that accelerates traveling waves, as shown in Fig. 69.
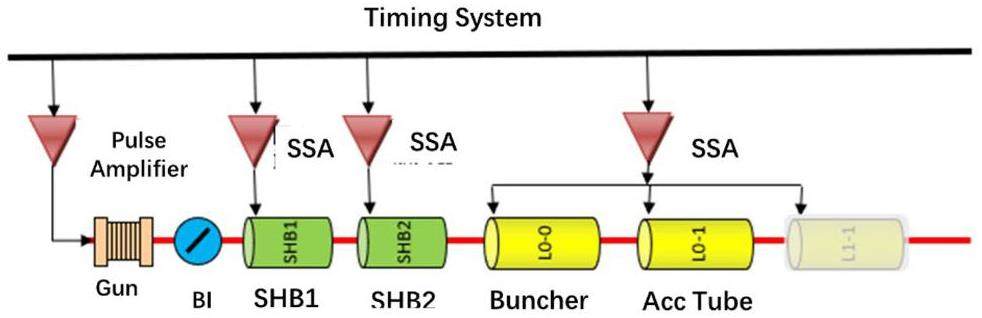
The two SHBs and one S-band fundamental buncher, downstream of the gun, longitudinally modulate the velocity of the non-relativistic electron beam and compress its bunch length, enabling effective injection into the ML. A 1.3 ns FWHM beam from the gun is compressed to approximately 10 ps FWHM after passing through this bunching system.
After bunching, the 10 ps beam is injected into the accelerating structure L0-1 and further accelerated to 65 MeV, which is sufficient for subsequent acceleration to 1.5 GeV in the ML for tungsten-target positron production. The fundamental buncher and accelerator L0-1 share a klystron power source, while the two SHBs are powered by independent solid-state amplifiers.
The beam dynamics of the BS are critical to overall accelerator performance. Simulations were performed using the well-established Parmela code. A commercial Y-796 cathode-grid assembly with a maximum emission current of 12 A paired with a 1.6 ns amplifier is used. The grid operates at 7 A, leaving a margin for changes in current. Figure 70 shows the initial phase space distribution of the thermionic electron beam used in the simulation.
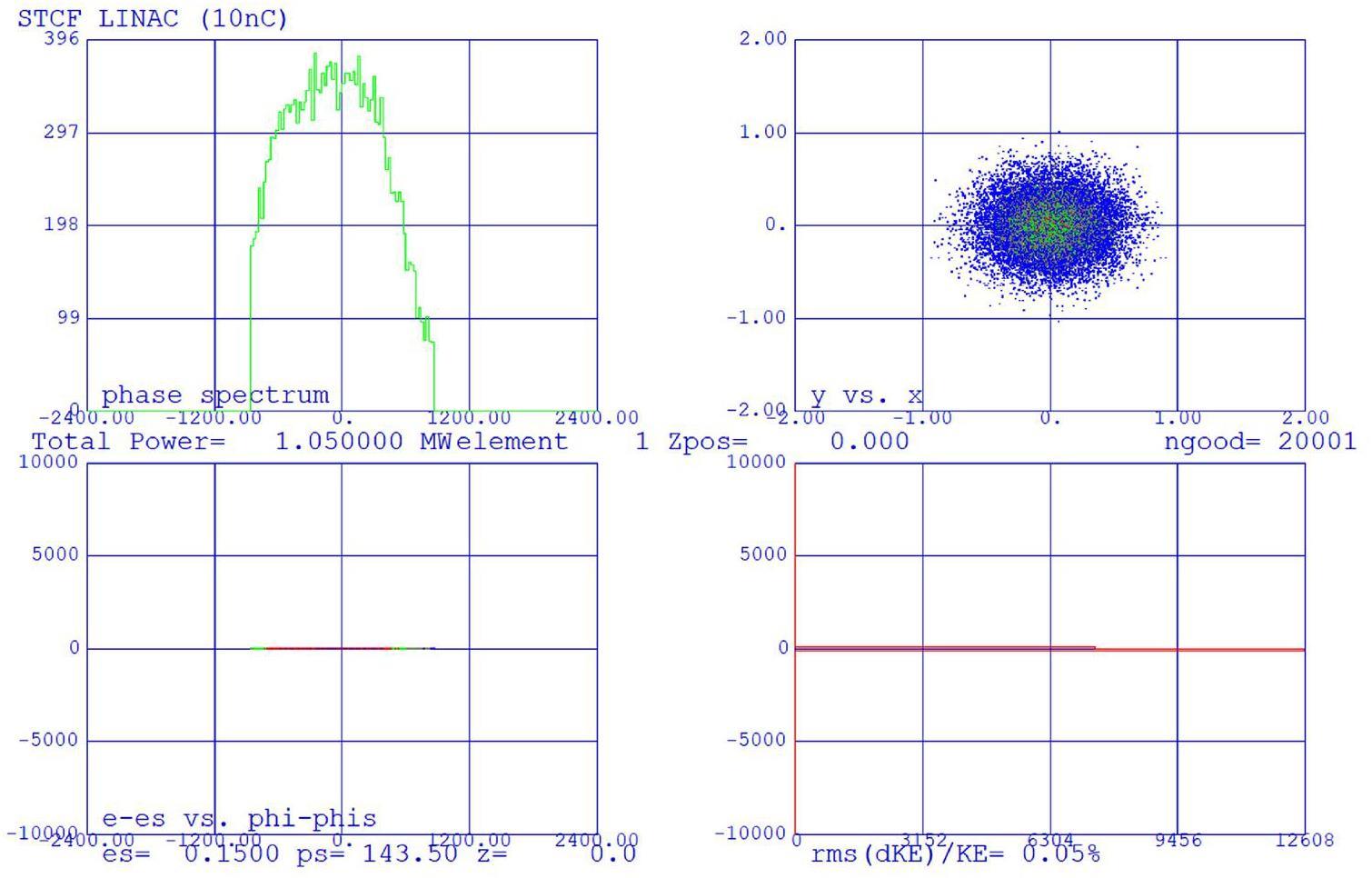
After extensive optimization, especially tuning the cavity voltages, phases, and drift distances of the SHBs and the cavity length and voltage of the fundamental buncher, key beam parameters such as transverse and longitudinal envelopes along the beamline were obtained, as shown in Fig. 71. The beam is well-focused both transversely and longitudinally, and a capture efficiency of 99.8% is achieved.
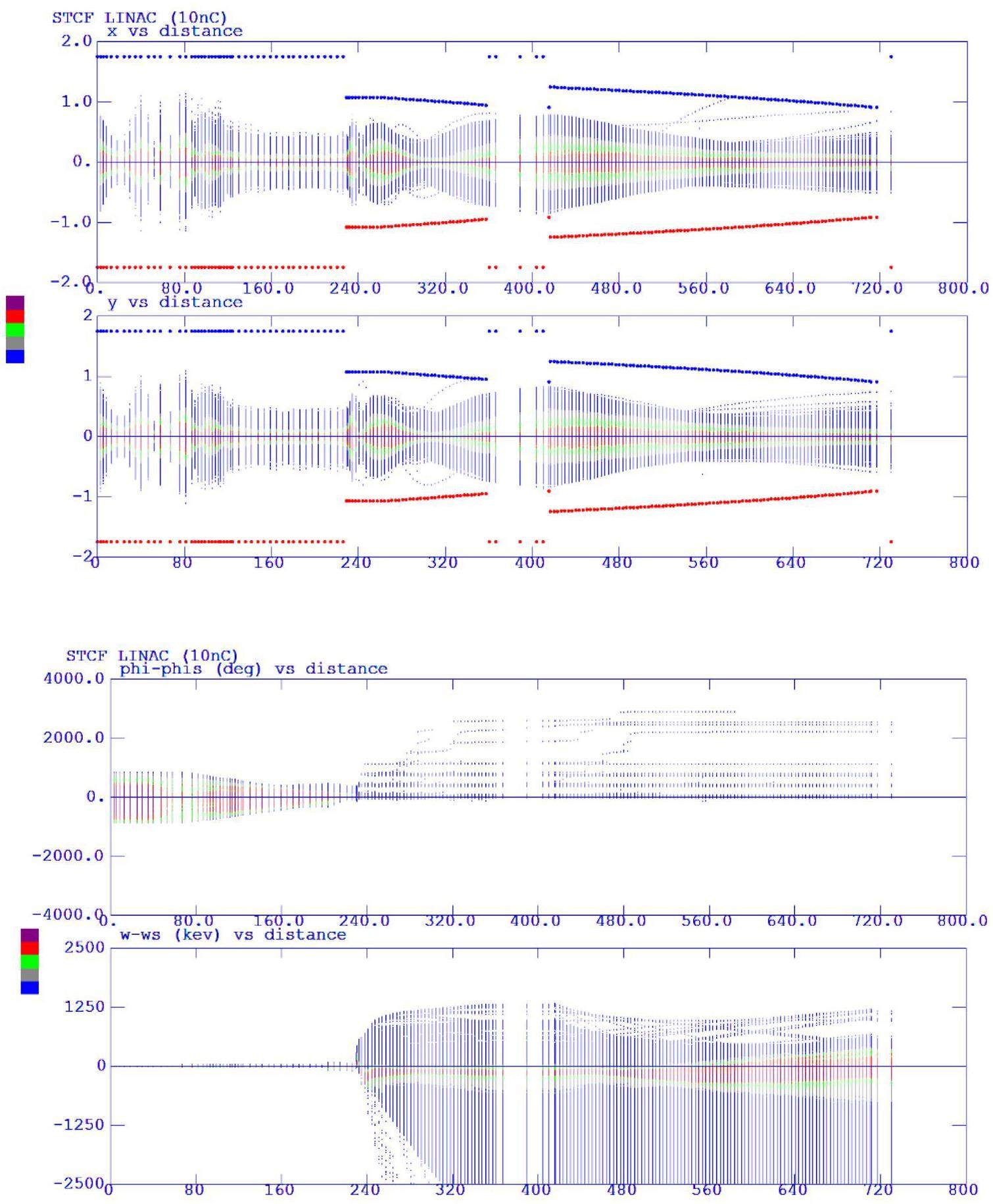
The evolutions of normalized emittance and phase space distribution at the exit of the BS are shown in Fig. 72. The normalized rms emittance is approximately 50 μm·rad. After the main bunch, there are approximately 5 to 6 satellite bunches; however, their particle count is only approximately 0.2% of the total. The main bunch has a charge of approximately 10.9 nC, which meets the target impact requirement of > 10 nC, as illustrated in Fig. 65.
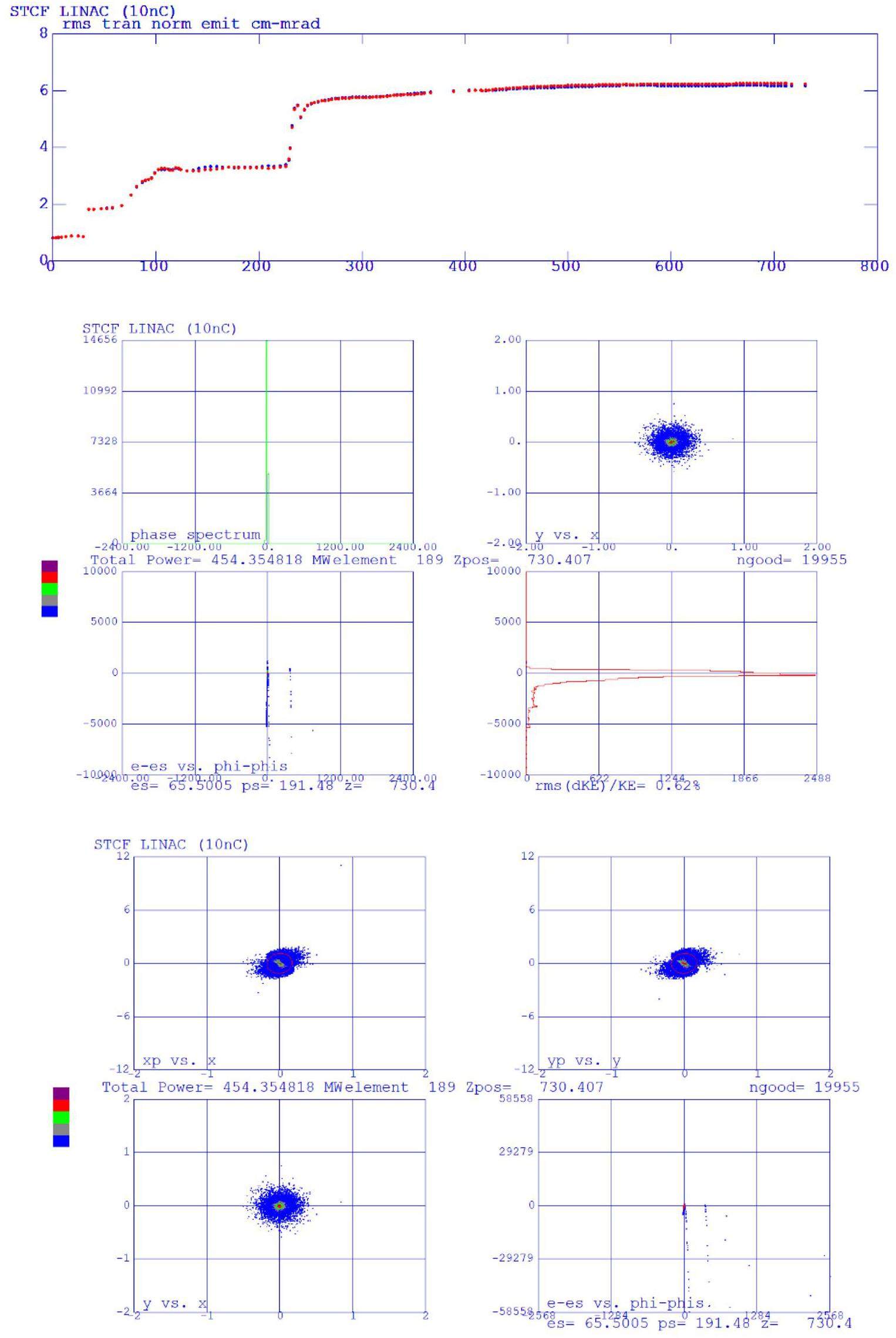
In the BS, solenoids and short magnetic lenses are effectively used for transverse beam confinement. This ensures good transverse parameters, such as envelope size and transmission efficiency, while preserving longitudinal compression. The magnetic field distribution of the BS is shown in Fig. 73.
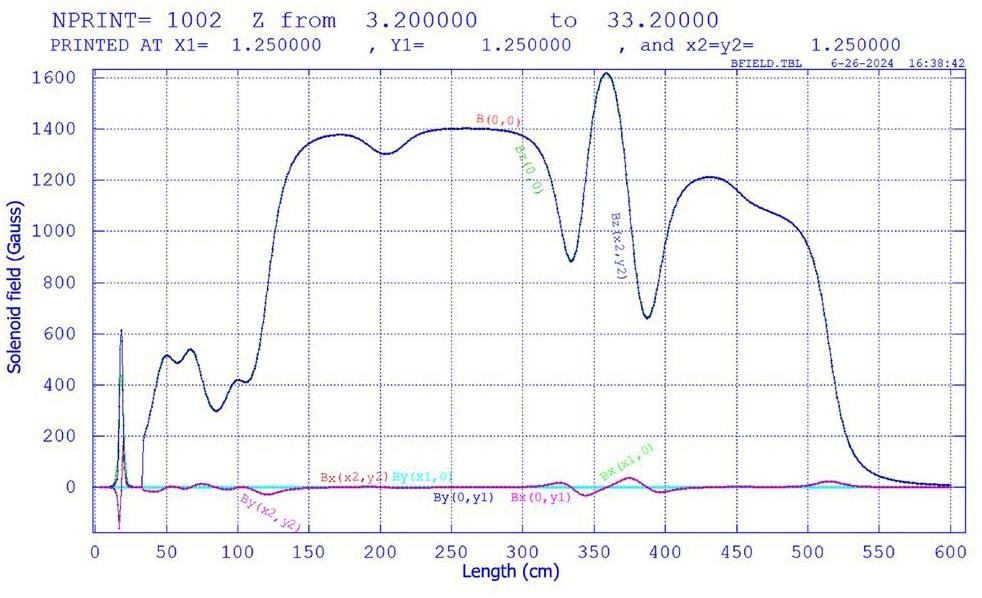
Pre-injector Section
As shown in Fig. 65, to allow the 10 nC thermionic cathode electron bunch to use the same linac section (EL1) as the 1.5 nC bunch produced by the PC source and preserve the beam quality of both modes, the thermionic beam must first be accelerated to 220 MeV. The PIS consists of a BS, three 50 MeV accelerating structures, and two sets of triplet lenses, as illustrated at the top of Fig. 74.
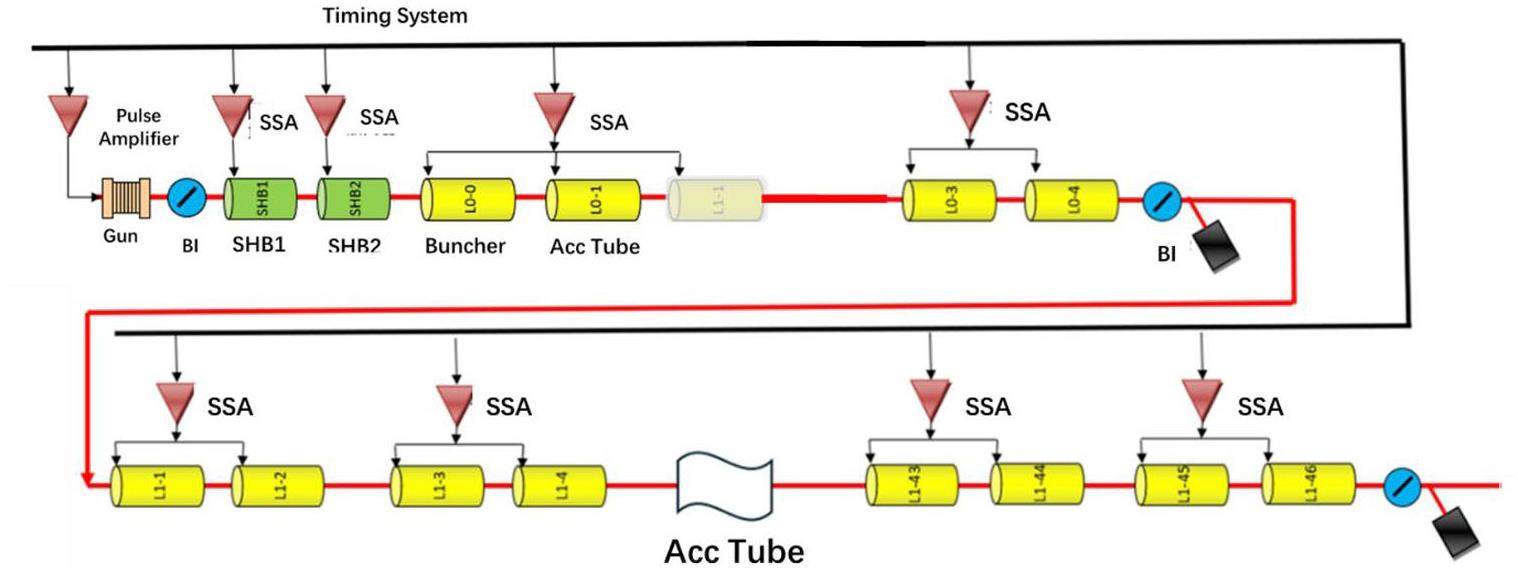
The fundamental buncher L0-0 and accelerating structures L0-1 and L0-2 share a single RF power source, while L0-3 and L0-4 are powered by another source. Two triplet lens assemblies are placed between L0-2/L0-3 and after L0-4 for transverse beam focusing.
Using the output distribution from L0-1 (shown in Fig. 72) as the input, we optimized the phases of L0-2, L0-3, and L0-4, as well as the two triplets. The resulting transverse and longitudinal envelopes along the beamline are shown in Fig. 75, indicating excellent transverse and longitudinal confinement.
The evolution of the normalized emittance, phase space at the pre-injector exit, and energy gain curve are shown in Fig. 76. The normalized rms emittance and phase space are well controlled, satisfying the requirements for merging with the photocathode beam and further acceleration.
Electron linacs EL1 and EL2
High-charge electron beams for positron production and high-quality electron beams for direct injection into the collider electron ring are both pre-accelerated through two separate low-energy sections and then merged in EL1, where they are accelerated to 1 GeV.
Key Design Considerations for the Merger Section
The layout of the merger section for the dual-electron-gun system in the STCF linac is shown in Fig. 77. Considering the low charge and low emittance characteristics of the photocathode electron beam, deflecting the photocathode beam into the ML is preferred. This arrangement minimizes the impact of dispersion from dipole magnets on beam quality and facilitates beam optics design. The design goal of the merger section is to align the beam center of the photocathode electron beam with that of the thermionic beam while preserving the former’s beam quality.
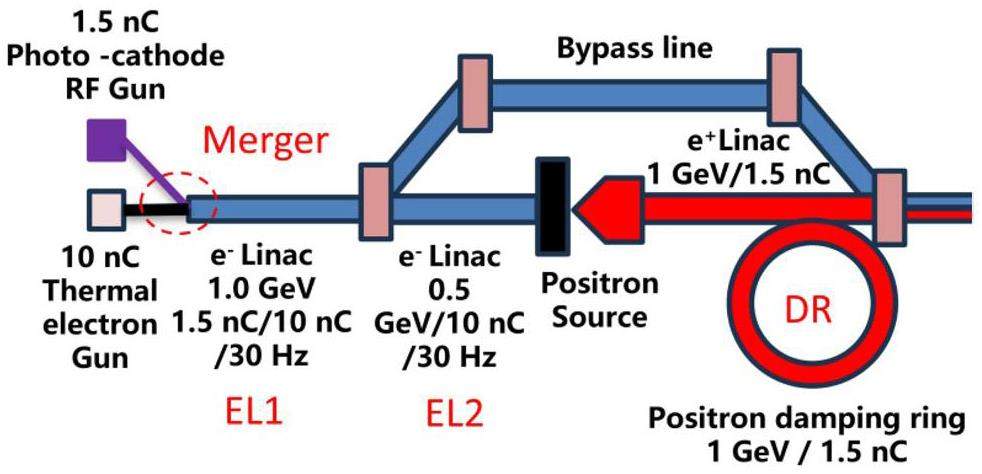
In our design, the photocathode and thermionic cathode electron guns are on the same horizontal plane. Hence, we implement horizontal-plane deflection for the PC beam. The merger section adopts a dogleg structure, consisting of two dipole magnets with identical parameters that deflect beams in opposite directions. This arrangement ensures that the beam propagates in the same direction before and after the dogleg while achieving lateral displacement to merge with the thermionic beam.
In practical terms, the PC beam must undergo bunch compression during transport to reduce energy spread. However, this compression introduces significant energy chirp/spread (1% rms, 6% peak-to-peak). When passing through dipole magnets, the horizontal emittance induced by this dispersion can increase by up to two orders of magnitude, severely degrading beam quality. Thus, the main challenge in merger beam optics design is not only to eliminate first-order dispersion but also to suppress higher-order dispersion terms, particularly the T_166 and T_266 matrix elements. Given space constraints, we fix the dipole length to 0.2 m and set the deflection angle to approximately 21.5°, resulting in a total merger length of approximately 7 m. The dogleg layout is shown in Fig. 78.
We used the beam tracking code Elegant [60] for optimization. Quadrupole magnets were employed to match the first-order dispersion and transverse Twiss functions. To minimize higher-order dispersion, sextupoles were inserted. Inspired by the Elettra approach [61], sextupole windings were added to the quadrupoles to provide additional sextupole components, further optimizing the emittance. The optimization results show that reducing both first- and second-order dispersion below 0.01 effectively restores emittance to the desired level.
To reflect realistic conditions, the beam charge was set to 1.5 nC in the simulation. Effects including SC, CSR in dipoles, and incoherent synchrotron radiation (ISR) at dipole edges were considered. Beam parameter optimization was performed using Simplex and second-generation genetic algorithms (NSGA2), with magnet parameters as variables. First, dispersion terms were minimized, followed by optimization of transverse Twiss parameters and emittance (Figs. 79, 80, 81, 82, 83).
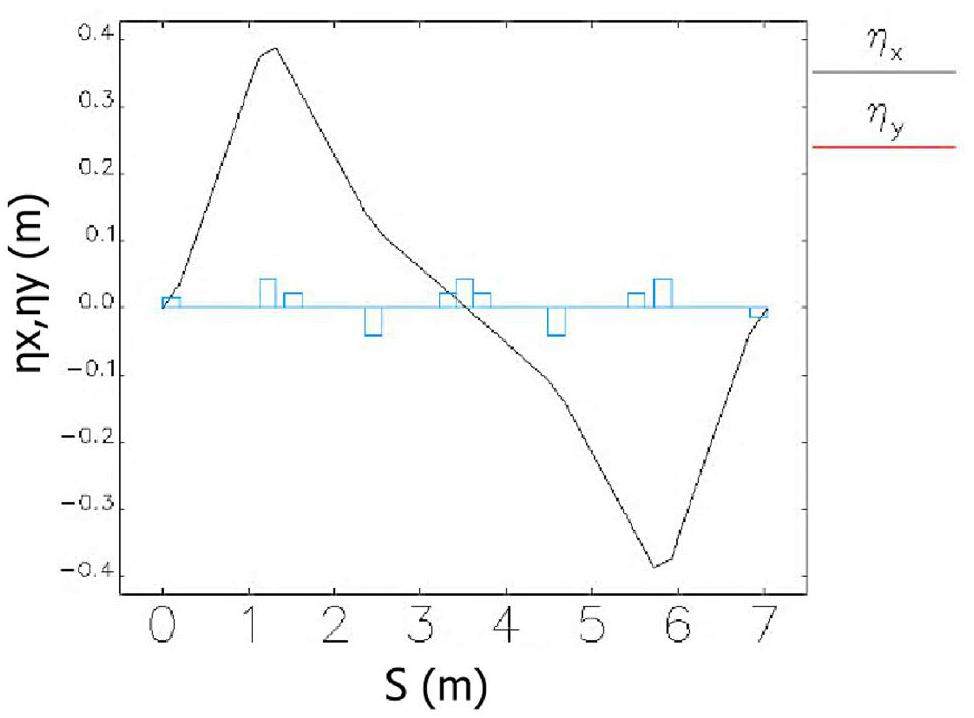
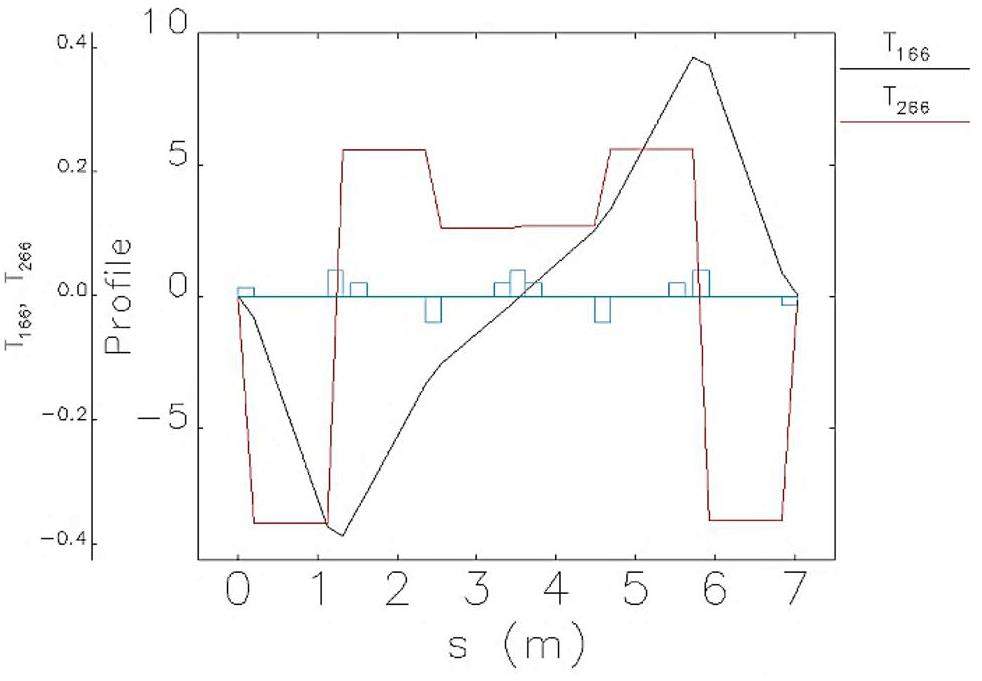
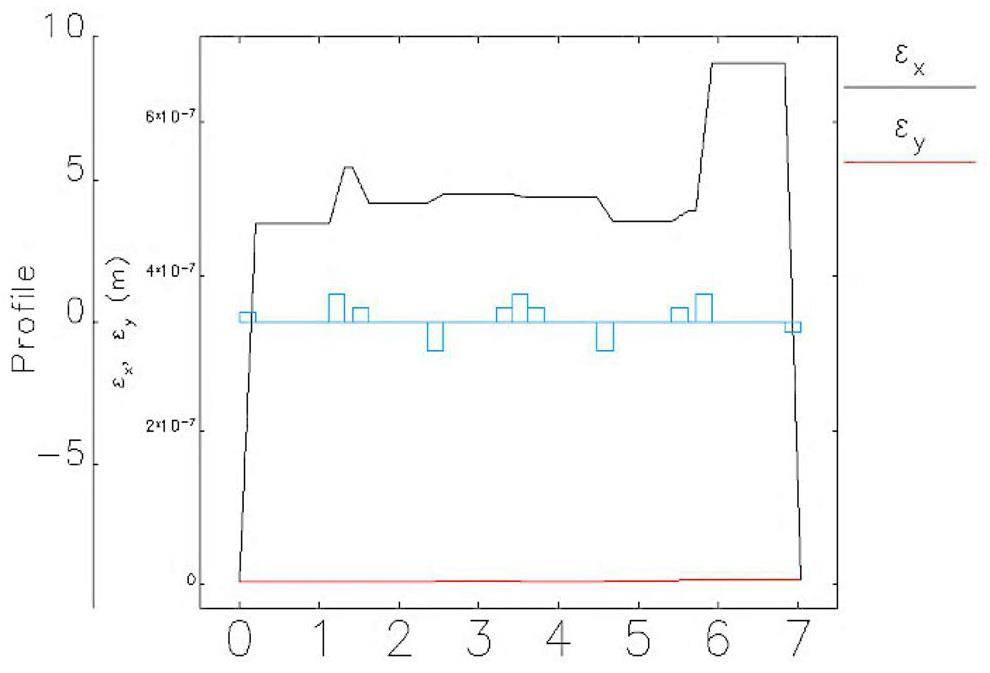
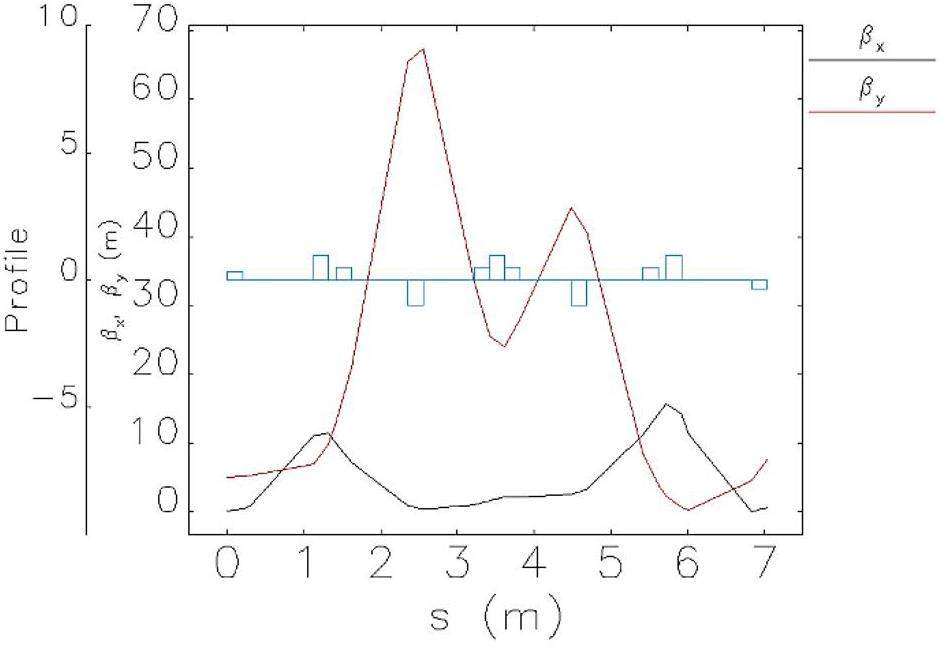
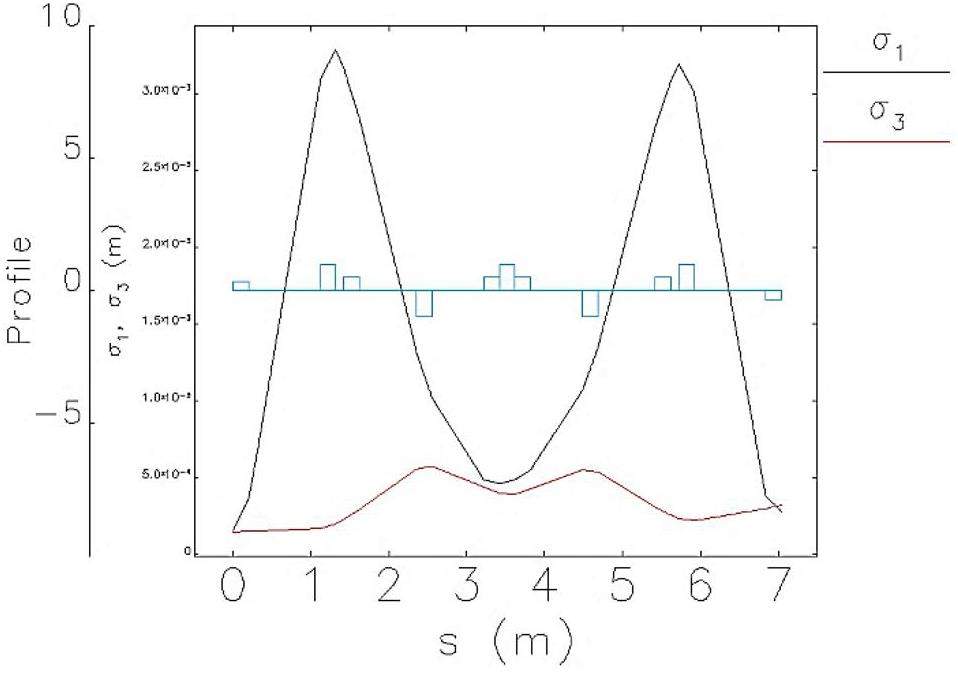
In conclusion, through the custom-designed dogleg, we successfully merged beams from the dual electron guns while restoring the horizontal emittance of the PC beam, even under significant energy spread, thus maintaining beam quality. The merged beams share the same beam center and can use the same ML, optimizing cost and equipment usage.
Key Design Considerations for EL1 and EL2
The 1.5 nC beam from the PC is directly injected into the collider electron ring via the bypass after acceleration in EL1. Therefore, the beam quality requirements for this beam are more stringent than for the 10 nC beam that is further accelerated in EL2 for positron production. Hence, EL1’s lattice is optimized for the 1.5 nC beam. The performance of the 10 nC beam in EL1 and EL2 was also simulated, with the resulting transverse and longitudinal envelopes, normalized emittance evolution, and phase space at the linac exit shown in Fig. 84.
The plots show that the transverse rms beam size at the linac exit is approximately 0.5 mm, the emittance is approximately 50 μm·rad, the energy reaches 1540 MeV, the transmission efficiency is 99.8%, the beam charge is 10.9 nC, and the rms energy spread is 1.87%. These parameters meet the requirements for tungsten target positron production.
The EL2 section differs slightly in design. A triplet magnet is placed for every four 50 MeV accelerating structures (i.e., after every 200 MeV energy increment). The total length of the thermionic cathode linac is approximately 110 m.
Positron production, capture, and pre-acceleration
As a high-luminosity electron–positron collider, the STCF requires a high-performance positron source capable of generating positron bunches with sufficient quantity and quality. This source is one of the core components of the STCF injector. The positron source of the STCF adopts the conventional method of positron production via electron beam bombardment of a high-Z target—currently the only viable approach for generating high-intensity positron beams.
The STCF design is currently considering both off-axis and bunch-swap injection schemes for the collider rings. The off-axis injection scheme requires a relatively low positron bunch charge and uses a lower primary electron energy of 1.5 GeV. This necessitates optimizing the subsequent capture and matching acceleration systems to ensure high positron yield from low-energy electron beams. In contrast, the swap-out injection scheme imposes significantly higher requirements on the positron yield and heat dissipation capacity of the target owing to the need for high-charge positron bunches (Table 17).
| No. | Parameter | Off-axis injection | Swap-out injection |
|---|---|---|---|
| 1 | Injected positron charge | 1.5 nC/30 Hz | 2.9 nC/90 Hz |
| 2 | Incident electron beam | 1.5 GeV/10 nC/30 Hz | 2.9 GeV/11.6 nC/90 Hz |
| 3 | Injection energy | 1.0 GeV | 1.0 GeV |
| 4 | Damping ring entry emittance | ≤1400 nm·rad | ≤1400 nm·rad |
To develop a high-quality, high-current positron source that meets the STCF requirements, two sets of target-converter systems, which are based on the two electron beam injection schemes, must be carefully designed and optimized. These include the positron conversion target, the adiabatic matching system (AMS), and the capture accelerating structure, which must be engineered to improve positron yield and meet the needs of both injection schemes.
Positron conversion target
The positron production process by electron beam bombardment is typically simulated using Monte Carlo codes such as EGS4, MCNP, FLUKA, or Geant4. These simulations determine the energy spread and angular distribution of positrons emerging from the high-Z target, providing input for the design of the downstream capture and matching systems. Figure 85 shows simulation results obtained using Geant4. It is worth noting that simulations performed using different codes often yield discrepancies in the positron angular and energy distributions, sometimes up to 10–20%. Since these results directly affect the design of the capture and matching systems, improving simulation precision and accuracy is crucial for the future development of positron sources for e+e- colliders.

The emittance of the electron beam and its spot size on the target significantly influence the distribution and angular spread of positrons produced after the target. Smaller spot sizes generally lead to higher positron collection efficiency; however, excessively small spot sizes may cause thermal damage to the target. For the STCF, the electron beam spot size is required to be ≤1 mm. In addition, the beam offset on the target affects the positron yield. Figure 86 illustrates this effect for a 1.5 GeV electron beam, with similar results observed for a 2.5 GeV beam. This necessitates a beam offset of less than 1 mm for the primary electron beam.
For the off-axis injection scheme, the positron source must deliver 1.5 nC at 30 Hz. Figure 87 presents the simulated positron yield for a 1.5 GeV electron beam with a 1 mm rms spot size incident on conversion targets of different thicknesses and materials. Gold and tungsten provide the highest positron yields. Considering cost-effectiveness, tungsten is selected as the target material. The optimal tungsten thickness is 13 mm, resulting in a positron production efficiency of approximately 4.1 positrons per incident electron.
Figure 88 presents the energy and angular distributions of positrons produced by 1.5 GeV electron beams with and without a 5% energy spread. The results indicate that a 5% energy spread has an acceptable effect on the resulting positron characteristics.
Positron accelerator PL design
The positron beam produced by electron bombardment of a target exhibits a wide energy spectrum and large divergence angles. To match it with the downstream accelerating structures, the positrons must be captured and converted into a beam with smaller divergence and larger transverse size. The conventional solution employs an adiabatic matching device (AMD) within an AMS, where the magnetic field gradually decreases along the longitudinal axis as Bz=B0/(1+az). During transport through the AMD, the transverse phase-space volume of the beam is conserved, enabling a transformation from small transverse size and large divergence to large transverse size and small divergence. After passing through the AMS, the positron energy spectrum remains broad and is dominated by low-energy positrons.
Because the positron energy spectrum contains a large fraction of low-energy particles (1–20 MeV), a specialized accelerating structure is required for effective capture. In the AMD, positrons follow helical trajectories due to the longitudinally varying magnetic field: low-energy positrons spiral outward, while high-energy positrons spiral inward. As they exit the AMD, the positron bunch both lengthens and widens. Therefore, the first accelerating structure must compress the positron bunch, increase its energy, and provide longitudinal phase-space matching. By choosing appropriate RF phases, a greater fraction of positrons can be efficiently accelerated.
To increase transverse acceptance and improve positron capture efficiency, larger-aperture accelerating structures are needed. However, placing large-aperture L-band accelerators within focusing solenoids would significantly increase cost. As a cost-effective alternative, the STCF design adopts S-band large-aperture (30 mm) accelerating structures with optimized RF phase settings for enhanced capture and acceleration. The initial stage comprises six specialized accelerating structures that boost the positron energy to 200 MeV. This stage is critical for determining the positron beam’s intensity, emittance, and energy spread, all of which strongly influence the designs of the DR, ML, and injection system.
Adiabatic Matching Device (AMD)
The strength and profile of the AMD magnetic field are determined by the energy spread and angular distribution of positrons emerging from the target. Optimizing the AMD is critical for improving positron capture. Figure 89 shows the STCF AMD design on the electron–positron verification platform, where a 5 µs, 15 kA pulsed current is applied through 13 coils to generate the field.
Owing to the large angular and momentum spread of positrons from the target, most would be lost without strong focusing. The capture system must have high acceptance. As positron beams have a small size but large divergence, while downstream accelerating structures allow larger sizes and smaller divergence, the AMD must perform the beam transformation shown in Fig. 90, enabling proper matching. Figure 91 shows angular variation after AMD; Figure 92 shows the energy spread and transverse beam size.
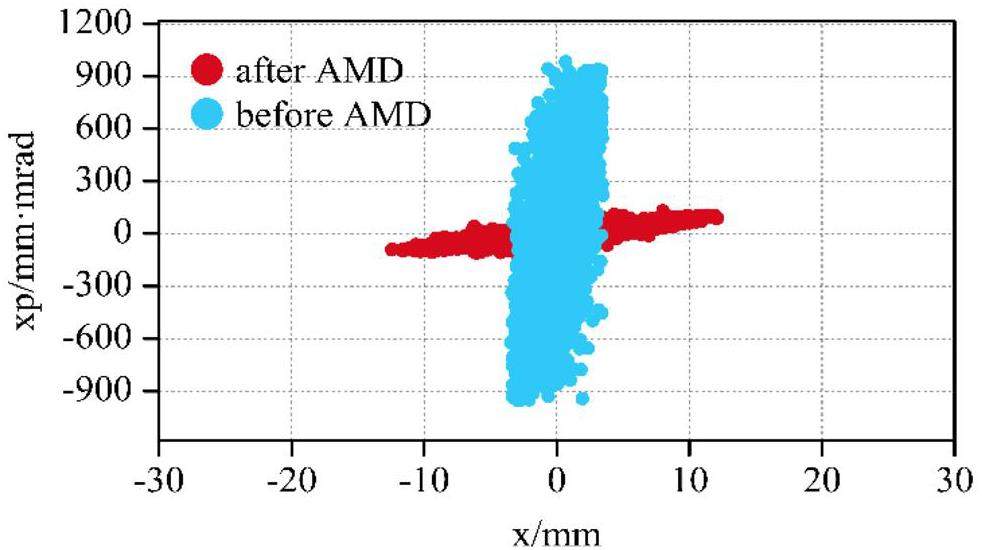
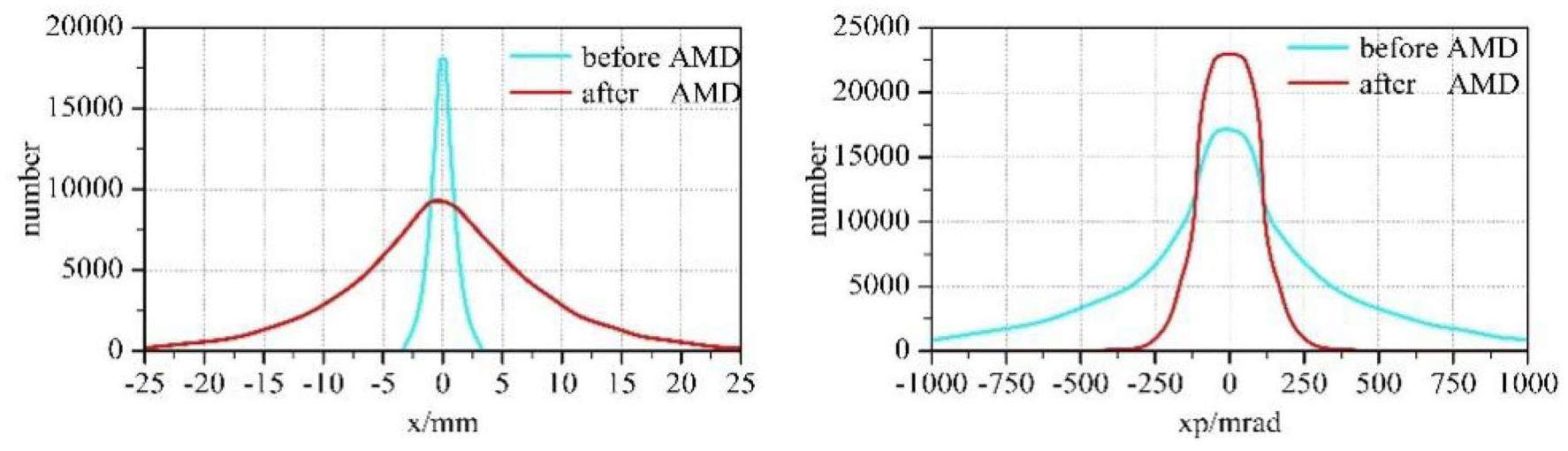
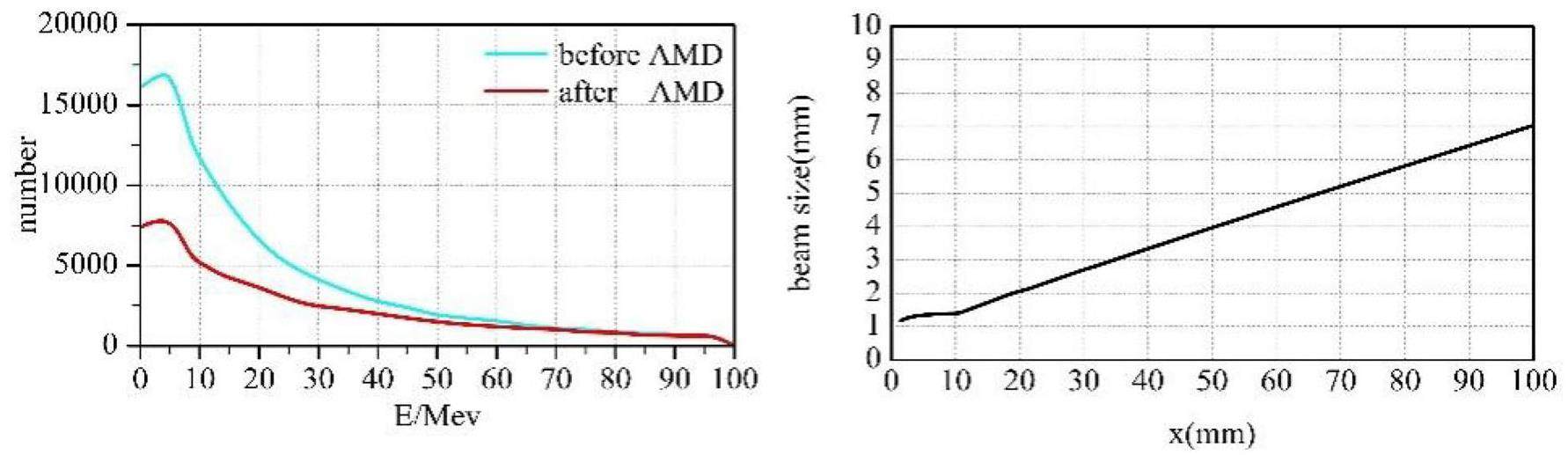
200 MeV Pre-Acceleration Section
Figure 93 illustrates the PAS-Pre section. Its structure includes the conversion target system, AMD, two 2 m large-aperture capture cavities, four 3 m capture cavities, solenoids for external focusing, a triplet lens for matching, and a chicane for momentum collimation. Geant4 simulations provide the energy and spatial distributions of 1.5 GeV positrons, which are captured in the AMD and two 2 m S-band accelerating sections. RF phase scans for these two sections yield the optimal phases of 20° and –40°, maximizing positron yield (see Figure 94). A final 3 m accelerating cavity boosts positrons to 200 MeV. Figure 95 shows particle tracking at this energy.

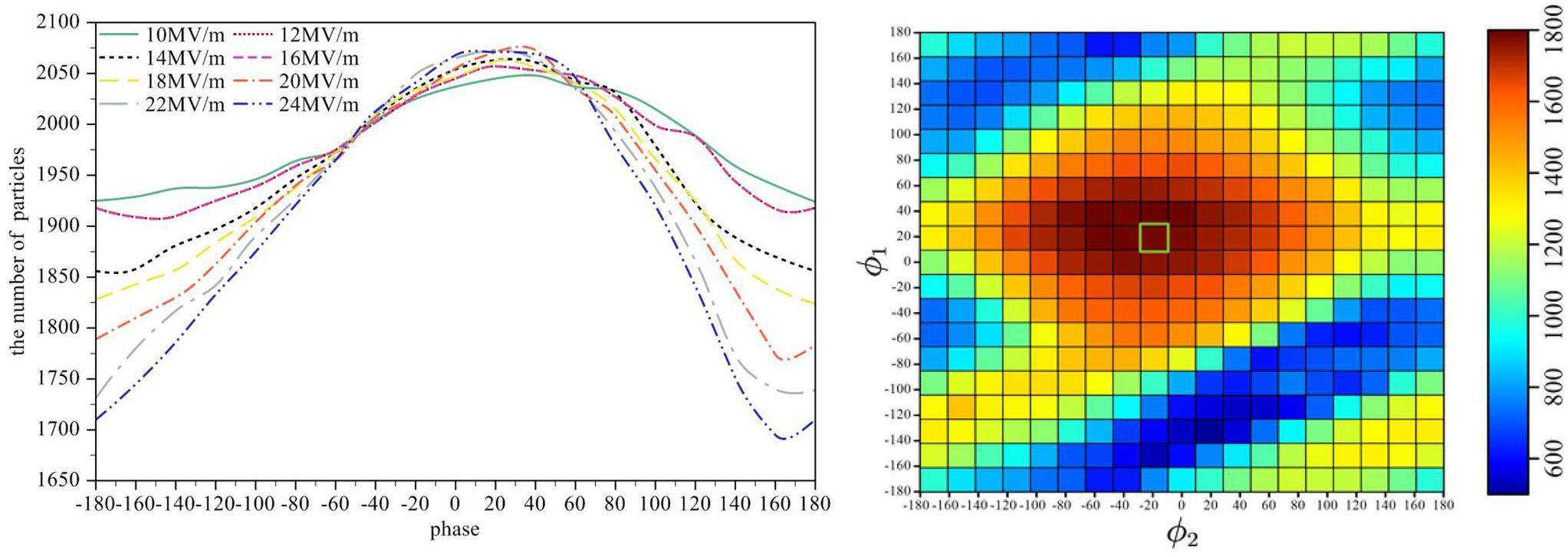
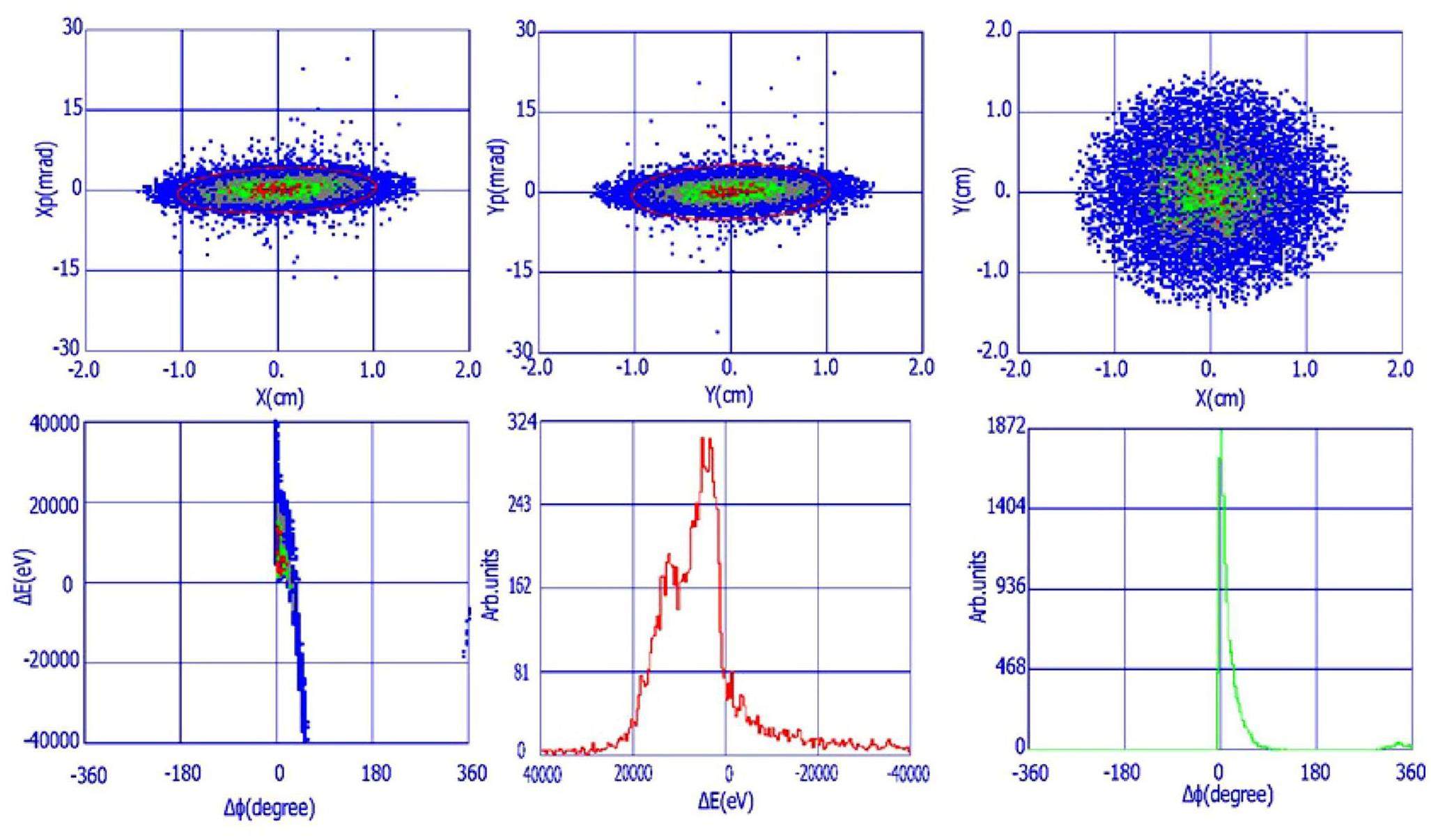
After optimization, the overall positron yield reaches 52.7% with an rms energy spread of 5.44%. Figure 96 shows the evolution of beam spot size, bunch length, and energy spread. Figure 97 presents the transverse and longitudinal dimensions. The main positron bunch is approximately 60 ps long and contains ≈90% of the particles.
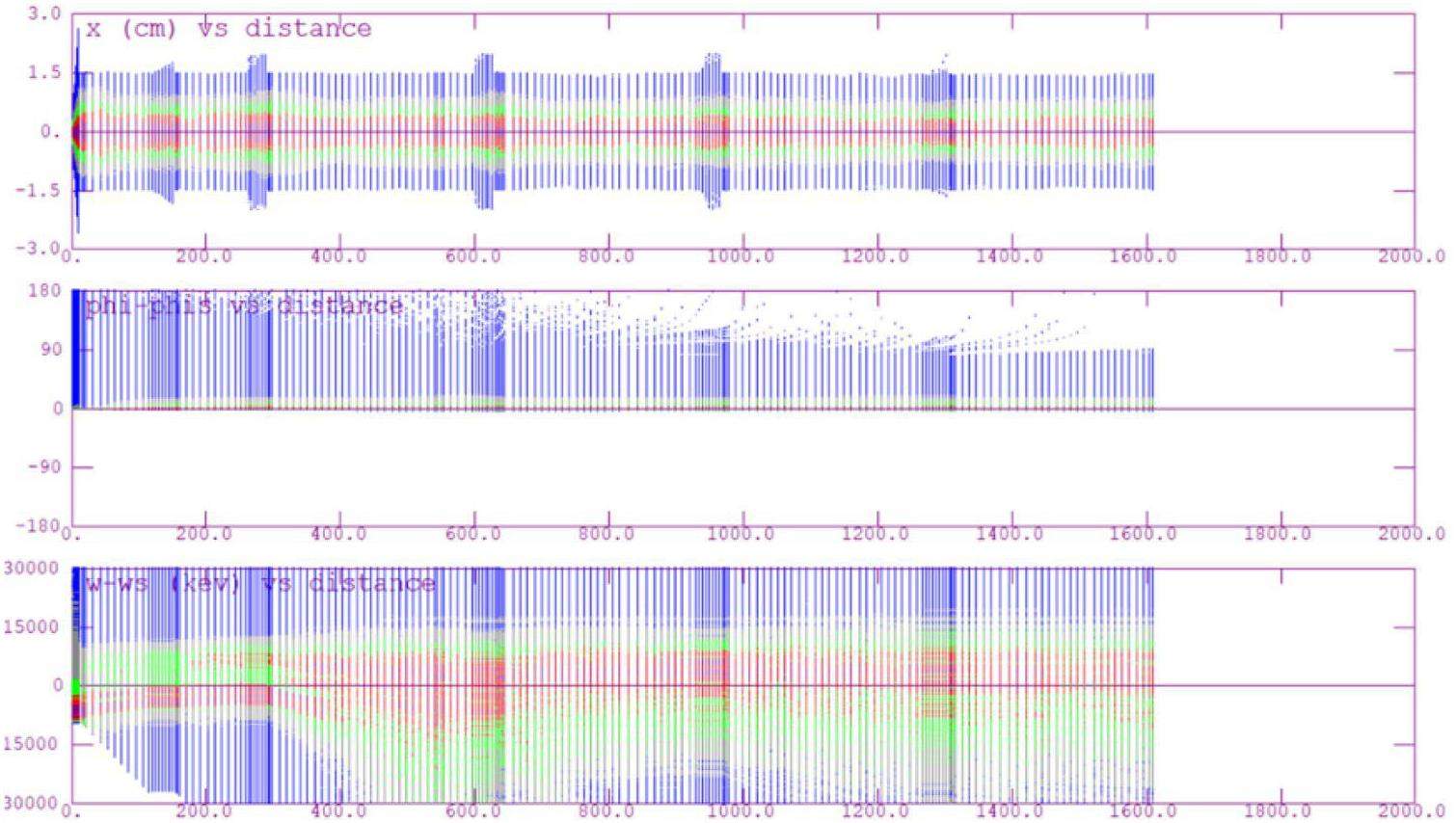
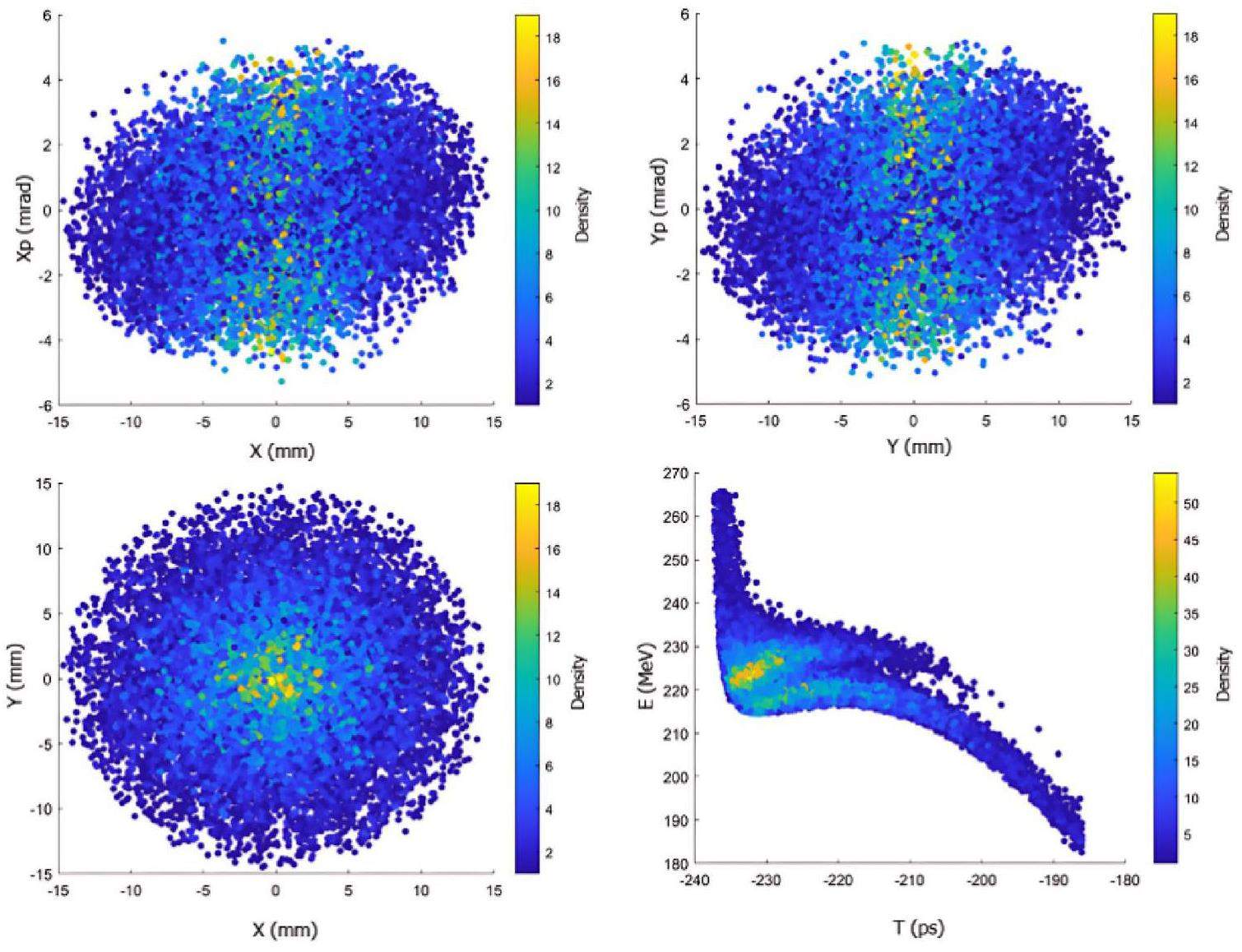
Magnetic Compression Design
Most high-energy electrons pass through the target and accompany positrons through the accelerator. To separate electrons from positrons, a chicane is introduced, which also compresses the positron bunch. The layout is shown in Fig. 98, with an 8° bend angle and 27.83 mm offset, yielding
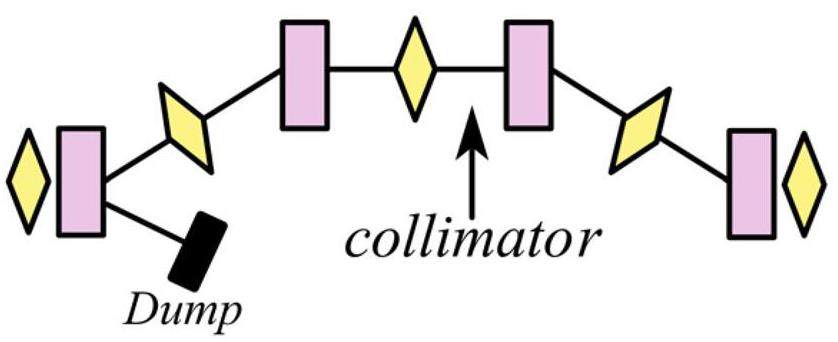
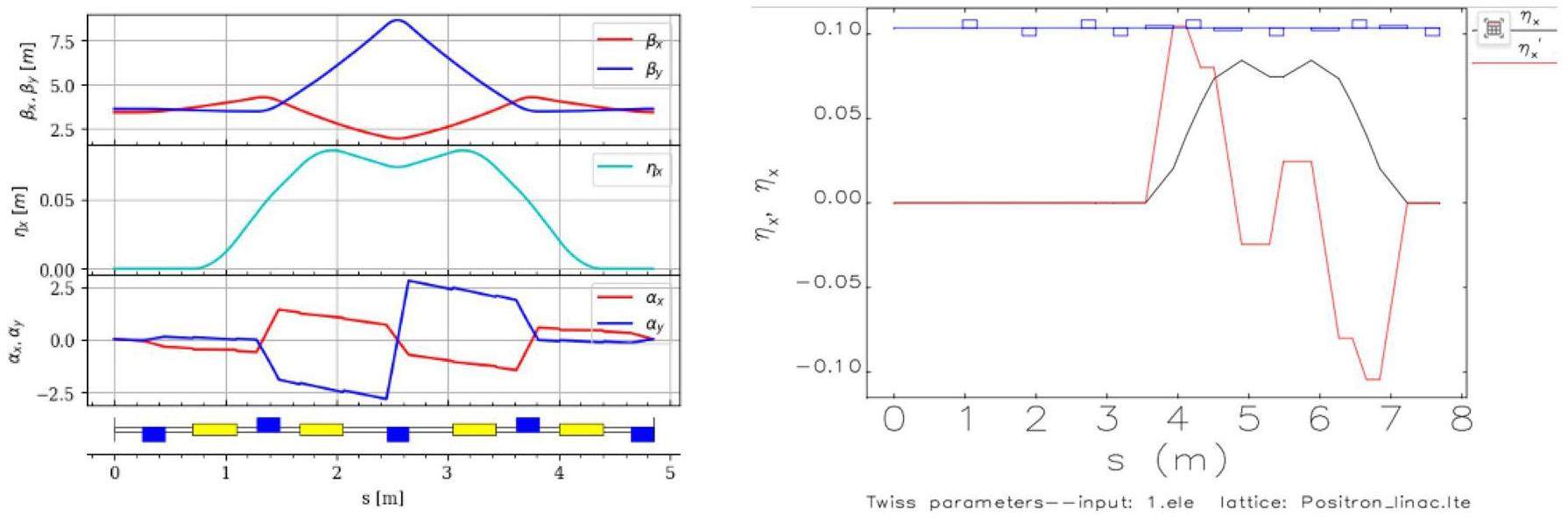
To match the positron beam with the DR, a horizontal collimator is placed at the chicane center to remove poor-quality positrons. For off-axis injection, the aperture is 10 mm. Figure 100 shows the filtering effect, reducing energy spread from 4.14% to 3.18%.
200 MeV to 1 GeV Positron Acceleration
After initial capture and acceleration to 200 MeV, positrons are separated from electrons via the chicane. Acceleration from 200 MeV to 1 GeV uses a triplet-focusing structure (see Fig. 101). Acceleration from 200 to 600 MeV uses 30 mm aperture S-band structures at 19 MeV/m. Acceleration from 600 MeV to 1 GeV uses 20 mm aperture structures at 23 MeV/m.
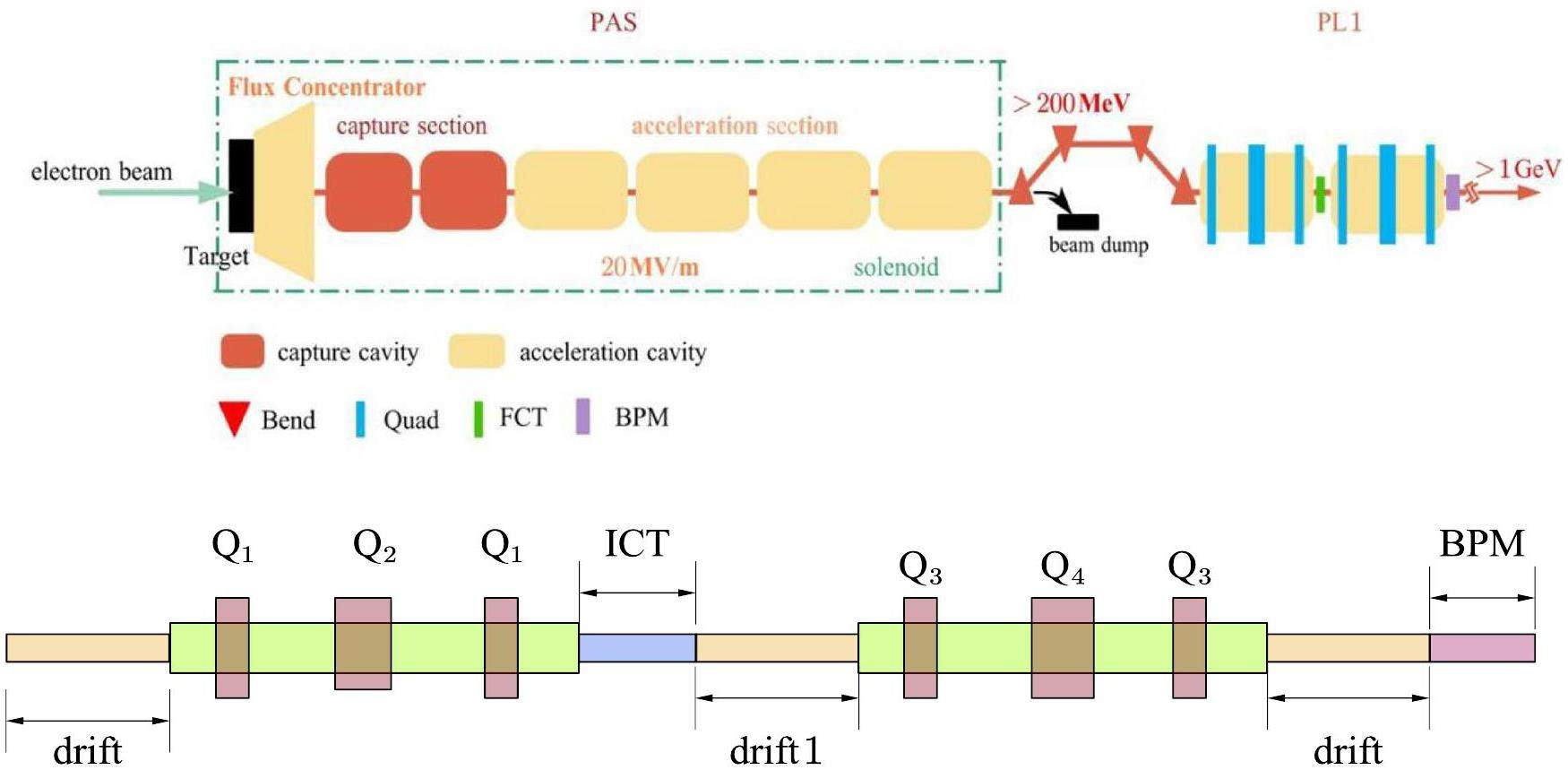
Figures 102 and 103 show the Twiss parameters and particle tracking results for the PAS section under off-axis injection. At 1 GeV, the rms energy spread is 0.77%, the positron yield is 0.153 (i.e., 1.53 nC per pulse), the rms bunch length is 5.62 ps, and the geometric emittances are
Positron damping ring
Design requirements
In the STCF off-axis injection scheme, the injector incorporates a 1.0 GeV positron DR, which reduces the emittance of positron bunches—produced through electron beam interactions with a target—via synchrotron radiation damping, bringing them to levels suitable for injection into the collider positron ring.
The layout of the DR system is shown in Fig. 104. It primarily consists of the injection and extraction beamlines and a circular synchrotron accelerator. Positron bunches generated by the positron source have a maximum charge of 1.5 nC and are injected into the DR through the injection line. The DR operates at an injection frequency of 30 Hz and stores five bunches simultaneously. Each bunch remains in the ring for 166.7 ms before extraction. The extraction frequency is also 30 Hz, with one bunch extracted per cycle and delivered to the subsequent linac section.
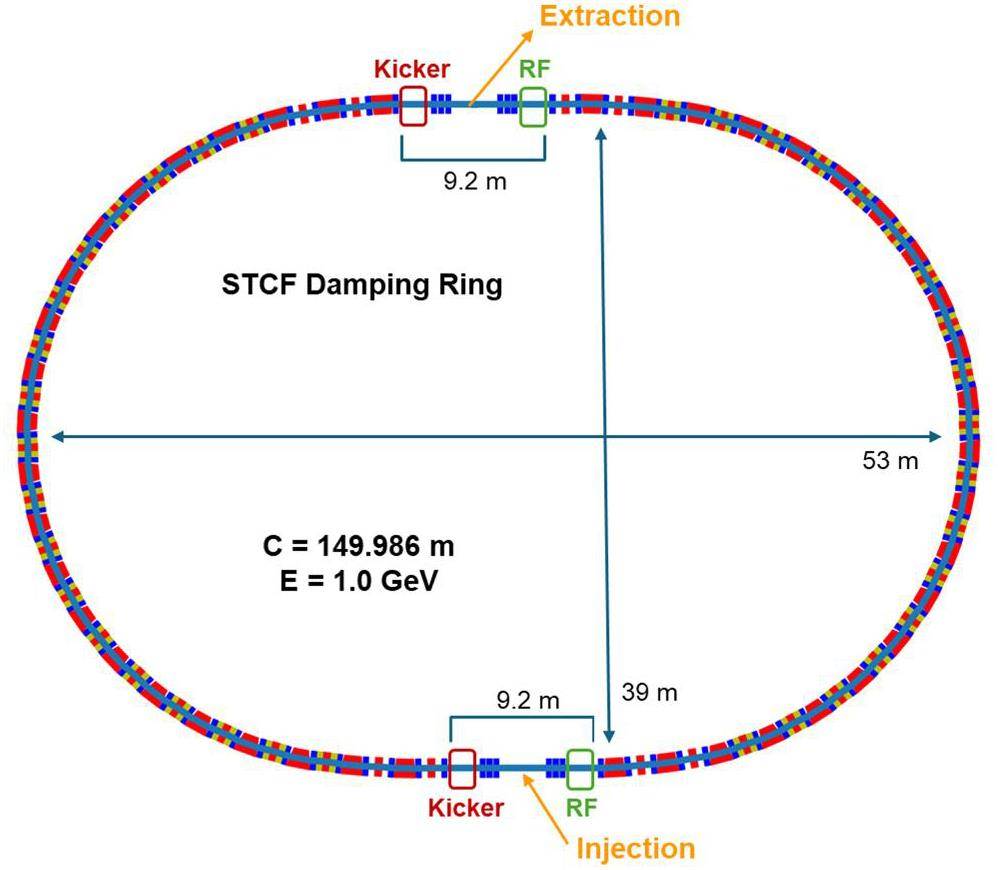
According to the collider ring design, the injected positron bunch emittance must be below 6 nm·rad at the nominal energy of 2 GeV, corresponding to a maximum emittance of 12 nm·rad at the DR energy of 1 GeV. To meet collider ring requirements while accounting for emittance growth during transport, the extracted bunch from the DR must have an emittance of less than 11 nm·rad. Currently, the full emittance (4 × rms) of the injected positron bunch is approximately 1400 nm·rad. Table 18 compares the design parameters of the STCF DR with those of similar international facilities [12, 37, 62].
| Parameter | CEPC | SuperKEKB | FCC-ee | STCF |
|---|---|---|---|---|
| Circumference (m) | 147 | 135.498 | 241.8 | 149.986 |
| Energy (GeV) | 1.1 | 1.1 | 1.54 | 1.0 |
| Natural emittance (nm·rad) | 43.85 | 42.6 | 1.16 | 8.25 |
| Horizontal injection emittance (nm·rad) | 1161 | 1400 | 1290 | 350 |
| Horizontal extraction emittance (nm·rad) | 77.2 (44.9)* | 43.5 | 1.81 | 8.26 |
| Horizontal damping time (ms) | 11.4 | 10.87 | 10.6*** | 28.8 |
| Storage time (ms) | 20 (40)* | 40 | 40 | 166.7 |
| Stored bunches Ntrain×nb | 2(4)*×1(2)** | 2×2 | 5×2 | 5×1 |
Damping ring optics design
The extracted emittance from the DR is calculated as follows:
The DR adopts a racetrack layout consisting of two straight sections and two 180° arcs, designed to minimize the total circumference and thereby reduce the damping time. Both straight sections are dispersion-free and house the injection and extraction elements as well as the RF cavity. The ring is based on a FODO lattice, which is sufficient to achieve a natural emittance in the nanometer-radian range. Although MBA lattices can provide even lower emittance, they do so at the cost of reduced dynamic aperture. The FODO structure employed here incorporates a Reverse Bend (RB) scheme, which enhances synchrotron radiation and enables low emittance.
Several RB strategies have been proposed internationally. In 1989, CERN introduced a scheme in the CLIC design where dipoles with opposite bending directions were embedded within focusing and defocusing quadrupole pairs; however, this configuration offered limited flexibility for phase advance tuning. Later, the ALS implemented a reversed central dipole (“Superbend”) within a triple-bend achromat (TBA) structure. A similar “positive–negative–positive” dipole pattern was adopted in the U.S. EIC design, though it is unsuitable for compact DRs. In 2005, KEK proposed a “positive–negative” dipole arrangement within each FODO cell for the SuperKEKB DR, which allows for tunable damping time and a compact layout. The STCF design adopts this latter scheme.
With the RB scheme, the damping time τ, natural emittance ε, and momentum compaction factor are calculated as follows [63, 64]:
The explicit forms are
Figure 105 and 106 show the dependence of the damping time, natural emittance, and momentum compaction factor on the reverse bend factor r. Considering damping time requirements and magnet fabrication feasibility, we choose r=0.3 as the design value.
Each arc contains 18 FODO cells (36 total in the ring). The phase advance per FODO cell is 90°. The forward and reverse dipoles are 1.0 m and 0.3 m long, respectively, both with a bending radius of 4.456 m and a field strength of 0.749 T. Each FODO cell is 3.0 m long. The Twiss parameters for the arc cell are shown in Fig. 107.
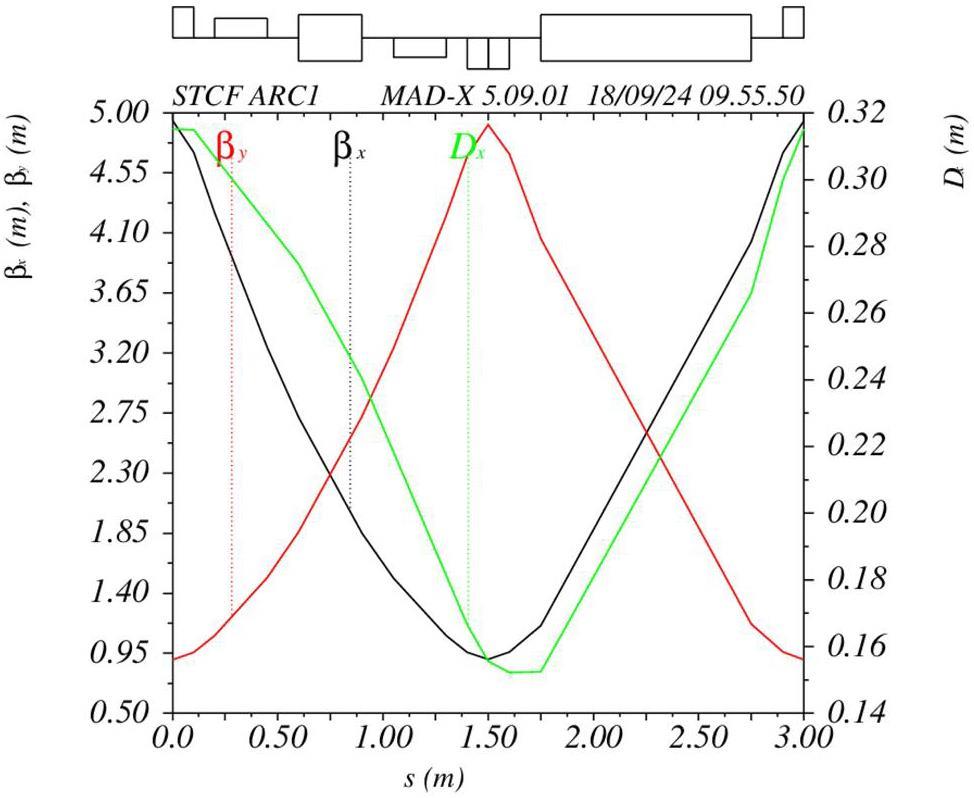
Each arc ends with two half-strength FODO cells for dispersion suppression. After that comes a straight section of approximately 9.2 m used for injection/extraction and housing the RF cavity. Twiss parameters for this region are shown in Fig. 108. The injection/extraction point lies at the center of the straight, with horizontal and vertical beta functions of 9.5 m and 1.0 m, respectively. The RF cavity positions are indicated in the figure. Downstream of the injection/extraction point, three quadrupoles lead to the kicker location. Global Twiss parameters are shown in Fig. 109.
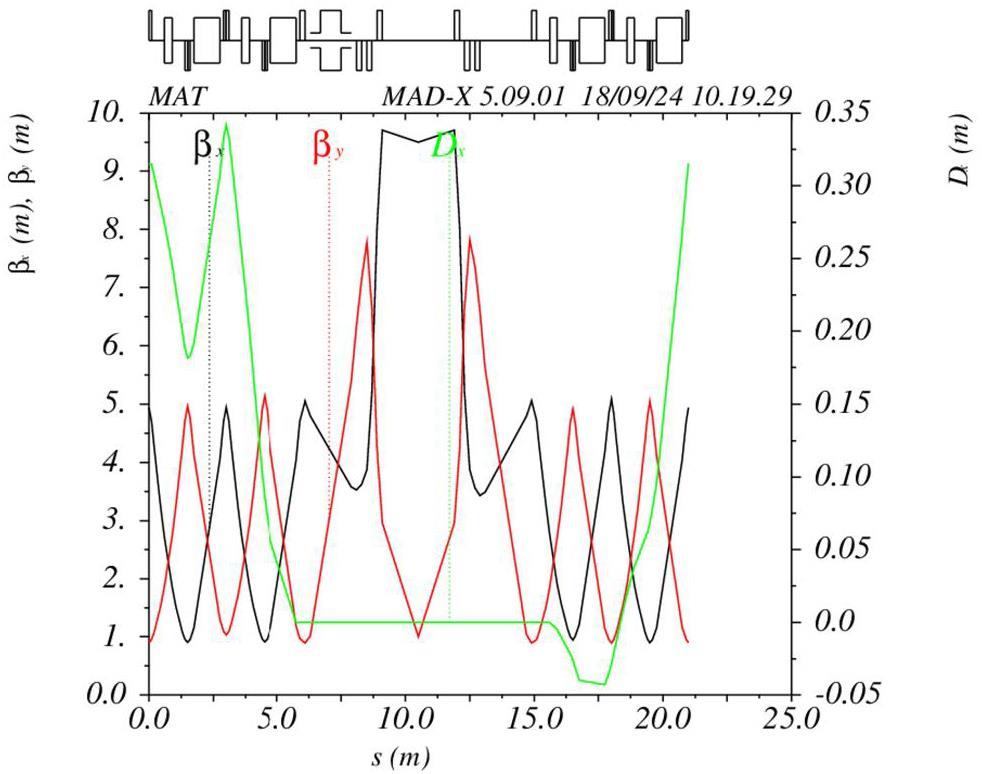
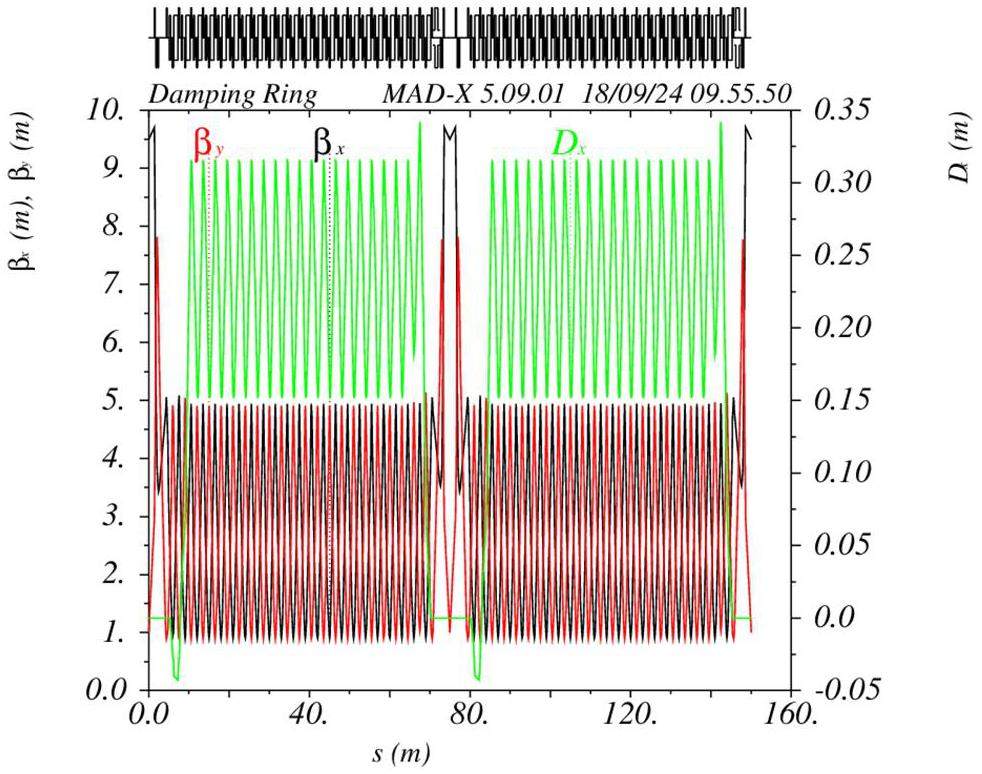
Figure 110 shows the dynamic aperture simulated with Elegant. The size of this aperture ten times that of the rms bunch size at the injection point in both transverse directions, fully meeting the injection requirement.
Figure 111 shows the emittance evolution of injected positrons as simulated using multi-particle tracking in Elegant. With a damping time of 28.8 ms and a design equilibrium emittance of 8.25 nm·rad, a 166.7 ms storage time ensures the emittance decreases from 350 nm·rad to approximately 8.4 nm·rad, which meets the extraction requirements (Table 19).
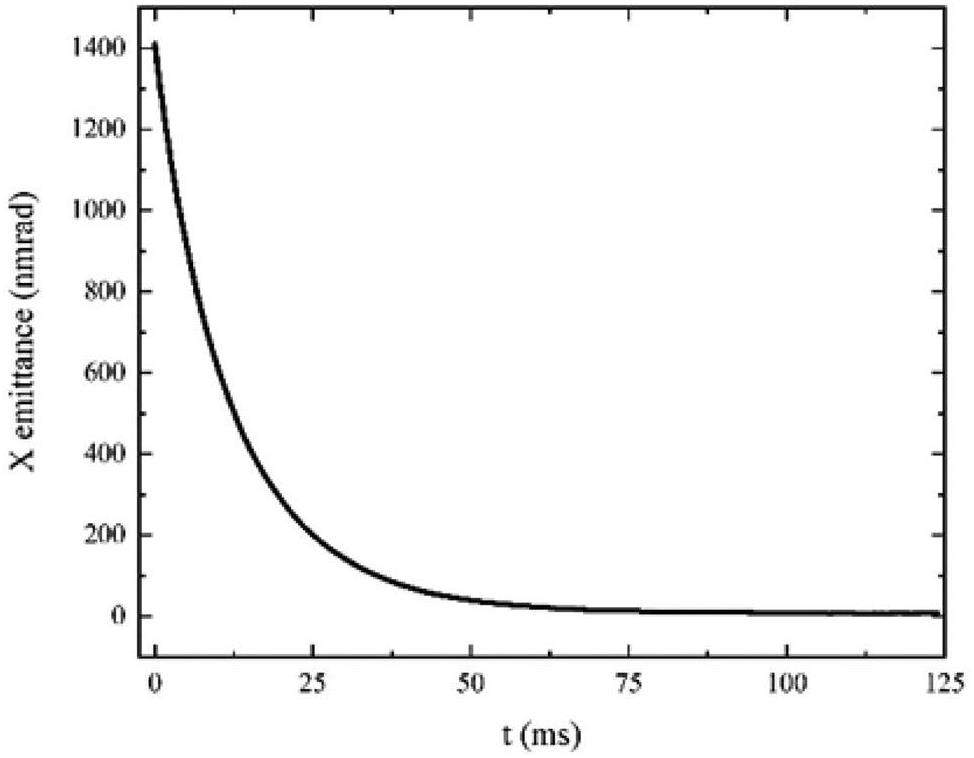
| Parameter | Value |
|---|---|
| Energy (GeV) | 1.0 |
| Circumference (m) | 149.986 |
| Number of bunches | 5 |
| Max charge per bunch (nC) | 1.5 |
| Max current (mA) | 15 |
| Arc FODO phase advance x/y (deg) | 90 / 90 |
| Dipole bending radius (m) | 4.456 |
| Dipole field strength (T) | 0.749 |
| Reverse bend factor, r | 0.3 |
| Synchrotron radiation loss per turn (keV) | 35 |
| Damping time, x/y/z (ms) | 28.8 / 28.6 / 14.2 |
| Storage time (ms) | 166.7 |
| Natural emittance x/y (nm·rad) | 8.25 / 0.1 |
| Injected emittance x/y (nm·rad) | 350 / 350 |
| Extracted emittance x/y (nm·rad) | 8.26 / 0.2 |
| Natural relative energy spread (%) | 0.031 |
| Momentum compaction factor | 0.0064 |
| RF frequency (MHz) | 499.7 |
| RF voltage (MV) | 0.2 |
| Harmonic number | 250 |
| Natural chromaticity x/y | –15.0 / –15.3 |
Injection and extraction design of the damping ring
The DR stores five positron bunches evenly distributed around the ring. After each bunch is extracted, it is replenished through bucket-to-bucket single-turn injection. During injection, a septum magnet deflects the incoming positron bunch from the transfer line into the acceptance of the DR. When the bunch center reaches the beam pipe center, a pulsed kicker magnet is used to remove the injection angle. The STCF DR employs a horizontal single-turn injection scheme, consisting of one injection kicker magnet and one injection septum magnet. The layout of the injection system is shown in Fig. 112.
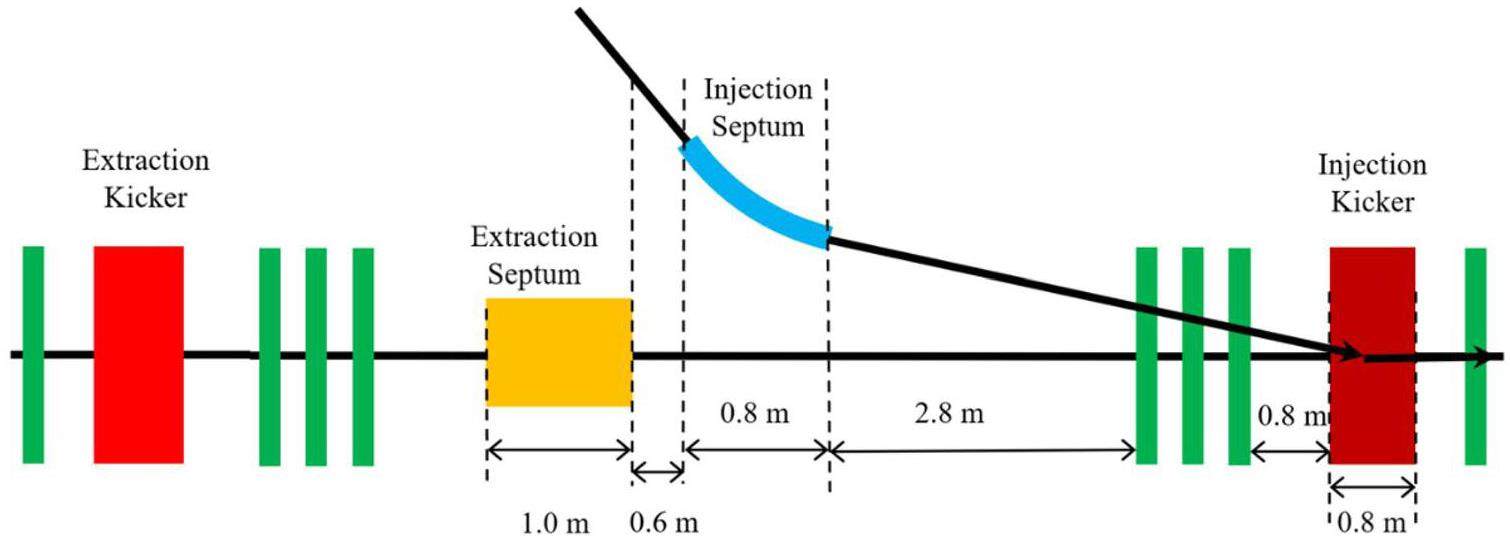
The exit of the septum magnet is located 9 mm from the reference orbit of the circulating beam. The horizontal acceptance is 8100 nm·rad. The septum blade has a thickness of 4 mm, and the injected beam envelope is 3.7 mm (corresponding to 1400 nm·rad). At the exit of the septum magnet, the center of the injected beam is 18 mm from the reference orbit, with an injection angle of –2.82 mrad. Parameters of the injection septum and kicker magnets are summarized in Tables 20 and 21, respectively.
| Parameter | Specification |
|---|---|
| Injection direction | Horizontal |
| Number of bunches | 1 |
| Kicker type | Stripline |
| Deflection angle (mrad) | 4.04 |
| Effective magnet length (mm) | 800 |
| Pulse width (ns) | < 2 |
| Rise time (ns) | < 35 |
| Parameter | Specification |
|---|---|
| Injection direction | Horizontal |
| Deflection angle (°) | 10 |
| Effective magnet length (mm) | 800 |
| Magnetic field strength (T) | 0.73 |
| Septum thickness (mm) | 4 |
The DR also employs a horizontal single-turn extraction scheme, utilizing one horizontal extraction septum and one extraction kicker magnet. The magnet parameters are identical to those listed in Tables 20 and 21. The layout of the extraction straight section is symmetric to that of the injection section.
At present, the STCF positron DR achieves an extracted emittance below 11 nm·rad after a storage time of 166.7 ms, satisfying the design requirements. The field strengths of the dipole, quadrupole, sextupole, and kicker magnets in the DR are all within feasible operational ranges. The engineering design of all components is technically achievable, with no evident risks, demonstrating the overall feasibility.
Injector physics design for swap-out injection
Electron source and main linac SEL1 for direct injection
Scheme 1–High-charge thermionic electron source
· System Design Requirements and Specifications
The beam parameters for swap-out injection are specified in Table 15. This design employs a thermionic electron source operating at an RF frequency of 2998.2 MHz. The final system output is a single bunch with a charge of 8.5 nC, geometric emittance ≤ 30 nm·rad, rms energy spread ≤ 0.5%, and rms bunch length ≤ 2.0 mm.
· Key Technologies and Design Strategy
The linac design is driven by the beam injection requirements of the collider rings. Based on the overall performance objectives, the system integrates beam bunching and acceleration structures, supported by both theoretical modeling and simulation studies. The interaction between multiple physical fields and the driving beam is analyzed to establish an accurate theoretical framework, guiding the design of the RF fields and focusing magnets. To enhance design efficiency, multi-objective optimization algorithms are employed. The optimized parameters obtained from these algorithms are then applied to 3D multi-particle beam dynamics simulations to evaluate the bunching system’s performance.
Key technical challenges include the design of SHBs, optimization of phase velocity distributions in non-uniform multi-cell structures, axial magnetic field design, longitudinal phase-space optimization during acceleration, and transverse matching of beam parameters.
· System Configuration
The swap-out injection linac comprises a bunching system and a relativistic main accelerating section, as illustrated in Fig. 113. The bunching system includes two subharmonic prebunchers operating at frequencies of 1/18 and 1/6 of the main RF frequency, an S-band traveling-wave buncher, and one velocity-of-light accelerating section. The ML consists of 68 SLAC-type accelerating structures, each 3 m in length.
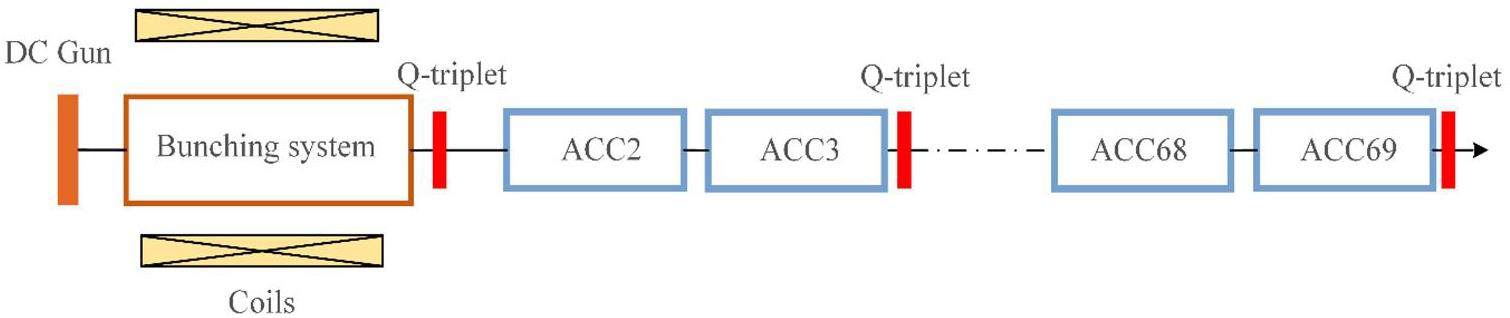
· Bunching System Design
The thermionic electron gun produces a bunch with an FWHM of 1.3 ns, a single-bunch charge of 8.5 nC, and a kinetic energy of 200 keV. Its longitudinal distribution and projections in the longitudinal and transverse directions are shown in Fig. 114.
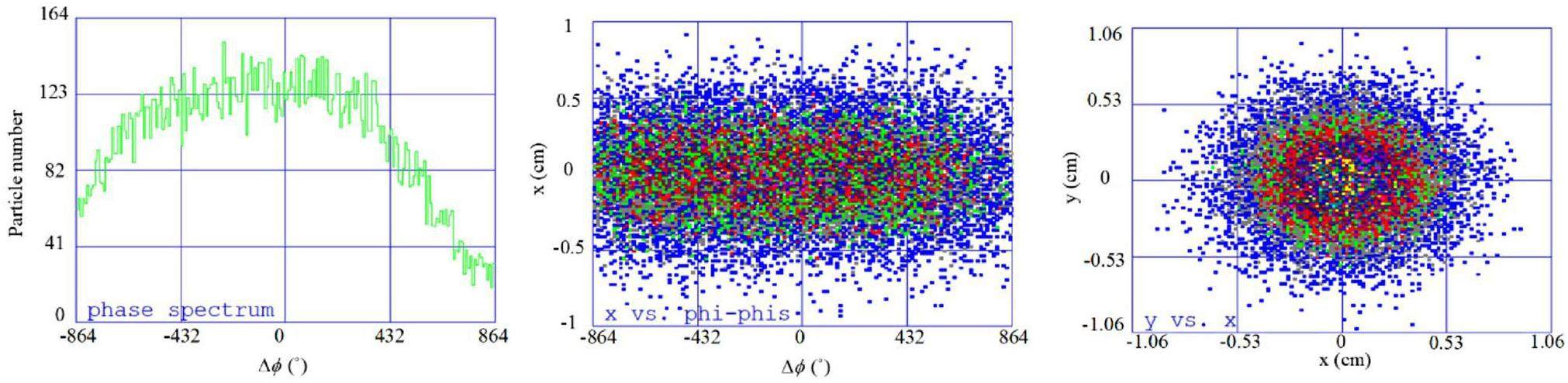
After passing through the two SHBs and the traveling-wave buncher (Fig. 113), the bunch is compressed to 5 ps (rms, 95% particles) and accelerated by a 3 m SLAC accelerating section to ≈60 MeV with an energy spread of 1.39% (rms, 95% particles). The traveling-wave buncher adopts a variable phase velocity and gradient disc-loaded waveguide structure. The accelerating field profiles for the buncher and the relativistic section are shown in Fig. 115 (left and right, respectively).
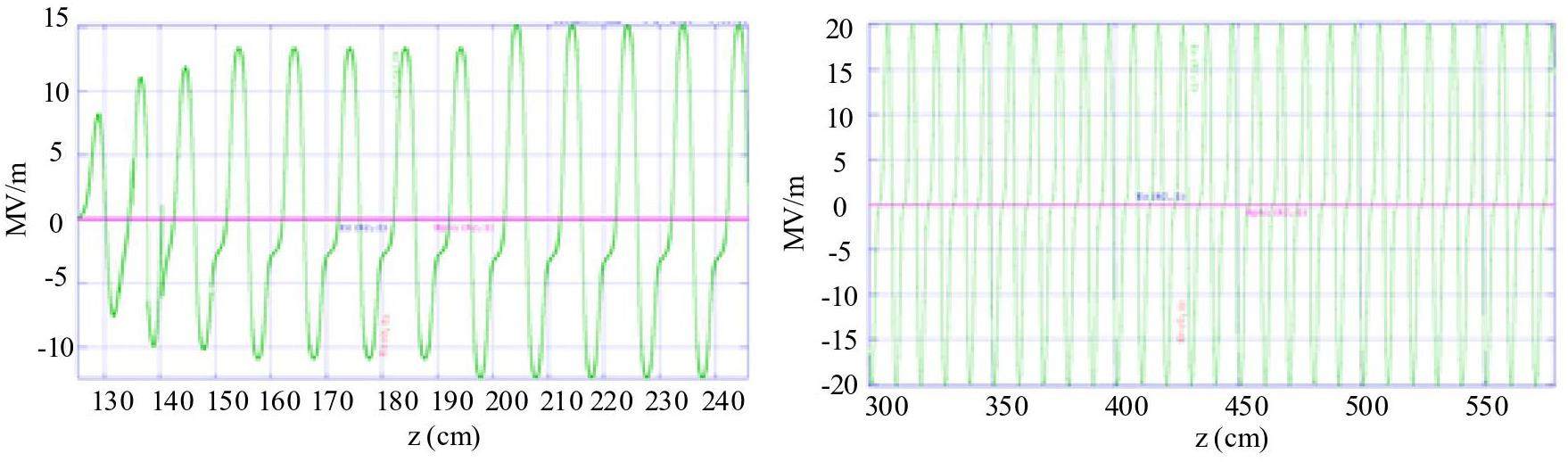
Figure 116 shows the beam energy gain at the output of the bunching system, and Figs. 117 and 118 show the transverse and longitudinal phase spaces.
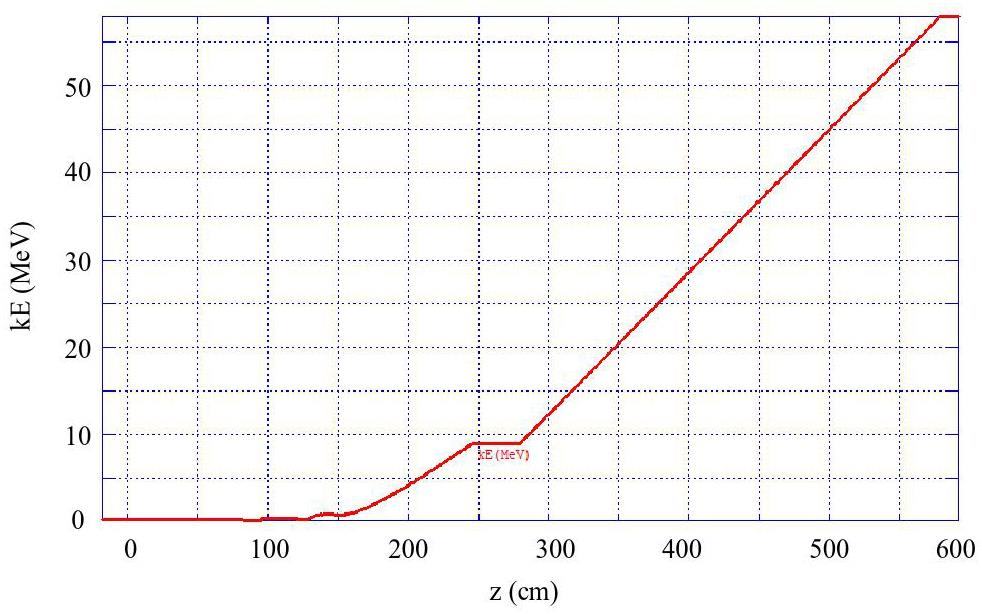
To limit transverse beam loss, a solenoidal focusing system is used to constrain the beam size. The magnetic field distribution along the BS is shown in Fig. 119. The evolution of transverse beam envelope, phase deviation, and energy deviation along the beamline is shown in Fig. 120. The evolution of key parameters, including rms bunch length, energy spread, normalized transverse emittance, and rms transverse size, is presented in Fig. 121.
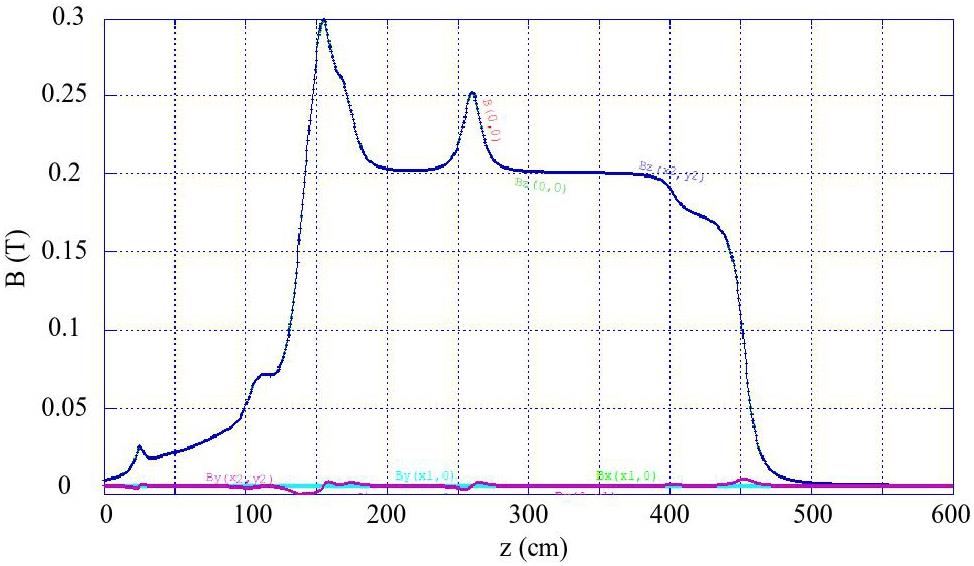
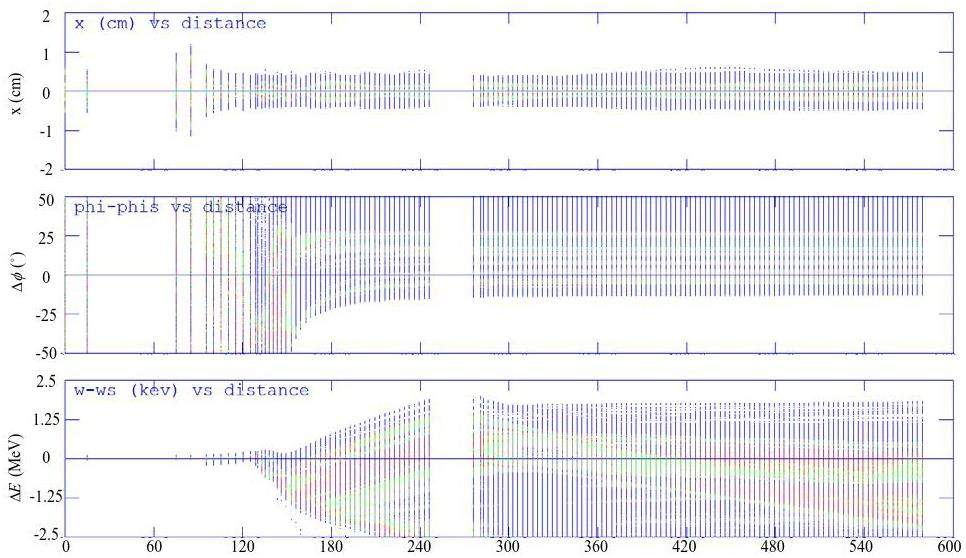
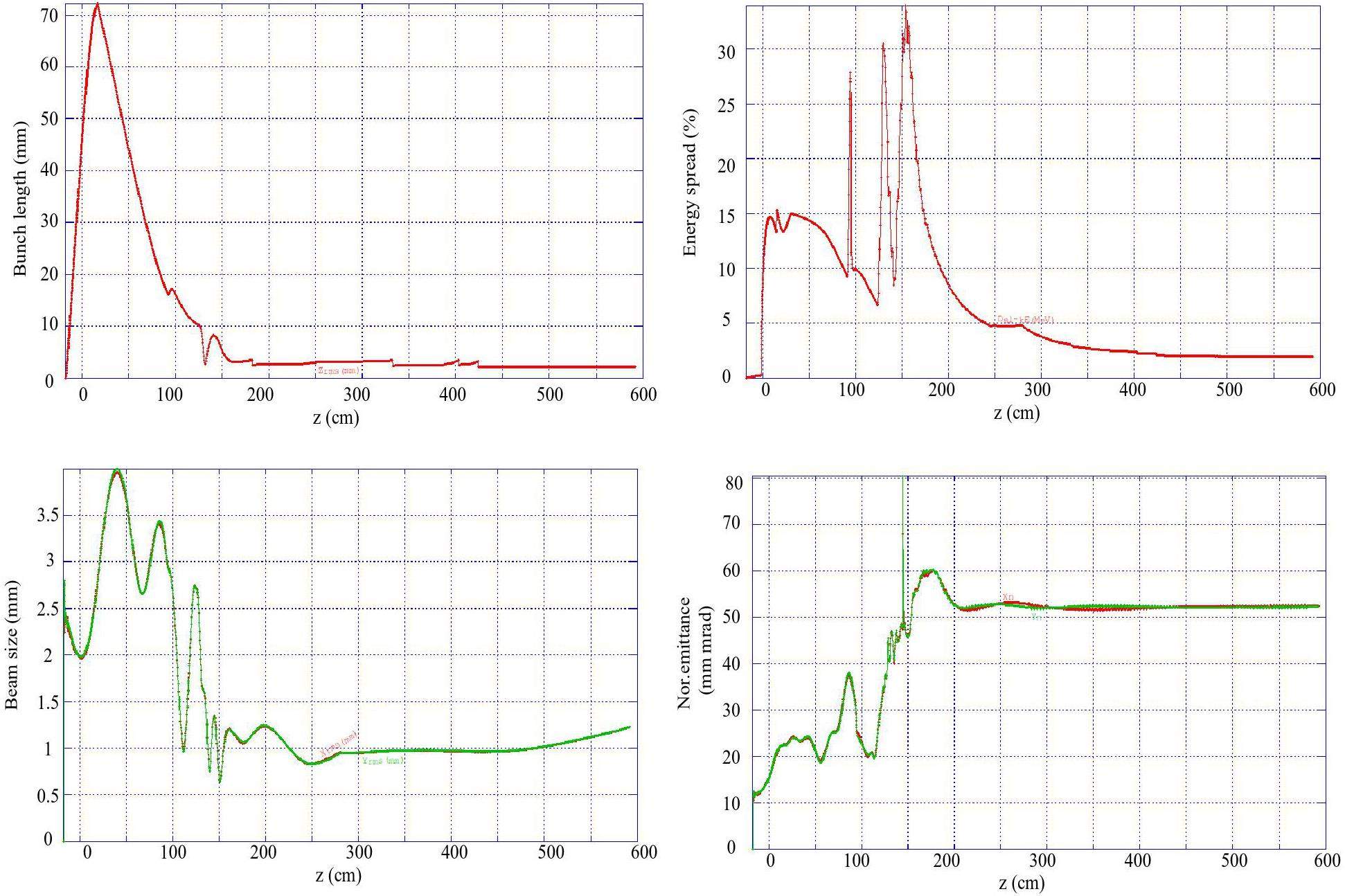
· Light-speed Linac Design
The light-speed accelerating section consists of 68 SLAC-type accelerating structures, each 3 m long, which increase the beam energy from approximately 60 MeV to a maximum of 3.5 GeV. To control the transverse beam properties, one quadrupole triplet (comprising three quadrupole magnets) is placed between every two accelerating sections to provide beam optics matching.
· Longitudinal Performance: The input beam energy to the relativistic linac is approximately 60 MeV, and it is accelerated to 3.51 GeV. The evolution of the energy spread and bunch length along the linac is shown in Fig. 122. At the linac exit, the rms bunch length is 4.87 ps (containing 95% of particles), and the rms energy spread is less than 0.5% (also for 95% of particles).
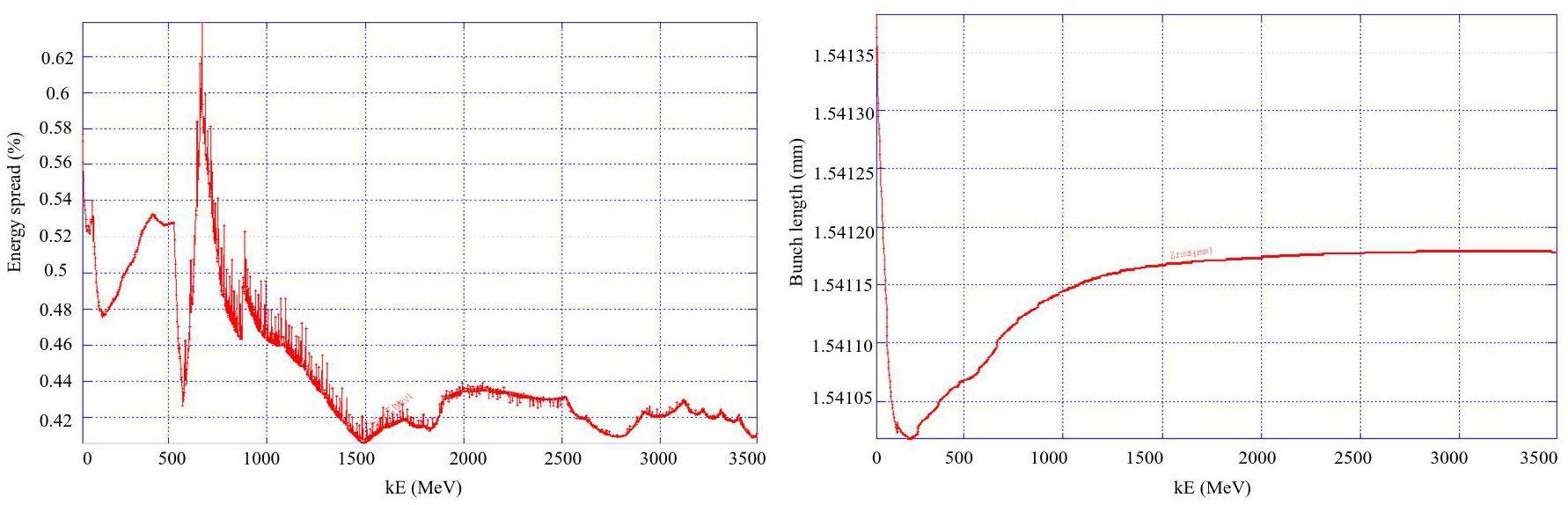
· Transverse Performance: Once the beam enters the relativistic linac, solenoids are no longer suitable for focusing high-energy beams. Therefore, triplet magnet systems are installed between every two accelerating structures to control the transverse beam size and match the beam optics by adjusting the quadrupole magnet currents. After optimization, the rms transverse beam size and normalized transverse emittance are shown in Fig. 123.
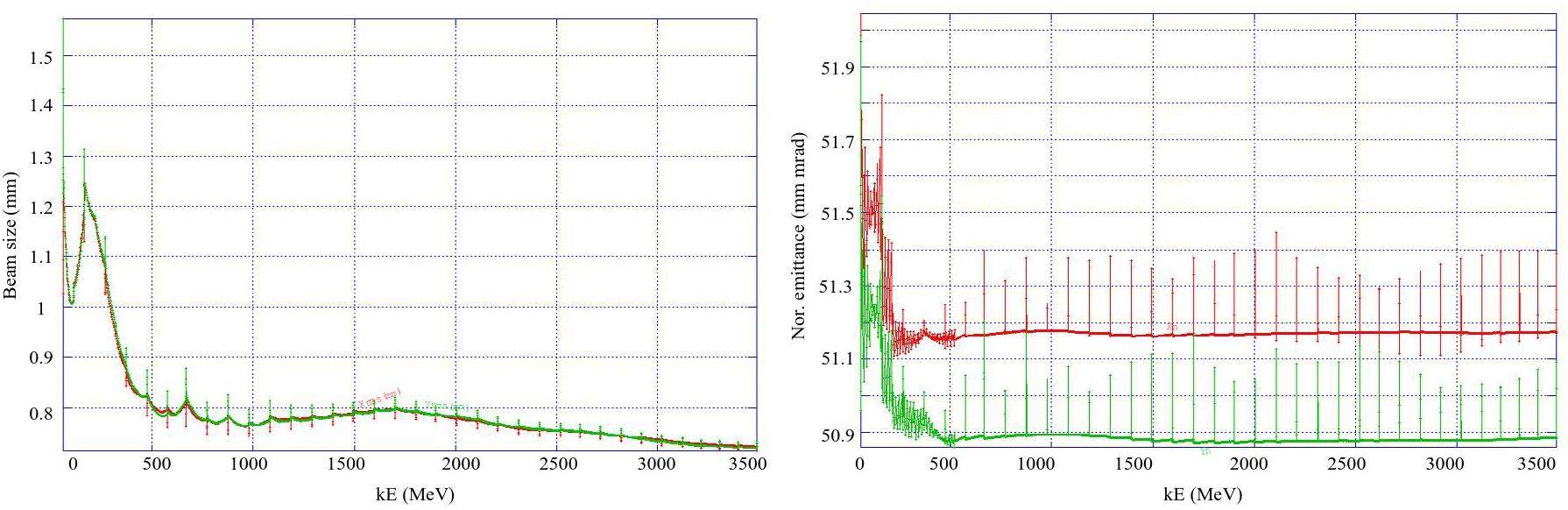
The overall performance of the SEL1 linac for the swap-out injection is summarized in Table 22. It successfully accelerates an 8.5 nC high-charge electron bunch to 3.5 GeV while maintaining a transmission efficiency of 99.97% and energy spread below 0.5%, meeting the STCF injector design requirements.
| Parameter | Value |
|---|---|
| Injected electron bunch charge (nC) | 8.5 |
| Injection beam energy (GeV) | 1–3.5 |
| Transmission efficiency (main bunch) (%) | 99.97 |
| Normalized emittance (mm·mrad) | ≤ 55 |
| Rms energy spread (for ≥95% of particles) (%) | ≤ 0.5 |
| Rms bunch length (for ≥95% of particles) (ps) | ≤ 4.9 |
· Performance at Different Output Energies
As noted above, the 68-section linac can be operated with adjustable RF power to achieve 1 and 2 GeV output energies. Figures 124, 125, 126, 127 show the evolution of energy spread and normalized emittance for the 1 and 2 GeV cases.
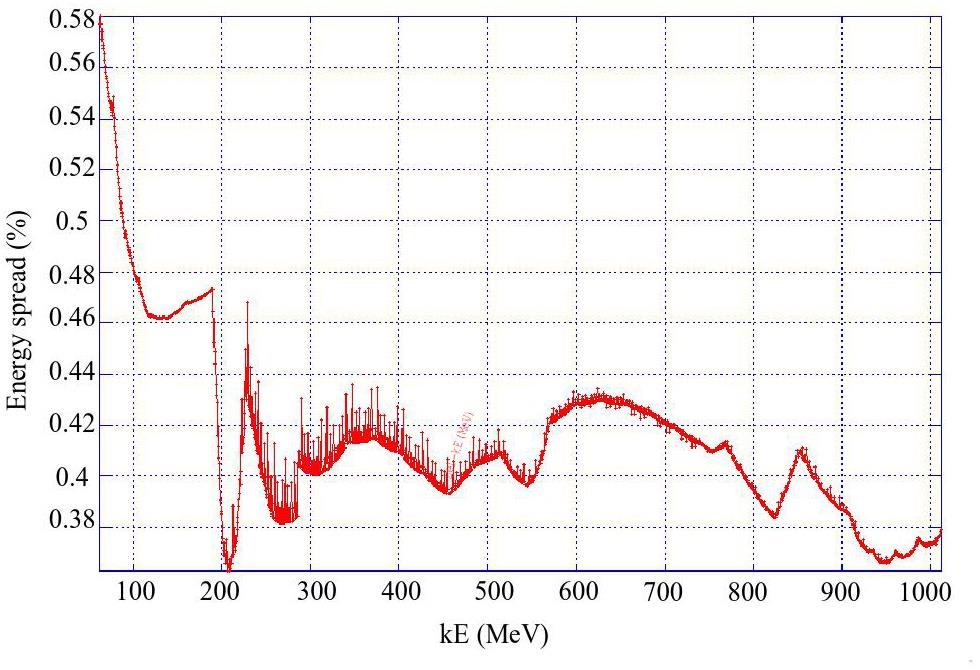
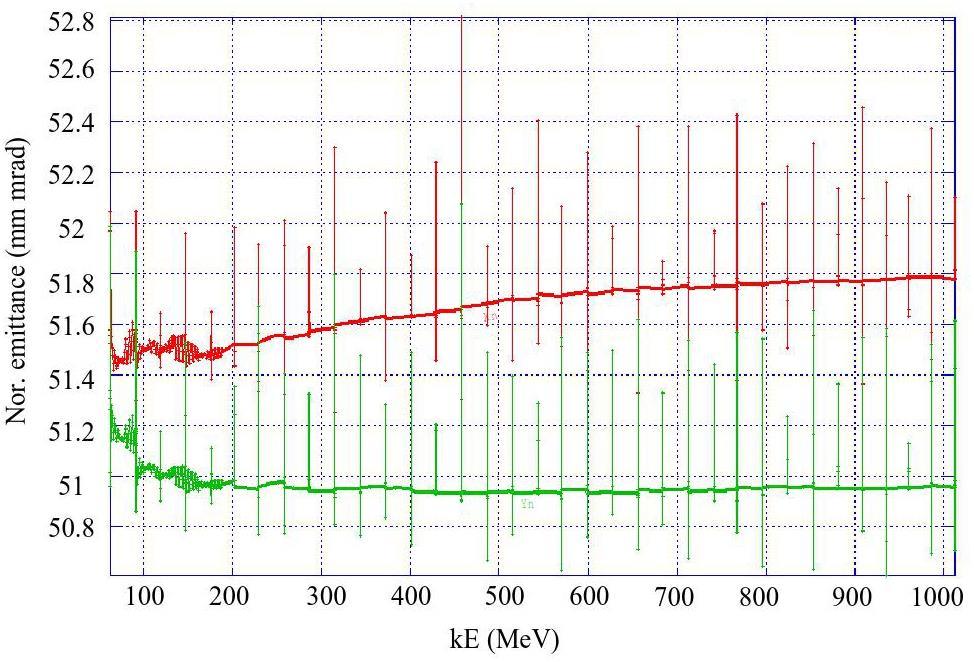
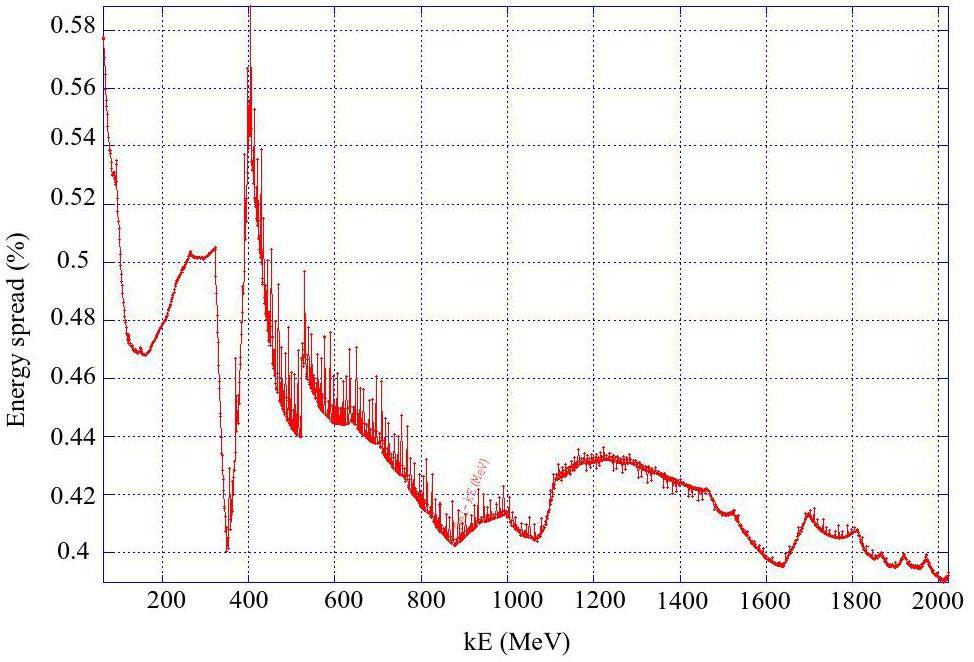
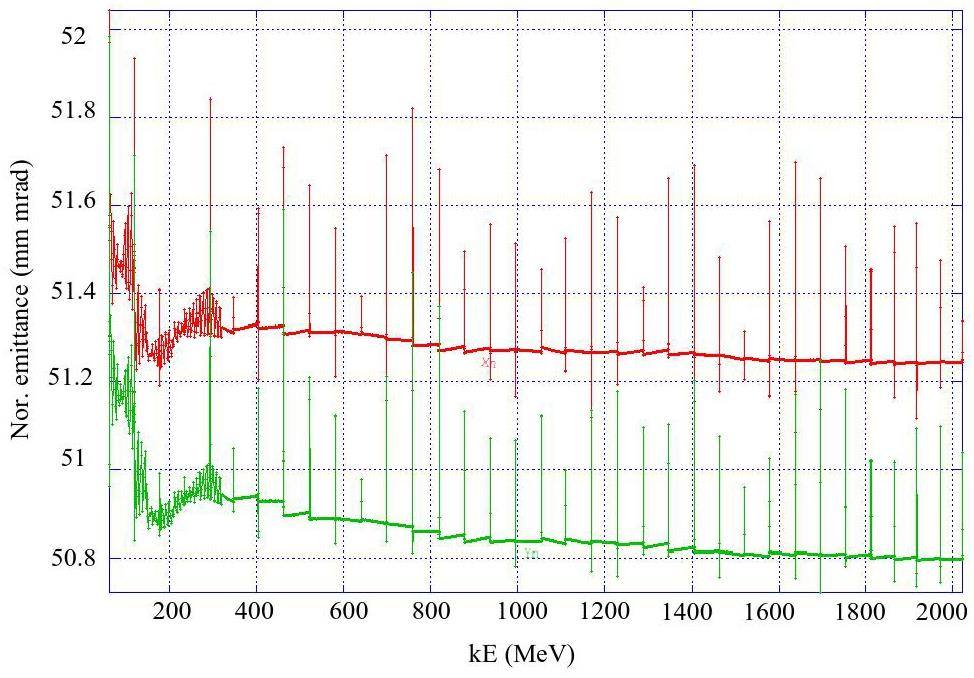
· Feasibility Analysis
· The input beam distribution in this design is derived from the HEPS electron source. The simulations incorporate a realistic upstream electron gun system, producing consistent and representative output parameters.
· The SuperKEKB injector in Japan adopts a similar configuration consisting of two SHBs + pre-buncher + buncher, with SHB frequencies of 1/25 and 1/5 of the main RF frequency. The CEPC in China also employs two SHBs + TW buncher operating at 1/18 and 1/6 of the main frequency. The present design is therefore consistent with established and successful international practices.
· Beam dynamics simulations were performed using Parmela. The results, presented in the previous section, confirm that the design meets the STCF collider requirements for high-charge direct injection.
· Conclusion
For the swap-out injection scheme, a high-charge linac design based on a thermionic electron gun is proposed. Two SHBs and a traveling-wave buncher are used to compress the high-charge electron beam, which is then accelerated through 68 accelerating structures to reach the injection energy. Beam dynamics simulations demonstrate that the beam achieves an energy of 3.5 GeV, with an rms energy spread below 0.5%, an rms bunch length below 4.9 ps, and an overall transmission efficiency of 99.97%, fully satisfying the STCF injection requirements.
Scheme 2 —L-band photocathode high-charge electron source
For the swap-out injection scheme, the STCF collider requires the injector to deliver high-quality electron bunches with a charge of at least 8.5 nC while satisfying strict emittance constraints. Traditionally, producing bunches with such high charge has relied on thermionic electron guns, which typically generate beams with high emittance (≈100 mm·mrad) and long bunch lengths (>100 ps). These characteristics lead to phase overlap during RF acceleration and necessitate beam scraping, making it challenging to meet the required emittance and energy spread specifications.
In contrast, L-band PC electron guns, developed over many years for free-electron laser (FEL) applications, present a promising alternative. These guns can simultaneously achieve high bunch charge and excellent beam quality. The L-band PC gun technology has been successfully demonstrated at facilities such as PITZ (Germany) and Tsinghua University [65, 66], achieving quantum efficiencies exceeding 5% and normalized emittances of approximately 1 μm/nC. It has also been adopted in major projects such as SHINE [67] and PWFA at BEPCII, establishing it as a mature and reliable solution for high-charge electron injectors (Fig. 128).
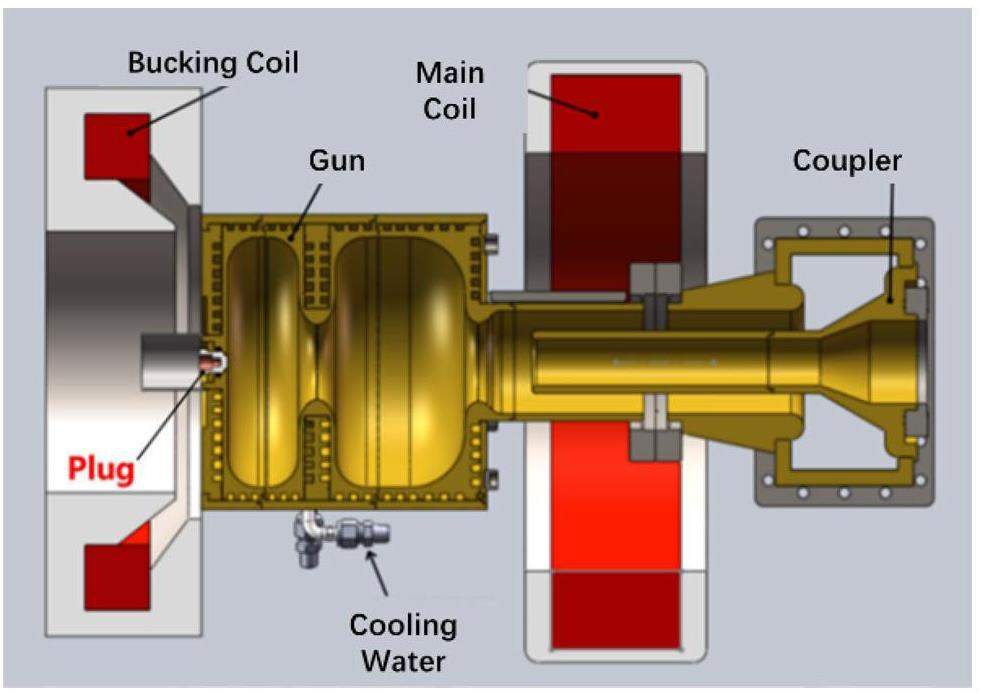
· Layout Overview
This scheme replaces the 8.5 nC thermionic gun in the injector layout (Fig. 65) with an L-band PC gun while retaining a positron line configuration similar to that of the off-axis injection scheme but with an increased positron production energy (>2.5 GeV).
The L-band PC gun has been experimentally demonstrated to operate stably at 5 nC @ 1 kHz. For the STCF, the required total yield is 240 nC/s (8.5 nC × 30 Hz), which this gun can satisfy. Considering RF power system constraints (≤ 100 Hz), the gun is configured for 8.5 nC @ 30 Hz operation. The feasibility of this design is currently under further study.
· Electron Bunch Generation and Acceleration
The low-energy section of the L-band PC injector primarily comprises the PC RF gun, a solenoid (SOL), two L-band accelerating structures (L1), two S-band accelerating structures (L2), one X-band linearizer section, and a magnetic chicane compressor. It is also equipped with several magnets and beam diagnostics components. Together with the PC, drive laser, solid-state and pulsed power sources, as well as vacuum, mechanical, power supply, control, radiation protection, and engineering systems, these elements form the complete low-energy section of the injector. The overall layout is illustrated in Fig. 129.

Since the exit energy of the L-band RF gun is relatively high (>7 MeV), a traditional RF buncher cannot be used for compression. Instead, magnetic compression is employed to reduce the bunch length and control the energy spread. Based on international experience with L-band PC RF guns, for bunch charges as high as 8.5 nC, the bunch length at the gun exit is relatively long. To address this, a pair of 1 m-long L-band accelerating structures is used for pre-acceleration to increase the beam energy, followed by two 3 m-long S-band accelerating structures (L2) and an X-band linearizer to introduce an energy chirp, which is subsequently compressed in a magnetic chicane. Finally, the beam is further accelerated beyond 1 GeV in section L3, comprising 20 S-band accelerating structures.
The PC gun is a PITZ-type L-band design, featuring 10 water-cooling channels on the cavity body and a coaxial RF coupler for power feed. The solenoid uses a combination of a bucking coil and a main solenoid, following the PITZ design. The performance parameters of the gun are summarized in Table 23.
| Parameter | Value |
|---|---|
| Operating frequency (MHz) | 1300 |
| Operating mode | Pulsed |
| Max repetition rate (kHz) | 1 |
| Duty cycle (%) | >0.4 |
| Cathode gradient (MV/m) | >50 |
| Dark current (pC/pulse) | <200 |
| Static vacuum (Pa) | <1×10-8 |
| Dynamic vacuum (Pa) | <5×10-8 |
As in the off-axis injection design, the optimization of the L-band PC low-energy section employs a multi-objective, multi-variable genetic algorithm integrated with ASTRA beam dynamics simulation software. 3D electromagnetic field maps of the actual components are used in the simulation, and the entire physical layout is modeled realistically.
During optimization, the longitudinal bunch length and transverse emittance of the electron beam at the injector exit are used as the main objectives. The tunable variables include the operational parameters and physical positions of the components described above. The thermal emittance of the PC is set to 1 mm·mrad/mm. The transverse distribution of the drive laser is set to a flat-top profile, while the longitudinal profile is Gaussian. The main optimized results of the low-energy section are presented in Figs. 130, 131, and 132.
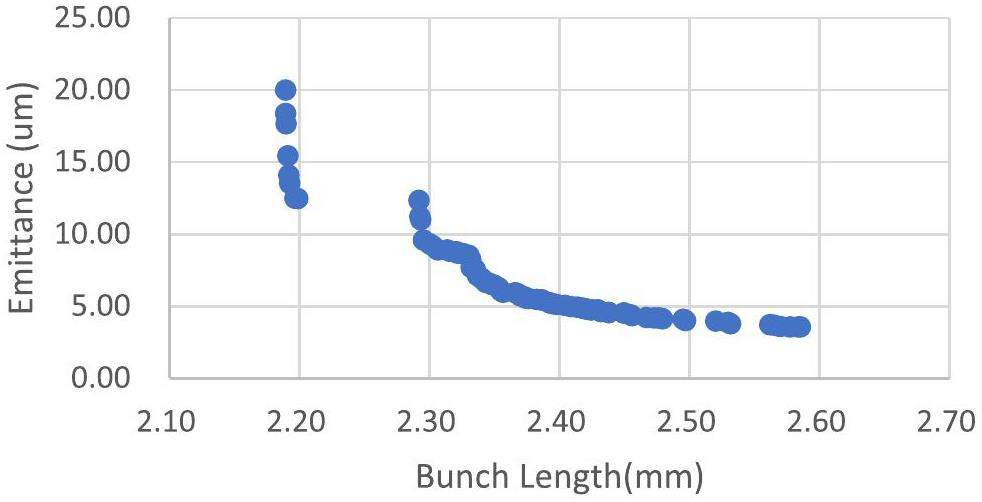
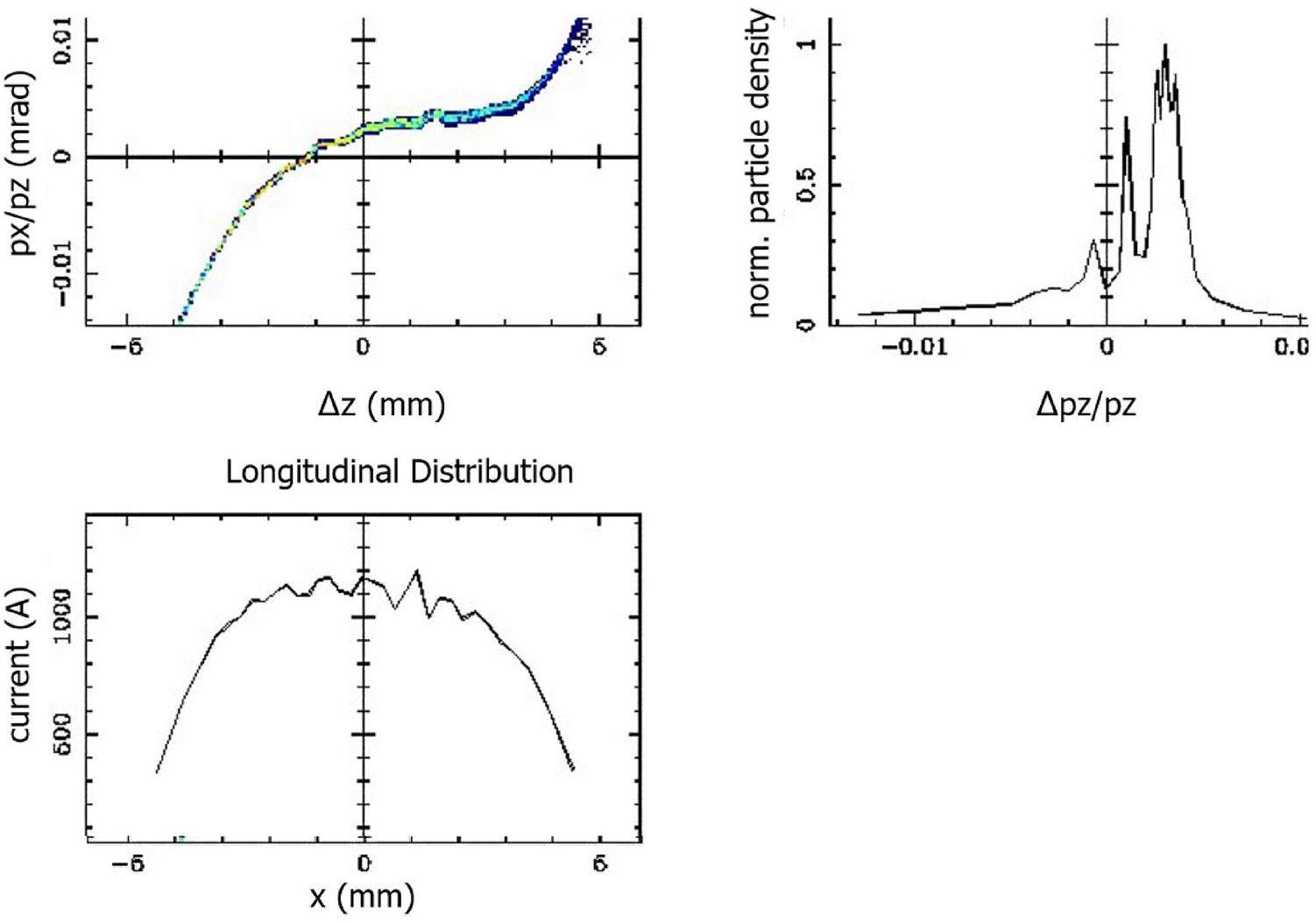
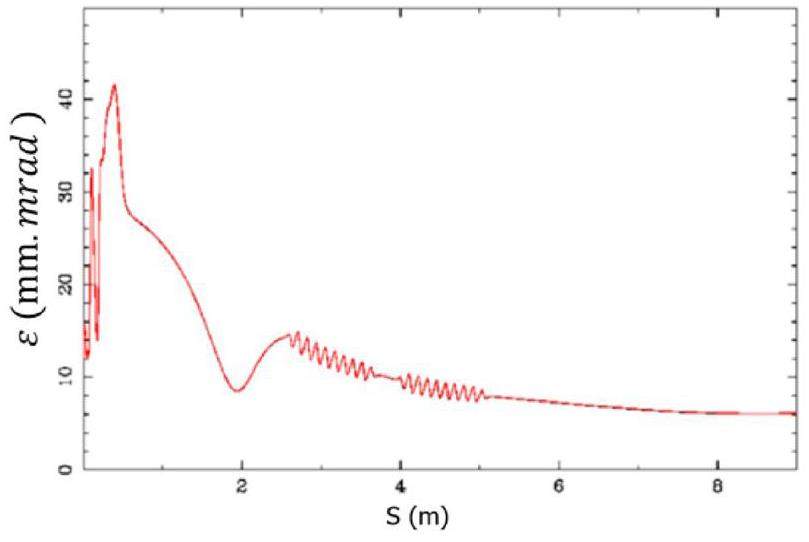
The above results demonstrate that at the L1 pre-buncher exit, the beam energy is 38.77 MeV, the bunch charge is 8.5 nC, the bunch length is 2.2 mm, the normalized emittance is 4.8 μm, and the peak current reaches 300 A. The longitudinal profile approximates a Gaussian distribution. The low-energy beam then passes through the L2 and X-band linearizer sections, where it is compressed at approximately 200 MeV. The bunch length is reduced from 2.2 mm to 0.8 mm (corresponding to approximately 2° of the S-band RF phase), as shown in Figure 133, before being accelerated to over 1 GeV.
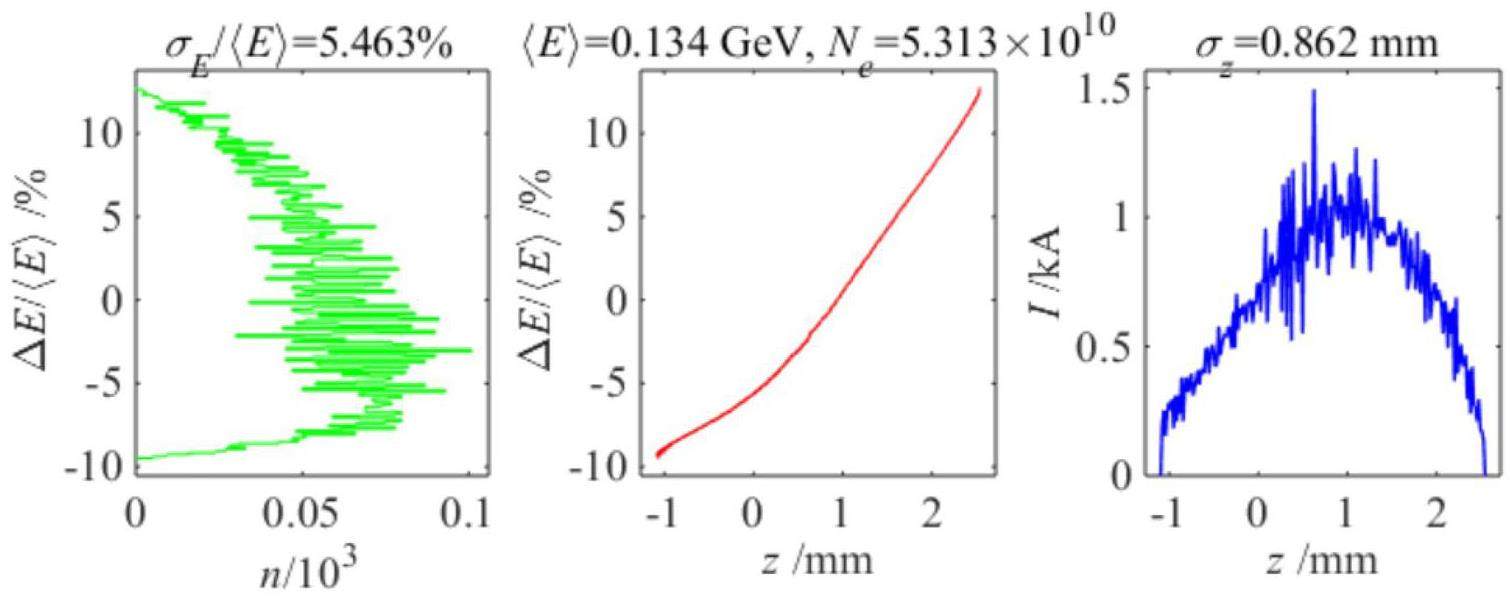
At the exit of the SEL1 section, the energy spread is approximately 0.38%, with the phase space and current distribution shown in Fig. 134.
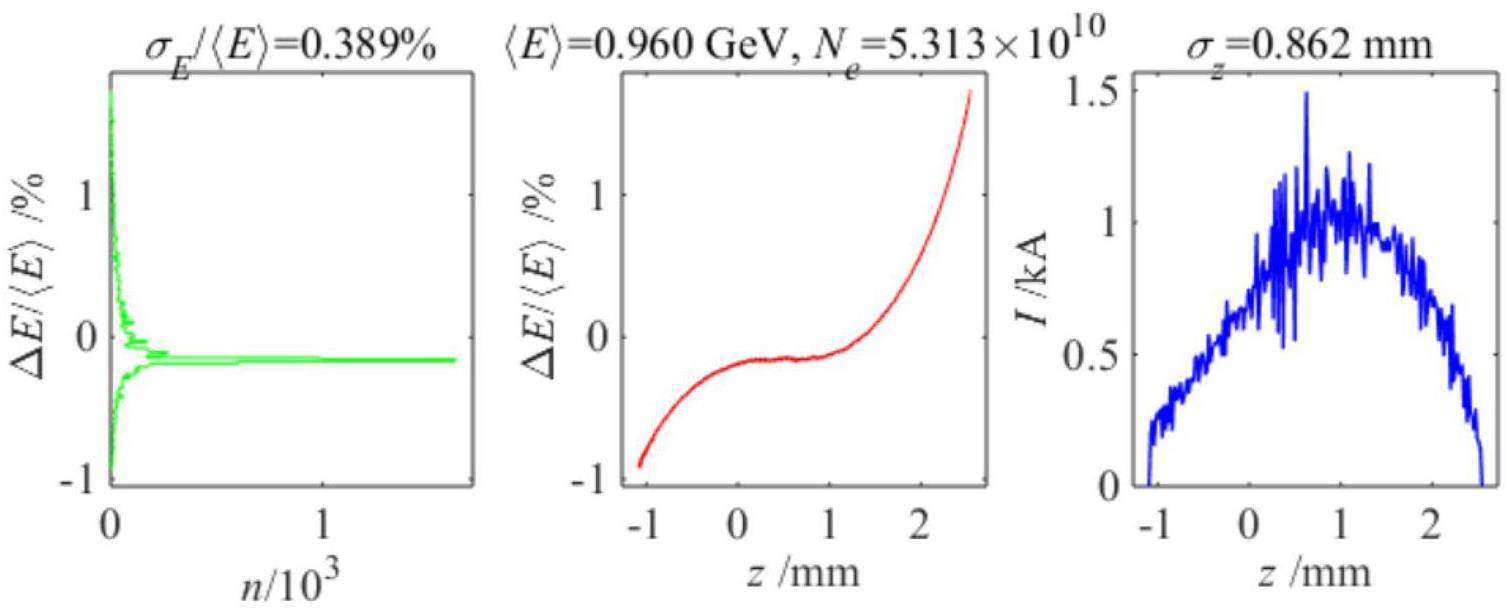
These results show that the L-band PC low-energy section achieves a shorter bunch length and lower emittance, making it suitable for direct injection. Moreover, both the cathode and drive laser offer sufficient operational margin, and the L-band PC gun shows potential to scale up to ≈10 nC, fully meeting the requirements of single-bunch swap-out injection.
Electron source and main accelerator section SEL2 for positron production
In the swap-out injection scheme, the thermionic electron source used for positron target bombardment is similar to that in the off-axis injection design, but with a higher bunch charge requirement of 11.6 nC. The low-energy section design is also identical, comprising a BS and a PIS. The main accelerator section, SEL2, increases the beam energy to 2.5 GeV while supporting an increased repetition rate of 90 Hz. A total of 46 accelerating structures are required in SEL2, resulting in an overall linac length of approximately 180 m, as illustrated in Fig. 135.
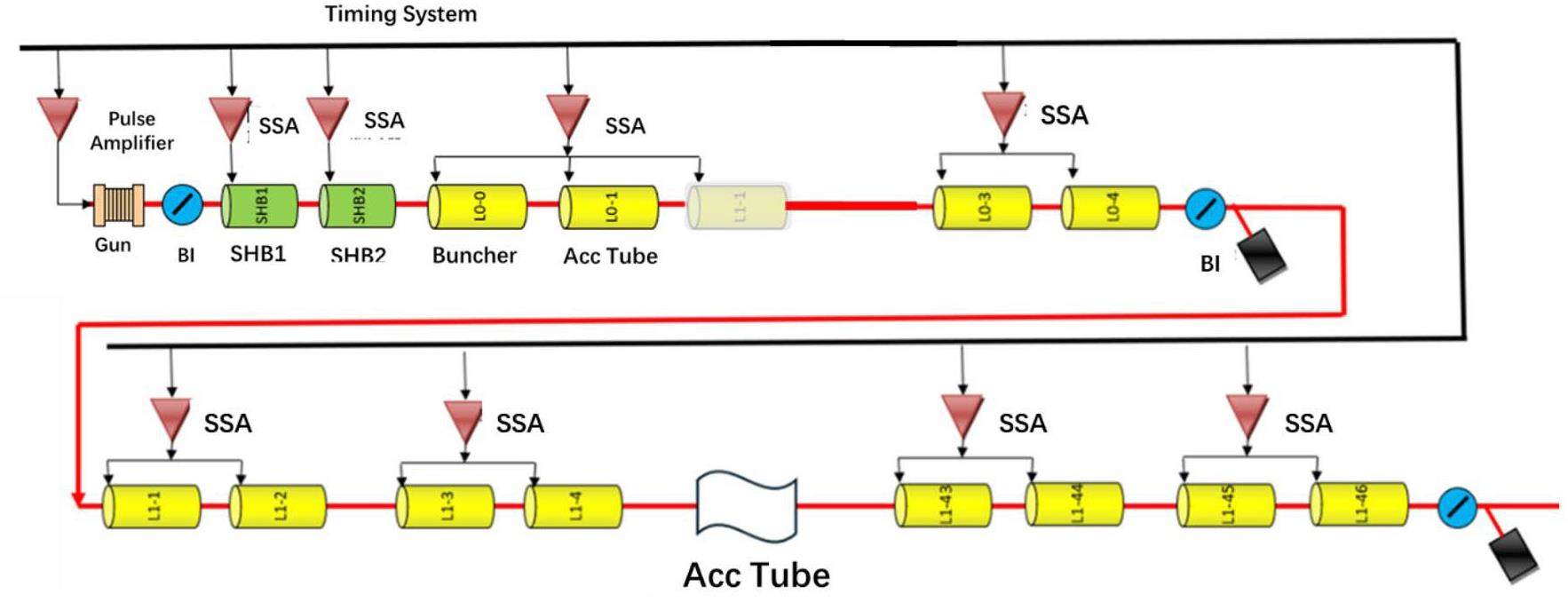
Tracking the 11.6 nC bunch through SEL2 yields the beam transverse and longitudinal envelopes, normalized emittance evolution along the beamline, and the final phase space distribution at the linac exit, as shown in Fig. 136.
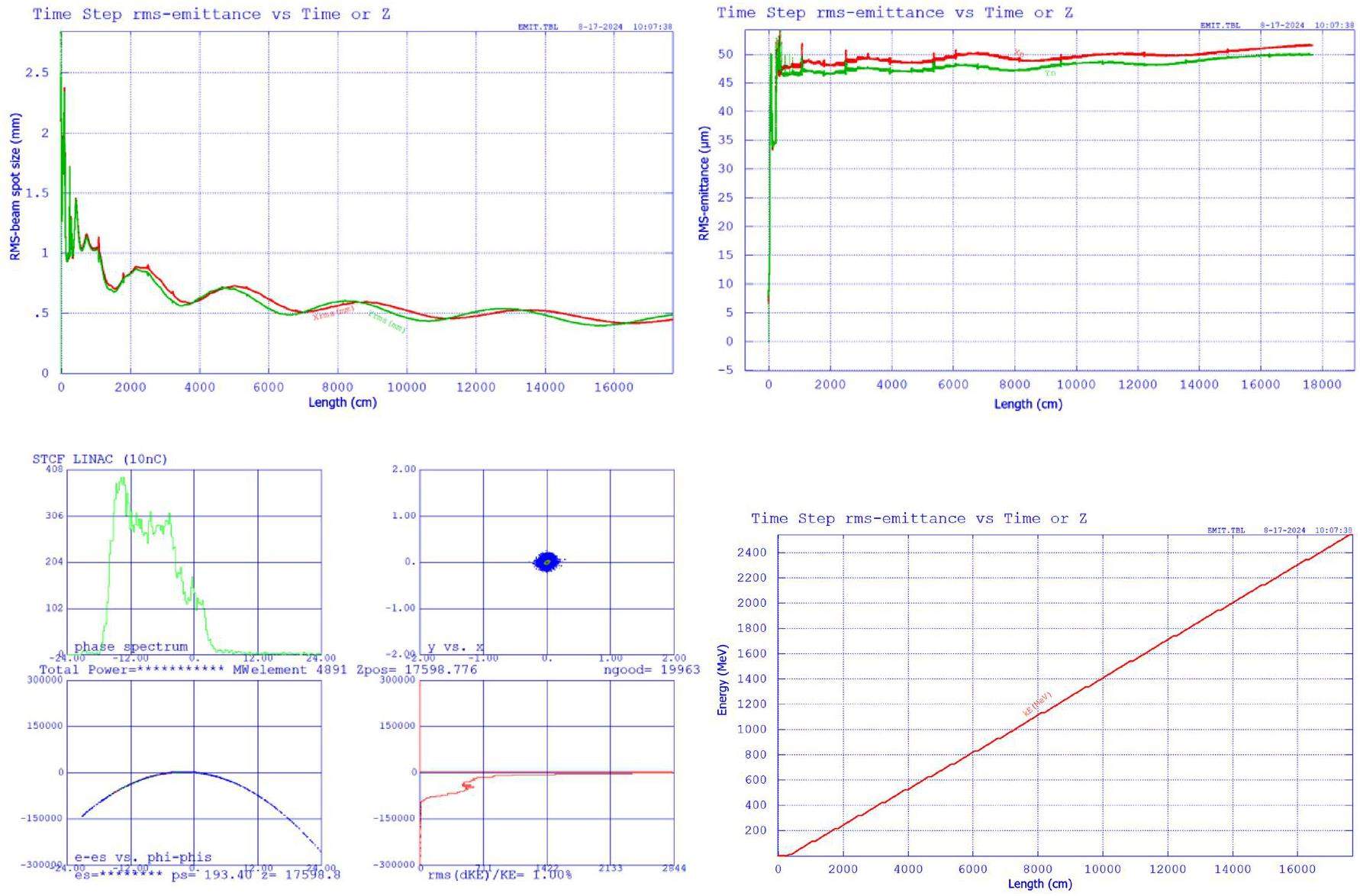
The figure shows that the rms transverse beam size at the exit is approximately 0.5 mm, with a normalized emittance of approximately 50 μm. The final energy is 2542 MeV, with a transmission efficiency of 99.8%, a bunch charge of 10.9 nC, and an rms energy spread of 1.76%, satisfying the requirements for tungsten target positron production.
As in the off-axis injection scheme, a triplet lens is placed every two 50 MeV accelerating structures before 1 GeV and every four 50 MeV accelerating structures after 1 GeV.
Positron production, capture, and pre-acceleration
The positron source is a key component of the STCF injector, responsible for generating positron bunches with sufficient quantity and quality. The STCF will adopt the conventional method of positron generation via electron beam bombardment of a target, which remains the only viable approach for producing high-intensity positron beams. Both off-axis injection and swap-out injection schemes are considered. The off-axis scheme employs a relatively low bombardment energy of 1.5 GeV, requiring careful optimization of the subsequent capture and matching accelerator systems to ensure adequate positron yield from low-energy electron beams. The swap-out injection scheme, by contrast, imposes a much higher bunch charge requirement, demanding greater positron yield and improved target heat dissipation performance. The positron source parameters for the swap-out injection scheme are summarized in Table 17.
Positron Conversion Target
For the swap-out injection scheme, the positron source must provide positron bunches with 2.5 nC at 90 Hz. Figure 137 shows the simulated positron yield for a 2.5 GeV electron beam incident on targets of different thicknesses and materials. Gold and tungsten produce the highest yields. Owing to cost considerations, tungsten is used as the target material, with an optimal thickness of 15 mm and a positron yield of 6.9 per incident electron.
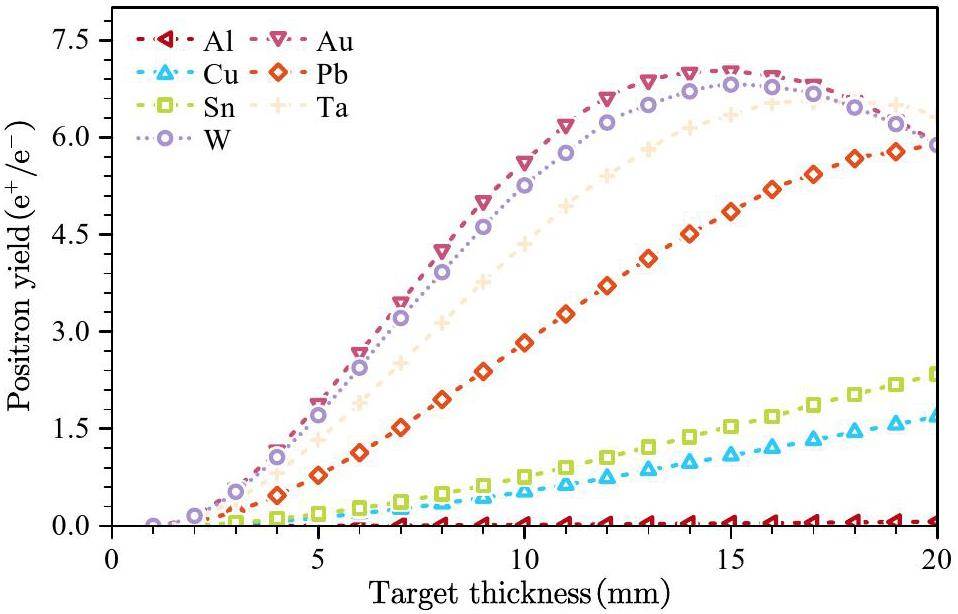
To optimize the downstream capture and acceleration of positrons, the energy and angular distribution of the positrons leaving the target must be known. Figure 138 compares the energy spectra and angular distributions of positrons produced by a 2.5 GeV electron beam with a 5% energy spread and by an ideal monoenergetic beam. The effect of the 5% energy spread on the positron distribution is found to be acceptable.
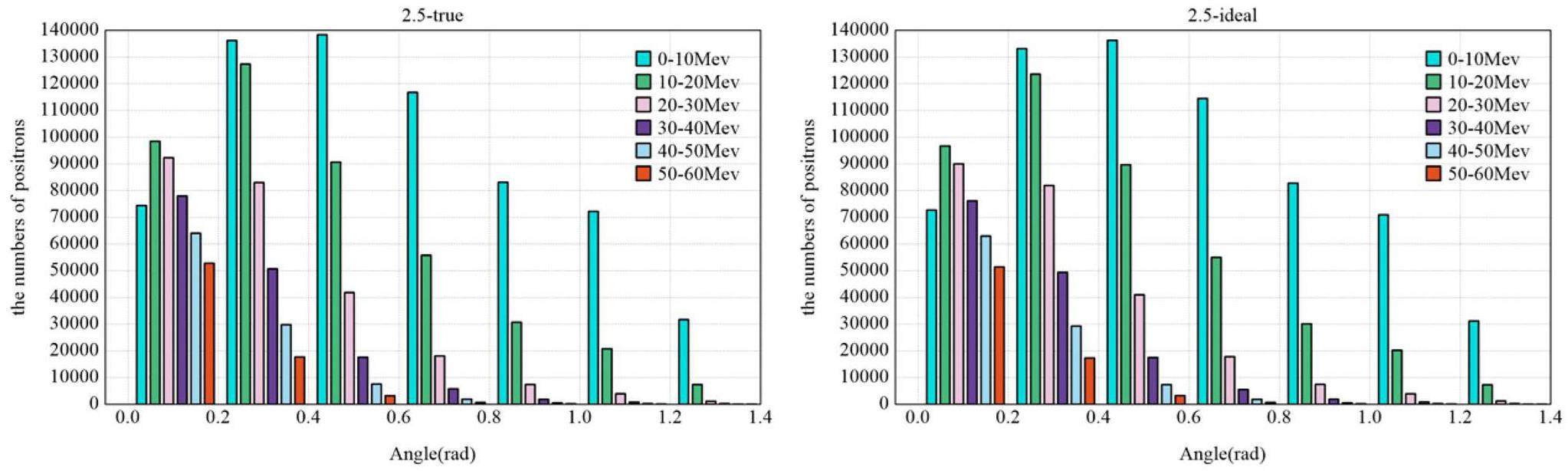
Design for the positron linac (PL)
This design, including the AMD, positron pre-accelerator, and main accelerator section, is nearly identical to the system used in the off-axis injection scheme. Therefore, it will not be discussed.
Positron accumulation ring
Design requirements and specifications
In the swap-out injection scheme of the STCF, the injector must supply full-charge electron and positron bunches of 8.5 nC to replace those in the collider rings with particle numbers less than the level required for collisions. owing to the relatively short beam lifetime, the bunches must be prepared at a high repetition rate.
Assuming the injector delivers bunches to the collider rings at a repetition rate of
To ensure that each bunch is sufficiently damped before extraction, we adopt a rotational injection mode. During the initialization phase, each of the
The bunch accumulation process uses multiple off-axis injections. The interval between injections is
Lattice design of the accumulation ring
The accumulation ring adopts a structure similar to the DR, consisting of periodic bending sections, dispersion suppression sections, and straight sections. The full ring comprises 56 periodic bending cells, 4 dispersion compression sections, and 2 straight sections. The overall ring structure is shown in Fig. 139, where blue indicates dipole magnets, red indicates quadrupole magnets, and green indicates sextupole magnets.
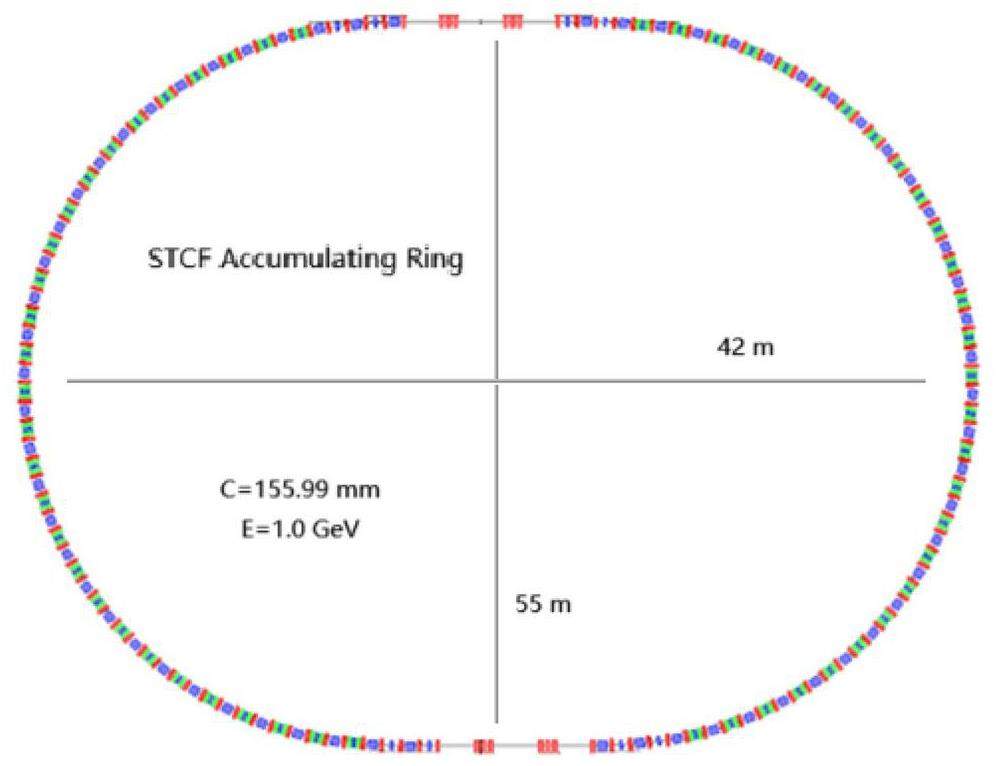
The periodic bending cell is illustrated in Fig. 140. It adopts a “one normal + one reverse” dipole layout within a FODO structure [12, 68], where the reverse dipole length is 0.3 times the normal dipole length and both have the same magnetic field strength. Each bending cell is 2.16 m long and bends positrons by 6°. The normal and reverse dipoles bend by 8.57° and 2.57°, respectively. Each cell includes one focusing quadrupole, one defocusing quadrupole, one focusing sextupole, and one defocusing sextupole.
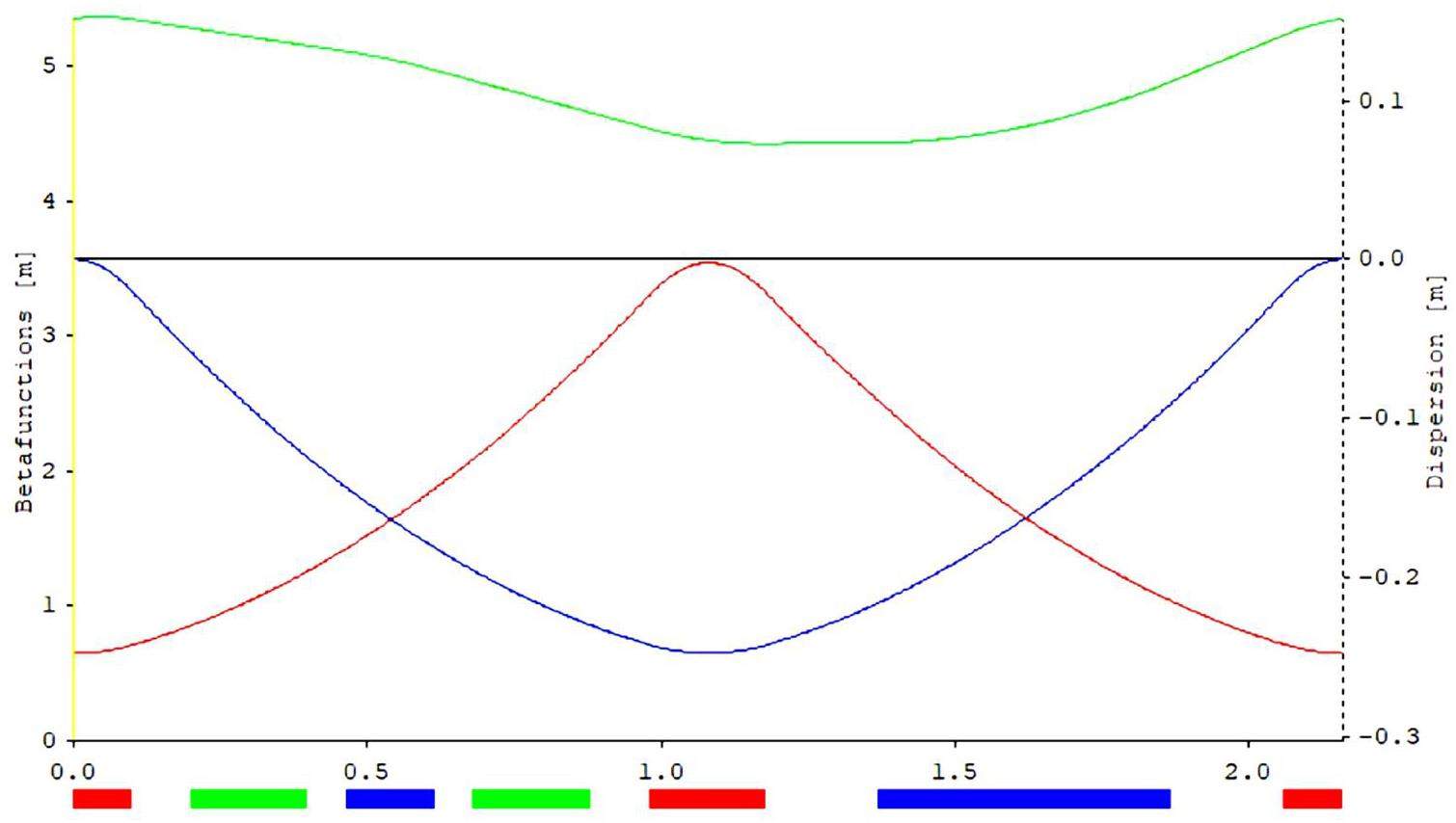
The dispersion suppression section is shown in Fig. 141. It follows a "half-bend" scheme, including two normal and two reverse dipole magnets, each with the same dimensions as those in the periodic bending cells but with half the magnetic field strength. This results in a total bend angle of 6°, matching the deflection in each bending cell.
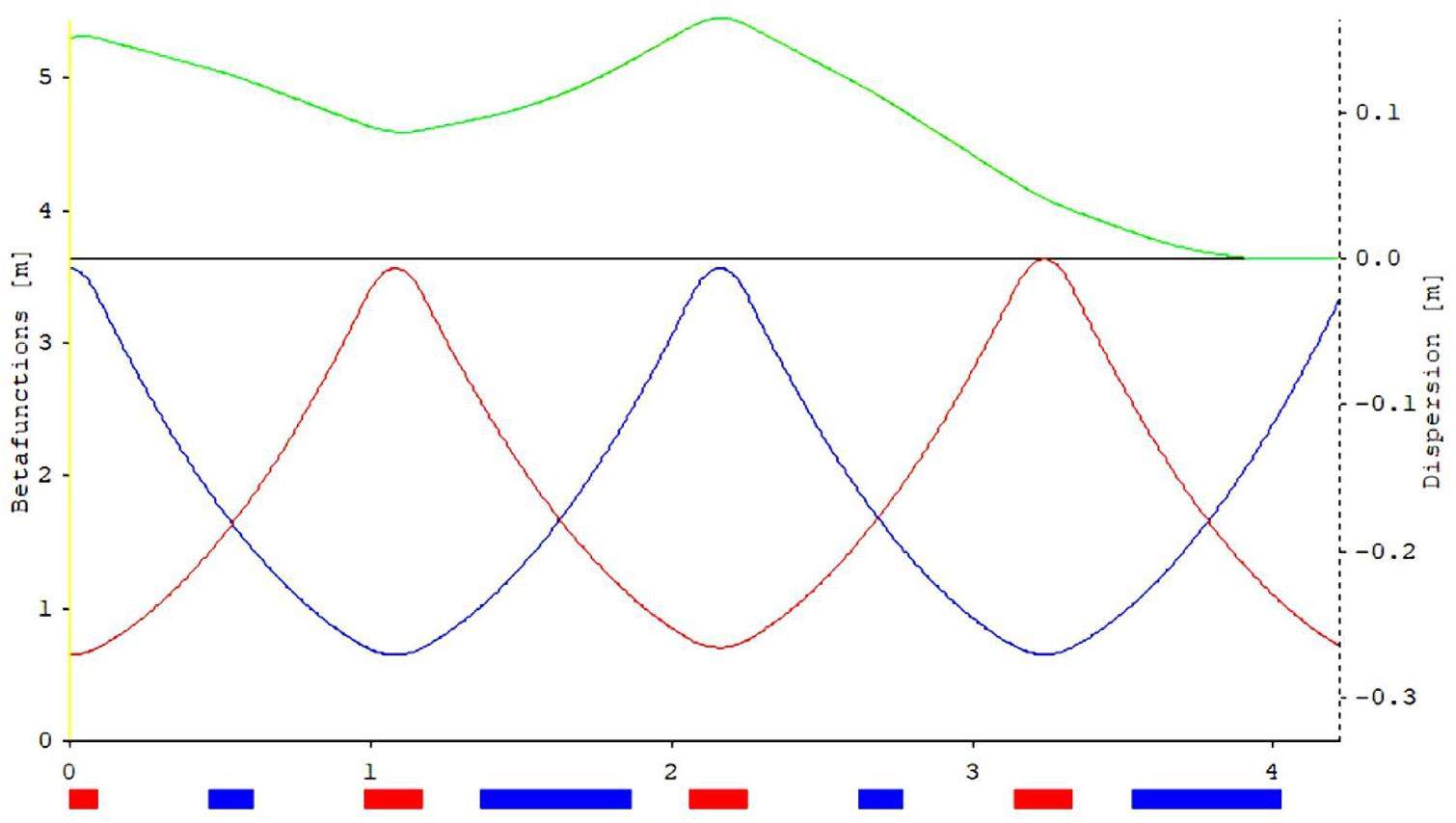
The structure of the straight section is shown in Fig. 142. Its primary function is to provide space for positron injection and extraction components, as well as RF cavities. The straight section consists of eight quadrupole magnets. After beam optics matching, the Twiss parameters at the injection/extraction point are set to βₓ = 9.5 m and βᵧ = 1 m. Downstream of this point, after three quadrupole magnets, space is reserved for the injection/extraction kicker magnet. The beam optics matching is completed across the full ring, and the full-ring Twiss parameters are shown in Fig. 143.
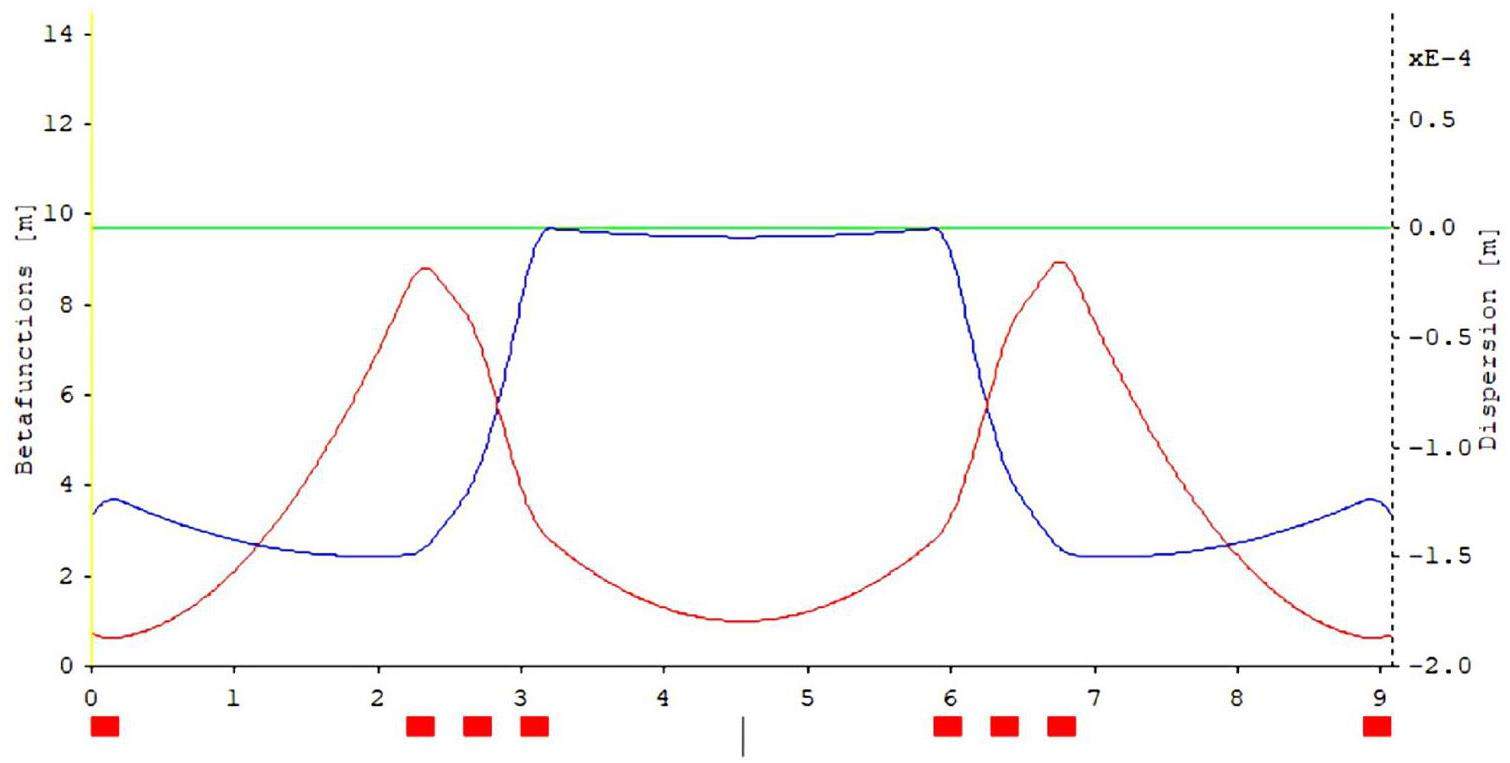
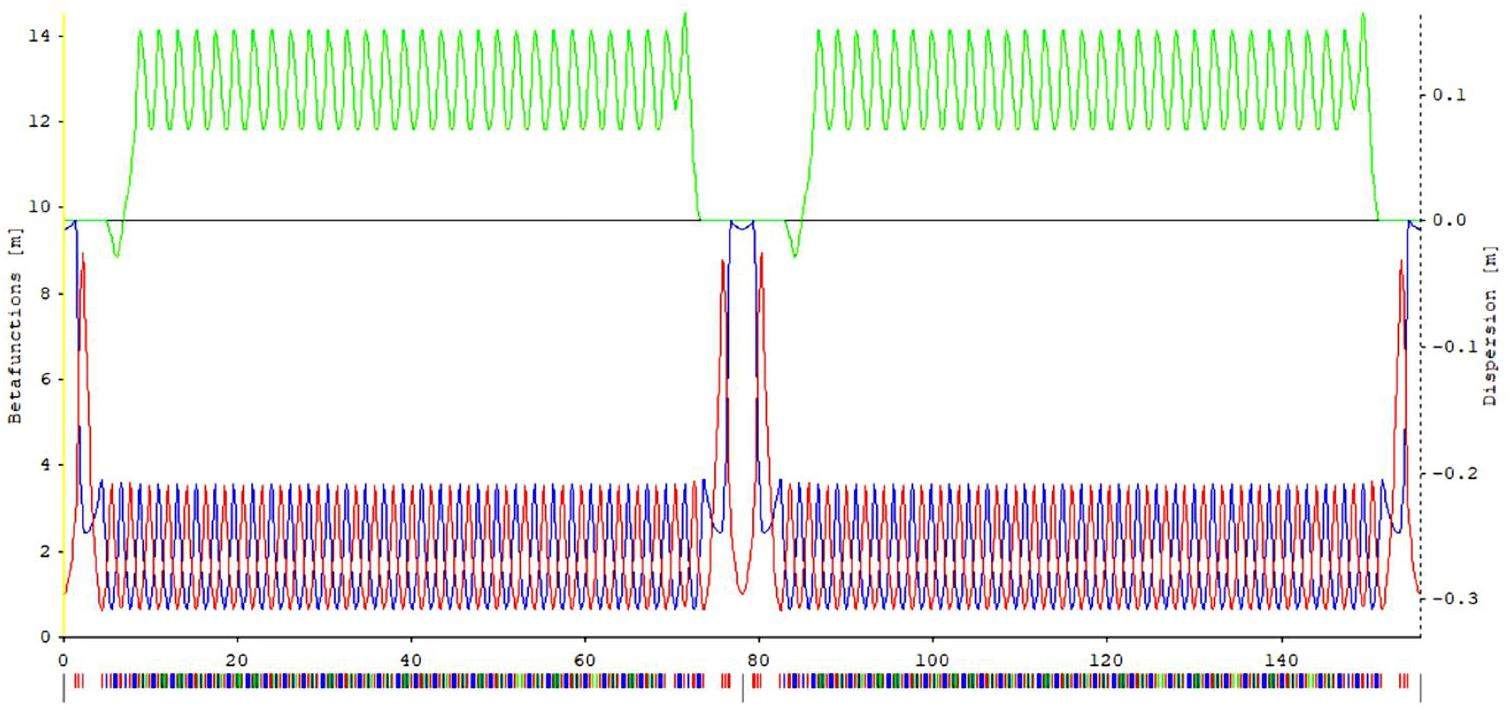
In the arc region, each periodic focusing cell provides a horizontal and vertical phase advance of 0.25·2π. After the linear optics design is completed, sextupole magnets are added in each periodic cell to correct the first-order chromaticity. The final full-ring horizontal and vertical phase advances are 16.714·2π and 17.424·2π, respectively. Figure 144 shows the working point of the accumulation ring. It is well-separated from fourth-order resonance lines, although it is relatively close to fifth-order resonances.
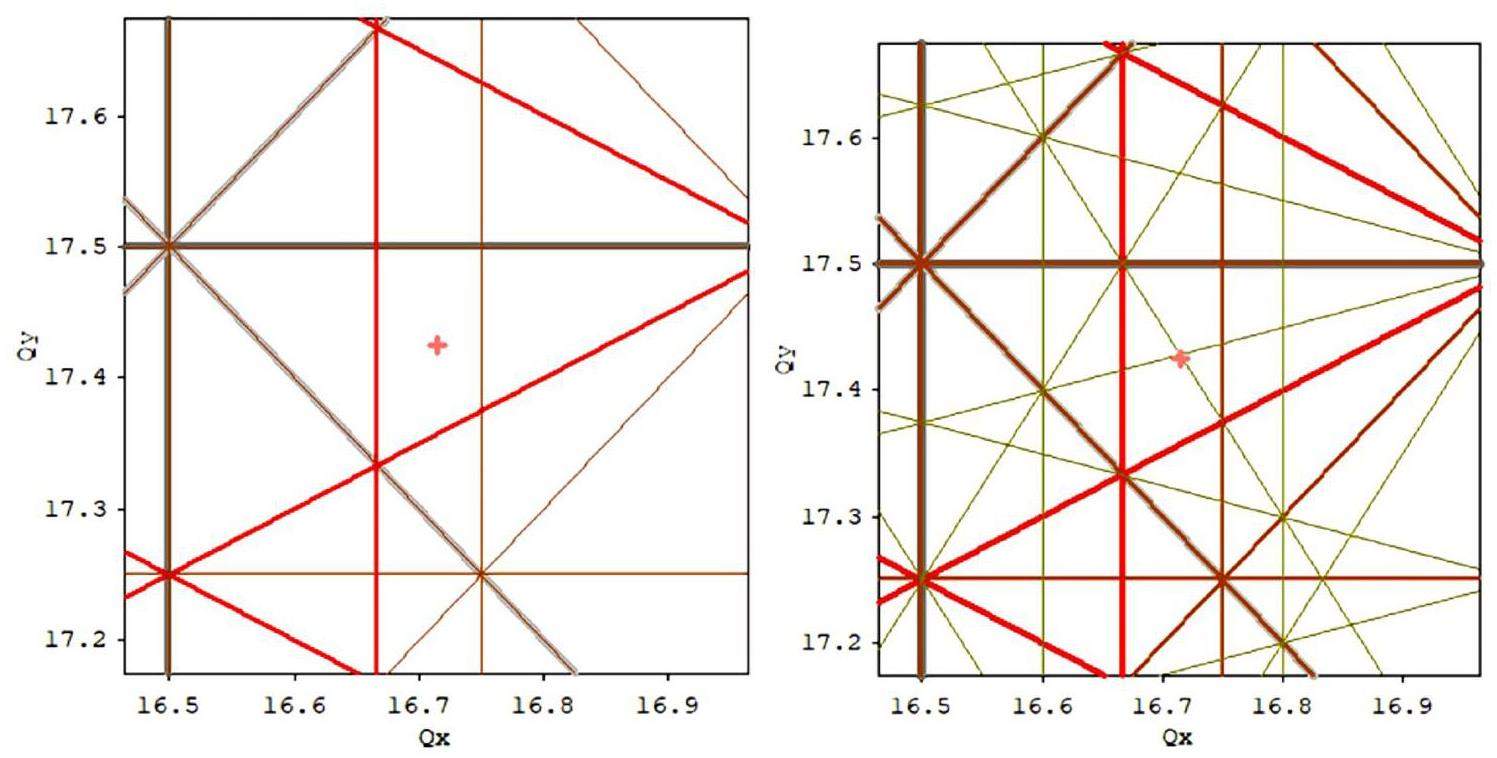
To ensure injection efficiency and reduce beam loss, the dynamic aperture must be analyzed. Dynamic apertures are influenced by nonlinear elements such as sextupoles. After correcting chromaticity with sextupoles, the impact of their nonlinearities must be considered [69]. Figure 145 shows the dynamic aperture. During injection, the positron beam envelope is approximately 3.6 mm, while the dynamic aperture in the horizontal direction is approximately 15 mm, roughly four times the beam envelope, indicating a reasonably large acceptance.
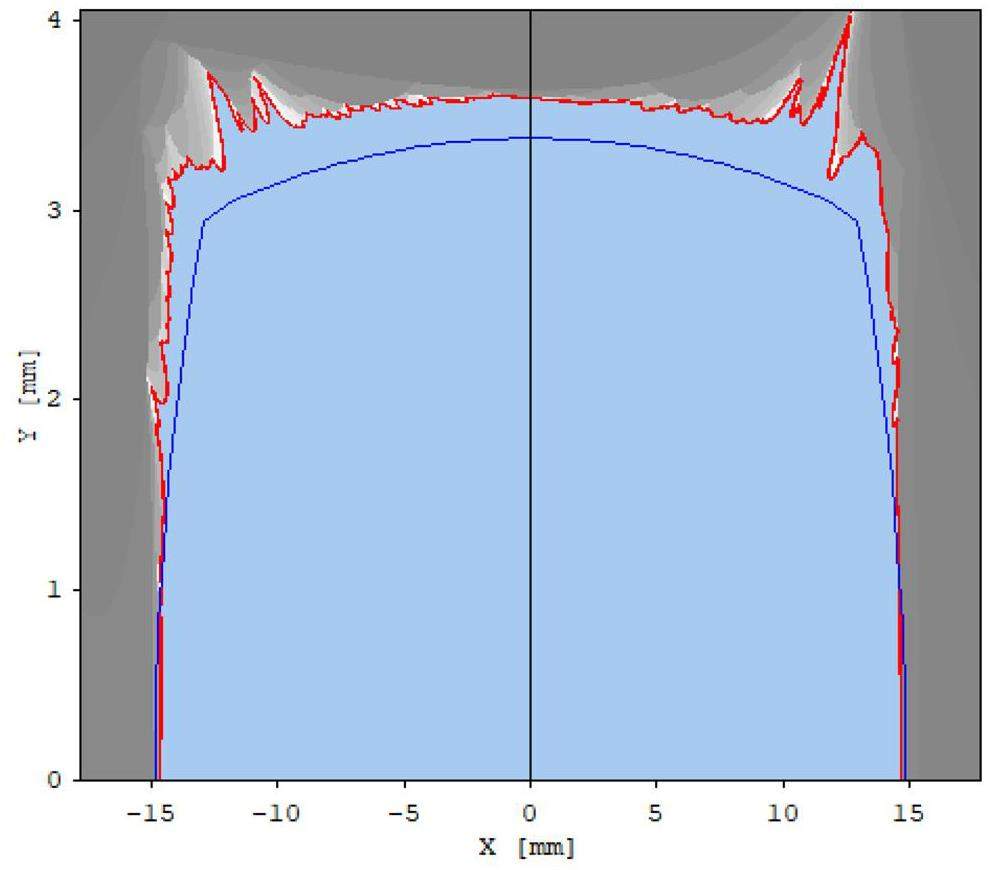
Beam lifetime is also an important factor in the design. By adjusting RF cavity voltage and frequency, harmonic number, and gas species, the beam lifetime is estimated to be approximately 140 s. Figure 146 shows the momentum acceptance, which meets the requirements for positron injection.
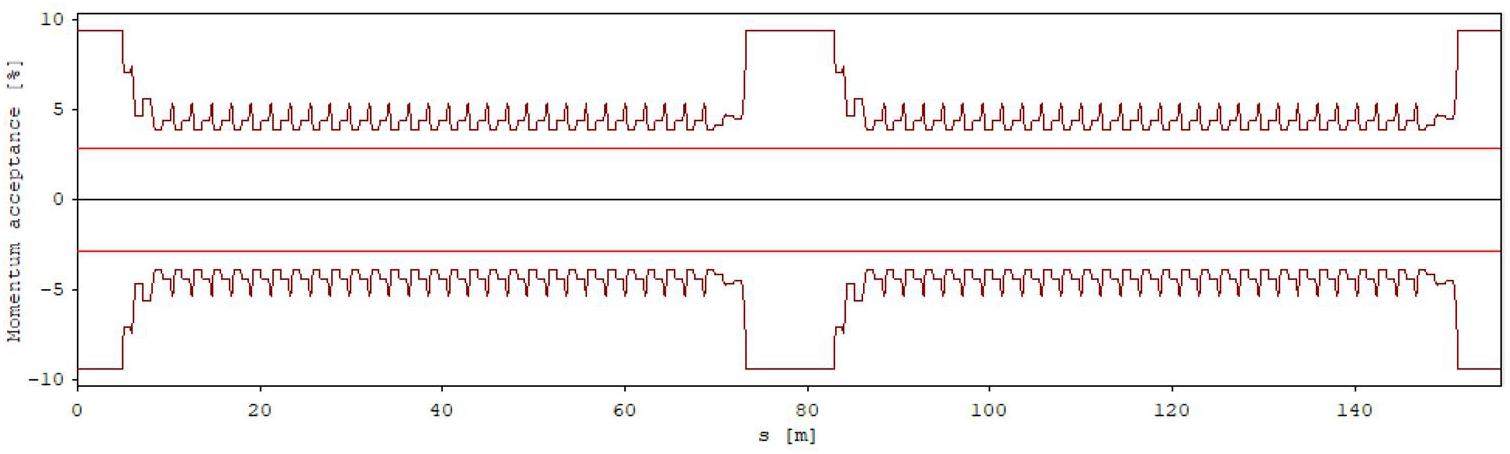
The final injection into each stored positron bunch occurs approximately 100 ms before extraction, allowing damping to occur. The extracted emittance
Here,
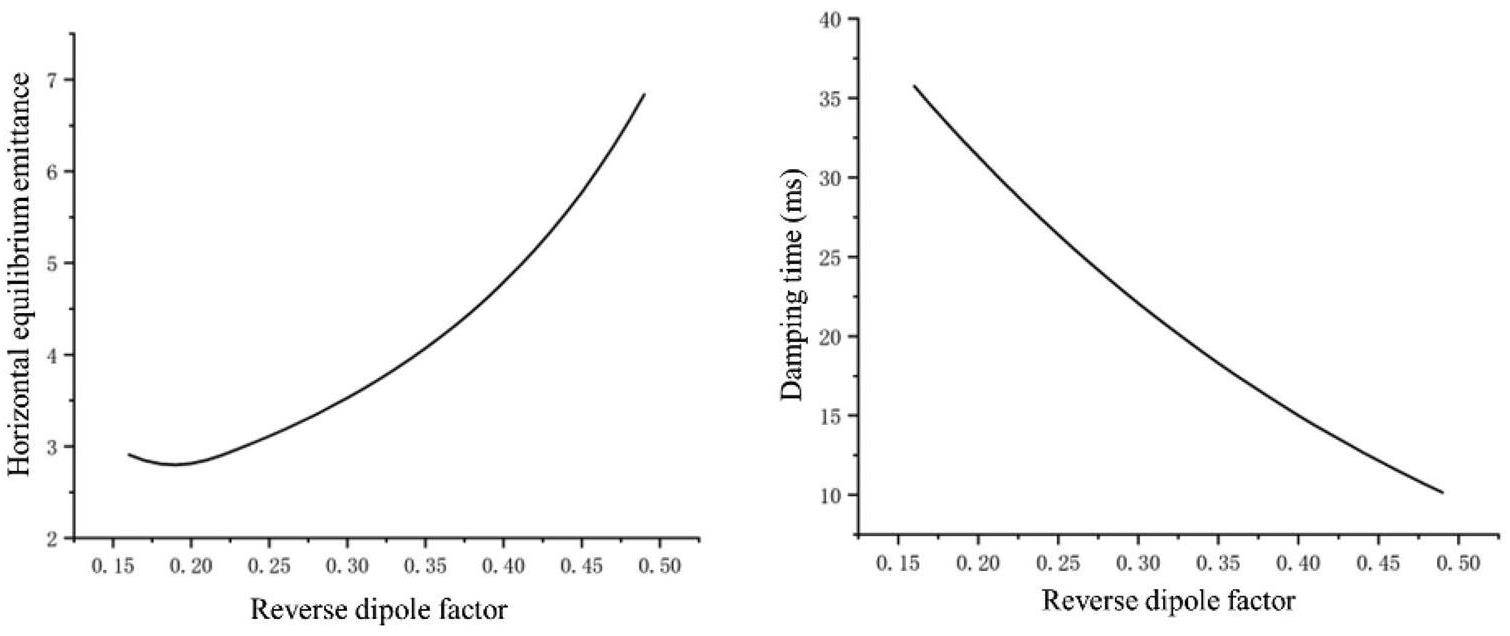
From Fig. 148, a reverse dipole magnet ratio between 0.25–0.3 yields the lowest extracted emittance. Therefore, a ratio of 0.3 is adopted as the feasible design choice. The key parameters of the accumulation ring are listed in Table 24.
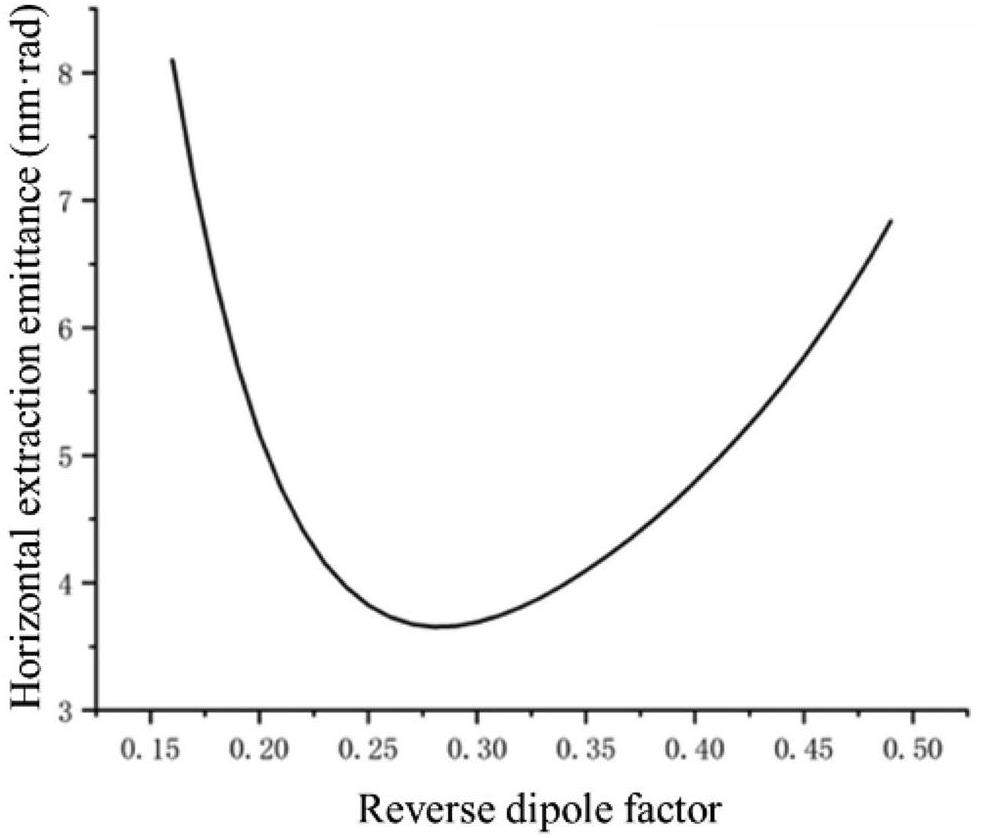
| Parameter | Value |
|---|---|
| Energy (GeV) | 1.0 |
| Circumference (m) | 155.99 |
| Number of bunches | 4 |
| Max bunch charge (nC) | 8.5 |
| Max current (mA) | 65.4 |
| FODO phase advance (x/y) (degree) | 90 / 90 |
| Dipole bending radius (m) | 3.337 |
| Dipole field strength (T) | 0.998 |
| Reverse dipole magnet ratio, r | 0.3 |
| Energy loss per turn (keV) | 47.5 |
| Damping time (x/y/z) (ms) | 21.9 / 21.9 / 11.0 |
| Storage time (ms) | 100 |
| Natural emittance (x/y) (nm·rad) | 3.52 / 0.1 |
| Injected emittance (x/y) (nm·rad) | 350 / 350 |
| Extracted emittance (x/y) (nm·rad) | 3.56 / 0.23 |
| Natural relative energy spread (%) | 0.0465 |
| Momentum compaction factor | 0.00273 |
| RF frequency (MHz) | 499.7 |
| RF voltage (MV) | 0.8 |
| Harmonic number | 260 |
| Natural chromaticity (x/y) | –21.4 / –22.3 |
| Working point (x/y) | 16.7 / 17.4 |
Beam accumulation and extraction scheme
The accumulation ring uniformly stores four bunches, each reaching the target charge after three accumulation cycles. For a given bunch, charge accumulation is performed via off-axis injection, as illustrated in Fig. 149. The positron bunch is deflected by a septum magnet toward the injection point, where a pulsed kicker magnet creates a local orbit bump that allows the injected bunch to enter the acceptance of the accumulation ring. The bump height is then gradually reduced, and the positron bunch undergoes synchrotron radiation damping to decrease its emittance.
During the first injection, the orbit bump is at its maximum height, and after injection, the bunch settles on the central orbit. For the second injection, since a circulating bunch already exists, the orbit bump must be reduced to avoid beam loss caused by interaction with the septum. The centroid of the newly injected bunch will therefore be offset from the central orbit, resulting in a substantially increased effective emittance. In the third injection, due to the short damping time, the circulating bunch still has a relatively large effective emittance, requiring a further reduction in bump height. After this injection, the beam continues to damp within the accumulation ring until it reaches the design emittance. Table 25 lists the key design parameters of the pulsed kicker magnet used for injection in the accumulation ring.
| Parameter | Specification |
|---|---|
| Injection direction | Horizontal |
| Number of accumulations | 3 |
| Kicker type | Stripline |
| Max deflection angle (mrad) | 11 |
| Effective length (mm) | 800 |
| Pulse width (ns) | < 2 |
| Rise time (ns) | < 130 |
In the current scheme, stringent requirements are imposed on the pulsed kicker magnet to minimize particle loss during accumulation. An alternative under consideration is splitting the accumulation ring into a DR and an accumulation ring. In this approach, the high-emittance positron bunch from the upstream system is damped in the DR and the low-emittance beam accumulates in the accumulation ring. This method relaxes hardware requirements and simplifies overall design complexity.
Main linac
The ML boosts the energy of the beam from the upstream electron and positron linacs from 1 GeV to 1.0 to 3.5 GeV, the injection energy required by the collider rings. Since the beam emittance from the preceding linacs is already determined, the primary design focus of this acceleration stage is to ensure sufficient energy gain.
General physics design
The ML uses the same RF frequency as the upstream linacs, 2998.2 MHz. A total of 40 RF power sources (klystrons) rated at 45–50 MW are employed. Each klystron, paired with a SLED energy multiplier, drives two 3 m-long accelerating structures. The accelerating structures operate at a phase slightly after the peak to compensate for the correlated energy spread introduced in the upstream sections, ensuring low-energy-spread acceleration from 1.0 to 3.5 GeV before injection into the collider rings. The layout of the accelerating units is shown in Fig. 150.
To prevent excessive beam envelope divergence, a quadrupole lens is installed in each drift section between two accelerating structures. Beam diagnostic elements are positioned between each power unit to monitor beam parameters. At the ML exit, quadrupole magnets and diagnostic instruments are placed between every two accelerating structures to facilitate matching with the downstream bending section and collision region, as illustrated in Fig. 151.

Quadrupole magnets located before and after the magnetic bunch compressor must be carefully configured to control the coherent synchrotron radiation (CSR) effect during compression and to enable post-compression beam diagnostics. Based on the lattice layout described above, the strengths of the quadrupole magnets in the triplet groups and FODO cells are optimized to ensure that the beam’s horizontal and vertical β-functions exhibit periodic oscillations in the L3 and L4 sections. In addition, appropriate quadrupole magnets are reserved at the entrance of the transport line to achieve Twiss parameter matching. The overall Twiss function distribution in the ML is shown in Fig. 152.
Error analysis
Longitudinal error analysis
Equipment parameter errors are the primary sources of beam parameter variations and can generally be categorized into longitudinal and transverse components. Longitudinal beam parameters—such as bunch length, energy, and arrival time—are affected by injected bunch charge and timing, amplitude and phase errors of the accelerating fields, and variations in the R56 of the bunch compressor.
Installation errors and vibrations in dipole and quadrupole magnets, magnetic field imperfections, and higher-order field components can lead to orbit deviations, residual dispersion, Twiss parameter mismatches, and emittance growth. Likewise, misalignment and vibration of accelerating structures induce transverse wakefields, resulting in additional orbit deviations and further emittance growth.
These errors can be classified by their timescales and bandwidths into static, slow-drift, and fast-varying categories. Static and slow-drift errors can be corrected using dedicated algorithms and slow feedback systems, whereas fast-varying errors must be mitigated by improving equipment stability to keep their effects within acceptable limits.
Given the similarities in analysis methods across subsystems, this subsection focuses on evaluating the effects of various errors and jitters on the beam in the S-band photoinjector under 1 nC operation (prior to 1 GeV) in the off-axis injection scheme. The beam jitter requirements at the injector exit, as determined by the collider ring physics goals, are summarized in Table 26.
| Parameter | Value |
|---|---|
| Energy jitter (%) | < 0.2 |
| Peak current jitter (%) | < 10 |
| Timing jitter (fs) | < 100 |
These variations are mainly driven by injection charge and timing jitter, RF phase and amplitude errors, and magnetic field deviations in the bunch compressor. Since different systems have multiple correlated sources and different achievable error margins, individual subsystems must have reasonable error tolerances.
Simulations were performed at various operating points, analyzing the sensitivity of beam jitter to each type of equipment jitter. The normalized sensitivities and final results are summarized in Table 27.
| Jitter source | Value | ΔE (%) | ΔI (%) | Δt (fs) |
|---|---|---|---|---|
| inj_dt | 0.25 ps | 0.0000 | 0.4333 | 17.20 |
| inj_dQ | 5% | 0.0390 | 2.5133 | 49.80 |
| L1_pha | 0.1° | 0.0525 | 0.0333 | 20.27 |
| L1_amp | 0.1% | 0.0207 | 5.3867 | 4.47 |
| Lx_pha | 0.4° | 0.0062 | 0.0400 | 3.53 |
| Lx_amp | 0.04% | 0.0037 | 0.2667 | 3.20 |
| L2_pha | 0.1° | 0.0093 | 0.0267 | 4.73 |
| L2_amp | 0.1% | 0.0140 | 0.0400 | 7.10 |
| L3_pha | 0.1° | 0.0157 | 0 | 0 |
| L3_amp | 0.1% | 0.0166 | 0 | 0 |
| L4_pha | 0.1° | 0.0157 | 0 | 0 |
| L4_amp | 0.1% | 0.0166 | 0 | 0 |
| BC1_R56 | 0.01% | 0.0047 | 0.0333 | 5.77 |
| Total | 0.08 | 5.97 | 57.75 |
As shown above, the beam stability at the S-band photoinjector exit meets the downstream collider ring injection requirements.
Transverse Errors and Correction
Due to unavoidable manufacturing and installation imperfections, components in the ML—particularly magnets—may introduce mechanical alignment errors. These errors produce non-ideal magnetic fields, leading to orbit distortions that can cause beam emittance growth and, in severe cases, beam loss due to excursions beyond the dynamic aperture. Therefore, precise control and correction of beam trajectory deviations are essential.
Because BPMs are also subject to alignment errors, BBA techniques are employed to calibrate and eliminate these offsets. Subsequent trajectory correction is performed using one-to-one, global, or dispersion-free correction methods to align the beam path as closely as possible with the ideal orbit.
Numerical simulations were conducted using the Elegant code’s built-in BBA and global correction algorithms. The initial error settings are summarized in Table 28. The results show that orbit distortions caused by these initial errors can be effectively corrected, with horizontal deviations reduced from the millimeter to the sub-100 μm level. Future simulations will incorporate more realistic error budgets to further refine the feedback and control system.
| Component | Δx/Δy (μm) | Δθ (mrad) | ΔK/K or ΔB/B (%) |
|---|---|---|---|
| Dipole magnets | 100 | 1 | 0.01 |
| Quadrupole magnets | 100 | 1 | 0.1 |
| BPMs | 100 | - | - |
| Accelerating tubes | 100 | - | - |
Using the global BBA correction method, Fig. 153 shows the horizontal trajectories of various seeds before and after correction. Pre-correction orbit deviations reached several mm, with values exceeding 10 mm near the bunch compressor. After correction, orbit deviations were reduced to below 100 μm, meeting the design requirements.
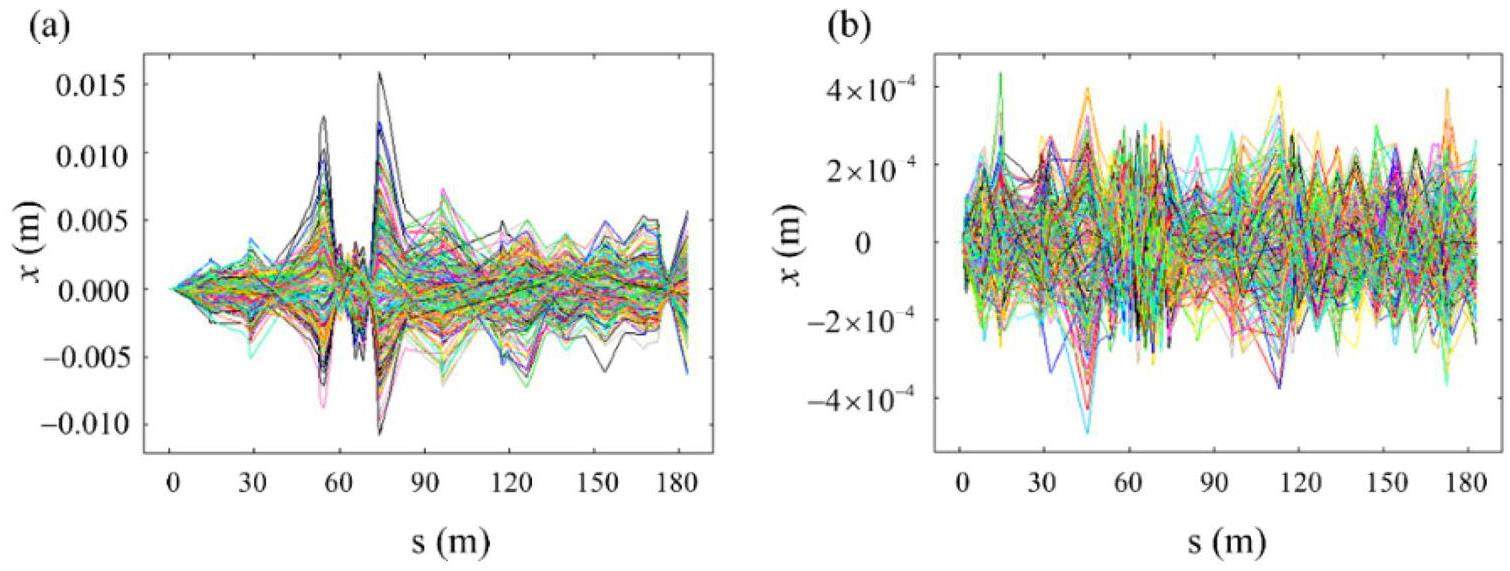
Off-axis beam injection and component misalignments introduce wakefield effects, leading to emittance growth. To evaluate this, simulations were performed on worst-case seed (i.e., largest pre-correction orbit deviation in Fig. 153). The results in Fig. 154 show that after BBA correction, the emittance growth due to wakefields is limited to within 10%.
Error analysis and correction for the ML follow the same procedures described above. Since the injection energy for the collider rings is adjustable from 1 to 3.5 GeV, the ML layout remains unchanged. When operation at a lower beam energy is required, some accelerating structures are switched off; however, wakefields induced by the passing bunches still degrade beam quality. By tuning the RF phase of the active accelerating structures, the energy spread increase from longitudinal wakefields can be effectively suppressed, while the transverse emittance growth caused by transverse wakefields is similarly controlled after BBA correction. The main beam parameters at ML exit energies of 1, 2, and 3.5 GeV are summarized below (Table 29).
| Energy | 1 GeV | 2 GeV | 3.5 GeV | |
|---|---|---|---|---|
| Rms energy spread (%) | 0.0783 | 0.0534 | 0.074 | |
| Rms bunch length (ps) | 1.5669 | 1.5671 | 1.5667 | |
| Nor. transverse emittance (μm·rad) | ||||
| x | 2.187 | 2.175 | 2.166 | |
| y | 1.678 | 1.499 | 1.449 | |
| Rms beam size (μm) | ||||
| x | 113.66 | 81.09 | 60.91 | |
| y | 152.95 | 109.18 | 82.04 | |
Beam transport lines
For collider rings with off-axis injection, the injector's beam transport lines are divided into five parts based on their regions and functions: the electron bypass section (Bypass), the DR transport section, the electron accumulation ring section, the positron accumulation ring section, and the injection transport sections to the collider rings. The Bypass and DR transport sections are used in the off-axis injection scheme, while the electron and positron accumulation ring are used in the swap-out injection scheme. The injection transport sections to the collider rings are shared by both schemes.
The transport sections of the positron damping and accumulation rings have one injection line and one extraction line. The injection transport sections of the collider rings have one transport line for the electron beam and one for the positron beam.
Bypass section
To reduce the cost and footprint of the linac during positron production, a beam bypass drift section is typically implemented to extract electron beams that have been accelerated to a specific energy. These beams can then either proceed to higher energy stages or serve as drive beams for the positron source. This approach is commonly adopted in facilities such as SuperKEKB, the Tau/Charm Factory, and CEPC. In this design, the Bypass section branches off from the 1 GeV electron linac, deflects horizontally to bypass the positron linac, and rejoins at the entrance of the 3.5 GeV positron/electron ML.
A schematic layout of the Bypass section is shown in Fig. 155. The total straight-line distance from start to end is approximately 160 m, with a horizontal offset of approximately 6 m from the linac. The Bypass section employs eight dipole magnets for beam steering, 35 quadrupole magnets for transverse focusing, and energy slits located in the bending regions for beam scraping and energy spread control. At the entrance of the Bypass, the electron beam parameters are as follows: 1.0 GeV energy, 0.2% rms energy spread, 1.5 nC charge, and 2 mm·mrad rms normalized emittance.

The beam optics of the Bypass section were matched using the MAD code. For initial Twiss parameters of βₓ,y = 20 m and αₓ,y = 1, the lattice layout and optical design results are shown in Fig. 156. The optimized Twiss parameters at the exit are βₓ,y = 20 m and αₓ,y = –1. The β-functions are symmetrically distributed and maintained below 50 m throughout the transport line, oscillating between 10 m and 40 m in the straight sections. The dispersion function reaches a maximum of 1.3 m in the bending region, which is sufficient for installing an energy slit, while both the dispersion and its derivative are zero in the straight sections. The transverse focusing system retains adjustment capability, allowing the lattice parameters to be tuned to match the downstream optical requirements of the positron and electron MLs under different initial conditions.
Beam dynamics tracking was carried out using the Elegant code. The simulated rms beam size and normalized emittance are shown in Fig. 157. The beam size and emittance exhibit symmetric distributions, with an rms beam size of approximately 0.2 mm at the exit. The normalized emittance is 2.14 mm·mrad horizontally and 2.0 mm·mrad vertically, showing only a 7% increase in the horizontal direction—meeting the requirements of both the ML and the collider rings. Owing to the Bypass transport line's R56 design value of 0.4 m, the bunch length increases slightly, while the energy spread remains nearly unchanged.
Damping ring transport section
Meeting the bunch length, energy spread, and β-functions at injection and extraction requirements of the positron DR requires the dedicated design of a transport line connecting the DR and the positron linac. Before injection into the DR, the positron beam must pass through an energy compression system (ECS) to reduce energy spread and meet the ring's energy acceptance requirements. After extraction from the DR, the positron beam must pass through a bunch compression system (BCS) to shorten the bunch length for appropriate matching with the subsequent linac.
A schematic layout of the DR transport section is shown in Fig. 158. The light red and dark red lines represent the injection and extraction lines, respectively. The lengths of both lines are approximately 95 m. The injection line consists of two chicane-based ECSs, a horizontal bending arc, and matching section. In total, 14 dipole magnets are used for horizontal steering and the chicane system, along with 30 quadrupole magnets for transverse focusing. Additionally, an approximately 1.3 m accelerating structure is used to provide an energy chirp for compression. The extraction line shares the same structure as the injection line, with only modifications to the chicane bend angles to accommodate different compression requirements.
At the entrance of the injection line, the positron beam has an energy of 1.0 GeV, an rms energy spread of 0.6%, a bunch charge of 1.5 nC, an rms bunch length of 1.5 mm, and rms normalized emittances of 165 mm·mrad horizontally and 75 mm·mrad vertically. Optics matching was performed using the MAD code. For initial Twiss parameters of βₓ = 10 m, βy = 55 m, αₓ = –1, and αy = 2, the lattice layout and optical design results are shown in Fig. 159. The optimized Twiss parameters at the exit are βₓ = 2 m, βy = 8 m, αₓ = 2, and αy = 0. The β-functions are symmetrically distributed, and the dispersion function reaches a maximum of 2.5 m in the Chicane section, while both the dispersion and its derivative are zero in the matching section. The transverse focusing system provides sufficient flexibility for optics matching under various initial beam conditions to satisfy the damping ring’s optics requirements.
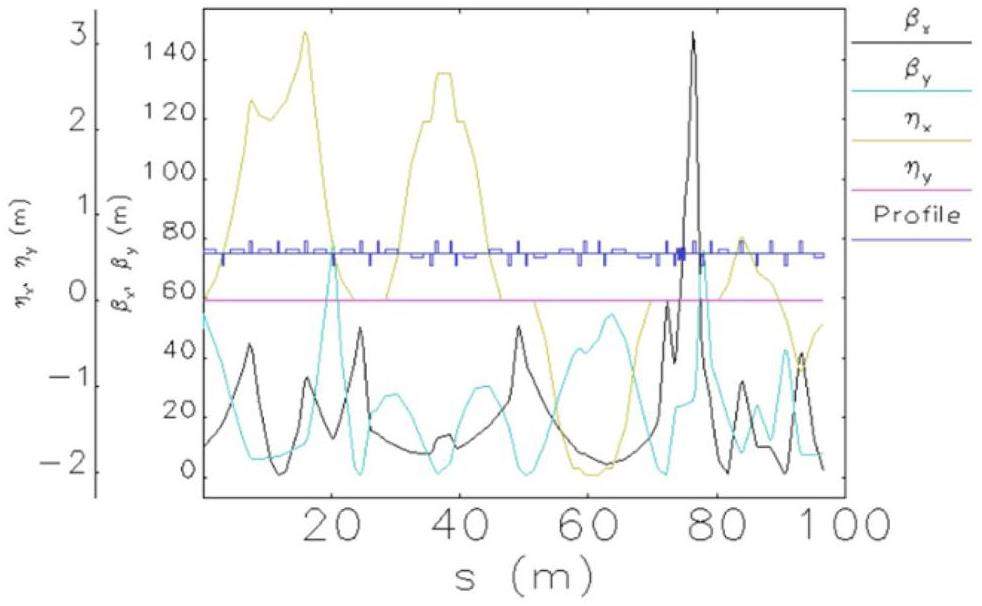
Beam dynamics tracking was carried out using the Elegant code. The simulated rms beam sizes and geometric emittances (with dispersion effects removed) are shown in Fig. 160. Just before injection into the DR, the rms horizontal and vertical beam sizes are both approximately 0.6 mm. The geometric emittances are 80 nm·rad horizontally and 39 nm·rad vertically, corresponding to emittance growths of 4.4% and 13.3%, respectively—both within the damping ring’s acceptance requirements.
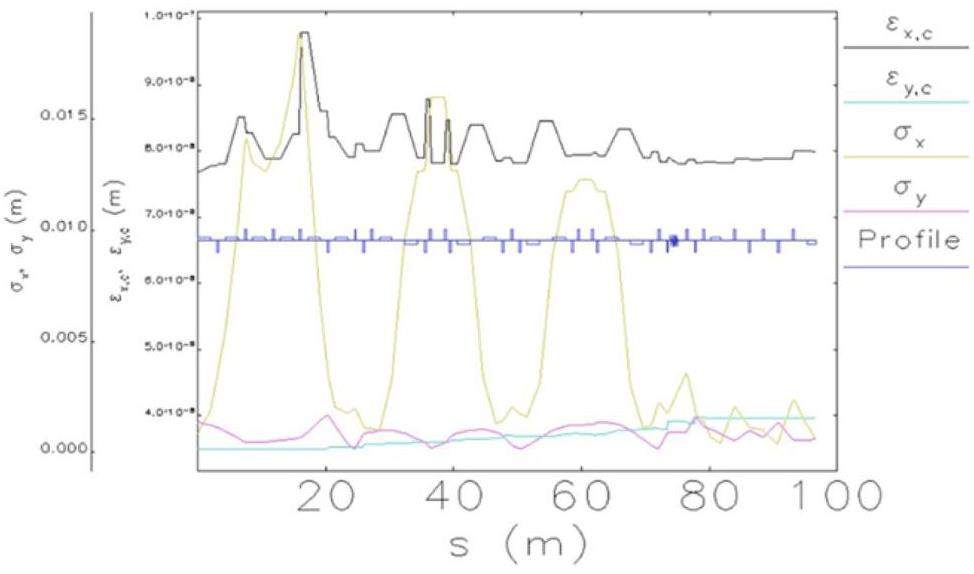
The transport matrix element R56 of the injection line is designed to be –1.48 m. Consequently, the rms bunch length increases to 9.1 mm, while the rms energy spread is reduced to 0.16%. A comparison of the energy distributions at the entrance and exit of the transport line is shown in Fig. 161, clearly demonstrating the expected energy compression effect.
Positron accumulation ring transport section
In the swap-out injection scheme, the positron beam must first be accumulated in the accumulation ring to reach the required bunch charge before being further accelerated and injected into the collider positron ring. The beam energy and quality in the positron accumulation ring transport line are similar to those in the DR transport section, and thus, the design can follow that of the positron DR transport system.
Collider ring injection transport section
The collider ring tunnel is assumed to be at ground level, while the injector is located partially underground, with a vertical height difference of 6.5 m. Consequently, the transport section connecting the injector to the collider ring consists of three main parts: a beam-splitting unit (±10° separation), a horizontal bending section, and a vertical bending section. The schematic layout is shown in Fig. 162. In this layout, the blue line represents the electron transport line, and the red line represents the positron transport line. The electron and positron beams are bent from two different directions and injected into opposite straight sections of the collider rings, located symmetrically to the IP.
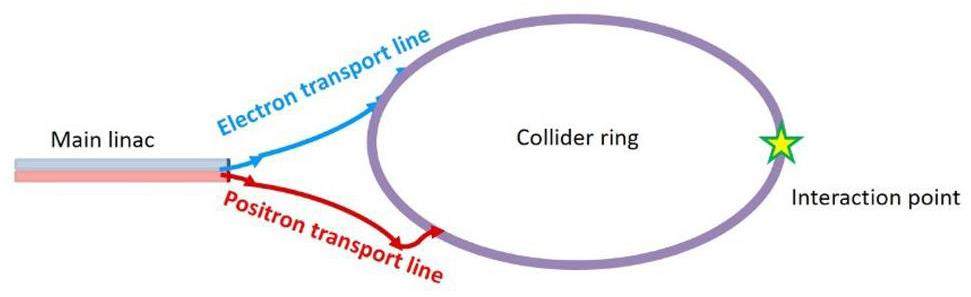
Taking the electron beamline as an example, the optical design of the horizontal bending section is shown in Fig. 163. This section comprises five 10° dipole magnets and twelve quadrupole magnets. The dispersion function is designed to be zero. The horizontal and vertical β-functions are 12.88 m and 1.404 m, respectively, with both α-functions set to zero. The evolution of the normalized horizontal and vertical emittances (excluding local growth due to energy spread in dispersive regions) is shown in Fig. 164. Compared with the initial values, the horizontal and vertical emittances increase by 33.3% and 1%, respectively. The bunch length increases slightly, while the energy spread remains nearly unchanged.
The optical design of the vertical bending section is shown in Fig. 165. This section consists of four 10° dipole magnets and eight quadrupole magnets. The dispersion function is also designed to be zero, with horizontal and vertical β-functions of 12.88 m and 1.404 m, respectively, and both α-functions equal to zero. The evolution of the normalized horizontal and vertical emittances (again excluding dispersion-induced growth) is shown in Fig. 166. Compared with the initial values, the horizontal emittance increases by 1%, while the vertical emittance increases by 54%. At the end of the electron beamline, the horizontal geometric emittance is approximately 1.2 nm·rad.
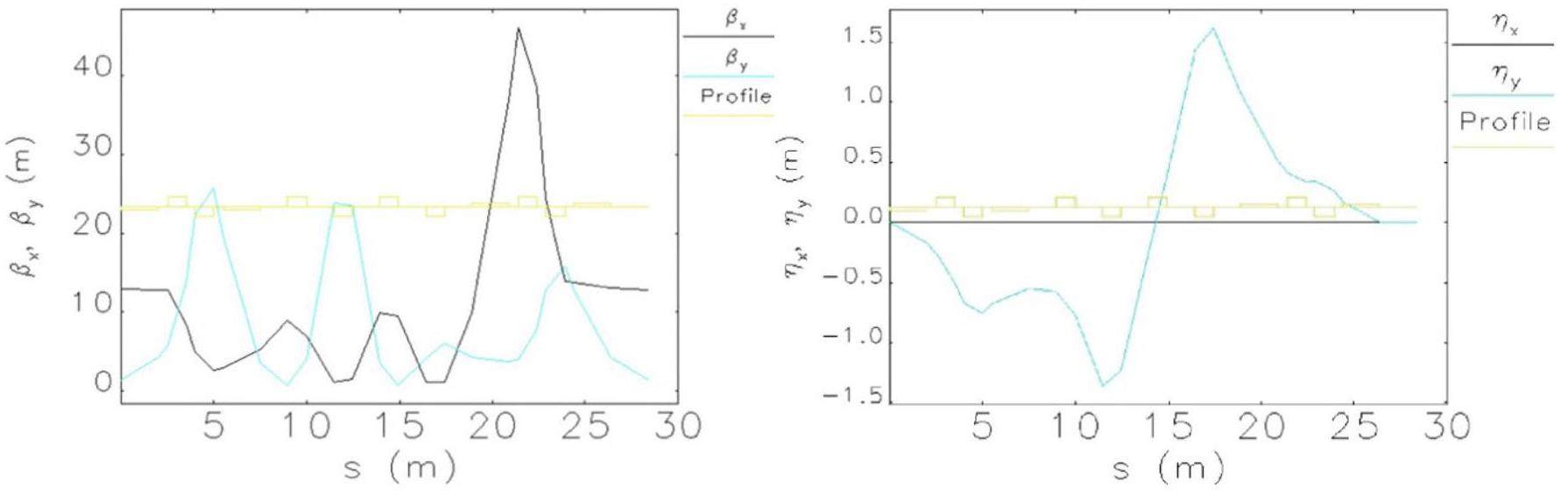
The collider ring injection transport lines comprise a total of eighteen 2 m dipole magnets and forty 1 m quadrupole magnets. Each transport line is approximately 100 m long and is designed with sufficient matching space and tuning flexibility. Particle tracking results confirm that the transverse emittances and Twiss parameters of the beams at the end of the line meet the injection requirements of the collider rings.
Compatible injector scheme for off-axis and swap-out injections
This scheme builds upon the previously described off-axis and swap-out injection concepts. While recognizing the performance advantages of the swap-out scheme and the cost-effectiveness and implementation simplicity of the off-axis approach, the core objective is to ensure that the STCF meets its stringent performance targets while enabling an initial construction based on the off-axis injection system that can later be upgraded to swap-out mode with minimal structural modifications. The main design parameters of the compatible injector scheme are summarized in Table 30.
| Parameter | Off-axis injection | Swap-out injection |
|---|---|---|
| Electron gun type | L-band photocathode / thermionic | L-band photocathode / thermionic |
| Linac RF frequency (MHz) | 2998.2 | 2998.2 |
| Electron bunch charge for collider e– ring (nC) | 1.0 | 8.5 |
| Positron bunch charge for collider e+ ring (nC) | 1.0 | 8.5 |
| Bunch energy/nominal energy (GeV) | 1.0–3.5 / 2.0 | 1.0–3.5 / 2.0 |
| Electron bunch geometric emittance (X/Y) (nm·rad) | ≤6 / 2 | ≤30 / 10 |
| Positron bunch geometric emittance (X/Y) (nm·rad) | ≤6 / 2 | ≤30 / 10 |
| Rms energy spread (%) | ≤0.1 | ≤0.25 |
| Rms bunch length (mm) | <7 | <7 |
| Electron injection repetition rate (Hz) | 30 | 30 |
| Positron injection repetition rate (Hz) | 30 | 30 |
| Positron target beam energy (GeV) | 1.0 | 2.5 |
| Positron target beam repetition rate (Hz) | 30 | 90 |
| Positron preparation ring type | Damping ring | Damping + Accum. ring |
| Preparation ring input bunch charge (nC) | 1.0 | 2.9 |
| Input emittance (X & Y) (nm·rad) | ≤350 | ≤350 |
| Input energy spread (%) | ≤0.1 | ≤0.3 |
| Output emittance (X / Y) (nm·rad) | ≤11 / 0.2 | ≤30 / 0.2 |
The layout of the compatible injector is shown in Fig. 1c. The specific strategy of the compatible injector scheme is as follows:
1. The injector layout is designed to satisfy the requirements of the swap-out scheme, but the initial accelerator hardware installation only needs to meet the off-axis injection specifications.
2. For the electron beam directly injected into the collider electron ring, an L-band PC electron gun is employed (as described in Sect. 3.3.1.2). The off-axis mode uses a bunch charge of 1.0 nC, whereas the swap-out mode operates with 8.5 nC.
3. For the electron linac used for positron production, the electron source delivers 11.6 nC in both modes. In off-axis mode, 1.0 GeV/30 Hz electron beams are used to strike the positron target; in swap-out mode, 2.5 GeV/90 Hz beams are used, which requires upgrading part of the transport line to a new 1.5 GeV linac section.
4. The positron target adopts a replaceable configuration—a conventional fixed tungsten target is used in off-axis mode, while a rotating tungsten target is used in the swap-out scheme.
5. The positron linac operates at 30 Hz in the off-axis mode and 90 Hz in the swap-out mode, both delivering 1.0 GeV output energy.
6. For positron damping and accumulation, a dual-ring configuration is employed. Initially, only the DR is constructed for off-axis injection. When upgraded to swap-out injection, an accumulation ring of the same circumference is added 0.8 m above the DR. Positrons first undergo emittance reduction in the DR, then are transferred to the accumulation ring to increase the bunch charge to 8.5 nC. The extraction repetition rates of the damping and accumulation rings are 90 Hz and 30 Hz, respectively.
7. The ML provides 2.5 GeV beam energy at a combined repetition rate of 30 Hz + 30 Hz for electrons and positrons. The bunch charges for off-axis and swap-out injection are 1.0 nC and 8.5 nC, respectively.
Technical system design
Conventional magnets and damping wigglers
Technical requirements and scope
In the STCF accelerator complex, aside from the superconducting magnets in the IR, this system is responsible for the design of all other magnets, including those in the collider rings, damping (or accumulation) rings, linacs, and beam transfer lines. It also covers the DW magnets in the collider rings. The magnet parameters and requirements are provided by the collider ring accelerator physics group and the injector accelerator physics group, respectively. The objective is to design all magnets to meet the performance specifications defined by the beam physics.
Based on current beam dynamics designs, the collider rings use dipole, quadrupole, sextupole, and DW magnets (octupoles and correctors are not yet finalized). The damping/accumulation ring magnets include dipoles, quadrupoles, and sextupoles. The electron and positron linacs include solenoid steering coils, dipoles for magnetic chicanes, analysis magnets, quadrupoles, and bi-directional correctors. The positron linac also features AMDs, large-aperture quadrupoles, and solenoids. Transfer lines include dipoles, quadrupoles, and bi-directional correctors.
Since the injector physics design spans multiple schemes with minimal variation in magnet requirements, this section focuses on magnet design for the off-axis injection scheme.
Key technologies and design approach
Due to the wide beam energy range of the STCF (1.0–3.5 GeV), the magnet design presents significant challenges. The magnetic field performance will be optimized for 2.0 GeV but must also ensure reliable operation at both the low (1.0 GeV) and high (3.5 GeV) ends of the range. Design margins must also be reserved to accommodate deviations from the nominal lattice configuration. At the upper energy limit of 3.5 GeV, high field strengths may bring some magnets close to saturation. Therefore, the beam dynamics groups will provide detailed performance requirements to guide the magnet design across the entire energy range.
Benefiting from decades of accelerator development and the successful construction of numerous large accelerator facilities in China, the design and fabrication techniques for conventional magnets [70, 71] are now highly mature. Based on the current requirements of the STCF, no insurmountable technical risks have been identified. All magnets—including DWs—will employ conventional electromagnet designs to achieve an optimal balance between performance, technical maturity, and cost-effectiveness.
Design strategy and system composition
Magnetic designs were performed with the Poisson code and Opera-3D for field calculations, while DW magnets were designed with Opera-3D and Radia code. The design goal is to achieve high field quality in constrained spaces by optimizing pole shapes, chamfers, and end shimming to suppress higher-order multipole components to meet beam dynamics requirements. The technical design of the magnets balances the requirements of accelerator physics, limitations of fabrication, and cost-effectiveness.
The system is organized into four subsystems:
· Magnets in the collider rings
· Magnets in the damping/accumulation ring
· Magnets in the linacs
· Magnets in the transfer lines
The magnets in the collider rings require the highest field quality due to large apertures and high fields. These will use silicon steel laminations of 0.5 mm thick (grade J23-50 from Wuhan Iron & Steel) with punched-lamination assembly. DR magnets, which have less stringent field quality requirements but still require a sufficient number of units, are also designed to be based on laminated construction.
The magnets used in the linacs and transfer lines—typically produced in smaller quantities and subject to less stringent field quality requirements—will primarily employ solid DT4 steel cores. These magnets will be fabricated using CNC or wire-cutting machining techniques, which can also ensure adequate field quality. However, for magnet types that require a large number of units and higher field uniformity, the laminated-core technique may still be adopted.
Feasibility designs and analysis
Collider ring magnets
The STCF collider is a dual-ring machine with a circumference of approximately 860 m. Iterations help define the collider ring accelerator physics parameters, which are used in the CDR report, for four main magnet types: dipoles, quadrupoles, sextupoles, and DWs. Following the specifications for each magnet type, the magnet group conducted feasibility studies and field modeling and has given the preliminary design results, including water cooling and electrical parameters.
Dipole Magnets
There are three types of dipole magnets (248 total for both rings), with gap sizes of 60 mm and 75 mm, and three types of effective lengths. An H-type yoke is proposed for its symmetric field; however, it requires a top/bottom split assembly that is less convenient for installing vacuum chambers. Figure 167 shows a 3D model and transverse field distribution of a typical arc dipole (B-ARC).
Quadrupole Magnets
Seven types of quadrupoles (706 units in total) are defined, with bore diameters of 50 mm, 60 mm, and 75 mm, and four effective lengths. The spaces for vacuum ante-chambers have been reserved in the designs. Figure 168 shows the 3D model and field profile of one quadrupole type (Q1-IR).
Sextupole Magnets
In addition to using two large-aperture sextupoles (60 mm and 75 mm in bore diameter) for chromaticity correction, a crab sextupole pair with a 75 mm aperture is required. Two rings have 192 sextupoles. Figure 169 shows the model and field profile of one sextupole type (Sext-IR).
Damping Wiggler Magnets
The primary function of the DW magnets in the STCF collider rings is reducing the radiation damping time. In addition, they help control the beam emittance and energy spread. As insertion devices in the storage ring, DWs are designed to minimize perturbations to the beam. To this end, the relative angle and position of the particle trajectory at the entrance and exit of the wiggler should remain unchanged. Although the central axis of the oscillatory particle trajectory within the magnet (i.e., the reference trajectory) may deviate from zero, it is preferable to maintain a zero-centered trajectory to suppress transverse sextupole field components within the same pole width. To achieve this, the wiggler employs two pairs of end-pole field-tapering structures at both ends.
The current wiggler design features an effective length of 4.8 m, a period length of 0.8 m, and a total of six periods (an even number). The peak magnetic field reaches 1.6 T with a vertical gap of 50 mm. A total of 32 such wigglers are planned for the double-ring configuration. The end-pole configuration follows the sequence (+1/4(①), −3/4(②), +1(③), −1, …, +1, −1, +3/4, −1/4), corresponding to 12 pole pairs. Figures 170 and 171 show the 2D magnetic model and the longitudinal on-axis magnetic field distribution of the DW. Future magnet optimization will focus on further increasing the achievable peak field, as required by the accelerator physics design.

Damping/accumulator ring magnets
The STCF DR has a circumference of approximately 150 m and operates at an energy of 1.0 GeV. The current accelerator physics design requires dipole, quadrupole, and sextupole magnets. The field strength and performance requirements for these magnets are relatively relaxed compared to those of the collider ring magnets. Hence, their design and fabrication are not expected to pose significant challenges. Preliminary modeling and estimates of the associated electrical and cooling parameters have been performed for each of the three types of magnets.
The magnets in the accumulator ring are similar to those in the DR; thus, they are not described here.
Dipole Magnets
The DR requires four types of dipole magnets: normal bending magnets (Normal-bend), reverse bending magnets (Reverse-bend), normal dispersion-matching dipoles (Normal-bend DPS), and reverse dispersion-matching dipoles (Reverse-bend DPS), with a total of 88 magnets. These dipoles also adopt an H-type structure and can be fabricated using either the laminated core technique or solid iron cores. The final choice will be determined during the engineering design phase. The 3D model is shown in Fig. 172 (left).

Quadrupole Magnets
The DR requires three types of quadrupole magnets, totaling 102 units. Among them, the Q-arc quadrupoles account for 86 units and will be fabricated using laminated steel cores for quality assurance. The small-batch quadrupoles may be fabricated using solid iron cores. The 3D model is shown in Fig. 172 (center).
Sextupole Magnets
The DR includes two types of sextupoles, SF and SD, totaling 72 units. These will be fabricated using solid DT4 iron cores with CNC machining for good precision. The 3D model is shown in Fig. 172 (right).
Linac magnets
Magnet parameters for the linacs are provided by the injector physics design group and pertain to the magnets in the electron linacs, positron linac, and ML. In the electron linacs, the magnet systems include 26 dipole correctors, 4 movable magnetic chicane dipoles, 2 analyzing dipoles, 43 quadrupole magnets, and several solenoid coils. The positron linac includes a magnetic horn, an 18 m-long solenoidal focusing coil, positron guiding solenoids, analyzing dipoles, 25 dipole correctors, 14 sets of combined-function quadrupole magnets, and 4 dipole magnets.
Although the linac magnets encompass a variety of types, most are produced in small quantities, except for the quadrupoles and dipole correctors. The requirements for field strength and field quality are relatively modest, posing no significant challenges to design or manufacturing. However, the long solenoidal focusing coil for positrons may present some fabrication challenges due to its large aperture and relatively high field strength. To develop the necessary expertise, a similar solenoid is already under construction as part of the electron–positron test platform within the framework of the STCF key technology R&D project. This effort will provide valuable fabrication experience for future STCF construction.
Transport line magnets
The magnets in the transport lines are mainly divided into three regions:
· Bypass Section: Includes 8 dipole magnets, 35 quadrupole magnets, and 2 bidirectional correction magnets.
· Transport Line Between the DR and the ML: Includes 14 dipole magnets, 30 quadrupole magnets, and 2 bidirectional correction magnets.
· Transport Lines Between the ML and Collider Rings: Also includes dipole, quadrupole, and bidirectional correction magnets (quantities to be determined).
The two first cases all operate in a fixed beam energy of 1.0 GeV, thus the magnets can be designed with less adjustability. However, the collider ring injection line magnets must operate with variable beam energies, ranging from 1.0 to 3.5 GeV. Hence, their design must be optimized for stable performance across the full energy range.
Summary
A feasibility study and analysis of the conventional and DW magnets for the STCF accelerator complex have been completed. Based on system design requirements, all magnets must meet the performance specifications defined by the accelerator physics design. These requirements apply to the collider rings, the damping/accumulation ring, the linac sections, and the beam transport lines.
Given the wide operating energy range of the collider rings, magnet performance is optimized at 2.0 GeV while ensuring compatibility at 1.0 GeV and 3.5 GeV. Detailed modeling of the magnets in the collider and damping rings has been carried out, and preliminary results confirm their feasibility. Initial estimates of electrical and cooling parameters have also been developed to support power supply design.
While the design and fabrication of conventional magnets pose no major technical risks—benefiting from decades of established domestic expertise—the electromagnetic damping wigglers remain more challenging. Achieving higher peak fields with excellent field quality, while controlling fabrication costs, will be a key technical focus in the next stage of development.
Magnet power supply system
The magnet power supply system provides stable or dynamically adjustable excitation currents for all types of magnets in the collider rings and injector. These currents generate the magnetic fields required for guiding charged particles along designed trajectories inside the accelerator, thereby enabling precise beam control.
Design requirements and specifications
The STCF power supply system comprises a large number of high-stability DC current sources characterized by excellent stability, low ripple, and minimal electrical noise. The required current stability ranges from 10 to 50 ppm, with current ripple on the order of 10–5. In addition to meeting stringent performance specifications, the system must also satisfy engineering requirements for layout, electromagnetic compatibility, and long-term reliability.
Based on their operational modes and power-delivery schemes, the STCF magnet power supplies are classified into two main types:
· Main Magnet Power Supplies: Unidirectional, high-stability static supplies serving dipole, quadrupole, and nonlinear magnets. For dipole and quadrupole magnets, long-term current stability and ripple must reach the 10 ppm level.
· Corrector Magnet Power Supplies: Bidirectional dynamic supplies used for beam-orbit correction magnets. Depending on bandwidth requirements, these are further divided into slow and fast corrector supplies. Fast corrector power supplies must achieve a small-signal response bandwidth of at least 5 kHz while maintaining low ripple, high output resolution, and excellent static stability.
Key technologies and design approach
Based on international engineering practices and established domestic technologies, the STCF power supply system adopts a digitally controlled switched-mode power supply (SMPS) topology, as shown in Fig. 173.
Each power supply consists of two main components: a converter and a controller. The converter serves as the core power-processing unit, performing voltage and current transformation, while the controller acts as the system’s brain, using closed-loop feedback control to maintain high output precision. Digital management modules handle analog/digital signal acquisition and adjustment.
Power supplies are classified into high-, medium-, and low-power categories. By analyzing load characteristics and physics requirements, the designs are standardized and grouped to reduce model variety and simplify manufacturing. Key design priorities include high-frequency operation, modularity, digital control, thermal redundancy, and hot-swappable capability. Costs are strictly controlled while ensuring all performance targets are met [72].
The primary factor affecting power supply stability is the design of the digital controller and feedback loop. The system employs a high-precision digital current feedback loop, complemented by output voltage feedback to suppress transients and feedforward voltage compensation to mitigate grid fluctuations.
A classic digital PID algorithm governs the closed-loop control, where precise tuning of proportional (Kp), integral (Ki), and derivative (Kd) gains is essential. A robust modeling and control framework enables adaptive self-tuning of these parameters under dynamic load conditions.
Design scheme and system configuration
The power supply system adopts a two-stage voltage conversion structure (see Fig. 174). The front-end AC/DC stage provides isolation and stabilized voltage, effectively suppressing low-frequency voltage ripple. The rear-end DC/DC stage ensures stable current output for magnet excitation [73].
The front-end AC/DC module can be implemented in several configurations, including a phase-shifted full-bridge PWM converter, a single-ended forward converter, or a 50 Hz transformer combined with a three-phase full-bridge rectifier. The rear-end DC/DC module is selected according to the excitation requirements of different magnet types. For unidirectional power supplies, a Buck chopper topology is used for its simplicity and reliability. For bidirectionalpower supplies, an H-bridge converter composed of four power switches is adopted. By adjusting the conduction time of the switches, both the magnitude and direction of the output current can be continuously and smoothly controlled.
According to the magnet coil parameters and requirements defined by the accelerator physics and magnet design, the collider rings include 248 dipole magnets, 706 quadrupoles, 192 sextupoles, and 32 DW magnets, along with numerous corrector magnets. The arc dipoles are powered in series by type, while those in the IR and beam crossing region are powered independently. Each DW magnet is energized by one of three independently grouped power supplies matched to different current levels. Quadrupole, sextupole, and corrector magnets are powered individually. Excluding corrector supplies (to be defined), the collider rings require a total of 1,062 power supplies.
The DR includes 88 dipole magnets (four types), 102 quadrupoles (three types), and 72 sextupoles (two types). All dipoles and sextupoles are powered in series, while quadrupoles are powered individually, resulting in approximately 108 power supplies in total. The accumulator ring is similar in scale and configuration to the DR; therefore, its power supply design is not described separately.
For the linac, the preliminary physical design requires approximately 241 power supplies, including 52 for correctors, 28 for solenoid guiding coils, one for the chicane dipole, two for analyzing dipoles, and 43 for quadrupoles. The positron linac uses 28 supplies for solenoids, 18 for long solenoidal focusing coils, one for the analyzing dipole, 50 for correctors, 14 for quadrupoles, and four for dipoles.
In the transport lines—including the electron bypass section, the section between the DR and linacs, and the two sections from the ML to the collider rings—approximately 364 power supplies are required: 37 for dipoles, 283 for quadrupoles, and 44 for correctors.
Power supplies are categorized into three power levels, with those in the same class sharing similar circuit topologies and control strategies [74]. High-power supplies—such as those for arc dipoles in the collider rings, DR dipoles, and selected DW magnets—typically operate near 100 kW. These use a “12-phase rectification + dual interleaved chopper” topology, consisting of an EMI input filter, circuit breaker, AC contactor, 12-phase transformer, 12-phase rectifier, input filter, DC/DC converter, high-frequency output filter, and current sampling circuit (see Fig. 175).
For power levels up to 300 kW, the main circuit consists of four power modules in a series–parallel configuration. Multilevel control is employed to meet ripple specifications and improve efficiency. The system incorporates two transformers with dual secondary windings, enabling 24-pulse rectification to minimize disturbances to the power grid.
For quadrupole and sextupole magnets in both the collider and DRs, most power supplies operate in the several-kilowatt range. The preferred topology is a digitally controlled phase-shifted full-bridge converter, which supports soft-switching to achieve high efficiency and compact construction. Each unit includes a three-phase rectifier and filter, a DC/DC converter, an output filter, current and voltage sensing circuits, control loops, and driver and protection circuits.
For corrector magnets and some low-power quadrupoles with outputs below 1 kW, the preferred circuit structure is a switching power supply combined with either a chopper or an H-bridge converter. The front end employs standard switch-mode power modules.
The digital controller serves as the core of high-precision regulation, capable of generating ultra-fine PWM signals with a minimum resolution of 78 ps, meeting the 10-ppm current stability requirement [75]. Integrated within the power supply chassis, the controller includes an FPGA-based control board and ADC/DAC modules. It communicates with the accelerator’s IOC system via Ethernet or optical fiber and interfaces with the orbit feedback system, local diagnostics, and synchronization signals from other supplies. The controller architecture follows a modular design, comprising a core daughterboard and motherboard backplane, which allows flexible upgrades of logic chips and control algorithms [76]. The overall design concept is illustrated in Fig. 176.
Feasibility analysis
Switch-mode power supplies (SMPS) are widely adopted for modern accelerator magnets owing to their high efficiency, wide operating range, and simple control. Digital regulation has become the mainstream solution for accelerator magnet supplies because of their excellent stability, configurability, and high integration.
The STCF power supply system shares similar design goals with facilities or projects such as the Hefei Light Source (HLS) and the Hefei Advanced Light Facility (HALF). Long-term R&D and construction experience from these facilities demonstrate the technical feasibility and maturity of this design.
Summary
Based on the requirements from accelerator physics and magnet design, we have adopted rational parameters and topologies for the magnet power supplies of the STCF accelerator complex. SMPS serves as the foundational architecture, supplemented by digital control, enabling high-precision software tuning of power loop parameters. Modular construction ensures that the system meets stringent performance goals, reliability, flexibility, and maintainability.
Ring RF system
Design requirements and specifications
The STCF ring RF system compensates for energy losses in the electron and positron beams of the collider and positron damping/accumulation rings, caused by synchrotron radiation, vacuum chamber impedance, and other effects. As a result, it is a critical subsystem directly influencing beam performance. The RF system design focuses on selecting suitable cavity technology and defining key physical parameters.
Operating at 499.7 MHz, harmonized with the 2998.2 MHz linac frequency, the ring RF system may employ either superconducting or room-temperature cavities. However, given the relatively low RF requirements of the damping/accumulation rings, the collider ring RF system can operate at reduced cavity voltage to also serve these rings—a cost-effective approach successfully implemented at SuperKEKB. Therefore, separate RF system studies for the damping/accumulation rings are unnecessary.
At a beam energy of 3.5 GeV and a beam current of 2 A, the synchrotron radiation power in the collider rings reaches 2.954 MW. Additional losses due to vacuum impedance, cavity wall dissipation, and HOMs will be further refined in collaboration with the accelerator physics design and are not yet included in the current estimate. Consequently, the RF system must provide an accelerating voltage of 6 MV and approximately 3 MW of beam power for each of the electron and positron beams.
To minimize the number of RF cavities—and thus fabrication cost—each cavity must deliver more than 0.5 MV of accelerating voltage and supply over 250 kW of RF power to the beam. The cavity design targets are summarized in Table 31. A minimum of 12 cavities per collider ring is required for normal operation, with 2–3 additional units reserved for redundancy. The high beam current and power impose stringent demands on both the RF input couplers and HOM dampers. Each cavity is driven by a dedicated RF power source and equipped with an LLRF control system that stabilizes its frequency, amplitude, and phase against beam loading and environmental fluctuations. Accurate beam control and synchronization are essential for machine stability and experimental data quality. Since phase drift in reference signals directly affects beam energy stability, a common reference signal must be distributed to all cavities to maintain inter-cavity phase synchronization. The design requirements for the LLRF system are listed in Table 32.
| Object | Target specifications |
|---|---|
| 499.7 MHz cavity | Accelerating voltage per cavity: ≥0.5 MV |
| Parameters | Target specifications |
|---|---|
| LLRF amplitude stability | 0.05% |
| LLRF phase stability | 0.05° |
| Reference signal frequency | 499.7 MHz |
| Integrated phase noise (jitter) | ≤30 fs (rms) |
| Long-term synchronization | ≤50 fs over 24 hours (rms) |
Key technologies and technical approach
Both superconducting and room-temperature RF cavities are widely used in modern electron–positron colliders. Superconducting cavities provide higher accelerating gradients and superior HOM damping but require complex cryogenic systems, involve higher maintenance costs, and are more sensitive to single-cavity failures. In contrast, room-temperature cavities offer greater operational stability, lower cost, and simpler maintenance, while still achieving adequate HOM suppression.
Given the low-energy, high-luminosity characteristics of the STCF collider rings—featuring high beam current but moderate cavity voltage requirements—a superconducting solution would be over-specified and constrained by coupler power limits. Considering cost, operational reliability, and maintainability, STCF adopts a room-temperature RF cavity design for both the collider rings and the positron damping/accumulation rings.
To compensate for beam loading under high-current operation, all cavities will operate with intentional detuning. As summarized in Table 33, among the four types of available room-temperature cavities, the ARES-type cavities used at SuperKEKB and the TM020-type cavities used at NanoTerasu exhibit single-cavity detuning frequencies much smaller than the revolution frequency, making them less susceptible to coupled-bunch instabilities driven by the fundamental mode. The ARES cavity employs a complex triple-cell configuration (storage, coupling, and accelerating cells), which makes fabrication difficult and costly. In contrast, the TM020 cavity, developed by KEK and RIKEN, features strong HOM damping, a compact structure, and high cavity voltage. Its total R/Q is approximately half that of conventional designs, significantly mitigating coupled-bunch instabilities. This cavity has demonstrated stable operation at approximately 250 kW per cavity in the NanoTerasu light source [77, 78].
| Cavity type | ARES (Japan) | PEP-II (USA) | BESSY-II (Europe) | TM020 (Japan) |
|---|---|---|---|---|
| Beam power (kW) | 3000 | 3000 | 3000 | 3000 |
| Total voltage (kV) | 6000 | 6000 | 6000 | 6000 |
| Number of cavities | 10 | 15 | 30 | 12 |
| Voltage per cavity | 600 | 400 | 200 | 500 |
| Wall loss per cavity (kW) | 209 | 23 | 6 | 49.7 |
| Beam power per cavity (kW) | 300 | 200 | 100 | 250 |
| Input power per cavity (kW) | 509 | 223 | 106 | 299.7 |
| Detuning per cavity (kHz) | 12 | 283 | 557 | 75 |
Accordingly, the TM020-type cavity is selected for the STCF collider ring RF system. At 3.5 GeV beam energy, each collider ring requires at least 12 cavities to provide 3 MW of beam power and 6 MV of accelerating voltage. Including operational margin, a total of 15 cavities per ring will be installed.
The core challenges of the LLRF system include stabilizing the cavity field amplitude and phase, maintaining accurate frequency control, and suppressing longitudinal coupled-bunch instabilities. The STCF LLRF system adopts a direct-sampling architecture with non-IQ demodulation algorithms, which enhance noise immunity—particularly against temperature drift and harmonic noise—while maintaining overall system stability [79].
The reference distribution system must provide phase-synchronized, low-jitter signals to all RF cavities. STCF employs a continuous-wave optical carrier scheme, in which the reference signal from the RF master oscillator (RMO) is transmitted along an optical fiber and partially reflected at the far end. The reflected signal is compared with the original to form a feedback loop, locking the receive-end phase.
Design scheme and system configuration
The RF system of the STCF collider rings consists of room-temperature RF cavities, solid-state power amplifiers, digital LLRF control systems, interlock and protection systems, and a reference distribution network. The room-temperature RF cavities supply the required accelerating voltage to the beam, compensating for radiation and other energy losses, while also ensuring a low HOM impedance environment. A 500 MHz solid-state RF amplifier with a maximum output power of 250 kW has been jointly developed by Chengdu Kaiteng Sifang Digital Broadcast Equipment Co., Ltd., the National Synchrotron Radiation Laboratory (NSRL), and the Institute of High Energy Physics, CAS. With minor upgrades, this amplifier can satisfy the power requirements of the STCF RF system. The digital LLRF system ensures stable amplitude and phase control of the cavity field. The interlock protection system guarantees equipment safety, while the reference distribution network ensures phase synchronization among all system nodes.
Design of the room-temperature RF cavity
The TM020-mode room-temperature cavity with HOM damping operates at 499.7 MHz. A higher R/Q value often leads to a larger cavity detuning frequency for compensating beam loading, increasing the risk of coupled-bunch instabilities due to the fundamental mode. To avoid this risk, the optimized R/Q was set to 77.2. The cavity adopts a nose-cone-shaped geometry. The electric and magnetic field distributions are shown in Fig. 177, and the optimized RF parameters are listed in Table 34.
| Parameter | Value |
|---|---|
| Operating frequency (MHz) | 499.7 |
| Shunt impedance (MΩ) | 5.03 |
| Unloaded quality factor | 65110 |
| Leakage power of the accelerating mode to the HOM damping slot / total power | 1.38% |
| Ep/Eacc | 2.12 |
| Bp/Eacc (mA/V) | 2.55 |
The cavity is equipped with elliptical coupling slots and ferrite dampers located at the magnetic field radial node. This ensures that the fundamental mode field remains confined, while unwanted HOMs can propagate into the damping system. Simulation results confirm that all the longitudinal monopole and transverse dipole modes are effectively suppressed to a beam current less than 2 A, as shown in Fig. 178, meeting the coupled-bunch instability (CBI) thresholds required by STCF.
The coupling section adopts a half-height WR1800 rectangular waveguide. The coupler features an asymmetric, off-center rectangular port on the broad side of the waveguide. An adjustable tuner near the coupling port enables the real-time tuning of the coupling strength by modifying the electromagnetic field distribution on both sides of the port. As shown in Fig. 179, with tuner insertion depth Insert_I varying from 0 mm to 67 mm, the coupling coefficient ranges from 0.99 to 10.25, satisfying operational needs.
A waveguide window isolates the vacuum inside the cavity from atmospheric pressure in the RF transmission system. The window comprises 99.5% high-purity alumina ceramic and matches the half-height WR1800 waveguide by optimizing the length, width, and thickness of the window. The transition between the main WR1800 waveguide and the coupler’s half-height WR1800 is realized via a step transformer. The final assembly model of the input coupler is shown in Fig. 180.
To ensure the stable operation of the high-power input coupler, thermal load issues, secondary electron multipacting, and stress must be evaluated. At a beam power of 250 kW per cavity, the cavity wall loss is 49.7 kW. Therefore, the input coupler is designed to stably operate at a CW power larger than 300 kW. For the waveguide couplers, suppressing secondary electron multipacting in the design phase is critical but complex. Simulations on the SEY at the coupling port and waveguide window have been performed. The results in Fig. 181 show that structural multipacting does not occur for CW operation at 300 kW.
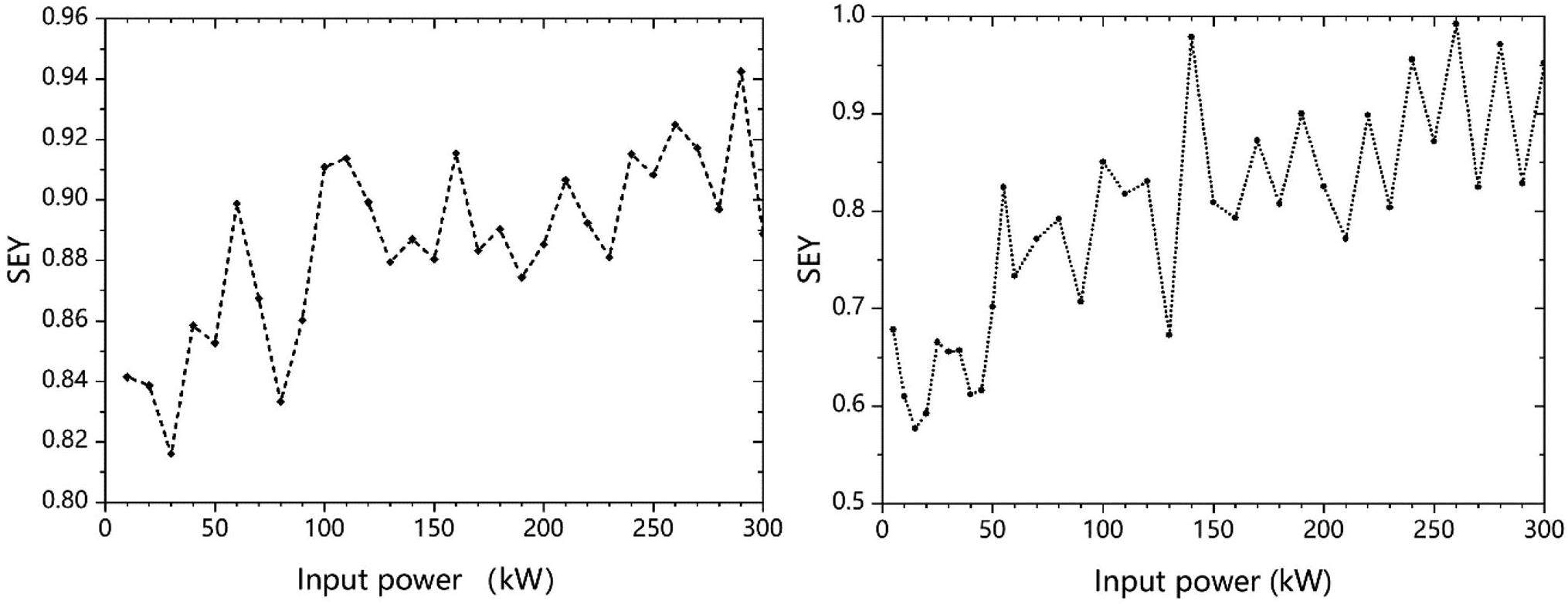
At a CW power of 300 kW, the RF forward pass through the coupler produces significant RF heating. Therefore, active water cooling is applied to the coupling port, tuner, and waveguide window, and air convection is provided to the ambient environment. The ceramic window of high-purity alumina contributes to resisting heat load but still requires water-cooling around its frame. With the discussed interventions, operation at a CW power of 300 kW results in a maximum temperature of 49.15 °C and produces stress and deformation that is within acceptable limits, as shown in Fig. 182.
Figure 183 shows the 3D model of the 499.7 MHz TM020 room-temperature RF cavity, combining the cavity and coupler designs. Each cavity provides a cavity voltage of 500 kV and RF power of 300 kW, with 250 kW contributing to the power of the beam. At least 12 such cavities per collider ring are required to meet performance goals. To ensure redundancy and prevent sustained operation at maximum capacity, additional cavities will be installed. In addition, designs with two input couplers per cavity are under development to further reduce power demands of each coupler.
Digital low-level RF (LLRF) system
The STCF comprises two separate collider rings for electrons and positrons, each equipped with at least 12 room-temperature RF cavities. Every cavity is controlled by an LLRF system. The overall design of the digital LLRF system is shown in Fig. 184. A direct RF sampling architecture is adopted, in which the 499.7 MHz signal is directly sampled by the ADC.
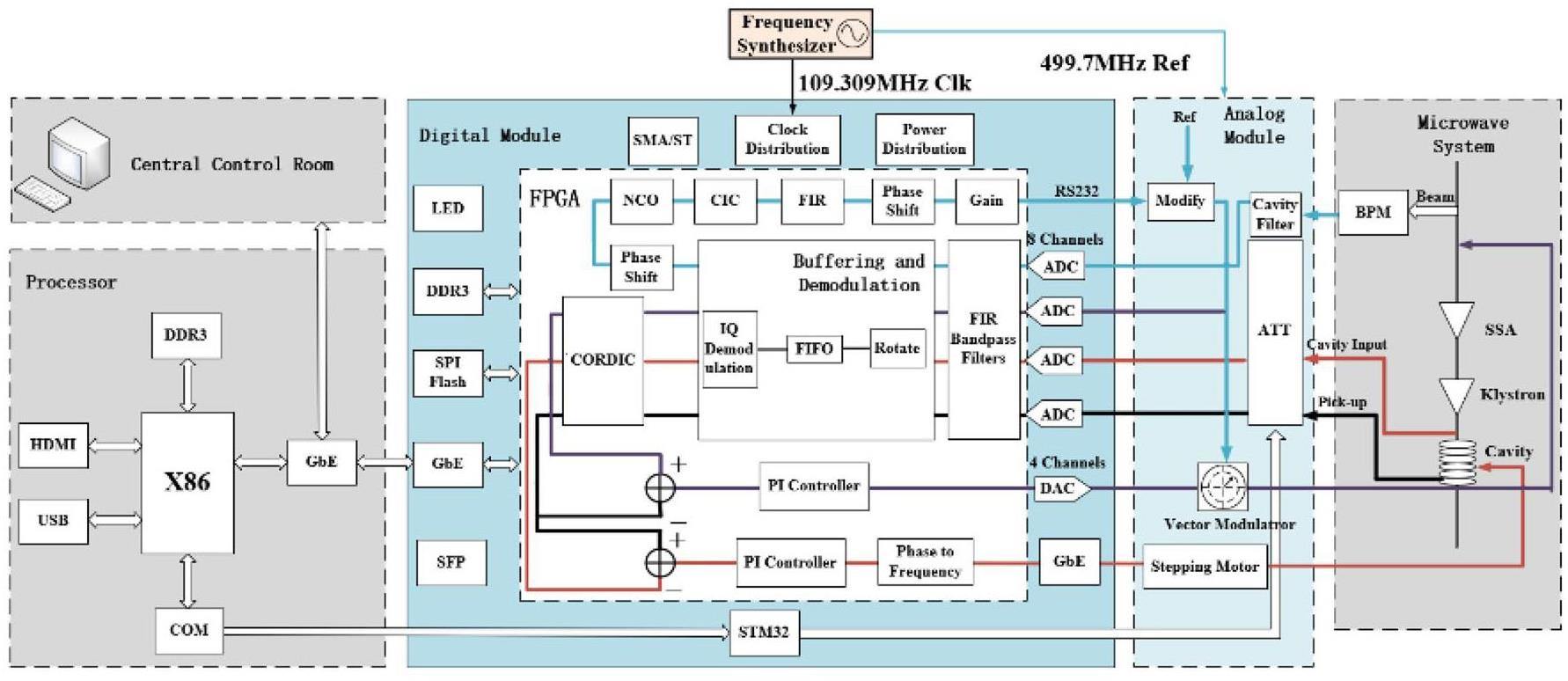
The LLRF system acquires the cavity input, reflected, and cavity field signals, as well as BPM signals. The reflected signal is used to monitor the cavity’s operational status, while the input and field signals are processed in real time by an FPGA-based logic unit. One output controls the solid-state amplifier and klystron to stabilize the RF field amplitude and phase; another drives the tuner mechanism to maintain frequency stability. In addition, a third control output modulates the reference signal from the frequency synthesis system to suppress longitudinal coupled-bunch instabilities, particularly in the zero-mode.
Interlock protection system
The interlock protection system provides rapid response to equipment faults, safeguarding RF components from potential damage. Implemented using FPGA technology, it offers both high reliability and fast reaction time. The data acquisition and interlock control software is developed within the Experimental Physics and Industrial Control System (EPICS) framework, with long-term data storage managed by the Archiver Appliance.
To enhance modularity and distributed control, the system operates on a Linux-based platform with full EPICS integration. Automated control is achieved through the EPICS sequencer module, enabling functions such as data acquisition, real-time analysis, and interlock event filtering.
Reference distribution system
As shown in Fig. 185, the synchronization system comprises a reference master oscillator (RMO), frequency synthesizer, synchronization modulator, transmitter, receiver, microwave phase compensation system, femtosecond phase comparator, and synchronization calibration controller.
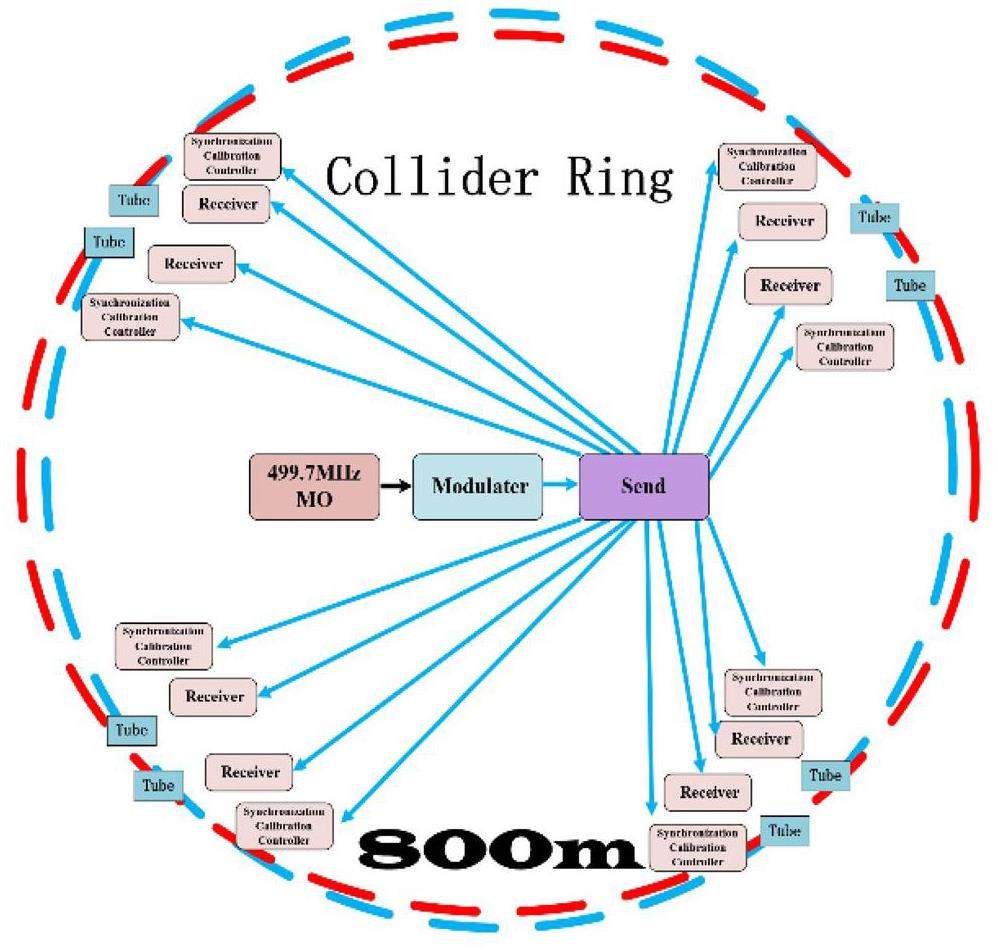
The RMO generates the reference signal, which is subsequently amplified and modulated. Using a continuous-wave laser carrier, the reference signal is distributed via optical fibers. A portion of the optical signal is reflected back to the transmitter, allowing the system to perform phase comparison and compensation using a femtosecond-level phase comparator and an adjustable optical delay line.
Feasibility analysis
In summary, while the TM020-mode room-temperature cavity offers significant technical advantages, it is a relatively new design with limited operational experience worldwide and poses challenges in precision mechanical fabrication. To ensure domestic production and technological independence, STCF is actively pursuing development through prototyping and manufacturing process studies.
To mitigate beam-loading effects, each cavity is intentionally detuned by 75 kHz. HOMs are effectively suppressed, preventing coupled-bunch instabilities. The NSRL has extensive experience in the development and operation of digital LLRF systems. Independently developed LLRF units have demonstrated reliable operation at the NSRL microwave test facility and have been successfully integrated into the SSRF RF system in collaboration with the Shanghai Synchrotron Radiation Facility (SSRF).
Summary
The conceptual design of the ring RF system—including the RF cavities, power sources, and LLRF systems—has been completed, and theoretical and simulation studies have been conducted for key technologies. Some components are under prototype development and fabrication testing. Most devices will adopt proven, cost-effective technologies and products to reduce risk and ensure a successful implementation.
Injection and extraction system
The STCF facility includes multiple circular accelerators: two collider rings (for electrons and positrons) and one positron DR (or accumulation ring). Each of these rings requires dedicated injection and extraction systems, which connect to the beam transport lines to ensure efficient electron and positron beam injection and extraction.
Design objectives
The overall objective is to satisfy the injection physics design requirements for each ring and to develop magnet systems that ensure efficient injection and extraction of both electron and positron beams.
Collider Rings: The current design accommodates two injection schemes—off-axis injection and swap-out injection—each with distinct requirements and technical challenges. For off-axis injection, the focus is on the structural design of nonlinear kicker magnets and the optimization of their magnetic field distribution. For swap-out injection, emphasis is placed on the electromagnetic design of stripline-type ultra-fast kickers and the development of prototypes. For beam abort and single-bunch swap-out extraction, kicker magnets with a long pulse width are developed for full-bunch train extraction, while the same ultra-fast kickers used for injection handle single-bunch extraction. Additionally, the thin pulsed septum magnet must be optimized to eliminate perturbations to the circulating beams.
DR: The ring stores 5 bunches spaced 100 ns apart, using an on-axis single-turn injection scheme to reduce dynamic aperture requirements. Ferrite-loaded transmission-line-type kicker magnets are employed to improve excitation efficiency, with a focus on achieving fast field rise times and impedance matching to suppress reflections. Extraction is single-bunch, technically similar to injection.
Accumulation Ring: This ring stores 4 bunches with 130 ns spacing, using local orbit bumps to allow multiple injections for positron accumulation. Kickers are similar to those in the DR and are technologically mature. Extraction is also single-bunch, with technical requirements comparable to those of injection.
Design requirements and key technical specifications
· Septum Magnets
Designs are being developed for two types of septum magnets: eddy-current focused and reverse-field. Key performance targets include a septum thickness ≤ 2 mm and a residual magnetic field on the circulating beam orbit < 0.1% of the main field. These parameters may be adjusted to meet specific physics design requirements.
· Nonlinear Kickers
Three types of nonlinear kickers are under development: air-core coil, pseudo-octupole, and shielded types. Critical criteria include a central magnetic field amplitude ≤ 5% of the injection field and a pulse width ≤ 3 μs, adjustable according to the physics design.
· Stripline-Type Ultra-Fast Kickers
These are currently in the design and prototyping stage. Key specifications include a magnetic field rise/fall time ≤ 2 ns and a total pulse width ≤ 6 ns, tunable to meet injection requirements.
The kickers and septum magnets are the core components of the injection and extraction systems for all three types of rings. Their main technical requirements are summarized in Table 35, while other structural parameters will be adjusted based on specific design details.
| Kickers | Septum magnets | |
|---|---|---|
| Collider rings | Off-axis: Central field ≤5%, pulse width ≤3 μs | Septum thickness ≤2 mm, residual field at orbit <0.1% |
| Swap-out: Rise time ≤2 ns, pulse width ≤6 ns | ||
| Damping ring | Single-turn injection: Rise time ≤90 ns, pulse ≤190 ns | Same as above |
| Accumulation ring | Off-axis injection: Rise time ≤120 ns, pulse ≤250 ns | Same as above |
Key technologies and technical approaches
· Septum Magnets
The primary function of septum magnets is to bring the injected beam path as close as possible to the stored beam trajectory, minimizing orbit disturbances and beam loss in off-axis injection schemes. For on-axis injection, they also reduce the required magnetic field strength of the kickers.
Technical approach at STCF: Based on injection physics requirements, theoretical electromagnetic analysis and parameter optimization are performed first. Numerical simulations using the OPERA code validate and refine the design. Comparative performance analyses of the two septum magnet types are conducted under different operational scenarios, and the final design is selected according to STCF-specific injection/extraction needs.
· Nonlinear Kickers
The defining feature of a nonlinear kicker is a zero magnetic field at the center, ensuring transparency to the stored beam, while producing sufficient field in the offset region to meet off-axis injection requirements.
Technical approach: Injection requirements are converted into magnetic field profile specifications. Three structural types are analyzed electromagnetically and parametrically. OPERA-based numerical simulations are used to validate and optimize the field profiles, and a comparative study identifies the final design based on injection/extraction physics.
· Stripline-Type Ultra-Fast Kickers
The swap-out injection scheme requires ultra-fast, precisely timed pulses within the narrow interval between adjacent bunches to steer the injected bunch into the pre-emptied bucket of the stored beam without perturbing the neighboring bunches.
Technical approach: Electromagnetic parameters are first analyzed theoretically. The structure is designed to meet the field waveform requirements specified by the physics design. CST simulations optimize pulse shape, pulse width, and flatness; minimize impedance mismatches with adjacent components; and ensure the desired time structure. Final performance is validated through prototyping and iterative testing.
Design scheme and system configuration
· Septum Magnets
Eddy-Current-Type Septum Magnet: A simulation model of the eddy-current-type septum magnet [80, 81] was constructed using OPERA, as shown in Fig. 186(a). The magnet is 650 mm long. The excitation current is a half-sine wave with a peak of 6270 A and a bottom width of 60 μs. The longitudinal distribution of the main magnetic field is presented in Fig. 186(b). Within the good field region, the peak field reaches 9832 Gs, the integrated field is 0.66686 T·m, and the leakage field at the circulating beam center is less than 0.01% of the main field.
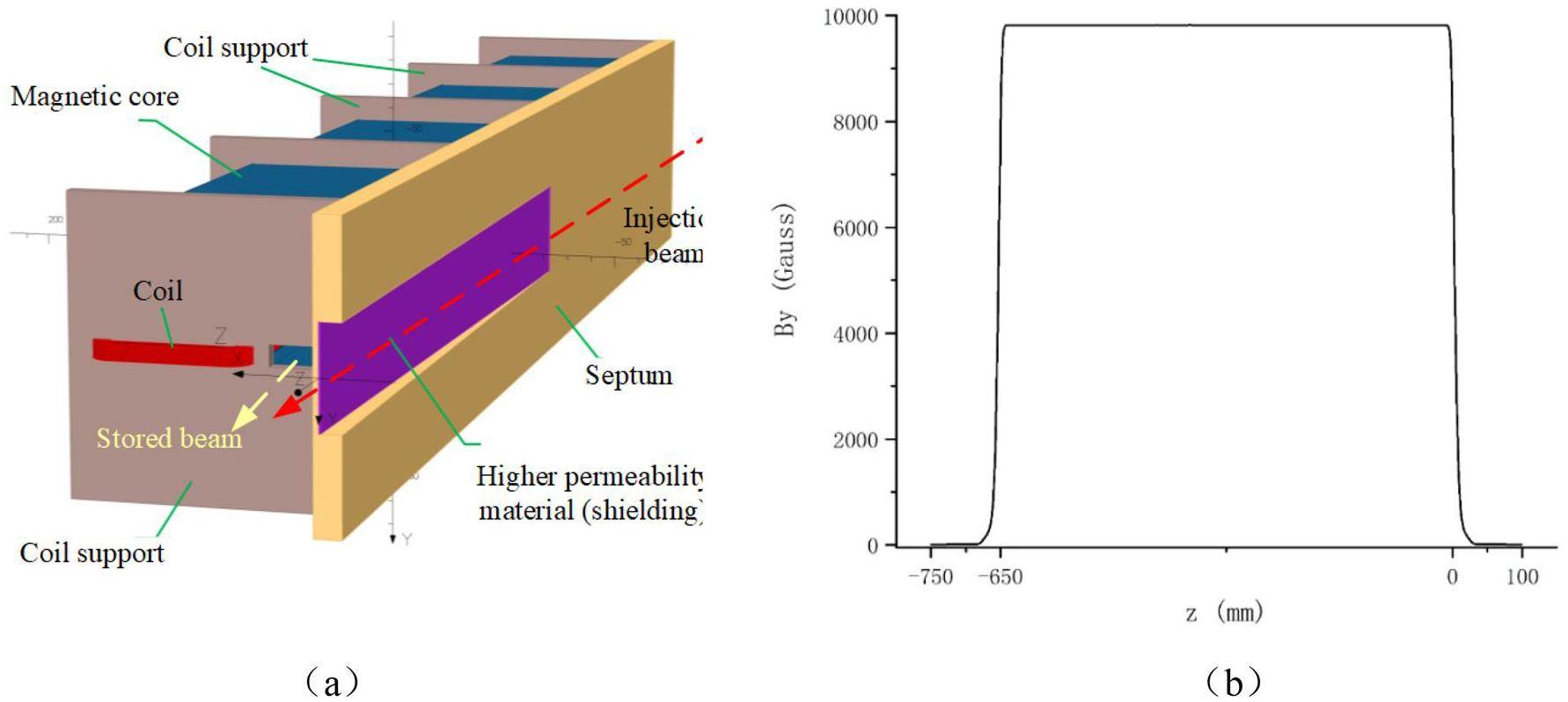
Opposite-Field-Type Septum Magnet: This design effectively comprises three dipole magnets [82]. The upstream and downstream compensating magnets each have a longitudinal length of 0.3 m, and the length of the central main septum magnet is 0.6 m, as illustrated in Figs. 187(a) and (b). The magnetic field distribution is shown in Fig. 187(c): the integrated magnetic field on the circulating beam side is canceled, while the integrated field on the injection beam side is doubled. Additionally, the electromagnetic forces on the septum plates cancel each other, reducing the structural design complexity of the coils.
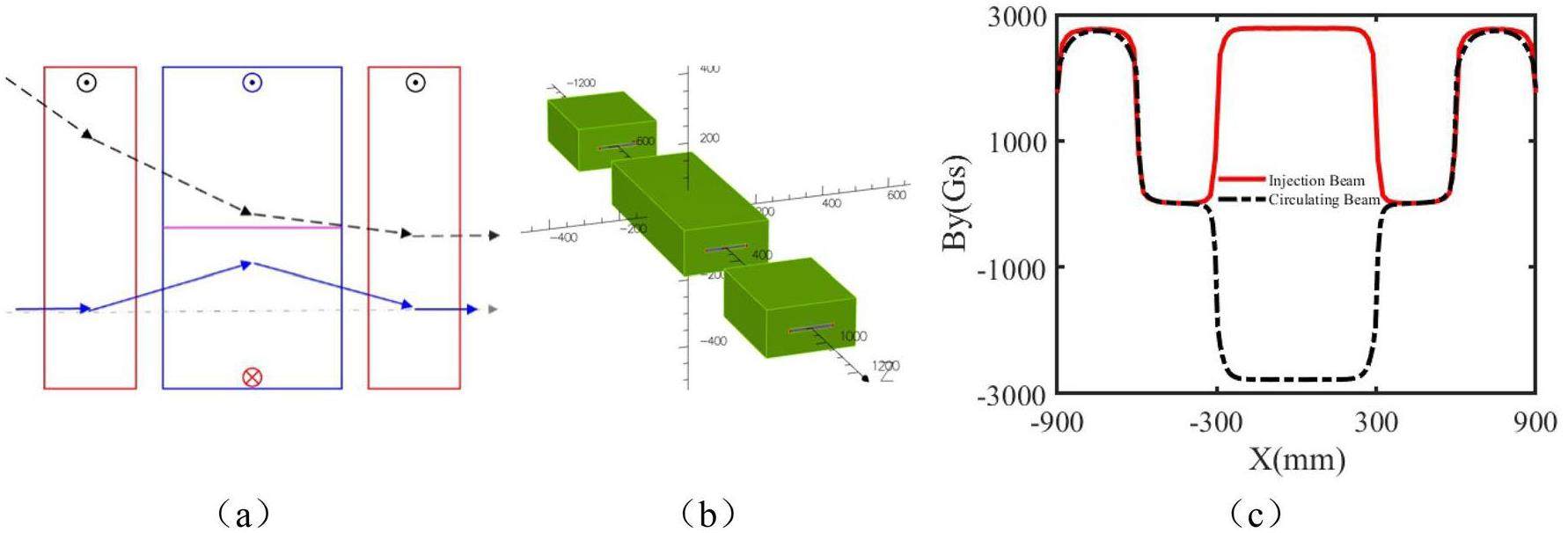
· Nonlinear Kicker Magnets
Air-Core Coil Type Nonlinear Kicker: As shown in Fig. 188, the required nonlinear magnetic field distribution is formed by adjusting the relative positions of eight current-carrying conductors [83, 84, 85]. Both 2D and 3D simulation models were built in OPERA, with results shown in Fig. 188(c). At the injection point x = –5 mm, the field magnitude is 297.20 Gs; while in the zero-field region (x = ±0.5 mm), the field is less than 0.28% of that at the injection point. The field distribution can be controlled by adjusting the conductor positions and excitation currents based on injection physics requirements.
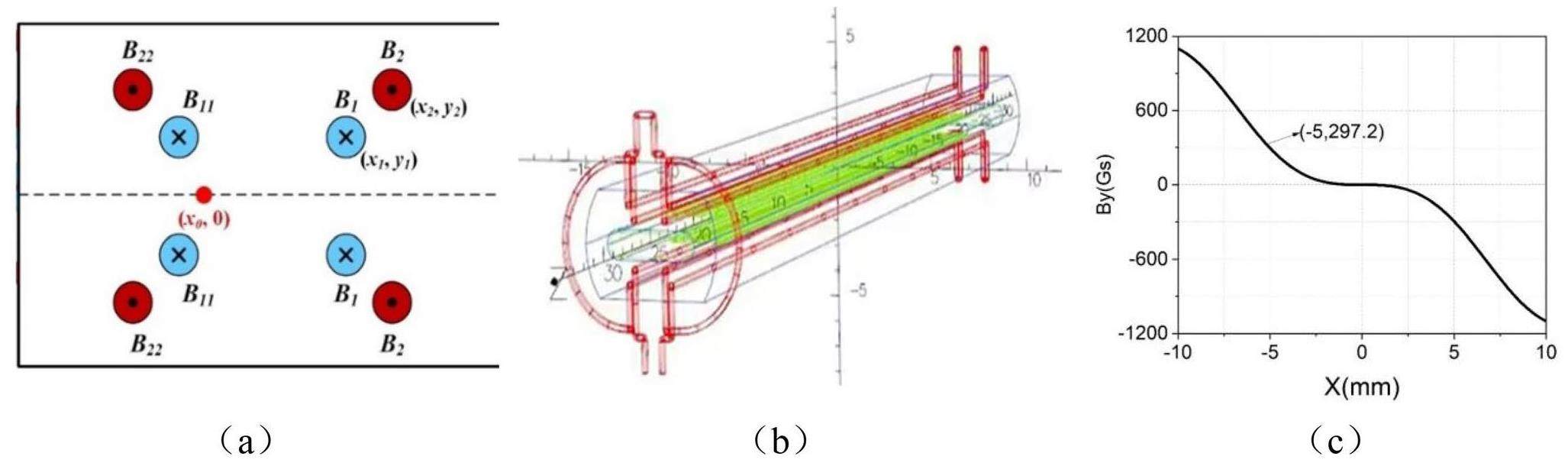
The engineering design of air-core coil-type nonlinear kickers has commenced. The design drawings are shown in Fig. 189. The driving power supply was successfully tested in mid-July 2025, followed by the fabrication of theprototype kicker. Comprehensive integration tests ofthe entire system were completed in September 2025, and the preliminary results confirmed the validity of the design.
Shielded-Type Nonlinear Kicker: The structure of the shielded-type nonlinear kicker is shown in Fig. 190(a). The magnet consists of two C-type ferrite cores, separated by eddy-current plates to form opposing magnetic fields. Two copper arc-shaped shielding plates are placed in the magnet center to suppress the central field via induced eddy currents, creating a flat zero-field region. The peak field distribution at a specific time simulated in OPERA is shown in Fig. 190(b). A key advantage of this design is its uniform field distribution at the injection point.
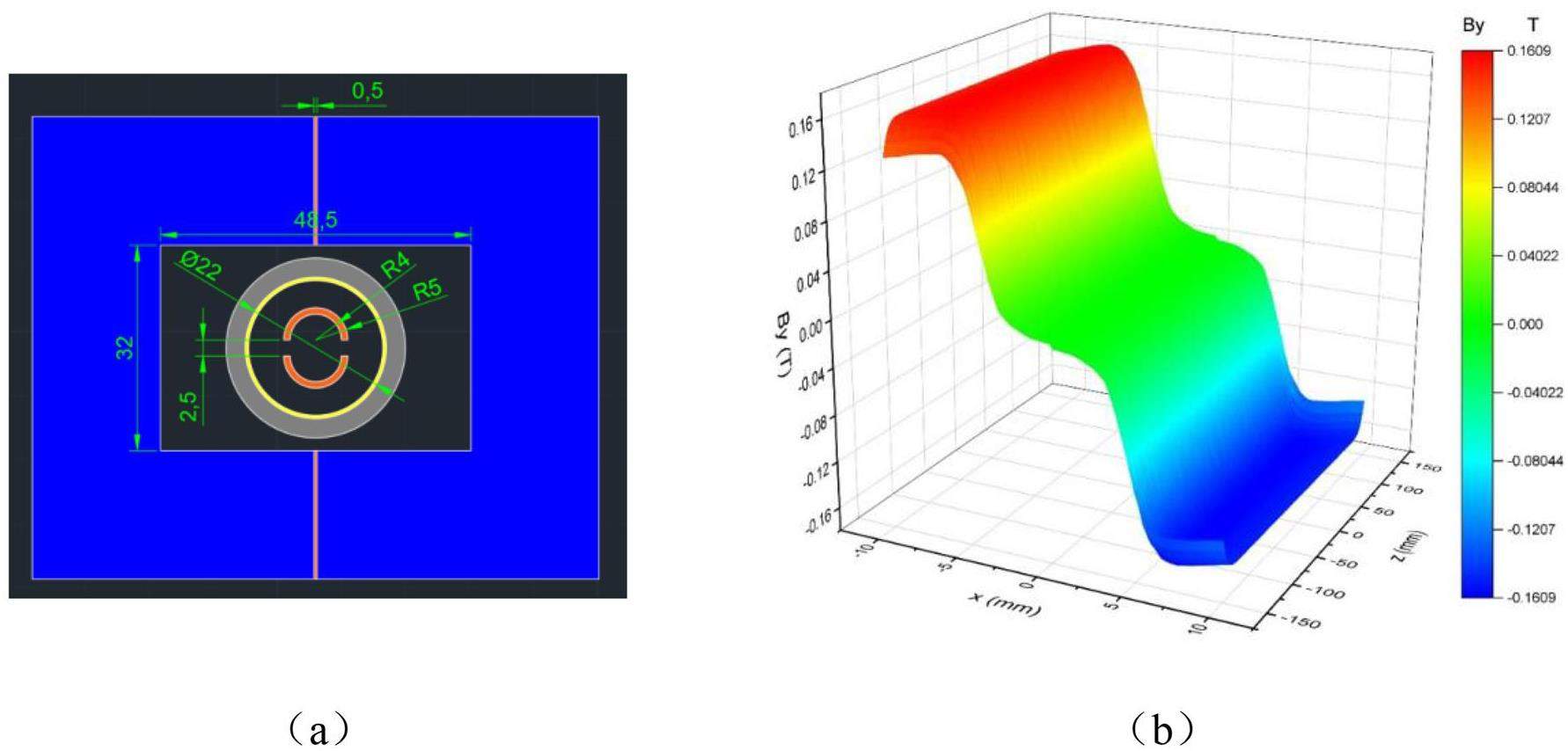
· Stripline-Type Kicker Magnet
To meet the strict time-structure requirements of pulsed electromagnetic fields for swap-out injection, the stripline kicker magnet’s electrode structure is optimized to match the impedance of the pulsed transmission cables, eliminating waveform distortion from distributed parameters [86]. Figure 191(a) shows the simulation model of the kicker, while Fig. 191(b) provides a cross-sectional view of the electrode and vacuum chamber. The yellow regions indicate the copper electrodes, which, together with the chamber, form a coaxial structure with an odd-mode impedance of 50 Ω, achieving impedance matching with the pulsed cables and enhancing response time and pulse quality. The effective electrode length is 300 mm, with a 12 mm gap between electrodes. Figure 191(c) shows the tapered end transition, designed to reduce beam coupling impedance.
Figure 192 shows the kicker center field distribution when the excitation voltage reaches 17.5 kV. Within the range y = –5 mm to 5 mm, the electric field exceeds 1.44 MV/m, with a field uniformity of 0.9%, and the magnetic flux density exceeds 48.2 Gs. These results indicate that the electric and magnetic fields have comparable effects on the electron beam.
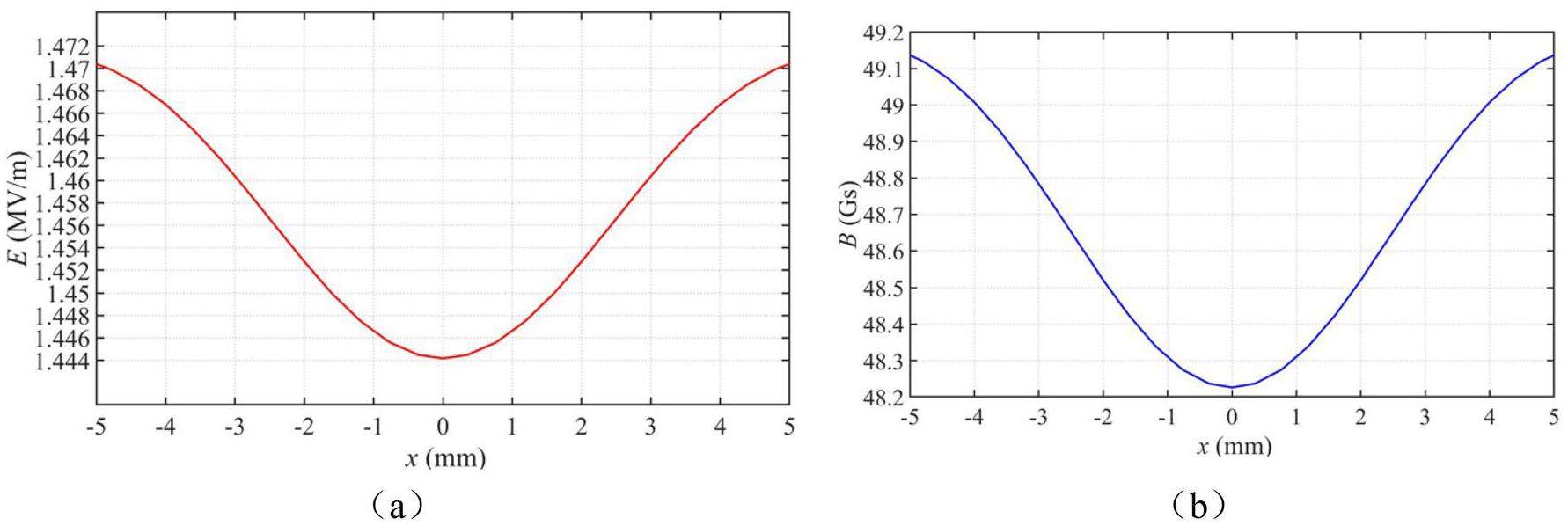
A comparison of beam coupling impedance before and after end-structure optimization is shown in Fig. 193(a), where the peak impedance decreases from 856.8 Ω to 390.72 Ω. Figure 193(b) shows the longitudinal impedance Z||/n per harmonic, with the effective impedance (Z||/n)0 dropping from 45.24 mΩ to 39.21 mΩ, a 13.33% reduction. Figure 193(c) presents the loss factor versus bunch length, with the optimized design consistently exhibiting lower losses. Figure 193(d) shows electrode power dissipation, with total loss reduced from 89.2 W to 59.4 W, a 33.4% decrease. These results demonstrate that the tapered end structure significantly mitigates beam coupling impedance and thermal effects. A conical-tapered transition section will be designed in the future to further reduce beam coupling impedance.
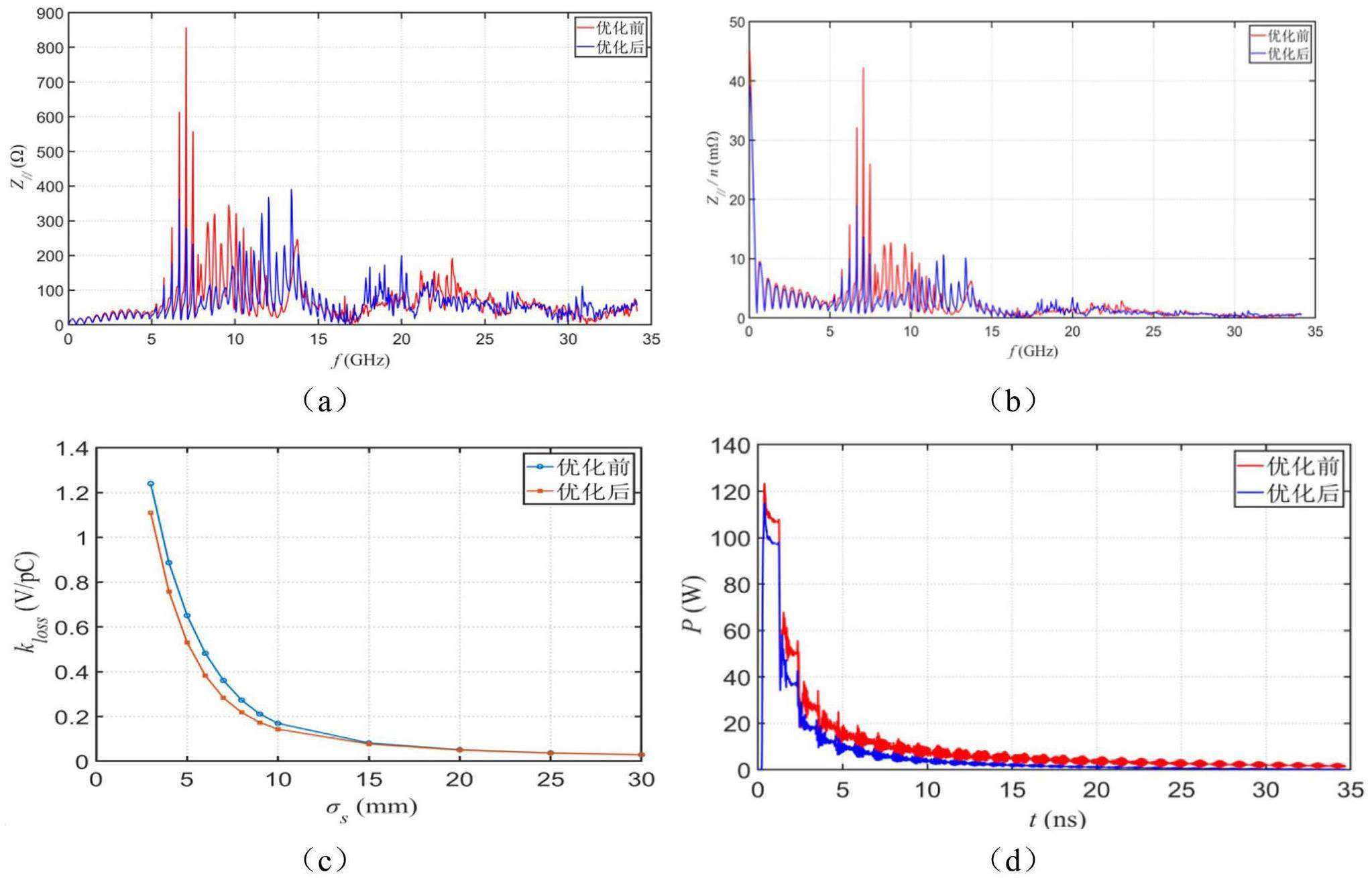
Feasibility analysis
· Septum Magnets
Eddy-current-type septum magnets are widely used in the accelerator field and represent a mature technology, with successful domestic development experience. In contrast, the opposite-field-type septum magnet is a relatively new international design and carries certain technical risks. To mitigate these risks, the team is advancing the design of both eddy-current and reverse-field septum magnets concurrently.
· Nonlinear Kicker Magnets
The air-core-coil nonlinear kicker magnet imposes stringent requirements on the positional accuracy of the excitation conductors. It also faces several engineering challenges, such as achieving the necessary machining precision of the ceramic vacuum chamber. These challenges will need to be addressed progressively during engineering implementation. In comparison, pseudo-octupole and shielded-type nonlinear kicker magnets carry lower technical risk and are based on more mature technologies.
· Stripline-Type Ultrafast Kicker Magnet
The stripline-type ultrafast kicker magnet must meet extremely strict timing requirements for its magnetic field structure. Its electromagnetic geometry, together with the pulse power supply, determines the response waveform of the magnetic field. The design is technically challenging and requires gradual refinement during engineering development. The necessary nanosecond-level fast-response pulsed power supply is commercially available from international vendors such as FID, without export restrictions. Additionally, the domestic team at IHEP (Institute of High Energy Physics, CAS) has relevant development experience. Therefore, the technical risks associated with the power supply are considered manageable.
Summary
A high-efficiency injection and extraction system is essential for achieving the ultra-high luminosity goals of STCF. Meeting the physical requirements for beam injection and extraction in the collider rings, DR, and accumulation ring necessitates specialized magnet designs. The focus is on addressing the most technically challenging magnet designs to ensure the safe and efficient operation of bunch swap-out injection, off-axis injection, and extraction processes.
Vacuum system
Technical requirements and design objectives
In the STCF accelerator complex, the vacuum system encompasses all environments requiring pressures below atmospheric levels, including both the collider rings and the injector components. The collider rings consist of the electron and positron rings, while the injector includes multiple accelerator sections: the electron linacs, positron linac, positron DR (or accumulator ring), ML, and various beam transport lines.
The vacuum requirements for the collider rings and injector are defined by the physics system. The vacuum system is designed to ensure that vacuum chambers and pumps maintain pressure levels across all accelerator components that satisfy the physical requirements of the STCF design.
According to specifications from the accelerator physics team, the dynamic vacuum pressure must be better than 1×10-7 Pa for the collider rings and 6.5×10-5 Pa for the injector. The corresponding static vacuum requirements are better than 2×10-8 Pa and 1.3×10-5 Pa, respectively.
The structural dimensions of the vacuum chambers for each section of the collider rings and injector are provided in the parameter tables from the accelerator physics design groups.
Key technologies and design approach
The most challenging part of the STCF vacuum system is the collider rings, with the primary challenges arising from two factors:
First, the high-current beams of 2 A generate intense synchrotron radiation, leading to high thermal loads and significant production of photoelectrons, which in turn trigger substantial gas desorption. This effect is particularly pronounced in the positron ring, which is sensitive to electron cloud formation. Additionally, the short bunch length and high bunch charge exacerbate HOM effects, imposing stringent requirements on the impedance of vacuum components.
Second, beam–gas scattering in the IR contributes significantly to experimental background, necessitating especially high vacuum levels in the IR, where space constraints make the installation of vacuum pumps challenging.
International experience from previous high-current e+e- colliders, such as KEKB [33, 87–88] and PEP-II [89, 90, 91], provides valuable guidance. The STCF vacuum design strategy incorporates:
· A carefully optimized global design.
· Arc-section vacuum chambers with antechambers to manage synchrotron radiation absorption and gas pumping.
· Appropriate material selection for vacuum chambers.
· Efficient vacuum pump configurations.
In the positron ring, additional electron cloud mitigation measures will be employed, including TiN coating, localized magnetic fields, and grooved chamber geometries. In the IR, non-evaporable getter (NEG) pumps will enhance local vacuum conditions, and low-impedance synchrotron radiation masks will be installed.
For the injector system—including the linacs, damping/accumulator rings, and transport lines—the vacuum requirements are conventional and well within the technological capabilities already established by several accelerator laboratories in China.
Design scheme and system composition
Collider ring vacuum system
The STCF collider rings are similar, each with a circumference of approximately 860 m. Each ring is divided into arc sections, straight sections, and the IR. The vacuum requirements for the collider rings are defined by accelerator physics, primarily based on factors such as beam–residual gas scattering—which contributes to experimental background near the IP—beam lifetime, and emittance growth. The design must also account for fast ion beam instabilities in the electron ring.
A key aspect of the collider ring vacuum system is the vacuum chamber design. Drawing from the experience of SuperKEKB [92], the positron ring will adopt a dual-symmetric side chamber design, as illustrated in Fig. 194. One side is used for absorbing synchrotron radiation, while the other is dedicated to pumping. For the electron ring, a single-sided chamber may also be considered. All vacuum chambers in the DW sections will adopt dual-side symmetry. Flanges, bellows, and vacuum pump ports must be equipped with RF shielding to minimize impedance contributions.
The pressure distribution in the collider ring vacuum system is determined by the gas load and the configuration of the pumping system. The design employs a vacuum chamber structure that integrates the beam duct with side chambers. Synchrotron radiation is directed onto the cooled sidewalls of the vacuum chamber to reduce photoelectron entry into the beam channel and suppress electron cloud formation. The pumping configuration combines both centralized and distributed pumping systems, which must efficiently remove the substantial gas loads generated by synchrotron radiation to achieve the vacuum levels required for acceptable beam lifetime. Once the distribution and rate of photon-induced desorption and thermal outgassing are quantified, the pumping scheme can be finalized. The collider rings will employ a combination of distributed NEG pumping and centralized ion pumping.
Collision ring arc section
In the arc sections of the collider rings, the vacuum pumping scheme uses NEG-coated chamber surfaces or distributed NEG strips in combination with centralized vacuum pumps (see Fig. 195). The centralized pumps consist of 400 L/s ion pumps paired with NEG hybrid pumps. For vacuum measurement in the arc section, a vacuum gauge and a cold cathode gauge are installed at the entrance of each standard cell, corresponding to one set every 4.7 m on average. Residual gas analyzers are placed at selected locations to monitor partial pressure distributions. The arc section is divided into 10 segments, each separated by full-metal gate valves equipped with RF shielding. Each segment also includes a roughing valve and a venting valve.
Collision ring straight section
The vacuum pumping strategy for the straight sections also employs either NEG-coated vacuum chamber surfaces or distributed NEG strips in combination with centralized vacuum pumps, configured as 400 L/s ion pumps paired with NEG hybrid systems. Vacuum measurement is implemented by placing a set of vacuum gauges and cold cathode gauges at the entrance of each standard cell, averaging one set every 5 m. Residual gas analyzers are installed at selected locations to monitor gas composition and partial pressures. Each straight section is divided into 10 segments, each isolated by RF-shielded full-metal gate valves, and each segment includes a roughing valve and a venting valve.
Interaction region
Based on the layout of beamline components near the IP (see Fig. 62), preliminary 3D modeling and simulations have been conducted. The beam pipe within the detector spectrometer relies on NEG coatings to maintain vacuum levels, providing an effective pumping speed of 500 L/s. In regions near the spectrometer, high-capacity NEG pumps and ion pumps are installed to remove gas loads generated by synchrotron radiation, delivering an effective pumping speed of 1000 L/s per m.
The IR is divided into 12 sections, each separated by all-metal gate valves equipped with RF shielding. Each section includes a roughing valve and a vent valve. The section containing the IP has very limited space, extending from the IP to the end of the cryostat, leaving no room for vacuum pumps or related components. Consequently, high-speed vacuum pumps are installed at more distant locations, accompanied by a vacuum gauge and cold cathode gauge to monitor vacuum levels. A residual gas analyzer is also installed to measure partial pressures. In the remaining sections, a vacuum gauge and cold cathode gauge are installed approximately every 10 m.
Based on the collider ring physics design, the preliminary list of major vacuum components is presented in Table 36.
| Component | Quantity | Material |
|---|---|---|
| Beam position monitors | 105 | Stainless steel |
| Various vacuum chambers | 458 | Oxygen-free copper |
| Ion pumps | 194 | — |
| NEG pumps | 158 | — |
| Vacuum valves | 102 | Stainless steel |
| Vacuum gauges | 96 | Stainless steel |
| Residual gas analyzers | 70 | — |
Linac vacuum system
The vacuum system for the injector linacs primarily consists of accelerating tubes, vacuum pipelines, and ion pumps. The DR (or accumulation ring) has a vacuum system similar to that of the collider rings but is somewhat simplified, relying mainly on ion pumps. The vacuum system for the transport lines is straightforward and also uses ion pumps.
Currently, two injection schemes are under consideration. In the off-axis injection scheme, the electron beam is directly injected into the collider electron ring through the linac and transport line, while the positron beam passes through the DR and then through the final-stage linac and transport line before being injected into the collider positron ring; this is referred to as the off-axis injection scheme. In the second scheme, the electron gun provides high-charge electron bunches that are directly accelerated and injected into the collider electron ring, while the positron beam is first accumulated in the accumulation ring to reach the required bunch charge, then accelerated by a downstream linac before injection into the collider positron ring; this is referred to as the bunch swap-out injection scheme.
The linac beamline includes the electron gun, pre-buncher, buncher, accelerating tubes, vacuum components, beam diagnostics, magnets, and ancillary microwave equipment such as waveguides and RF power loads. The vacuum system components include the electron gun, S-band accelerating tubes, collimators, vacuum chambers for diagnostics, bellows, ion pumps, valves, and turbopump stations for initial vacuum setup. All vacuum valves are all-metal gate or angle valves.
Vacuum in the accelerating tubes is maintained by sputter ion pumps located at pumping ports near the input and output couplers. Two 3 m accelerating tubes form a 6 m segment, with a 100 L/s sputter ion pump at each microwave input interface and another pump at the output of the first tube, between the two. Shielded bellows separate adjacent 6 m segments, and an all-metal gate valve is installed every two 6 m segments for vacuum isolation. Outside the accelerating tubes, sputter ion pumps are placed approximately every 2 m along the beamline.
A cold cathode gauge is installed at the input of the upstream accelerating tube in each 6 m segment to monitor vacuum levels.
Based on accelerator physics parameters and the selected injection schemes, the major vacuum components required for the two schemes are listed preliminarily in Table 37.
| Component | Off-axis | Swap-out | Material |
|---|---|---|---|
| Thermionic e-gun | 1 | 2 | – |
| Photocathode e-gun | 1 | 0 | – |
| S-band accel. tubes | 100 | 133 | OFHC Copper |
| X-band accel. tubes | 1 | 0 | OFHC Copper |
| Beam diagnostics | 40 | 45 | Stainless Steel |
| Vacuum chambers | 300 | 400 | Stainless Steel |
| Magnetic chicanes | 2 | 1 | – |
| Ion pumps | 343 | 473 | – |
| Vacuum valves | 27 | 36 | Stainless Steel |
| Vacuum gauges | 203 | 278 | Stainless Steel |
Damping ring (accumulation ring) vacuum system
In the off-axis injection scheme, the positron DR is used to reduce the emittance of positron bunches generated at the target through synchrotron radiation damping, achieving the emittance required for injection into the collider positron ring. In the swap-out injection scheme, the positron accumulation ring is used to accumulate charge and optimize emittance. Both systems include injection and extraction lines, with the ring having a circumference of approximately 150 m.
According to the DR design, the vacuum system can be divided into eight relatively independent sections by all-metal gate valves. Each section is equipped with roughing and venting valves. Initial evacuation of the system is performed using oil-free turbopump stations, and the vacuum is subsequently maintained by conventional sputter ion pumps. Ion pumps rated at 100 L/s are installed approximately every 6 m, each paired with a vacuum gauge and a cold cathode gauge. The transport line vacuum system includes approximately 32 ion pumps, 27 vacuum gauges, and nine VAT gate valves.
Beam transport line vacuum system
The beam transport lines are divided into four parts according to area and function: the electron beam bypass line, the DR (accumulation ring) transport section, the positron–electron merging section, and the final injection section into the collider rings.
The main vacuum chambers in the transport lines have circular cross-sections, while rectangular cross-sections are used in dipole magnet regions depending on the magnetic aperture and deflection or splitting angles. All vacuum chambers are constructed from low-magnetic-permeability stainless steel.
The pumping system employs conventional 50 L/s sputter ion pumps, installed approximately every 5 m along the beam path. Cold cathode vacuum gauges are placed every 10 m, and all-metal gate valves are installed every 20 m.
Based on the structural and design parameters provided by the accelerator physics team, the preliminary list of vacuum components required for the two injection schemes is shown in Table 38.
| Component | Off-axis | Swap-out | Material |
|---|---|---|---|
| Circular vacuum chambers | 87 | 59 | Stainless steel |
| Rectangular chambers | 38 | 30 | Stainless steel |
| Ion pumps | 82 | 50 | – |
| Vacuum valves | 29 | 19 | Stainless steel |
| Vacuum gauges | 47 | 29 | Stainless steel |
Vacuum control and interlock
The vacuum control system primarily consists of ion pumps and their power supplies, radiation-resistant vacuum gauges, and isolation gate valves. Ion pump power supplies include built-in protection functions and interface with the EPICS control system via 0–5 V analog output signals. These signals are used both for safety interlocks in the accelerating tubes and for displaying ion current and voltage. Gauge output signals are transmitted through high-voltage cables to vacuum meters, which are then processed and monitored by the control system.
Gate valve operation is interlocked with vacuum gauge readings. When vacuum at a specific location degrades below a predefined threshold, the two nearest gate valves automatically close to protect adjacent vacuum sections. During accelerator maintenance, only the affected segment needs to be purged with nitrogen gas, preventing exposure of the entire vacuum system to atmospheric pressure and preserving vacuum integrity in other regions.
Feasibility analysis
The design, construction, and operation of the STCF collider ring vacuum system present significant technical challenges, particularly in the positron ring, which requires additional measures to suppress electron cloud instabilities. While these technologies are largely mature internationally and BEPCII provides a strong domestic reference, there is currently no precedent in China for designing or operating an electron storage ring with circulating currents above 1 A.
In recent years, China has made substantial advances in ultra-high vacuum technologies through the construction of large-scale accelerator facilities and improvements in industrial capabilities. These include high-temperature-tolerant copper production, extrusion of non-standard structural profiles, and widespread application of NEG coatings in new-generation light sources such as HEPS and HALF. TiN coating technology has been extensively used in the CSNS accelerator. For the collider IR, vacuum chamber design techniques such as remotely controlled vacuum connections (RVC) have also been applied domestically. Although further R&D is required for some critical vacuum structures and technologies before construction begins, the overall technical risks are considered manageable.
The injector vacuum system can be fully realized using mature and well-established technologies and presents no technical risk.
Summary
The STCF accelerator vacuum system is extensive and complex, with a total vacuum pipeline length of approximately 2500 m. Each accelerator section requires specific design approaches and vacuum technologies. Through comprehensive surveys and preliminary design studies, a basic structure and framework for the vacuum system have been established. The design plans and technical approaches for each subsystem have been preliminarily clarified, providing a solid foundation for continued technical development. Key vacuum technologies requiring further R&D have also been identified.
Beam instrumentation system
Design requirements and specifications
The beam instrumentation system is a critical diagnostic tool for accelerator operation and tuning. It measures a wide range of beam parameters, providing essential support for machine commissioning, suppression of beam instabilities, and optimization of beam position and angle at the collision point. It also forms the data foundation for beam dynamics analysis and the evaluation of integrated luminosity performance. The STCF beam instrumentation system is designed to support both the collider rings and the injector, enabling accurate measurement and stabilization of beam parameters. Its primary objective is to maintain stable beam operation at a high luminosity of 5 × 1034 cm-2s-1, with time resolution sufficient to distinguish bunch spacing at integer multiples of 2 ns (expected to be 4–6 ns), while delivering high-precision data for beam dynamics analysis. The technical specifications are listed in Table 39.
| Beam parameter | Measurement method | Specification | Value/Detail |
|---|---|---|---|
| Beam position | Button electrodes and digital processors | Closed orbit resolution | SA: 50 nm @ 10 Hz; FA: 100 nm @ 10 kHz |
| Turn-by-turn resolution | 1 μm | ||
| Bunch-by-bunch resolution | 5 μm (transverse), 0.2 ps (longitudinal) | ||
| Dynamic range | -50 to 0 dBm | ||
| Beam current | DCCT, PCT, data acquisition system | Measurement range | 0.01–3000 mA |
| Resolution | 2 μA | ||
| Accuracy (>200 mA) | 10 μA | ||
| Bunch charge | BPM sum signal with fast digitizers or photodiodes | Measurement range | 0.1–50 mA |
| Resolution | 25 μA @ 50 mA | ||
| Betatron tune | Sweep/FFT method | Update rate | 1 Hz |
| Resolution | 1×10-4 | ||
| Beam size & Emittance | Absolute (X-ray diffraction imaging) | Range | 10–50 μm |
| Resolution | 2 μm | ||
| Relative (X-ray pinhole imaging) | Range | 20–80 μm | |
| Resolution | 5 μm | ||
| Relative (visible/X-ray interferometry) | Range | 5–50 μm | |
| Resolution | 1 μm | ||
| Bremsstrahlung | Dedicated detector | Measure polarization | – |
| Bunch length | Streak camera (visible light) | Range | 20–100 ps |
| Resolution | 2 ps | ||
| Bunch-by-bunch feedback | Transverse feedback (stripline, FPGA) | Bandwidth | 250 MHz |
| Drive power | 50–100 W | ||
| Damping time | 0.1–0.3 ms | ||
| Longitudinal feedback (RF cavity, FPGA) | Bandwidth | 250 MHz | |
| Drive power | 100–200 W | ||
| Damping time | 0.5 ms | ||
| IP feedback | Slow and fast feedback | Stability | Better than 10% of beam size |
| BPM drift compensation | Capacitive sensor and temperature probe | Resolution | 50–100 nm |
| Beam loss | Scintillator | Time response | ≤8 ns |
| Optical fiber | Spatial resolution | ≤1 m |
Key technologies and development strategy
In the collider rings, BPMs will be installed adjacent to quadrupole magnets, using button electrodes with heterodyne detection and high-speed, high-precision electronics to enable turn-by-turn and bunch-by-bunch position measurements. Visible photon monitors will employ diamond-coated extraction mirrors to minimize thermal deformation caused by synchrotron radiation. An X-ray bunch size monitor based on coded aperture imaging will provide bunch-by-bunch measurements of transverse beam size, while an X-ray interferometry system will offer higher-resolution diagnostics. At the IP, a large-angle bremsstrahlung radiation monitor will measure the polarization of emitted light to infer geometric characteristics of the colliding beams.
Bunch-by-bunch transverse and longitudinal feedback systems will integrate low-noise front-end electronics and high-resolution digital filters to suppress instabilities. The collision point feedback system will detect orbit offsets in the IR, which are linearly related to experimental luminosity, and will also use the luminosity monitor signal to maximize and stabilize luminosity.
In the injector, beam position will be monitored using stripline pickups combined with high-speed, high-resolution electronics for bunch-by-bunch measurements. Bunch charge and length will be measured via passive resonant cavities, providing a large dynamic range and good signal-to-noise ratio. For high-resolution measurements of longitudinal beam structure, a transverse deflecting cavity may also be employed.
Most of the beam diagnostics technologies required for the STCF collider rings and injector have been validated at the NSRL’s HALF [93], SuperKEKB at KEK [94], and the BEPCII/BEPCII-U collider in China [95]. Key techniques are also being developed as part of the STCF Key Technology R&D project [96].
The development strategy for STCF beam instrumentation will follow the principles outlined below:
· Prioritize mature and proven technologies when performance specifications are met.
· Draw design references from the latest international projects of similar scope, subject to expert review.
· Undertake targeted development—via internal R&D or collaborations—will address diagnostics tasks beyond existing technological capabilities, supported by pre-research programs.
Design scheme and system configuration
Beam instrumentation system of the collider rings
BPM and Displacement/Temperature Monitoring
Each STCF collider ring is equipped with 402 button-type BPMs, positioned as uniformly as possible near each quadrupole magnet. The number of BPMs can be adjusted in response to updates in the physical design, similar to other beam diagnostic instruments. BPMs near the injection points provide real-time monitoring of the injected beam, while those near the collision region deliver precise position measurements prior to collisions, ensuring effective beam interactions. Uniformly distributed BPMs also enable comprehensive monitoring throughout the entire ring. For the current STCF collider ring parameters, the button-type BPM probe design has been optimized. Its resonant mode frequencies are well separated from the operating frequency of 499.7 MHz and are shifted away from higher harmonics generated during multi-bunch operation. The BPM probe structure is shown in Fig. 196.
The four electrode signals from each BPM are transmitted via long cables to the BPM electronics, where the analog signals are conditioned before computing the 3D position of each bunch. For transverse position measurements, the system captures the peak negative signal from each bunch, while longitudinal phase measurements require sampling near the BPM signal’s zero-crossing. Based on these signal characteristics and measurement requirements, the system specifications for bunch-by-bunch 3D position measurements are summarized in Table 40.
| Parameter | System component | Minimum requirement | Recommended configuration |
|---|---|---|---|
| Number of channels | — | 4 | 8 |
| Analog bandwidth | Acquisition board | 500 MHz | >1 GHz |
| Oscilloscope | 500 MHz | >6 GHz | |
| Sampling rate | Acquisition board | 500 MS/s | >1 GS/s |
| Oscilloscope | 5 GS/s | >20 GS/s | |
| Sampling resolution | — | 8-bit | >10-bit |
Two acquisition methods are considered. One employs high-bandwidth, high-sampling-rate oscilloscopes [97], which offer high precision but require complex data processing due to their non-phase-locked nature and limited memory depth, making them less suitable for online, real-time bunch-by-bunch monitoring.
To meet STCF’s requirements, a high-speed data acquisition board is selected for real-time, online bunch-by-bunch 3D position monitoring. The system block diagram is shown in Fig. 197. Domestic signal processors have achieved 1 GSPS [98] sampling rates, enabling the development of an integrated processor that combines an analog front-end with eight ADC channels and a digital FPGA-based module. The processor also supports external clock and trigger inputs.
As a high-current machine, STCF experiences thermal variations from synchrotron radiation and other effects, which can affect BPM measurements. Temperature monitoring and compensation are therefore necessary. Following methods implemented at SuperKEKB [99], temperature sensors are installed near BPM probes to monitor environmental fluctuations in real time. The BPM processor collects both position and temperature data, which are then used to build compensation models correcting temperature-induced displacement errors. Feedback control systems may later be added to apply real-time corrections.
The button-type BPM probe design and signal processing capabilities ensure effective operation across the full 1–3.5 GeV energy range of STCF. Although beam characteristics such as shape, intensity, and pulse width may vary with energy, these variations have minimal impact on BPM measurement precision. Additionally, the BPM electronics feature high-sensitivity amplification and filtering circuits, maintaining a high signal-to-noise ratio and resolution under varying beam conditions.
Bunch-by-Bunch Feedback and Tune Measurement
The bunch-by-bunch feedback system suppresses coupled-bunch instabilities [100] and comprises three main components: oscillation signal detection, digital signal processing, and feedback implementation.
Oscillation signals acquired by the front-end RF circuit are filtered, amplified, and down-converted to remove the DC component before ADC sampling and transmission to a digital signal processor. Within the FPGA, appropriately ordered digital filters extract beam oscillation information, and a 90° phase shift can be implemented via FIR filtering algorithms. The processed signal is then converted by a DAC, delayed, amplified by a power amplifier, and applied to the beam through a kicker to suppress instabilities [101].
High-frequency beam signals are mixed with nfRF to generate an oscillation signal near fRF/2 with an improved signal-to-noise ratio [102]. To capture beam oscillations at the fundamental frequency, the digital signal processor operates at a 500 MHz sampling rate, with high-order FIR filters in a high-performance FPGA providing both phase shifting and DC component removal (Fig. 198).
The feedback actuator is the feedback kicker. The feedback signal, generated by the digital signal processor and amplified by an RF power amplifier, is applied to the kicker. In the longitudinal feedback system, the baseband signal must first be modulated to the operating frequency band of the power amplifier and longitudinal kicker. The kicker then generates an electromagnetic field that applies a corrective kick to the bunch, damping its transverse or longitudinal oscillation. To suppress all coupled-bunch instability modes, the bandwidths of the power amplifier and kicker must be at least The central frequencies differ between the transverse and longitudinal feedback channels.
Compared with SuperKEKB, whose collider rings are 3016 m in circumference [103], the STCF collider rings are significantly shorter at approximately 860 m, resulting in a shorter revolution period. Additionally, while SuperKEKB’s low-energy ring operates at 4 GeV, the STCF beam energy is tunable from 1 to 3.5 GeV. Thus, the damping time in STCF is expected to be shorter than in SuperKEKB, which is advantageous.
High-energy beams impose more stringent requirements on the electronics of bunch-by-bunch feedback systems. Digital signal processors must provide high-resolution, fast-sampling, low-latency feedback signals. The entire system, including power amplifiers, must operate with minimal latency to ensure precise and timely correction.
Beam tune is a critical machine parameter that must be continuously monitored and recorded, as it is directly related to beam quality and stability. Other parameters, such as the envelope function and chromaticity, can be derived from tune measurements. Because the amplitude of free oscillations is very small during stable operation, an excitation signal must be applied to the beam for measurement. To avoid disturbing the entire beam, a single bunch can be selectively excited while remaining undamped within the bunch-by-bunch feedback system, ensuring that all other bunches remain stable while the tune is measured.
Interaction Point Feedback
Beam orbit deviations at the IP can lead to significant luminosity losses and must be corrected. Such deviations may arise from vertical motion of the final focus (FF) magnets due to ground vibrations or mechanical fluctuations in cryogenic components, such as cold boxes, which produce closed orbit distortions at the IP that cannot be fully compensated.
The collision point feedback system uses beam–beam kick measurements to correct these deviations, exploiting the linear relationship between beam–beam deflection and beam displacement at the IP. By measuring changes in BPM readings near the IP caused by beam–beam kicks, the system can infer orbit deviations. Correction signals are calculated in real time and applied via correction magnets. Operating in a high-frequency closed-loop mode, this feedback system dynamically compensates for orbit errors caused by mechanical noise or ground motion, ensuring precise alignment of the colliding beams at the IP and enhancing collision efficiency and luminosity [104, 105].
The IP feedback system primarily relies on beam position signals, supplemented by luminosity and beam-induced radiation measurements. To measure beam positions as close to the IP as possible, two eight-electrode BPMs are positioned approximately 60 cm to the left and right of the IP (subject to updates based on MDI design evolution). At this location, the electron and positron beams remain co-linear, and each BPM must monitor both beams simultaneously. Based on STCF beam parameters, maintaining orbit deviations within 5% of the bunch size at the IP requires BPM resolution better than 5 μm. In the horizontal plane, where the beam size is very small, beam–beam kicks are no longer sufficiently sensitive to serve as indicators of collisions (Fug. 199).
BPM dimensions are optimized based on the beam pipe diameter, signal strength, resolution requirements, and beam parameters. The chamber diameter matches the transverse beam size and vacuum chamber design. The diameter of the button electrodes balances signal strength and spatial resolution while meeting bandwidth requirements. Because the beam pipe near the IP has a small aperture, the power output of the BPM near the IP is much higher than that of conventional BPMs; hence, specialized feedthroughs must be designed (Fig. 200).
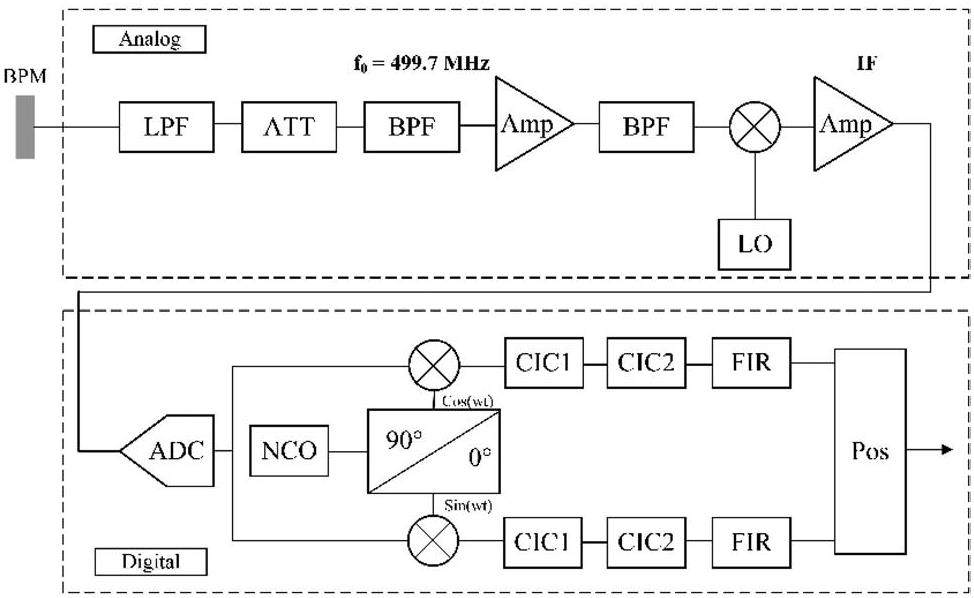
The analog section uses low-pass and band-pass filters to convert beam signals into passband signals centered at the RF frequency of 499.7 MHz. An analog mixer then down-converts the 499.7 MHz component of the BPM signal to an IF signal to reduce the impact of ADC clock jitter on the signal-to-noise ratio.
To ensure that the FOFB system operates with low latency and high bandwidth, the power sources of fast correction magnets must respond rapidly. The IP fast feedback system requires a correction magnet power supply with a bandwidth of at least 10 kHz. Fast corrector magnets must be capable of precise magnetic field control to minimize orbit correction errors and suppress feedback jitter around the target value. Improving power supply resolution requires reducing the quantization error of the DAC chips.
STCF may operate at energies ranging from 1 to 3.5 GeV. Beam–beam effects are energy-dependent and become more pronounced at lower energies. As energy increases, the same position offset results in smaller BPM signal changes, thereby raising the resolution requirements of the BPMs.
Beam Diagnostics Based on Synchrotron Radiation
High-energy charged particle bunches emit SR when deflected, with the SR characteristics reflecting the beam parameters at the light emission location, making it a valuable non-interceptive diagnostic tool. Considering the beam characteristics of the STCF, both X-rays and visible light from SR will be used to measure the transverse dimensions and length of the electron and positron bunches.
The beam size in the transverse direction and emittance can be monitored through X-ray diffraction imaging, X-ray pinhole imaging, and synchrotron light interferometry. Emittance is typically calculated by combining accurate measurements of the bunch transverse size with the beam’s Twiss parameters.
X-ray diffraction imaging is a direct method for observing the beam spot. Figure 201 illustrates a beam size measurement system based on Fresnel zone plate (FZP) X-ray diffraction imaging [106]. The synchrotron light is first monochromatized by a monochromator and then imaged directly through two FZPs. The system typically operates with a total magnification factor of 15–30. This method offers high spatial resolution but may be affected by diffraction effects, limiting its overall measurement range.
X-ray pinhole imaging uses a small aperture to project the transverse beam profile [107]. As shown in Fig. 202, X-rays extracted from the vacuum chamber pass through a pinhole and illuminate a downstream fluorescent screen, where the image is converted to visible light and recorded by a CCD camera for profile reconstruction. This method is simple, monochromator-free, robust to thermal loads, and reliable. However, it has lower resolution than diffraction-based methods.
Synchrotron light interferometry is implemented using a Michelson-type stellar interferometer [108]. After passing through a double slit, optical filters, and a focusing system, the light forms an interference pattern on a detector. The contrast of this pattern is used to deduce the beam spot size. This method can achieve sub-micrometer resolution but requires a complex optical path.
Bunch length is typically measured using a streak camera [109], which is capable of recording ultrafast optical phenomena. It can simultaneously provide information about light intensity, temporal structure, and spatial (or spectral) distribution.
In designing the STCF synchrotron light diagnostic system, beam energy variability must be considered. Beam energy affects both the synchrotron spectrum and radiation divergence: higher energies lead to an increased yield of high-energy (X-ray) photons and a narrower radiation cone. Therefore, optical elements must accommodate a wide dynamic range, and energy absorbers and related components must be designed with sufficient thermal capacity and safety margins.
Beam Loss Monitoring
According to the beam loss diagnostics requirements of the STCF, a hybrid detector configuration combining optical fibers and scintillators is adopted. Optical fibers are installed along the DR and linac to monitor abrupt losses and localize the position of the loss event. Scintillator detectors are deployed along the dual-ring collider to provide a prompt response to frequent beam loss incidents. The entire beam loss monitoring system is designed to provide high spatial and temporal resolution.
In future upgrades, a self-developed scintillator detector with an overall response time below 2 ns will be considered to realize bunch-by-bunch resolution. This will contribute to maintaining high operational luminosity.
Beam diagnostics system in the injector
Beam Diagnostics in the Linacs and Transfer Lines
The beam diagnostics system for the linacs and transfer lines with energies of 1–3.5 GeV includes independent subsystems for beam position measurements, bunch charge measurements, beam transverse profile measurements, kinetic energy measurements, and energy spread measurements.
The beam position measurement system mainly consists of BPM probes (stripline and button types), signal transmission cables, digital BPM (DBOM) electronics, timing/trigger distribution systems, and frequency synthesizers. The BPM probes receive beam position signals, which are processed by DBPM electronics to extract beam position data, and feed them to the control network. This system is primarily used for position and orbit measurement and BBA.
The beam charge measurement system mainly includes integrated current transformers (ICTs), signal transmission cables, digital oscilloscopes for current signal acquisition, and data processing terminals. The ICT signal is oversampled using digital oscilloscopes, and the collected waveform is processed to determine the bunch charge.
The beam transverse profile measurement system is based on view screen optical imaging. It includes beam spot screens, screen vacuum chambers, motion mechanisms, telecentric optical lenses, digital cameras, cabling, image processing terminals, motor drivers, and controllers. The local beam diagnostics station sends camera trigger signals via coaxial cables to the cameras. Control signals for stepper motors are sent via Ethernet to operate the screen actuators. Captured beam spot images are also transmitted via Ethernet to the server for remote control and image acquisition.
Beam energy and energy spread measurements are conducted using a spectrometer system. The beam is deflected by a bending magnet onto an energy-dispersive screen. By measuring the beam spot on the screen, beam energy and energy spread can be calculated. The imaging and motion control system for the energy screen shares infrastructure with the transverse profile system.
Beam Diagnostics in the Damping Ring
The positron beam of 1 GeV is injected into the DR to reduce its emittance through SR damping. Once the target emittance is achieved, the beam is injected into the collider. The diagnostics system in the DR uses this process to monitor the evolution of beam parameters, ensuring the beam meets injection requirements [110].
Beam position monitoring in the DR typically uses button-type BPMs. The four electrodes of a button BPM detect the bunch signal, which is transmitted through feedthroughs and coaxial cables to the readout electronics. The electronics compare the four signals (typically using difference-over-sum algorithms) to determine beam position. This system is simple, based on mature technology, easy to fabricate, and compatible with commercially available readout electronics.
A fluorescent screen is used during tuning phases to observe the beam spot position and shape. To ensure impedance continuity, a custom-designed beam shielding chamber that ensures that the vacuum chamber remains smooth when the screen is retracted is required.
A DC current transformer (DCCT) is employed to measure the DC current in the DR. The system includes a probe and its associated electronics. The probe is typically installed in the straight sections, and commercially available models with various apertures are available.
Beam loss in the DR is monitored using a combination of optical fibers and dual PIN diodes. Optical fibers cover the ring to enable the real-time localization of loss events, while dual PIN diodes are deployed at key points for localized radiation monitoring.
Charge monitors such as FCT/ICT are installed at the injection and extraction points of the DR to assess overall transmission efficiency. An optical transition radiation (OTR) screen is installed at the extraction point to measure beam spot size and calculate the transverse emittance, ensuring that the beam satisfies injection requirements.
Feasibility analysis
Most subsystems, such as BPMs, bunch-by-bunch feedback, beam loss monitors, and synchrotron radiation monitors, are based on mature, standardized, and well-validated technologies already implemented at facilities such as HALF, HEPS, and SuperKEKB. These solutions meet the engineering requirements and are feasible for deployment, posing no significant technical risks. Some of the more demanding technologies, compared to those in existing storage ring light sources or colliders, have already been applied in FEL facilities and have undergone verification through dedicated R&D initiatives and beam test platforms.
Most technology subsystems will rely on domestically procured or independently developed equipment. For subsystems involving imported components—such as zone plates, streak cameras, and precision displacement stages—alternative strategies are under consideration, including diversifying import sources and developing domestic substitutes.
Summary
Based on the technical specifications and requirements derived from the STCF accelerator physics design, the beam diagnostics system will provide measurements of parameters including beam position and closed orbit, DC and bunch-by-bunch current, tune (working point), beam transverse profile and emittance, bunch length, and beam losses. These measurements support beam commissioning and accelerator physics studies.
The overall system is largely composed of well-established technologies that have been used at other facilities, with a few cutting-edge components expected to be validated within the next 2–3 years. Whenever possible, the system will utilize domestically produced and self-developed equipment. Future collaboration with leading domestic research institutes and instrumentation manufacturers will be pursued to promote localization and develop viable domestic alternatives.
Interaction region superconducting magnet system
Design requirements and layout
To achieve extreme compression of the beam spot size at the IP and thereby enhance the luminosity of the STCF collider, a set of high-gradient superconducting quadrupole magnets is installed symmetrically on both sides of the IP, positioned as close as possible to it. These magnets are placed within the experimental spectrometer, where available space is severely constrained. In addition, they must effectively cancel the solenoidal magnetic field of the detector to prevent adverse effects on the accelerator beam.
Following accelerator physics requirements, the superconducting quadrupole magnets in the IR adopt a double-aperture design and accommodate a beam crossing angle of 60 mrad. The distance from the front face of the focusing quadrupole magnet to the IP (denoted as L*) is 900 mm (see Sect. 2.1). A conceptual layout of the IR superconducting magnet (IRSM) system is shown in Fig. 203. Each IRSM system, symmetrically placed on either side of the IP, comprises two sets of superconducting quadrupole magnets (QD0 and QF1), one anti-solenoid (AS), and two sets of corrector coils. These superconducting magnets operate within the 1.0 T solenoidal field generated by the detector spectrometer. The main physical parameters of the magnets are summarized in Table 41.
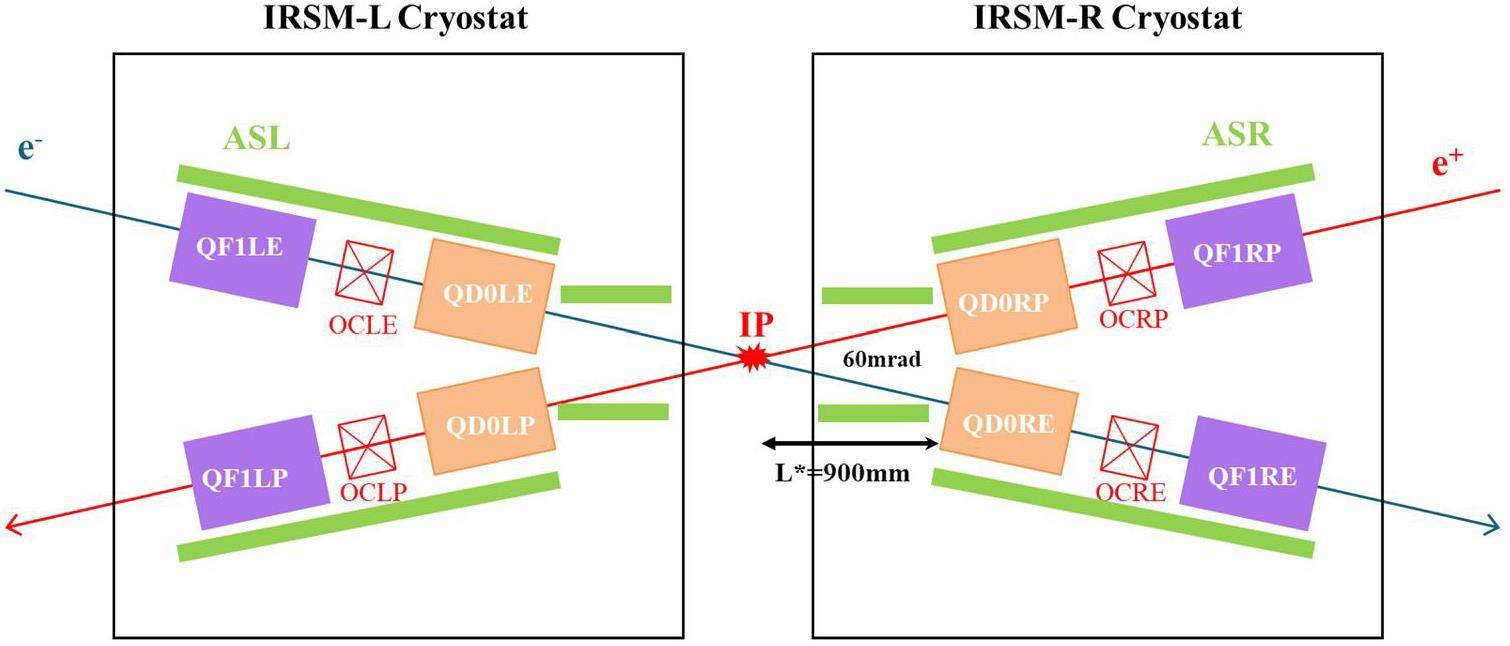
| Coil type | Parameter | QD0_e+/e– | QF1_e+/e– |
|---|---|---|---|
| Quadrupole | Field gradient (T/m) | 50 | 40 |
| Integrated field harmonic (excluding b2) | ≤0.2 ‰ @R=10 mm | ≤0.2 ‰ @R=15 mm | |
| Beam pipe inner radius (mm) | 15 | 25 | |
| Magnetic length (mm) | 400 | 300 | |
| Distance from IP (mm) | 900 | 1800 | |
| Coil inner radius (mm) | 20–22 | 20–22 | |
| Coil outer radius (mm) | ≤27 | ≤27 | |
| Correctors | Multipole orders | a1, b1, a2 | a1, b1, a2 |
| Strength @Rref | 0.016/0.016/0.6 | 0.03/0.03/0.3 | |
| Anti-solenoid | Integrated field | Within ±2 m from IP, residual field less than 1% of detector solenoidal field |
Key technologies and roadmap selection
Double-aperture superconducting quadrupoles in the IR are a critical and distinguishing feature of new-generation electron–positron colliders. To date, only SuperKEKB in Japan has completed the engineering design and fabrication of such a system. Other projects such as the FCC-ee at CERN, SCTF in Russia, and CEPC in China remain in the key technology R&D phase.
The focusing quadrupole coils are the core components of the IR quadrupole magnets. Several technical options exist for their construction:
· Cosine-theta (cos2θ) coils, as adopted by SuperKEKB [111]
· Serpentine coils, as used in BEPCII [112]
· Canted Cosine Theta (CCT) coils, adopted by FCC-ee [113] and SCTF at BINP [114]
Table 42 compares the IR quadrupole magnet technologies used in various international e+e- collider projects. The key technical requirements include high magnetic field gradient, excellent field uniformity, compact structure, and light weight. After evaluation, the STCF has selected the CCT coil technology route for the prototype IR quadrupole magnet owing to its design flexibility, superior magnetic field quality, lighter structure, and smaller end curvature.
| Collider | SuperKEKB | FCC-ee | CEPC | SCTF | STCF |
|---|---|---|---|---|---|
| Country/Region | Japan | Europe | China | Russia | China |
| Beam energy (e–/e+) (GeV) | 7.0/4.0 | 104.5/104.5 | 120/120 | 1.3/1.3 | 3.5/3.5 |
| Beam crossing angle (mrad) | 83 | 30 | 33 | 60 | 60 |
| L* distance (mm) | 935 | 2200 | 2200 | 905 | 900 |
| Detector field (T) | 1.5 | 2.0 | 3.0 | 1.0 | 1.0 |
| Quadrupole coil technology | cos2θ | CCT | cos2θ | CCT | CCT |
| Max gradient (T/m) | 68.9 | 100 | 142.3 | 100 | 50 |
| Magnetic length (mm) | 334 | 1200 | 1210 | 200 | 400 |
Design scheme and system configuration
Double-aperture superconducting quadrupole magnets
Each of the two quadrupole magnet assemblies comprises two vertically focusing magnets (QD0) and two horizontally focusing magnets (QF1). These magnets are symmetrically arranged on both sides of the IP, with a total crossing angle (2θ) of 60 mrad between the electron and positron beams. The front end of the QD0 is located 0.9 m from the IP, while that of the QF1 is positioned 1.8 m away. The relative positions of the eight quadrupole magnets are illustrated in Fig. 203, and their design specifications are listed in Table 41.
Due to the high field gradient and extremely compact spatial constraints, the QD0 magnet development presents the greatest challenge. Consequently, the main R&D effort on superconducting quadrupole coils is focused on the QD0. At the entrance of QD0, the center-to-center spacing between the electron and positron beam pipes is 54 mm. Considering the end length of the CCT-type magnet and assuming an equivalent field length of 450 mm, the center spacing at a 60 mrad beam crossing angle decreases to 52.52 mm. This indicates that the maximum outer diameter of each quadrupole coil is 26.26 mm.
Accounting for the beam pipe wall thickness of 1 mm, an installation clearance of 3 mm, and a helium channel thickness (installed directly on the inner surface of QD0) of 1 mm, the minimum required inner diameter of the QD0 coil is 20 mm. The available radial space for coil construction is therefore less than 6.26 mm, making this one of the most technically demanding components. A schematic of the radial space allocation is shown in Fig. 204.
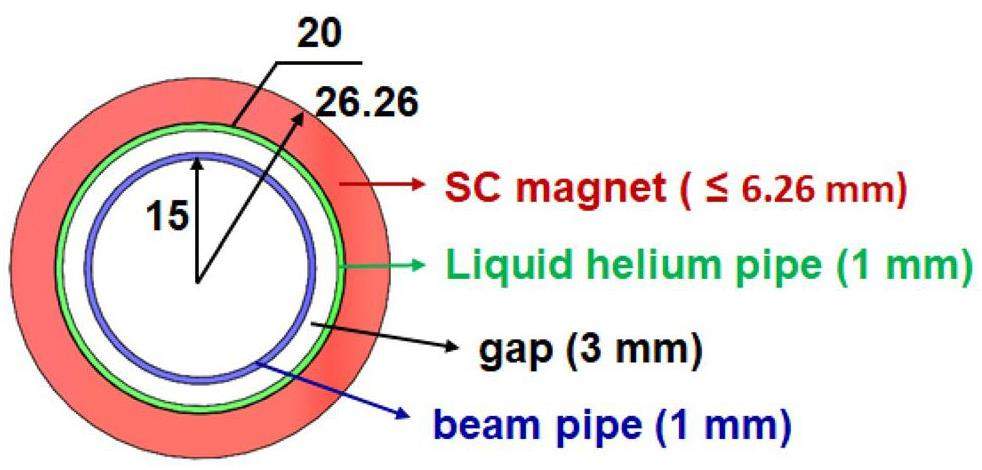
To mitigate magnetic hysteresis loss and enhance field stability, superconducting wires with a fine filament diameter (<10 μm) are prioritized for coil design. The test prototype of the QD0 uses superconducting wire with filaments less than 10 μm in diameter. The main design parameters for the CCT QD0 magnet are listed in Table 43. The magnetic field contour and current load line are shown in Fig. 205.
| Parameter | Value |
|---|---|
| Good field region radius (mm) | 10 |
| Coil inner radius (mm) | 20 |
| Max QD0 outer radius (mm) | <26.23 |
| Operating current (A) | 638 |
| Peak field on coil (T) | 1.64 |
| Field gradient (T/m) | 50 |
| Magnetic length (mm) | 400 |
| Superconductor working point (at 4.2 K) | 67% |
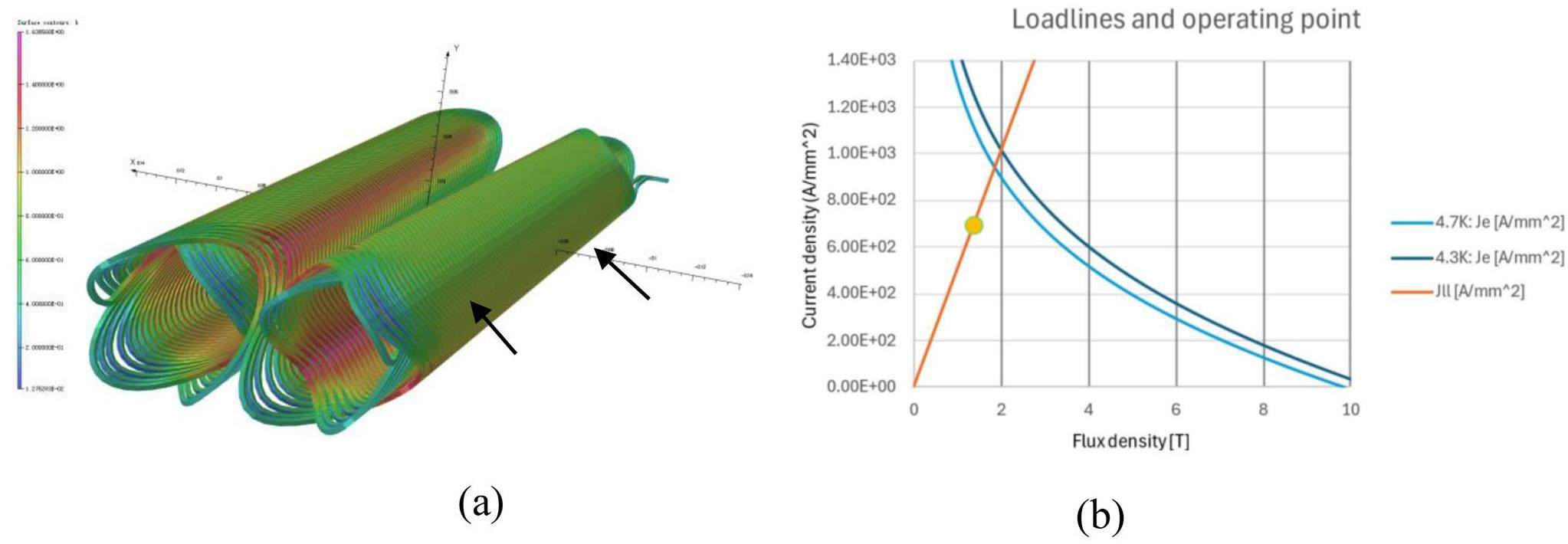
The maximum magnetic field on the quadrupole coil is 1.64 T, and the working point is at 67% of the load line. The QD0 coil is wound with superconducting wire of 0.9 mm diameter, using a pattern of 2 strands horizontally and 2 layers vertically, with 4 strands wound in parallel along pre-machined grooves on the CCT former.
Owing to the electromagnetic coupling between the two apertures of the double-aperture quadrupole magnet, a cross-talk compensation technique is applied. This involves introducing reversed harmonic components and optimizing the overall coil trajectory.
Table 44 summarizes the optimized values of the 1st to 10th order harmonics of the QD0 double-aperture superconducting magnet. After optimization, the integrated harmonics of each order are less than 2 units (<0.2‰).
| Harmonic order | An (T·m) | Unit (An) | Bn (T·m) | Unit (Bn) |
|---|---|---|---|---|
| 1 | 3.41×10–6 | 0.17 | –1.17×10–6 | –0.06 |
| 2 | 2.80×10–6 | 0.14 | 2.04×10–1 | 10000 |
| 3 | –1.56×10–6 | –0.08 | –4.27×10–6 | –0.21 |
| 4 | –3.47×10–6 | –0.17 | –2.64×10–7 | –0.01 |
| 5 | –3.32×10–6 | –0.16 | 3.87×10–6 | 0.19 |
| 6 | 1.13×10–6 | 0.06 | –2.98×10–6 | –0.15 |
| 7 | 4.58×10–7 | 0.02 | –2.94×10–6 | –0.14 |
| 8 | –6.61×10–7 | –0.03 | 2.99×10–6 | 0.15 |
| 9 | 2.20×10–7 | 0.01 | –2.70×10–7 | –0.01 |
| 10 | –8.51×10–8 | –0.00 | 2.97×10–7 | 0.01 |
The groove-embedded former structure is designed based on the CCT coil parameters. The inner and outer formers are shown in Fig. 206. Both formers are machined with helical grooves according to the CCT trajectory equations, with opposite winding inclinations. The inner and outer formers are aligned via positioning pins. Jumper and terminal structures are designed into the former to ensure continuous winding and allow for wire joint welding. The maximum mechanical stress in the CCT magnet coil is 1.6 MPa and within allowable limits.
Anti-field superconducting solenoid
The superconducting magnet system is embedded within the detector and operates under the background field of the detector solenoid, which is approximately 1.0 T. To eliminate the influence of the detector’s magnetic field on the beam trajectory, a set of anti-solenoid coils (including field screening and field compensation coils) is used to compensate for the integral magnetic field. The specific technical requirements are as follows:
1. The residual integrated field within the beam pipe from the IP to QD0 and beyond QF1 must be ≤ 0.01 T·m;
2. The residual longitudinal magnetic field within the beam pipe from QD0 to QF1 must be ≤ 300 Gs;
3. The field distribution of the anti-solenoid must satisfy the vertical beam divergence constraint;
4. The axial layout and outer diameter must comply with the mechanical detector interface (MDI) spatial constraints.
The anti-solenoid coils adopt a “NbTi-conductor, low-temperature superconducting coil + vacuum impregnation” technical approach. The coils are arranged in a stepped configuration along the central axis and powered in series. An additional current lead is included in the central coils to enable fine adjustment of the integral field during beam commissioning and operation.
As part of the combination magnet, the field-screening anti-solenoid coils are positioned between the quadrupole magnets and the outer cryostat. The structure consists of the NbTi anti-solenoid coils, coil former, mechanical supports, and current leads. Specifically:
1. The anti-solenoid coils generate a counteracting field to the spectrometer field; their parameters are listed in Table 45;
| Superconductor parameters | Coil parameters | ||
|---|---|---|---|
| Bare wire size (mm2) | 1.38×0.93 | Operating current (A) | 231 |
| Insulated size (mm2) | 1.48×1.03 | Peak field (T) | 4.11 T |
| Cu/SC ratio | 1.7 | Io/Ic | 20% |
| RRR | 150 | Number of coils | 15 |
| Filament count | 1500 | Coil length (m) | 1.905 |
| Filament diameter (μm) | 19 | Inductance (H) | 3.0 |
| Critical current (4.2 K, 5 T)(A) | 1400 | Stored energy (MJ) | 0.081 |
2. The coil former maintains the geometric profile of the coils;
3. The support structure connects the coil former to the combination magnet cryostat, providing mechanical stability and thermal isolation;
4. The end current leads power the anti-solenoid, while a center-tapped lead allows integral field tuning.
Figure 207(a) shows the half-model layout of the detector coil and the anti-solenoid (right side only), with the spectrometer yoke iron hidden for clarity. Figure 207(b) illustrates the magnetic field distribution: the blue curve represents the spectrometer field, the red curve the anti-solenoid field, and the black curve the resulting field after superposition. The QD0 and QF1 locations (marked by black dots) exhibit nearly zero net axial field, confirming successful integral compensation.
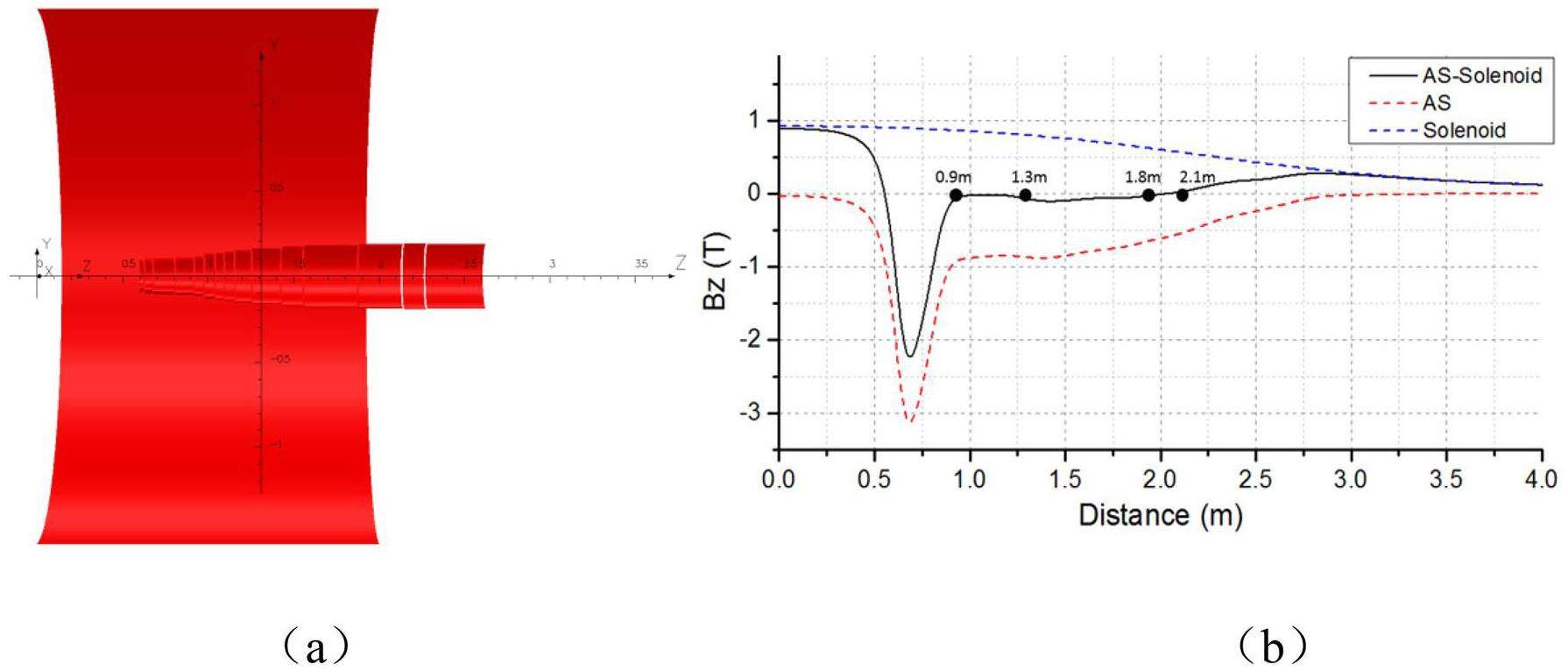
Corrector magnets and coils
Among various types of accelerator magnets, harmonic correction coils (or harmonic trim coils) are essential components. They are typically categorized into field correction coils and orbit correction coils, as summarized in Table 41.
Field correction coils are used to improve magnetic field quality and correct quadrupole misalignments. By generating higher-order fields that counteract the intrinsic multipole components of the magnet, they enhance field uniformity and stability, thereby ensuring consistent particle trajectories.
Orbit correction coils primarily include low-order correction coils that generate forces or coupling terms to adjust the dispersion function and correct motion coupling induced by alignment or magnetic errors. The a1 and b1 coils produce horizontal and vertical dipole fields, respectively, to correct beam orbits and control dispersion. The a2 coil generates a skew quadrupole field to mitigate x-y coupling.
Owing to the spatial constraints imposed by the IR layout (e.g., the crossing angle and L*), only approximately 6 mm of radial space is available—insufficient to accommodate both quadrupole and correction coils. Consequently, a self-compensating harmonic design based on a CCT-type quadrupole coil is adopted, leveraging high-precision CNC machining of the coil former. This approach may eliminate the need for dedicated field correction coils. However, saddle-type coils remain under consideration as candidates for low-order, beam-based corrections.
Currently, the initial specifications for the orbit correction coils, including their order and strength, are summarized in Table 46. The correction coils are positioned longitudinally between QD0 and QF1 and are wound in single-layer configurations with low current. The inner radius of these trim coils matches that of the quadrupole magnets (20 mm). At a reference radius of 10 mm, the design strengths of the a₁ and b₁ coils for QD0 are 0.016 T·m. The design and simulated magnetic field distribution of the a1 (b1) coil are shown in Fig. 208. The design parameters will continue to evolve as the machine optics and physics requirements become further refined.
| Magnet | Rref (mm) | A1 (T·m) | B1 (T·m) | A2 (T) | B2 (T) |
|---|---|---|---|---|---|
| QD0 | 10 | 0.016 | 0.016 | 0.6 | 0.6 |
| QF1 | 15 | 0.03 | 0.03 | 0.3 | 0.3 |
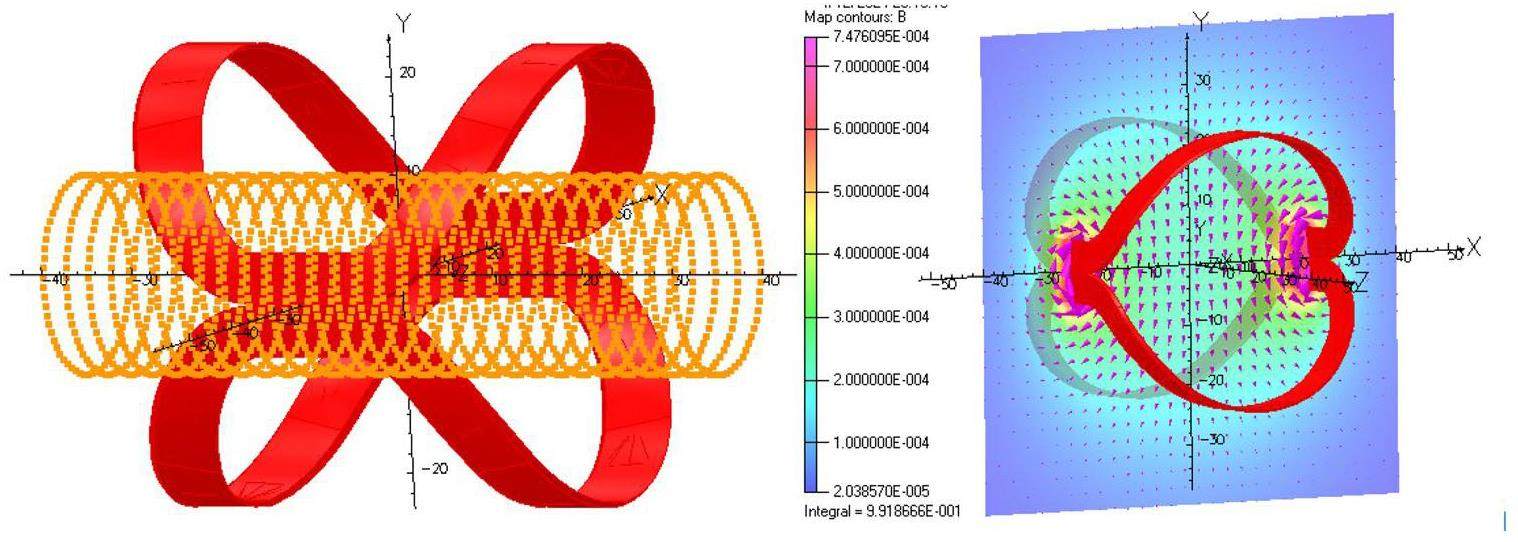
Cryostat for the interaction region superconducting magnet system
To meet the cryogenic requirements of the IRSM, the cryogenic system provides 4.5 K subcooled helium to cool the superconducting magnets and their current leads. It simultaneously provides sturdy mechanical support to extend the superconducting magnets into the detector. The system consists of cryostats, distribution valve boxes, and transfer lines. Each cryostat handles a thermal load of approximately 37.2 W and is cooled by a helium refrigerator with a total cooling capacity of 1000 W at 4.5 K. The refrigerator delivers up to 24 g/s of subcooled liquid helium to each IRSM system.
The core technical challenges of the IRSM cryogenic system are the thermal insulation of components and the precise allocation and control of cryogenic working fluids. The technical route to address these challenges involves the following steps:
1. Based on the magnet and current lead configuration, the structure of the cryostat is determined and designed for thermal insulation. The static thermal load at 4.2 K is analyzed and used in combination with the dynamic thermal load from magnet operation to determine the required total cooling power.
2. From the cooling requirement, the subcooled helium flow rate and pressure are estimated. These parameters are then used to design the cryogenic transfer lines, whose insulation structure is also optimized to minimize transmission losses.
3. Using the determined flow and pressure requirements, the flow scheme of the distribution valve box is designed to allocate, regulate, and recycle the cryogen efficiently. Adequate monitoring and control components are installed to ensure precise system regulation.
4. Based on the valve box flow scheme, its structure is finalized and thermally insulated. The cooling losses in the distribution stage are then calculated, and the final total cooling requirement of the system is determined, which in turn defines the upper-level refrigerator capacity.
Referencing the cryostat design for SuperKEKB’s IR magnets [115, 116] and adapting it for the STCF IRSM geometry, the cryostat is designed to be composed of an outer shell, liquid helium vessel, liquid nitrogen radiation shields, and a support structure. The internal cross-section is shown in Fig. 209. The cryogenic structure of the magnet cryostat is illustrated in Fig. 210. The liquid helium vessel is suspended by eight titanium alloy (Ti-6Al-4V) rods installed at inclined angles. This layout ensures that the relative positions of support points remain unchanged upon cool-down to 4.5 K.

The cryogenic distribution system layout depends on the spatial configuration of the cryostats and the refrigerator. It consumes cooling power during operation, and thus, the structure, process, and scale of the valve boxes and transfer pipelines directly affect the overall system performance. The transfer and distribution system must meet the following technical specifications: room-temperature vacuum pressure < 1.0 × 104 Pa and a total leak rate < 5.0 × 10–9 Pa·m3/s. Within the valve box, helium flow is split, collected, regulated, and routed as required. The cryostat and valve box are connected by a 4-channel cryogenic transfer line that has the cross-sectional structure shown in Fig. 211. The heat load of the 4.5 K line is less than 0.3 W/m. Liquid nitrogen at 77 K is split into two paths in the valve box, supplying the valve box radiation shield and the shields on the cryostat via the transfer line. Subcooled helium at 4.5 K flows to the cryostat, cools the magnet, and then returns via a helium vapor return line to the valve box.
Feasibility analysis
All superconducting magnets will be based on domestically available NbTi superconducting wire, thereby avoiding any risk of foreign export restrictions.
For the superconducting quadrupole coils, the design target has been set more stringently than the technical requirement to provide adequate margin against potential magnetic field quality deviations during production. Since the groove shape of the CCT coil support structure determines both the conductor path and magnetic field quality, tight control over the machining precision of the coil formers is essential. In addition, careful control of coil fabrication and assembly tolerances is required to prevent degradation of magnetic field quality due to misalignments.
The prototyping effort for the QD0 magnet will explore and verify the CCT-based technical approach, providing the experience needed for full-scale development. The high-gradient, high-field-quality double-aperture quadrupole coils form the core of the IRSM system. The CCT approach has already been validated through prototype work in the FCC-ee project, and the STCF team will build on both international developments and domestic expertise through multiple expert reviews and prototype iterations.
The anti-solenoid will adopt an integrated stepped support structure with pull-rod lifting mechanisms and end mounting holes. The support will be fabricated as a welded structure with full machining to ensure accurate coaxial alignment across the multiple stepped coils. The anti-solenoid itself will be vacuum-impregnated to produce a compact, precise, high-strength coil capable of generating a high-quality reverse field and withstanding electromagnetic forces resulting from coupling with the spectrometer magnet. The design, fabrication, and testing of NbTi-based anti-solenoid coils are well-established technologies in China and pose no technical risk.
Orbit correction coils are designed based on SuperKEKB specifications. Their technical approach is similar to that of the superconducting quadrupole coils but simplified through the use of single-turn, single-layer saddle coils, making them highly feasible.
Cryogenic cooling for the superconducting magnets in the IR is a mature technology, widely applied in both domestic and international accelerators. In particular, the SuperKEKB and BEPCII-U projects have conducted comprehensive simulation and experimental studies that clarified the thermal-hydraulic characteristics of subcooled helium and magnet behavior during cooldown, steady operation, and warmup. Proven technologies and protocols are already in place. As the technical requirements of STCF are consistent with those of these established projects, the cryogenic system and distribution infrastructure are considered mature and technically feasible.
Summary
The core component of the IRSM system—the high-gradient quadrupole coil—has completed conceptual design and meets STCF requirements for both field gradient and field quality. Prototype development of the CCT-type coil is underway, focusing on electromagnetic optimization of the double-aperture layout and harmonic control. Other components, such as the anti-solenoid and correction coils, employ mature technologies or off-the-shelf solutions, ensuring manageable technical risk for the overall system.
Electron source system
Design requirements and specifications
The primary options for the STCF electron source system are thermionic grid-controlled electron guns and PC RF electron guns, which serve as critical components of the STCF injector. Injector schemes for both off-axis injection and bunch swap-out injection in the collider rings have been studied and incorporated into the overall accelerator design.
In the off-axis injection scheme, the directly injected electron beam is generated by an S-band PC electron gun with a bunch charge of 1.5 nC, while the positron beam is produced by accelerating 10 nC bunches from a thermionic electron gun to 1.5 GeV for target bombardment. In the bunch swap-out injection scheme, the electron beam is generated by either a thermionic or an L-band PC electron gun with an 8.5 nC bunch charge, and the positron beam is produced by accelerating 11.6 nC bunches from a thermionic electron gun to 2.5 GeV before striking the target.
A compatible injector scheme supporting both injection options has been finalized, with the off-axis scheme planned for initial implementation. In this configuration, the electron beam directly injected into the collider electron ring is generated by an L-band PC gun producing 1.0 nC per bunch. The positron beam is produced by accelerating 11.6 nC bunches from a thermionic gun to 1.0 GeV before striking the target. For the bunch swap-out injection scheme, the same L-band PC gun is used to deliver 8.5 nC per bunch, while the positron beam is generated from 11.6 nC bunches accelerated to 2.5 GeV prior to target impact. The bunch swap-out injection places significantly higher performance demands on the electron source system compared to the off-axis injection.
The design requirements and specifications for the electron guns in the compatible injector scheme, applicable to both off-axis and swap-out injection modes, are summarized in Table 47.
| Injection scheme | Electron source | Expected specification |
|---|---|---|
| Off-axis injection | Thermionic | Beam current ≥ 16 A, anode voltage > 150 kV, repetition rate 30 Hz |
| Photocathode | L-band (1300 MHz) gun, static vacuum ≤ 1×10-7 Pa, bunch charge ≥ 1.0 nC | |
| Swap-out injection | Thermionic | Beam current ≥ 16 A, anode voltage > 150 kV, repetition rate 90 Hz |
| Photocathode | L-band (1300 MHz) gun, bunch charge ≥ 8.5 nC, repetition rate 30 Hz |
Key technologies and technical roadmap
Thermionic electron gun: physical design and optimization
The thermionic electron gun system consists of the gun, a cathode-grid assembly, and a pulsed high-voltage supply of up to 200 kV. The gun design must address factors such as beam energy, structural voltage hold-off capability, high-current stable emission, beam transverse size and divergence angle, ease of fabrication, assembly, and maintenance, long operational lifetime, and reliability. Achieving high current requires an ultra-high vacuum, which requires special attention.
The gun design was optimized using the EGUN simulation software. The design provides the gun with a perveance of 0.2 μP and a voltage of 200 kV, allowing it to deliver electron bunches of up to 16 nC with beam quality suitable for the injector. The SHB and accelerator system were designed in coordination with beam dynamics studies to ensure the feasibility and appropriateness of the electron gun parameters.
Photocathode electron gun: core technologies and physical design
The generation of 1.0 nC per bunch using an L-band PC microwave gun is a mature technology and is applicable to the off-axis injection scheme. The bunch swap-out scheme requires at least 8.5 nC per bunch, and plans are in place to use an L-band gun to meet this requirement.
The core technologies involved include the structural design of the RF electron gun, PC preparation, the load-lock system, and laser shaping schemes. The gun’s acceleration, focusing, and laser beam shaping must also be optimized.
Technical roadmap selection
For the thermionic gun system, EGUN simulations were used to perform design optimization. SHBs and accelerator sections were also designed with beam dynamics to validate performance.
For the PC source technology, the feasibility of using Cs2Te semiconductor cathodes in an L-band gun to produce 8.5 nC and 1.0 nC per bunch has been confirmed. In the future, GaAs PCs may be considered for generating polarized electron beams.
Design scheme and system composition
The electron source system consists of both the thermionic and PC electron gun systems.
Thermionic electron gun design scheme
CST simulations for the electron gun have been performed, and the results shown in Fig. 212 indicate that the extracted beam charge and quality meet the requirements of the STCF injector.
The gun cavity is primarily composed of a cathode, anode, focusing electrode, insulating ceramic tube, corona rings, and structural support. To prevent breakdown, corona rings are installed on both the vacuum (inner) and atmospheric (outer) sides of the welded area between the ceramic tube and metal. The 3D design of the thermionic electron gun is shown in Fig. 213.

This thermionic gun uses the EIMAC Y796 cathode-grid assembly or a component of equivalent specifications. The beam pulse generator for the electron gun includes a DC power supply, a control box, and a pulser. The pulser’s DC supply is continuously adjustable from 0 to 1 kV, with the pulse having an FWHM of approximately 1.1 ns and a base width of approximately 1.6 ns.
Photocathode electron gun design scheme
An L-band gun is used as the PC electron gun used for direct electron beam injection under both the off-axis and bunch swap-out schemes, as illustrated in Fig. 214. This gun is compatible with high-quantum-efficiency semiconductor PCs. The L-band cavity is relatively large, and the aperture between the full and half cells provides sufficient space to support the generation of high-charge electron bunches.
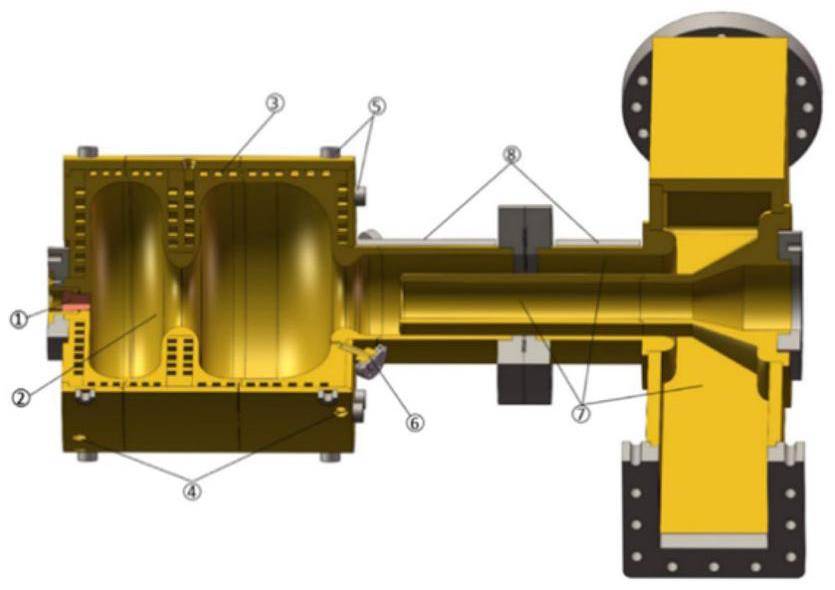
Feasibility analysis
Thermionic electron guns are mature technologies that have been widely adopted in accelerator facilities such as SuperKEKB and BEPCII [117]. It is well established that beam currents of approximately 12 A can be extracted at 150 kV. Simulations indicate that 16 A can be achieved at 200 kV, demonstrating the feasibility of the design. The remaining key subsystems are also technically mature, indicating a high overall level of feasibility.
For the L-band PC gun, Tsinghua University’s accelerator laboratory has extensive experience in both design and operation. Internationally, research groups such as PITZ (Germany) have conducted long-term and in-depth studies of L-band guns, which have been successfully deployed in large-scale facilities such as the European XFEL. At Argonne National Laboratory, the AWA project developed L-band PC guns capable of operating with bunch charges at the tens-of-nC level. Tsinghua University has also designed L-band guns [118] for the China Academy of Engineering Physics and the SHINE facility in Shanghai. Established precedents exist for high-charge optimization of L-band guns to support single-bunch charges of approximately 10 nC.
For polarized electron sources, design approaches can draw on international experience. For example, Jefferson Lab operates a high-performance polarized source [119], and the EIC project has proposed next-generation polarized sources capable of producing 7–16 nC per bunch. The STCF project will continue to survey and analyze these proven and emerging technologies to inform upgrade pathway decisions.
Summary
The thermionic electron gun system comprises the gun body, cathode-grid assembly, and a 200 kV pulsed high-voltage power supply. In addition to gun design, achieving high beam current depends critically on maintaining an ultra-high-vacuum environment, which will be a key focus during system development. SHBs and accelerator sections have been designed and analyzed through beam dynamics studies to verify and confirm the feasibility and appropriateness of the gun parameters.
The L-band high-gradient RF gun forms the core of the PC electron source and determines the upper limits of bunch charge, repetition rate, and beam quality. Innovations have been introduced in the structural design of the L-band PC gun to accommodate large-charge semiconductor cathodes, including integration with a cathode load-lock system.
The L-band gun cavity geometry has been optimized to generate high-charge bunches while maintaining good beam quality. The gun must also ensure long-term, stable operation with high-quantum-efficiency PCs to deliver large-charge, high-quality electron beams.
Linac RF system
Design requirements and specifications
The accelerating structures of the microwave system not only provide the strong electric fields required for electron and positron beam acceleration and bunching but also function as vacuum components, maintaining the required vacuum environment during beam transport. The reference signal synchronization system distributes low-phase-noise reference signals across the RF stations of the facility, ensuring synchronization among the microwave and clock systems driven by multiple power sources. It also provides precise timing references for other time-critical subsystems of STCF. The digital LLRF system automatically regulates the amplitude and phase of the accelerating field, maintaining them near their set values and forming a closed feedback loop with the beam pulse. The key parameters and design targets are summarized in Table 48.
| Parameter | Value |
|---|---|
| Main operating frequency (MHz) | 2998.2 |
| Accelerating structure operating temperature (°C) | 35 |
| Effective gradient of accelerating structures (conventional for electrons) (MV/m) | ≥ 20 |
| Pulse mode | Single-bunch acceleration |
| Aperture of positron accelerating structures (mm) | 30 |
| Effective gradient of positron accelerating structures (MV/m) | ≥ 15 |
| Phase stability (rms, online closed loop) (°) | 0.09 |
| Amplitude stability (rms, online closed loop) | 0.04% |
| Phase noise jitter at reference signal input (rms) (fs) | ≤30 |
| Synchronization accuracy (long-term) (fs) | ≤50 @24h (rms) |
Key technologies and technical path
Since the STCF linacs operate predominantly in pulsed mode, the baseline design adopts room-temperature traveling-wave accelerating structures with pulsed power operation (including pulse compressors in the waveguide system). This configuration offers a high performance-to-cost ratio. Considering the high bunch charge requirements of the injector, the S-band frequency is selected as the principal frequency for the linacs, with an operating frequency of 2998.2 MHz, which is six times the collider ring RF frequency of 499.7 MHz.
System design
The RF system is designed to accommodate the two injector configurations currently under parallel study: the injector for the off-axis injection scheme and that for the bunch swap-out injection scheme in the collider rings. For the swap-out injection option, multiple linac configurations have been considered for delivering the electron beam to the collider electron ring. The RF system design described in this section corresponds to the configuration employing a thermionic electron source.
Off-axis injection scheme microwave system design
The microwave system is organized into multiple acceleration sections. Table 49 summarizes the types of accelerator structures, the number of structures, the peak klystron power requirements, and the power distribution strategies for each beamline segment. The corresponding final beam energy at the end of each segment and the overall topological layout are shown in Fig. 215. In the off-axis injection scheme, the macro pulse repetition rate of the klystrons is 30 Hz. According to the physical design, each 3 m conventional accelerating structure provides an energy gain of 50 MeV.
| Beamline | Frequency (MHz) | Acc. structure type | Quantity | Peak power per klystron (MW) | RF power source to Acc. structures ratio | Number of RF power sources |
|---|---|---|---|---|---|---|
| PGun | 2998.2 | RF gun | 1 | 10 | 1:1 | 1 |
| 2998.2 | 3 m Std. Acc. structure | 4 | 50 | 1:2 | 2 | |
| 11992.8 | X-band Acc. structure | 1 | 6 | 1:1 | 1 | |
| TGun | 166.57 | Subharmonic pre-buncher (SHB1) | 1 | - | 1:1 | 1 |
| 499.7 | Subharmonic pre-buncher (SHB2) | 1 | - | 1:1 | 1 | |
| 2998.2 | Buncher | 1 | Shared use of next RF power source | 1 | ||
| 2998.2 | 3 m Std. Acc. structure | 4 | 50 | 1:2 | 2 | |
| EL1 | 2998.2 | 3 m Std. Acc. structure | 16 | 50 | 1:2 | 8 |
| EL2 | 2998.2 | 3 m Std. Acc. structure | 10 | 50 | 1:2 | 5 |
| PAS | 2998.2 | 2 m large aperture Acc. structure | 1 | 50 | 1:1 | 1 |
| 2998.2 | 3 m Large aperture Acc. structure | 14 | 50 | 1:2 | 7 | |
| PL1 | 2998.2 | 3 m Std. Acc. structure | 8 | 50 | 1:2 | 4 |
| ML | 2998.2 | 3 m Std. Acc. structure | 50 | 50 | 1:2 | 25 |
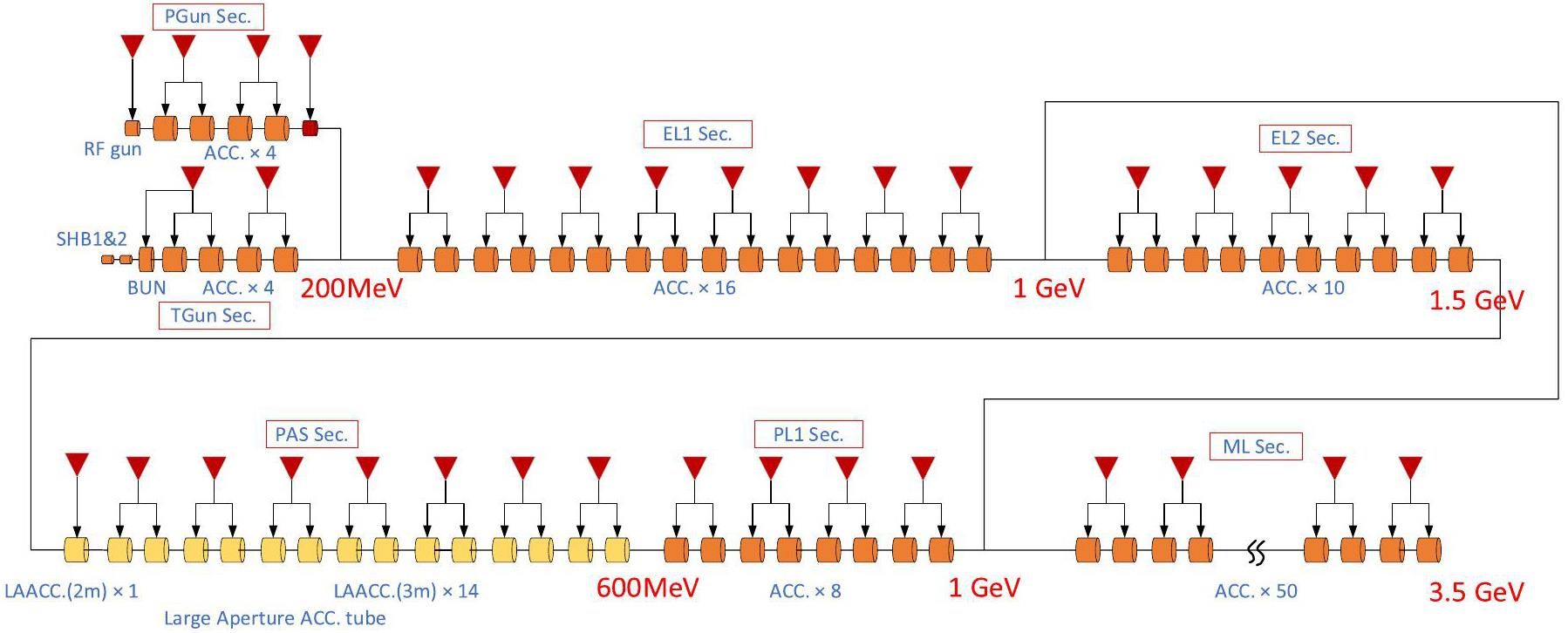
Figure 215 illustrates the sequential arrangement of the accelerating structures and the distribution of RF sources across the various linac sections in the off-axis injection scheme.
Swap-out injection scheme microwave system design
The swap-out injection scheme requires more powerful linacs. The layout is similarly divided by acceleration sections, each with its corresponding number of accelerating structures, RF power sources, and macropulse repetition rates. Table 50 provides the detailed configuration. The beam energy at the end of each section and the overall topological layout are illustrated in Fig. 216. According to the physical design of the injector, each 3 m standard accelerating structure provides an energy gain of 50 MeV.
| Beamline | Frequency (MHz) | Acc. structure type | Quantity | Peak power per klystron (MW) | Power source to Acc. structures ratio | Repetition rate (Hz) | Number of RF sources | |
|---|---|---|---|---|---|---|---|---|
| TGun | 166.57 | Subharmonic pre-buncher (SHB1) | 1 | – | 1:1 | 90 | 1 | |
| 499.7 | Subharmonic pre-buncher (SHB2) | 1 | – | 1:1 | 90 | 1 | ||
| 2998.2 | Buncher | 1 | – | Shared use of next RF power source | 90 | – | ||
| 2998.2 | 3 m Std. standard Acc. structure | 4 | 50 | 1:2 | 90 | 2 | ||
| EL1 | 2998.2 | 3 m Std. standard Acc. structure | 46 | 50 | 1:2 | 90 | 23 | |
| EL2 | 166.57 | Subharmonic pre-buncher (SHB1) | 1 | – | 1:1 | 30 | 1 | |
| 499.7 | Subharmonic pre-buncher (SHB2) | 1 | – | 1:1 | 30 | 1 | ||
| 2998.2 | Buncher | 1 | - | Shared use of next RF power source | 30 | 0 | ||
| PAS | 2998.2 | 3 m Std. Standard Acc. structure | 20 | 50 | 1:20 | 90 | 110 | |
| 2998.2 | 2 m large aperture Acc. structure | 14 | 50 | 1:2 | 90 | 7 | ||
| PL1 | 2998.2 | 3 m Large aperture Acc. structure | 8 | 50 | 1:2 | 90 | 4 | |
| ML | 2998.2 | 3 m Std. standard Acc. structure | 14 | 50 | 1:2 | 30 | 25 |
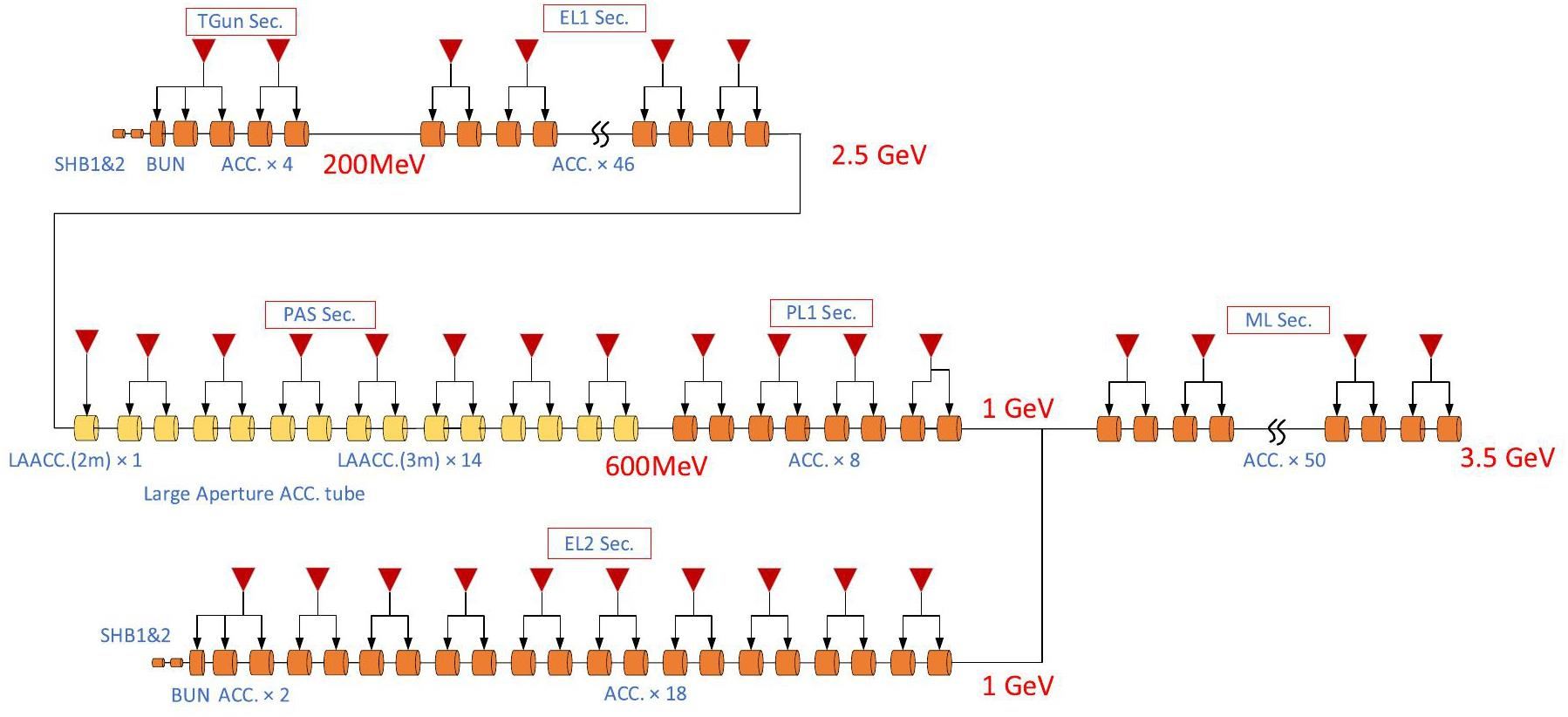
This figure illustrates the sequential configuration of the accelerating structures and their associated RF power sources along the injector beamline designed for the bunch swap-out injection scheme. The use of 2998.2 MHz S-band accelerating structures and subharmonic pre-bunchers enables effective beam manipulation at high bunch charges and across varying repetition rates, depending on the specific beamline function. The overall layout is optimized for compactness and high accelerating efficiency to meet the performance requirements of the swap-out injection configuration.
System composition
The microwave system primarily comprises the accelerating structures, reference signal distribution and synchronization systems, digital LLRF systems and their auxiliary equipment, as well as solid-state amplifiers and microwave transmission components. The solid-state amplifier and microwave transmission subsystems adopt standard, well-established designs and are therefore not discussed in detail here.
Traveling-wave accelerating structures
The accelerating structures for the STCF linacs include standard traveling-wave accelerating tubes, large-aperture traveling-wave accelerating tubes, and subharmonic pre-bunching cavities.
The standard accelerating structures are designed with elliptical-rounded irises and incorporate internal water-cooling channels [120]. Based on the power source layout shown in Figs. 215 and 216, these structures can achieve a maximum energy multiplication factor of 1.94 and an average effective accelerating gradient of up to 23.5 MV/m. The key design parameters are summarized in Table 51.
| Parameter | Value |
|---|---|
| Frequency (MHz) | 2998.2 |
| Operating temperature (℃) | 30 |
| Number of cells | 90 |
| Length (mm) | 3165 |
| Cell length (mm) | 33.330 |
| Disk thickness (mm) | 4 |
| Iris diameter (2a) (mm) | 25.31–18.89 |
| Shunt impedance (MΩ/m) | 63.41–74.37 |
| Quality factor | 15,510–15403 |
| Group velocity, vg/c | 0.0264–0.0101 |
| Filling time (μs) | 0.57 |
| Accelerating gradient (with pulse compressor) (MV/m) | 23.5 |
The large-aperture accelerating structures are employed for positron capture and initial acceleration. These structures utilize fixed iris diameters, while the gradient distribution is adjusted by modifying the nose-cone lengths [121]. The structure dimensions and cavity distribution are optimized to ensure a uniform distribution of peak surface electric fields. According to the injector design requirements, two types of large-aperture structures are implemented: one 2 m tube and fourteen 3 m tubes. The 2 m tube, located immediately downstream of the positron target, serves as the primary capture structure and is powered by a single 40 MW klystron, with an assumed waveguide loss of 0.6 dB. Each pair of 3 m structures is powered by a standard microwave station. The corresponding design parameters are listed in Table 52. The subharmonic pre-bunching cavities adopt a standard standing-wave single-cell design.
| Parameter | 2 m tube | 3 m tube |
|---|---|---|
| Frequency (MHz) | 2998.2 | 2998.2 |
| Operating temperature (℃) | 30 | 30 |
| Number of cells | 60 | 90 |
| Length (mm) | 2165 | 3165 |
| Iris diameter (2a) (mm) | 30 | 30 |
| Cell length (mm) | 33.330 | 33.330 |
| Nose-cone length, d (mm) | 9.34–11.97 | 8.42–12.33 |
| Shunt impedance (MΩ/m) | 53.27–48.45 | 54.37–47.60 |
| Quality factor | 13998–12877 | 14318–12695 |
| Group velocity, vg/c | 0.027–0.020 | 0.030–0.020 |
| Fill time (μs) | 0.28 | 0.41 |
| Accelerating gradient (with pulse compressor) (MV/m) | 21.59 | 20.90 |
Low-level RF (LLRF) processor
The LLRF system employs a down-conversion sampling scheme. The detected signal is mixed with a local oscillator (LO) signal and passed through a band-pass filter to obtain an intermediate frequency (IF), which is then sent to the FPGA via an ADC for demodulation [122]. A direct conversion scheme is used for signal output, generating VM signals with lower phase noise and eliminating the need for digital modulation using numerically controlled oscillators (NCOs) in the FPGA or DSP, thereby improving system reliability. Feedback control can be implemented using either amplitude–phase or IQ control schemes. In the amplitude–phase feedback scheme, two independent loops are used to detect and regulate amplitude and phase separately [123].
Reference signal synchronization system
The reference signal synchronization system of the STCF injector provides low-phase-noise 2998.2 MHz signals for lasers and microwave power sources. It ensures phase synchronization between microwave stations along the linacs and supplies reference signals to other time-sensitive systems. The system maintains a phase drift of less than 100 fs (rms) over 24 hours. The overall configuration is shown in Fig. 217 and includes synchronized reference signals to LLRF units and calibration terminals near the accelerating structures. The principle is based on modulating the RF reference signal from the RMO onto a continuous optical carrier transmitted via fiber. A portion of the signal is reflected at the remote end and returned to the transmitter, where it is compared with the reference. Phase locking between the sender and receiver is achieved by adjusting the fiber length based on this phase comparison [124].
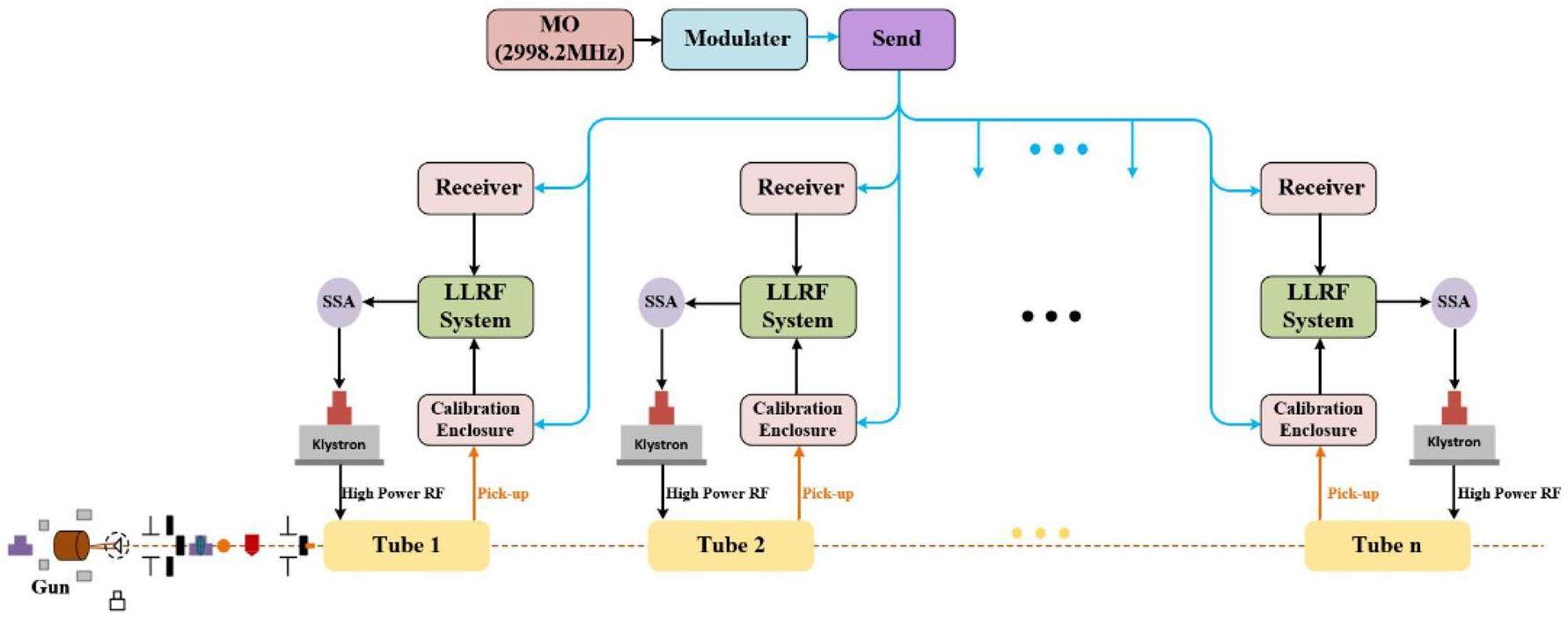
Feasibility analysis
The linac microwave system adopts mature, cost-effective technologies and products, presenting no insurmountable technical risks. The NSRL has extensive experience in designing and fabricating constant-gradient accelerating structures. The 3 m, 2π/3-mode traveling-wave accelerating tubes have been successfully applied in the HLS-II injector, demonstrating excellent performance and reliability. The ongoing construction of the HALF linac will further enhance this experience. The previously untested large-aperture accelerating structures are currently being verified through the STCF key technology R&D project using the positron–electron beam test platform. NSRL also has extensive experience in microwave transmission and LLRF systems and maintains close collaboration with IHEP, IMP, and Tsinghua University, ensuring smooth project development.
Summary
The design of the linac microwave system comprehensively considers performance requirements, technical feasibility, and cost-effectiveness based on the physical design of the STCF injector. A detailed and rational technical route has been established, prioritizing mature and proven technologies to minimize technical risks while meeting application demands. The design achieves a balance between innovation and practicality, providing a solid foundation for subsequent system integration and optimization.
Linac microwave power source system
Design requirements and specifications
The STCF injector comprises multiple segments of electron and positron linacs. The microwave power source system supplies S-band (2998 MHz) microwave power to the linac microwave system, enabling full-energy injection of electrons and positrons into the collider rings. The system primarily consists of high-power S-band klystrons and corresponding pulse modulators.
According to the collider’s physics design, both off-axis and swap-out injection schemes are considered, each requiring a distinct injector configuration. The RF power system described here corresponds to the design using a thermionic electron source for direct electron beam injection, consistent with the microwave system.
In the off-axis injection scheme, the macro-pulse repetition rate is 30 Hz. The microwave power source system includes a total of 56 pulsed power units: one 6 MW X-band source, one 10 MW S-band source, and 54 45 MW S-band sources.
In the swap-out injection scheme, the macro-pulse repetition rates are 30 Hz and 90 Hz. The microwave power source system includes 72 pulsed power units, all employing 45 MW S-band klystrons. The system is developed based on the selected injection scheme, with emphasis on microwave power source stability.
Key technologies and roadmap selection
The linac microwave power source system consists of S-band and X-band klystrons and their associated high-voltage pulse modulators. It also integrates auxiliary systems such as the microwave drive and LLRF, vacuum, waveguide transmission, and water cooling subsystems.
For low repetition rates (<50 Hz), high-power S-band klystrons—such as the commercial Canon E37302A—are technically mature and readily available. With support from the Institute of High Energy Physics (IHEP, CAS), domestic manufacturers, including Hanguang Tech (Hubei) and the CETC No. 12 Institute, have developed indigenous 2998 MHz klystrons. The Hanguang high-power klystron is currently undergoing validation at the Wuhan Light Source.
Given the need for large-scale deployment in major facilities and potential procurement constraints, advancing the maturity of domestically developed high-peak-power klystrons is essential.
For the modulator design, a “fractional turn ratio transformer” type solid-state modulator is selected due to its superior performance characteristics and alignment with modern trends in modulator technology [125]. This design reduces insulation requirements, offers excellent pulse stability and uniformity, eliminates lifetime limitations associated with thyratrons, enables low-voltage power supply operation, and provides improved electromagnetic compatibility and safety. These advantages support stable system operation and facilitate future upgrades [126].
Design scheme and system configuration
The microwave power source system delivers microwave power with specified stability and performance to accelerate electrons and positrons in the STCF linacs. Different injector configurations require tailored microwave system integration.
Microwave power source configuration for off-axis injection scheme
For the off-axis injection scheme, the system includes 56 pulsed microwave power units: one 6 MW X-band unit, one 10 MW S-band unit, and 54 45 MW S-band units. The system layout is shown in Fig. 218.
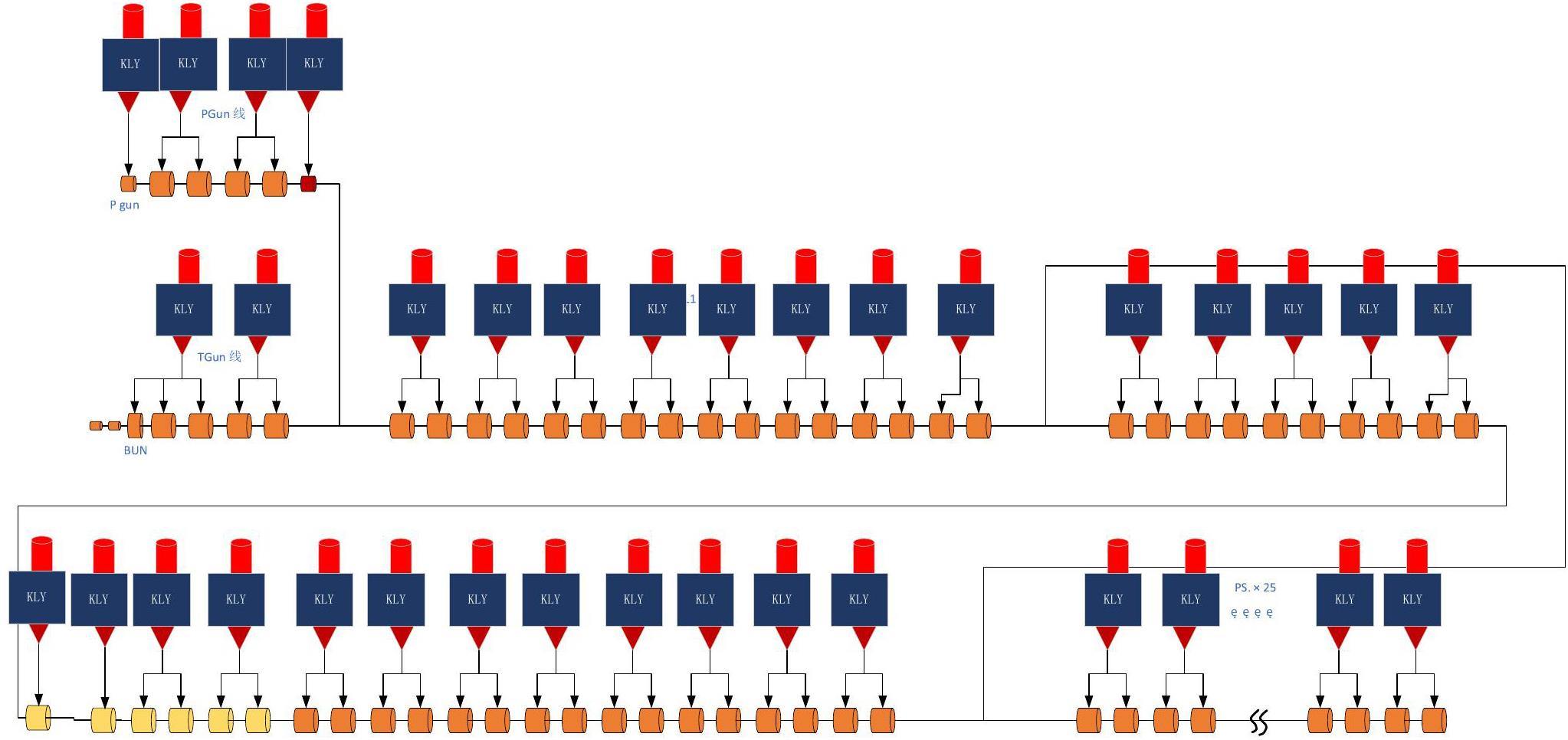
In this scheme, the macro-pulse repetition rate for the klystrons reaches up to 90 Hz (ML section). The specific performance requirements of the involved RF power sources are listed in Tables 53 and 54.
| Parameter | Specification |
|---|---|
| Microwave frequency (MHz) | 2998.2 |
| Maximum repetition rate (Hz) | 90 |
| Klystron peak power (MW) | 45 |
| Modulator peak power (MW) | 130 |
| Pulse flat-top width (μs) | ≥ 4.0 |
| Pulse high voltage stability (rms) | Jitter ≤ 0.03% |
| Output pulse rise time jitter (rms) (ns) | ≤ 10 ns |
| Parameter | Specification |
|---|---|
| Microwave frequency (MHz) | 11,992 |
| Maximum repetition rate (Hz) | 30 |
| Klystron peak power (MW) | 6 |
| Modulator peak power (MW) | 20 |
| Pulse flat-top width (μs) | ≥ 4.0 |
| Pulse high voltage stability (rms) | Jitter ≤ 0.03% |
| Output pulse rise time jitter (rms) (ns) | ≤ 10 |
Microwave power source system configuration for swap-out injection scheme
For the swap-out injection scheme, the system consists of 72 sets of pulsed power equipment, all utilizing S-band 45 MW RF sources. The macro-pulse repetition rate of the klystrons reaches up to 90 Hz in the EL1, PAS, and PL1 beamlines. The system layout is illustrated in Fig. 219.
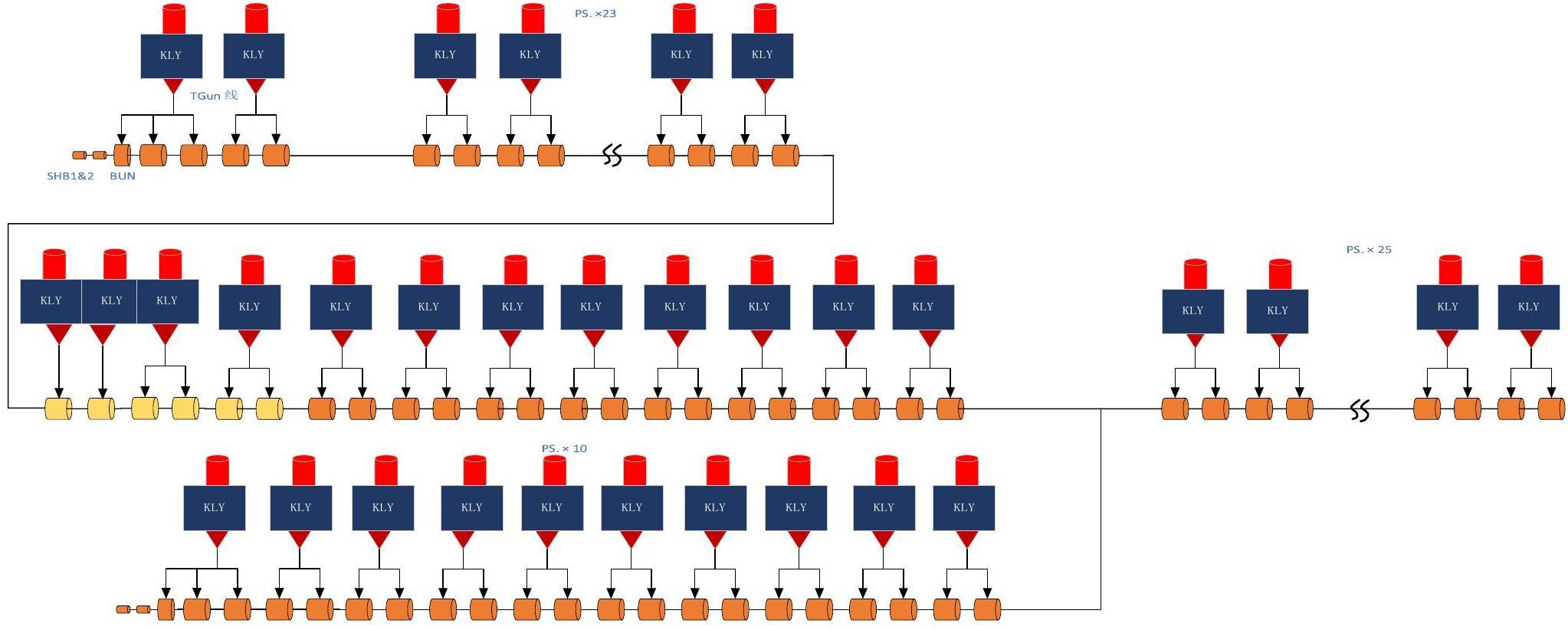
According to the operating parameters of the klystrons and the injector physics requirements, and with a margin considered in the design, the fractional-turn transformer-type solid-state modulator paired with the 45 MW klystrons has the parameters shown in Table 55.
| Parameter | Design value |
|---|---|
| Pulse voltage (kV) | 335 |
| Pulse current (A) | 400 |
| Modulator pulse power (MW) | 135 |
| Pulse width (μs) | 4 |
| Maximum repetition rate (Hz) | 90 |
| Pulse amplitude stability (rms) | < 0.03% |
| Output pulse rise jitter (rms) (ns) | < 10 |
Given the large number of RF sources required for the STCF, the design of the microwave power source system follows a modular design philosophy. The system is standardized as much as possible, adopting a unified design across multiple frequency bands to simplify the complexity of high-power systems and enhance maintenance efficiency. This modular, highly integrated, compact, and reliable approach applies to both the X-band 6 MW and S-band 45 MW klystrons and their associated high-voltage pulse modulators.
Each microwave power unit comprises a klystron, a modulator, and auxiliary power supplies. The solid-state modulator includes a pulse transformer and oil tank, solid-state modulation components, a high-voltage power supply, auxiliary power units, and measurement devices. Although the klystron structure varies across frequency bands and power levels, the modulation components are designed using a unified modular architecture, and the auxiliary power supplies are standardized as much as possible to facilitate engineering implementation and large-scale production.
Taking the main 45 MW klystron power unit as an example, the system diagram is shown in Fig. 220.
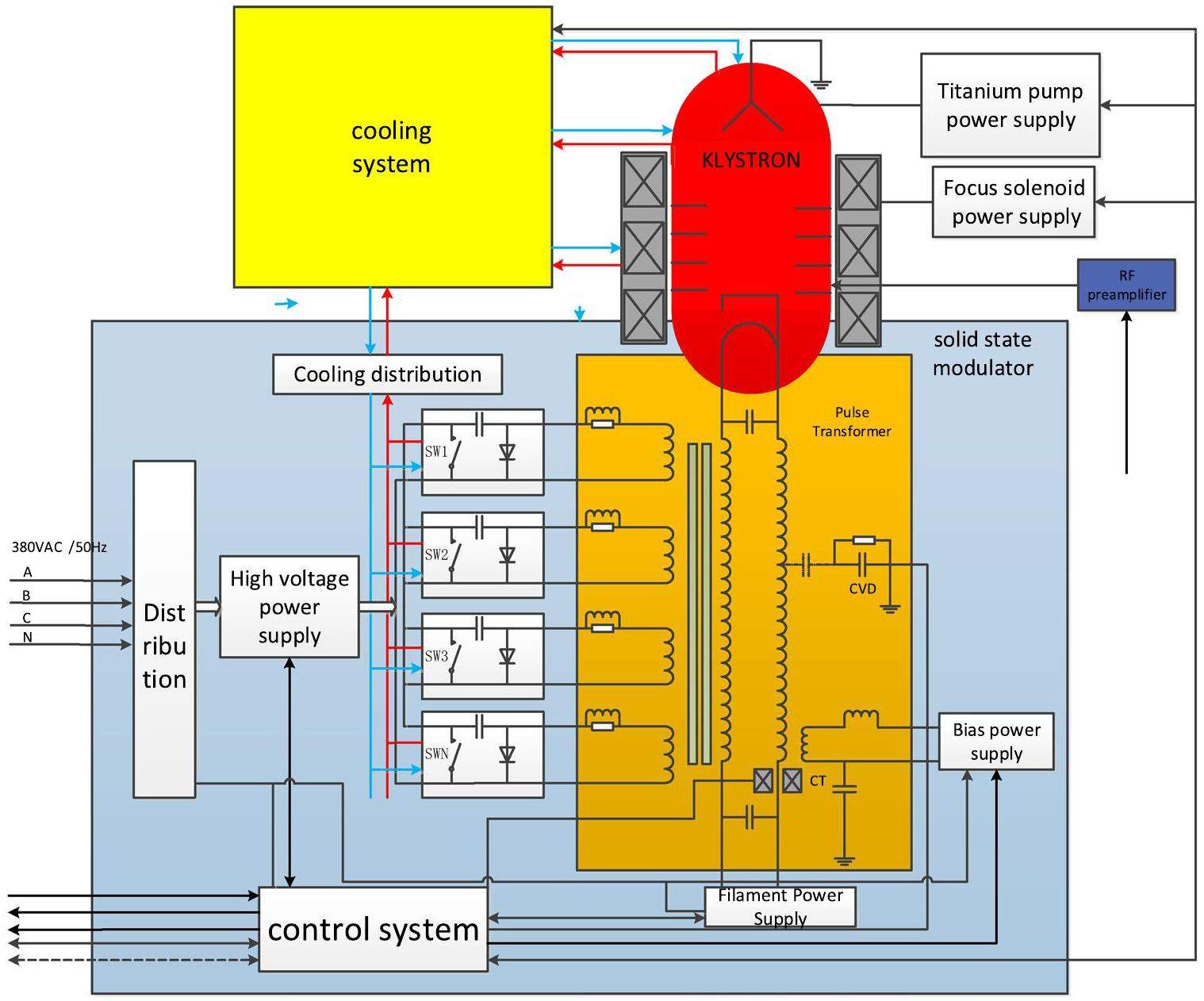
Each 45 MW microwave power unit consists of a klystron, a matching high-voltage pulse modulator, and an auxiliary power supply. A DC power supply of approximately 1 kV provides input to the solid-state pulse modulator, which converts it into pulsed voltage applied to the primary winding of the pulse transformer. The primary-to-secondary turns ratio is designed to deliver the required cathode pulse voltage. The auxiliary power supply includes units for the titanium pump, cathode heater, and focusing solenoid. The pulse modulator converts electrical energy into microwave power, which is then delivered to the accelerating structures in the linacs.
An engineering layout diagram of a single 45 MW microwave power source unit is shown in Fig. 221.

Feasibility analysis
For pulse repetition rates up to 50 Hz, commercial klystrons such as Canon’s E37302A are technically mature and widely deployed in accelerator facilities. Domestic manufacturers, including Hanguang Technology and the CETC No.12 Institute, have the capability to develop 2998 MHz klystrons, and their high-power designs are currently being tested at the Wuhan Light Source. To mitigate procurement risks, it is necessary to further advance the maturity of these domestic klystrons through dedicated beam test platforms.
For higher repetition rates (up to 90 Hz), the limiting factor is the klystron’s performance. Discussions with Canon and Hanguang indicate that high-repetition variants of existing products are technically feasible, with further development possible during STCF’s R&D phase.
The pulsed modulator adopts an advanced fractional-turn transformer-type solid-state design, offering high integration, maintainability, and reliability. This approach is already applied at the HALF. The system's auxiliary power units—including the focusing solenoid, filament, biasing transformer, and titanium pump supplies—use mature, digitally controlled technology, widely adopted at facilities such as HLS and HALF.
Summary
The linac microwave power source system is based on a technically advanced and feasible overall design, demonstrating high system maturity.
Positron source system
Design requirements and specifications
The STCF positron source uses the conventional method of bombarding a tungsten target with an electron beam to generate the required positron beam. As a core component of the STCF injector, the positron source must support both off-axis and swap-out injection schemes in the collider rings, with priority given to off-axis injection during initial construction. In the off-axis scheme, the electron beam has an energy of 1.5 GeV, a single-bunch charge of 10 nC, and a repetition rate of 30 Hz (1.5 GeV/10 nC/30 Hz) to bombard the target. The swap-out injection scheme requires a more demanding electron beam of 2.5 GeV/11.6 nC/90 Hz, resulting in significantly higher average power on the target and stricter requirements for positron yield, target thermal resilience, and cooling performance. With the compatible injector design, the initial off-axis injection phase achieved target beam parameters of 1.0 GeV/11.6 nC at 30 Hz. In the subsequent upgrade to swap-out injection, the electron beam on the positron target is increased to 2.5 GeV/11.6 nC at 90 Hz.
To develop a high-intensity, high-quality positron source suitable for STCF, it is essential to master the design and manufacturing techniques of key components such as the positron conversion target, AMD, and the capture accelerating structures. The main parameter specifications of the STCF positron source are listed in Table 56.
| Parameter | Off-axis injection | Swap-out injection |
|---|---|---|
| Positron beam for collider injection | 1.0 nC / 30 Hz | 8.5 nC / 30 Hz |
| Electron beam on target | 1.0 GeV/11.6 nC/30 Hz | 2.5 GeV/11.6 nC/90 Hz |
| Average power (W) | 348 | 2443 |
| Peak energy deposition density (PEDD, J/g) | 5.6 | 32.2 |
| AMD magnetic field (T) | 0.5–5 | 0.5–5 |
| Positron conversion efficiency (%) | 9.1 | 25 |
| Solenoidal magnetic field (T) | 0.5 | 0.5 |
| Aperture of accelerating structure (mm) | 30 | 30 |
Key technologies and technical approaches
Given the high positron current requirements of STCF, only positron sources based on conventional electron beams bombarding a heavy-element target can meet the injection specifications. The positron source comprises three main components: the conversion target system, the matching system, and the capture accelerator system.
Positron conversion target system
The primary function of the conversion target is to generate electron–positron pairs from a high-energy electron beam. Tungsten is typically chosen as the target material due to its high atomic number, high-temperature resistance, favorable performance, and low cost. Target structures may include amorphous tungsten, single-crystal tungsten, and multilayer composite designs. STCF plans to adopt a conventional single-layer amorphous tungsten target, balancing operational stability with technical maturity.
Since the target directly absorbs the electron beam energy, thermal management is critical. STCF has designed two cooling schemes according to the injection mode: a conventional fixed tungsten target for off-axis injection and a wobbling water-cooled target for swap-out injection, which improves heat dissipation.
Positron matching system
Post-target positrons exhibit large divergence angles and wide energy spreads. The matching system collects and transforms these positrons in phase space. Two common designs are the quarter-wavelength transformer (QWT) and AMD. Since the AMD provides superior energy dispersion acceptance compared to the QWT, the STCF positron source adopts the AMD as its matching system, leveraging the pulsed high-strength magnetic field to facilitate the capture and phase-space manipulation of positrons.
Capture and acceleration section
As positrons traverse the AMD under a longitudinally varying magnetic field, they undergo Larmor rotation. Low-energy positrons spiral outward, while high-energy positrons remain near the axis, resulting in a large transverse size and extended bunch length at the AMD exit. To improve capture efficiency, STCF employs large-aperture (30 mm) S-band accelerating structures in the pre-acceleration section. A 0.5 T solenoidal field suppresses beam divergence and accelerates positrons to 200 MeV. A chicane structure deflects the beam, and a collimator removes positrons that do not meet damping requirements. Finally, positrons are accelerated to 1 GeV via standard linear acceleration. Additional details on beam dynamics are provided in Sect. 3.
Design scheme and system composition
Positron target design
PEDD is a critical parameter for evaluating the thermal shock tolerance of a tungsten conversion target. Research at SLAC indicates that the upper PEDD limit for tungsten is 35 J/g [127, 128]; exceeding this limit can cause severe damage. For off-axis injection (1.0 GeV/11.6 nC/30 Hz), simulations (Fig. 222) indicate a safe PEDD of 12.6 J/g. The target is fixed and surrounded by a water-cooled copper jacket (Fig. 223).
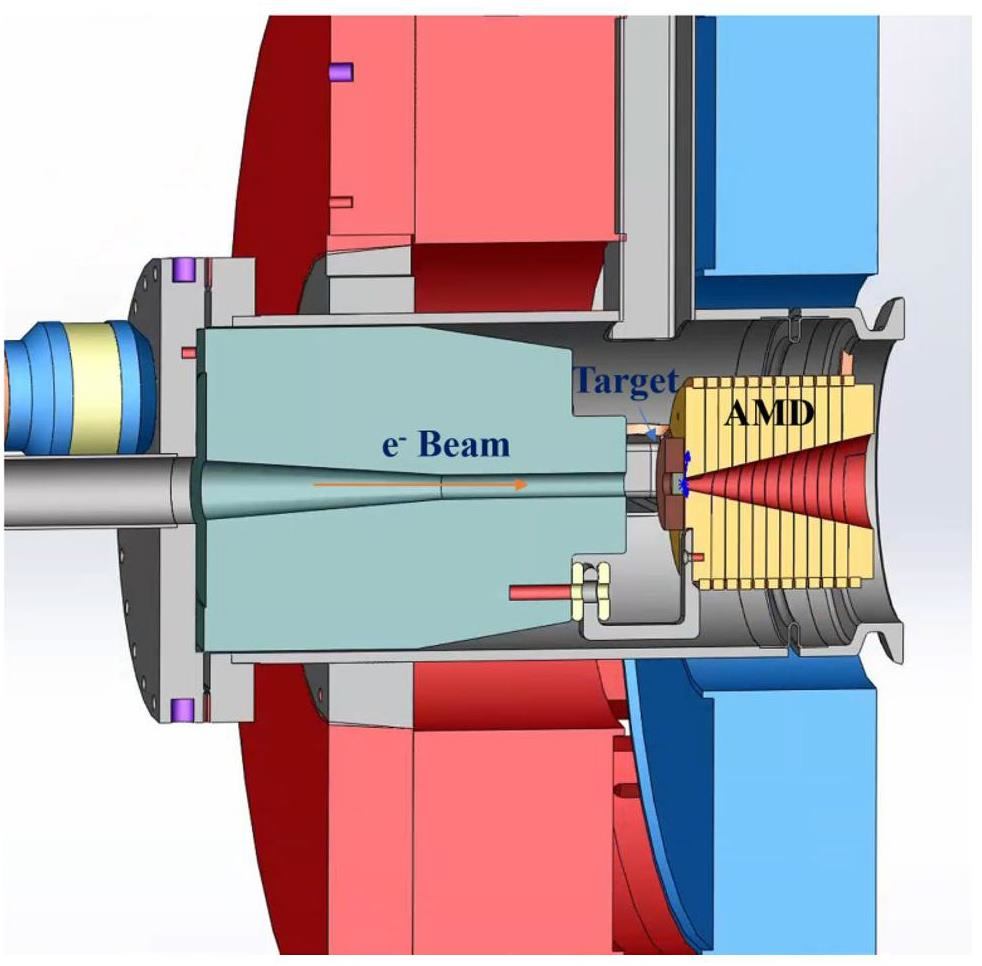
For the swap-out injection mode, a 2.5 GeV/11.6 nC/90 Hz electron beam with a diameter of 1 mm is used for positron production. Simulations, shown in Fig. 224, indicate a PEDD of 32.2 J/g in the tungsten target, which is close to the damage threshold. Thus, a new target design is required to ensure lifetime and reliability.
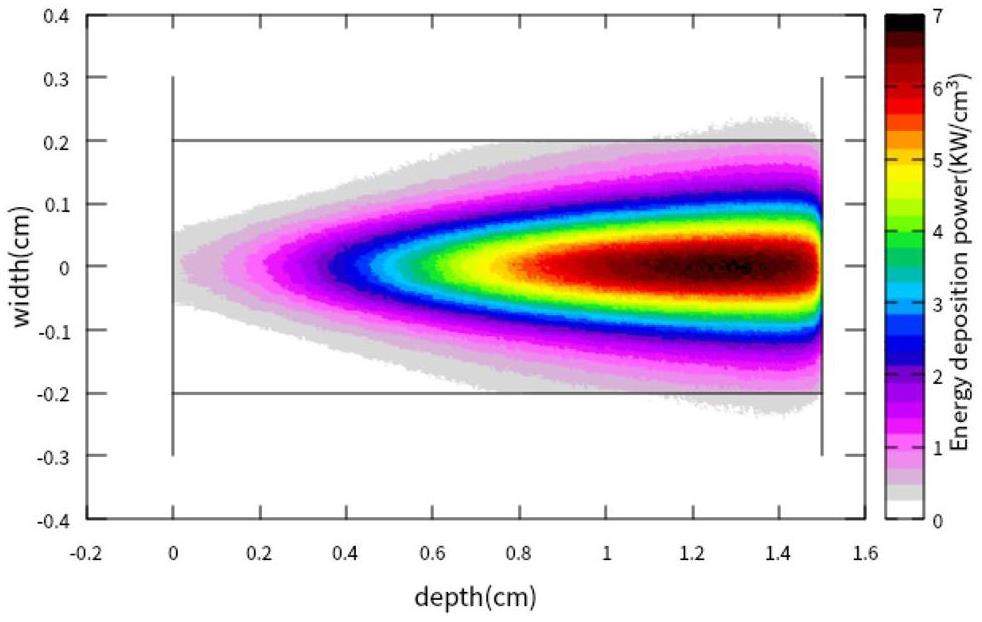
High-energy pulsed electron beams cause thermal shock and long-term heating effects. Shock can damage the target mechanically, while the high temperatures due to the heat deposition can change the tungsten lattice. Experimental results show that tungsten recrystallization begins at 800–900 °C, reducing yield strength and positron yield [129]. ILC uses a rotating water-cooled target [130]; however, this design has vacuum sealing challenges, which is unsuitable for STCF.
To address thermal issues, STCF proposes a wobbling water-cooled target design (Fig. 225). Simulations show that without motion, the target temperature peaks at 1515 °C, above the recrystallization point. With a wobbling motion, the temperature drops to 394 °C, preventing lattice damage and ensuring target longevity (Fig. 226).
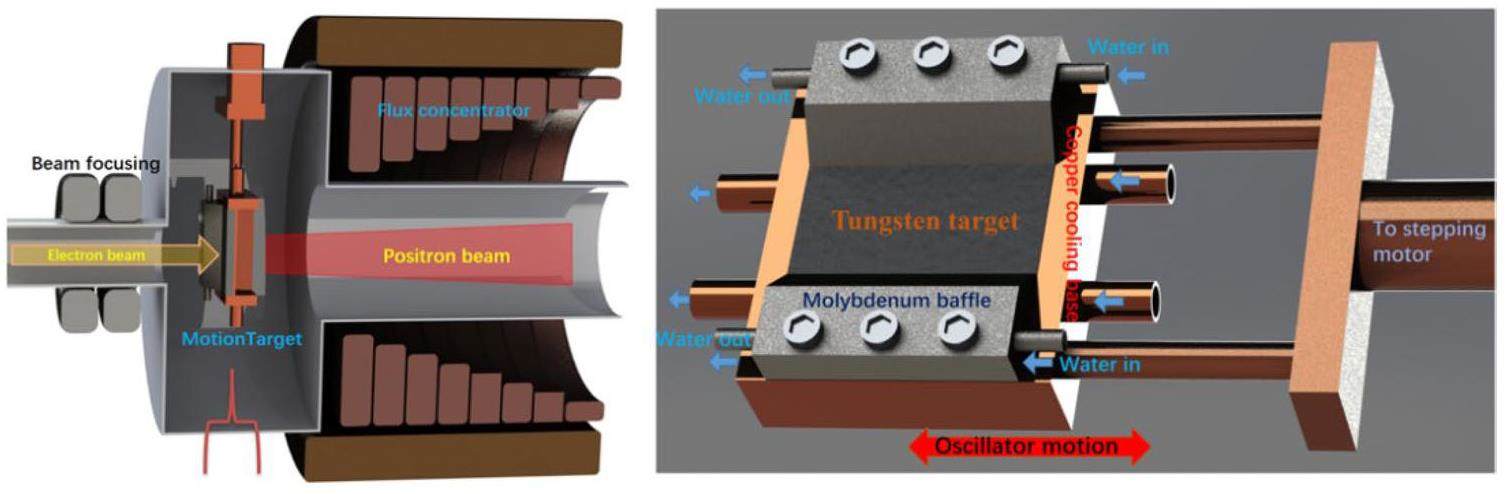
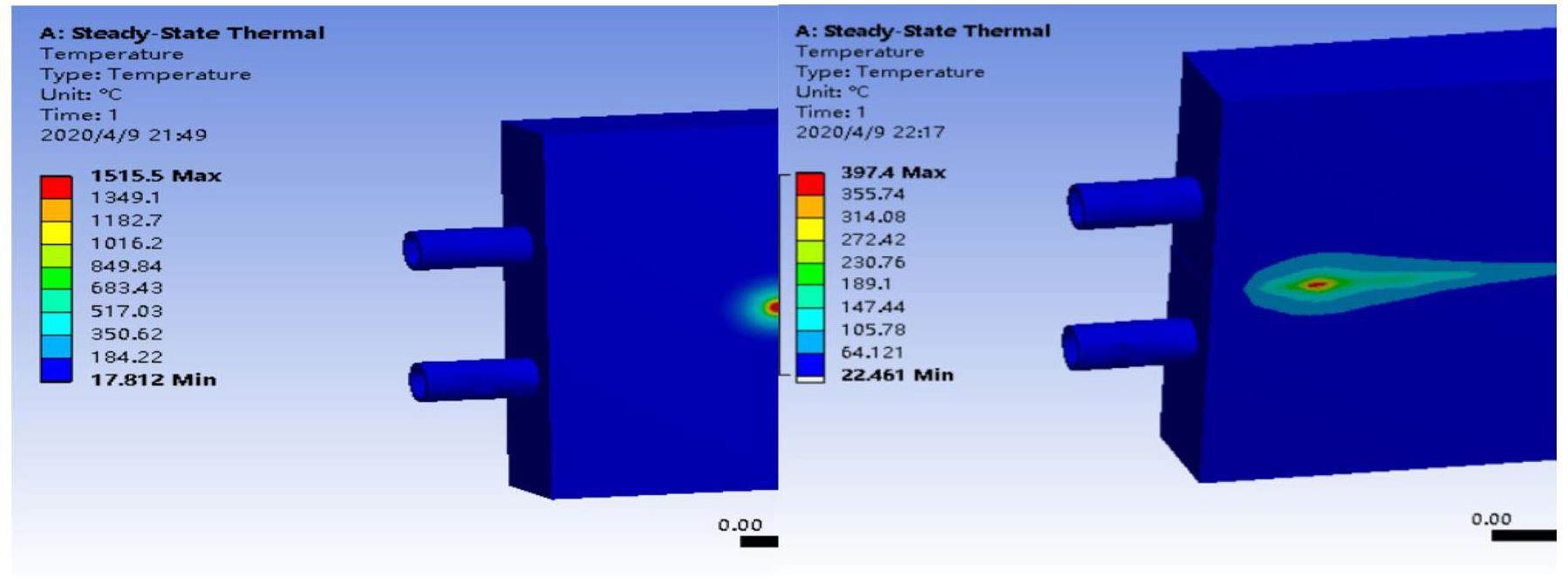
AMD design
The positron beam produced by the electron bombardment of the conversion target features a wide energy spectrum and large angular divergence. To ensure effective matching with downstream accelerating structures, positrons must be captured and transformed into a beam with small divergence and larger transverse size. STCF will adopt an AMD to perform this transformation and optimize positron collection, capture, and acceleration. The design parameters of the STCF AMD are shown in Table 57.
| Parameter | Value |
|---|---|
| Peak pulsed current (kA) | ≥15 |
| Pulse width (FWHM) (μs) | 5 ± 0.5 |
| Pulse waveform | Half-sine wave |
| Repetition rate (Hz) | 50 |
| Long-term stability (8 h) | 0.5% |
| Charging peak voltage (kV) | 15 |
| Time jitter (ns) | ±20 ns |
| Equivalent load inductance (μH) | 0.8 |
The AMD consists of a radially centered conductor surrounded by a primary coil. The central conductor is formed by several connected thin disks. When a time-varying current flows through the primary coil, magnetic flux is induced in the conical central conductor. Owing to skin effects, the induced current flows along the inner surface, generating a peak magnetic field at the center. The design target for the AMD peak field is above 5 T. Figure 227 shows simulation results under an excitation current of 15 kA and a pulse width of 5 μs, indicating a peak field exceeding 6 T, satisfying design requirements.
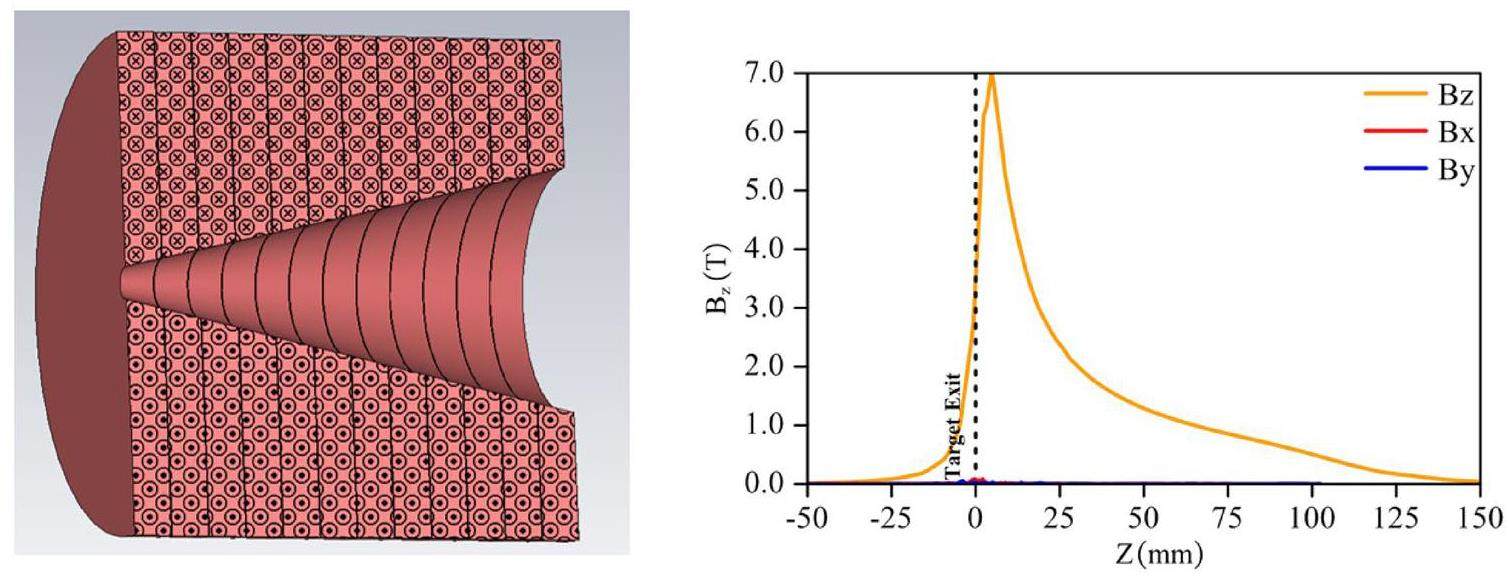
Positron capture and acceleration design
The key challenge of a positron accelerator lies in the capture and matching acceleration section, which differs significantly from conventional electron accelerators. To enhance capture efficiency by increasing transverse acceptance, large-aperture accelerating structures are often employed. For instance, a 1298 MHz L-band cavity with a 35 mm aperture provides approximately three times the acceptance of a 20 mm S-band cavity. However, L-band structures have larger outer diameters, which substantially increases the cost of the solenoid magnet surrounding the accelerating structure.
To balance performance and cost, STCF adopts a compromise solution: a 30 mm aperture S-band accelerating structure, with optimized RF phase to enhance capture and acceleration efficiency. This large-aperture S-band section is positioned immediately after the positron target. A 0.5 T solenoidal field surrounds the structure to suppress beam divergence and maximize positron yield. Downstream, the positron beam passes through a chicane for charge separation, and a collimator removes off-spec particles. The positrons are then accelerated conventionally to 1 GeV. Figure 228 shows the layout of the capture and acceleration section. The detailed lattice design is provided in Sect. 3 on injector beam dynamics.
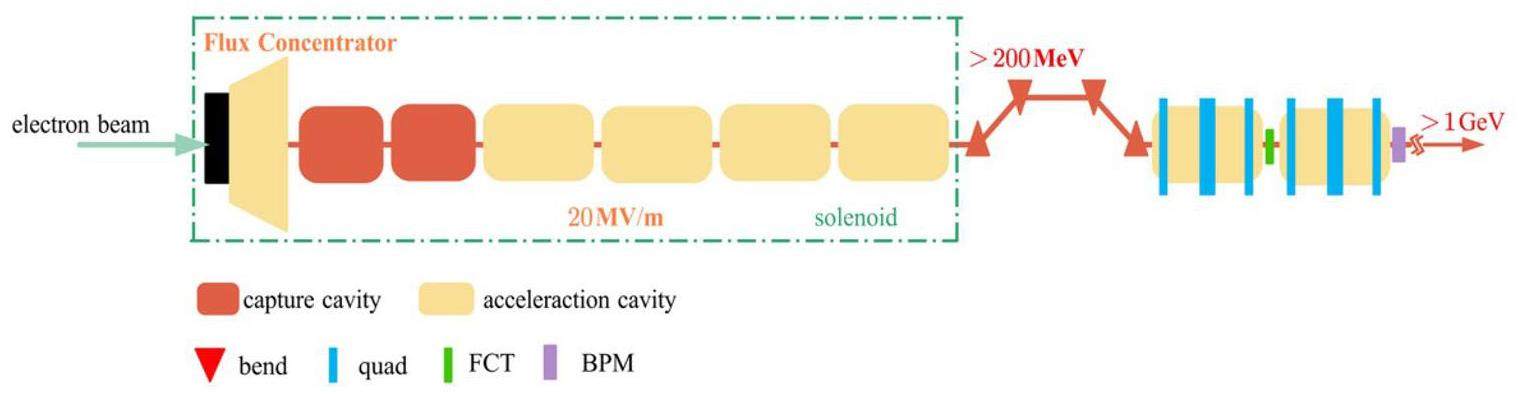
Feasibility analysis
Positron generation via high-energy electron bombardment is a well-established technique. In the off-axis injection scheme of STCF, producing positron bunches of 1.0 nC using an electron beam of 1.0 GeV/11.6 nC/30 Hz presents no significant challenges. However, the swap-out injection scheme requires an electron beam of 2.5 GeV/11.6 nC/90 Hz to bombard the tungsten target, imposing much higher demands on the positron source—a first-of-its-kind challenge in China.
Such high average power may cause thermal management and lifetime issues for the positron target. These risks can be mitigated through optimized target designs, such as the use of movable targets. The STCF key technology R&D project includes a positron-electron beam test platform for validating critical components and simulating high-power beam impacts. Preliminary experimental studies have been conducted, providing a strong technical foundation for future development.
In conclusion, despite certain technical challenges, the positron source design is feasible. STCF possesses the theoretical foundation, experimental experience, and engineering capabilities to ensure the positron source meets the collider’s injection requirements.
Summary
The positron source is a critical subsystem for achieving high luminosity in STCF. It uses conventional high-energy electron bombardment on a target to generate positrons. To meet luminosity goals, the source must deliver a high-current positron beam, imposing stringent demands on the target’s yield efficiency, thermal resilience, and heat dissipation. This necessitates the development of a high-power, high-reliability positron target and an optimized positron collection, matching, and acceleration system. Together, these components ensure the positron source meets the requirements of both injection schemes under consideration for STCF.
Control system
The accelerator control system provides comprehensive management of all equipment within the injector and collider rings, serving as the operational platform for both commissioning and routine operation of STCF. It must meet the needs of accelerator physicists and engineers for device monitoring, data acquisition, and analysis while remaining flexible enough for future upgrades. Specifically, the control system shall:
· Initialize the accelerator and transition it into operational status under safe interlock conditions.
· Enable operators to adjust device parameters as required by physicists to achieve optimal performance.
· Utilize beam diagnostics to optimize beam performance and satisfy physics requirements during commissioning.
· Safely bring the accelerator to shutdown status under interlock supervision.
Additionally, the system shall:
· Support device status inspection and alarm functionalities.
· Provide a timing system to synchronize signals among subsystems.
· Maintain a central database for machine parameters and operational data to support online and offline physics analysis.
· Establish a beam tuning software development platform to assist in achieving accelerator physics objectives.
Design requirements and specifications
Based on STCF’s practical requirements and referencing the control systems of BEPCII and SuperKEKB, the main design requirements and specifications are:
· Control Network: Must support accelerator-wide data communication. Core backbone switches must support 40 Gb/s, while access layer switches must support 10 Gb/s.
· Device Control: Must monitor and control all accelerator equipment. Parameter monitoring refresh rate ≥ 2 Hz; parameter setting response time < 200 ms.
· Timing System: Must ensure trigger signal synchronization. Delay and pulse width of each signal should be independently adjustable. Inter-signal jitter < 30 ps.
· Interlock System: Must ensure operational safety. Fast interlock intra-station signal response < 10 μs; inter-station response < 100 μs. Slow interlock intra-station response < 20 ms; inter-station response < 100 ms.
Beam Tuning Platform: Must support remote device control and remain open and extensible, providing tools and interfaces for developing and debugging beam tuning software.
Key technologies and strategy
Large-scale accelerator control systems increasingly adopt integrated solutions based on mature technologies and commercial products, reducing development cost and timeline while ensuring reliability. Due to the diversity and geographic spread of STCF devices, a distributed architecture will be employed.
After evaluating major control frameworks used in large accelerator facilities—such as EPICS [131], TANGO [132], DOOCS [133], TINE [134], MADOCA [135], and commercial SCADA systems—EPICS stands out as a mature and widely adopted solution.
EPICS is a software toolkit based on the distributed control system (DCS) standard for developing and operating distributed control systems. Originally co-developed in the early 1990s by LANL and ANL for large accelerator facilities, EPICS has evolved through global collaboration, with ongoing contributions to core software, device drivers, record types, and application tools.
EPICS features modularity, scalability, and ease of maintenance and upgrades. It has been used in over 100 major research infrastructures worldwide, including:
· Colliders: KEKB (Japan)
· Synchrotron light sources: Diamond (UK)
· Free electron lasers: LCLS I/II (USA)
· Spallation neutron sources: SNS (USA), ESS (Europe)
In China, EPICS underpins the control systems of BEPCII, HLS, SSRF, CSNS, SXFEL, and SHINE. Considering performance, development schedule, and resource availability, the STCF control system will adopt EPICS as its core framework.
Design scheme and system composition
Based on the EPICS architecture, the STCF control system is organized into three layers:
· Operator Interface Layer (OPI)
· Input/Output Control Layer (IOC)
· Device Control Layer (DCL)
The overall architecture is illustrated in Fig. 229.
The control system is composed of the following major components:
· Control platform
· Control network
· High-level application software
· Device control
· Interlock system
· Timing system.
Control Platform
The control platform provides a reliable and stable runtime environment for the control system. It includes central servers capable of long-term stable operation, storage systems, a high-reliability network, OPI systems, and various support services such as account management, network file systems, time synchronization, channel access, and version control. These components ensure the consistency, integrity, and security of control software and data.
Control Network
The control network acts as the nervous system of the entire control infrastructure, connecting all subsystems. Its performance and reliability are critical to overall system effectiveness, covering communication, network security, and operational management. A star topology is adopted, with the central server room at its core. Local control stations are connected to core switches via fiber optics, with dual redundancy employed for the core switch. The network is divided into the backbone control network, local device networks, and dedicated data networks.
High-Level Application Software
High-level applications support accelerator operation and beam tuning. Key functions include system status monitoring and control, real-time and historical data access and analysis, event logging, alarm management, and accelerator physics tuning. Key components include graphical user interfaces, data archivers, alarm systems, and beam tuning toolkits.
Device Control
The system provides comprehensive control of all accelerator subsystems. Based on device type, it is divided into multiple subsystems: magnet power supply control, vacuum control, cryogenic control, electron source control, injection/extraction control, RF and microwave control, power system control, beam diagnostics, motion control, and more. All control software is developed and run under EPICS. Control hardware includes protocol converter servers, network switches, IOC controllers, and other auxiliary servers.
Interlock System
The interlock system, or Machine Protection System (MPS), protects critical equipment from beam-related damage by aborting the beam or disabling power when abnormal conditions are detected. It consists of a PLC-based slow interlock and an FPGA-based fast interlock system. A layered design is adopted, with a master station handling inter-subsystem logic and slave stations managing internal logic and protection.
Timing System
The timing system delivers precision timing and trigger signals to devices such as electron guns, kickers, modulators, microwave systems, RF cavities, and beam diagnostics, ensuring synchronized operation. White Rabbit technology is employed, including master nodes, WR switches, and slave nodes. The master node locks to the RF reference signal, while WR switches distribute synchronized time and frequency signals via optical fibers to downstream switches or end nodes. The end nodes generate trigger signals for connected devices.
Feasibility analysis
Key components of the STCF accelerator control system include the control platform, device control, interlock system, and timing system. EPICS, a widely adopted control framework in the global accelerator community, has been selected for development and operation. Most control solutions have already been successfully validated at HLS and SSRF, significantly reducing overall system risk. Mature and stable device support/driver support is available for EPICS-based device integration.
The fast and slow interlock systems, as well as the White Rabbit timing system, have already been deployed and are operating stably in the SHINE injector. This demonstrates solid technical experience across major subsystems of the STCF control system. No significant technical barriers or unforeseen risks are anticipated during construction.
Summary
Large-scale accelerator control systems are complex engineering challenges due to:
· High device count and variety
· Interface complexity
Critical success factors include:
· Unified architecture design
· Standardized protocols
Through extensive studies of international systems and STCF-specific requirements analysis, we have:
· Established a distributed EPICS-based architecture
· Defined preliminary standards, protocols, and specifications
This foundation ensures efficient progression to detailed design and implementation.
Mechanics system
The STCF accelerator complex consists of two main parts: the injector and the collider rings. Within the collider rings, the machine detector interface (MDI) section at the IR has a unique structural design.
The collider consists of two intersecting electron and positron storage rings at the IR. The injector features two design schemes based on off-axis and swap-out injection in the collider rings. While their layouts differ, the main linac (0–2.5 GeV, alternating acceleration of electrons and positrons) is shared by both schemes. Other accelerator segments are largely similar, and the linac’s mechanical support system is comparable to conventional linacs.
Each ring of the dual-ring collider contains four arc sections and four long straight sections. The primary devices are housed in a radiation-shielded tunnel. Beamline elevation is 1.2 m, with the inner ring 3.5 m from the tunnel’s inner wall and the outer ring 1.5 m from the outer wall. Arc sections are composed of standard cells with nearly identical structures (Sect. 2.2).
The IR MDI mechanical system is highly specialized, with a complex arrangement of components, confined spatial constraints, and stringent alignment requirements. It is one of the most challenging aspects of collider design [136]. The IR, located at the center of the detector, contains an ultra-thin IP chamber, superconducting magnets with multiple coils, and cryostats. It integrates cryogenic, magnetic, vacuum, and detector systems within a 7 m-long region (diameter under 300 mm), where conventional mechanical and adjustment components cannot be installed or operated.
The collider rings also require beam collimators to adjust the physical aperture using movable absorbers, define beam acceptance, and scatter or absorb halo particles outside the acceptance. Collimators help localize beam losses, reduce radiation in critical areas, suppress experimental background in the IR, and protect sensitive instrumentation [137].
Beam dumps absorb high-energy discarded beams. As part of the engineering infrastructure, dumps maximize energy absorption and provide sufficient radiation shielding to protect surrounding equipment, the environment, and personnel [138].
Design requirements and specifications
Accelerator mechanics design requirements
The mechanical system adopts a modular, stepwise integration approach. Major accelerator components are grouped into independent support assemblies, pre-installed offline, then integrated into units and finally into the full accelerator on site [136].
Design parameters vary with component requirements, but the overall mechanical system must meet criteria related to adjuster selection, range, resolution, structural dynamic stability, cost-effectiveness, disassembly workflow, and alignment methodology. Table 58 summarizes the mechanical adjustment specifications.
| Parameter | Specification |
|---|---|
| Horizontal adjustment range (X/Y) (mm) | ±10 |
| Horizontal resolution (X/Y) (μm) | ≤10 |
| Vertical adjustment range (Z) (mm) | ±8 |
| Vertical resolution (Z) (μm) | ≤5 |
Interaction Region Design Requirements
The IR includes: the IP vacuum chamber inside the detector, bellows, remote vacuum connection (RVC) structures, BPMs, superconducting magnets and cryostats (IRSM), as well as surrounding room-temperature magnets, cryo-pipelines, and movable platforms.
Key component specifications:
1. IP Chamber
· Material: Beryllium + Tantalum
· Inner beryllium pipe diameter: 30 mm
· IP chamber length: 1000 mm
· Vacuum: better than 5×10-8Pa
2. Movable Platform
· Foundation flatness: < 0.5 mm
· Guide rail parallelism after installation: < 0.05 mm
· Guide rail flatness after installation: < 0.05 mm
· Alignment accuracy of platform: < 0.1 mm
· Positioning accuracy of platform: < 0.2 mm
3. RVC (Remote Vacuum Connection)
· Alignment accuracy between IRSM vacuum chamber and IR vacuum chamber bellows: < 0.1 mm
· Remote-controlled locking/unlocking capability
· Remote vacuum diagnostics and pumping capability
· Must meet vacuum requirements of the IR
Beam Collimator Design Requirements
Primary design specifications for the beam collimator include:
· Length (beam direction): 1000 mm
· Taper angle of scraper: < 0.15 rad
· Travel range of scraper: ≥ 24 mm (Din=60 mm); ≥ 23.5 mm (Din=67 mm)
· Motion positioning accuracy: < 50 μm
· Radiation tolerance: ≥ 1 MGy
Beam Dump Design Requirements
Main specifications for the beam dump system include:
· Positioning accuracy: ≤ 0.1 mm
· Environmental radiation dose: < 2.5 μSv/h
· Must meet vacuum specifications
Key technologies and technical approaches
The primary challenges in accelerator mechanical support lie in meeting the stability and precision requirements imposed by beam physics and the accelerator components themselves. For most components not subject to extremely tight tolerances, conventional mechanical alignment and support designs are generally sufficient.
For the IR, the mechanical system includes several critical technologies:
Key Technology 1: IP Chamber Fabrication. The central beryllium vacuum chamber, with a wall thickness of only 0.4–0.6 mm, presents major challenges in welding and assembly. Ensuring uniform cooling performance is particularly difficult, as coolant must circulate through a cavity 200 mm in length with only a 1 mm gap.
Key Technology 2: RVC. This device must enable reliable and convenient remote operation. Key challenges include selecting a suitable sealing material for the vacuum interface, achieving precise mechanical alignment, and maintaining long-term vacuum integrity under operational conditions.
Key Technology 3: IP Chamber Integration with Detector. The innermost layer of the detector (ITKW/ITKM) has a diameter of only 70 mm, while the IP chamber reaches a maximum radial size of 100 mm. This extremely limited space requires that the entire assembly be integrated externally and installed as a single unit. Ensuring accurate positioning and future maintainability is a significant design challenge.
Key Technology of Beam Collimators. The beam absorber (scraper) is exposed to multiple effects, including energy deposition, synchrotron radiation, Touschek scattering, and beam-induced impedance heating. Design must address these factors through simulation-driven material selection and structural optimization, reducing impedance while ensuring high reliability and long operational life.
Design scheme and system composition
Accelerator mechanical design scheme and system composition
Injector Mechanics
The injector system is designed for two injection schemes—off-axis and swap-out—in alignment with the collider ring layout (Fig. 1). The injector mechanical systems cover linac segments for both electrons and positrons, including the shared ML, the positron target station, the damping/accumulation ring, and associated beam transport lines.
The main component of the injector is the accelerating structure. Its support design largely follows standard practice established by domestic synchrotron light sources. Mechanical prototypes for the STCF injector support structures will be refined based on the finalized injector lattice.
Collider Ring Mechanics
The STCF collider employs a dual-ring layout, composed of an electron ring and a positron ring, as illustrated in Fig. 230. Both rings lie in the same horizontal plane and intersect at the IP and at the symmetric crossing point opposite the IP. Each ring is two-fold symmetric, with the arcs of the inner and outer rings slightly differing in length due to the crossing geometry, resulting in approximately 2 m spacing between rings.
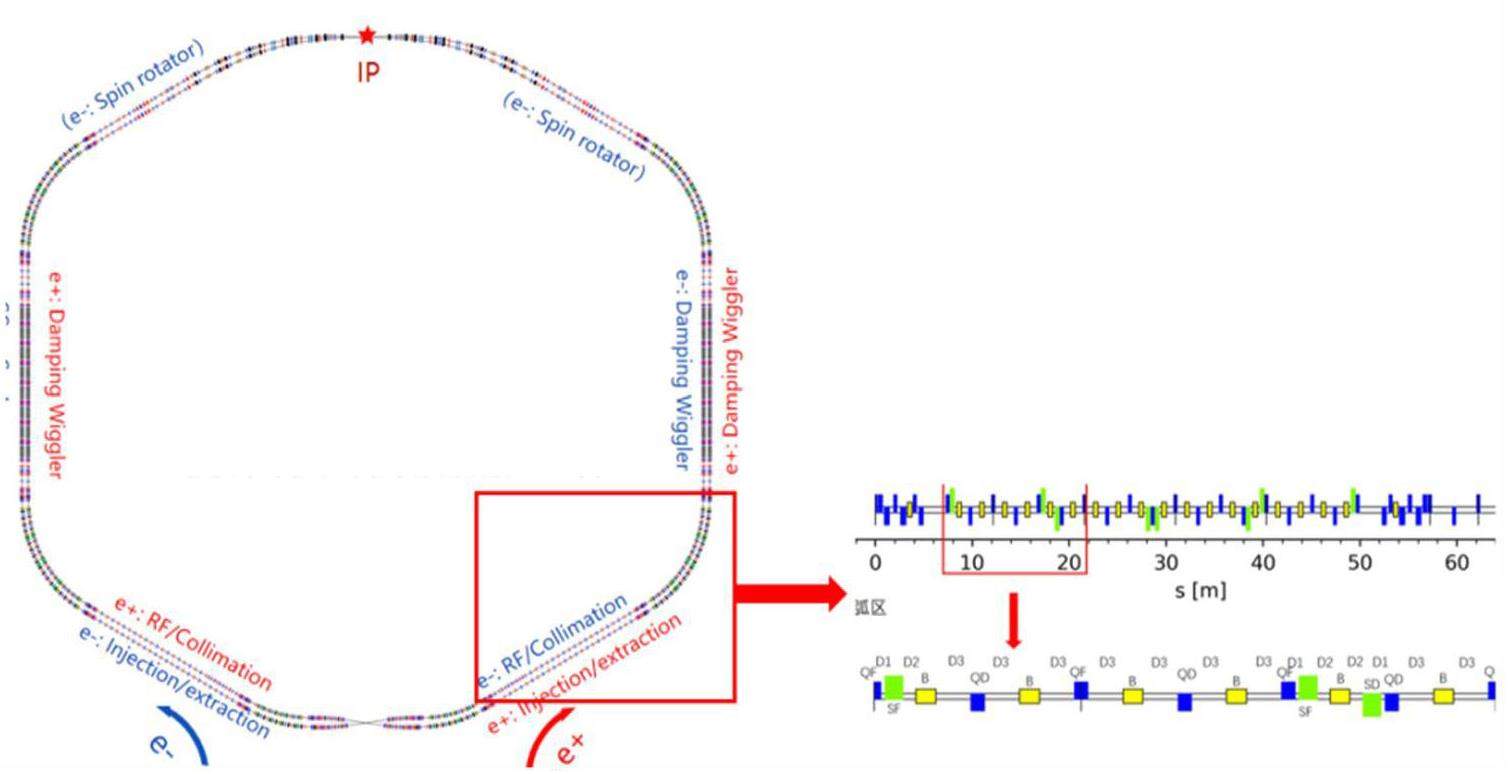
Each ring includes one IR, four large arc sections (each with a 60° bend), two short arc sections (each with a 30° bend), one crossing region, and several straight sections. The total ring circumference is 860.321 m.
Taking a short arc section as an example, Fig. 231 (left) shows the mechanical support system layout. The tunnel is 7.5 m wide, with each ring 2.5 m from the tunnel wall. Beamline height is 1.2 m, and spacing between the rings is 2 m. The tunnel height is 4.5 m, with ring-shaped lifting equipment installed overhead.
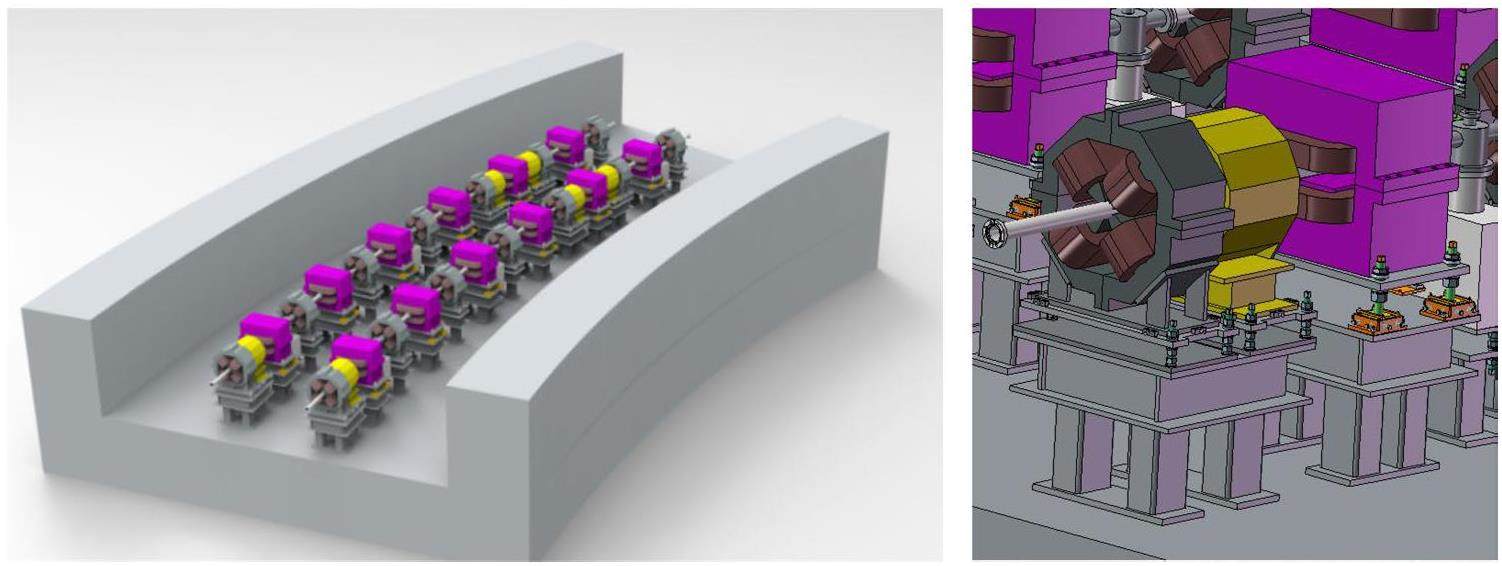
In the local support structure, second-order (B2) magnets are mounted on individual supports, while fourth-order (B4) and sixth-order (B6) magnets are installed on a shared girder. Each magnet is equipped with three-directional mechanical adjusters, as shown in Fig. 231 (right).
Structure and Design Scheme of the Interaction Region
The composition of the IR is shown in Fig. 232. The STCF IR is defined as the ±8 m region centered on the IP. It includes the beryllium IP vacuum chamber extending into the detector, bellows, RVCs, BPMs, superconducting magnets and cryostats (IRSM), room-temperature magnets outside the cryostat, cryogenic piping, and support structures, such as movable platforms.
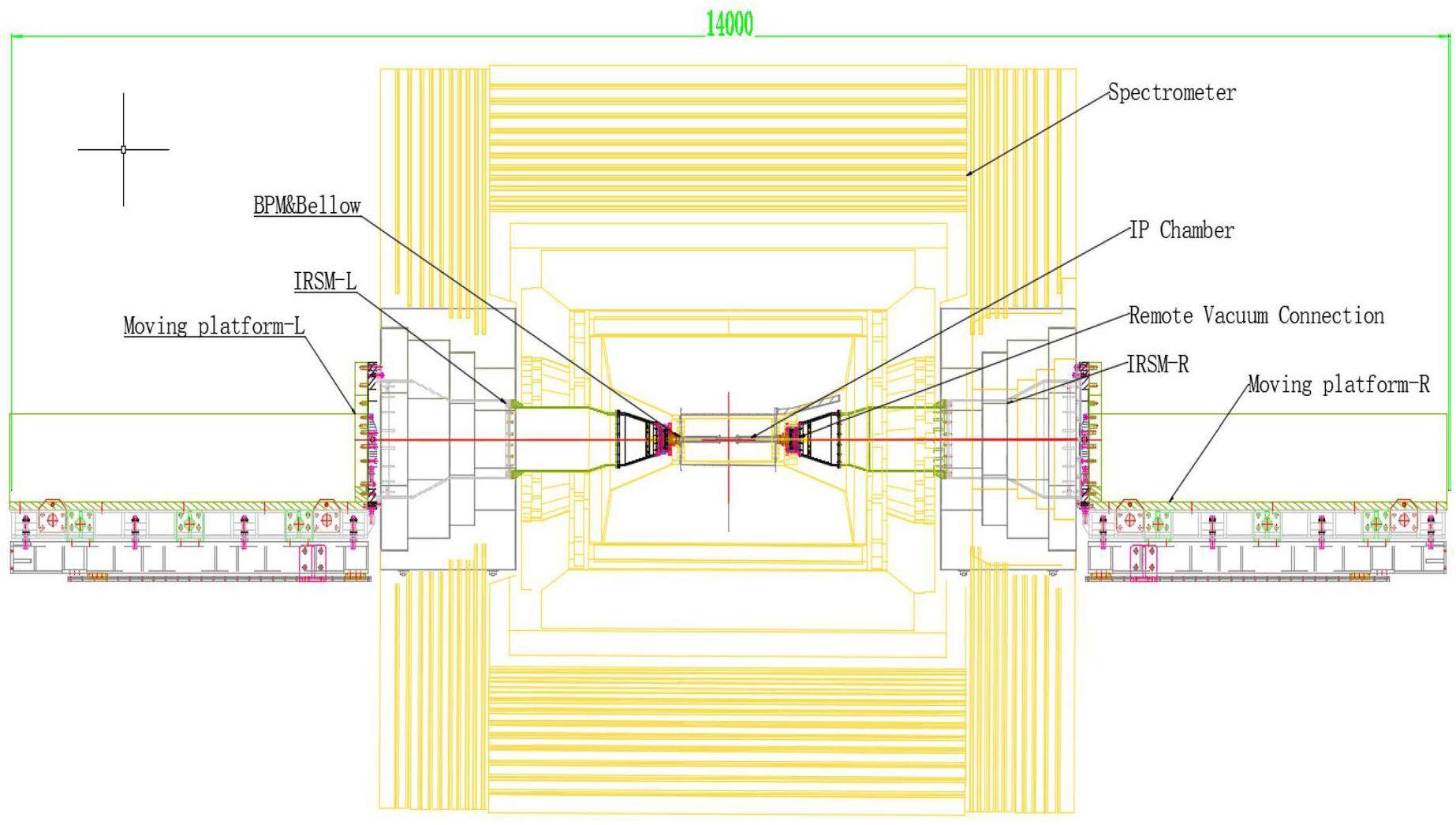
Figure 62 illustrates the crossing angle of the electron and positron beams in the IR, as well as the positions and lengths of the associated beamline components. A beryllium vacuum chamber is located at the collision point in the detector center, with bellows at both ends connecting it to the upstream and downstream vacuum chambers. These bellows are designed to accommodate thermal expansion of the beryllium chamber and provide flexible connections between vacuum sections. The outer vacuum chambers are connected to the superconducting magnet vacuum chambers via RVCs, which are critical mechanical-vacuum components of the IR. These connectors enable automatic alignment and remote locking/unlocking of vacuum flanges, facilitating equipment installation and maintenance.
The IRSM magnets, along with the upstream and downstream warm magnets, are mounted on a movable platform. The cryogenic valve box and transfer lines supplying liquid helium to the IRSM magnets are also installed on the platform’s sides. Figure 233 depicts the mechanical structure of the movable platform, based on the physical design.
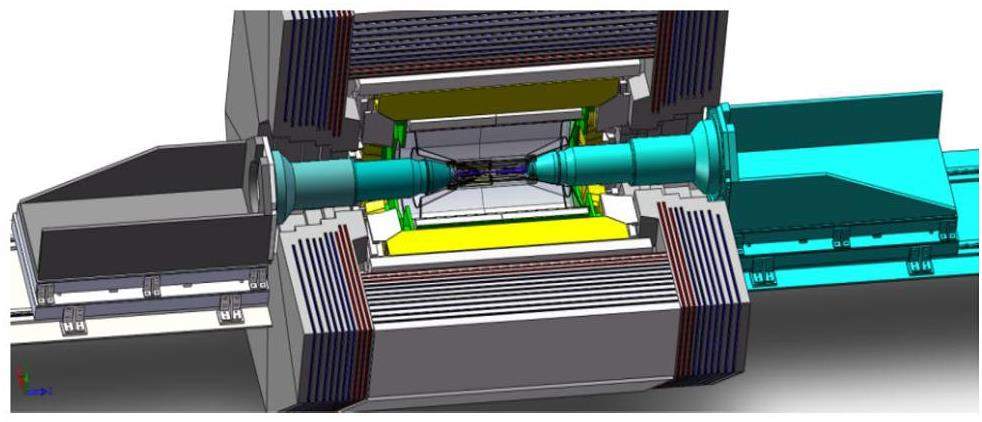
IP Chamber Design Scheme
The IP beam pipe is designed symmetrically around the IP. To minimize the material budget in the IR, beryllium is used due to its low density and high radiation transparency, making it ideal for high-energy physics applications [138]. According to the preliminary MDI design, the central beryllium beam pipe adopts a double-layer structure: the inner tube has an inner diameter of φ30 mm and a wall thickness of 0.6 mm, internally coated with 10 μm of gold. The outer tube has a wall thickness of 0.4 mm, with a 1.0 mm gap between layers through which electric spark oil or paraffin is circulated [136, 139, 140]. The beryllium section is 205 mm long, and the total beam pipe length is 1000 mm.
The beryllium section is flanked by tantalum pipes that transition from φ30 mm circular diameters to a special elliptical shape with a long diameter of 60 mm and a short diameter of 30 mm at the flange ends (see Fig. 234). These tantalum sections are water-cooled, with their inner walls coated with 10 μm of copper [5]. To prevent deformation from long-span sagging, the beam pipe is supported by an axial alignment system and fixed to the detector inner chamber for precise installation. The outer structure includes inlet and outlet piping for coolant circulation and integrated sensors for monitoring.
Movable Platform Design Scheme
Ensuring the alignment accuracy of accelerator beamline components in the MDI region requires precise mechanical design and motion control of the movable platform (see Fig. 235). Due to space constraints, the IRSM on the platform is implemented as a cantilever structure. Finite element analysis, assuming a uniform 2 ton load on the IRSM, indicates a deflection of 0.29 mm at the platform end, as shown in Fig. 236.
RVC Structure Design Scheme
Based on the RVC design used in SuperKEKB, a related RVC concept was proposed for the STCF. When the IRSM is pushed into the detector region, initial flange alignment is achieved via two tapered pins. A remote handle rotates a gear disc, gradually pushing the vacuum flange faces together. Clamping force is provided by custom butterfly springs. A prototype of the STCF RVC structure is shown in Fig. 237.
Structure and Design Scheme of the Beam Collimators
Based on design experience from major international colliders and synchrotron radiation sources, the STCF beam collimator primarily consists of the absorber, vacuum chamber, motion control system, support and adjustment mechanism, water-cooling system, and radiation shielding structure, as illustrated in Fig. 238.
To handle high thermal loads from direct beam impact, Touschek scattering, beam impedance, and synchrotron radiation, the absorber material is preliminarily selected as Glidcop-AL-15, a dispersion-strengthened copper reinforced with nano-scale alumina. The vacuum chamber of the collimator is 800 mm long, with 100 mm shielding bellows installed at both upstream and downstream ends.
To reduce impedance contributions, the vertical internal surfaces of the vacuum chamber are capped with plates to eliminate cavity-like structures. A tapered end section of 100 mm length is designed with optimized slanted surfaces to ensure a smooth longitudinal transition. Comb-shaped RF shielding fingers are installed between the absorber and vacuum chamber along the longitudinal gap of the beam, while spring-shaped RF shielding fingers are added across the vertical gaps.
Structure and Design Scheme of the Beam Dump Station
The beam dump station mainly comprises an absorber, shielding structure, and support and adjustment mechanism, as shown in Fig. 239.
Feasibility analysis
The mechanical support schemes for accelerators have been widely adopted in major facilities worldwide and thoroughly validated, providing a solid foundation for implementation.
The IP chamber design is optimized based on experience from SuperKEKB. However, further refinements are needed in physics design, mechanical integration, fabrication, and detector interfacing. Prototype development and mock installation tests are recommended. Only after repeated validation and verification that design specifications are met should the system be deployed for operational use.
The RVC design must satisfy both vacuum integrity and remote operability requirements. Mechanical prototyping and preliminary studies are recommended, including the establishment of a vacuum docking simulation platform. The system should undergo repeated testing to verify performance before final implementation.
The beam collimator adopts a relatively mature technical approach. Nonetheless, critical processes such as material bonding, machining, and welding require further validation to ensure safety and reliability for large-scale engineering deployment.
The beam dump station design is well-established. Thermal and radiation shielding analyses, based on actual beam energy and power parameters, confirm that the design meets all operational requirements.
Summary
The total beamline length of the STCF accelerator exceeds 2.5 km and includes numerous beamline elements with diverse requirements. The side-by-side layout of the double storage rings in the collider presents demanding challenges for mechanical system integration and tunnel space allocation.
Mechanical support requirements for the collider ring arc sections are similar to those in existing domestic and international accelerator facilities. With the recent development and operation of new accelerators in China, technical and manufacturing capabilities are sufficiently mature to meet these requirements.
However, the mechanical system of the IR represents a particular challenge for STCF. It involves multiple subsystems, complex interfaces, and high technical risks. A thorough review of successful and unsuccessful experiences from similar international facilities will be conducted. Based on this analysis, detailed scheme design and technical studies will be carried out in combination with the overall STCF design and current engineering capabilities in China. Only after rigorous prototyping, testing, and verification will the system be implemented in the full-scale project.
Alignment system
Design requirements and specifications
The alignment task of the STCF accelerator is to ensure a smooth beam trajectory along the magnetic centers of components for both the electron and positron beams under high-precision control. Therefore, alignment is generally implemented in two phases. During the construction period of STCF, a unified control network is established across the facility using high-precision alignment instruments and optimized schemes. Equipment is adjusted to its theoretical positions within specified accuracy ranges, providing the initial trajectory for accelerator operation. In the operation phase, online monitoring of equipment positions and trajectory smoothing is performed.
As shown in Table 59, the alignment precision requirements for the STCF collider rings are as follows: within and between supports, the relative horizontal alignment precision of components is 50 μm, and the vertical precision is 100 μm. Additionally, the attitude angle control precision for all magnet equipment must be better than 0.1 mrad. The absolute precision of the closed orbit circumference of the collider rings should be better than 2 mm.
| Parameter | Index |
|---|---|
| Relative horizontal precision within a support (mm) | 0.050 |
| Relative vertical precision within a support (mm) | 0.100 |
| Relative horizontal precision between supports (mm) | 0.050 |
| Relative vertical precision between supports (mm) | 0.100 |
| Magnet attitude angle precision (mrad) | 0.100 |
| Superconducting quadrupole magnets in the IP region (mm) | 0.020 |
| Ring closed orbit circumference precision (mm) | 2.000 |
Overall, the alignment accuracy requirements are highest and most stringent for the collider rings. The damping and accumulation rings require similar precision but are less challenging due to their smaller scale. The linacs and transport lines of the STCF injector have the lowest precision requirements, as listed in Table 60.
| Parameter | Precision |
|---|---|
| Accelerator structure position precision (mm) | 0.1 |
| Accelerator structure attitude angle precision (mrad) | 0.1 |
| Corrector magnet position precision (mm) | 0.5 |
| Corrector magnet attitude angle precision (mrad) | 0.5 |
Moreover, equipment alignment and monitoring in the constrained and compact IR, as well as trajectory smoothing and differential control in the dual-ring structure, are among the key alignment challenges.
Key technologies and roadmap selection
Considering the high-precision alignment requirements in the compact IR and the dual-ring structure of the STCF tunnel, the following core alignment technologies are identified:
FSI-based high-precision positioning technology for compact regions
For precise alignment of superconducting quadrupole magnets in the compact MDI region, traditional methods such as multi-laser systems requiring cooperative targets are impractical. Frequency Scanning Interferometry (FSI) is therefore employed. FSI uses a laser with linearly varying frequency as the light source. Due to time delays in the measured distance, the reference and return beams generate a small and stable frequency difference upon overlap, producing an interference beat signal. This method offers a wide measurement range, high precision, strong anti-interference ability, and low return power requirements (suitable for non-cooperative diffuse reflection surfaces). FSI is also being considered for alignment systems in FCC-ee [141, 142] and CEPC study projects.
Multi-sensor fusion monitoring of deformation in confined spaces
Distributed fiber optic sensor technologies, widely used in tunnels and bridges, are adopted for long-term deformation monitoring of key equipment nodes in the MDI region. These sensors provide real-time data with high precision, interference resistance, and distributed sensing capabilities. Fiber Bragg Grating (FBG) sensors can achieve distance measurement precision on the order of tens of microns, with each sensor segment covering centimeter-scale ranges. By placing multiple FBG sensors at critical locations, long-term mechanical deformation monitoring becomes feasible. This approach has also been applied in FCC-ee [3] and CEPC and can be supplemented with CCD or other fusion sensor technologies.
Trajectory smoothing and ring-to-ring differential control for dual-ring layouts
Trajectory smoothing is essential for high-precision alignment and serves as a key guarantee for accelerator tuning. Given that the STCF collider adopts a dual-ring structure for electrons and positrons with limited tunnel space and correlated alignment errors between the two rings, dedicated research is needed on alignment-based trajectory smoothing and differential control in such a configuration [144].
Accurate magnet center determination and high-precision transfer techniques
Precise determination of magnet centers is critical for successful alignment and beam tuning. Depending on magnet design, techniques such as rotating coil, vibrating wire, magnetic targets, image-based methods, capacitive wire position sensors, coordinate measurement machines (CMMs), and precision photogrammetry are used for reference point extraction and high-precision mapping [145].
Accuracy and efficiency enhancement under strong reference constraints in tunnel alignment networks
Owing to the STCF’s large scale and the long-term need for alignment maintenance, precision, efficiency, and reliability must be improved under strong-reference-constrained tunnel alignment control networks. This is achieved by providing geometric constraints (position and attitude) to the laser tracker stations, thereby controlling cumulative measurement errors in the secondary network and resolving directional instability in intermediate sections [146-149].
Design scheme and system composition
The STCF alignment system is designed with seven key processes:
· Establishment and measurement of the first-level surface control network;
· Establishment and measurement of the second-level tunnel control network;
· Extraction and calibration of physical centers of equipment;
· Pre-alignment installation of magnet units on support structures;
· Initial alignment of equipment inside the tunnel;
· Beamline trajectory smoothing and dual-ring differential control alignment;
· Monitoring of ground settlement and deformation.
Establishment and measurement of first-level surface control network
The first-level control network consists of permanent control points for the injector, collider rings, and surface installations. It is typically constructed using downward excavation and permanent rock pile foundations, with vertical projections aligned to the building roof. Measurements are performed using GNSS receivers and total stations. This network serves two purposes:
· Maintain global spatial relationships between the linacs, transport lines, DR, and collider rings;
· Provide absolute accuracy constraints to ensure relative positional requirements from the physics design are met across the facility.
Establishment and measurement of second-level tunnel control network
The second-level control network is deployed along the tunnel every 3–6 m, with five reference points per segment: two on the floor, one each on the inner and outer walls, and one on the ceiling. Reference points are custom-machined and permanently bonded to tunnel surfaces with epoxy. This network reestablishes a unified facility coordinate system and provides essential spatial positioning references for equipment installation.
Extraction and calibration of physical centers of STCF equipment
The physical center of STCF equipment refers to the magnetic or electric center, which is not directly observable and must be transformed into a mechanical center for alignment. This transformation introduces inevitable conversion error, so strict control of extraction accuracy is essential. For components with moderate accuracy requirements, the mechanical center is used as a substitute. The standard edge method laser trackers enable measurement and extraction of the mechanical center with up to 0.05 mm accuracy.
Pre-alignment installation of equipment on support structures
Pre-alignment installation is performed in controlled laboratory environments using high-precision tools. Equipment is locally aligned on support modules before tunnel installation, improving local alignment precision and reducing installation time and complexity during assembly.
Initial alignment of equipment in the tunnel
Once equipment is coarsely positioned in the tunnel, laser trackers use the tunnel control network to reestablish the facility-wide coordinate system, enabling accurate alignment of magnets and other components to their theoretical spatial positions.
Beamline trajectory smoothing and dual-ring differential control alignment
Tunnel foundation settlement, environmental effects, and installation errors can cause deviations from theoretical trajectories, resulting in trajectory irregularities that affect machine tuning. A global smoothing algorithm is used post-installation to minimize local corrections while achieving globally optimized beamline smoothness. Given the unique dual-ring layout of the STCF, additional studies and optimization are required for differential control and trajectory smoothing between the two rings to meet operational physics requirements.
Monitoring of ground deformation
Foundation movement can cause cumulative displacement of accelerator equipment. Long-term monitoring is therefore required to track such deformations and enable timely correction during operational maintenance.
Feasibility analysis
Unlike fourth-generation diffraction-limited synchrotron light sources, which require sub-micron alignment precision over entire storage rings, the most stringent alignment requirements at STCF are concentrated in the IR. Multiple fourth-generation light sources, such as HEPS, have been successfully constructed and commissioned both in China and internationally. In comparison, the technical solutions proposed for STCF are generally mature and feasible.
Among STCF subsystems, the collider rings pose the greatest alignment precision challenge, followed by the DR, linacs, and beam transport lines. The IR of the collider rings is particularly complex due to limited space, cryogenic conditions, and the need for high precision in hard-to-access locations. The dual-ring structure further increases complexity compared to single-ring light sources.
Targeted research has been conducted on five key technologies:
· FSI-based high-precision alignment in confined spaces;
· Multi-sensor deformation monitoring in elongated enclosed environments;
· Dual-ring trajectory smoothing and differential control;
· High-precision magnetic center extraction;
· High-efficiency accuracy enhancement under strong-reference tunnel control networks.
These studies indicate that the alignment requirements of the STCF can be realized with good confidence.
Summary
Through the systematic description of the STCF alignment system—including design, specifications, core technologies, system composition, and feasibility analysis—it can be concluded that the proposed technical approach is highly executable and capable of meeting the alignment requirements of the STCF accelerator.
Radiation protection system
The STCF accelerator is a high-energy electron–positron collider comprising multiple linac sections, a damping/accumulation ring, several beam transport lines, and two collider rings. The maximum beam energy for both electrons and positrons is 3.5 GeV, with a center-of-mass energy range of 2–7 GeV and a maximum circulating current of 2 A in the collider rings. In addition to synchrotron X-ray radiation emitted during normal operation, other radiation sources include bremsstrahlung produced by interactions between the beam and residual gas and secondary particles generated when beam losses interact with accelerator components and shielding materials via nuclear reactions. These sources can result in radiation exposure to personnel and the surrounding environment.
The primary goal of radiation shielding is to ensure that the dose outside shielding structures remains within design and regulatory limits. Following the ALARA principle (As Low As Reasonably Achievable), radiation exposure to personnel and the environment should be minimized. Accordingly, the radiation protection system is an essential component of the STCF facility. It encompasses studies and design considerations for operational and maintenance radiation fields, shielding calculations and layout, dose estimation, monitoring systems, personnel safety interlocks, personal and environmental dose monitoring, evaluation of radioactive gaseous, liquid, and solid waste, and overall radiation safety management.
System design requirements and criteria
Dose constraint values and limits
According to the Basic Standards for Ionizing Radiation Protection and the Safety of Radiation Sources (GB 18871-2002) [150] and Regulations for Radiation Protection of Particle Accelerators (GB 5172-85) combined with the specific needs of the STCF project, the following requirements must be met:
· Basic Dose Limits:
· For occupational exposure, the average effective dose limit over five consecutive years is 20 mSv/year.
· For members of the public: the annual effective dose limit for individuals in critical groups is 1 mSv.
· Dose Constraints (used for design purposes):
· STCF radiation workers: 5 mSv/year
· Visiting scientists or users: 1 mSv/year, assuming up to 400 hours of work per year
· General public: 0.1 mSv/year
Dose rate control levels
Under normal operating conditions, the ambient dose equivalent rate at 30 cm from the shielding surface of the beamline enclosure must be less than 2.5 μSv/h.
Under beam-loss accident scenarios, the maximum accumulated dose at the outer surface of the shielding must be less than 1 mSv per incident.
Control levels for induced radioactive gases and clearance levels for solid waste
Induced radioactive gas control levels are based on the exemption activity concentration limits in Appendix A, Table A1 of GB 18871-2002 [150], assuming an air density of 1.225×10–3 g/cm3. The control limits of induced radioactive gas in tunnel during STCF operation are given in Table 61.
| Isotope | 3H | 7Be | 14C | 15O | 35S | 37Ar | 38Cl | 41Ar |
|---|---|---|---|---|---|---|---|---|
| Limit | 1.23×103 | 1.23×100 | 1.23×101 | 1.23×10–1 | 1.23×102 | 1.22×103 | 1.22×10–2 | 1.23×10–1 |
For radioactive solid waste, the clearance levels are also based on Appendix A1 of GB 18871-2002 [150]. Table 62 lists the clearance levels of solid radioactive waste.
| Isotope | Activity conc. (Bq/g) | Total activity (Bq) | Isotope | Activity conc. (Bq/g) | Total activity (Bq) |
|---|---|---|---|---|---|
| 3H | 1.0×106 | 1.0×109 | 56Mn | 1.0×101 | 1.0×105 |
| 46Sc | 1.0×101 | 1.0×100 | 56Co | 1.0×101 | 1.0×105 |
| 48V | 1.0×101 | 1.0×106 | 57Co | 1.0×102 | 1.0×106 |
| 51Cr | 1.0×103 | 1.0×105 | 58Co | 1.0×101 | 1.0×106 |
| 51Mn | 1.0×101 | 1.0×107 | 99Mo | 1.0×102 | 1.0×106 |
| 52Mn | 1.0×101 | 1.0×105 | 52mMn | 1.0×101 | 1.0×105 |
| 54Mn | 1.0×101 | 1.0×106 | 58mCo | 1.0×104 | 1.0×107 |
| 55Fe | 1.0×104 | 1.0×106 | 99mTc | 1.0×102 | 1.0×107 |
Wastewater discharge standards
According to GB 18871-2002, Section 8.6.2, radioactive wastewater may be discharged to regular municipal sewage systems with a flow rate at least 10 times higher than the discharge rate, after treatment and approval by regulatory authorities. The discharge limits are
· Monthly total discharged activity: ≤ 10 ALImin
· Per-discharge activity: ≤ 1 ALImin
· After each discharge, flush the system with water at least 3× the discharge volume.
Note: ALImin refers to the smaller value between the annual intake limits for ingestion or inhalation relevant to occupational exposure.
Key technologies and technical approaches
Source term analysis
As a high-energy electron–positron accelerator, the STCF involves a variety of beam–matter interactions, including interactions of electrons and positrons with residual gas, collimators and targets, vacuum chamber walls, and with each other during beam–beam collisions. Electromagnetic cascades and nuclear reactions dominate these processes, giving rise to ionizing radiation fields (instantaneous and mixed) and the formation of radioactive nuclei inside target materials (induced radioactivity). The radiation sources therefore include both prompt radiation and induced radioactivity.
Sources of prompt radiation include:
· Random beam losses from particles in the beam halo striking the vacuum chamber walls (modeled as uniform loss);
· Sudden loss of an entire bunch (100% loss of a beam bunch);
· Bremsstrahlung generated by beam interaction with residual gas;
· Point losses from positron targets, positron linac sections, electron and positron storage rings, damping/accumulation rings, and main linacs;
· Radiation from electron–positron collisions;
· Beam losses during machine tuning and at beam dumps (e.g., from bunch swap-out or beam abort scenarios during injection in swap-out mode).
· The secondary particles generated in prompt radiation can carry energies up to the full incident beam energy and may also initiate activation processes in nearby materials.
Induced radioactivity arises when particles lost during beam operation interact with components, vacuum walls, targets, and other structures. The resulting prompt radiation further induces nuclear reactions in surrounding materials, shielding, air, and water, converting stable nuclei into radioactive isotopes. After beam shutdown, prompt radiation ceases, but induced radioactivity persists. The produced isotopes decay over time, emitting gamma and beta radiation, which can pose hazards to personnel and the environment. Evaluation and mitigation strategies are therefore required to manage these risks effectively.
Key activation products include:
· Activated structural materials (e.g., Cu, Fe, stainless steel, Al, Al alloys): 54Mn、52mMn、56Mn、58V、51Cr
· Activated shielding concrete: 22Na、24Na、54Mn
· Activated air: 3H、7Be、11C、13N、15O、41Ar
· Activated cooling water: 11C、13N、15O、7Be、3H
· Activated soil and groundwater: 7Be、3H、22Na
Shielding calculation methods
The radiation shielding design for STCF follows internationally recognized methodologies for electron accelerator shielding, combining empirical formulas with Monte Carlo simulations. The final design integrates simulation results with proven engineering practices:
· Empirical formulas: Primarily based on Jenkins and Sakano’s methods.
· Monte Carlo simulations: Performed using FLUKA.
· Skyshine (air-scattered radiation): Calculated using the semi-empirical Stapleton formula.
· Engineering references: Drawn from experiences at BEPC [151–154], Beijing High Energy Photo Source [155], HALF, and similar domestic and international facilities.
Radiation monitoring system
The STCF radiation monitoring subsystem will be a state-of-the-art, fully integrated system designed in compliance with the latest legal requirements and international standards. Key considerations in the design include:
· Results from preliminary hazard assessments;
· Latest technological developments;
· Unique beam time structure and radiation field characteristics.
The system will continuously measure environmental dose rates in both accelerator operational areas and surrounding interior/exterior zones. If dose levels exceed predefined thresholds in a controlled radiation zone, alarms will be triggered, including remote alerts to the control room. Additional capabilities include:
· Remote monitoring;
· Long-term data storage;
· Offline data analysis.
A critical challenge is ensuring detector responsiveness under STCF-specific conditions: ultra-high beam loss rates, high beam energies, complex secondary particle distributions, and time-structured radiation. Evaluation will be required to determine whether conventional detectors suffice or if new detectors need to be developed.
Personnel safety interlock subsystem (PSIS)
The STCF Personnel Safety Interlock Subsystem (PSIS), due to its unique application environment, must comply not only with low-voltage electrical system design standards but also with radiation protection regulations. Drawing on best practices and operational experience from national and international accelerator facilities, the PSIS for STCF is designed with the following principles [153]:
· Hardware reliability;
· Optimal shutdown logic;
· Fail-safe operation;
· Redundancy;
· Defense-in-depth;
· Self-diagnosis and inspection;
· Human-centered design.
A critical aspect is the logical structure of the interlock system. The PSIS is tightly integrated with the radiation monitoring system to ensure coordinated and safe accelerator operation.
Design scheme and system architecture
STCF accelerator tunnel shielding design
In the shielding design, FLUKA simulations were conducted under two beam loss scenarios: uniform loss along the beam envelope and sudden full-bunch loss. Neutron and photon energy spectra were calculated at various distances from copper and stainless-steel targets impacted by high-energy electron beams. Using the shielding design objectives, radiation shielding formulas, and beam loss assumptions, radiation dose rates and primary shielding thicknesses were determined for each accelerator section under various operating conditions. Dose calculations account for both public and occupational occupancy: public occupancy is assumed year-round with a factor of 1, while workers are assumed to be present for up to 2000 h per year. Depending on the location, occupancy factors of 1 or 1/10 are applied to accessible areas outside the shielding walls.
To meet STCF radiation protection objectives, dose rates on the surface of shielding walls and on the ground above underground tunnels were calculated using the specified beam loss scenarios and shielding thicknesses. These calculations ensure that, even under assumed beam loss conditions, shielding walls reduce dose rates in accessible areas to levels consistent with STCF design goals.
Shielding strategies vary by tunnel location. The injector’s accelerator sections, tentatively located 6.5 m underground, use concrete combined with soil overburden for shielding. The collider ring tunnel, situated at or near ground level, relies primarily on concrete shielding. In special areas, shielding may include heavy concrete combined with steel plates. Personnel access corridors employ maze-type shielding and shielding doors, with shielding thicknesses determined through source term simulations.
Personnel safety interlock subsystem
The Personnel Safety Interlock Subsystem (PSIS) is built on the interlock control infrastructure and supported by an access control monitoring system. Guided by principles of digitalization, networking, integration, and human-centered design, the system ensures personnel safety in radiation-controlled areas, such as tunnels, and helps prevent radiation accidents.
The PSIS is managed by programmable logic controllers (PLCs) and complemented by access control systems and interlock keys, with the following core functions:
· Prevent personnel from entering zones where prompt radiation is present.
· Prevent radiation generation while personnel remain in controlled zones.
· Prevent uncontrolled radiation leakage from controlled areas.
A conceptual system diagram is shown in Fig. 240 [153].
When the accelerator is operating in beam mode, interlocks are activated for the corresponding areas, prohibiting personnel access. After shutdown, access for maintenance is permitted. Each interlock zone includes multiple interlock doors and shielding doors, all equipped with status indicators, interlock control boxes, access control readers, emergency open buttons, and interlock key systems.
Within each tunnel zone, emergency stop buttons are installed every 10 m along walkways, ensuring at least two stop points per zone. Search and clearance buttons, along with audio-visual alarms, are installed at exits, remote corners, and blind spots. PSIS input and output signals interface with the accelerator management system, ventilation control, high-power equipment systems, and on-site interlock hardware, including stop buttons, clearance buttons, access readers, and interlock key devices.
Radiation monitoring subsystem
The radiation monitoring system includes area monitoring, individual dose monitoring, and environmental monitoring:
· Area Monitoring: Combines fixed online monitors with mobile survey instruments.
· Environmental Monitoring: Employs fixed radiation monitors for continuous observation and periodic sampling and analysis of environmental media.
· Personnel Dosimetry: Primarily uses passive dose badges, supplemented by personal alarm dosimeters. Personnel are monitored quarterly.
Routine area radiation monitoring ensures workplace safety and verifies that protective measures prevent accidental exposure to staff and the public.
As illustrated in Fig. 241, the system consists of:
· Local detectors for real-time area and environmental dose rate measurements;
· Data transmission and acquisition systems to send information to the central control and data storage center;
· Functions including threshold alarms, data archiving, information publication, and interfacing with interlock controls.
To ensure reliable control and communication under varying conditions, the system supports four communication channels: Ethernet, wireless, GPRS, and offline logging.
Feasibility analysis
The STCF project team brings together researchers from across the country with expertise in relevant fields. Domestically, substantial experience already exists in the design and operation of radiation protection systems for high-energy electron accelerators, providing a solid foundation for the successful implementation of this project. The shielding calculation software required is internationally recognized, mature, and open-source, with controlled access rights. Consequently, the proposed research topics, technical approach, and design scheme are all feasible.
Summary
The radiation protection system for the STCF facility encompasses source term analysis, shielding calculations, the radiation monitoring subsystem, and the radiation safety interlock subsystem. The facility’s complex structure, high beam loss rate, unique beam timing, and generation of complex secondary particles present significant challenges to radiation protection design. However, by leveraging the design experience of major domestic electron accelerator facilities, the project team is well-positioned to implement an effective radiation protection system for STCF. Continuous iteration and close integration with the physical design will be essential to deliver a radiation protection solution that fully meets all safety and regulatory requirements.
Key technology R&D
Overview
As described in Sect. 1, the STCF accelerator will extensively adopt mature accelerator technologies. Over the past two decades, China has built numerous accelerator facilities at the international level, establishing a solid foundation in accelerator technology. At the same time, the capabilities of China’s manufacturing industry have significantly improved, enabling domestic mastery of world-class accelerator technologies and equipment fabrication techniques—an important advantage for constructing the STCF accelerator.
However, STCF also requires several technologies that are not yet fully mastered by the project team or even within China. In some cases, the required technical specifications exceed the current international state-of-the-art, or the technologies themselves have not been fully validated globally. Despite these challenges, adopting these novel technologies is crucial to achieving the performance goals of a new-generation collider. It is a well-established practice in the international accelerator and high-energy physics communities to drive technological advancement through sustained R&D and targeted pre-construction development. This approach is essential not only for delivering cutting-edge accelerator facilities but also for advancing accelerator science as a whole.
The STCF project will follow a similar strategy, strengthening national collaboration, forming strong partnerships, and organizing dedicated R&D campaigns to master key technologies during both pre-research and construction phases. Where necessary, temporary substitution with mature technologies may be used during construction, accepting modest trade-offs in device performance. These temporary solutions would be replaced with advanced technologies once fully developed and validated.
During the conceptual design phase, the accelerator team conducted systematic studies of the physical design and coordinated closely between physical and technical system design. This process allowed the team to identify the complete set of technical requirements for building the STCF accelerator, including both established technologies and key technologies yet to be mastered. Through active international collaboration, the team also gained a comprehensive understanding of design approaches and technical levels of third-generation electron–positron colliders worldwide, providing a strong foundation for targeted R&D and engineering-oriented technical pre-research.
Given the varying degrees of technical maturity, difficulty, and criticality of the required technologies, phased R&D programs are necessary. During early project development, the team received strong support from the Ministry of Science and Technology, the National Natural Science Foundation of China (NSFC), the Chinese Academy of Sciences, and the University of Science and Technology of China (USTC), enabling significant progress. However, due to the complexity of the STCF accelerator, a large-scale collaborative effort was required for comprehensive design and research, which was not fully achieved during the initial stage. Consequently, early-phase R&D work was not fully systematic and only partially addressed certain key technologies.
Since 2023, with joint support from Anhui Province, the City of Hefei, and USTC through a provincial science and technology special initiative, the STCF team has conducted focused R&D on critical technologies, achieving major advances, particularly in accelerator-related areas. Section 5.2 presents specific progress and deployment of these R&D initiatives. Additional key technologies and engineering techniques still requiring validation—including follow-up work from the current R&D program—will be addressed in the next project phase to ensure STCF can commence construction as planned in 2027 or 2028, as detailed in Sect. 5.3.
Ongoing R&D on key technologies
With support from the Anhui Provincial “STCF Key Technology R&D Project” and the National Key R&D Program project titled “Physics and Key Technology Research on High-Luminosity Electron–Positron Accelerators and Detectors in the GeV Energy Range”, the STCF accelerator team is actively pursuing R&D on several critical accelerator technologies. These include: superconducting magnet technology for the IR, high-power RF technology for the collider rings, high-precision beam diagnostics and fast feedback systems, beam injection technology, MDI mechanical integration, high-charge S-band PC electron sources, large-aperture S-band accelerating structures, and high-power positron target technology.
For the injector-related technologies—such as the PC electron source, large-aperture accelerating structures, and positron target—the team plans to integrate prototype systems into a newly constructed test platform for electron and positron beam experiments. The major R&D efforts under way are outlined below.
Superconducting magnet technology for the interaction region
As a third-generation electron–positron collider, STCF adopts a large crossing-angle collision scheme, requiring the FF superconducting quadrupoles to be positioned as close as possible to the IP. This design faces significant constraints, making the development of IRSMs a major technical challenge.
On both sides of the IP, a set of double-aperture combined superconducting magnets is located deep within the detector. These magnets must provide strong focusing to minimize beam size at the collision point while incorporating orbit correction, higher-order multipole correction, and solenoidal field compensation functions. The core of each magnet set consists of two double-aperture quadrupole magnets and includes compensation solenoids, correction coils, harmonic compensation coils, and anti-solenoid windings. These magnets feature multiple coil types, high gradient, and high magnetic field precision. The current layout of the IR magnets is shown in Fig. 62.
The complexity of this magnet system is further increased by strict spatial constraints, including limited separation between apertures and restricted outer dimensions. Internationally, few precedents exist. The only operational example is the SuperKEKB collider in Japan, which uses an asymmetric-energy beam scheme with different magnet requirements. Its performance has been suboptimal, and upgrades are under consideration. Within China, no prior R&D exists on double-aperture combined superconducting IR magnets. However, the Institute of High Energy Physics (IHEP) developed a single-aperture combined superconducting magnet for BEPCII using the serpentine winding technique originally developed by BNL and a single-aperture prototype for CEPC using the Cos2θ winding technique. These efforts provide useful references for STCF.
The STCF team has identified IRSM development as a top-priority key technology. Experts in superconducting magnet R&D were consulted to evaluate four design technologies—CCT, cos2θ, DCT, and serpentine winding. After comparative studies and international input, the CCT (canted cosine-theta) scheme was selected as the baseline for STCF IR magnet prototyping.
Prototyping is divided into two stages: the first stage develops the CCT-based design, manufacturing process, and a double-aperture quadrupole prototype; the second stage develops a full engineering prototype of the combined magnet system based on refined accelerator optics requirements. The design and prototype goals are listed in Table 63.
| Item | Parameter | Design target | Prototype target |
|---|---|---|---|
| Magnet assembly | Double-aperture angle | 60 mrad | 60 mrad |
| Distance from IP to Q-center | 1100 mm | 1100 mm | |
| Quadrupole and correction coils | Field gradient | ≥ 50 T/m | ≥ 50 T/m |
| High-order field error | ≤ 0.2 ‰ | ≤ 1.0 ‰ | |
| Cross-talk | ≤ 30 Gauss | N/A | |
| Magnetic length | ≤ 400 mm | ≤ 400 mm | |
| Coil inner diameter | ≈22 mm | ≈22 mm | |
| Coil outer diameter | ≤ 27 mm | ≤ 27 mm | |
| Anti-solenoid coil | Field strength | ≥ 1 T | N/A |
| Integrated field (within ±2 m of IP) | Suppress to ≤ 1% of detector solenoid field | N/A |
The R&D process includes the following steps: (1) considering accelerator optics and spatial constraints to perform 2D/3D magnetic field calculations using tools such as OPERA; (2) structural design of the full system, including thermal, electrical, and mechanical properties, using 3D CAD and finite element analysis tools; (3) selection of coil materials and support structure designs suitable for cryogenic operation; (4) machining and winding trials of CCT coil supports; (5) fabrication of a prototype superconducting magnet; (6) vertical cryogenic testing to verify operational current and magnetic field quality; (7) refinement of the magnetic design and manufacturing process for future engineering models.
RF technology R&D for the collider ring
STCF will operate with high beam currents (≈2 A) and low emittance, making beam–cavity interaction effects—such as beam loading and HOM instabilities—critical concerns. These challenges place stringent requirements on the RF system, particularly the development of accelerating cavities capable of handling high power (≈300 kW) with low R/Q and deeply damped HOMs.
Although similar challenges have been addressed internationally, domestic R&D in this area lags significantly. Advances in technology now demand cavity designs that are more effective and economical than previous generations. After reviewing RF cavities used in global storage rings of both e+e- colliders and synchrotron light sources, the team identified the 500 MHz room-temperature TM020 cavity, developed jointly by Spring-8 and KEK, as a promising candidate for STCF (see Sect. 4.3 for details).
While the NanoTerasu light source in Japan has deployed this cavity type, STCF’s much higher beam current imposes significantly greater demands on both the cavity and power coupler. This necessitates dedicated domestic development of the TM020 cavity and high-power coupler, including mechanical design, fabrication techniques, and tuning systems. Development of the LLRF system is also essential, as it forms the foundation for stable RF operation and beam feedback.
The ring RF technology development will proceed in stages. The current phase focuses on building a TM020 prototype cavity to study its mechanical and RF properties, along with high-power coupler development and tuning strategies. In the next phase, improvements based on this work will enable construction of an engineering prototype that meets all operational requirements for STCF.
Beam instrumentation technology R&D
Compared with fourth-generation synchrotron light sources under construction, STCF operates at much higher beam currents and achieves extremely small beam spots at the IP. Compared to colliders like SuperKEKB, STCF operates at lower energies, where collective effects such as IBS are more pronounced. Under conditions of intense radiation background and strong collective effects, accurate and timely beam parameter measurements—and precise, fast tuning capabilities—are key limiting factors for STCF performance. The overall performance targets for STCF’s beam diagnostics system must significantly exceed the capabilities of BEPCII and SuperKEKB, ensuring stable beam operation under high-luminosity conditions. This requires the development of advanced diagnostics for high-precision bunch-by-bunch spatial resolution, suppression of instabilities via bunch-by-bunch feedback, and interaction-point-based luminosity feedback. These efforts are actively pursued.
Bunch-by-bunch precision diagnostics for the collider rings
To reduce noise from multiple front-end components, a low-noise signal-conditioning front-end is under development, paired with a high-sampling-rate, high-bandwidth multi-channel oscilloscope for initial signal observation and offline data analysis.
A phase-resolved sampling technique is being developed, sampling at two fixed-delay points near the signal peak to suppress phase jitter effects on peak value determination. Combined with a modal-matching amplitude and phase extraction algorithm, this approach enables 3D position and charge measurements using only eight original sampling channels, achieving high signal-to-noise ratio and integration. An integrated bunch-by-bunch 3D position signal processor is under development, featuring an eight-channel data acquisition system. The prototype includes both an analog front-end electronics module (with 8-channel ADCs) and a digital processing module based on FPGA, and supports external clocking and triggering.
Based on this system, transient analysis of off-axis beam injection can be performed. After injection, differences in the initial conditions between the injected and stored bunches cause the injected bunches to undergo damped oscillations in both longitudinal and transverse dimensions around the stored beam’s equilibrium position. Eventually, they merge fully. Bunch-by-bunch precision diagnostics enables detailed observation of this evolution.
Collision stability and feedback technologies
This segment involves two critical areas: a fast bunch-by-bunch feedback technique to suppress collective beam instabilities and a luminosity-oriented feedback technique at the IP.
The bunch-by-bunch feedback system includes RF signal processors, digital processors, broadband linear power amplifiers, and transverse and longitudinal kickers. Given STCF’s high beam current (≈2 A), multiple kickers may be required in the same direction. Custom processors are under development to support multiple independent-phase feedback outputs. Broadband amplifiers, currently dominated by foreign suppliers at high cost, are being developed domestically to reduce dependency.
Beam–beam interactions and micro-vibrations affecting the final focus superconducting magnets, particularly in the vertical plane, can cause closed orbit distortions and collision angle changes at the IP, leading to luminosity jitter. Interaction-point orbit feedback can mitigate this. For example, a single-chamber dual-beam BPM with eight electrodes, currently under international study, can measure relative displacement of electron and positron beams. When combined with the detector’s luminosity monitoring system, this enables real-time orbit corrections to stabilize luminosity. These technologies are under exploratory study by the STCF beam instrumentation team in the pre-research phase.
MDI technology R&D
The MDI at the IR is one of the most complex challenges in collider engineering (see Sects. 2.12 and 4.13). It must satisfy interrelated requirements from multiple domains. For example, the accelerator physics design specifies the position, aperture, and field configuration of the IP superconducting magnet assembly. At the same time, the detector imposes stringent constraints on the transverse boundaries of these accelerator components. The close spacing between dual-aperture superconducting quadrupoles and limited volume for coil supports and cryostats severely constrains mechanical integration. Moreover, the vacuum system must achieve ultra-high vacuum without dedicated pumps, while accounting for beam losses, beam-gas interactions, and radiation backgrounds from bremsstrahlung and synchrotron radiation, which add to local heat loads.
Mechanical support, maintenance procedures, and the interface with external vacuum sections (RVCs) are further complicated by the location inside the large spectrometer. During R&D, multiple constraints must be studied, viable structural solutions proposed, and prototype models developed. These activities must iteratively co-evolve with accelerator and detector physics designs, which will continue to change in subsequent STCF design phases.
Prototyping begins with a 3D mechanical model, built using geometry data from the collider optics, superconducting magnet layout, vacuum system, and detector structure. This model supports integrated assembly planning, handling strategies, and co-design with other systems. A full-scale (1:1) mechanical integration prototype (one side) will then be fabricated to verify the mechanical design and installation process.
Collider ring injection technology R&D
Because the STFC has a small dynamic aperture and extremely short beam lifetime, each of the collider rings requires an injection and extraction system with exceptional performance. In particular, the proposed swap-out injection scheme imposes stringent timing requirements: the pulsed kicker magnet must respond within just a few nanoseconds and operate at high repetition rates, posing major technical challenges.
In the R&D phase, the team is not only supporting the ongoing injection system design (see Sect. 4.4) but is also developing and testing two kicker magnet prototypes: One is an ultra-fast pulsed kicker for the swap-out injection scheme and the other is a nonlinear pulsed kicker for the traditional off-axis injection scheme. Although similar devices have been developed and even operated both internationally and domestically, the technology is still evolving. STCF places higher demands on performance than current systems. The goal is to achieve full mastery of pulsed injection kicker technologies that meet STCF requirements.
Injector-related technology R&D and the e+/e- test platform
Key injector technologies
To achieve the ultra-high luminosity design goals of STCF, the collider must operate with high beam currents, a small dynamic aperture, and short beam lifetimes. This necessitates top-up injection using high-charge, low-emittance electron and positron bunches at a moderate repetition rate. Minimizing luminosity perturbation from the injected beams is essential.
Whether employing off-axis or swap-out injection, the injector must support high-repetition, high-charge beams with excellent beam quality. This places much stricter demands on beam performance and control precision compared with BEPCII. Therefore, targeted R&D on key enabling injector technologies is required.
Current R&D efforts focus on developing a high-charge photoinjector, an S-band RF system with energy compression, a high-power solid-state modulator, large-aperture S-band positron accelerating structures, a high-power positron target, an AMD, and diagnostics for precise measurement of bunch charge and bunch length.
Electron–positron beam test platform
To support the injector-related key technologies described above, the STCF team has designed an integrated electron–positron beam test platform—also referred to as the beam test facility—where multiple R&D components can be evaluated within a unified experimental environment. The platform includes a high-charge photoinjector, a 100 MeV electron linac, a positron production target and an AMD, a 100 MeV positron linac, as well as comprehensive beam diagnostics and a beam dump system. The system parameters are summarized in Table 64.
| No. | Parameter description | Design target |
|---|---|---|
| 1 | Electron beam energy (MeV) | 100 |
| 2 | Electron bunch charge (nC) | 8 |
| 3 | RF frequency (MHz) | 2998 |
| 4 | Macro-pulse repetition rate (Hz) | Max 50 (1 Hz at high charge) |
| 5 | Energy stability | 0.1% rms |
| 6 | Bunch length (rms) (ps) | 4 |
| 7 | Beam spot at positron target (rms) (mm) | ≈2 |
| 8 | Positron beam energy (MeV) | 100 |
| 9 | Positron yield (e+/e-) | 0.1% |
This test platform is being co-developed with the klystron and accelerating structure test facility of the HALF, sharing infrastructure and space. The layout is shown in Fig. 242.
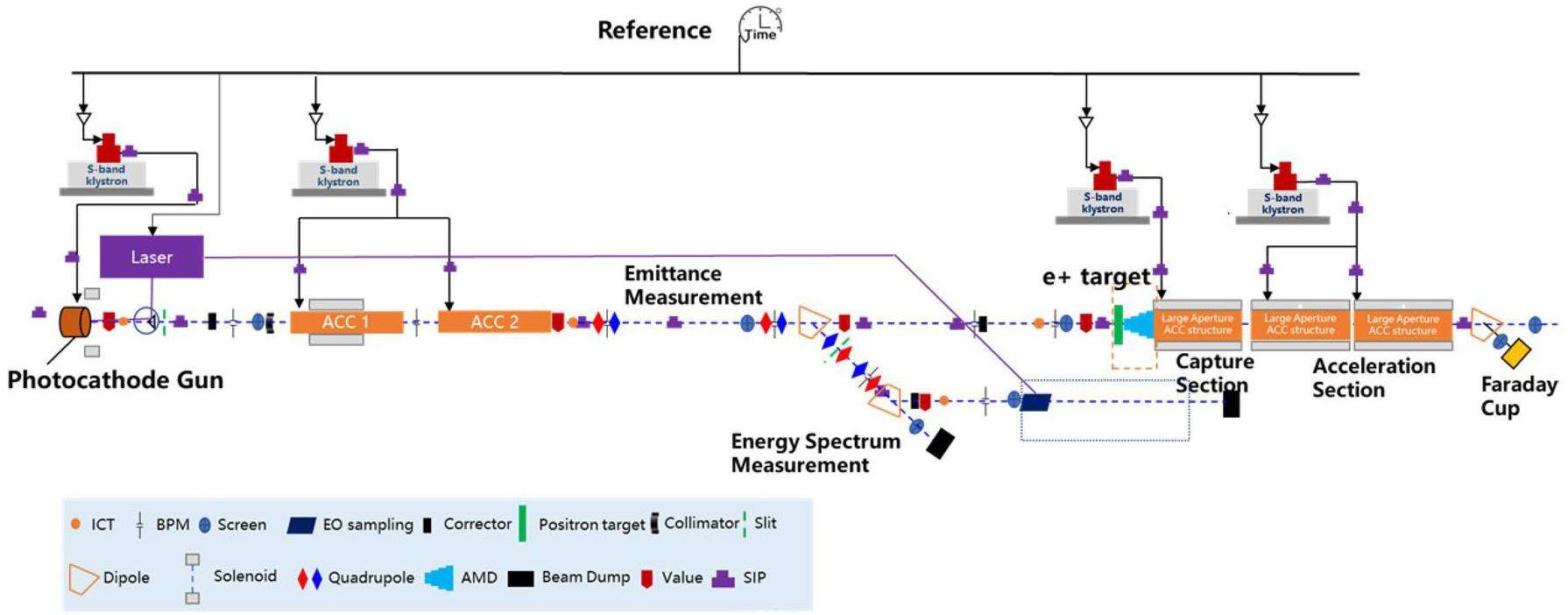
The test facility will address the following six major technical tasks:
1. Develop a high-charge, low-emittance S-band PC electron gun;
2. Construct a 100 MeV electron linac to accelerate electrons from the photoinjector and deliver them either to the positron production target or to an upstream beam dump;
3. Build a positron target and an AMD;
4. Construct a 100 MeV positron linac to capture and accelerate positrons using large-aperture accelerating structures;
5. Transport both electron and positron beams to a diagnostics beamline and a downstream beam dump;
6. Carry out precision beam diagnostics for both species to validate physical models of the STCF injector and verify beam quality, stability, and measurement techniques.
Future R&D on key accelerator technologies
Continuation of current key technology R&D
Some of the ongoing STCF accelerator technology development efforts involve significant technical challenges that require a staged approach. The first stage is primarily exploratory, focusing on prototype-level validation to identify technical bottlenecks and establish feasible processes—often referred to as the “proof-of-principle” stage. The second stage builds upon this foundation to achieve full technical performance through system integration and engineering-level implementation, culminating in the development of qualified engineering prototypes.
One of the core areas requiring continued advancement is the superconducting magnet system in the IR. Building on the current prototype of a double-aperture superconducting quadrupole magnet, the next step is to develop a full engineering model. This model must accommodate the mechanical and spatial constraints defined by the MDI region, satisfy updated physical parameters driven by machine optics, and integrate high-order harmonic correction coils and anti-solenoid compensation coils. In addition, the coil and compact cryostat structures must be jointly optimized. The resulting engineering prototype will undergo rigorous performance validation before being qualified for deployment.
Another key area is the high-power RF system for the storage rings. The initial phase of research has focused on the structural design, machining processes, and LLRF controls of a TM020-type room-temperature cavity. However, to meet STCF’s high-current operational requirements, subsequent R&D must address the development of high-power input couplers and structural optimizations to enhance power handling and electromagnetic performance. The ultimate objective is to produce a TM020-type cavity that fully meets STCF specifications at the engineering prototype level.
Additional accelerator technology development
Following the completion of the STCF conceptual design and external expert evaluations, it has become clear that several technologies—originally considered secondary or of uncertain necessity—are, in fact, indispensable for STCF construction and must be addressed through targeted R&D. These technologies are not yet sufficiently mature for direct application in STCF and should therefore be prioritized for dedicated development.
In many cases, the fundamental knowledge base and technical infrastructure already exist domestically. However, current performance levels do not meet the stringent requirements of STCF. Consequently, these technologies must be elevated to the status of key technical areas, with focused efforts to develop engineering-level prototypes that satisfy project specifications.
Furthermore, certain technologies are currently available only from established international suppliers and have not yet been developed domestically. To mitigate potential supply chain risks during STCF construction, it is essential to initiate parallel domestic development of these systems. Even if early-stage performance falls short of foreign counterparts, such efforts will strengthen future self-reliance and reduce strategic vulnerabilities during the STCF engineering phase.
Requirements for utility infrastructure
Large-scale accelerator facilities impose exceptionally stringent demands on utility systems, far exceeding those of conventional research laboratories or civilian buildings. These systems represent a critical component of the overall engineering design and construction process. Based on the preliminary technical layout of the STCF accelerator, the major infrastructure requirements have been largely defined. They include the construction of injector tunnels, collider ring tunnels, experimental and testing halls, and various equipment rooms. Four to five equipment access points will be established at key locations, such as the linac and DR area, the beam crossing points of the collider rings, and the experimental detector hall.
The collider rings and injector impose extensive requirements on public infrastructure, encompassing civil construction, power supply and energy management, HVAC systems, process cooling water, cryogenics, water supply and drainage, geodetic surveying and alignment, networking and computing infrastructure, transportation and logistics, as well as system installation and integration. Moreover, since many accelerator components operate within radiation-controlled areas, the infrastructure must not only meet operational and technical needs but also fully comply with radiation protection and safety standards.
Electrical power and system grounding requirements
The primary power consumers of the STCF accelerator include the collider rings, linac, DR, and beam transport lines. Major energy-consuming systems consist of the RF power sources, magnet power supplies, microwave sources for the linac, cooling water pumps, and air-conditioning units. The total estimated power demand is approximately 80 MVA.
A dedicated 110 kV substation with dual external transmission lines will be constructed within the STCF site. A 10 kV distribution network will deliver power to substations in each building, where it will be stepped down and distributed to the accelerator systems. To ensure high power quality for sensitive equipment, power conditioning devices and UPS or energy storage systems will be installed where required.
Dedicated grounding networks will be implemented in the tunnel areas for systems such as the RF, power sources, and injection systems. A combined or M-type grounding configuration will be adopted, achieving a grounding resistance of less than 0.5 Ω to minimize interference from common-mode conduction. Copper busbars will be routed along tunnel walls, with reserved grounding terminals provided for equipment connection. The grounding system will comply with IEC 62561 and GB/T 33588 standards, ensuring full electromagnetic compatibility.
Water and cooling requirements
During accelerator operation, most of the electrical energy consumed by the machine systems is converted into heat, which must be effectively removed to maintain operational temperature limits and ensure long-term stability. For example, magnet coils generate resistive heat during excitation and therefore require direct internal water cooling. Temperature fluctuations in the cooling water can lead to variations in the magnetic field, adversely affecting beam stability. As such, the temperature stability of the cooling water must meet the precision requirements of the magnets and other sensitive components.
In addition to water-cooled magnets, other systems requiring process cooling water include DC and pulsed power supplies, electronics racks, RF equipment, and cryogenic devices. The total thermal load from the STCF accelerator equipment is estimated at approximately 30 MW. Most water-cooled systems operate at a nominal pressure of 0.4 MPa, with a maximum of 0.6 MPa, and require an inlet water temperature of 22±0.5 °C.
Both primary and secondary cooling water will be sourced from the municipal water supply, with an approximate total flow rate of 1500 m3/h. Several distributed water stations located around the accelerator will supply secondary cooling water to the machine systems. Heat extracted by the secondary water loops will be transferred to the primary circuit, which will be cooled either by air or through heat recovery systems.
The campus water supply and drainage system must also meet the needs of both equipment and personnel. Wastewater from cooling towers and filtration systems will undergo treatment prior to discharge, and a comprehensive drainage network will be implemented throughout the facility.
Compressed air requirements
The compressed air system at STCF is designed to provide clean, stable, and reliable compressed air to all terminal devices requiring pneumatic actuation, including vacuum valves and other pneumatic components within the injector and collider ring areas. The purified compressed air must meet the quality standards specified in Table 65.
| Type | Oil content (mg/m3) | Contained particle size (μm) | Dew point (°C) |
|---|---|---|---|
| Instrumentation-grade air | < 0.01 | < 0.1 | –40 |
Ventilation and air conditioning requirements
To maintain beam orbit stability, in addition to ensuring the stability of power supplies and minimizing mechanical deformation of magnets and their supports, the tunnel environment—particularly within the collider rings—must meet stringent environmental control requirements. The ambient temperature in the collider ring tunnel shall be maintained at 24 ± 0.1 °C, with a relative humidity ≤ 50%.
A transverse ventilation scheme will be adopted for the collider ring tunnel, divided into distributed ventilation sectors around the ring. The ductwork and air outlets are specifically designed to ensure uniform humidity and temperature control during operation. To maintain airflow in the event of duct failures, air will be supplied bi-directionally from both ends using symmetrical configurations.
Rapid air exchange systems will be installed to provide fresh air for personnel entry and to remove smoke or hazardous gases in emergencies. The fresh air exchange rate shall be at least 0.5 air changes per hour.
Cryogenic requirements
STCF employs two superconducting magnet subsystems located in the IR, each comprising multiple magnet coils housed within a cryostat extending into the detector volume on either side of the IP. These magnets require cryogenic cooling at 4.5 K and 1.5 bar. Each superconducting magnet has a thermal load of approximately 37.2 W and requires 2.0 g/s of cold helium gas for current lead cooling. The thermal shield operates at 77 K, and the magnet cooldown rate must be limited to below 10 K per hour.
To ensure stable operation of the IRSM systems, a dedicated cryogenic system will be constructed to supply low-temperature fluids at the required pressure and temperature while removing thermal loads. The system design emphasizes reliability, safety, and maintainability. Cooling will be provided via subcooled liquid helium at a pressure between saturation and the critical point (2.3 bar), with two local valve boxes controlling helium flow to and from the cryostats. In addition to operational cooling, the cryogenic system will support prototyping and performance testing. It will include helium and nitrogen subsystem. The helium system comprises storage tanks, refrigerators, cryogenic transfer lines, valve boxes, and helium recovery and purification systems.
The nitrogen system supplies liquid nitrogen for refrigerator precooling, purifier cooling, and thermal shield cooling.
Reliable cryogenic operation requires supporting utilities such as water cooling, electrical power, compressed air, and ventilation. The helium compressor, turbine expanders, and associated components require approximately 30 m3/h of cooling water and 800 kW of electrical power. Electrical power will be provided via three-phase five-wire or single-phase three-wire systems from the main distribution panel. Major electrical loads include helium compressors, heaters, mechanical and turbomolecular pumps, cranes, fans, HVAC units, and lighting.
Compressed air is required to operate all pneumatic valves in the cryogenic system—including control, shut-off, and gate valves. A 15 m3 air storage tank will be installed, and the system will consume approximately 45 Nm3/h of instrumentation compressed air.
Geodetic surveying
The STCF facility requires the establishment of a comprehensive geodetic reference infrastructure, including a dedicated reference network and precise gravity leveling. This infrastructure will support all project phases—from initial construction through long-term operation—ensuring the accurate spatial positioning and alignment of accelerator components.
Ground settlement and micro-vibration requirements
Ground vibrations—arising from micro-seismic activity, environmental sources (e.g., machinery or human activity), and internal facility equipment—can induce beam trajectory drift and emittance growth. Site selection and foundation design must therefore minimize vibration transmission. Based on beam dynamics, mechanical coupling, and feedback system constraints, the collider tunnel floor must meet a vibration criterion where the rms displacement integrated over the 1–100 Hz frequency range within any one-second interval is less than 30 nm.
The injector tunnel floor must support loads up to 100 kN/m2, with flatness deviations of less than 4 mm per 25 m and less than 10 mm over the total length, including transfer lines. The collider tunnel floor must support up to 200 kN/m2, with the same flatness criteria and less than 10 mm deviation around the full circumference.
Uneven ground settlement during operation can affect beam trajectories. The allowable differential settlement rate is limited to < 10 μm per 10 m per year for the collider tunnel and < 20 μm per 10 m per year for the injector tunnel. Real-time and long-term ground monitoring systems will be implemented to ensure continuous compliance with these criteria.
Communications, computing, and data services
STCF accelerator control and operations demand robust infrastructure for data transmission, telephony, and wireless communication, supported by a dedicated fiber-optic network. A central data center will be established to provide computing resources, data storage, operational support, diagnostics, and secure network access.
Digital modeling
To achieve fully integrated visualization and planning for the STCF project, 3D digital models will be developed for all key areas, including accelerator tunnels, detector halls, and equipment rooms. These models will be integrated with the engineering design database to support layout optimization, ensure compliance with machine requirements, and reserve space for future upgrades.
Transport and logistics
The transportation, storage, and installation of STCF technical components will be organized based on detailed specifications regarding device type, quantity, size, weight, testing locations, operational positioning, storage conditions, and vibration sensitivity. Custom transport and installation tools will be designed according to tunnel dimensions and engineering layout constraints.
Logistics planning will also address the movement of personnel, equipment, and materials within tunnel sections and equipment halls. Workflow analysis, including installation rates (e.g., number of magnets installed per day), will inform the development of an efficient, safe, and coordinated logistics strategy to meet installation schedules and overall project milestones.
Design of beam optics for the Future Circular Collider e+e−-collider rings
. Phys. Rev. Accel. Beams 19,Super Tau-Charm Facility of China
. Physics 49, 513 (2020). https://doi.org/10.7693/wl20200803Suppression of beam-beam resonances in crab waist collisions
. in: Proceedings of EPAC08, Genoa, Italy, June 23-27, 2008. Conf. Proc. C 0806233 (2008)Touschek lifetime and luminosity optimization for Russian Super Charm Tau factory
. J. Instrumen. 19,Chromaticity correction of the interaction region
.First- and second-order charged particle optics
. AIP Conference Proceedings, 127, 62-138. (1985). https://doi.org/10.1063/1.35177PAMKIT
. https://pypi.org/project/PAMKIT/SAD home page. (n.d.)
. RetrievedSuperKEKB operation using crab waist collision scheme
. Eur. Phys. J. Plus 136, 1023 (2021). https://doi.org/10.1140/epjp/s13360-021-01979-8Local chromatic correction Arc & Final Focus
,CEPC technical design report - accelerator
. Radiat. Detect. Technol. Methods 8(1), 1-1105 (2024). https://doi.org/10.1007/s41605-024-00463-yFinal focus designs for crab waist colliders
. Phys. Rev. Accel. Beams 19,Dynamic aperture studies in e+e− factories with crab waist
. IR’07 proceedings, Part of CARE HHH APD Workshop on Interaction Regions for the LHC Upgrade, DAFNE and SuperB (IR'07) Frascati, Italy, 6-9 November 2007, Conf. Proc. C 0711071 (2008) 114-116.Dynamic aperture limit caused by IR nonlinearities in extremely low-beta B factories
. Proceedings of IPAC’10,Advanced damper system with a flexible and fine-tunable filter for longitudinal coupled-bunch instabilities caused by the accelerating mode in SuperKEKB
. Nucl. Instum. Meth. Phys. Res. A 953,Compact HOM-damping structure of a beam-accelerating TM020 mode rf cavity
. Nucl. Instum. Meth. Phys. Res. A 1064,Fundamental cavity impedance and longitudinal coupled-bunch instabilities at the High Luminosity Large Hadron Collider
. Phys. Rev. Accel. Beams 20,Graphics-processing-unit-accelerated simulation for longitudinal beam dynamics of arbitrary bunch trains in electron storage rings
. Phys. Rev. Accel. Beams 24,Transient beam loading effects in harmonic rf systems for light sources
. Phys. Rev. ST Accel. Beams 5,Simulations and experimental results of beam-beam effects in SuperKEKB
. Phys. Rev. Accel. and Beams 26,Luminosity limit due to the beam-beam interactions with or without crossing angle
. Phys. Rev. ST Accel. Beams 7,Coherent beam-beam instability in collisions with a large crossing angle
. Phys. Rev. Lett. 119,Test of “Crab-Waist” collisions at the DAΦNE Φ factory
. Phys. Rev. Lett. 104,Collective effects in a diffraction-limited storage ring
, J. Synchrotron Rad. 21, 937-960 (2014). https://doi.org/10.1107/S1600577514015215Microwave instability threshold from coherent wiggler radiation impedance in storage rings
. Phys. Rev. Accel. Beams 26,The SuperKEKB has broken the world record of the Luminosity
.Electron cloud in accelerators
. Int. J. Mod. Phys. A 29,KEK B-factory Design Report, KEK Report 95-7
(1995).Status of the APS-U Project
,Top-up injection schemes for future circular lepton collider
. Nucl. Instrum.Meth. Phys. Res. A 880, 98-106 (2018). https://doi.org/10.1016/j.nima.2017.10.075Review of Top-up Injection Schemes for Electron Storage Rings
, Proc. of IPAC2018,SuperKEKB Design Report
, (2020). https://www-linac.kek.jp/linac-com/report/skb-tdr/Alignment & stability challenges for FCC-ee
. EPJ Tech. Instrum. 10, 8 (2023). https://doi.org/10.1140/epjti/s40485-023-00096-3Emittance optimization with dispersion free steering at LEP
. Phys. Rev. ST-Accel. Beams 3,Experimental determination of storage ring optics using orbit response measurements
. Nucl. Instrum. Methods Phys. Res. A 388, 27-36 (1997). https://doi.org/10.1016/S0168-9002(97)00309-4First beam loss measurements in the SuperKEKB positron ring using the fast luminosity monitor diamond sensors
. Phys. Rev. Accel. Beams 22,Low impedance movable collimators for SuperKEKB
. Proceedings of the IPAC2017, 14-19 (2017).Beam-beam effects investigation and parameters optimization for a circular e+e− collider at very high energies
. Phys. Rev. ST-Accel. Beams 17,Small-Beta Collimation at SuperKEKB to Stop Beam-Gas Scattered Particles and to Avoid Transverse Mode Coupling Instability
, Conf. Proc. C 1205201, 1104 (2012)PEP-II: An Asymmetric B Factory: Conceptual Design Report June 1993, SLAC Report, SLAC-418, LBL-PUB-5379, CALT-68-1869
, (1993)Development of a hybrid collimator bonding tantalum and carbon-fiber-composite for SuperKEKB
. Nucl. Instrum. Meth Phys. Res. Sect. A 1059,Low-Z collimator for SuperKEKB
. Nucl. Instrum. Meth. Phys. Res. Sect. A 1047,Collimator challenges at SuperKEKB and their countermeasures using nonlinear collimator
. Phys. Rev. Accel. Beams 27,Damping Ring Design and Physics Issues
[EB/OL], (2007). https://pcwww.liv.ac.uk/~awolski/Teaching/USPAS/Houston/DampingRings-Lecture4.pdfThe research on magnetic properties of permanent magnet and magnetic field of prototype for Cryogenic Permanent Magnet Undulator
, PhD Thesis,Study on the Effect of Undulator Dynamic Field Integral and the Shimming Method
; PhD Thesis,Study on the effects of insertion devices at SSRF
. PhD Thesis,Elementary spinor algebra for polarized beams in storage rings
. Particle Accelerators,11, 219-231 (1981)A spin rotator for the compact linear collider
, Proceedings of IPAC10,Pelegant: A parallel accelerator simulation code for electron generation and tracking
. AIP Conf. Proc. 877, 241-247 (2006). https://doi.org/10.1063/1.2409141FERMI@Elettra Conceptual Design Report, Sincrotrone Trieste
,FCC-ee: The lepton collider
. Eur. Phys. J. Spec. Top. 228, 261-623 (2019). https://doi.org/10.1140/epjst/e2019-900045-4Reverse bending magnets in a combined-function lattice for the CLIC damping ring
, 1989 IEEE Particle Accelerator Conference vol.1613, 1611-1613 (1989).Reverse-bend FODO lattice applied to damping ring for SuperKEKB
. Nucl. Instrum. Meth. Phys. Res. Sect. A 556, 13-19 (2006). https://doi.org/10.1016/j.nima.2005.10.010Development of an L-band photocathode RF gun at Tsinghua University
. Nucl. Instrum. Meth. Phys. Res. Sect. A 985,RF Performance of a Next-Generation L-Band RF Gun at PITZ
. Proc. of LINAC2022,Physics design and beam dynamics optimization of the SHINE accelerator
. Proc. of FLS2023,Reverse-bend FODO lattice applied to damping ring for SuperKEKB
. Nucl. Instrum. Meth. Phys. Res. Sect. A 556, 13-19 (2006). https://doi.org/10.1016/j.nima.2005.10.010Study on the magnetic focusing structure and related dynamics of diffraction limit storage ring
. PhD Thesis,ESRF-EBS project, EBS storage ring technical report
(SEE-LS: A 4th generation synchrotron light source for science and technology. CERN Yellow Report: CERN-2020-001, Chapter 11: Power supplies
Advanced Photon Source Upgrade Project Preliminary Design Report - Chapter 4: Accelerator Upgrade, ANL Report: APSU-2.01-RPT-002
(2017)SLS 2.0 Storage Ring Technical Design Report - Chapter 2.3: Power supplies, PSI Bericht Nr. 21-02
,High-stability magnet power supplies for SuperKEKB
. Proc of IPAC2017, 3391-3393 (2017).Compact HOM-damping structure of a beam-accelerating TM020 mode rf cavity
. Nucl. Instrum. Meth. Phys. Res. A 1064,High-power tests of the compactly HOM-damped TM020 cavities for a next generation light source
, Proceedings of IPAC2023,The design of LLRF system for STCF storage ring
, Mod. Phys. Lett. A 39,Fast kicker systems for ALS-U
. Proc. of IPAC2014,Strip-line kicker and fast pulser R&D for the HEPS on-axis injection system
, Nucl. Instrum. Meth. Phys. Res. Sect. A 920, 1-6 (2019). https://doi.org/10.1016/j.nima.2018.12.009Modeling of eddy current effects in an opposite-field septum
. Nucl. Instrum. Meth. Phys. Res. Sect. A 597, 142-148 (2008). https://doi.org/10.1016/j.nima.2008.09.010Septum magnet design for compact storage ring
. Nucl. Instrum. Meth. Phys. Res. Sect. A 1023,Suppression of eddy-current effects in beam injection using a pulsed sextupole magnet with a new ceramic chamber
. Phys. Rev. Accel. Beams. 25,Design and research of HLS pulsed octupole magnet injection scheme
. Nuclear Techniques 38, 24-29 (2015). (in Chinese)Development of a pulsed octupole magnet system for studying the dynamics of transverse beam instabilities in electron storage rings
. Nucl. Instrum. Meth. Phys. Res. Sect. A 581, 589-600 (2007). https://doi.org/10.1016/j.nima.2007.08.120Development of copper beam ducts with antechambers for advanced high-current particle storage rings
. Vacuum 84, 694-698 (2009). https://doi.org/10.1016/j.vacuum.2009.06.027Experience at the KEK B-Factory vacuum system
. Prog. Theor. Exp. Phys. 2013,An Asymmetric B Factory Based on PEP: Conceptual Design Report (Vacuum Part), SLAC, SLAC-0372
,PEP-II Asymmetric B-Factory: R&D Results, LBL-32098, ESG-204, LLNL-UCRL-JC-110287, SLAC PUB-5785, ABC-75
, (1992)Set-up of PEP-II longitudinal feedback systems for even/odd bunch spacings
. AIP Conf. Proc. 648, 474-482 (2002). https://doi.org/10.1063/1.1524435Design and construction of the SuperKEKB vacuum system
. J. Vac. Sci. Technol. A 30,Design of the button-type beam position monitor for the electron storage ring of Hefei Advanced Light Facility
. 2024 9th International Conference on Electronic Technology and Information Science (ICETIS),Development and implementation of advanced beam diagnostic and abort systems in SuperKEKB
. Nucl. Instrum. Meth. Phys. Res. Sect. A 1072,Longitudinal impedance measurements and simulations of a three-metal-strip kicker
. Nucl. Sci. Tech. 34, 57 (2023). https://doi.org/10.1007/s41365-023-01212-4Design of bunch length and charge monitor based on cavity resonator for injector of Super Tau-Charm Facility
. Nuclear Techniques (in Chinese) 47,Bunch-by-bunch three-dimensional position and charge measurement in a storage ring
. Phys. Rev. Accel. Beams 24,High performance generic beam diagnostic signal processor for SHINE
, Proc. of IBIC 2024,Beam instrumentation for the SuperKEKB rings
, Proc. of IBIC2012,Bunch by bunch feedback systems for the KEKB rings
. Proc. of the 2001 Particle Accelerator Conference (Cat. No.01CH37268),Bunch-by-bunch beam transverse feedback electronics designed for SSRF
. IEEE Trans. Nucl. Sci. 64, 1395-1400 (2017). https://doi.org/10.1109/TNS.2017.2696975Transverse and longitudinal bunch-by-bunch feedback for storage rings
. Proc. of IPAC2018,Bunch by bunch feedback system for Super KEKB rings
. Proc. of the 13th Annual Meeting of Particle Accelerator Society of JapanInteraction point orbit feedback system at SuperKEKB
. Proc. of IPAC2015,Recent progress of dithering system at SuperKEKB
. Proc. of IPAC2017,Measurement of an electron-beam size with a beam profile monitor using Fresnel zone plates
. Nucl. Instrum. Meth. Phys. Res. Sect. A 506, 41-49 (2003). https://doi.org/10.1016/S0168-9002(03)01392-5The beam-based calibration of an X-ray pinhole camera at SSRF
. Chinese Phys. C 36, 80-83 (2012). https://doi.org/10.1088/1674-1137/36/1/014Source size measurement options for low-emittance light sources
. Phys. Rev. Accel. Beams 23,Bunch length and impedance measurements at SPEAR3
. Proc. of EPAC'08, Genoa, Italy, June 23-27, 2008. Conf. Proc. C 0806233 (2008)Systematic approach to damping ring design
. Phys. Rev. ST Accel. Beams 4,A SuperKEKB beam final focus superconducting magnet system
. Nucl. Instum. Meth. Phys. Res. A 1021,Design and optimization of the superconducting quadrupole magnet Q1a in CEPC interaction region
. IEEE Trans. Appl. Supercond. 32,The FCC-ee interaction region magnet design
. Proc. of IPAC2016,Superconducting CCT quadrupole test at Budker INP
. 39,Cryogenic systems of SuperKEKB final focusing superconducting magnets
. Nucl. Instrum. Meth. Phys. Res. Sect. A 1058,Design and construction of the magnet cryostats for the SuperKEKB interaction region
. IEEE Trans. Appl. Supercond. 28,New electron gun system for BEPCII
. Proceedings of the 2005 Particle Accelerator Conference,Development of an L-band photocathode RF gun at Tsinghua University
. Nucl. Instrum. Meth. Phys. Res. Sect. A 958,Vacuum characterization and improvement for the Jefferson Lab polarized electron source
. Proc. of IPAC2015,High gradient, high reliability, and low wake-field accelerating structures for the FERMI FEL
. Rev. Sci. Instrum. 88,RF Design of Traveling-Wave Accelerating Structures for the FCC-ee Pre-injector Complex
, Proc. of Linac2022,The European XFEL LLRF system
. Proc. of IPAC 2012, 55-57 (2012).Design and performance of LLRF system for CSNS/RCS
. Chinese Phys. C 39,Next generation CW reference clock transfer system with femtosecond stability
. Proc. of PAC2013,Upgrade and operation experience of solid-state switching klystron modulator in NSLS-II Linac
. Proc. of NAPAC2019,RF system performance in SwissFEL
. Proc. of LINAC,SuperKEKB positron source target protection scheme
. Proc. of IPAC2013,Analysis of beam-induced damage to the SLC positron production target. PACS2001
. Proceedings of the 2001 Particle Accelerator Conference (Cat. No.01CH37268),Thermal research of a single crystal tungsten target positron source for the STCF project in China
. Nucl. Instrum. Meth. Phys. Res. Sect. A 1039,A design of an electron driven positron source for the international linear collider
. Nucl. Instrum. Meth. Phys. Res. Sect. A 953,SuperKEKB mechanical assembly at IR. Workshop on the mechanical optimization of the FCC-ee MDI, Geneva, Switzerland
, (2018): https://indico.cern.ch/event/694811Low-Z collimator for SuperKEKB
. Nucl. Instum. Meth. Phys. Res. A 1047,Movable collimator system for SuperKEKB
. Phys. Rev. Accel. Beams 23,Research on the beam pipe and its thermal control system of the Beijing Electron-Positron Collider
. PhD Thesis,Validation of the crab-cavities internal monitoring strategy
. Proc. of 14th International Workshop on Accelerator Alignment,Robust optical instrumentation for accelerator alignment using frequency scanning interferometry
. Proc. of IPAC2021,Frequency scanning interferometry based deformation monitoring system for the alignment of the FCC-ee machine detector interface
. Meas. Sci. Technol. 34,Stability analysis of tunnel control network and beam orbit smoothing of particle accelerator
, PhD Thesis,Research on the magnetic center measurement methods for accelerator magnetic components
, PhD Thesis,Error analysis and application of laser tracker's bundle adjustment in the tunnel alignment measurement of particle accelerator
. Geomatics and Information Science of Wuhan University 48(6), 919-925 (2023). (in Chinese) https://doi.org/10.13203/j.whugis20200718Improved adjustment method applied in transformation of laser tracker
. Chinese J. Lasers 51,Fixing positions and orientations of laser trackers during bundle adjustment in multi-station measurements
. Meas. Sci. Technol. 32,Two efficient recursive total least squares solutions based on the grouping strategy
. IEEE Trans. Instrum. Measure. 73,Study on radiation field in the injection area of Beijing Electron-Positron Collider (BEPC II)
. Radiation Protection 37(1), 12-17 (2017) (in Chinese)Measurement of prompt radiation field in the linear accelerator tunnel of BEPC II
. Nuclear Electronics Detection Technology 36(8), 880-884 (2016). (in Chinese)Personal safety interlock access control system for the major upgrade project of Beijing Electron-Positron Collider (BEPC II)
. Proc. of the National Symposium on Radioactive Effluent and Environmental Monitoring and Assessment 544-549 (2002). (in Chinese)Environmental radiation during beam tuning and operation of Beijing Electron-Positron Collider
. Radiation Protection 10, 1-10 (1990) (in Chinese)Study on Key Problems of Radiation Protection for the Accelerator at the High Energy Photon Source
, PhD Thesis,
