Introduction

Neodymium isotopes play a crucial role in nuclear processes. They are important fission products that are widely used in activation analysis and reactor physics research [1-3]. Their neutron capture and photonuclear properties affect key areas of nuclear science, including neutron economy [4], fuel cycle management [5], radiation shielding [6], and nuclear astrophysics [7]. Neodymium has seven naturally stable isotopes, namely, ^{142,143,144,145,146,148,150}Nd, with abundances of 27.15%, 12.17%, 23.798%, 23.798%, 8.293%, 17.189%, and 5.638%, respectively [3]. Accurate knowledge of their photonuclear cross-sections is essential for enhancing fission reactor modeling, activation analysis, and broader applications, such as reactor design and nucleosynthesis studies.

Early studies of photonuclear reactions used broad-spectrum bremsstrahlung light sources from electron linear accelerators and quasi-monochromatic positron annihilation sources based on time-of-flight methods [8]. Between 1962 and 1987, the Lawrence Livermore National Laboratory [9] and the Saclay Laboratory [10] conducted numerous experiments using quasi-monochromatic light sources, yielding precise photoneutron cross-section data. However, Berman’s review highlighted discrepancies between the (γ,n) and (γ,2n) cross sections from the two laboratories, emphasizing the need for further investigation.

New photonuclear reaction data have been obtained through experiments at facilities such as NewSUBARU and Oslo [11]. Advances in light source and neutron detection technologies have led to the development of high-quality experimental facilities. Recently, the Shanghai Advanced Research Institute completed an SLEGS facility using inverse Compton backscattering [12], which has attracted significant attention. The China Nuclear Data Center (CNDC) collaborates with the SLEGS facility to improve measurement techniques and theoretical evaluations with the goal of establishing a comprehensive photonuclear reaction database.

To enhance the quality of photonuclear reaction cross-section data and resolve inconsistencies, the International Atomic Energy Agency (IAEA) has organized two Coordinated Research Projects (CRPs) on photonuclear reactions. A recent CRP, conducted from 2016 to 2020, updated the IAEA’s photonuclear data and established a reference database for photon strength functions (PSF) [13-15]. The CNDC actively participated in both the CRPs, making significant contributions through experimental evaluations and theoretical calculations.

In theoretical approaches, two types of models are used to predict the strength function: phenomenological models and microscopic models [16-21]. The most commonly used phenomenological models include the Standard Lorentzian (SLO) model [22, 23], Enhanced Generalized Lorentzian (EGLO) model [24, 25], and Generalized Fermi-Liquid (GFL) model [26]. Microscopic models encompass the Finite Fermi Gas theory [27, 28], semi-classical thermodynamic approach [29], non-relativistic Quasiparticle Random Phase Approximation (QRPA) based on the BCS ground state [30], and relativistic Quasi-Particle Random Phase Approximation (RQRPA) based on the covariant density functional theory [31-33]. Phenomenological methods usually rely heavily on large amounts of experimental data; however, there are conflicts between the data measured by the Saclay Laboratory and the Livermore National Laboratory. Therefore, microscopic methods are required for this purpose.

QRPA has been the most popular microscopic method.. The QRPA and RQRPA methods have been successful for spherical nuclei; however, for deformed nuclei, the QRPA matrix becomes large, requiring significant computational and storage resources [34]. To address this, the finite-amplitude method (FAM) was introduced, which avoids the construction and diagonalization of the full QRPA matrix. Instead, FAM iteratively solves the linear response problem by calculating the fields excited by the one-body transition operators [35-37]. In 2020, A. Bjelcic and T. Niksic developed a QFAM model based on relativistic EDFs (DIRQFAM program) to compute the multipole response of even-even deformed nuclei [38], and in 2023, DIRQFAM2.0 was released with updates including meson exchange interactions and a new solver method [39].

The aim of this work is to better describe the experimental photon absorption cross-section using the microscopic method, as the photon absorption cross-section calculated by QFAM still shows a significant discrepancy with the experimental results. In this study, we calculated the photon-absorption cross-sections of even-even Nd isotopes using DIRQFAM2.0 and compare the results with experimental data. Section 2 outlines the theoretical framework of relativistics and introduces an approximation method for optimizing the system to align it with the experimental data. In Sect. 3, we discuss our results in detail. Finally, Section 4 presents the conclusions and future prospects of this study.

Theoretical Framework

The theoretical photoabsorption cross section σ_abs(ϵγ) as a function of gamma ray energy ϵγ is taken as the sum of the terms ${\sigma }_{\text{abs}}\left({ϵ}_{\gamma }\right)={\sigma }_{\text{GDR}}\left({ϵ}_{\gamma }\right)+{\sigma }_{\text{QD}}\left({ϵ}_{\gamma }\right)\mathrm{,}$ (1) where the component σ_GDR(ϵγ) corresponds to the excitation of the GDR and σ_QD(ϵγ) is a quasideuteron contribution (a photoabsorption by a neutron–proton pair), which is taken in accordance with the model proposed by Chadwick et al. [40, 41].

The GDR component σ_GDR(ϵγ) of the total photoabsorption cross section is equal to that of the electric dipole gamma rays ${\sigma }_{E1}\left({ϵ}_{\gamma }\right)$, which is proportional to the strength function $R_{E1}\left({ϵ}_{\gamma }\right)$ $\begin{array}{ll}{\sigma }_{E1}\left({ϵ}_{\gamma }\right)\hfill & =\frac{16{\pi }^3}{9}\frac{e^2}{\hslash c}{ϵ}_{\gamma }{R}_{E1}\left({ϵ}_{\gamma }\right)\mathrm{,}\hfill \end{array}$ (2) where the isovector dipole strength function $R_{E1}\left({ϵ}_{\gamma }\right)$ can be calculated using a microscopic model, such as the RQRPA equations [31, 42-44]. In standard notation, these equations can be written in matrix form as $\left(\begin{array}{cc}{A}^J& B^J\\ B^{*J}& A^{*J}\end{array}\right)\left(\begin{array}{c}{X}^{\nu J}\\ Y^{\nu J}\end{array}\right)={\omega }^{\nu }\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}{X}^{\nu J}\\ Y^{\nu J}\end{array}\right)\mathrm{.}$ (3) For each RQRPA energy, ων, $X^{\nu }$, and $Y^{\nu }$ denote the corresponding forward- and backward-going two-quasiparticle amplitudes, respectively.

The RQRPA equation can be solved by directly diagonalizing the A and B matrices (3) for the spherical nuclei. However, for deformed systems, the dimensionality of these matrices increases rapidly, and such calculations were only possible approximately a decade ago [45, 46]. To overcome the challenges of implementing matrix-based RPA for deformed heavy nuclei, FAM was introduced as an efficient alternative for calculating the multipole response functions. FAM has been successfully applied in numerous studies, both in coordinate space and on the harmonic oscillator basis [38, 39, 47, 48].

2.2

Tiny Smearing Approximation method

While the relativistic QFAM approach offers a highly efficient solution to the standard RQRPA problem, it does not provide direct access to the RQRPA eigenfrequencies Ω_i However, the method proposed in Ref. [51], which is based on contour integration in a complex plane, enables the extraction of RQRPA transition matrix elements and eigenfrequencies from relativistic QFAM calculations.

In this section, the TSA method is introduced, which provides an efficient approach for connecting the relativistic QFAM strength function with the RQRPA transition matrix elements. As is well known, the response function is $R(\omega )=\frac{\text{d}B(\omega )}{\text{d}\omega }={\displaystyle \sum _i}{\left|\langle i\left|\widehat{F}\right|0\rangle \right|}^2\frac{\gamma /\pi }{{\left(\omega -{\text{Ω}}_i\right)}^2+{\gamma }^2}\mathrm{,}$ (9) where $\text{d}B(\omega )/\text{d}\omega$ is the strength function of the relativistic QFAM, ${\left|\langle i\left|\widehat{F}\right|0\rangle \right|}^2$ is the RQRPA transition matrix elements, and Ω_i is the eigenfrequency. If γ is sufficiently small, such as γ=0.01 MeV, when ω=Ω_k, ${\displaystyle \sum _i}\frac{{\left|\langle i\left|\widehat{F}\right|0\rangle \right|}^2}{{\left(\omega -{\text{Ω}}_i\right)}^2+{\gamma }^2}\approx {\left|\langle k\left|\widehat{F}\right|0\rangle \right|}^2\frac{1}{{\gamma }^2}$ (10) becomes extremely larger, therefore, the transition matrix elements of the RQRPA can be approximated by ${\left|\langle i\left|\widehat{F}\right|0\rangle \right|}^2\approx \frac{\text{d}B(\omega )}{\text{d}\omega }\pi \gamma {|}_{\omega ={\text{Ω}}_i\mathrm{,}\gamma =0.01}\mathrm{.}$ (11)

In Fig. 1, we present the isovector Giant Dipole Resonance (GDR) response of ¹⁴²Nd, calculated using DD-PC1 parameterization with a separable pairing interaction and N_shells=20 oscillator shells. The purple columns represent the ${\left|\langle i\left|\widehat{F}\right|0\rangle \right|}^2$ obtained from the spherical RQRPA calculations, whereas the red curve corresponds to the relativistic QFAM results for $\pi \gamma \text{d}B(\omega )/\text{d}\omega$ calculated with a smearing parameter of γ=0.01 MeV. This comparison demonstrated that Eq. (11) provides an excellent approximation, as both the RQRPA transition matrix elements and eigenfrequencies closely match the results obtained from the relativistic QFAM.

Fig. 1Full-screen View

(Color online) The isovector Giant dipole response of ¹⁴²Nd calculated using the DD-PC1 parameterization with a separable pairing interaction and N_shells=20 oscillator shells. The purple columns represent the results obtained from spherical RQRPA calculations, while the red curve corresponds to the relativistic QFAM calculations

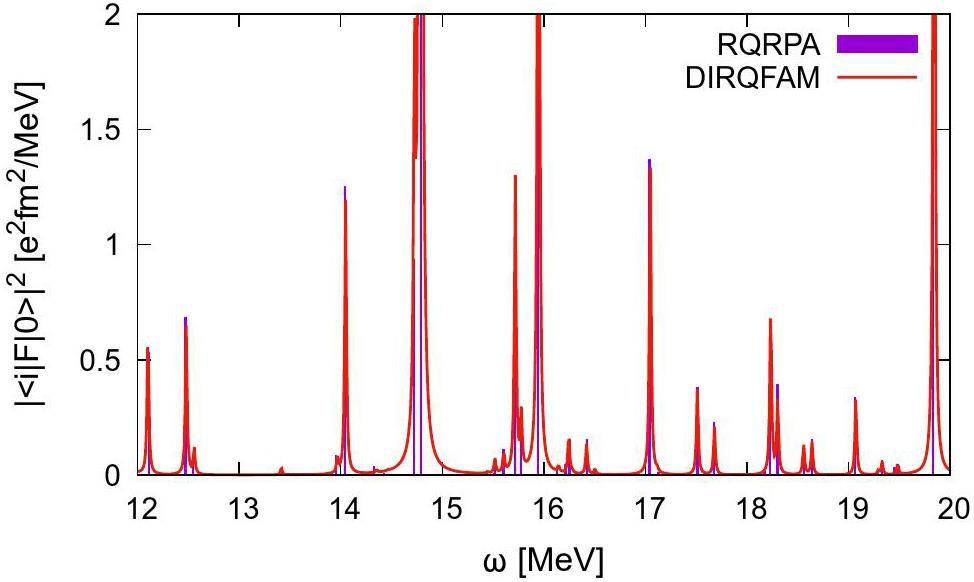
In practice, once we know the transition matrix elements ${\left|\langle i\left|\widehat{F}\right|0\rangle \right|}^2$, the response function with arbitrary smearing γ larger than 0.01 MeV can be calculated using the empirical formula: $R(\omega )\approx {\displaystyle \sum _i}\frac{\text{d}B(\omega )}{\text{d}\omega }\pi \gamma {|}_{\omega ={\text{Ω}}_i\mathrm{,}\gamma =0.01}\frac{\text{Γ}/\pi }{{\left(\omega -{\text{Ω}}_i\right)}^2+{\text{Γ}}^2}\mathrm{,}$ (12) where Γ is the Lorentz width in the RQRPA calculation. In Fig. 2, we present a comparison of the photon-absorption cross-section for ¹⁴²Nd calculated by QFAM using γ=0.5 MeV and 1.0 MeV, alongside TSA results obtained with γ=0.01 MeV. The solid lines represent the relativistic QFAM calculations, whereas the dashed lines correspond to the photon-absorption cross-sections computed using the TSA method. As shown in the figure, the TSA results closely matched the relativistic QFAM calculations, demonstrating the effectiveness of the approximation. Neither γ=1.00 MeV nor 0.50 MeV accurately reproduces the experimental data.

Fig. 2Full-screen View

(Color online) Comparison of the photon-absorption cross-section for ¹⁴²Nd calculated by relativistic QFAM (solid lines) using γ=0.5 and γ=1.0 MeV with TSA results (dashed lines) using γ=0.01 MeV. The black dots are the experimental data

Calculations and discussion

The photon absorption cross-sections of Nd isotopes were first measured in 1971 by Carlos et al., [52]. In this study, we employed the relativistic QFAM method to calculate the photon-absorption cross sections for even-even Nd isotopes.

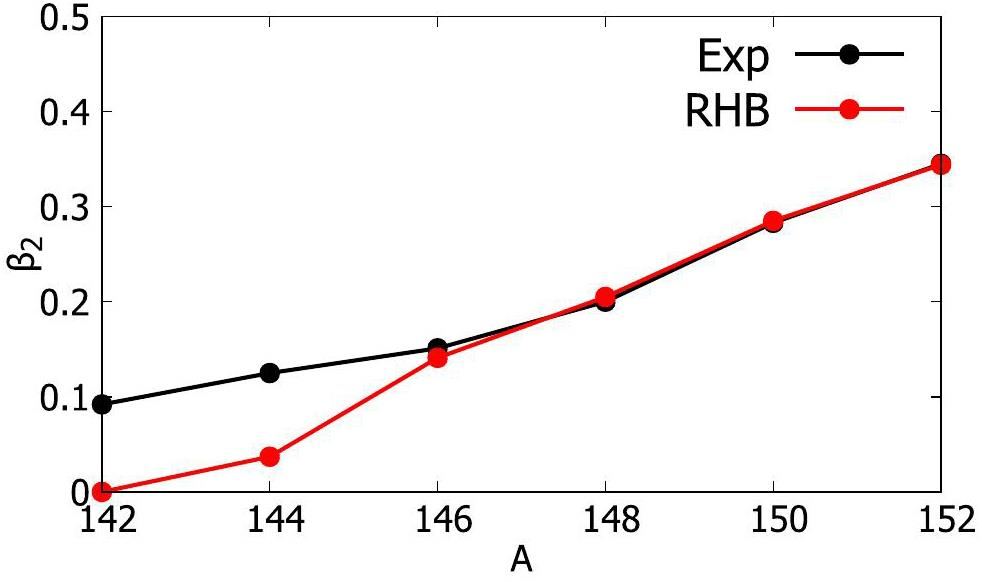
First, we solved the RHB equation using the DD-PC1 relativistic density functional combined with a separable pairing interaction to calculate the ground-state properties of even-even Nd isotopes. In Fig. 3, we compare the quadrupole deformations between the experimental data [53] and those obtained from the RHB calculations for ¹⁴²Nd to ¹⁵²Nd. Experimentally, the deformation of Nd isotopes increases with neutron number. While the RHB calculations accurately reproduced the deformation for isotopes beyond ¹⁴⁶Nd, they predicted ¹⁴²Nd and ¹⁴⁴Nd to be closer to spherical configurations, deviating from the experimental observations.

Fig. 3Full-screen View

Comparison of quadrupole deformations between experimental data (black) and RHB calculations (red) for ¹⁴²Nd to ¹⁵²Nd

In our previous work [16], we constructed microscopic GDR parameters using relativistic quasiparticle random phase approximation (RQRPA) for spherical nuclei. We now extend this approach by constructing microscopic GDR parameters based on the Dirac Quasiparticle Finite Amplitude Method (relativistic QFAM) combined with the TSA method.

In this study, we introduce an energy-dependent width parameter, defined as $\text{Γ}(\omega )=\delta \text{Γ}\sqrt{\omega }\mathrm{,}$ (13) where δΓ is the first parameter to be fitted to experimental data. The photon-absorption cross-section is then expressed as $\sigma (\omega )=\frac{16{\pi }^3}{9}\frac{e^2}{\hslash c}G\times \omega R(\omega +\delta \omega )\mathrm{,}$ (14) where G is the strength parameter used to adjust the height of the cross-section and $R(\omega )$ represents the strength function using the TSA method (as defined in Eq. (12)), and δω accounts for the energy shift. Using the MINUIT package [54], we optimized the three parameters to enhance the relativistic QFAM calculations for the photon absorption cross-section of even-even Nd isotopes. As shown in Table 1, the total χ² value between the relativistic QFAM results and experimental photon-absorption cross-sections was reduced by nearly an order of magnitude through the application of the TSA method.

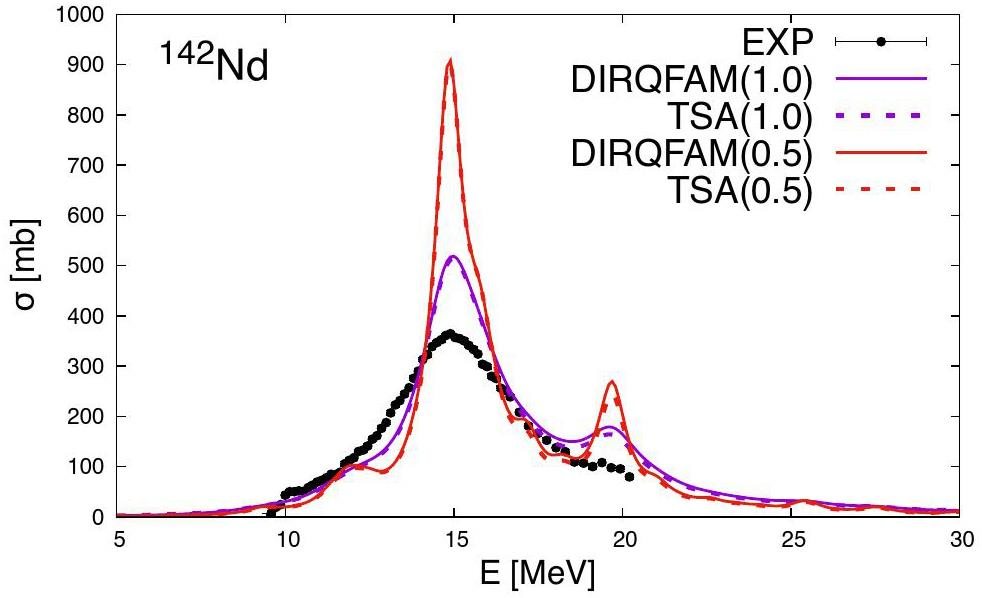
In Fig. 4, we display the Kπ=0^-(yellow solid line) and Kπ=1^-(orange dashed line) components of the photon-absorption cross section obtained from the relativistic QFAM calculations with smearing γ=1.0, the total photon-absorption cross section obtained from the relativistic QFAM calculations (purple solid line), the results using the TSA method (red solid line), compared with the experimental data [52] and evaluated data of IAEA-2019 [55] or JENDL-5 [56] (black dotted dashed line). Only the JENDL-5 evaluation database predicted the photon absorption cross section of ¹⁵²Nd.

Fig. 4Full-screen View

(Color online) Comparison of relativistic QFAM calculations (purple solid line), the Kπ=0^-(yellow solid line) and Kπ=1^-(orange dashed line) components of the photon-absorption cross-section and TSA results (red solid line) with experimental photon-absorption cross-sections (black dots) and evaluated data (black dashed line) for even-even Nd-isotope ranging from ¹⁴²Nd to ¹⁵²Nd

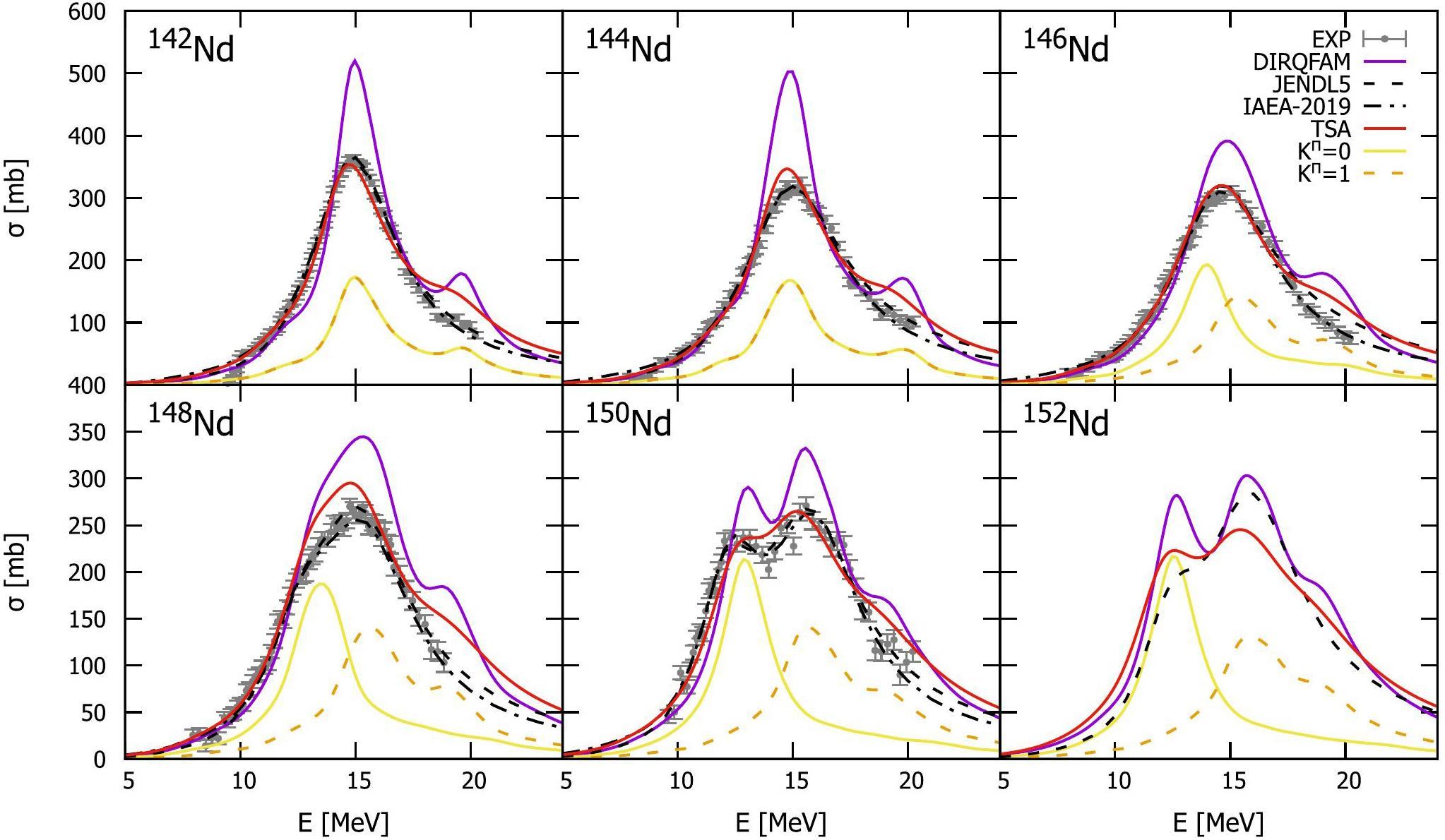
As shown in Fig. 4, the centroid energy calculated using relativistic QFAM aligns well with the experimental data. For ¹⁴²Nd and ¹⁴⁴Nd, only a single peak was observed in the photon absorption cross section, as the deformation of these nuclei was minimal. Consequently, the centroid energies of the Kπ=0^- and Kπ=1^- components were nearly identical. For ¹⁴⁶Nd to ¹⁵²Nd, the Kπ=0^- and Kπ=1^- components are separated because these nuclei are well deformed. For ¹⁵⁰Nd and ¹⁵²Nd, there are two distinct peaks in the photon absorption cross-section owing to splitting of the GDR.

By employing Eqs. (13) and (14), the parameters δΓ, G, and δω were adjusted by fitting to the experimental data of Carlos et al. [52] for even-even Nd isotopes using the TSA method. This optimization significantly improves the agreement with the experimental data compared to relativistic QFAM calculations. The results demonstrate the effectiveness of the TSA method in accurately reproducing the photon absorption cross sections of Nd isotopes.

Finally, we predicted for ¹⁵²Nd and compared it with the evaluation data from the JENDL-5 library [56]. Our calculated photon absorption cross sections are significantly smaller than the JENDL-5 data, but are more consistent with the cross-sections of ¹⁵⁰Nd.

Conclusion

In this study, we demonstrated that the GDR strength functions calculated by relativistic QFAM with any appropriate smearing parameter γ can be efficiently obtained using the TSA method. This approach significantly reduces the computational cost of calculating photon-absorption cross-sections with relativistic QFAM and allows for the incorporation of energy-dependent Lorentzian broadening.

We extend this approach by constructing microscopic GDR parameters based on relativistic QFAM combined with the TSA method, which can describe the photon absorption cross-section of even-even Nd isotopes using only three parameters.

In the future, we will broaden our investigation of photon absorption cross-sections to include a wider range of atomic nuclei using this TSA method based on relativistic QFAM. Additionally, we will explore the impact of different interactions, such as the density-dependent meson exchange (DD-ME2) parameter set and the pairing strength on the photon absorption cross-section.